All Exams >
UGC NET >
3 Months Preparation for UGC NET Paper 1 >
All Questions
All questions of Venn Diagrams for UGC NET Exam
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.Q.Which of the following diagrams indicates the best relation between Travelers, Train and Bus ?- a)
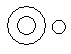
- b)
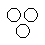
- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Q.
Which of the following diagrams indicates the best relation between Travelers, Train and Bus ?
a)
b)
c)
d)

|
Iq Funda answered |
The best relation between Travelers, Train, and Bus can be represented in a Venn diagram, where Travelers are represented as a larger circle containing both Train and Bus circles. This is because travelers can choose either train or bus as their mode of transportation, and some may use both. Here's the explanation:
Travelers
- Travelers are people who move from one place to another for various reasons, such as work, leisure, or other purposes.
Train
- A train is a mode of transportation that runs on a railway track and can carry passengers or goods.
- Some travelers may choose to travel by train due to various factors such as cost, comfort, or availability.
Bus
- A bus is a mode of transportation that runs on roads and can carry passengers.
- Some travelers may choose to travel by bus due to factors such as cost, convenience, or accessibility.
Venn Diagram: Option C
- In option C, we have a large circle representing Travelers, which includes two smaller circles representing Train and Bus.
- This diagram shows that there are travelers who use trains, travelers who use buses, and some travelers who may use both modes of transportation.
- This representation captures the relationship between travelers and their choice of transportation, whether it's by train, bus, or both.
Travelers
- Travelers are people who move from one place to another for various reasons, such as work, leisure, or other purposes.
Train
- A train is a mode of transportation that runs on a railway track and can carry passengers or goods.
- Some travelers may choose to travel by train due to various factors such as cost, comfort, or availability.
Bus
- A bus is a mode of transportation that runs on roads and can carry passengers.
- Some travelers may choose to travel by bus due to factors such as cost, convenience, or accessibility.
Venn Diagram: Option C
- In option C, we have a large circle representing Travelers, which includes two smaller circles representing Train and Bus.
- This diagram shows that there are travelers who use trains, travelers who use buses, and some travelers who may use both modes of transportation.
- This representation captures the relationship between travelers and their choice of transportation, whether it's by train, bus, or both.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Hospital, Nurse and Patient ?- a)
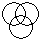
- b)

- c)
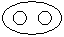
- d)
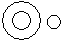
Correct answer is option 'C'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Hospital, Nurse and Patient ?
a)
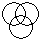
b)

c)

d)
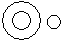

|
Kirti Yadav answered |
Hospital consists of nurse and patient but nurse and patient are of two different nature.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Judge, Thieves and Criminals ?- a)
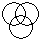
- b)
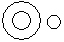
- c)
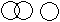
- d)
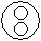
Correct answer is option 'B'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Judge, Thieves and Criminals ?
a)
b)
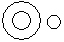
c)
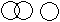
d)
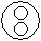

|
Avi Chakraborty answered |
All the thieves are criminals while judge is different from these.
290 students of MBA (International Business) in a reputed Business School have to study foreign language in Trimesters IV and V. Suppose the following information are given(i) 120 students study Spanish
(ii) 100 students study Mandarin
(iii) At least 80 students, who study a foreign language, study neither Spanish nor MandarinThen the number of students who study Spanish but not Mandarin could be any number from- a)20 to 110
- b)80 to 100
- c)50 to 80
- d)80 to 170
Correct answer is option 'A'. Can you explain this answer?
290 students of MBA (International Business) in a reputed Business School have to study foreign language in Trimesters IV and V. Suppose the following information are given
(i) 120 students study Spanish
(ii) 100 students study Mandarin
(iii) At least 80 students, who study a foreign language, study neither Spanish nor Mandarin
(ii) 100 students study Mandarin
(iii) At least 80 students, who study a foreign language, study neither Spanish nor Mandarin
Then the number of students who study Spanish but not Mandarin could be any number from
a)
20 to 110
b)
80 to 100
c)
50 to 80
d)
80 to 170

|
G.K Academy answered |
Atleast 80 students study neither Spanish nor Mandarin.
Hence, maximum number of students who study atleast one language = 290 – 80 = 210
Hence, maximum number of students who study atleast one language = 290 – 80 = 210
Minimum number of students who study both languages = 100 + 120 – 210 = 10
∴ Maximum number of students who study Spanish but not Mandarin = 120 – 10 = 110
Maximum number of students who study both languages = smaller value of 100 and 120 = 100
∴ Minimum number of students who study Spanish but not Mandarin = 120 – 100 = 20
Hence, the range could be any number from 20 to 110.
Hence, option (a).
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Travelers, Train and Bus ?- a)
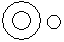
- b)
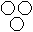
- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Travelers, Train and Bus ?
a)
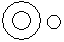
b)
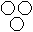
c)

d)


|
Ishani Rane answered |
Bus and Train are different from each other but some travelers travel by bus and some travel by train.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Profit, Dividend and Bonus ?- a)
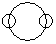
- b)

- c)
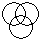
- d)
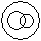
Correct answer is option 'B'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Profit, Dividend and Bonus ?
a)

b)

c)
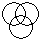
d)


|
Niti Iyer answered |
Bonus and Dividend are different from each other. But both these are parts of profit.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Boys, Girls and Students ?- a)
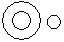
- b)

- c)
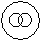
- d)
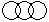
Correct answer is option 'D'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Boys, Girls and Students ?
a)
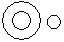
b)

c)
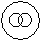
d)
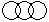

|
Sanjana Tiwari answered |
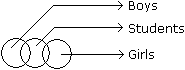
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Women, Mothers and Engineers ?- a)

- b)
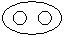
- c)

- d)

Correct answer is option 'A'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Women, Mothers and Engineers ?
a)

b)

c)

d)


|
Partho Nambiar answered |
All mothers are women and some mothers and some women may be engineers.
There are 3 clubs A, B & C in a town with 40, 50 & 60 members respectively. While 10 people are members of all 3 clubs, 70 are members in only one club. How many belong to exactly two clubs?- a)20
- b)25
- c)50
- d)70
Correct answer is option 'B'. Can you explain this answer?
There are 3 clubs A, B & C in a town with 40, 50 & 60 members respectively. While 10 people are members of all 3 clubs, 70 are members in only one club. How many belong to exactly two clubs?
a)
20
b)
25
c)
50
d)
70

|
G.K Academy answered |
We know that x + y + z = T and x + 2y + 3z = R, where
x = number of members belonging to exactly 1 set = 70
y = number of members belonging to exactly 2 sets
z = number of members belonging to exactly 3 sets = 10
T = Total number of members
R = Repeated total of all the members = (40 + 50 + 60) = 150
Thus we have two equations and two unknowns. Solving this we get y = 25
x = number of members belonging to exactly 1 set = 70
y = number of members belonging to exactly 2 sets
z = number of members belonging to exactly 3 sets = 10
T = Total number of members
R = Repeated total of all the members = (40 + 50 + 60) = 150
Thus we have two equations and two unknowns. Solving this we get y = 25
So, 25 people belong to exactly 2 clubs.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Tall man, Black haired people and Indians ?- a)
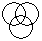
- b)
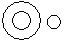
- c)

- d)
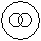
Correct answer is option 'A'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Tall man, Black haired people and Indians ?
a)
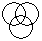
b)
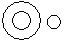
c)

d)
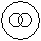

|
Nayanika Basu answered |

Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Examination, Questions and Practice ?- a)
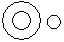
- b)
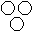
- c)

- d)
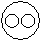
Correct answer is option 'C'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Examination, Questions and Practice ?
a)
b)
c)

d)


|
Harshitha Desai answered |
Some questions are asked in examination and some in practice but examination and practice are different from each other.
In a class of 60, along with English as a common subject, students can opt to major in Mathematics, Physics, Biology or a combination of any two. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. In an English test, the average mark scored by students majoring in Mathematics is 45 and that of students majoring in Biology is 60. However, the combined average mark in English, of students of these two majors, is 50. What is the maximum possible number of students who major ONLY in Physics?
- a)15
- b)25
- c)20
- d)30
Correct answer is option 'A'. Can you explain this answer?
In a class of 60, along with English as a common subject, students can opt to major in Mathematics, Physics, Biology or a combination of any two. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. In an English test, the average mark scored by students majoring in Mathematics is 45 and that of students majoring in Biology is 60. However, the combined average mark in English, of students of these two majors, is 50. What is the maximum possible number of students who major ONLY in Physics?
a)
15
b)
25
c)
20
d)
30

|
Aspire Academy answered |
Let the number of persons who do not take any juice and the number of persons who take all 4 types of juices be ‘x’.
As there are ‘x’ people who take atleast 4 types of juices there should be ‘2x’ people who take atleast 3 types of juices.
This means the number of people who take exactly 3 types of juices = 2x – x = x.
As there are ‘2x’ people who take atleast 3 types of juices there should be ‘4x’ people who take atleast 2 types of juices.
This means the number of people who take exactly 2 types of juices = 4x – x – x = 2x.
As there are ‘4x’ people who take atleast 2 types of juices there should be ‘8x’ people who take atleast 1 type of juices.
This means the number of people who take exactly 1 type of juices = 8x – 4x = 4x.
Thus the total number of people in the Gym = x + 4x + 2x + x + x = 9x.
9x = 207 => x = 23.
The number of people who take exactly 2 types of juices = 2x = 46.
As there are ‘x’ people who take atleast 4 types of juices there should be ‘2x’ people who take atleast 3 types of juices.
This means the number of people who take exactly 3 types of juices = 2x – x = x.
As there are ‘2x’ people who take atleast 3 types of juices there should be ‘4x’ people who take atleast 2 types of juices.
This means the number of people who take exactly 2 types of juices = 4x – x – x = 2x.
As there are ‘4x’ people who take atleast 2 types of juices there should be ‘8x’ people who take atleast 1 type of juices.
This means the number of people who take exactly 1 type of juices = 8x – 4x = 4x.
Thus the total number of people in the Gym = x + 4x + 2x + x + x = 9x.
9x = 207 => x = 23.
The number of people who take exactly 2 types of juices = 2x = 46.
In a certain village, 22% of the families own agricultural land, 18% own a mobile phone and 1600 families own both agricultural land and a mobile phone. If 68% of the families neither own agricultural land nor a mobile phone, then the total number of families living in the village is:- a)20000
- b)10000
- c)8000
- d)5000
Correct answer is option 'A'. Can you explain this answer?
In a certain village, 22% of the families own agricultural land, 18% own a mobile phone and 1600 families own both agricultural land and a mobile phone. If 68% of the families neither own agricultural land nor a mobile phone, then the total number of families living in the village is:
a)
20000
b)
10000
c)
8000
d)
5000

|
Aim It Academy answered |
Let total number of families in the village be T
Number of families own agricultural land, n(A) = 0.22T
Number of families own agricultural land, n(A) = 0.22T
Number of families own mobile phone, n(M) = 0.18T
Number of families own both agricultural land and mobile phone, n(A ⋂ M) = 1600
Number of families own agricultural land or mobile phone, n(A ⋃ M) = T – 0.68T = 0.32T
∴ n(A ⋃ M) = n(A) + n(M) – n(A ⋂ M)
∴ n(A ⋂ M) = 0.08T
0.08T = 1600 ⇒ T = 20000
Hence, option (a).
400 students were admitted to the 2018-19 MBA batch. 200 of them did not choose “Business Statistics”. 100 of them did not choose “International Management’. There were 80 students who did not choose any of the two subjects. Find the number of students who chose both Business Statistics and International Management.- a)220
- b)180
- c)280
- d)300
Correct answer is option 'B'. Can you explain this answer?
400 students were admitted to the 2018-19 MBA batch. 200 of them did not choose “Business Statistics”. 100 of them did not choose “International Management’. There were 80 students who did not choose any of the two subjects. Find the number of students who chose both Business Statistics and International Management.
a)
220
b)
180
c)
280
d)
300

|
Maitri Sengupta answered |
Given Information:
- Total number of students admitted to the 2018-19 MBA batch = 400
- Number of students who did not choose "Business Statistics" = 200
- Number of students who did not choose "International Management" = 100
- Number of students who did not choose either subject = 80
Calculations:
Let's denote:
- Number of students who chose both "Business Statistics" and "International Management" as x
- Number of students who chose only "Business Statistics" as y
- Number of students who chose only "International Management" as z
From the given information, we can create the following equations:
x + y = 200 (Total number of students who chose "Business Statistics")
x + z = 100 (Total number of students who chose "International Management")
x + y + z + 80 = 400 (Total number of students admitted)
Now, we can solve these equations to find the values of x, y, and z.
From the first two equations:
y = 200 - x
z = 100 - x
Substitute these values in the third equation:
x + (200 - x) + (100 - x) + 80 = 400
300 - x + 80 = 400
380 - x = 400
-x = 20
x = 20
Therefore, the number of students who chose both "Business Statistics" and "International Management" is 20.
Therefore, the correct answer is option B) 180.
- Total number of students admitted to the 2018-19 MBA batch = 400
- Number of students who did not choose "Business Statistics" = 200
- Number of students who did not choose "International Management" = 100
- Number of students who did not choose either subject = 80
Calculations:
Let's denote:
- Number of students who chose both "Business Statistics" and "International Management" as x
- Number of students who chose only "Business Statistics" as y
- Number of students who chose only "International Management" as z
From the given information, we can create the following equations:
x + y = 200 (Total number of students who chose "Business Statistics")
x + z = 100 (Total number of students who chose "International Management")
x + y + z + 80 = 400 (Total number of students admitted)
Now, we can solve these equations to find the values of x, y, and z.
From the first two equations:
y = 200 - x
z = 100 - x
Substitute these values in the third equation:
x + (200 - x) + (100 - x) + 80 = 400
300 - x + 80 = 400
380 - x = 400
-x = 20
x = 20
Therefore, the number of students who chose both "Business Statistics" and "International Management" is 20.
Therefore, the correct answer is option B) 180.
Out of 60 families living in a building, all those families which own a car own a scooter as well. No family has just a scooter and a bike. 16 families have both a car and a bike. Every family owns at least one type of vehicle and the number of families that own exactly one type of vehicle is more than the number of families that own more than one type of vehicle. What is the sum of the maximum and minimum number of families that own only a bike?- a)24
- b)34
- c)54
- d)44
Correct answer is option 'D'. Can you explain this answer?
Out of 60 families living in a building, all those families which own a car own a scooter as well. No family has just a scooter and a bike. 16 families have both a car and a bike. Every family owns at least one type of vehicle and the number of families that own exactly one type of vehicle is more than the number of families that own more than one type of vehicle. What is the sum of the maximum and minimum number of families that own only a bike?
a)
24
b)
34
c)
54
d)
44

|
Learning Education answered |
From the information given in the question, the following Venn Diagram can be constructed:
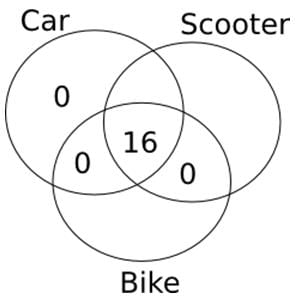
So, in order to maximize the number of families that own only a bike, we can put the remaining 44 families in ‘only bike’ region.

So, in order to maximize the number of families that own only a bike, we can put the remaining 44 families in ‘only bike’ region.
Similarly, in order to minimize the number of families that own only a bike, we can put the remaining 44 families in ‘only scooter’ region.
So, the maximum number of families that own only a bike is 44 and the minimum number of families that own only a bike is 0.
So, sum = 44 + 0 = 44
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Factory, Product and Machinery ?- a)

- b)
- c)

- d)
Correct answer is option 'D'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Factory, Product and Machinery ?
a)

b)

c)

d)

|
|
Nikita Singh answered |
Product and Machinery are different from each other but both are found in Factory.
A premier B-school, which is in process of getting an AACSB accreditation, has 360 second year students. To incorporate sustainability into their curriculum, it has offered 3 new elective subjects in the second year namely Green Supply Chain, Global Climate Change & Business and Corporate Governance. Twelve students have taken all the three electives, and 120 students study Green Supply Chain. There are twice as many students who study Green Supply Chain and Corporate Governance but not Global Climate Change and Business, as those who study both Green Supply Chain and Global Climate Change & Business but not Corporate Governance, and 4 times as many who study all the three. 124 students study Corporate Governance. There are 72 students who could not muster up the courage to take up any of these subjects. The group of students who study both Green Supply Chain and Corporate Governance but not global Climate Change & Business is exactly the same as the group made up to the students who study both Global Climate Change & Business and Corporate Governance. How many students study Global Climate Change & Business only?- a)176
- b)104
- c)152
- d)188
Correct answer is option 'B'. Can you explain this answer?
A premier B-school, which is in process of getting an AACSB accreditation, has 360 second year students. To incorporate sustainability into their curriculum, it has offered 3 new elective subjects in the second year namely Green Supply Chain, Global Climate Change & Business and Corporate Governance. Twelve students have taken all the three electives, and 120 students study Green Supply Chain. There are twice as many students who study Green Supply Chain and Corporate Governance but not Global Climate Change and Business, as those who study both Green Supply Chain and Global Climate Change & Business but not Corporate Governance, and 4 times as many who study all the three. 124 students study Corporate Governance. There are 72 students who could not muster up the courage to take up any of these subjects. The group of students who study both Green Supply Chain and Corporate Governance but not global Climate Change & Business is exactly the same as the group made up to the students who study both Global Climate Change & Business and Corporate Governance. How many students study Global Climate Change & Business only?
a)
176
b)
104
c)
152
d)
188

|
Rithika Chakraborty answered |
Understanding the Problem
To solve the problem, we need to set up variables for the number of students in each category of elective subjects.
Given Data
- Total students = 360
- Students not taking any subject = 72
- Students taking Green Supply Chain (G) = 120
- Students taking Corporate Governance (C) = 124
- Students taking all three subjects = 12
- Let:
- x = Students taking G and C but not Global Climate Change (X)
- y = Students taking G and X but not C
- z = Students taking X and C but not G
Relationships between the groups
- According to the problem:
- \( x = 2y \)
- \( x = z \)
- \( y = 12 \) (since 12 students take all three subjects)
Calculating Students in Each Category
Using the relationships:
- \( y = 12 \) (students taking all three)
- \( x = 2y = 2 \times 12 = 24 \)
- \( z = x = 24 \)
Calculating Total Students Taking Each Subject
Using the inclusion-exclusion principle:
- Total taking G and C = \( 120 + 124 - (x + y + z + 12) \)
Set the equation:
- \( 120 + 124 - (24 + 12 + 24 + 12) = 360 - 72 \)
- Solve for students taking Global Climate Change only:
Final Calculation
Total students studying:
- \( G + C + X - G \cap C - G \cap X - C \cap X + G \cap C \cap X = 288 \)
Thus, the students studying Global Climate Change only = \( 360 - 72 - (students in G + C + both) = 104 \).
Conclusion
The number of students studying Global Climate Change & Business only is:
Answer: 104 (Option B).
To solve the problem, we need to set up variables for the number of students in each category of elective subjects.
Given Data
- Total students = 360
- Students not taking any subject = 72
- Students taking Green Supply Chain (G) = 120
- Students taking Corporate Governance (C) = 124
- Students taking all three subjects = 12
- Let:
- x = Students taking G and C but not Global Climate Change (X)
- y = Students taking G and X but not C
- z = Students taking X and C but not G
Relationships between the groups
- According to the problem:
- \( x = 2y \)
- \( x = z \)
- \( y = 12 \) (since 12 students take all three subjects)
Calculating Students in Each Category
Using the relationships:
- \( y = 12 \) (students taking all three)
- \( x = 2y = 2 \times 12 = 24 \)
- \( z = x = 24 \)
Calculating Total Students Taking Each Subject
Using the inclusion-exclusion principle:
- Total taking G and C = \( 120 + 124 - (x + y + z + 12) \)
Set the equation:
- \( 120 + 124 - (24 + 12 + 24 + 12) = 360 - 72 \)
- Solve for students taking Global Climate Change only:
Final Calculation
Total students studying:
- \( G + C + X - G \cap C - G \cap X - C \cap X + G \cap C \cap X = 288 \)
Thus, the students studying Global Climate Change only = \( 360 - 72 - (students in G + C + both) = 104 \).
Conclusion
The number of students studying Global Climate Change & Business only is:
Answer: 104 (Option B).
In an amusement park along with the entry pass a visitor gets two of the three available rides (A, B and C) free. On a particular day 77 opted for ride A, 55 opted for B and 50 opted for C; 25 visitors opted for both A and C, 22 opted for both A and B, while no visitor opted for both B and C. 40 visitors did not opt for ride A and B, or both. How many visited with the entry pass on that day?- a)102
- b)115
- c)130
- d)150
Correct answer is option 'D'. Can you explain this answer?
In an amusement park along with the entry pass a visitor gets two of the three available rides (A, B and C) free. On a particular day 77 opted for ride A, 55 opted for B and 50 opted for C; 25 visitors opted for both A and C, 22 opted for both A and B, while no visitor opted for both B and C. 40 visitors did not opt for ride A and B, or both. How many visited with the entry pass on that day?
a)
102
b)
115
c)
130
d)
150

|
Aspire Academy answered |
Let the Venn diagram be as shown in the figure,
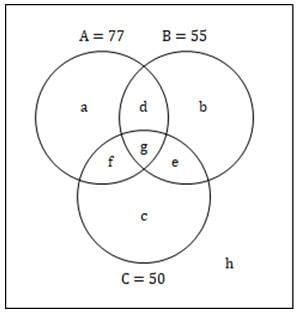
No one can take all three rides, hence g = 0.

No one can take all three rides, hence g = 0.
22 people take rides A and B,
∴ d = 22
∴ d = 22
25 people take rides A and C,
∴ f = 25
∴ f = 25
50 people take ride C,
∴ c = 50 – 25 = 25.
∴ c = 50 – 25 = 25.
40 people don’t take A or B or both,
∴ 40 = c + h
⇒ h = 40 – 25 = 15
∴ 40 = c + h
⇒ h = 40 – 25 = 15
∴ Total number of people visiting the park = (77 + 55 + 50 – 25 – 22) + 15 = 150.
Hence, option (d).
Shyam visited Ram during his brief vacation. In the mornings they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e. either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?- a)32
- b)24
- c)30
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Shyam visited Ram during his brief vacation. In the mornings they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e. either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?
a)
32
b)
24
c)
30
d)
None of these

|
Learning Education answered |
Let the number of days in the vacation be x
They played tennis for x - 14 days
They did yoga for x - 24 days
So, they did yoga or played tennis for x - 14 + x - 24 = 2x - 38 days
2x – 38 = 22
=> x = 30
They played tennis for x - 14 days
They did yoga for x - 24 days
So, they did yoga or played tennis for x - 14 + x - 24 = 2x - 38 days
2x – 38 = 22
=> x = 30
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Teacher, Writer and Musician ?- a)
- b)

- c)
- d)
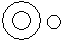
Correct answer is option 'A'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Teacher, Writer and Musician ?
a)
b)

c)

d)
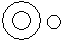

|
Niti Iyer answered |
A teacher may or may not be a writer and musician. Similarly a musician may or may not be a teacher and writer and so a writer may or may not be a teacher and musician.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Hockey, Football and Cricket ?- a)
- b)
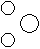
- c)

- d)
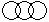
Correct answer is option 'B'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Hockey, Football and Cricket ?
a)

b)
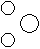
c)

d)
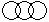

|
Nayanika Basu answered |
All these three games are different from each other.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between India, Haryana and World ?- a)
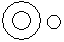
- b)
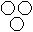
- c)
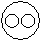
- d)

Correct answer is option 'D'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between India, Haryana and World ?
a)
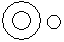
b)
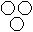
c)

d)


|
Mahesh Mehta answered |
Haryana is in India and India is in the World.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Earth, Sea and Sun ?- a)
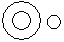
- b)
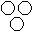
- c)
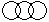
- d)
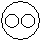
Correct answer is option 'A'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Earth, Sea and Sun ?
a)
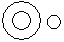
b)
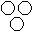
c)
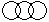
d)


|
Yashvi Chauhan answered |
Sea is a part of Earth while Sun is different from these two.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Author, Lawyer and Singer ?- a)
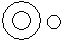
- b)
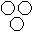
- c)
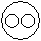
- d)

Correct answer is option 'B'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Author, Lawyer and Singer ?
a)
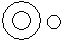
b)
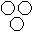
c)

d)


|
Sparsh Mehra answered |
All the three are different professions.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Mercury, Zinc and Metal ?- a)
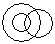
- b)
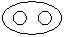
- c)
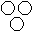
- d)

Correct answer is option 'B'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Mercury, Zinc and Metal ?
a)
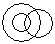
b)

c)
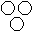
d)


|
Mahesh Mehta answered |
Mercury and Zinc both are different from one another but belong to metal.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Moon, Sun and Earth ?- a)

- b)
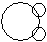
- c)
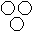
- d)
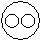
Correct answer is option 'C'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Moon, Sun and Earth ?
a)

b)

c)
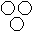
d)


|
Yashvi Chauhan answered |
All the three are different from each other.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Lion, Dog and Snake ?- a)

- b)
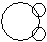
- c)
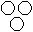
- d)
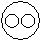
Correct answer is option 'C'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Lion, Dog and Snake ?
a)

b)

c)
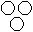
d)


|
Maulik Unni answered |
All the three are different from each other.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Pigeon, Bird and Dog ?- a)
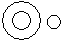
- b)
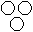
- c)
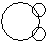
- d)
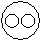
Correct answer is option 'A'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Pigeon, Bird and Dog ?
a)
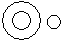
b)
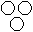
c)

d)


|
Kirti Yadav answered |
All the pigeons are birds while dog is different from these.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Bulb, Lamp and Light ?- a)
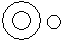
- b)
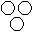
- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Bulb, Lamp and Light ?
a)
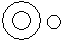
b)
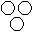
c)

d)


|
Dipanjan Shah answered |
Bulb and Lamp are different from each other but light is obtained from both.
Directions to Solve Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams. Question - Which of the following diagrams indicates the best relation between Iron, Lead and Nitrogen ?- a)
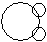
- b)
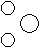
- c)

- d)
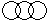
Correct answer is option 'B'. Can you explain this answer?
Directions to Solve
Each of these questions given below contains three elements. These elements may or may not have some inter linkage. Each group of elements may fit into one of these diagrams at (A), (B), (C), (D) and/or (E). You have to indicate the group of elements which correctly fits into the diagrams.
Question - Which of the following diagrams indicates the best relation between Iron, Lead and Nitrogen ?
a)

b)
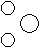
c)

d)
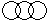

|
Sanjana Tiwari answered |
All these three elements are different from each other
Chapter doubts & questions for Venn Diagrams - 3 Months Preparation for UGC NET Paper 1 2025 is part of UGC NET exam preparation. The chapters have been prepared according to the UGC NET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UGC NET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Venn Diagrams - 3 Months Preparation for UGC NET Paper 1 in English & Hindi are available as part of UGC NET exam.
Download more important topics, notes, lectures and mock test series for UGC NET Exam by signing up for free.
3 Months Preparation for UGC NET Paper 1
231 videos|447 docs|128 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









