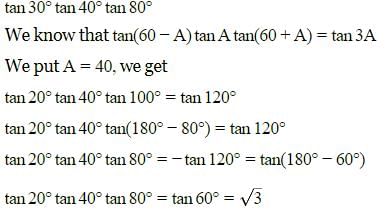All Exams >
JEE >
6 Months Preparation for JEE >
All Questions
All questions of Basic Mathematics for Physics for JEE Exam
In which quadrant are sin, cos and tan positive?a)... moreIInd quadrantb)IVth quadrantc)IIIrd quadrantd)Ist quadrantCorrect answer is 'D'. Can you explain this answer?

|
Anshu Joshi answered |
- All three of them are positive in Quadrant I
- Sine only is positive in Quadrant II
- Tangent only is positive in Quadrant III
- Cosine only is positive in Quadrant IV

Can you explain the answer of this question below:tan x = - 5/12, x lies in the second quadrant. So sinx=?
- A:
5/13
- B:
-5/13
- C:
-12/13
- D:
12/13
The answer is a.
tan x = - 5/12, x lies in the second quadrant. So sinx=?
5/13
-5/13
-12/13
12/13
|
|
Krishna Iyer answered |
tanx = -5/12
Therefore perpendicular = -5, base = 12
Applying pythagoras theorem,
(hyp)2 = (per)2 + (base)2
⇒ (-5)2 + (12)2
hyp = [25+144]1/2
hyp = (169)1/2
hyp = 13
sinx = perpendicular/hypotenous
= -5/13
In second quadrant, only sin x, cosec x are positive
So. sinx = 5/13
Therefore perpendicular = -5, base = 12
Applying pythagoras theorem,
(hyp)2 = (per)2 + (base)2
⇒ (-5)2 + (12)2
hyp = [25+144]1/2
hyp = (169)1/2
hyp = 13
sinx = perpendicular/hypotenous
= -5/13
In second quadrant, only sin x, cosec x are positive
So. sinx = 5/13
SinA = 1/√10 , SinB= 1/√5 If A and B are both acute angles,then , A+B=?- a)300
- b)750
- c)600
- d)450
Correct answer is option 'D'. Can you explain this answer?
SinA = 1/√10 , SinB= 1/√5 If A and B are both acute angles,then , A+B=?
a)
300
b)
750
c)
600
d)
450
|
|
Riya Banerjee answered |
We know that:
Sin θ = Opposite / Hypotenuse
Sin θ = Opposite / Hypotenuse
∴ SinA = 1/√10
CosA= 3/√10
similarly, SinB = 1/√5
CosB= 2/√5
CosA= 3/√10
similarly, SinB = 1/√5
CosB= 2/√5
⇒ Multiply:
Cos(A+B)= CosA x CosB - SinA x SinB
Cos(A+B)= CosA x CosB - SinA x SinB
Substituting the value in above equation we get:
= 3/√10 x 2/√5 - 1/√10 x 1/√5
= 6/√50 - 1/√50
= 6-1/5√2. ........(√50=5√2)
= 1/ √2
= 6/√50 - 1/√50
= 6-1/5√2. ........(√50=5√2)
= 1/ √2
we know that, sin 45 = 1/ √ 2 therefore
sinθ / cosθ = 45
sinθ / cosθ = 45
What is the value of sin 7π ?
- a)1
- b)-1
- c)-1/2
- d)0
Correct answer is option 'D'. Can you explain this answer?
What is the value of sin 7π ?
a)
1
b)
-1
c)
-1/2
d)
0
|
|
Om Desai answered |
Sin 7π = Sin 7*180 = Sin 2π * 7 = 0
# Remember Sin nπ =0
# Remember Sin nπ =0
The next term of the sequence 1, 2, 4, 7,11,…. Is- a)18
- b)17
- c)16
- d)15
Correct answer is option 'C'. Can you explain this answer?
The next term of the sequence 1, 2, 4, 7,11,…. Is
a)
18
b)
17
c)
16
d)
15

|
Imk Pathsala answered |
The given series is: 1,2,4,7,11,...
Difference between second and first term = 2 - 1 = 1
Difference between third and second term = 4 - 2 = 2
Difference between fourth and third term = 7 - 4 = 3
Difference between fifth and fourth term = 11 - 7 = 4
Difference between sixth and fifth term = 16 - 11 = 5
Difference between second and first term = 2 - 1 = 1
Difference between third and second term = 4 - 2 = 2
Difference between fourth and third term = 7 - 4 = 3
Difference between fifth and fourth term = 11 - 7 = 4
Difference between sixth and fifth term = 16 - 11 = 5
cos 68° cos 8° + sin 68° sin 8° = ?
- a)1/2
- b)1/4
- c)1
- d)0
Correct answer is option 'A'. Can you explain this answer?
cos 68° cos 8° + sin 68° sin 8° = ?
a)
1/2
b)
1/4
c)
1
d)
0
|
|
Lavanya Menon answered |
We know,
cosA cosB + sinA sinB = cos(A-B)
cosA cosB + sinA sinB = cos(A-B)
cos 68° cos 8° + sin 68° sin 8° = Cos (68-8) = Cos60°
=1/2
=1/2
In which quadrant are sin, cos and tan positive?- a)IInd quadrant
- b)IVth quadrant
- c)IIIrd quadrant
- d)Ist quadrant
Correct answer is option 'B'. Can you explain this answer?
In which quadrant are sin, cos and tan positive?
a)
IInd quadrant
b)
IVth quadrant
c)
IIIrd quadrant
d)
Ist quadrant
|
|
Nandini Patel answered |
For an angle in the fourth quadrant the point P has positive x coordinate and negative y coordinate. Therefore: In Quadrant IV, cos(θ) > 0, sin(θ) < 0 and tan(θ) < 0 (Cosine positive). The quadrants in which cosine, sine and tangent are positive are often remembered using a favorite mnemonic.
Can you explain the answer of this question below:What is the value of 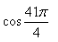
- A:√3/2
- B:1/2
- C:1
- D:1/√2
The answer is d.
What is the value of 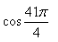
A:
√3/2
B:
1/2
C:
1
D:
1/√2
|
|
Harshitha Mehta answered |
We know ,π = 180deg
So cos 41π/4 = Cos( 41*180/4)
= Cos (1845deg)
= Cos (1800 + 45)
= Cos (10π + π/4)
= Cos (π/4)
= 1/√2
cos(π/4 -x) cos ( π/4 -y)-sin(π/4-x) sin( π/4 -y)=- a)cos(x-y)
- b)sin(x-y)
- c)cos(x+y)
- d)sin(x+y)
Correct answer is option 'D'. Can you explain this answer?
cos(π/4 -x) cos ( π/4 -y)-sin(π/4-x) sin( π/4 -y)=
a)
cos(x-y)
b)
sin(x-y)
c)
cos(x+y)
d)
sin(x+y)

|
Infinity Academy answered |
Cos(π/4-x)cos (π/4-y) - sin (π/4-x) sin(π/4-y)
= CosA*Cos B - Sin A*Sin B
= Cos (A+B)
= cos(π/4-x+π/4-y)
= cos(π/2-x-y)
= cos{π/2 - (x+y)}
= sin(x+y)
= Cos (A+B)
= cos(π/4-x+π/4-y)
= cos(π/2-x-y)
= cos{π/2 - (x+y)}
= sin(x+y)
What is the range of cos function?
- a)[-1,0]
- b)[0,1]
- c)[-1,1]
- d)[-2,2]
Correct answer is option 'C'. Can you explain this answer?
What is the range of cos function?
a)
[-1,0]
b)
[0,1]
c)
[-1,1]
d)
[-2,2]
|
|
Om Desai answered |
Just look at the graph of cosine.
We know , Range of a function is the set of all possible outputs for that function. If you look at any 2π interval, the cosine function is periodic after every 2π. as you can see it value range between -1 to 1 along the y-axis . So the range for cos function is [-1,1]
Sin(n+1)A sin(n+2)A + cos(n+1)A cos(n+2)A=- a)sinA
- b)sin2A
- c)cosA
- d)cos2A
Correct answer is option 'C'. Can you explain this answer?
Sin(n+1)A sin(n+2)A + cos(n+1)A cos(n+2)A=
a)
sinA
b)
sin2A
c)
cosA
d)
cos2A
|
|
Gaurav Kumar answered |
sin(n+1)Asin(n+2)A + cos(n+1)Acos(n+2)A = cos (n+1)Acos(n+2)A + sin(n+1)Asin(n+2)A = cos{A(n+2-n-1)} = cos (A.1) = cos A
Which of the following cannot be the value of cos θ .- a)1
- b)-1
- c)√2
- d)0
Correct answer is option 'C'. Can you explain this answer?
Which of the following cannot be the value of cos θ .
a)
1
b)
-1
c)
√2
d)
0
|
|
Naina Sharma answered |
√2 cannot be the value for Cosθ.
The values of Cos θ at different angles are given below :
Cos0°=1
Cos30°=√3/2
Cos45°=1/√2
Cos60°=1/2
Cos90°=0
What is the sign of the sec θ and cosec θ in second quadrant respectively?- a)positive and negative
- b)positive and positive
- c)negative and negative
- d)negative and positive
Correct answer is option 'D'. Can you explain this answer?
What is the sign of the sec θ and cosec θ in second quadrant respectively?
a)
positive and negative
b)
positive and positive
c)
negative and negative
d)
negative and positive
|
|
Preeti Iyer answered |
In quadrant sin, cos tan, cot, sec, cosec all +ve .In second quadrant sin and cosec are +ve. in 3rd quadrant tan and cot are positive.And in 4th cos and sec are +ve. 

Can you explain the answer of this question below:sin(60° + A) cos(30° – B) + cos(60° + A) sin(30° – B) is equal to- A:sin(A + B)
- B:sin(A – B)
- C:cos(A – B)
- D:cos(A + B)
The answer is c.
sin(60° + A) cos(30° – B) + cos(60° + A) sin(30° – B) is equal to
A:
sin(A + B)
B:
sin(A – B)
C:
cos(A – B)
D:
cos(A + B)
|
|
Lavanya Menon answered |
L.H.S. = sin(60+A)cos(30−B)+cos(60+A)sin(30−B)
= sin[(60+A)+(30−B)] (Using, sin(A+B)sinAcosB+cosAsinB)
= sin(90+A−B)
= sin(90+(A−B))
= cos(A−B) (Using, sin(90+θ)=cosθ) = R.H.S.Hence Proved.
= sin[(60+A)+(30−B)] (Using, sin(A+B)sinAcosB+cosAsinB)
= sin(90+A−B)
= sin(90+(A−B))
= cos(A−B) (Using, sin(90+θ)=cosθ) = R.H.S.Hence Proved.
If a, b, c, d are in H.P., then ab + bc + cd is- a)3 b d
- b)(a + b) (c + d)
- c)3 a d
- d)3 a c
Correct answer is option 'C'. Can you explain this answer?
If a, b, c, d are in H.P., then ab + bc + cd is
a)
3 b d
b)
(a + b) (c + d)
c)
3 a d
d)
3 a c
|
|
Rajesh Gupta answered |
Since a,b,c are in H.P, so b = 2ac/(a+c).
Also, b,c,d are in H.P, so c = 2bd/(b+d).
Therefore, (a+c)(b+d) = 2ac/b × 2bd/c
⇒ab+cb+ad+cd = 4ad
⇒ab+bc+cd = 3ad
Also, b,c,d are in H.P, so c = 2bd/(b+d).
Therefore, (a+c)(b+d) = 2ac/b × 2bd/c
⇒ab+cb+ad+cd = 4ad
⇒ab+bc+cd = 3ad
What is the sign of the sinA and tanA in third quadrant respectively- a)negative and positive
- b)positive and positive
- c)negative and negative.
- d)positive and negative
Correct answer is option 'A'. Can you explain this answer?
What is the sign of the sinA and tanA in third quadrant respectively
a)
negative and positive
b)
positive and positive
c)
negative and negative.
d)
positive and negative
|
|
Suresh Iyer answered |
The sign of the sinA and tanA in third quadrant is negative and positive.
In an A.P., sum of first p terms is equal to the sum of first q terms. Sum of its first p + q terms is- a)0
- b)- ( p + q)
- c)p + q
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
In an A.P., sum of first p terms is equal to the sum of first q terms. Sum of its first p + q terms is
a)
0
b)
- ( p + q)
c)
p + q
d)
none of these.

|
Trisha Vashisht answered |
Sp = Sq
⇒ p/2(2a+(p−1)d) = q/2(2a+(q−1)d)
⇒ p(2a+(p−1)d) = q(2a+(q−1)d)
⇒ 2ap + p2d − pd = 2aq + q2d − qd
⇒ 2a(p−q) + (p+q)(p−q)d − d(p−q) = 0
⇒ (p−q)[2a + (p+q)d − d] = 0
⇒ 2a + (p+q)d − d = 0
⇒ 2a + ((p+q) − 1)d = 0
⇒ Sp+q = 0
⇒ p/2(2a+(p−1)d) = q/2(2a+(q−1)d)
⇒ p(2a+(p−1)d) = q(2a+(q−1)d)
⇒ 2ap + p2d − pd = 2aq + q2d − qd
⇒ 2a(p−q) + (p+q)(p−q)d − d(p−q) = 0
⇒ (p−q)[2a + (p+q)d − d] = 0
⇒ 2a + (p+q)d − d = 0
⇒ 2a + ((p+q) − 1)d = 0
⇒ Sp+q = 0
Which term of the sequence 8 – 6i, 7 – 4i, 6 – 2i, ….is a real number ?- a)7th
- b)6th
- c)5th
- d)4th
Correct answer is option 'D'. Can you explain this answer?
Which term of the sequence 8 – 6i, 7 – 4i, 6 – 2i, ….is a real number ?
a)
7th
b)
6th
c)
5th
d)
4th
|
|
Preeti Iyer answered |
a = 8−6i
d = 7−4i−8+6i
= −1+2i
an = a+(n−1)d
a+ib = 8−6i+(n−1)(−1+2i)
a+ib = 8−6i+(−1)(n−1)+(n−1)2i
= − 6+2(n−1)=0
= 2(n−1) = 6
n = 4
an = 8−6i+(4−1)(−1+2i)
= 8−6i−3+6i = 5
4th term = 5
d = 7−4i−8+6i
= −1+2i
an = a+(n−1)d
a+ib = 8−6i+(n−1)(−1+2i)
a+ib = 8−6i+(−1)(n−1)+(n−1)2i
= − 6+2(n−1)=0
= 2(n−1) = 6
n = 4
an = 8−6i+(4−1)(−1+2i)
= 8−6i−3+6i = 5
4th term = 5
The next term of the sequence 1, 5, 14, 30, 55, …… is
- a)95
- b)91
- c)90
- d)80
Correct answer is option 'B'. Can you explain this answer?
The next term of the sequence 1, 5, 14, 30, 55, …… is
a)
95
b)
91
c)
90
d)
80
|
|
Mihir Chaudhary answered |
The sequence is obtained by adding consecutive odd numbers, starting with 1.
1 + 0 = 1
1 + 3 = 4
4 + 5 = 9
9 + 7 = 16
16 + 9 = 25
So the next term in the sequence is 25.
Therefore, the complete sequence is:
1, 5, 14, 30, 55, 25
1 + 0 = 1
1 + 3 = 4
4 + 5 = 9
9 + 7 = 16
16 + 9 = 25
So the next term in the sequence is 25.
Therefore, the complete sequence is:
1, 5, 14, 30, 55, 25
The eleventh term of the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, ….. is- a)89
- b)66
- c)72
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The eleventh term of the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, ….. is
a)
89
b)
66
c)
72
d)
none of these
|
|
Nandini Iyer answered |
The sequence is the Fibonacci series
1+1 = 0
1+2 = 3
2+3 = 5
3+5 = 8
5+8 = 13
8+13 = 21
13+21 = 34
21+34 = 55
34+55 = 89
The 11th term will be 89.
1+1 = 0
1+2 = 3
2+3 = 5
3+5 = 8
5+8 = 13
8+13 = 21
13+21 = 34
21+34 = 55
34+55 = 89
The 11th term will be 89.
The sum of 40 A.M.’s between two number is 120. The sum of 50 A.M.’s between them is equal to- a)150
- b)130
- c)160
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The sum of 40 A.M.’s between two number is 120. The sum of 50 A.M.’s between them is equal to
a)
150
b)
130
c)
160
d)
none of these
|
|
Mira Sharma answered |
Let A1, A2, A3, , A40 be 40 A.M's between two numbers 'a' and 'b'.
Then,
a, A1, A2, A3, , A40, b is an A.P. with common difference d = (b - a)/(n + 1) = (b - a)/41
[ where n = 40]
now,
A1, A2, A3, , A40 = 40/2( A1 + A40)
A1, A2, A3, , A40 = 40/2(a + b)
[ a, A1, A2, A3, , A40, b is an Ap then ,a + b = A1 + A40]
sum of 40A.M = 120(given)
120= 20(a + b)
=> 6 = a + b --(1)
Again ,
consider B1, B2, B50 be 50 A.M.'s between two numbers a and b.
Then, a, B1, B2,, B50, b will be in A.P. with common difference = ( b - a)/51
now , similarly,
B1, B2, ... , B50 = 50/2(B1 + B2)
= 25(6) -from(1)
= 150
If a, 4, b are in A.P.; a, 2, b are in G.P.; then a, 1, b are in- a)G.P.
- b)H.P.
- c)A.P.
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If a, 4, b are in A.P.; a, 2, b are in G.P.; then a, 1, b are in
a)
G.P.
b)
H.P.
c)
A.P.
d)
none of these
|
|
Lekshmi Chopra answered |
Given: a, 4, b are in A.P. and a, 2, b are in G.P.
To find: a, 1, b are in which progression.
Solution:
Let d be the common difference in the A.P.
Then, 4 - a = b - 4 = d ...(1)
Let r be the common ratio in the G.P.
Then, 2/a = b/2 = r ...(2)
From equation (1), we get:
b - a = 4 - 4a
a - 4a + b = 4
(1 - 4 + 1)r = 4 - a
-3r = 4 - a
r = (a - 4)/3
From equation (2), we get:
b = 2r/a
b = 2(a - 4)/(3a)
Substituting the value of b in equation (1), we get:
(a - 4)/(3a) - a = d
(a - 4) - 3a^2 d = 0
3a^2 - a + 4d = 0
Using the formula for the sum of n terms of an H.P., we get:
a, 1, b are in H.P. with sum 3/(a + 1/b) = 3/(a + 2/(a - 4)/3) = (3a(a - 4))/(4a^2 - 4a - 24)
Simplifying, we get:
3(a - 4)/(4a - 6) = 3(1 - 4/a)/(4 - 6/a)
Therefore, a, 1, b are in H.P.
Hence, the correct option is (b).
To find: a, 1, b are in which progression.
Solution:
Let d be the common difference in the A.P.
Then, 4 - a = b - 4 = d ...(1)
Let r be the common ratio in the G.P.
Then, 2/a = b/2 = r ...(2)
From equation (1), we get:
b - a = 4 - 4a
a - 4a + b = 4
(1 - 4 + 1)r = 4 - a
-3r = 4 - a
r = (a - 4)/3
From equation (2), we get:
b = 2r/a
b = 2(a - 4)/(3a)
Substituting the value of b in equation (1), we get:
(a - 4)/(3a) - a = d
(a - 4) - 3a^2 d = 0
3a^2 - a + 4d = 0
Using the formula for the sum of n terms of an H.P., we get:
a, 1, b are in H.P. with sum 3/(a + 1/b) = 3/(a + 2/(a - 4)/3) = (3a(a - 4))/(4a^2 - 4a - 24)
Simplifying, we get:
3(a - 4)/(4a - 6) = 3(1 - 4/a)/(4 - 6/a)
Therefore, a, 1, b are in H.P.
Hence, the correct option is (b).
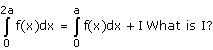
- a)
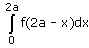
- b)
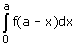
- c)
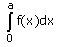
- d)
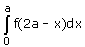
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
|
Vikas Kapoor answered |
Option d is correct, because it is the property of definite integral
∫02a f(x) dx = ∫0a f(x) dx + ∫0a f(2a – x) dx
∫02a f(x) dx = ∫0a f(x) dx + ∫0a f(2a – x) dx
The number of terms common to the Arithmetic progressions 3, 7, 11, …., 407 and 2, 9, 16, …., 709 is- a)14
- b)21
- c)51
- d)28
Correct answer is option 'A'. Can you explain this answer?
The number of terms common to the Arithmetic progressions 3, 7, 11, …., 407 and 2, 9, 16, …., 709 is
a)
14
b)
21
c)
51
d)
28
|
|
Geetika Shah answered |
First A.P′s sequence is 3,7,11,....,407
General term will be 4k+3 k≤101
Second A.P's sequence is 2,9,16,....,709
General term will be 7p+2 p≤101
The common terms will be 51,79,...,28m + 51
28m + 51 ≤ 407
⟹ 28k ≤ 356
⟹ k ≤ 12.71
And adding the 2 starting number count of the 2 A.P′s i.e. 3 & 2
Number of common terms will be 12 + 2 = 14
General term will be 4k+3 k≤101
Second A.P's sequence is 2,9,16,....,709
General term will be 7p+2 p≤101
The common terms will be 51,79,...,28m + 51
28m + 51 ≤ 407
⟹ 28k ≤ 356
⟹ k ≤ 12.71
And adding the 2 starting number count of the 2 A.P′s i.e. 3 & 2
Number of common terms will be 12 + 2 = 14
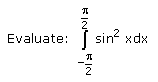
- a)π
- b)π/2
- c)2π
- d)π/4
Correct answer is option 'B'. Can you explain this answer?
a)
π
b)
π/2
c)
2π
d)
π/4

|
Tarun Kaushik answered |
For sin2(X), we will use the cos double angle formula:
cos(2X) = 1 - 2sin2(X)
The above formula can be rearranged to make sin2(X) the subject:
sin2(X) = 1/2(1 - cos(2X))
You can now rewrite the integration:
∫sin2(X)dX = ∫1/2(1 - cos(2X))dX
Because 1/2 is a constant, we can remove it from the integration to make the calculation simpler. We are now integrating:
1/2 x ∫(1 - cos(2X)) dX
= 1/2 x (X - 1/2sin(2X)) + C]-pi/4 to pi/4
∫sin2(X) dX = [1/2X - 1/4sin(2X)]-pi/4 to pi/4 + C
½[-pi/2] - 1/4sin(2(-pi/4)] - ½[pi/2] - 1/4sin(2(pi/4)]
= π/2
cos(2X) = 1 - 2sin2(X)
The above formula can be rearranged to make sin2(X) the subject:
sin2(X) = 1/2(1 - cos(2X))
You can now rewrite the integration:
∫sin2(X)dX = ∫1/2(1 - cos(2X))dX
Because 1/2 is a constant, we can remove it from the integration to make the calculation simpler. We are now integrating:
1/2 x ∫(1 - cos(2X)) dX
= 1/2 x (X - 1/2sin(2X)) + C]-pi/4 to pi/4
∫sin2(X) dX = [1/2X - 1/4sin(2X)]-pi/4 to pi/4 + C
½[-pi/2] - 1/4sin(2(-pi/4)] - ½[pi/2] - 1/4sin(2(pi/4)]
= π/2
pth term of an H.P. is qr and qth term is pr, then rth term of the H.P. is- a)pq
- b)1
- c)pqr2
- d)pqr
Correct answer is option 'A'. Can you explain this answer?
pth term of an H.P. is qr and qth term is pr, then rth term of the H.P. is
a)
pq
b)
1
c)
pqr2
d)
pqr
|
|
Raghav Bansal answered |
Given pth term of HP = qr
So pth term of AP = 1/qr
a+(p−1)d = 1/qr....(1)
and qth term of HP = pr
so qth term of AP = 1/pr
a + (q−1)d = 1/pr.....(2)
subtracting equation 1 and 2 we get,
(p−q)d = (p−q)/pqr
d = 1/pqr
Now from equation 1,
a = 1/qr − (p−1)/pqr
= (p−p+1)/pqr = 1/pqr
So rth term of AP = a+(r−1)d = 1/pqr + (r − 1)/pqr = 1/pq
So, rth term of HP = pq
So pth term of AP = 1/qr
a+(p−1)d = 1/qr....(1)
and qth term of HP = pr
so qth term of AP = 1/pr
a + (q−1)d = 1/pr.....(2)
subtracting equation 1 and 2 we get,
(p−q)d = (p−q)/pqr
d = 1/pqr
Now from equation 1,
a = 1/qr − (p−1)/pqr
= (p−p+1)/pqr = 1/pqr
So rth term of AP = a+(r−1)d = 1/pqr + (r − 1)/pqr = 1/pq
So, rth term of HP = pq
If cos a + 2cos b + cos c = 2 then a, b, c are in- a)2b = a+c
- b)b2 = a x c
- c)a = b = c
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If cos a + 2cos b + cos c = 2 then a, b, c are in
a)
2b = a+c
b)
b2 = a x c
c)
a = b = c
d)
none of these
|
|
Hansa Sharma answered |
cos A + 2 cos B + cos C = 2
⇒ cos A + cos C = 2(1 – cos B)
⇒ cos A + cos C = 2(1 – cos B)
2 cos((A + C)/2) × cos((A-C)/2 = 4 sin²(B/2)
2 sin(B/2) cos((A-C)/2) = 4 sin² (B/2)
cos((A-C)/2) = 2 sin (B/2)
cos((A-C)/2) = 2 cos((A+C)/2)
cos((A-C)/2) – cos((A+C)/2) = cos((A+C)/2)
cos((A-C)/2) = 2 sin (B/2)
cos((A-C)/2) = 2 cos((A+C)/2)
cos((A-C)/2) – cos((A+C)/2) = cos((A+C)/2)
2 sin(A/2) sin(C/2) = sin(B/2)
⇒ 2 {√(s-b)(s-c)√bc} × {√(s-a)(s-b)√ab} = √(s-a)(s-c)√ac
⇒ 2 {√(s-b)(s-c)√bc} × {√(s-a)(s-b)√ab} = √(s-a)(s-c)√ac
2(s – b) = b
a + b + c – 2b = b
a + c – b = b
a + c = 2b
a + b + c – 2b = b
a + c – b = b
a + c = 2b
In a triangle ABC, tan A/2 = 5/6, tan B/2 = 20/37, then tan C/2 is equal to:
- a)2/5
- b)100/222
- c)34/37
- d)5/2
Correct answer is option 'A'. Can you explain this answer?
In a triangle ABC, tan A/2 = 5/6, tan B/2 = 20/37, then tan C/2 is equal to:
a)
2/5
b)
100/222
c)
34/37
d)
5/2
|
|
Anjali Sharma answered |
In triangle ABC,
► Sum of all three angles = 1800
► A + B + C = 180 = A + B = 180 - C
► Sum of all three angles = 1800
► A + B + C = 180 = A + B = 180 - C
devide by 2 both side
A/2 + B/2 = 180/2 - C/2
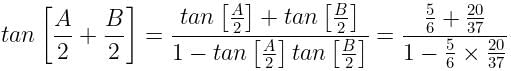
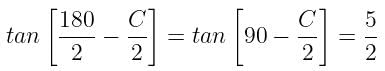
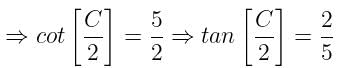
Identify the odd one out from the following- a)sin2θ + cos2θ=1
- b)sec2θ = 1 + tan2θ
- c)sec2θ + tan2θ = 1
- d)cosec2 θ = 1 + cot2 θ
Correct answer is option 'C'. Can you explain this answer?
Identify the odd one out from the following
a)
sin2θ + cos2θ=1
b)
sec2θ = 1 + tan2θ
c)
sec2θ + tan2θ = 1
d)
cosec2 θ = 1 + cot2 θ
|
|
Sonal Mestry answered |
Bcoz in trigonometry, we have only 3 identities which are A, B and D respectively. but we trigo don't have C type identity or formula.
The value of 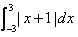 is:
is:- a)10
- b)17/2
- c)7/2
- d)5
Correct answer is option 'A'. Can you explain this answer?
The value of 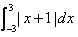 is:
is:
a)
10
b)
17/2
c)
7/2
d)
5

|
Sushil Kumar answered |
∫(-3 to 3) (x+1)dx
= ∫(-3 to -1) (x+1)dx + ∫(-1 to 3) (x+1) dx
= [x2 + x](-3 to -1) + [x2 + x](-1 to 3)
= [½ - 1 - (9/2 - 3)] + [9/2 + 3 - (½ - 1)]
= -[-4 + 2] + [4 + 4]
= -[-2] + [8]
= 10
The next term of the sequence, 2, 6, 12, 20, …..is- a)30
- b)28
- c)40
- d)24
Correct answer is option 'A'. Can you explain this answer?
The next term of the sequence, 2, 6, 12, 20, …..is
a)
30
b)
28
c)
40
d)
24
|
|
Lavanya Menon answered |
The given sequence is based on the following pattern:
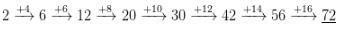
∴ Required number = 30.
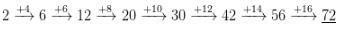
∴ Required number = 30.
The number of numbers between n and n2 which are divisible by n is- a)n – 2
- b)n
- c)n – 1
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of numbers between n and n2 which are divisible by n is
a)
n – 2
b)
n
c)
n – 1
d)
none of these
|
|
Hansa Sharma answered |
Between n & n2, numbers divisible by n are:
2n, 3n, 4n, ….... (n – 1)n
No. of numbers = (n – 1) – 2 + 1 = n – 2
2n, 3n, 4n, ….... (n – 1)n
No. of numbers = (n – 1) – 2 + 1 = n – 2
The value of 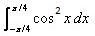 is:
is:- a)
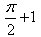
- b)
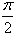
- c)
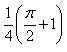
- d)
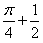
Correct answer is option 'D'. Can you explain this answer?
The value of 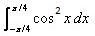 is:
is:
a)
b)
c)
d)
|
|
Samyak Jain answered |
1/2(cos π/2 + 1 -[cos(π/2-π/4)+1])=1/2+π/4
In an A.P., sum of first p terms is q and sum of first q terms is p. Sum of its p + q terms is- a)0
- b)- ( p + q)
- c)p + q
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
In an A.P., sum of first p terms is q and sum of first q terms is p. Sum of its p + q terms is
a)
0
b)
- ( p + q)
c)
p + q
d)
none of these
|
|
Om Desai answered |
Let the first term of the given AP be ‘a' and the common difference be ‘d'. Then, the sum of first ‘n' terms of the AP is given by:
Sn = n/2 {2a+(n-1)d} …….(1)
Here, it is given that:
Sp = q and Sq = p
Using (1), we get:-
q = p/2 {2a+(p-1)d}
and p = q/2 {2a+(q-1)d}
i.e. 2a + (p-1)d = 2q/p …..(2)
and 2a + (q-1)d = 2p/q …..(3)
Subtracting (3) from (2), we get:
(p - 1 - q + 1)d = 2q/p - 2p/q
So, d = 2(q2 - p2)/pq(p-q)
i.e. d = -2(p+q)/pq
Now, substituting the value of ‘d' in eq.n (2), we get:
2a + (p-1){-2(p+q)/pq} = 2q/p
i.e. 2a= 2q/p + 2(p-1)(p+q)/pq
This gives:
a = (p2 + q2 - p - q + pq)/pq
So, we have
Sp+q = (p+q)/2 { 2(p2+q2-p-q+pq)/pq - (p+q-1) 2 (p+q)/pq}
i.e. Sp+q = (p+q)/pq { p2+q2-p-q+pq-p2-pq-qp-q2+p+q}
So, Sp+q = -(p+q)
Sn = n/2 {2a+(n-1)d} …….(1)
Here, it is given that:
Sp = q and Sq = p
Using (1), we get:-
q = p/2 {2a+(p-1)d}
and p = q/2 {2a+(q-1)d}
i.e. 2a + (p-1)d = 2q/p …..(2)
and 2a + (q-1)d = 2p/q …..(3)
Subtracting (3) from (2), we get:
(p - 1 - q + 1)d = 2q/p - 2p/q
So, d = 2(q2 - p2)/pq(p-q)
i.e. d = -2(p+q)/pq
Now, substituting the value of ‘d' in eq.n (2), we get:
2a + (p-1){-2(p+q)/pq} = 2q/p
i.e. 2a= 2q/p + 2(p-1)(p+q)/pq
This gives:
a = (p2 + q2 - p - q + pq)/pq
So, we have
Sp+q = (p+q)/2 { 2(p2+q2-p-q+pq)/pq - (p+q-1) 2 (p+q)/pq}
i.e. Sp+q = (p+q)/pq { p2+q2-p-q+pq-p2-pq-qp-q2+p+q}
So, Sp+q = -(p+q)
tan x = - 5/12, x lies in the second quadrant. So sinx=?- a)5/13
- b)-5/13
- c)-12/13
- d)12/13
Correct answer is option 'A'. Can you explain this answer?
tan x = - 5/12, x lies in the second quadrant. So sinx=?
a)
5/13
b)
-5/13
c)
-12/13
d)
12/13
|
|
Raghav Bansal answered |
tanx = -5/12
Therefore perpendicular = -5, base = 12
Applying pythagoras theorem,
(hyp)2 = (per)2 + (base)2
⇒ (-5)2 + (12)2
hyp = [25+144]1/2
hyp = (169)1/2
hyp = 13
sinx = perpendicular/hypotenous
= -5/13
In second quadrant, only sin x, cosec x are positive
So. sinx = 5/13
Therefore perpendicular = -5, base = 12
Applying pythagoras theorem,
(hyp)2 = (per)2 + (base)2
⇒ (-5)2 + (12)2
hyp = [25+144]1/2
hyp = (169)1/2
hyp = 13
sinx = perpendicular/hypotenous
= -5/13
In second quadrant, only sin x, cosec x are positive
So. sinx = 5/13
What is the maximum or minimum point for the curve y = -3x2 − 12x + 5 ?- a)A minimum at (-2, 17)
- b)A maximum at (-2, 17)
- c)A minimum at (2, -31)
- d)A maximum at (2, -31)
Correct answer is option 'B'. Can you explain this answer?
What is the maximum or minimum point for the curve y = -3x2 − 12x + 5 ?
a)
A minimum at (-2, 17)
b)
A maximum at (-2, 17)
c)
A minimum at (2, -31)
d)
A maximum at (2, -31)
|
|
Rahul Basu answered |
Identifying the Curve
The given equation is in the form of a quadratic function: y = -3x^2 - 12x + 5. This is a downward-facing parabola due to the negative coefficient of the x^2 term.
Finding the Vertex
To find the vertex of the parabola, we can use the formula x = -b / 2a, where a = -3 and b = -12. Substituting these values, we get x = -(-12) / 2(-3) = 2. This means the x-coordinate of the vertex is 2.
Substitute x into the Equation
Next, substitute the x-coordinate back into the original equation to find the y-coordinate. y = -3(2)^2 - 12(2) + 5 = -3(4) - 24 + 5 = -12 - 24 + 5 = -31.
Conclusion
The vertex of the parabola is at (2, -31), which means the curve has a maximum point at (2, -31). Therefore, the correct answer is option B.
The given equation is in the form of a quadratic function: y = -3x^2 - 12x + 5. This is a downward-facing parabola due to the negative coefficient of the x^2 term.
Finding the Vertex
To find the vertex of the parabola, we can use the formula x = -b / 2a, where a = -3 and b = -12. Substituting these values, we get x = -(-12) / 2(-3) = 2. This means the x-coordinate of the vertex is 2.
Substitute x into the Equation
Next, substitute the x-coordinate back into the original equation to find the y-coordinate. y = -3(2)^2 - 12(2) + 5 = -3(4) - 24 + 5 = -12 - 24 + 5 = -31.
Conclusion
The vertex of the parabola is at (2, -31), which means the curve has a maximum point at (2, -31). Therefore, the correct answer is option B.
If log27x = 1/6 , then x is equal to- a)9
- b)27
- c)√3
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
If log27x = 1/6 , then x is equal to
a)
9
b)
27
c)
√3
d)
None of the above
|
|
Akshay Kapoor answered |
Given:
log27x = 1/6
To find:
The value of x
Solution:
Step 1: Rewrite the equation in exponential form
log27x = 1/6 can be rewritten as 27^(1/6) = x
Step 2: Simplify the right side
27^(1/6) can be expressed as the sixth root of 27, which is equal to 3. Therefore, x = 3.
Conclusion:
The value of x is √3. Hence, the correct answer is option 'C'.
log27x = 1/6
To find:
The value of x
Solution:
Step 1: Rewrite the equation in exponential form
log27x = 1/6 can be rewritten as 27^(1/6) = x
Step 2: Simplify the right side
27^(1/6) can be expressed as the sixth root of 27, which is equal to 3. Therefore, x = 3.
Conclusion:
The value of x is √3. Hence, the correct answer is option 'C'.
If log10 2 = 0.3010 and log10 3 = 0.4771. Find the value of log10 4.5 ? - a)0.6545
- b)0.2256
- c)0.5656
- d)0.6532
Correct answer is option 'D'. Can you explain this answer?
If log10 2 = 0.3010 and log10 3 = 0.4771. Find the value of log10 4.5 ?
a)
0.6545
b)
0.2256
c)
0.5656
d)
0.6532

|
Top Rankers answered |
log10 2 = 0.3010 and log10 3 = 0.4717
Now,
log10 4.5 = log10 (9/2)
= log10 9 - log10 2 (∵ log(m/n) = log m - log n)
= log10 32 - log10 2
= 2log10 3 - log10 2
= 2(0.4771) - 0.3010 = 0.6532
Now,
log10 4.5 = log10 (9/2)
= log10 9 - log10 2 (∵ log(m/n) = log m - log n)
= log10 32 - log10 2
= 2log10 3 - log10 2
= 2(0.4771) - 0.3010 = 0.6532
In a triangle ABC, cosec A (sin B cos C + cos B sin C) equals:
- a)c/a
- b)a/c
- c)1
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
In a triangle ABC, cosec A (sin B cos C + cos B sin C) equals:
a)
c/a
b)
a/c
c)
1
d)
none of these
|
|
Neha Sharma answered |
cosec A (sin B cos C + cos B sin C)= cosec A × sin(B+C)
= cosec A × sin(180 – A)
= cosec A × sin A
= cosec A × 1/cosec A
= 1
= cosec A × sin(180 – A)
= cosec A × sin A
= cosec A × 1/cosec A
= 1
The number of numbers between 105 and 1000 which are divisible by 7 is- a)127
- b)142
- c)128
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of numbers between 105 and 1000 which are divisible by 7 is
a)
127
b)
142
c)
128
d)
none of these
|
|
Tanuja Kapoor answered |
Clearly, the numbers between 105 and 1000 which are divisible by 7 are 112,119,126,...,994.
This is an AP with first term a=112, common difference d=7 and last term l = 994.
Let there be n terms in this AP. Then,
an = 994
Let there be n terms in this AP. Then,
an = 994
⇒ a + (n − 1)d
994 = 112 + (n − 1) × 7
994 = 105 + 7n
∴ 7n = 889
∴ n = 127
If acos x + bsin x = c, then the value of (asin x – bcos x)² is:
- a)a² + b² + c²
- b)a² - b² - c²
- c)a² - b² + c²
- d)a² + b² - c²
Correct answer is option 'D'. Can you explain this answer?
If acos x + bsin x = c, then the value of (asin x – bcos x)² is:
a)
a² + b² + c²
b)
a² - b² - c²
c)
a² - b² + c²
d)
a² + b² - c²
|
|
Preeti Iyer answered |
(acos x + bsin x)² + (asin x – bcos x)² = a² + b²
⇒ c² + (asin x – bcos x)² = a² + b²
⇒ (asin x – bcos x)² = a² + b² – c²
⇒ c² + (asin x – bcos x)² = a² + b²
⇒ (asin x – bcos x)² = a² + b² – c²
Chapter doubts & questions for Basic Mathematics for Physics - 6 Months Preparation for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Basic Mathematics for Physics - 6 Months Preparation for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily