All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Number System for GMAT Exam
How many prime numbers exist between 200 and 220? - a)0
- b)1
- c)2
- d)3
Correct answer is option 'B'. Can you explain this answer?
How many prime numbers exist between 200 and 220?
a)
0
b)
1
c)
2
d)
3

|
Manasa Gupta answered |
Odd numbers between 200 and 220 are:
201, 207, 210, 213, 219 are divisible by 3 (because the sum of their digits is divisible by 3).
205, 215 are divisible by 5.
Hence, we have to check just the following numbers: 203, 209, 211 and 217. Now,
203 = 7*29 (Not prime).
209 = 11*19 (Not prime).
211 = Prime
217 = 7*31 (Prime).
205, 215 are divisible by 5.
Hence, we have to check just the following numbers: 203, 209, 211 and 217. Now,
203 = 7*29 (Not prime).
209 = 11*19 (Not prime).
211 = Prime
217 = 7*31 (Prime).
So there is only one prime number between 200 and 220.
Is the product of two numbers x and y a prime number?
1) x + y = even
2) x is even
- a)Exactly one of the statements can answer the question
- b)More information is required as the information provided is insufficient to answer the question
- c)Each statement can answer the question individually
- d)Both statements are required to answer the question
Correct answer is option 'B'. Can you explain this answer?
Is the product of two numbers x and y a prime number?
1) x + y = even
2) x is even
a)
Exactly one of the statements can answer the question
b)
More information is required as the information provided is insufficient to answer the question
c)
Each statement can answer the question individually
d)
Both statements are required to answer the question
|
|
Lavanya Menon answered |
-
If x+y is even, it doesn't provide any information about whether xy is prime or not. For instance, 2+4=6 is even, and 2×4=8 is not a prime number, but 2+6=8 is even, and 2×6=12 is also not prime. So, statement 1 alone is insufficient.
-
If x is even, it also doesn't provide any information about whether xy is prime or not. For example, if x=2, y can be any number, and the product xy might or might not be prime. So, statement 2 alone is insufficient.
Combining the two statements doesn't provide any new information; it doesn't help determine whether the product of x and y is prime.
Therefore, the correct answer is:
2. More information is required as the information provided is insufficient to answer the question
Is x divisible by y?
1) x is a multiple of (y + 1)
2) y > 1
- a)Exactly one of the statements can answer the question
- b)More information is required as the information provided is insufficient to answer the question
- c)Each statement can answer the question individually
- d)Both statements are required to answer the question
Correct answer is option 'B'. Can you explain this answer?
Is x divisible by y?
1) x is a multiple of (y + 1)
2) y > 1
a)
Exactly one of the statements can answer the question
b)
More information is required as the information provided is insufficient to answer the question
c)
Each statement can answer the question individually
d)
Both statements are required to answer the question

|
Gitanjali Kumar answered |
= 0 (incomplete statement)
If m and n are two different prime numbers, then the least common multiple of the two numbers must equal which one of the following? - a)mn
- b)m - n
- c)m + n
- d)m + mn
Correct answer is option 'A'. Can you explain this answer?
If m and n are two different prime numbers, then the least common multiple of the two numbers must equal which one of the following?
a)
mn
b)
m - n
c)
m + n
d)
m + mn

|
Dhruv Mehra answered |
Prime numbers do not have common factors. Hence, the least common multiple of a set of such numbers equals the product of the numbers. For example, the LCM of 11 and 23 is 11 • 23. So, the answer is a) mn
If x is an integer, is x! + (x + 1) a prime number?1) x < 102) x is even- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
If x is an integer, is x! + (x + 1) a prime number?
1) x < 10
2) x is even
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Dhruv Mehra answered |
Stmt1
x <10> x can be 2 so 2!+3 = 5 - prime
But x can be 3 so 3!+4 = 10 - Non prime
So InSuff
Stmt2
x is even.
x can be 2 so 2!+3 = 5 - prime
But x can be 14 so 14! + 15 is not prime
Combine 1 and 2 you will see x! + x + 1 is prime
Which of the following could be the median of a set consisting of 6 different primes? - a)3
- b)9.5
- c)12.5
- d)39
Correct answer is option 'D'. Can you explain this answer?
Which of the following could be the median of a set consisting of 6 different primes?
a)
3
b)
9.5
c)
12.5
d)
39
|
|
Aditya Deshmukh answered |
Median of a set containing 6 different primes
median will be average of 3rd and 4th prime.
All prime greater than 2 are odd. So 3th and 4th primes are odd and their sum will be even and the median will be an integer. 3rd prime will be greater than 2 or 3(first 2 primes)
If k is a positive integer, is k a prime number?
1) k is the sum of three consecutive prime numbers
2) k has only 2 factors
- a) Exactly one of the statements can answer the question
- b) statement 2 can answer the question individually
- c)Both statements are required to answer the question
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'B'. Can you explain this answer?
If k is a positive integer, is k a prime number?
1) k is the sum of three consecutive prime numbers
2) k has only 2 factors
a)
Exactly one of the statements can answer the question
b)
statement 2 can answer the question individually
c)
Both statements are required to answer the question
d)
More information is required as the information provided is insufficient to answer the question
|
|
Aditya Kumar answered |
Statement 1: k is the sum of three consecutive prime numbers
2 + 3 + 5 = 10, which is not a prime number.
11 + 13 + 17 = 41, which is a prime number.
Therefore Statement 1 Alone is Insufficient. Answer options could be B, C or E
Statement 2: k has only 2 positive factors
If k has only 2 positive factors, then they have to be 1 and k itself, which is the definition of a prime number. k is a prime number.
Therefore Statement 2 Alone is Sufficient.
2 + 3 + 5 = 10, which is not a prime number.
11 + 13 + 17 = 41, which is a prime number.
Therefore Statement 1 Alone is Insufficient. Answer options could be B, C or E
Statement 2: k has only 2 positive factors
If k has only 2 positive factors, then they have to be 1 and k itself, which is the definition of a prime number. k is a prime number.
Therefore Statement 2 Alone is Sufficient.
Is integer y divisible by 16?1) y2 is divisible by 162) y3 is divisible by 16- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
Is integer y divisible by 16?
1) y2 is divisible by 16
2) y3 is divisible by 16
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Krithika Datta answered |
Answer: D
Explanation:
To determine if integer y is divisible by 16, we need to know if y is a multiple of 16.
Statement 1: y^2 is divisible by 16
- If y^2 is divisible by 16, it means that y is a multiple of 4. However, this does not necessarily mean that y is a multiple of 16. For example, y could be 4, 8, or 12, all of which satisfy statement 1 but are not divisible by 16. Therefore, statement 1 alone is insufficient to answer the question.
Statement 2: y^3 is divisible by 16
- If y^3 is divisible by 16, it means that y is a multiple of 2 and a multiple of 4. However, this still does not guarantee that y is a multiple of 16. For example, y could be 8, which satisfies statement 2 but is not divisible by 16. Therefore, statement 2 alone is also insufficient to answer the question.
Combining both statements:
- From statement 1, we know that y is a multiple of 4. From statement 2, we know that y is a multiple of 2 and a multiple of 4. Therefore, y must be a multiple of 8. However, this still does not guarantee that y is a multiple of 16. For example, y could be 8, 16, 24, or any multiple of 8, all of which satisfy both statements but only some of which are divisible by 16. Therefore, even when both statements are considered together, we cannot determine if y is divisible by 16. Hence, more information is required to answer the question.
Therefore, the correct answer is option D - more information is required as the information provided is insufficient to answer the question.
Explanation:
To determine if integer y is divisible by 16, we need to know if y is a multiple of 16.
Statement 1: y^2 is divisible by 16
- If y^2 is divisible by 16, it means that y is a multiple of 4. However, this does not necessarily mean that y is a multiple of 16. For example, y could be 4, 8, or 12, all of which satisfy statement 1 but are not divisible by 16. Therefore, statement 1 alone is insufficient to answer the question.
Statement 2: y^3 is divisible by 16
- If y^3 is divisible by 16, it means that y is a multiple of 2 and a multiple of 4. However, this still does not guarantee that y is a multiple of 16. For example, y could be 8, which satisfies statement 2 but is not divisible by 16. Therefore, statement 2 alone is also insufficient to answer the question.
Combining both statements:
- From statement 1, we know that y is a multiple of 4. From statement 2, we know that y is a multiple of 2 and a multiple of 4. Therefore, y must be a multiple of 8. However, this still does not guarantee that y is a multiple of 16. For example, y could be 8, 16, 24, or any multiple of 8, all of which satisfy both statements but only some of which are divisible by 16. Therefore, even when both statements are considered together, we cannot determine if y is divisible by 16. Hence, more information is required to answer the question.
Therefore, the correct answer is option D - more information is required as the information provided is insufficient to answer the question.
If the product of the integers a, b, c, and d is 1155 and if a > b > c > d > 1, then what is the value of a – d?
- a)2
- b)8
- c)10
- d)11
Correct answer is option 'B'. Can you explain this answer?
If the product of the integers a, b, c, and d is 1155 and if a > b > c > d > 1, then what is the value of a – d?
a)
2
b)
8
c)
10
d)
11

|
Jatin Kapoor answered |
Based on the given information, we know that the product of the integers a, b, c, and d is 1,155.
We also know that a < b="" />< c="" />< />
To find the values of a, b, c, and d, we can start by finding the prime factorization of 1,155.
The prime factorization of 1,155 is 3 * 5 * 7 * 11.
Since a < b="" />< c="" />< d,="" we="" need="" to="" distribute="" these="" prime="" factors="" in="" ascending="" order="" among="" the="" />
Let's start with the smallest prime factor, which is 3.
We have three possibilities for distributing the factor of 3 among the integers:
1. a = 3, b = 1, c = 1, d = 385
2. a = 1, b = 3, c = 1, d = 385
3. a = 1, b = 1, c = 3, d = 385
Next, let's consider the next smallest prime factor, which is 5.
We can distribute the factor of 5 among the integers in the following ways:
1. a = 3, b = 5, c = 1, d = 77
2. a = 3, b = 1, c = 5, d = 77
3. a = 1, b = 3, c = 5, d = 77
Now let's consider the next prime factor, which is 7.
We can distribute the factor of 7 among the integers in the following ways:
1. a = 3, b = 5, c = 7, d = 11
2. a = 3, b = 7, c = 5, d = 11
3. a = 3, b = 7, c = 11, d = 5
4. a = 5, b = 3, c = 7, d = 11
5. a = 5, b = 7, c = 3, d = 11
6. a = 5, b = 7, c = 11, d = 3
7. a = 7, b = 3, c = 5, d = 11
8. a = 7, b = 5, c = 3, d = 11
9. a = 7, b = 5, c = 11, d = 3
Finally, let's consider the last prime factor, which is 11.
We can distribute the factor of 11 among the integers in the following ways:
1. a = 3, b = 5, c = 7, d = 11
2. a = 3, b = 7, c = 5, d = 11
3. a = 3, b = 7, c = 11, d = 5
4. a = 5, b = 3, c = 7, d = 11
5. a = 5, b = 7, c = 3, d = 11
6. a = 5, b = 7, c = 11, d = 3
7.
We also know that a < b="" />< c="" />< />
To find the values of a, b, c, and d, we can start by finding the prime factorization of 1,155.
The prime factorization of 1,155 is 3 * 5 * 7 * 11.
Since a < b="" />< c="" />< d,="" we="" need="" to="" distribute="" these="" prime="" factors="" in="" ascending="" order="" among="" the="" />
Let's start with the smallest prime factor, which is 3.
We have three possibilities for distributing the factor of 3 among the integers:
1. a = 3, b = 1, c = 1, d = 385
2. a = 1, b = 3, c = 1, d = 385
3. a = 1, b = 1, c = 3, d = 385
Next, let's consider the next smallest prime factor, which is 5.
We can distribute the factor of 5 among the integers in the following ways:
1. a = 3, b = 5, c = 1, d = 77
2. a = 3, b = 1, c = 5, d = 77
3. a = 1, b = 3, c = 5, d = 77
Now let's consider the next prime factor, which is 7.
We can distribute the factor of 7 among the integers in the following ways:
1. a = 3, b = 5, c = 7, d = 11
2. a = 3, b = 7, c = 5, d = 11
3. a = 3, b = 7, c = 11, d = 5
4. a = 5, b = 3, c = 7, d = 11
5. a = 5, b = 7, c = 3, d = 11
6. a = 5, b = 7, c = 11, d = 3
7. a = 7, b = 3, c = 5, d = 11
8. a = 7, b = 5, c = 3, d = 11
9. a = 7, b = 5, c = 11, d = 3
Finally, let's consider the last prime factor, which is 11.
We can distribute the factor of 11 among the integers in the following ways:
1. a = 3, b = 5, c = 7, d = 11
2. a = 3, b = 7, c = 5, d = 11
3. a = 3, b = 7, c = 11, d = 5
4. a = 5, b = 3, c = 7, d = 11
5. a = 5, b = 7, c = 3, d = 11
6. a = 5, b = 7, c = 11, d = 3
7.
Is x divisible by y?1) (x – 1) is divisible by y2) x > y- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
Is x divisible by y?
1) (x – 1) is divisible by y
2) x > y
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Avantika Dey answered |
Sorry, the given information is incomplete. Please provide the complete information to solve the problem.
What is the greatest common factor of positive integers x and y?1) x and y share only one common factor. ?2) x and y are unique prime numbers. ?- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'C'. Can you explain this answer?
What is the greatest common factor of positive integers x and y?
1) x and y share only one common factor. ?
2) x and y are unique prime numbers. ?
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Manasa Kulkarni answered |
To find the greatest common factor (GCF) of positive integers x and y, we need to determine the largest number that divides both x and y without leaving a remainder. Let's analyze each statement separately:
1) x and y share only one common factor:
In this case, if x and y have only one common factor, then their GCF would be that common factor. For example, if x=5 and y=10, their only common factor is 5, so the GCF would be 5. Therefore, statement 1 alone is sufficient to answer the question.
2) x and y are unique prime numbers:
If x and y are unique prime numbers, then their only common factor would be 1. This is because prime numbers are only divisible by 1 and themselves. Therefore, the GCF of x and y in this case would be 1. Thus, statement 2 alone is also sufficient to answer the question.
Conclusion:
Both statements 1 and 2 individually provide sufficient information to determine the GCF of positive integers x and y. Therefore, each statement can answer the question individually. Thus, the correct answer is option C.
1) x and y share only one common factor:
In this case, if x and y have only one common factor, then their GCF would be that common factor. For example, if x=5 and y=10, their only common factor is 5, so the GCF would be 5. Therefore, statement 1 alone is sufficient to answer the question.
2) x and y are unique prime numbers:
If x and y are unique prime numbers, then their only common factor would be 1. This is because prime numbers are only divisible by 1 and themselves. Therefore, the GCF of x and y in this case would be 1. Thus, statement 2 alone is also sufficient to answer the question.
Conclusion:
Both statements 1 and 2 individually provide sufficient information to determine the GCF of positive integers x and y. Therefore, each statement can answer the question individually. Thus, the correct answer is option C.
Is the product of three integers xyz a prime number?1) x = -y2) z = 1 - a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
Is the product of three integers xyz a prime number?
1) x = -y
2) z = 1
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Lavanya Menon answered |
Correct Answer :- a
Explanation : xyz will be prime only when x = 1, y = -1, z = -2
or x = -1, y = 1, z = -2
(Sufficient)
if z=1, no other possible values of x and y make a prime product.
Is the product of two numbers x and y a prime number?1) x/y = prime2) x and y are consecutive integers- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'B'. Can you explain this answer?
Is the product of two numbers x and y a prime number?
1) x/y = prime
2) x and y are consecutive integers
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Aditya Kumar answered |
Correct Answer :- b
Explanation : Both the statements are required to answer the question.
Because it is given x and y are consecutive integers
Let x = 2, y = 1
When dividing x/y = 2/1
= 2(prime).
Is the product of two numbers x and y a prime number?1) x + y = prime2) y is not prime- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
Is the product of two numbers x and y a prime number?
1) x + y = prime
2) y is not prime
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Meera Rana answered |
Correct Answer :- d
Explanation : Given: x,y are integers > 0.
is x*y = prime?
prime number = 1*prime.
statement 1:
x = prime - y
possible values of x,y:
(3,1): product is a prime
(4,1):product is not a prime
not sufficient
statement 2:
y ≠≠ prime
nothing is specified about x.
not sufficient
combining both statements,
possible values of x,y:
(3,1): product is a prime
(4,1):product is not a prime
If k is a positive integer. Is k a prime number??1) No integers between "2" and "square root of k" inclusive divides k evenly2) No integers between 2 and k/2 divides k evenly, and k is greater than 5. - a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'C'. Can you explain this answer?
If k is a positive integer. Is k a prime number??
1) No integers between "2" and "square root of k" inclusive divides k evenly
2) No integers between 2 and k/2 divides k evenly, and k is greater than 5.
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Tanvi Deshpande answered |
Statement 1:
Property of a prime number: k is a prime number if no integer between 2 and square root of k (inclusive) is a factor of k.
Sufficient
Statement 2:
k/2 >= sqrt(k)
So it satisfies the above-mentioned property.
Sufficient
How many multiples of 2 exist between -10 and 10?
- a)4
- b)5
- c)9
- d)8
Correct answer is option 'C'. Can you explain this answer?
How many multiples of 2 exist between -10 and 10?
a)
4
b)
5
c)
9
d)
8

|
Sanskriti Ahuja answered |
Multiples of 2 between -10 and 10 are -8, -6, -4, -2, 0, 2, 4, 6, 8
If k is a positive integer, is k a prime number??1) k can be written as 6n + 1, where n is a positive integer.2) k > 4!- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
If k is a positive integer, is k a prime number??
1) k can be written as 6n + 1, where n is a positive integer.
2) k > 4!
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Preitee Ranjan Pradhan answered |
The answer is wrong here I guess
bkz in statement 1 k can be 7 or be 25
one is prime another is not.
statement 2 says k>24,so k can be 29 or be 30
again Not sufficient
combining k can be 25 or 31
again not sufficient
answer should be E
bkz in statement 1 k can be 7 or be 25
one is prime another is not.
statement 2 says k>24,so k can be 29 or be 30
again Not sufficient
combining k can be 25 or 31
again not sufficient
answer should be E
Is the integer x a prime number?
1) x + 1 is prime
2) x + 2 is not prime
- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
Is the integer x a prime number?
1) x + 1 is prime
2) x + 2 is not prime
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Srikar Mukkavilli answered |
1 alone can't answer as 2 is prime and 2+1=3 is also prime, also 4 is not prime and 4+1=5 is prime ( ambiguous )
2 alone can't answer as 2 is prime and 2+2=4 is not prime, also 4 is not prime and 4+2=6 is also not prime ( ambiguous )
1 and 2 together also can't answer as 2 is prime and 2+1=3 is also prime and 2+2=4 is not prime, also 4 is not prime and 4+1=5 is prime and 4+2=6 is also not prime( ambiguous )
Hence, more information is required to answer the question.
Please upvote if you find it useful!
2 alone can't answer as 2 is prime and 2+2=4 is not prime, also 4 is not prime and 4+2=6 is also not prime ( ambiguous )
1 and 2 together also can't answer as 2 is prime and 2+1=3 is also prime and 2+2=4 is not prime, also 4 is not prime and 4+1=5 is prime and 4+2=6 is also not prime( ambiguous )
Hence, more information is required to answer the question.
Please upvote if you find it useful!
How many odd positive integers divide the positive integer n completely?
(1) 16 is the highest power of 2 that divides n
(2) n has a total of 68 factors and 3 prime factors.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to theproblem are needed.
Correct answer is option 'C'. Can you explain this answer?
How many odd positive integers divide the positive integer n completely?
(1) 16 is the highest power of 2 that divides n
(2) n has a total of 68 factors and 3 prime factors.
(1) 16 is the highest power of 2 that divides n
(2) n has a total of 68 factors and 3 prime factors.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to theproblem are needed.
|
|
Aarav Sharma answered |
Step 1 & 2: Understand Question and Draw Inference
- n is an integer > 0
- We can write: n = P1a * P2b * P3c ….where P1 , P2 , P3 ..etc. are prime numbers and a, b, c are positive integers
To Find: Number of odd positive integers divide n?
- These are the factors that do not have 2 as their prime factor.
- So, the factors which can be written in the form P1a * P2b ….where P1, P2 ... etc. are greater than 2. The number of such factors = (a+1) (b+1)….
- So, we need to find the powers of all odd prime factors of n.
Step 3 : Analyze Statement 1 independent
- 16 is the highest power of 2 that divides n
Statement-1 tells us that the prime number 2 comes 16 times in n.
So, for n = P1a * P2b * P3c ….we know that P1 = 2 and a = 16.
However it does not tell us anything about the powers of odd prime factors of n.
Hence statement-1 is insufficient to answer the question.
So, for n = P1a * P2b * P3c ….we know that P1 = 2 and a = 16.
However it does not tell us anything about the powers of odd prime factors of n.
Hence statement-1 is insufficient to answer the question.
Step 4 : Analyze Statement 2 independent
2. n has a total of 68 factors and 3 prime factors.
Statement-2 tells us that n has a total of 68 factors and 3 prime factors.
So, for n = P1a * P2b * P3c we know that (a+1) (b+1) (c+1) = 68.
Now, let’s find the number of ways in which 68 can be expressed as a product of 3 integers > 1.
68 = 2 * 2 * 17.
So, (a, b, c) = (1, 1, 16). However, we do not know:
If 2 is a prime factor of n AND
Even if 2 is a prime factor of n, the power of 2 in n.
So, we cannot in any way find out the number of odd positive integers that divide n.
Hence statement-2 is insufficient to answer the question.
Statement-2 tells us that n has a total of 68 factors and 3 prime factors.
So, for n = P1a * P2b * P3c we know that (a+1) (b+1) (c+1) = 68.
Now, let’s find the number of ways in which 68 can be expressed as a product of 3 integers > 1.
68 = 2 * 2 * 17.
So, (a, b, c) = (1, 1, 16). However, we do not know:
If 2 is a prime factor of n AND
Even if 2 is a prime factor of n, the power of 2 in n.
So, we cannot in any way find out the number of odd positive integers that divide n.
Hence statement-2 is insufficient to answer the question.
Step 5: Analyze Both Statements Together (if needed)
Since we do not have a unique answer from either step 3 or 4, we need to
analyze both the steps together.
Step-3 tells us that P1 = 2 and a = 16.
Step- 4 tells us that n = P1a * P2b * P3c and (a+1) (b+1) (c+1) = 68.
Combining both the steps, we can say that (b+1) (c+1) = 4 i.e. there are a total
of 4 odd factors of n.
Hence statements 1 and 2 together are sufficient to answer the question.
analyze both the steps together.
Step-3 tells us that P1 = 2 and a = 16.
Step- 4 tells us that n = P1a * P2b * P3c and (a+1) (b+1) (c+1) = 68.
Combining both the steps, we can say that (b+1) (c+1) = 4 i.e. there are a total
of 4 odd factors of n.
Hence statements 1 and 2 together are sufficient to answer the question.
Answer : C
If x and y are nonzero integers, is x/y an integer?
(1) x is the product of 2 and some other integer.
(2) There is only one pair of positive integers whose product equals y.
- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
If x and y are nonzero integers, is x/y an integer?
(1) x is the product of 2 and some other integer.
(2) There is only one pair of positive integers whose product equals y.
(1) x is the product of 2 and some other integer.
(2) There is only one pair of positive integers whose product equals y.
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Preitee Ranjan Pradhan answered |
A says X is even that's all no other meaning
x/y =2/2=1 answer can Yes
x/y= 14/3 non integer answer can be No
so A is not sufficient
B says Y =2,no value of x I know ,so I can frame anything for x to make the ratio x/y to get integer and non interger.
Not sufficient
combining X is even and Y is 2 ,yes any even integer to 2 will be an integer
ANS IS C
x/y =2/2=1 answer can Yes
x/y= 14/3 non integer answer can be No
so A is not sufficient
B says Y =2,no value of x I know ,so I can frame anything for x to make the ratio x/y to get integer and non interger.
Not sufficient
combining X is even and Y is 2 ,yes any even integer to 2 will be an integer
ANS IS C
If x and y are prime numbers, which of the following CANNOT be the sum of x and y? - a)5
- b)9
- c)16
- d)23
Correct answer is option 'D'. Can you explain this answer?
If x and y are prime numbers, which of the following CANNOT be the sum of x and y?
a)
5
b)
9
c)
16
d)
23

|
Arya Roy answered |
In order odd number to be the sum of two prime numbers one must be even, so 2, and another odd.
Now, 23=2+21. Since 21 is not a prime then 23 cannot be written as the sum of two prime numbers.
Is integer y divisible by 24? 1) y is divisible by 6 ?2) y is divisible by 4 ?- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
Is integer y divisible by 24?
1) y is divisible by 6 ?
2) y is divisible by 4 ?
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Raghavendra Sharma answered |
If y divisible by 24. The rule says if number is divisible by all factors of other number the last number is a factor of the first
So, 24=3*2*2*2
S1. y is divisible by 6, which 3*2. Do not know about 2*2. Not sufficient
S2. y is divisible by 4, which 2*2. Do not know about 3*2. Not sufficient
S1+S2 says that y divisible by 3*2 and 2*2. Trick is that it is enough to be 3*2*2=12 to be divisible by 4 and 6 but not enough to be divisible by 24. But if we have 3*2*2*2=24 it is enough for all. Not sufficient.
What is the value of integer x?1) The lowest common multiple of x and 16 is 48. ?2) The greatest common factor of x and 16 is 4. - a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
What is the value of integer x?
1) The lowest common multiple of x and 16 is 48. ?
2) The greatest common factor of x and 16 is 4.
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Siddharth Pillai answered |
Ans.
(1) The lowest common multiple of x and 16 is 48 --> x can be 3, 6, 12, 24, or 48. Not sufficient.
(2) The greatest common factor of x and 16 is 4 --> x can take more than one value, for example, 4, 12, 20, .. (basically any number of the form 4*odd). Not sufficient.
(1)+(2) The most important property of LCM and GCD is: for any positive integers x and y,
x∗y=GCD(x,y)∗LCM(x,y). According to this 16x=48*4 --> x=12. Sufficient.
Answer: C.
What is the value of integer x?
1) The lowest common multiple of x and 7 is 28. ?
2) The greatest common factor of x and 7 is 1.
- a)Both statements are required to answer the question
- b)Exactly one of the statements can answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
What is the value of integer x?
1) The lowest common multiple of x and 7 is 28. ?
2) The greatest common factor of x and 7 is 1.
a)
Both statements are required to answer the question
b)
Exactly one of the statements can answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Maya Khanna answered |
Explanation:
To find the value of integer x, we need to consider the given statements one by one.
Statement 1: The lowest common multiple of x and 7 is 28.
From this statement, we know that the LCM of x and 7 is 28. We know that 28 is a multiple of 7. Therefore, x must also be a multiple of 7. We can find the value of x by dividing 28 by 7.
x = 28/7 = 4
Statement 1 alone is sufficient to answer the question.
Statement 2: The greatest common factor of x and 7 is 1.
From this statement, we know that x and 7 have no common factors other than 1. This means that x and 7 are co-prime. However, we cannot find the value of x with this information alone. For example, x could be 6, 8, 10, etc. Therefore, statement 2 alone is not sufficient to answer the question.
Therefore, the answer is option A, i.e. statement 1 alone is sufficient to answer the question.
To find the value of integer x, we need to consider the given statements one by one.
Statement 1: The lowest common multiple of x and 7 is 28.
From this statement, we know that the LCM of x and 7 is 28. We know that 28 is a multiple of 7. Therefore, x must also be a multiple of 7. We can find the value of x by dividing 28 by 7.
x = 28/7 = 4
Statement 1 alone is sufficient to answer the question.
Statement 2: The greatest common factor of x and 7 is 1.
From this statement, we know that x and 7 have no common factors other than 1. This means that x and 7 are co-prime. However, we cannot find the value of x with this information alone. For example, x could be 6, 8, 10, etc. Therefore, statement 2 alone is not sufficient to answer the question.
Therefore, the answer is option A, i.e. statement 1 alone is sufficient to answer the question.
An integer greater than 1 that is not prime is called composite. If the two-digit integer n is greater than 20, is n composite?
1) The tens digit of n is a factor of the units digit of n
2) The tens digit of n is 2
- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
An integer greater than 1 that is not prime is called composite. If the two-digit integer n is greater than 20, is n composite?
1) The tens digit of n is a factor of the units digit of n
2) The tens digit of n is 2
1) The tens digit of n is a factor of the units digit of n
2) The tens digit of n is 2
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Gowri Chakraborty answered |
Given: n>20n>20 --> two digit integer can be written as follows: n=10b+a>20n=10b+a>20 --> 2≤b≤92≤b≤9, 0≤a≤90≤a≤9.
(1) The tens digit of n is a factor of the units digit of n. This statement implies that a=kba=kb, (0≤k≤40≤k≤4) --> n=10b+a=10b+kb=b(10+k)n=10b+a=10b+kb=b(10+k) --> as b≥2b≥2, nn will always be composite and factor of bb. Sufficient
(2) The tens digit of n is 2. This statement implies that b=2b=2, but nn can be for instance composite 25 or prime 29. Not sufficient.
If the dimensions of a rectangle (in inches) is equal to a prime number that lies between 55 and 65, exclusive, which of the
following statements must be true?
I. There is only one other rectangle that has integral dimensions and the same area as the given rectangle
II. There is only one other rectangle that has integral dimensions and the same perimeter as the given rectangle
III. The area of the given rectangle is 3599 square inches.- a)I only
- b)II only
- c)III only
- d)I and II only
- e)None of the above
Correct answer is option 'A'. Can you explain this answer?
If the dimensions of a rectangle (in inches) is equal to a prime number that lies between 55 and 65, exclusive, which of the
following statements must be true?
I. There is only one other rectangle that has integral dimensions and the same area as the given rectangle
II. There is only one other rectangle that has integral dimensions and the same perimeter as the given rectangle
III. The area of the given rectangle is 3599 square inches.
following statements must be true?
I. There is only one other rectangle that has integral dimensions and the same area as the given rectangle
II. There is only one other rectangle that has integral dimensions and the same perimeter as the given rectangle
III. The area of the given rectangle is 3599 square inches.
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
None of the above

|
Ujwal Iyer answered |
Given:
- Length of the rectangle (inches) = {59, 61}
- Breadth of the rectangle (inches) = {59, 61}
- Note that we’re not given that Length and Breadth are distinct integers.
So, it would be wrong to assume so.
To Find: Which of the 3 given statements must be true?
Approach:
- We’ll evaluate the 3 statements one by one. They will qualify as must be true statements only if no exception is found to those statements.
Working out:
- Evaluating Statement I
- There is only one other rectangle that has integral dimensions and the same area as the given rectangle
- This statement talks about the area of the given rectangle. So, let us first see what are the different possible values for the area of the given rectangle. We find that 3 values of area are possible:
- 59*59
- 59*61
- 61*61
- Let’s evaluate the first possibility, where the area of the given rectangle is 59*59
In how many ways can 59*59 be expressed as a product of 2 integers?
- Way 1 - (59)*(59)
- Way 2 - (1)*(59*59)
- This means, only 2 rectangles are possible whose area is 59*59:
- A rectangle each of whose side is 59 inches
- This is the given rectangle
- A rectangle whose one side is 1 inch and the other is 59*59 inches
- A rectangle each of whose side is 59 inches
- Thus, apart from the given rectangle, there is only one other rectangle that can have the same area as the given rectangle
- We can do a similar analysis for the other 2 possible values of the area (59*61 and 61*61). We’ll get the same result – that there is only one other rectangle that can have the same area as the given rectangle
- The reason why the other 2 values will also yield the same result is that these 2 values of the area too are a product of prime numbers, like the first possibility was. So, the analysis and the conclusion will be similar.
- Thus, Statement 1 holds true for each of the 3 possible values of the area of the given rectangle. Therefore, this statement is a must be true statement.
- Evaluating Statement II
- There is only one other rectangle that has integral dimensions and the same perimeter as the given rectangle
- This statement talks about the perimeter of the given rectangle. So, let’s first evaluate what the perimeter of the given rectangle will be. We find that 3 values are possible for the perimeter:
- 2(59+59)
- 2(59+61)
- 2(61+61)
- Let’s evaluate the first possible value of the perimeter, 2(59+59) and see
how many different rectangles can have this perimeter - All the following pairs of length and breadth lead to the same perimeter:
- (59 – 1, 59 + 1), that is, (58, 60)
- (59 – 2, 59 + 2), that is, (57, 61)
- (59 – 3, 59 + 3), that is, (56, 62)
- And so on . . .
- Thus, we see that there are more than one rectangles that can have the same perimeter as the given rectangle if the perimeter of the given rectangle is 2(59+59)
- Since Statement II has proved untrue for one possible value of the Perimeter, it is definitely not a must be true statement.
- Note: You may have done your analysis with one of the 2 other possible values of the perimeter. That’s perfectly okay. The line of reasoning will be the same and will lead to the same conclusion as above.
- Evaluating Statement III
- The area of the given rectangle is 3599 square inches.
- As discussed in Statement I, 3 values of Area of the given rectangle are possible:
- 59*59
- 59*61
- 61*61
- Therefore, we cannot say definitely what the area of the given rectangle is. We can only say that the area can be 59*59 or 59*61 or 61*61 square inches
- So, Statement III is not true.
Looking at the answer choices, we see that the correct answer is Option A
How many unique divisors does 222 have?- a)4
- b)6
- c)8
- d)10
Correct answer is option 'C'. Can you explain this answer?
How many unique divisors does 222 have?
a)
4
b)
6
c)
8
d)
10

|
Manoj Ghosh answered |
222 is an even composite number. It is composed of three distinct prime numbers multiplied together. It has a total of
eight divisors.
If m has the smallest prime number as its only prime factor, is ∛m an integer?
(1) m2 is divisible by 32
(2) √m is divisible by 4- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If m has the smallest prime number as its only prime factor, is ∛m an integer?
(1) m2 is divisible by 32
(2) √m is divisible by 4
(1) m2 is divisible by 32
(2) √m is divisible by 4
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.
|
|
Anaya Patel answered |
Step 1 & 2: Understand Question and Draw Inference
Given:
- Positive integer m
- The only prime factor of m = the smallest prime number
- The smallest prime number is 2
- So, m = 2n , where n is a positive integer
To find:
So, in order to answer the question, we need to find if n is a multiple of 3 or not
Step 3 : Analyze Statement 1 independent
- m2 is divisible by 32
- m2 = 22n
- 32 = 25
- Since m2 is divisible by 32, m2 must be greater than or equal to 32
- Since n is an integer, the minimum possible value of n is 3.
- So possible values of n = {3, 4, 5, 6 . . . }
- Thus n may or may not be a multiple of 3
Step 4 : Analyze Statement 2 independent
Since √m is divisible by 4, √m must be greater than or equal to 4
- So possible values of n = {4, 5, 6 . . . }
- Thus n may or may not be a multiple of 3
Statement 2 alone is not sufficient to answer the question.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: n = {3, 4, 5, 6 . . . }
- From Statement 2: n = {4, 5, 6 . . . }
- By combining both statements: n = {4, 5, 6 . . . }
We’ve still not been able to determine if n is a multiple of 3.
So, even the two statements together are not sufficient to answer the question.
Answer: Option E
So, even the two statements together are not sufficient to answer the question.
Answer: Option E
If h(x) = product of all the multiples of 3 from 3 to x, inclusive, then the smallest prime factor of h(150) + 1 must be………- a)between 2 and 10
- b)between 11 and 20
- c)between 21 and 40
- d)greater than 40
Correct answer is option 'D'. Can you explain this answer?
If h(x) = product of all the multiples of 3 from 3 to x, inclusive, then the smallest prime factor of h(150) + 1 must be………
a)
between 2 and 10
b)
between 11 and 20
c)
between 21 and 40
d)
greater than 40

|
Talent Skill Learning answered |
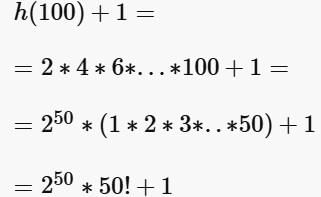
- Now, two numbers h(100)=250∗50!h(100)=250∗50! and h(100)+1=250∗50!+1h(100)+1=250∗50!+1 are consecutive integers.
- Two consecutive integers are co-prime, which means that they don't share ANY common factor but 1.
- For example 20 and 21 are consecutive integers, thus only common factor they share is 1.
- As h(100)=250∗50!h(100)=250∗50! has ALL prime numbers from 1 to 50 as its factors, then, according to the above, h(100)+1=250∗50! +1h(100)+1=250∗50! +1 won't have ANY prime factor from 1 to 50.
- Hence pp (>1>1), the smallest prime factor of h(100)+1h(100)+1 must be more than 50.
- Hence, option D is correct
If 375y = x2 and x and y are positive integers, then which of the following must be an integer? I. y/15 II. y/30 III. y2/25 - a)I only
- b)III only
- c)I and II only
- d)I, II, and III
Correct answer is option 'C'. Can you explain this answer?
If 375y = x2 and x and y are positive integers, then which of the following must be an integer?
I. y/15 II. y/30 III. y2/25
a)
I only
b)
III only
c)
I and II only
d)
I, II, and III

|
Dipanjan Mehra answered |
To determine which of the given expressions must be an integer, we need to simplify the given equation and analyze the resulting terms.
Given: 375y = x^2
1. Expressing x^2 in terms of y:
Since x and y are positive integers, we can rewrite the equation as:
x^2 = 375y
2. Analyzing the factors of the right-hand side:
The prime factorization of 375 is 3 * 5^3. Therefore, any factorization of x^2 must include an even number of 3s and an even number of 5s to yield a perfect square.
3. Analyzing the factors of the left-hand side:
The prime factorization of x^2 must also include an even number of 3s and an even number of 5s. This implies that the prime factorization of x must include an even number of 3s and an even number of 5s as well.
Now, let's analyze each of the given expressions:
I. y/15:
To determine if y/15 is an integer, we need to check if y is divisible by 15. Since the prime factorization of 15 is 3 * 5, which are also factors of x, it follows that y/15 is an integer. Therefore, option I is correct.
II. y/30:
To determine if y/30 is an integer, we need to check if y is divisible by 30. However, the prime factorization of 30 includes a factor of 2, which is not necessarily a factor of x. Therefore, y/30 may not be an integer. Therefore, option II is not correct.
III. y^2/25:
To determine if y^2/25 is an integer, we need to check if y^2 is divisible by 25. Since the prime factorization of 25 includes a factor of 5, which is also a factor of x, it follows that y^2/25 is an integer. Therefore, option III is correct.
In conclusion, options I and III must be integers, while option II may or may not be an integer. Therefore, the correct answer is option C (I and II only).
Given: 375y = x^2
1. Expressing x^2 in terms of y:
Since x and y are positive integers, we can rewrite the equation as:
x^2 = 375y
2. Analyzing the factors of the right-hand side:
The prime factorization of 375 is 3 * 5^3. Therefore, any factorization of x^2 must include an even number of 3s and an even number of 5s to yield a perfect square.
3. Analyzing the factors of the left-hand side:
The prime factorization of x^2 must also include an even number of 3s and an even number of 5s. This implies that the prime factorization of x must include an even number of 3s and an even number of 5s as well.
Now, let's analyze each of the given expressions:
I. y/15:
To determine if y/15 is an integer, we need to check if y is divisible by 15. Since the prime factorization of 15 is 3 * 5, which are also factors of x, it follows that y/15 is an integer. Therefore, option I is correct.
II. y/30:
To determine if y/30 is an integer, we need to check if y is divisible by 30. However, the prime factorization of 30 includes a factor of 2, which is not necessarily a factor of x. Therefore, y/30 may not be an integer. Therefore, option II is not correct.
III. y^2/25:
To determine if y^2/25 is an integer, we need to check if y^2 is divisible by 25. Since the prime factorization of 25 includes a factor of 5, which is also a factor of x, it follows that y^2/25 is an integer. Therefore, option III is correct.
In conclusion, options I and III must be integers, while option II may or may not be an integer. Therefore, the correct answer is option C (I and II only).
If x is a positive integer, is x prime?1) x has the same number of factors as y2, where y is a positive integer greater than 2.
2) x has the same number of factors as z, where z is a positive integer greater than 2.- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
If x is a positive integer, is x prime?
1) x has the same number of factors as y2, where y is a positive integer greater than 2.
2) x has the same number of factors as z, where z is a positive integer greater than 2.
2) x has the same number of factors as z, where z is a positive integer greater than 2.
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Sameer Rane answered |
If x is a positive integer, is x prime?
(1) x has the same number of factors as y^2, where y is a positive integer greater than 2.
y^2 is a perfect square. The number of distinct factors of a positive perfect square is ALWAYS ODD, while the number of factors of a prime is two (1 and itself). Thus since x has the same number of factors as a perfect square it cannot be a prime. Sufficient.
(2) x has the same number of factors as z, where z is a positive integer greater than 2. Clearly insufficient.
Is the product of two numbers x and y a prime number?1) x is even2) y is odd- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
Is the product of two numbers x and y a prime number?
1) x is even
2) y is odd
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Anaya Patel answered |
Correct Answer :- d
Explanation : Given: x,y are integers > 0.
is x*y = prime?
prime number = 1*prime.
statement 1:
x is even
possible values of x,y:
(1,2): product is a prime
(1,4):product is not a prime
not sufficient
statement 2:
y is odd
nothing is specified about x.
not sufficient
combining both statements,
possible values of x,y:
(3,1): product is a prime
(4,1):product is not a prime
What is the value of x?
1) x has exactly 3 factors.
2) 10 < x < 45
- a)Both statements are required to answer the question
- b)Exactly one of the statements can answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
What is the value of x?
1) x has exactly 3 factors.
2) 10 < x < 45
a)
Both statements are required to answer the question
b)
Exactly one of the statements can answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Talent Skill Learning answered |


Integer x represents the product of all integers between 1 and 25, inclusive. The smallest prime factor of (x + 1) must be _____. - a)between 1 and 10 ?
- b)between 11 and 20
- c)between 21 and 25
- d)greater than 25
Correct answer is option 'D'. Can you explain this answer?
Integer x represents the product of all integers between 1 and 25, inclusive. The smallest prime factor of (x + 1) must be _____.
a)
between 1 and 10 ?
b)
between 11 and 20
c)
between 21 and 25
d)
greater than 25

|
Kirti Roy answered |
Solution:
To find the smallest prime factor of (x+1), we need to find the value of x first.
Value of x:
x = 1 × 2 × 3 × … × 25
x = 25!
Now, we need to find the smallest prime factor of (x+1).
Smallest Prime Factor:
To find the smallest prime factor of (x+1), we need to add 1 to x and factorize it until we get the smallest prime factor.
x+1 = 25! + 1
Now, we need to factorize 25!+1 to find the smallest prime factor.
25!+1 = 2^k × m
where k is a non-negative integer and m is an odd integer.
We cannot factorize 25!+1 easily as it is a large number. However, we can use Wilson's theorem to simplify the expression.
Wilson's Theorem:
If p is a prime number, then (p-1)! ≡ -1 (mod p)
Using Wilson's theorem, we can say that:
24! ≡ -1 (mod 25)
Multiplying both sides by 25, we get:
25 × 24! ≡ -25 (mod 25)
25! ≡ -25 (mod 25)
25!+1 ≡ 0 (mod 25)
This means that 25 is a factor of 25!+1.
Now, we can say that:
25!+1 = 25 × k
where k is a positive integer.
Therefore, the smallest prime factor of (x+1) is greater than 25. Hence, the correct answer is option D.
To find the smallest prime factor of (x+1), we need to find the value of x first.
Value of x:
x = 1 × 2 × 3 × … × 25
x = 25!
Now, we need to find the smallest prime factor of (x+1).
Smallest Prime Factor:
To find the smallest prime factor of (x+1), we need to add 1 to x and factorize it until we get the smallest prime factor.
x+1 = 25! + 1
Now, we need to factorize 25!+1 to find the smallest prime factor.
25!+1 = 2^k × m
where k is a non-negative integer and m is an odd integer.
We cannot factorize 25!+1 easily as it is a large number. However, we can use Wilson's theorem to simplify the expression.
Wilson's Theorem:
If p is a prime number, then (p-1)! ≡ -1 (mod p)
Using Wilson's theorem, we can say that:
24! ≡ -1 (mod 25)
Multiplying both sides by 25, we get:
25 × 24! ≡ -25 (mod 25)
25! ≡ -25 (mod 25)
25!+1 ≡ 0 (mod 25)
This means that 25 is a factor of 25!+1.
Now, we can say that:
25!+1 = 25 × k
where k is a positive integer.
Therefore, the smallest prime factor of (x+1) is greater than 25. Hence, the correct answer is option D.
If p is a prime number greater than 2, what is the value of p?
1) There are a total of 100 prime numbers between 1 and p + 1
2) There are a total of p prime numbers between 1 and 3912
- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'C'. Can you explain this answer?
If p is a prime number greater than 2, what is the value of p?
1) There are a total of 100 prime numbers between 1 and p + 1
2) There are a total of p prime numbers between 1 and 3912
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Palak Yadav answered |
Solution:
Given, p is a prime number greater than 2.
Statement 1: There are a total of 100 prime numbers between 1 and p
- This statement alone is not sufficient to determine the value of p as there can be multiple values of p that satisfy this condition. For example, if p = 547, then there are 100 prime numbers between 1 and 547. But if p = 541, then there are also 100 prime numbers between 1 and 541. Hence, we cannot determine the value of p from this statement alone.
Statement 2: There are a total of p prime numbers between 1 and 3912
- This statement alone is sufficient to determine the value of p. We know that all prime numbers less than or equal to 3912 are less than or equal to p. Hence, we can use the Sieve of Eratosthenes to count the number of prime numbers between 1 and 3912. This will give us the value of p. For example, if there are 200 prime numbers between 1 and 3912, then p = 200.
Therefore, statement 2 alone is sufficient to answer the question.
Hence, the correct answer is option C.
Given, p is a prime number greater than 2.
Statement 1: There are a total of 100 prime numbers between 1 and p
- This statement alone is not sufficient to determine the value of p as there can be multiple values of p that satisfy this condition. For example, if p = 547, then there are 100 prime numbers between 1 and 547. But if p = 541, then there are also 100 prime numbers between 1 and 541. Hence, we cannot determine the value of p from this statement alone.
Statement 2: There are a total of p prime numbers between 1 and 3912
- This statement alone is sufficient to determine the value of p. We know that all prime numbers less than or equal to 3912 are less than or equal to p. Hence, we can use the Sieve of Eratosthenes to count the number of prime numbers between 1 and 3912. This will give us the value of p. For example, if there are 200 prime numbers between 1 and 3912, then p = 200.
Therefore, statement 2 alone is sufficient to answer the question.
Hence, the correct answer is option C.
Which of the following CANNOT be the greatest common divisor of two different prime numbers a and b? - a)a - b
- b)b - a
- c)2a - b
- d)a + b
Correct answer is option 'D'. Can you explain this answer?
Which of the following CANNOT be the greatest common divisor of two different prime numbers a and b?
a)
a - b
b)
b - a
c)
2a - b
d)
a + b

|
Saumya Shah answered |
Explanation:
To find the greatest common divisor (GCD) of two numbers, we need to identify the largest number that can divide both numbers without leaving a remainder. In this case, we are given that the numbers are prime, which means they are only divisible by 1 and themselves.
Let's consider each option and see if it can be the GCD of the two prime numbers a and b:
a) a - b:
If a is greater than b, then a - b will be a positive number. The GCD cannot be greater than the smaller of the two numbers, so a - b cannot be the GCD.
b) b - a:
Similar to the previous case, if b is greater than a, then b - a will be a positive number. The GCD cannot be greater than the smaller of the two numbers, so b - a cannot be the GCD.
c) 2a - b:
In this case, we have a linear combination of the two numbers. If a and b are both odd prime numbers, then 2a - b will be an even number. The GCD of two odd prime numbers cannot be an even number, so 2a - b cannot be the GCD.
d) a + b:
The sum of two prime numbers will always be greater than either of the two numbers. The GCD cannot be greater than the smaller of the two numbers, so a + b cannot be the GCD.
Conclusion:
Out of the given options, only option D (a b) can be the GCD of two different prime numbers a and b. The GCD of two different prime numbers is always equal to 1.
To find the greatest common divisor (GCD) of two numbers, we need to identify the largest number that can divide both numbers without leaving a remainder. In this case, we are given that the numbers are prime, which means they are only divisible by 1 and themselves.
Let's consider each option and see if it can be the GCD of the two prime numbers a and b:
a) a - b:
If a is greater than b, then a - b will be a positive number. The GCD cannot be greater than the smaller of the two numbers, so a - b cannot be the GCD.
b) b - a:
Similar to the previous case, if b is greater than a, then b - a will be a positive number. The GCD cannot be greater than the smaller of the two numbers, so b - a cannot be the GCD.
c) 2a - b:
In this case, we have a linear combination of the two numbers. If a and b are both odd prime numbers, then 2a - b will be an even number. The GCD of two odd prime numbers cannot be an even number, so 2a - b cannot be the GCD.
d) a + b:
The sum of two prime numbers will always be greater than either of the two numbers. The GCD cannot be greater than the smaller of the two numbers, so a + b cannot be the GCD.
Conclusion:
Out of the given options, only option D (a b) can be the GCD of two different prime numbers a and b. The GCD of two different prime numbers is always equal to 1.
If 6x = 8y = 14z, then what is a possible sum of positive integers x, y, and z?
- a)52
- b)58
- c)60
- d)61
Correct answer is option 'D'. Can you explain this answer?
If 6x = 8y = 14z, then what is a possible sum of positive integers x, y, and z?
a)
52
b)
58
c)
60
d)
61
|
|
Rajeev Menon answered |
We are given the equation 6x=8y=14z. To find a possible sum of x, y, and z, let's approach this systematically.
Step 1: Express x, y, and z in terms of a common variable
Let k be the constant such that:
6x=8y=14z=k
So,
x=k6,y=k8,z=k14
Step 2: Find the least common value of k
To ensure x, y, and z are integers, k must be a common multiple of 6, 8, and 14. The least common multiple (LCM) of 6, 8, and 14 is 168.
Thus, let k=168
Step 3: Calculate the values of x, y, and z
- x=168/6=28
- y=168/8=21
- z=168/14=12
Step 4: Find the sum of x, y, and z
The sum is:
x+y+z=28+21+12=61
Conclusion:
A possible sum of the positive integers x, y, and z is 61
Which of the following can be the least common multiple of two distinct integers a and b? - a)a
- b)b
- c)a - b
- d)a + b
Correct answer is option 'D'. Can you explain this answer?
Which of the following can be the least common multiple of two distinct integers a and b?
a)
a
b)
b
c)
a - b
d)
a + b

|
Devika Yadav answered |
Explanation:
The least common multiple (LCM) of two distinct integers a and b is the smallest positive integer that is divisible by both a and b.
To find the LCM of two numbers, we need to find the prime factorization of each number and then take the highest power of each prime factor that appears in either factorization.
For example, let's say we want to find the LCM of 12 and 18:
- The prime factorization of 12 is 2^2 x 3
- The prime factorization of 18 is 2 x 3^2
To find the LCM, we take the highest power of each prime factor:
- The highest power of 2 is 2^2
- The highest power of 3 is 3^2
Therefore, the LCM of 12 and 18 is 2^2 x 3^2 = 36.
Now, let's look at the answer choices:
a) a: This cannot be the LCM unless b = 1.
b) b: This cannot be the LCM unless a = 1.
c) a - b: This cannot be the LCM unless a and b are consecutive integers.
d) ab: This is a possible LCM because it is divisible by both a and b, and it is the smallest possible product of a and b that is divisible by both a and b.
Therefore, the correct answer is option D: ab.
The least common multiple (LCM) of two distinct integers a and b is the smallest positive integer that is divisible by both a and b.
To find the LCM of two numbers, we need to find the prime factorization of each number and then take the highest power of each prime factor that appears in either factorization.
For example, let's say we want to find the LCM of 12 and 18:
- The prime factorization of 12 is 2^2 x 3
- The prime factorization of 18 is 2 x 3^2
To find the LCM, we take the highest power of each prime factor:
- The highest power of 2 is 2^2
- The highest power of 3 is 3^2
Therefore, the LCM of 12 and 18 is 2^2 x 3^2 = 36.
Now, let's look at the answer choices:
a) a: This cannot be the LCM unless b = 1.
b) b: This cannot be the LCM unless a = 1.
c) a - b: This cannot be the LCM unless a and b are consecutive integers.
d) ab: This is a possible LCM because it is divisible by both a and b, and it is the smallest possible product of a and b that is divisible by both a and b.
Therefore, the correct answer is option D: ab.
Which of the following CANNOT be the greatest common divisor of two positive integers a and b?
- a)a - 2b
- b)a
- c)b
- d)1
Correct answer is option 'A'. Can you explain this answer?
Which of the following CANNOT be the greatest common divisor of two positive integers a and b?
a)
a - 2b
b)
a
c)
b
d)
1

|
Swara Dasgupta answered |
The greatest common divisor (GCD) of two positive integers a and b is the largest positive integer that divides both a and b without leaving a remainder.
Out of the given options, the only number that cannot be the GCD of two positive integers a and b is option 4, a - 2b.
To see why, consider the following example: let a = 10 and b = 4. The factors of 10 are 1, 2, 5, and 10, and the factors of 4 are 1, 2, and 4. The common factors of 10 and 4 are 1 and 2, and the greatest common factor is 2.
Now, if we substitute a = 10 and b = 4 into the expression a - 2b, we get:
a - 2b = 10 - 2(4) = 2
Since 2 is the GCD of 10 and 4, it is possible for a - 2b to be the GCD of two positive integers. However, there are other cases where a - 2b is not the GCD of two positive integers, so it cannot be concluded that a - 2b is always a valid option for the GCD of two positive integers.
Therefore, the correct answer is option 4, a - 2b.
Is integer y divisible by 16?1) y is divisible by 82) 2y is divisible by 16- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
Is integer y divisible by 16?
1) y is divisible by 8
2) 2y is divisible by 16
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Sahana Mehta answered |
Solution:
To determine whether y is divisible by 16, we need to check whether it is divisible by 2^4.
Statement 1: y is divisible by 8
If y is divisible by 8, then it is also divisible by 2^3. However, we cannot determine whether y is divisible by 2^4. For example, y could be 8, 16, or 24, which are all divisible by 8 but only 16 is divisible by 2^4. Thus, statement 1 alone is insufficient.
Statement 2: 2y is divisible by 16
If 2y is divisible by 16, then it is also divisible by 2^4. However, we cannot determine whether y is divisible by 2^4. For example, if 2y = 32, then y could be 16, which is divisible by 2^4, or it could be any odd integer, which is not divisible by 2^4. Thus, statement 2 alone is insufficient.
Combined statements:
If we combine the two statements, we know that y is divisible by 8 and 2y is divisible by 16. From statement 1, we know that y is divisible by 2^3, and from statement 2, we know that 2y is divisible by 2^4. Therefore, y must be divisible by 2^4. For example, if 2y = 32, then y = 16, which is divisible by 2^4. However, if 2y = 48, then y = 24, which is not divisible by 2^4. Thus, even when the statements are combined, we cannot determine whether y is divisible by 2^4.
Therefore, the correct answer is option (D) - more information is required as the information provided is insufficient to answer the question.
To determine whether y is divisible by 16, we need to check whether it is divisible by 2^4.
Statement 1: y is divisible by 8
If y is divisible by 8, then it is also divisible by 2^3. However, we cannot determine whether y is divisible by 2^4. For example, y could be 8, 16, or 24, which are all divisible by 8 but only 16 is divisible by 2^4. Thus, statement 1 alone is insufficient.
Statement 2: 2y is divisible by 16
If 2y is divisible by 16, then it is also divisible by 2^4. However, we cannot determine whether y is divisible by 2^4. For example, if 2y = 32, then y could be 16, which is divisible by 2^4, or it could be any odd integer, which is not divisible by 2^4. Thus, statement 2 alone is insufficient.
Combined statements:
If we combine the two statements, we know that y is divisible by 8 and 2y is divisible by 16. From statement 1, we know that y is divisible by 2^3, and from statement 2, we know that 2y is divisible by 2^4. Therefore, y must be divisible by 2^4. For example, if 2y = 32, then y = 16, which is divisible by 2^4. However, if 2y = 48, then y = 24, which is not divisible by 2^4. Thus, even when the statements are combined, we cannot determine whether y is divisible by 2^4.
Therefore, the correct answer is option (D) - more information is required as the information provided is insufficient to answer the question.
Set A consists of 8 distinct prime numbers. If x is equal to the range of set A and y is equal to the median of set A, is the product xy even? ?1) The smallest integer in the set is 5.2) The largest integer in the set is 101. ?- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
Set A consists of 8 distinct prime numbers. If x is equal to the range of set A and y is equal to the median of set A, is the product xy even? ?
1) The smallest integer in the set is 5.
2) The largest integer in the set is 101. ?
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Pallabi Deshpande answered |
As long as the set A doesn't contain a 2, x (the range of set A) is always even. Thus, xy is even.
(2) doesn't tell us anything. If the set contains {2,3,5,7,11,13,17,101}, x (the range) is odd and y (the median) is 9 which is odd. So, xy is odd. And of course, we can remove the 2 and then xy will be even.
If a and b are positive integers and x = 4a and y = 9b, which of the following is a possible units digit of xy?- a)1
- b)4
- c)5
- d)7
- e)8
Correct answer is option 'B'. Can you explain this answer?
If a and b are positive integers and x = 4a and y = 9b, which of the following is a possible units digit of xy?
a)
1
b)
4
c)
5
d)
7
e)
8

|
Kavya Chakraborty answered |
To find the units digit of xy, we need to find the units digit of both x and y separately and then multiply them together.
Given that x = 4a and y = 9b, we need to determine the units digit of 4a and the units digit of 9b.
Finding the Units Digit of 4a:
The units digit of any number multiplied by 4 will always end in 0, 4, 8, or 2. Therefore, the units digit of 4a will be either 0, 4, 8, or 2.
Finding the Units Digit of 9b:
The units digit of any number multiplied by 9 will always end in 1, 9, 7, or 3. Therefore, the units digit of 9b will be either 1, 9, 7, or 3.
Multiplying the Units Digits:
To find the units digit of xy, we need to multiply the units digit of x (0, 4, 8, or 2) with the units digit of y (1, 9, 7, or 3).
When we multiply the units digits, we get the following possibilities:
0 * 1 = 0
0 * 9 = 0
0 * 7 = 0
0 * 3 = 0
4 * 1 = 4
4 * 9 = 6
4 * 7 = 8
4 * 3 = 2
8 * 1 = 8
8 * 9 = 2
8 * 7 = 6
8 * 3 = 4
2 * 1 = 2
2 * 9 = 8
2 * 7 = 4
2 * 3 = 6
From the above possibilities, we can see that the units digit of xy can be either 0, 4, 6, or 8. Therefore, the correct answer is option B: 4.
Given that x = 4a and y = 9b, we need to determine the units digit of 4a and the units digit of 9b.
Finding the Units Digit of 4a:
The units digit of any number multiplied by 4 will always end in 0, 4, 8, or 2. Therefore, the units digit of 4a will be either 0, 4, 8, or 2.
Finding the Units Digit of 9b:
The units digit of any number multiplied by 9 will always end in 1, 9, 7, or 3. Therefore, the units digit of 9b will be either 1, 9, 7, or 3.
Multiplying the Units Digits:
To find the units digit of xy, we need to multiply the units digit of x (0, 4, 8, or 2) with the units digit of y (1, 9, 7, or 3).
When we multiply the units digits, we get the following possibilities:
0 * 1 = 0
0 * 9 = 0
0 * 7 = 0
0 * 3 = 0
4 * 1 = 4
4 * 9 = 6
4 * 7 = 8
4 * 3 = 2
8 * 1 = 8
8 * 9 = 2
8 * 7 = 6
8 * 3 = 4
2 * 1 = 2
2 * 9 = 8
2 * 7 = 4
2 * 3 = 6
From the above possibilities, we can see that the units digit of xy can be either 0, 4, 6, or 8. Therefore, the correct answer is option B: 4.
Can a batch of identical cookies be split evenly between Laurel and Jean without leftovers and without breaking a cookie?
1) If the batch of cookies were split among Laurel, Jean and Marc, there would be one cookie left over.
2) If Peter eats three of the cookies before they are split, there will be no leftovers when the cookies are split evenly between Laurel and Jean.- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
Can a batch of identical cookies be split evenly between Laurel and Jean without leftovers and without breaking a cookie?
1) If the batch of cookies were split among Laurel, Jean and Marc, there would be one cookie left over.
2) If Peter eats three of the cookies before they are split, there will be no leftovers when the cookies are split evenly between Laurel and Jean.
1) If the batch of cookies were split among Laurel, Jean and Marc, there would be one cookie left over.
2) If Peter eats three of the cookies before they are split, there will be no leftovers when the cookies are split evenly between Laurel and Jean.
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question

|
Pallavi Jain answered |
From first statement we can say that the number of cookies is 3x+1
since this can be even or odd depending on x we can't say the cookies will be evenly split
from second statement alone we know that number of cookies is 2y+3
this Is always odd and cookies can't be evenly distributed ever
hence option A
since this can be even or odd depending on x we can't say the cookies will be evenly split
from second statement alone we know that number of cookies is 2y+3
this Is always odd and cookies can't be evenly distributed ever
hence option A
The product of the largest two factors of a positive integer n is 16875. What is the difference between the largest positive integer that divides √n and the smallest odd factor greater than 1 of √n?- a)2
- b)12
- c)13
- d)222
- e)223
Correct answer is option 'B'. Can you explain this answer?
The product of the largest two factors of a positive integer n is 16875. What is the difference between the largest positive integer that divides √n and the smallest odd factor greater than 1 of √n?
a)
2
b)
12
c)
13
d)
222
e)
223

|
Jhanvi Saha answered |
Understanding the problem:
Given that the product of the largest two factors of a positive integer n is 16875, we need to find the difference between the largest positive integer that divides n and the smallest odd factor greater than 1 of n.
Solution:
Finding the prime factorization of 16875:
16875 = 3 * 5^3 * 11
Finding the factors of n:
Since the largest two factors of n multiply to 16875, they must be 225 and 75. This means n = 225.
Finding the largest positive integer that divides n:
The largest positive integer that divides 225 is 225 itself.
Finding the smallest odd factor greater than 1 of n:
The smallest odd factor greater than 1 of n is 3.
Calculating the difference:
The difference between the largest positive integer that divides n and the smallest odd factor greater than 1 of n is:
225 - 3 = 222
Therefore, the correct answer is option B (222).
Which of the following CANNOT be the greatest common divisor of two positive integers a and b?
- a)1
- b)a + b
- c)a - b
- d)a
Correct answer is option 'B'. Can you explain this answer?
Which of the following CANNOT be the greatest common divisor of two positive integers a and b?
a)
1
b)
a + b
c)
a - b
d)
a

|
Arya Roy answered |
Divisor of a positive integer cannot be more than that integer (for example integer 4 doesn't have a divisor more than 4, the largest divisor it has is 4 itself), so greatest common divisor of two positive integers x and y can not be more than a or b.
So answer will be a + b.
So answer will be a + b.
For any integer x greater than 1, x! denotes the product of all integers from 1 to x, inclusive. What is the hundred-thousands
digit of 25!?- a)0
- b)2
- c)4
- d)5
- e)8
Correct answer is option 'A'. Can you explain this answer?
For any integer x greater than 1, x! denotes the product of all integers from 1 to x, inclusive. What is the hundred-thousands
digit of 25!?
digit of 25!?
a)
0
b)
2
c)
4
d)
5
e)
8

|
Prisha Mukherjee answered |
Given:
- x is an integer > 1
- Then x! = 1*2*3………x
To Find:: Hundred-thousand digit of 25!
- 25! = 1*2*3…..25
- Hundred-thousand digit of 25! is the digit, that comes at the 6 place from
- the rightmost digit, in the value of 25!.
Approach:
- Let’s first try to find the number of zeroes at the end in 25!. If there are more than 5 zeroes, then the hundred-thousands digit will be 0
- Now, 0 can occur only when a 5 is multiplied with an even number
- So, if 5 is multiplied with any multiple of 2, it will result in a zero.
- So, we would try to find the number of 2s and 5s in 25!, i.e. the power of 2 and 5 in 25!
- Let’s take a simple example to understand how we can find this. Consider a number p = 1*2*3*4. We need to find the power of 2 in p.
- Now, powers of 2 will occur in multiples of 2. So, we should first find the multiples of 2 in p. They are 2 and 4. However all multiples of 2 will not contain only 2 . Some of them may contain higher powers of 2. For example, here 4 contains 22.
- So, when we are finding multiples of 2, we should also find the multiples of higher powers of 2 in p.
- Hence, 2 will occur 2 + 1 = 3 times in p
- Using the same analogy, we will find the power of 2 and 5 in 25!
- Once we get the power of 2 and 5 in 25!, we can calculate the number of zeroes at the end of 25
Working out:
3. As 25! has 222 and 56 in it, 25! will have 10 in it
- This is because 5 is the limiting factor here, as it has a lesser power than 2.
4. So, 25! will have 6 zeroes at the end. Hence, the hundred-thousands digit will be 0.
Answer A
A positive integer n has 3 prime factors. Is n odd?
(1) The total number of factors of n is odd.
(2) The prime factors of n when arranged in ascending order form an evenly spaced set.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'B'. Can you explain this answer?
A positive integer n has 3 prime factors. Is n odd?
(1) The total number of factors of n is odd.
(2) The prime factors of n when arranged in ascending order form an evenly spaced set.
(1) The total number of factors of n is odd.
(2) The prime factors of n when arranged in ascending order form an evenly spaced set.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Prisha Mukherjee answered |
Statement 1: The total number of factors of n is odd.
Statement 2: The prime factors of n when arranged in ascending order form an evenly spaced set.
To determine if n is odd, we need to determine if it has an odd number of prime factors. Let's analyze each statement separately:
Statement 1: The total number of factors of n is odd.
The total number of factors of n can be found by multiplying the exponents of its prime factors plus one. For example, if n = 2^a * 3^b * 5^c, then the total number of factors would be (a+1) * (b+1) * (c+1).
If the total number of factors is odd, it means that at least one of the exponents (a, b, or c) must be even. This is because when we add 1 to an even exponent, we get an odd number. However, if all three exponents are odd, then multiplying three odd numbers would result in an odd total number of factors.
Therefore, statement 1 alone is sufficient to answer the question.
Statement 2: The prime factors of n when arranged in ascending order form an evenly spaced set.
An evenly spaced set means that the difference between any two consecutive terms is the same. In this case, it means that the difference between the prime factors should be the same. For example, if the prime factors are 2, 5, and 8, the difference between consecutive terms is 3, which is the same.
However, knowing that the prime factors form an evenly spaced set does not provide any information about whether n is odd or even. We can have both odd and even numbers that satisfy this condition.
Therefore, statement 2 alone is not sufficient to answer the question.
Conclusion:
From the analysis above, we can conclude that statement 1 alone is sufficient to answer the question, while statement 2 alone is not. Therefore, the correct answer is option B.
Statement 2: The prime factors of n when arranged in ascending order form an evenly spaced set.
To determine if n is odd, we need to determine if it has an odd number of prime factors. Let's analyze each statement separately:
Statement 1: The total number of factors of n is odd.
The total number of factors of n can be found by multiplying the exponents of its prime factors plus one. For example, if n = 2^a * 3^b * 5^c, then the total number of factors would be (a+1) * (b+1) * (c+1).
If the total number of factors is odd, it means that at least one of the exponents (a, b, or c) must be even. This is because when we add 1 to an even exponent, we get an odd number. However, if all three exponents are odd, then multiplying three odd numbers would result in an odd total number of factors.
Therefore, statement 1 alone is sufficient to answer the question.
Statement 2: The prime factors of n when arranged in ascending order form an evenly spaced set.
An evenly spaced set means that the difference between any two consecutive terms is the same. In this case, it means that the difference between the prime factors should be the same. For example, if the prime factors are 2, 5, and 8, the difference between consecutive terms is 3, which is the same.
However, knowing that the prime factors form an evenly spaced set does not provide any information about whether n is odd or even. We can have both odd and even numbers that satisfy this condition.
Therefore, statement 2 alone is not sufficient to answer the question.
Conclusion:
From the analysis above, we can conclude that statement 1 alone is sufficient to answer the question, while statement 2 alone is not. Therefore, the correct answer is option B.
1727 has a units digit of:- a)1
- b)2
- c)3
- d)7
- e)9
Correct answer is option 'C'. Can you explain this answer?
1727 has a units digit of:
a)
1
b)
2
c)
3
d)
7
e)
9

|
Sreemoyee Nambiar answered |
To determine the units digit of a number, we only need to consider the last digit of the number. In this case, we need to find the units digit of 1727.
To find the units digit of a number, we divide it by 10 and check the remainder. The remainder will give us the units digit.
Dividing 1727 by 10:
Since the remainder is 7, the units digit of 1727 is 7. Therefore, the correct answer is option 'C'.
To find the units digit of a number, we divide it by 10 and check the remainder. The remainder will give us the units digit.
Dividing 1727 by 10:
- 1727 ÷ 10 = 172 remainder 7
Since the remainder is 7, the units digit of 1727 is 7. Therefore, the correct answer is option 'C'.
If x is a positive integer, what is the units digit of (24)(2x + 1)(33)(x + 1)(17)(x + 2)(9)(2x)?- a)4
- b)6
- c)7
- d)8
- e)9
Correct answer is option 'D'. Can you explain this answer?
If x is a positive integer, what is the units digit of (24)(2x + 1)(33)(x + 1)(17)(x + 2)(9)(2x)?
a)
4
b)
6
c)
7
d)
8
e)
9

|
Arjun Iyer answered |
For problems that ask for the units digit of an expression, yet seem to require too much computation, remember the Last Digit Shortcut. Solve the problem step-by-step, but recognize that you only need to pay attention to the last digit of every intermediate product. Drop any other digits.
So, we can drop any other digits in the original expression, leaving us to find the units digit of:
(4)(2x + 1)(3)(x + 1)(7)(x + 2)(9)(2x)
(4)(2x + 1)(3)(x + 1)(7)(x + 2)(9)(2x)
This problem is still complicated by the fact that we don’t know the value of x. In such situations, it is often a good idea to look for patterns. Let's see what happens when we raise the bases 4, 3, 7, and 9 to various powers. For example: 31 = 3, 32 = 9, 33 = 27, 34 = 81, 35 = 243, and so on. The units digit of the powers of three follow a pattern that repeats every fourth power: 3, 9, 7, 1, 3, 9, 7, 1, and so on. The patterns for the other bases are shown in the table below:

The patterns repeat at least every fourth term, so let's find the units digit of (4)(2x + 1)(3)(x + 1)(7)(x + 2)(9)(2x) for at least four consecutive values of x:
x = 1: units digit of (43)(32)(73)(92) = units digit of (4)(9)(3)(1) = units digit of 108 = 8
x = 2: units digit of (45)(33)(74)(94) = units digit of (4)(7)(1)(1) = units digit of 28 = 8
x = 3: units digit of (47)(34)(75)(96) = units digit of (4)(1)(7)(1) = units digit of 28 = 8
x = 4: units digit of (49)(35)(76)(98) = units digit of (4)(3)(9)(1) = units digit of 108 = 8
x = 1: units digit of (43)(32)(73)(92) = units digit of (4)(9)(3)(1) = units digit of 108 = 8
x = 2: units digit of (45)(33)(74)(94) = units digit of (4)(7)(1)(1) = units digit of 28 = 8
x = 3: units digit of (47)(34)(75)(96) = units digit of (4)(1)(7)(1) = units digit of 28 = 8
x = 4: units digit of (49)(35)(76)(98) = units digit of (4)(3)(9)(1) = units digit of 108 = 8
The units digit of the expression in the question must be 8.
Alternatively, note that x is a positive integer, so 2x is always even, while 2x + 1 is always odd. Thus,
(4)(2x + 1) = (4)(odd), which always has a units digit of 4
(9)(2x) = (9)(even), which always has a units digit of 1
(4)(2x + 1) = (4)(odd), which always has a units digit of 4
(9)(2x) = (9)(even), which always has a units digit of 1
That leaves us to find the units digit of (3)(x + 1)(7)(x + 2). Rewriting, and dropping all but the units digit at each intermediate step,
(3)(x + 1)(7)(x + 2)
= (3)(x + 1)(7)(x + 1)(7)
= (3 × 7)(x + 1)(7)
= (21)(x + 1)(7)
= (1)(x + 1)(7) = 7, for any value of x.
(3)(x + 1)(7)(x + 2)
= (3)(x + 1)(7)(x + 1)(7)
= (3 × 7)(x + 1)(7)
= (21)(x + 1)(7)
= (1)(x + 1)(7) = 7, for any value of x.
So, the units digit of (4)(2x + 1)(3)(x + 1)(7)(x + 2)(9)(2x) is (4)(7)(1) = 28, then once again drop all but the units digit to get 8.
The correct answer is D.
Chapter doubts & questions for Number System - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Number System - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily










