All questions of Ratio And Proportion for GMAT Exam
Can you explain the answer of this question below:According to the Boyle’s law, at a constant temperature, pressure of a definite mass of gas is inversely proportional to the volume. If the pressure is reduced by 20%, find the respective change in volume.
- A:
-33.33%
- B:
+25%
- C:
-25%
- D:
+33.33%
The answer is b.
According to the Boyle’s law, at a constant temperature, pressure of a definite mass of gas is inversely proportional to the volume. If the pressure is reduced by 20%, find the respective change in volume.
-33.33%
+25%
-25%
+33.33%
|
|
Ishan Chaudhary answered |
Arun has a certain amount of money in the denomination of 1 rupee and 10 rupee notes . T he number of 1 rupee notes multiplied by the number of 10 rupee notes is equal to the total money (in rupees) that he has. What is the total number of ten rupee notes that he can have?- a)11
- b)13
- c)15
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
|
|
Dhruv Verma answered |
Two-fifth of Anil’s salary is equal of Bhuvan’s salary and seven -ninth of Bhuvan’s salary is equal to Chandra’s salary. The sum of the salary of all of them is Rs 770. Which of the following is the salary of each?- a)300, 225, 250
- b)500, 425, 375
- c)450, 180, 140
- d)520, 610, 475
Correct answer is option 'C'. Can you explain this answer?
|
|
Anaya Patel answered |
A metal trader buys 2 kinds of silver foils, the ratio of their prices being 1:4. He sells the alloy at Rs 90 per kg so that he can make a profit of 20%. If the ratio of their quantities present in a alloy is 6:1 respectively, find the purchase price of the foil present in lesser quantity.
- a)Rs 52.5
- b)Rs 55
- c)Rs 47.5
- d)Rs 45
Correct answer is option 'A'. Can you explain this answer?

|
Arya Roy answered |

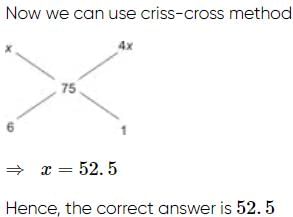
Anand and Bhavana have a few one rupee, 50 paise and 25 paise coins each. The total amount with each of them is Rs 5. The number of coins of two of the three types of coins that Anand has are equal and same is the case for the coins that Bhavana has. If Anand has the maximum possible total number of coins, then find the maximum possible total number of coins that Bhavana can have given that she has fewer coins than Anand.- a)16
- b)12
- c)10
- d)9
Correct answer is option 'B'. Can you explain this answer?
|
|
Nandita Kaur answered |
Can you explain the answer of this question below:The difference between the two positive numbers is 10 and the ratio between them is 5:3. Find the product of the two numbers.
- A:
375
- B:
325
- C:
275
- D:
125
The answer is a.
The difference between the two positive numbers is 10 and the ratio between them is 5:3. Find the product of the two numbers.
375
325
275
125

|
Subham Basu answered |
An alloy of manganese, tin and bronze contains 90% bronze, 7% manganese and 3% tin. A second alloy of bronze and tin is melted with the first and the mixture contains 85% of bronze, 5% of manganese and 10% of tin. What is the percentage of bronze in the second alloy?- a)67.5%
- b)72.5%
- c)77.5%
- d)82.5%
Correct answer is 'B'. Can you explain this answer?

|
Sameer Rane answered |
Can you explain the answer of this question below:A and B invest Rs 12,000 and Rs 16,000 respectively in a business. At the year-end, they share the profit in the ratio of 3:1. If A has invested his capital for the whole year, for how many months B has invested his capital?
- A:
4 months
- B:
3 months
- C:
6 months
- D:
8 months
The answer is b.
A and B invest Rs 12,000 and Rs 16,000 respectively in a business. At the year-end, they share the profit in the ratio of 3:1. If A has invested his capital for the whole year, for how many months B has invested his capital?
4 months
3 months
6 months
8 months
|
|
Saranya Kaur answered |
Gandhiji owns cows, some black and some white. He finds that 4 black cows and 3 white cows gave the same amount of milk in 5 days as 3 black cows and 5 white cows gave in 4 days. What is the ratio of milk given by a black cow in a day to that given by a white cow in a day?- a)8 : 5
- b)5 : 8
- c)3 : 5
- d)5 : 3
Correct answer is option 'B'. Can you explain this answer?

|
Janhavi Nambiar answered |
The sum of four numbers is 253. The ratio of the first number to the second number is 2:3. The ratio of the second number to the third number is 5:6. The ratio of the third number to the fourth number is 8:9. What is the average of the second number and the third number?- a)72
- b)132
- c)60
- d)66
Correct answer is option 'D'. Can you explain this answer?
|
|
Anaya Patel answered |
2nd no.= B , 3rd no.= C , 4th no. = D
A: B =2:3
A/B = 2/3
x/B =2/3
B= 3x/2
B:C=5:6
(3x/2)/ C= 5/6
C=( 6×3x)/2×5= 9x/5
C= 9x/5
C:D= 8:9
9x/5/ D = 8/9
D= (9x×9)/8×5= 81x/40
D= 81x/40
A+B+C+D= 253. (GIVEN)
x+ 3x/2+9x/5+81x/40
Lcm = 40
(40x+ 60x+ 72x+81x)/40= 253
253x= 253×40
X= (253×40)/253= 40
Ist no.(A)= X= 40
2no.(B)= 3x/2=( 3 × 40)/2= 60
3rd no.(C)= 9x/5 = (9×40)/5= 72
4th no.(D)= 81x/40=( 81×40/)/40= 81
Average of numbers= sum of observations/ total no.of observations
Average of 2nd no. & 3rd no.= (60+72)/2= 132/2= 66
Four numbers in the ratio of 1:3:4:7 add up to give a sum of 75. Find the value of the biggest number.- a)42
- b)35
- c)49
- d)63
Correct answer is option 'B'. Can you explain this answer?
|
|
Kavya Saxena answered |
15x = 75
x = 75/15
x = 5
So, 1x = 1*5 = 5
3x = 3*5 = 15
4x = 4*5 = 20
7x = 7*5 = 35
Bidhan is planning to buy a bike worth Rs 35,000, provided his brother agrees to lend him 3/2 times the money. Bidhan contributes and the financer provides 3 times the brother’s contribution. How much does Bidhan’s brother contribute?- a)5,000
- b)7,500
- c)10,000
- d)7,000
Correct answer is option 'B'. Can you explain this answer?
|
|
Nikita Singh answered |
The sum of the ages of the 4 members of Sinha family is 140 years. 5 years ago the ages of the 4 members Nishu, Vicky, Mrs Sinha and Mr Sinha were in the ratio of 2 : 3 : 7 : 8 . After how many years would Nishu be as old as the present age of his mother?- a)10yrs
- b)17yrs
- c)30 yrs
- d)32 yrs
Correct answer is option 'C'. Can you explain this answer?
|
|
Lavanya Menon answered |
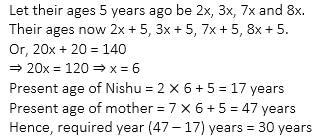
A and B invested Rs 12,000 and Rs 18,000 respectively in a business for the whole year. At the year-end, there was a total profit of Rs 2,000. What is the share of A in the profit?- a)Rs 800
- b)Rs 1,200
- c)Rs 1,600
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
|
|
Advait Saini answered |
A and B have invested different amounts in a business:
- A's investment: Rs 12,000
- B's investment: Rs 18,000
Total Investment
- Total investment by both A and B = Rs 12,000 + Rs 18,000 = Rs 30,000
Profit Distribution
The total profit at the year-end is Rs 2,000. The profit is shared based on the ratio of their investments.
Calculating the Ratio
- A's investment = Rs 12,000
- B's investment = Rs 18,000
- Ratio of A’s investment to B’s investment = 12,000 : 18,000
To simplify:
- Divide both sides by 6
- A : B = 2 : 3
Finding A's Share in Profit
To determine A's share in the profit, we first calculate the total parts in the ratio. The total parts = 2 (for A) + 3 (for B) = 5 parts.
Next, we find out how much each part is worth:
- Value of each part = Total Profit / Total Parts = Rs 2,000 / 5 = Rs 400
Now, we can calculate A's share:
- A's share = 2 parts * Value of each part = 2 * Rs 400 = Rs 800
Conclusion
Thus, A's share in the profit is Rs 800, which corresponds to option 'A'.
Anil started a manufacturing unit with a certain amount of money. After a few months, Dheeraj became his partner, contributing three times of what Anil had contributed. At the end of the year, each was entitled to half the total profit. If Anil started the unit in January, then when did Dheeraj join as a partner?- a)August
- b)September
- c)July
- d)October
Correct answer is option 'B'. Can you explain this answer?

|
Shraddha Dasgupta answered |

In a fort there are 1600 soldiers fighting a battle against their enemy. On a particular day after their morning meal the balance provision inside the fort is only sufficient for 12 days at the rate of 1.2 kg per day. If by the evening 400 soldiers die then for how many days will the provision be sufficient for remaining men at the rate of 1.6 kg per day. (Assume soldiers eat either in morning or in evening).- a)10
- b)8
- c)18
- d)12
Correct answer is option 'D'. Can you explain this answer?
|
|
Alok Verma answered |
= (1600) (12) (1.2)
Total number of soldiers left at the end of the day 1200
Now we have to calculate that for how long is available provision enough for the left-out soldiers
(1200) (x) (1.6)
(1600) (12) (1.2) = (1200) (x) (1.6)
Solving it for the value of x
We get x = 12
The provision is sufficient for 1200 soldiers for 12 days.
A certain investment grows at an annual interest rate of 8%, compounded quarterly. Which of the following equations can be solved to find the number of years, x, that it would take for the investment to increase by a factor of 16?- a)16 = (1.02)x/4
- b)2 = (1.02)x
- c)16 = (1.08)4x
- d)2 = (1.02)x/4
- e)1/16 = (1.02)4x
Correct answer is option 'B'. Can you explain this answer?

|
Hridoy Desai answered |
The given investment grows at an annual interest rate of 8% compounded quarterly. We need to find the equation that can be solved to determine the number of years it would take for the investment to increase by a factor of 16.
Understanding Compound Interest:
Compound interest is calculated using the formula:
A = P(1 + r/n)^(nt)
Where:
A = the final amount
P = the principal amount (initial investment)
r = annual interest rate (as a decimal)
n = number of times interest is compounded per year
t = number of years
In this case, the interest is compounded quarterly, so n = 4.
Approach:
To find the equation that can be solved for the number of years, we need to set up the equation using the given information.
Solution:
Let's analyze each option and see which one fits our requirements:
a) 16 = (1.02)^(x/4)
This equation does not have the factor of 16 on the right side, so it cannot be solved to find the number of years.
b) 2 = (1.02)^x
This equation has the factor of 16 on the right side (2^4 = 16), so it can be solved to find the number of years.
c) 16 = (1.08)^(4x)
This equation has the interest rate of 8% compounded annually, which does not match the given information. Therefore, it cannot be solved to find the number of years.
d) 2 = (1.02)^(x/4)
This equation does not have the factor of 16 on the right side, so it cannot be solved to find the number of years.
e) 1/16 = (1.02)^(4x)
This equation has the factor of 16 on the left side (1/16 = (1/2)^4), but it does not match the given interest rate of 8% compounded quarterly. Therefore, it cannot be solved to find the number of years.
Conclusion:
Out of the given options, only option b) 2 = (1.02)^x fits the requirements and can be solved to find the number of years it would take for the investment to increase by a factor of 16.
Read the passage below and solve the questions based on it.
A book having pages between 4,000 and 5,000 is divided into four parts, each part being divided into chapters. The total number of pages in each of the four parts is the same. The ratio of the chapters across all the parts is 6:5:10:14. The number of chapters in the fourth part is 70
Q.What is the total number of pages in the book?
- a)4,000
- b)4,800
- c)4,200
- d)4,600
Correct answer is option 'C'. Can you explain this answer?
A book having pages between 4,000 and 5,000 is divided into four parts, each part being divided into chapters. The total number of pages in each of the four parts is the same. The ratio of the chapters across all the parts is 6:5:10:14. The number of chapters in the fourth part is 70

|
Palak Yadav answered |
► Now in D there are 70 chapters
Therefore, A:B:C:D = 30:25:50:70 [ Multiplying Each by 5 ]
L.C.M of 30, 25, 50, 70 is 1050
So each part should have 1050 pages.
So total pages = 4 x 1050 = 4200 ans.
Can you explain the answer of this question below:Two cogged wheels of which one has 32 cogs and other 54 cogs, work into each other. If the latter turns 80 times in three quarter of a minute, how often does the other turn in 8 seconds? (Assume equal size cogs and equi-spaced).
- A:
24
- B:
16
- C:
32
- D:
8
The answer is a.
Two cogged wheels of which one has 32 cogs and other 54 cogs, work into each other. If the latter turns 80 times in three quarter of a minute, how often does the other turn in 8 seconds? (Assume equal size cogs and equi-spaced).
24
16
32
8

|
Dhruv Mehra answered |
Jim needs $1,000 to buy a new flat-screen TV. Since he has only $7, he borrows the remanining balance from his sister Mary. The loan will be repaid in 3 annual installments at an interest rate of 10%, compounded annually. The formula for calculating the monthly payment P is P = (L x C x r) / (C – 1) where L = amount of the loan, r = annual interest rate, and C = compounding factor = (1 + r)N where N = number of annual payments. How much does Jim have to pay Mary at the end of each of the next 3 years (rounded to the nearest penny)?- a)$357.67
- b)$375.85
- c)$387.40
- d)$399.30
- e)$433.33
Correct answer is option 'D'. Can you explain this answer?

|
Jatin Kapoor answered |
L = amount of the loan = 1000 – 7 = 993
r = annual interest rate = 10% = 0.1
C = compounding factor = (1 + r)N = (1.1)3 = (1.1)(1.1)(1.1) = 1.21(1.1) = 1.331
Hence P = (993 x 1.331 x 0.1) / (1.331 – 1) = (993 x 1.331 x 0.1) / 0.331 = (993/.331) x 1.331 x 0.1.
Note that 993 is an integral multiple of 0.331 and 993/0.331 = 993000/331 = 3000.
Hence P = (993/0.331) x 1.331 x 0.1 = 3000 x 1.331 x 0.1 = 399.30
The correct answer is D.
Louie takes out a three-month loan of $1000. The lender charges him 10% interest per month compounded monthly. The terms of the loan state that Louie must repay the loan in three equal monthly payments. To the nearest dollar, how much does Louie have to pay each month?- a)333
- b)383
- c)402
- d)433
- e)483
Correct answer is option 'C'. Can you explain this answer?

|
Navya Yadav answered |
i = monthly interest rate = 10% = 0.1
c = compound growth rate = 1 + i = 1.1
x = monthly payment (to be calculated)
Balance after month 1: Pc – x
Balance after month 2: [Pc – x]c – x = Pc2 – x(c+1)
Balance after month 3: [Pc2 - x(c+1)]c - x = Pc3 - x(c2+c+1)
x(c2+c+1) = Pc3
x = (Pc3) / (c2+c+1) Note that c = 1.1; c2 = 1.21; c3 = 1.331
x = 1331 / 3.31
A man has rs.480 in the denominations of one-rupee notes, five-rupee notes and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has ?- a)100
- b)50
- c)78
- d)90
Correct answer is option 'D'. Can you explain this answer?
|
|
Aisha Gupta answered |
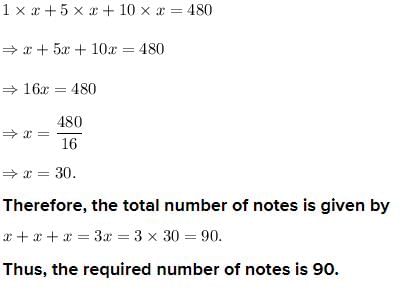
A is proportional to B. B is inversely proportional to C. C is proportional to the square of D. D is directly proportional to the cube root of E. Assuming positive integers, if A increases then E- a)Increases
- b)Decreases
- c)Cannot say
- d)Could increase or decrease
Correct answer is option 'B'. Can you explain this answer?

|
Akanksha Datta answered |
Three friends A, B and C started a venture with capitals in the ratio of 4:1:15. At the end of every quarter A halves his capital, while B doubles his capital and C leaves his capital untouched. This process is repeated till the end of the year. If at the end of the year B ’ s share of the profit is Rs 22,000, what is the total profit?
- a)Rs 88,000
- b)Rs 1,10,000
- c)Rs 2,25,000
- d)Rs 1,21,000
Correct answer is option 'D'. Can you explain this answer?

|
Bhavya Saha answered |
Read the passage below and solve the questions based on it.
There are certain number of apples, guavas and oranges in a basket. The number of each variety is more than one. The ratio of the number of apples to the number of guavas is equal to the ratio of the number of guavas lo the number of oranges.Q.If the total number of fruits is 61, then find the number of guavas.- a)16
- b)20
- c)25
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
There are certain number of apples, guavas and oranges in a basket. The number of each variety is more than one. The ratio of the number of apples to the number of guavas is equal to the ratio of the number of guavas lo the number of oranges.

|
Akanksha Datta answered |
Now start using the options.
Option (b) satisfies the relationship (16/20 = 20/25)
The ratio of the age of Sita and her mother is 2:3. N years from now, ratio of their ages will become 3:5. What is the value of N?- a)Infinite
- b)1
- c)More than 1 but finite
- d)Not possible
Correct answer is option 'D'. Can you explain this answer?
|
|
Aarav Sharma answered |
The ratio of the age of Sita and her mother is 2:3.
N years from now, the ratio of their ages will become 3:5.
To find:
The value of N.
Solution:
Let's assume the current ages of Sita and her mother to be 2x and 3x respectively (since the ratio of their ages is given as 2:3).
After N years, the age of Sita will be 2x + N and the age of her mother will be 3x + N.
According to the given condition, the ratio of their ages after N years will be 3:5.
Therefore, we can write the equation as:
(2x + N) / (3x + N) = 3/5
Cross-multiplying, we get:
5(2x + N) = 3(3x + N)
10x + 5N = 9x + 3N
(10x - 9x) = (3N - 5N)
x = -2N
Since x represents the age, it cannot be negative. Hence, the equation does not have a valid solution.
Therefore, it is not possible to determine the value of N that satisfies both conditions.
Answer:
The value of N is not possible.
P works twice as fast as Q, whereas P and Q together can work three times as fast as R. If P, Q and R together work on a job, in what ratio should they share the earnings?- a)2:1:1
- b)4:2:1
- c)4:3:2
- d)4:2:3
Correct answer is option 'A'. Can you explain this answer?

|
Akanksha Datta answered |
Hence, earning should be distributed in the ratio of their efficiency, i.e., 2 : 1 : 1.
Jolene entered an 18-month investment contract that guarantees to pay 2 percent interest at the end of 6 months, another 3 percent interest at the end of 12 months, and 4 percent interest at the end of the 18 month contract. If each interest payment is reinvested in the contract, and Jolene invested $10,000 initially, what will be the total amount of interest paid during the 18-month contract?- a)$ 506.00
- b)$726.24
- c)$900.00
- d)$920.24
- e)$926.24
Correct answer is option 'E'. Can you explain this answer?

|
Navya Yadav answered |
$10,000 (initial investment)
+ $200 (1% interest on $10,000 principal
= $100, so 2% = 2 × $100) = $10,200
⇒ $10,200 + $306 (1% interest on $10,200 principal = $102, so 3% = 3 × $102) = $10,506
⇒ + $420.24 (1% interest on $10,506 principal = $105.06, so 4% = 4 × $105.06) = $10,926.24
The final value is $10,926.24 after an initial investment of $10,000. Thus, the total amount of interest paid is $926.24 (the difference between the final value and the amount invested).
The correct answer is E.
Donald plans to invest x dollars in a savings account that pays interest at an annual rate of 8% compounded quarterly. Approximately what amount is the minimum that Donald will need to invest to earn over $100 in interest within 6 months?- a)$1500
- b)$1750
- c)$2000
- d)$2500
- e)$3000
Correct answer is option 'D'. Can you explain this answer?

|
Navya Yadav answered |
P = principal investment
r = interest rate (annual)
n = number of times per year interest is compounded
t = number of years
2500 = x
A man has 25 paise, 50 paise and 1 Rupee coins. There are 220 coins in all and the total amount is 160. If there are thrice as many 1 Rupee coins as there are 25 paise coins, then what is the number of 50 paise coins?- a)60
- b)80
- c)100
- d)120
Correct answer is option 'A'. Can you explain this answer?
|
|
Rajeev Kumar answered |
The first, second and third class fares between two railway stations, Patna and Lucknow were 10:8:3 and the number of first, second and third class passengers between the two stations was is 3:4:10. If total sales of the ticket is Rs 16,100, find the money obtained by the sales of second class tickets.- a)Rs 5,250
- b)Rs 5,600
- c)Rs 6,400
- d)Rs 6,650
Correct answer is option 'B'. Can you explain this answer?
|
|
Aarav Sharma answered |
Given information:
- The ratio of first, second, and third class fares between Patna and Lucknow is 10:8:3.
- The ratio of first, second, and third class passengers between the two stations is 3:4:10.
- The total sales of tickets is Rs 16,100.
Step 1: Calculate the total ratio of fares.
The total ratio of fares can be found by adding up the individual ratios: 10 + 8 + 3 = 21.
Step 2: Calculate the proportion of each fare.
To find the proportion of each fare, divide each individual fare ratio by the total ratio of fares:
First class fare proportion = 10/21
Second class fare proportion = 8/21
Third class fare proportion = 3/21
Step 3: Calculate the total sales from each fare.
To find the total sales from each fare, multiply the total sales by the proportion of each fare:
Total sales from first class fare = (10/21) * Rs 16,100
Total sales from second class fare = (8/21) * Rs 16,100
Total sales from third class fare = (3/21) * Rs 16,100
Step 4: Calculate the money obtained by the sales of second class tickets.
From step 3, we can see that the total sales from second class fare is:
Total sales from second class fare = (8/21) * Rs 16,100
Simplifying this expression, we get:
Total sales from second class fare = Rs 5,600
Therefore, the money obtained by the sales of second class tickets is Rs 5,600, which corresponds to option B.
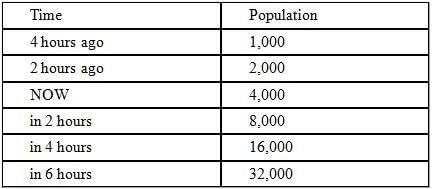
The population of locusts in a certain swarm doubles every two hours. If 4 hours ago there were 1,000
locusts in the swarm, in approximately how many hours will the swarm population exceed 250,000 locusts?- a)6
- b)8
- c)10
- d)12
- e)14
Correct answer is option 'D'. Can you explain this answer?
locusts in the swarm, in approximately how many hours will the swarm population exceed 250,000 locusts?

|
Navya Yadav answered |

Wes works at a science lab that conducts experiments on bacteria. The population of the bacteria multiplies at a constant rate, and his job is to notate the population of a certain group of bacteria each hour. At 1 p.m. on a certain day, he noted that the population was 2,000 and then he left the lab. He returned in time to take a reading at 4 p.m., by which point the population had grown to 250,000. Now he has to fill in the missing data for 2 p.m. and 3 p.m. What was the population at 3 p.m.?- a)50000
- b)62500
- c)65000
- d)86666
- e)125000
Correct answer is option 'A'. Can you explain this answer?

|
Jatin Kapoor answered |
2,000(x3) = 250,000
x3 = 250,000/2,000 = 125
x = 5
An investor purchased a share of non-dividend-paying stock for p dollars on Monday. For a certain number of days, the value of the share increased by r percent per day. After this period of constant increase, the value of the share decreased the next day by q dollars and the investor decided to sell the share at the end of that day for v dollars, which was the value of the share at that time. How many working days after the investor bought the share was the share sold, if
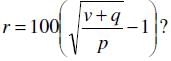
- a)Two working days later.
- b)Three working days later.
- c)Four working days later.
- d)Five working days later.
- e)Six working days later.
Correct answer is option 'B'. Can you explain this answer?
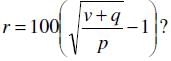

|
Navya Yadav answered |
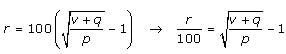

→
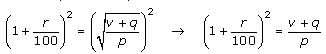
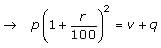
→
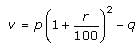
Let’s compare this simplified equation to the compound interest formula. Notice that r in this simplified equation (and in the question) is not the same as the r in the compound interest formula. In the formula, the r is already expressed as a decimal equivalent of a percent, in the question the interest is r percent. The simplified equation, however, deals with this discrepancy by dividing r by 100.
In our simplified equation, the cost of the share of stock (p), corresponds to the principal (P) in the formula, and the final share price (v) corresponds to the final value (F) in the formula. Notice also that the exponent 2 corresponds to the x in the formula, which is the number of compounding periods. By comparing the simplified equation to the compound interest formula, we see that the equation tells us that the share rose at the daily interest rate of p percent for TWO days. Then the share lost a value of q dollars on the third day, i.e. the “– q” portion of the expression. If the investor bought the share on Monday, she sold it three days later on Thursday.
The correct answer is B.
Chapter doubts & questions for Ratio And Proportion - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|

Contact Support
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|














