All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Time and Work for GMAT Exam
If ‘x’ men can finish ‘x’ similar projects in ‘x’ days, then in how many days can ‘2x’ men can finish ‘2x’ similar projects? Assume that each man works with same efficiency.- a)x/2
- b)x
- c)3x/2
- d)2x
- e)5x/2
Correct answer is option 'B'. Can you explain this answer?
If ‘x’ men can finish ‘x’ similar projects in ‘x’ days, then in how many days can ‘2x’ men can finish ‘2x’ similar projects? Assume that each man works with same efficiency.
a)
x/2
b)
x
c)
3x/2
d)
2x
e)
5x/2

|
Pallabi Sengupta answered |
Solution:
Given, x men can finish x similar projects in x days.
Let's assume that each man will take 1 day to complete one project. (The efficiency of each man is the same).
So, x men can complete x projects in x days.
Therefore, 1 man can complete 1 project in x days.
Now, we need to find the number of days taken by 2x men to complete 2x similar projects.
Let's solve this using the formula "Men, days and work done".
Men, days and work done:
In the case of Men, days and work done, the formula is given as:
Men1 × Days1 × Work1 = Men2 × Days2 × Work2
where,
Men1, Men2 are the number of men in the first and second cases respectively.
Days1, Days2 are the number of days taken in the first and second cases respectively.
Work1, Work2 are the amount of work done in the first and second cases respectively.
Using the above formula, we can solve the problem.
Let's assume that 2x men can complete 2x projects in y days.
So, we have,
x × x × x = 2x × y × 2x
x^2 = 4xy
y = x/4
Therefore, 2x men can complete 2x similar projects in x/4 days.
Hence, the correct option is (B) x.
Given, x men can finish x similar projects in x days.
Let's assume that each man will take 1 day to complete one project. (The efficiency of each man is the same).
So, x men can complete x projects in x days.
Therefore, 1 man can complete 1 project in x days.
Now, we need to find the number of days taken by 2x men to complete 2x similar projects.
Let's solve this using the formula "Men, days and work done".
Men, days and work done:
In the case of Men, days and work done, the formula is given as:
Men1 × Days1 × Work1 = Men2 × Days2 × Work2
where,
Men1, Men2 are the number of men in the first and second cases respectively.
Days1, Days2 are the number of days taken in the first and second cases respectively.
Work1, Work2 are the amount of work done in the first and second cases respectively.
Using the above formula, we can solve the problem.
Let's assume that 2x men can complete 2x projects in y days.
So, we have,
x × x × x = 2x × y × 2x
x^2 = 4xy
y = x/4
Therefore, 2x men can complete 2x similar projects in x/4 days.
Hence, the correct option is (B) x.
A rectangular reservoir is filled with water till one-fifth of the height of the reservoir. If an outlet at the bottom of the reservoir is unplugged, the water in the reservoir will drain completely in 1 hour. If the outlet remains plugged and the inlet tap at the head of the reservoir is opened, the reservoir will fill to the brim in 2 hours. In how much time will the reservoir fill to the brim if the outlet is unplugged 30 minutes after the inlet tap is opened?- a)3 hours
- b)3 hours 30 minutes
- c)4 hours 30 minutes
- d)5 hours
- e)The reservoir will never be filled to the brim
Correct answer is option 'B'. Can you explain this answer?
A rectangular reservoir is filled with water till one-fifth of the height of the reservoir. If an outlet at the bottom of the reservoir is unplugged, the water in the reservoir will drain completely in 1 hour. If the outlet remains plugged and the inlet tap at the head of the reservoir is opened, the reservoir will fill to the brim in 2 hours. In how much time will the reservoir fill to the brim if the outlet is unplugged 30 minutes after the inlet tap is opened?
a)
3 hours
b)
3 hours 30 minutes
c)
4 hours 30 minutes
d)
5 hours
e)
The reservoir will never be filled to the brim
|
|
Priya Singhania answered |
Given:
- Let the length and the breadth (of the base) of the reservoir be L and B, and let its height be H
- Time taken to drain the water in the reservoir is 1 hour
- Time taken to fill the reservoir completely (when V/5 water is already there) is 2 hours
To Find: Time taken to fill the reservoir if outlet is unplugged 30 minutes after inlet is opened
Approach:
- Here, 30 minutes is the time for which only the inlet pipe is opened
- (Volume that remains to be filled after 30 minutes of inlet) = (Volume that initially needed to be filled) – (Volume of water pumped in through the inlet in 30 minutes)
- And, Net Rate of Filling = Rate of Filling – Rate of Draining
Working out:
- Finding the Volume that Remains to be filled after 30 minutes of inlet
- (Volume that remains to be filled after 30 minutes of inlet) = (Volume that initially needed to be filled) – (Volume of water pumped in through the inlet in 30 minutes)
Looking at the answer choices, we see that the correct answer is Option B
Lindsay can paint 1/x of a certain room in 20 minutes. What fraction of the same room can Joseph paint in 20 minutes if the two of them can paint the room in an hour, working together at their respective rates?- a)1/3x
- b)3x/(x – 3)
- c)(x – 3) / 3x
- d)x / (x – 3)
- e)(x – 3) / x
Correct answer is option 'C'. Can you explain this answer?
Lindsay can paint 1/x of a certain room in 20 minutes. What fraction of the same room can Joseph paint in 20 minutes if the two of them can paint the room in an hour, working together at their respective rates?
a)
1/3x
b)
3x/(x – 3)
c)
(x – 3) / 3x
d)
x / (x – 3)
e)
(x – 3) / x

|
Sharmila Singh answered |
We can solve this problem as a VIC (Variable In answer Choice) and plug in values for the variable x. Let’s say x = 6. (Note that there is a logical restriction here in terms of the value of x. Lindsay has to have a rate of less than less than 1 room per hour if she needs Joseph’s help to finish in an hour).
If Lindsay can paint 1/6 of the room in 20 minutes (1/3 of an hour), her rate is 1/2.
rt = w
r(1/3) = 1/6
r = 1/2
rt = w
r(1/3) = 1/6
r = 1/2
Let J be the number of hours it takes Joseph to paint the entire room. Joseph’s rate then is 1/J. Joseph and Lindsay’s combined rate is 1/2 + 1/J, which can be simplified:
1/2 + 1/J → J / 2J + 2 / 2J → (J + 2) / 2J
1/2 + 1/J → J / 2J + 2 / 2J → (J + 2) / 2J
If the two of them finish the room in one hour, using the formula of rt = w, we can solve for J.
rt = w and t = 1 (hour), w = 1 (job)
((J + 2) / 2J )(1) = 1 → J + 2 = 2J → J =2
That means that Joseph’s rate is 1/2, the same as Lindsay’s. The question though asks us what fraction of the room Joseph would complete in 20 minutes, or 1/3 of an hour.
rt = w
(1/2)(1/3) = w
w = 1/6
rt = w and t = 1 (hour), w = 1 (job)
((J + 2) / 2J )(1) = 1 → J + 2 = 2J → J =2
That means that Joseph’s rate is 1/2, the same as Lindsay’s. The question though asks us what fraction of the room Joseph would complete in 20 minutes, or 1/3 of an hour.
rt = w
(1/2)(1/3) = w
w = 1/6
Now we must look at the answer choices to see which one is equal to 1/6 when we plug in x = 6. Only C works: (6 – 3) / 18 = 1/6.
The correct answer is C.
Suzy and Marie decide to help Leslie with her thesis. Suzy can type 3 chapters per hour, Leslie can type 5 chapters per hour, and Marie can type 6 chapters per hour. If the thesis contains 28 chapters, how many hours with it take the three of them, working together, to complete the thesis?- a)1/2
- b)3/4
- c)1
- d)2
- e)14/3
Correct answer is option 'D'. Can you explain this answer?
Suzy and Marie decide to help Leslie with her thesis. Suzy can type 3 chapters per hour, Leslie can type 5 chapters per hour, and Marie can type 6 chapters per hour. If the thesis contains 28 chapters, how many hours with it take the three of them, working together, to complete the thesis?
a)
1/2
b)
3/4
c)
1
d)
2
e)
14/3

|
Avantika Sengupta answered |
Step 1: Question statement and Inferences
The question asks for the amount of time that the three friends, working together at their respective rates, will take to complete the thesis. You are given the rates of each friend, and you can infer that the rates are consistent. In other words, the women typing will consistently complete the same number of chapters per hour.
Step 2: Finding required values
Use the rates that the three friends type. Per each hour, Suzy, Marie, and Leslie type 3, 5, and 6 chapters each, respectively. The thesis contains 28 chapters total.
Step 3: Calculating the final answer
In the first hour working together, Suzy, Marie, and Leslie type 3, 5, and 6 chapters each, thus typing a total of 14 chapters together. In the second hour, they type the same number of chapters, for a total of 14. At the end of this second hour, they have typed 28 chapters, which is the entire thesis.
Working together, it will take the three friends 2 hours to type the thesis.
Answer: Option (D)
In how many days can 12 men and 15 women complete a job, if 8 men can do the same job in 12 days? Assume the rate of working of all men is same and rate of working of all women is same.(1) 20 women can do the same job in 10 days.(2) 24 men and 5 women can complete the same job in 40/11 days.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
In how many days can 12 men and 15 women complete a job, if 8 men can do the same job in 12 days? Assume the rate of working of all men is same and rate of working of all women is same.
(1) 20 women can do the same job in 10 days.
(2) 24 men and 5 women can complete the same job in 40/11 days.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Manasa Gupta answered |
The question is asking how long it would take 12 men and 15 women to complete a certain job. It tells you that 8 men complete this job in 12 days.
Let the total amount of work involved in completing the job be W.
Work done by 8 men in 12 days = W
Work done by 8 men in 1 day = W/12
Work done by 1 man in 1 day = W/96 . . . Equation 1
So, work done by 12 men in 1 day = 12W/96 = W/8
Let one woman working alone complete the job in d days.
So, work done by 1 woman in 1 day =W/d . . . Equation 2
So, work done by 15 women in 1 day = 15W/d
Work done by 12 men and 15 women working together in 1 day = W/8 + 15W/d=(1/8+15/d)W
Once we know the value of d, we will be able to know the value of the coefficient of w in the above equation.
The reciprocal of this coefficient will be equal to the total time taken by 12 men and 15 women to complete the task.
So, we need to find the value of d.
Step 3: Analyze Statement 1
20 women can do the same job in 10 days.
Work done by 20 women in 10 days = W
Work done by 20 women in 1 day = W/10
Work done by 1 woman in 1 day =W/200 . . . Equation 3
Comparing Equation 3 with Equation 2:
d=200
Thus, Statement 1 is sufficient to arrive at a unique value of the time taken by 12 men and 15 women
to complete the job
Step 4: Analyze Statement 2
24 men and 5 women can complete the same job in 40/11 days.
Work done by 24 men and 5 women in 40/11 days = W
Work done by 24 men and 5 women in 1 day =
Using Equations 1 and 2 we can write:
Thus, we have a linear equation in d.
By solving this equation, we will be able to find the value of d
Thus, Statement 2 too is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
You get unique answers in steps 3 and 4, so this step is not required
Answer: Option (D)
A copy machine, working at a constant rate, makes 35 copies per minute. A second copy machine, working at a constant rate, makes 55 copies per minute. Working together at their respective rates, how many copies do the two machines make in half an hour?- a)90
- b)2700
- c)4500
- d)5400
- e)324000
Correct answer is option 'B'. Can you explain this answer?
A copy machine, working at a constant rate, makes 35 copies per minute. A second copy machine, working at a constant rate, makes 55 copies per minute. Working together at their respective rates, how many copies do the two machines make in half an hour?
a)
90
b)
2700
c)
4500
d)
5400
e)
324000

|
Arnab Kumar answered |
To find the total number of copies made by both machines in half an hour, we need to calculate the combined rate at which they work.
1. Calculate the rate of the first copy machine:
The first copy machine makes 35 copies per minute.
2. Calculate the rate of the second copy machine:
The second copy machine makes 55 copies per minute.
3. Calculate the combined rate of both machines:
To calculate the combined rate, we add the rates of both machines.
Combined rate = Rate of machine 1 + Rate of machine 2
Combined rate = 35 copies/minute + 55 copies/minute
Combined rate = 90 copies/minute
4. Calculate the total number of copies made in half an hour:
Since there are 60 minutes in an hour, half an hour would be 30 minutes.
To find the total number of copies made in half an hour, we multiply the combined rate by the number of minutes.
Total copies made = Combined rate * Number of minutes
Total copies made = 90 copies/minute * 30 minutes
Total copies made = 2700 copies
Therefore, the two copy machines make a total of 2700 copies in half an hour. Hence, the correct answer is option B) 2700.
1. Calculate the rate of the first copy machine:
The first copy machine makes 35 copies per minute.
2. Calculate the rate of the second copy machine:
The second copy machine makes 55 copies per minute.
3. Calculate the combined rate of both machines:
To calculate the combined rate, we add the rates of both machines.
Combined rate = Rate of machine 1 + Rate of machine 2
Combined rate = 35 copies/minute + 55 copies/minute
Combined rate = 90 copies/minute
4. Calculate the total number of copies made in half an hour:
Since there are 60 minutes in an hour, half an hour would be 30 minutes.
To find the total number of copies made in half an hour, we multiply the combined rate by the number of minutes.
Total copies made = Combined rate * Number of minutes
Total copies made = 90 copies/minute * 30 minutes
Total copies made = 2700 copies
Therefore, the two copy machines make a total of 2700 copies in half an hour. Hence, the correct answer is option B) 2700.
Tom, working alone, can paint a room in 6 hours. Peter and John, working independently, can paint the same room in 3 hours and 2 hours, respectively. Tom starts painting the room and works on his own for one hour. He is then joined by Peter and they work together for an hour. Finally, John joins them and the three of them work together to finish the room, each one working at his respective rate. What fraction of the whole job was done by Peter?- a)1/9
- b)1/6
- c)1/3
- d)7/18
- e)4/9
Correct answer is option 'E'. Can you explain this answer?
Tom, working alone, can paint a room in 6 hours. Peter and John, working independently, can paint the same room in 3 hours and 2 hours, respectively. Tom starts painting the room and works on his own for one hour. He is then joined by Peter and they work together for an hour. Finally, John joins them and the three of them work together to finish the room, each one working at his respective rate. What fraction of the whole job was done by Peter?
a)
1/9
b)
1/6
c)
1/3
d)
7/18
e)
4/9

|
Janani Sharma answered |
Peter's individual rate is 1 job / 3 hours.
Peter joins Tom and they work together for another hour; Peter and Tom's respective individual rates can be added together to calculate their combined rate: 1/6 + 1/3 = 1/2.
Working together then they will complete 1/2 of the job in the 1 hour they work together.
Peter joins Tom and they work together for another hour; Peter and Tom's respective individual rates can be added together to calculate their combined rate: 1/6 + 1/3 = 1/2.
Working together then they will complete 1/2 of the job in the 1 hour they work together.
At this point, 2/3 of the job has been completed (1/6 by Peter alone + 1/2 by Peter and Tom), and 1/3 remains.
When John joins Tom and Peter, the new combined rate for all three is: 1/6 + 1/3 + 1/2 = 1.
The time that it will take them to finish the remaining 1/3 of the job can be solved:
rt = w → (1)(t) = 1/3 → t = 1/3.
The question asks us for the fraction of the job that Peter completed. In the hour that Peter worked with Tom he alone completed: rt = w → w = (1/3)(1) = 1/3 of the job.
In the last 1/3 of an hour that all three worked together, Peter alone completed:
(1/3)(1/3) = 1/9 of the job.
Adding these two values together, we get 1/3 + 1/9 of the job = 4/9 of the job.
The time that it will take them to finish the remaining 1/3 of the job can be solved:
rt = w → (1)(t) = 1/3 → t = 1/3.
The question asks us for the fraction of the job that Peter completed. In the hour that Peter worked with Tom he alone completed: rt = w → w = (1/3)(1) = 1/3 of the job.
In the last 1/3 of an hour that all three worked together, Peter alone completed:
(1/3)(1/3) = 1/9 of the job.
Adding these two values together, we get 1/3 + 1/9 of the job = 4/9 of the job.
The correct answer is E.
A rectangular tank has the dimensions of its base as 30 metres by 20 metres and a height of 10 metres. There are two taps attached to the tank such that each tap working alone at a constant rate can fill the tank completely in 60 hours and 90 hours respectively. One of the walls of the tank has holes along the height of the tank at a regular distance of 2 metres and the first such hole is 2 metres above the base of the tank. The rate of water outflow from each hole is 10m per hour. If both the taps are opened simultaneously in the empty tank, approximately how many hours will it take to fill the tank completely?- a)36
- b)42
- c)48
- d)54
- e)60
Correct answer is option 'B'. Can you explain this answer?
A rectangular tank has the dimensions of its base as 30 metres by 20 metres and a height of 10 metres. There are two taps attached to the tank such that each tap working alone at a constant rate can fill the tank completely in 60 hours and 90 hours respectively. One of the walls of the tank has holes along the height of the tank at a regular distance of 2 metres and the first such hole is 2 metres above the base of the tank. The rate of water outflow from each hole is 10m per hour. If both the taps are opened simultaneously in the empty tank, approximately how many hours will it take to fill the tank completely?
a)
36
b)
42
c)
48
d)
54
e)
60
|
|
Disha Ahuja answered |
Given data:
Dimensions of the tank: Length = 30m, Width = 20m, Height = 10m
Rate of filling the tank by tap 1 = 1/60 of the tank per hour
Rate of filling the tank by tap 2 = 1/90 of the tank per hour
Rate of water outflow from each hole = 10m per hour
Distance between holes = 2m
First hole is 2m above the base of the tank
To find: Time taken to fill the tank completely when both taps are opened simultaneously
Let's calculate the volume of the tank:
Volume = Length × Width × Height
Volume = 30m × 20m × 10m
Volume = 6000 cubic meters
Let's calculate the rate of water outflow from each hole:
Rate of water outflow from each hole = 10m per hour
Let's calculate the rate of water outflow from all the holes:
Number of holes = (Height - Distance of first hole from base) / Distance between holes + 1
Number of holes = (10m - 2m) / 2m + 1
Number of holes = 4 + 1
Number of holes = 5
Rate of water outflow from all the holes = Rate of water outflow from each hole × Number of holes
Rate of water outflow from all the holes = 10m per hour × 5
Rate of water outflow from all the holes = 50m per hour
Let's calculate the combined rate of filling the tank by both taps:
Combined rate of filling the tank = Rate of filling by tap 1 + Rate of filling by tap 2
Combined rate of filling the tank = 1/60 + 1/90
Combined rate of filling the tank = (3 + 2) / (3 × 60)
Combined rate of filling the tank = 5 / 180
Combined rate of filling the tank = 1/36 of the tank per hour
Now, let's calculate the time taken to fill the tank completely when both taps are opened simultaneously:
Time = Volume / Combined rate of filling the tank
Time = 6000 cubic meters / (1/36 of the tank per hour)
Time = 6000 cubic meters × 36 hours
Time = 216000 hours
Approximately, it will take 216000 hours to fill the tank completely when both taps are opened simultaneously.
Therefore, the correct answer is option (B) 42.
Dimensions of the tank: Length = 30m, Width = 20m, Height = 10m
Rate of filling the tank by tap 1 = 1/60 of the tank per hour
Rate of filling the tank by tap 2 = 1/90 of the tank per hour
Rate of water outflow from each hole = 10m per hour
Distance between holes = 2m
First hole is 2m above the base of the tank
To find: Time taken to fill the tank completely when both taps are opened simultaneously
Let's calculate the volume of the tank:
Volume = Length × Width × Height
Volume = 30m × 20m × 10m
Volume = 6000 cubic meters
Let's calculate the rate of water outflow from each hole:
Rate of water outflow from each hole = 10m per hour
Let's calculate the rate of water outflow from all the holes:
Number of holes = (Height - Distance of first hole from base) / Distance between holes + 1
Number of holes = (10m - 2m) / 2m + 1
Number of holes = 4 + 1
Number of holes = 5
Rate of water outflow from all the holes = Rate of water outflow from each hole × Number of holes
Rate of water outflow from all the holes = 10m per hour × 5
Rate of water outflow from all the holes = 50m per hour
Let's calculate the combined rate of filling the tank by both taps:
Combined rate of filling the tank = Rate of filling by tap 1 + Rate of filling by tap 2
Combined rate of filling the tank = 1/60 + 1/90
Combined rate of filling the tank = (3 + 2) / (3 × 60)
Combined rate of filling the tank = 5 / 180
Combined rate of filling the tank = 1/36 of the tank per hour
Now, let's calculate the time taken to fill the tank completely when both taps are opened simultaneously:
Time = Volume / Combined rate of filling the tank
Time = 6000 cubic meters / (1/36 of the tank per hour)
Time = 6000 cubic meters × 36 hours
Time = 216000 hours
Approximately, it will take 216000 hours to fill the tank completely when both taps are opened simultaneously.
Therefore, the correct answer is option (B) 42.
John starts reading a book from the first page onwards and reads each page only once. Every day, he reads twice the number of pages read by him the previous day. If the book has 400 pages, will John still be reading the book on the 6 day after he starts reading it?
(1) On the fifth day of reading the book, John reads more than 180 pages
(2) John reads 52 more pages on the fourth day of reading the book than he reads on the third day- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'B'. Can you explain this answer?
John starts reading a book from the first page onwards and reads each page only once. Every day, he reads twice the number of pages read by him the previous day. If the book has 400 pages, will John still be reading the book on the 6 day after he starts reading it?
(1) On the fifth day of reading the book, John reads more than 180 pages
(2) John reads 52 more pages on the fourth day of reading the book than he reads on the third day
(1) On the fifth day of reading the book, John reads more than 180 pages
(2) John reads 52 more pages on the fourth day of reading the book than he reads on the third day
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Tarun Khanna answered |
Step 1 & 2: Understand Question and Draw Inference
- Let’s assume John reads x pages on the first day.
- Number of pages read by John on second day = 2x
- Number of pages read by John on the third day = 22 x
- Number of pages read by John on 4th day = 23 x
- Number of pages read by John on 5th day = 24 x
- Total pages read by John in 5 days = x +2x +4x +8x +16x = 31x
- Number of pages in the book = 400
To Find: Is 31x ≥ 400 ?
- If Yes, then John will have finished the book before 6 day. So, he will not be reading the book on the 6 day
- If No, then John will still be reading the book on the 6 day
Step 3 : Analyze Statement 1 independent
- On the fifth day of reading the book, John reads more than 180 pages
- Number of pages read on 5 day = 16 x> 180.
- x > 11
- So, x = 12 < 12. Something or x = 13 > 12.something
- Number of pages read on 5 day = 16 x> 180.
- Insufficient to answer
Step 4 : Analyze Statement 2 independent
(2) John reads 52 more pages on the fourth day of reading the book than he reads on the third day
- Number of pages read on third day = 4x
- Number of pages read on fourth day = 8x
- Extra number of pages read on the fourth day compared to the third day = 8x – 4x = 4x
4x = 52, i.e. x = 13
Therefore, the answer to the question 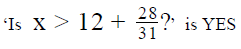
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step-4, this step is not required.
Answer: B
A can do a particular work in 6 days . B can do the same work in 8 days. A and B signed to do it for Rs. 3200. They completed the work in 3 days with the help of C. How much is to be paid to C?A.- a)Rs. 380
- b)Rs. 600
- c)Rs. 420
- d)Rs. 400
- e)Rs. 450
Correct answer is option 'D'. Can you explain this answer?
A can do a particular work in 6 days . B can do the same work in 8 days. A and B signed to do it for Rs. 3200. They completed the work in 3 days with the help of C. How much is to be paid to C?A.
a)
Rs. 380
b)
Rs. 600
c)
Rs. 420
d)
Rs. 400
e)
Rs. 450

|
Mainak Chakraborty answered |
Amount of work A can do in 1 day = 1/6
Amount of work B can do in 1 day = 1/8
Amount of work A + B can do in 1 day = 1/6 + 1/8 = 7/24
Amount of work A + B + C can do = 1/3
Amount of work C can do in 1 day = 1/3 - 7/24 = 1/24
work A can do in 1 day: work B can do in 1 day: work C can do in 1 day
= 1/6 : 1/8 : 1/24 = 4 : 3 : 1
Amount to be paid to C = 3200 × (1/8) = 400
Amount of work B can do in 1 day = 1/8
Amount of work A + B can do in 1 day = 1/6 + 1/8 = 7/24
Amount of work A + B + C can do = 1/3
Amount of work C can do in 1 day = 1/3 - 7/24 = 1/24
work A can do in 1 day: work B can do in 1 day: work C can do in 1 day
= 1/6 : 1/8 : 1/24 = 4 : 3 : 1
Amount to be paid to C = 3200 × (1/8) = 400
Alan alone can build (1/x) th of a wall in 1 day. If Alan & Mike together can build the entire wall in 2 days, then what fraction of the wall can Mike alone build in 1 day?- a)2x/(x-2)
- b)(x – 2)/2x
- c)1/2x
- d)1/(x-2)
- e)(x-2)*2x
Correct answer is option 'B'. Can you explain this answer?
Alan alone can build (1/x) th of a wall in 1 day. If Alan & Mike together can build the entire wall in 2 days, then what fraction of the wall can Mike alone build in 1 day?
a)
2x/(x-2)
b)
(x – 2)/2x
c)
1/2x
d)
1/(x-2)
e)
(x-2)*2x

|
Ankita Chauhan answered |
Given, Alan alone can build (1/x)th of a wall in one day.
Let's assume that Mike alone can build (1/y)th of the same wall in one day.
Together, Alan and Mike can build the entire wall in two days.
Using the formula for work, we can write:
1/x + 1/y = 1/2 (as the wall is built in two days)
We need to find the fraction of the wall that Mike alone can build in one day, which is (1/y).
Solving for (1/y), we get:
1/y = (2xy)/(x + 2y)
Simplifying further, we get:
1/y = (x + 2y - x)/(x + 2y)
1/y = 1 - (x/(x + 2y))
1/y = (x + 2y - x)/(x + 2y)
1/y = (2y)/(x + 2y)
1/y = 2/(x/2 + y)
Comparing this with the options given, we can see that option (B) matches:
(1/y) = (x + 2y - x)/(x + 2y) = (x + 2y)/(2x + 2y) = (x + 2y)/(2(x/2 + y)) = (x + 2y)/(2x) = (x/2 + y)/x = (x + 2y)/(2x) = (x + 2y)/(2x) = (x + 2)/2x
Therefore, the correct answer is option (B).
Let's assume that Mike alone can build (1/y)th of the same wall in one day.
Together, Alan and Mike can build the entire wall in two days.
Using the formula for work, we can write:
1/x + 1/y = 1/2 (as the wall is built in two days)
We need to find the fraction of the wall that Mike alone can build in one day, which is (1/y).
Solving for (1/y), we get:
1/y = (2xy)/(x + 2y)
Simplifying further, we get:
1/y = (x + 2y - x)/(x + 2y)
1/y = 1 - (x/(x + 2y))
1/y = (x + 2y - x)/(x + 2y)
1/y = (2y)/(x + 2y)
1/y = 2/(x/2 + y)
Comparing this with the options given, we can see that option (B) matches:
(1/y) = (x + 2y - x)/(x + 2y) = (x + 2y)/(2x + 2y) = (x + 2y)/(2(x/2 + y)) = (x + 2y)/(2x) = (x/2 + y)/x = (x + 2y)/(2x) = (x + 2y)/(2x) = (x + 2)/2x
Therefore, the correct answer is option (B).
Machine A can complete a certain job in X hours. Machine B can complete the same job in y hours. If A and B work together at their respective rates to complete the job, which of the following represents the fraction of the job that B will not have to complete because of A's help?- a)(x – y)/ (x + y)
- b)x / (y – x)
- c)(x + y) / xy
- d)y / (x – y)
- e)y / (x + y)
Correct answer is option 'E'. Can you explain this answer?
Machine A can complete a certain job in X hours. Machine B can complete the same job in y hours. If A and B work together at their respective rates to complete the job, which of the following represents the fraction of the job that B will not have to complete because of A's help?
a)
(x – y)/ (x + y)
b)
x / (y – x)
c)
(x + y) / xy
d)
y / (x – y)
e)
y / (x + y)

|
Avantika Dey answered |
We can solve this problem as a VIC (Variable In Answer Choice) and plug in values for the two variables, x and y. Let's say x = 2 and y = 3.
Machine A can complete one job in 2 hours. Thus, the rate of Machine A is 1/2.
Machine B can complete one job in 3 hours. Thus, the rate of Machine B is 1/3.
The combined rate for Machine A and Machine B working together is: 1/2 + 1/3 = 5/6.
Using the equation (Rate)(Time) = Work, we can plug 5/6 in for the combined rate, plug 1 in for the total work (since they work together to complete 1 job), and calculate the total time as 6/5 hours.
The question asks us what fraction of the job machine B will NOT have to complete because of A's help. In other words we need to know what portion of the job machine A alone completes in that 6/5 hours.
A's rate is 1/2, and it spends 6/5 hours working. By plugging these into the RT=W formula, we calculate that, A completes (1/2)(6/5) = 3/5 of the job. Thus, machine B is saved from having to complete 3/5 of the job.
If we plug our values of x = 2 and y = 3 into the answer choices, we see that only answer choice E yields the correct value of 3/5.
Working individually, Abe, Bosky, and Chris could do the same job in 12, 24 and 36 hours respectively. They decided to work in cycles of 3 hours with each person working exactly for an hour in a cycle. If they could start the work in any order and only one person works on the job at any given time, what was the minimum amount of time in which the job could be completed? - a)18
- b)19
- c)20
- d)21
- e)22
Correct answer is option 'B'. Can you explain this answer?
Working individually, Abe, Bosky, and Chris could do the same job in 12, 24 and 36 hours respectively. They decided to work in cycles of 3 hours with each person working exactly for an hour in a cycle. If they could start the work in any order and only one person works on the job at any given time, what was the minimum amount of time in which the job could be completed?
a)
18
b)
19
c)
20
d)
21
e)
22

|
Nayanika Bajaj answered |
Understanding Each Person's Work Rate
- Abe can complete the job in 12 hours, so his work rate is 1/12 of the job per hour.
- Bosky can finish it in 24 hours, giving him a work rate of 1/24 of the job per hour.
- Chris requires 36 hours, translating to a work rate of 1/36 of the job per hour.
Calculating Combined Work in One Cycle
In one cycle of 3 hours, each person works for 1 hour:
- Abe's contribution: 1/12 of the job
- Bosky's contribution: 1/24 of the job
- Chris's contribution: 1/36 of the job
Now, we sum their contributions:
- Total work done in one cycle = (1/12 + 1/24 + 1/36)
To combine these fractions, we find a common denominator, which is 72:
- 1/12 = 6/72
- 1/24 = 3/72
- 1/36 = 2/72
Thus, the total work done in one cycle:
- Total = (6 + 3 + 2) / 72 = 11/72 of the job
Calculating Total Cycles Needed
To find out how many cycles are required to complete the job:
- If 11/72 of the job is done per cycle, the total cycles needed to complete 1 job is:
Total cycles = 72/11 ≈ 6.545 cycles
Since they can only work complete cycles, they will need 7 cycles.
Determining Total Time
Each cycle is 3 hours, so:
- Total time = 7 cycles * 3 hours/cycle = 21 hours
However, since they only need to finish the remaining work after 6 cycles, let’s calculate how much work they complete in 6 cycles:
- Work done in 6 cycles = 6 * (11/72) = 66/72 = 11/12 of the job
This means 1/12 of the job remains after 6 cycles.
Finishing the Remaining Work
In the next hour (the start of the 7th cycle), Abe can finish the remaining 1/12 of the job alone.
Therefore, the total time taken to complete the job:
- 6 cycles (18 hours) + 1 more hour = 19 hours
Conclusion
Thus, the minimum amount of time to complete the job is 19 hours, making the correct answer option 'B'.
- Abe can complete the job in 12 hours, so his work rate is 1/12 of the job per hour.
- Bosky can finish it in 24 hours, giving him a work rate of 1/24 of the job per hour.
- Chris requires 36 hours, translating to a work rate of 1/36 of the job per hour.
Calculating Combined Work in One Cycle
In one cycle of 3 hours, each person works for 1 hour:
- Abe's contribution: 1/12 of the job
- Bosky's contribution: 1/24 of the job
- Chris's contribution: 1/36 of the job
Now, we sum their contributions:
- Total work done in one cycle = (1/12 + 1/24 + 1/36)
To combine these fractions, we find a common denominator, which is 72:
- 1/12 = 6/72
- 1/24 = 3/72
- 1/36 = 2/72
Thus, the total work done in one cycle:
- Total = (6 + 3 + 2) / 72 = 11/72 of the job
Calculating Total Cycles Needed
To find out how many cycles are required to complete the job:
- If 11/72 of the job is done per cycle, the total cycles needed to complete 1 job is:
Total cycles = 72/11 ≈ 6.545 cycles
Since they can only work complete cycles, they will need 7 cycles.
Determining Total Time
Each cycle is 3 hours, so:
- Total time = 7 cycles * 3 hours/cycle = 21 hours
However, since they only need to finish the remaining work after 6 cycles, let’s calculate how much work they complete in 6 cycles:
- Work done in 6 cycles = 6 * (11/72) = 66/72 = 11/12 of the job
This means 1/12 of the job remains after 6 cycles.
Finishing the Remaining Work
In the next hour (the start of the 7th cycle), Abe can finish the remaining 1/12 of the job alone.
Therefore, the total time taken to complete the job:
- 6 cycles (18 hours) + 1 more hour = 19 hours
Conclusion
Thus, the minimum amount of time to complete the job is 19 hours, making the correct answer option 'B'.
Peter, Mark and John work in the marketing department of an e-learning firm. Peter can answer 25 emails in an hour, Mark can answer 40 percent more emails in an hour than Peter and John takes 1/6 lesser time to answer the same number of emails as Peter. By what percentage should Peter increase his speed so that the three employees can together answer 1/6 more emails than they currently do?- a)25%
- b)30%
- c)50%
- d)60%
- e)75%
Correct answer is option 'D'. Can you explain this answer?
Peter, Mark and John work in the marketing department of an e-learning firm. Peter can answer 25 emails in an hour, Mark can answer 40 percent more emails in an hour than Peter and John takes 1/6 lesser time to answer the same number of emails as Peter. By what percentage should Peter increase his speed so that the three employees can together answer 1/6 more emails than they currently do?
a)
25%
b)
30%
c)
50%
d)
60%
e)
75%

|
Shreya Basu answered |
Given:
- Number of emails answered by Peter in 1 hour = 25
- Number of emails answered by Mark in 1 hour = 25 + 40% of 25
- Time taken by John to answer 25 emails =
To Find: Percentage by which Peter should increase his speed so that all 3 can answer 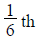 more emails than they currently do?
more emails than they currently do?
Approach:
2. So, to find the percentage by which Peter should increase his speed, we should first find the extra number of emails that he needs to answer.
3. For finding the extra number of emails that he needs to answer, we need to find the total number of emails currently answered by Peter, John and Mark together in 1 hour and number of increased emails they need to answer together.
3. For finding the extra number of emails that he needs to answer, we need to find the total number of emails currently answered by Peter, John and Mark together in 1 hour and number of increased emails they need to answer together.
- We are given the number of emails answered by Peter and Mark in 1 hour.
- As we know that John can answer 25 email in 5/6 hours, we can find the number of emails answered by John in 1 hour
Working out:
- Number of emails answered by Mark in 1 hour = 25 + 40% of 25 = 25 + 10 = 35
- Number of emails answered by John in 1 hour =
- So, the number of emails currently being answered by Peter, mark and John combined = 25 + 35 + 30 = 90
- Number of emails they should answer in case of 1/6 increase = 90 +
emails
- As there are 105 – 90 = 15 more emails that need to answered, these should be answered by Peter.
- So, Peter should answer 15 more emails per hour
- Hence, Peter’s speed should increase by
- Hence, Peter’s speed should increase by
So, Peter should increase his speed by 60%
Answer : D
Two machines A and B worked at variable rates. The average number of items produced per day by machine A could be expressed as Ra (x) = ax(x + 1) and the average number of items produced per day by machine B could be expressed as Rb (x) = bx(x-1), where x was the number of consecutive days worked and a, b were constants. If machine B produced 90 more items when it worked for 4 consecutive days than when it worked for to 3 consecutive days and machine A produced a total of 232 items when it worked in two intervals of 3 consecutive days and 4 consecutive days, how many items was produced by machines A and B working together for 10 consecutive days?- a)3855
- b)4485
- c)4900
- d)5200
- e)5675
Correct answer is option 'C'. Can you explain this answer?
Two machines A and B worked at variable rates. The average number of items produced per day by machine A could be expressed as Ra (x) = ax(x + 1) and the average number of items produced per day by machine B could be expressed as Rb (x) = bx(x-1), where x was the number of consecutive days worked and a, b were constants. If machine B produced 90 more items when it worked for 4 consecutive days than when it worked for to 3 consecutive days and machine A produced a total of 232 items when it worked in two intervals of 3 consecutive days and 4 consecutive days, how many items was produced by machines A and B working together for 10 consecutive days?
a)
3855
b)
4485
c)
4900
d)
5200
e)
5675

|
Pranav Mehta answered |
Given:
- Average number of items produced per day by machine A , Ra (x) = ax(x + 1)
- x is the number of consecutive days worked and a is a constant
- Machine A produced 232 items when it worked for two intervals of 3 consecutive days and 4 consecutive days
- Average number of items produced per day by machine B, Rb (x) = bx(x-1)
- x is the number of consecutive days worked and b is a constant
- Machine B produced 90 more items when it worked for 4 consecutive days than when it worked for 3 consecutive days
To Find: Number of items produced by machine A and B working together for 10 consecutive days
Approach:
- We know that Number of items produced = Rate of producing items * Time taken
- As we are given the time taken to be 10 days, we need to find the rate of producing items for both machines A and B, i.e. we need to find the values of Ra (x) and Rb (x)
- For finding the values of R (x) and R (x), we need to find the values of a and b, i.e. we need an equation each in a and b.
- As we are given the number of items produced by machine A in a certain time interval and the number of items produced by machine B in a certain time interval, we will use this information to find the values of a and b.
Working out:
- Rate of producing items of machine A
- Number of items produced working for 3 consecutive days = ax(x+1)*x = 3a(3+1) * 3 = 36a
- Number of items produced working for 4 consecutive days = ax(x+1)*x= 4a(4+1) * 4 = 80a
- So, total number of items produced = 36a +80a = 116a = 232
- a = 2
- Rate of producing items of machine B
- Number of items produced working for 4 consecutive days = bx(x-1)*x = 4a(4-1) * 4 = 48b
- Number of items produced working for 3 consecutive days = bx(x-1)*x = 3a(3-1) * 3 = 18b
- So, extra items produced = 48b – 18b = 30b = 90
- b = 3
- Number of items produced by machine A working for 10 consecutive days = ax(x+1)*x = 2*10 *(10+1)*10 = 2200
- Number of items produced by machine B working for 10 consecutive days = bx(x-1)*x = 3*10*(10-1)*10 = 2700
- Total number of items produced by machine A and machine B working together for 10 consecutive days = 2200 + 2700 = 4900
Answer : C
P can lay railway track between two stations in 16 days. Q can do the same job in 12 days. With the help of R, they completes the job in 4 days. How much days does it take for R alone to complete the work?- a) 9(3/5) days
- b)9(1/5) days
- c)9(2/5) days
- d)10 days
- e)None of the above
Correct answer is option 'A'. Can you explain this answer?
P can lay railway track between two stations in 16 days. Q can do the same job in 12 days. With the help of R, they completes the job in 4 days. How much days does it take for R alone to complete the work?
a)
9(3/5) days
b)
9(1/5) days
c)
9(2/5) days
d)
10 days
e)
None of the above

|
Avantika Sengupta answered |
Amount of work P can do in 1 day = 1/16
Amount of work Q can do in 1 day = 1/12
Amount of work P, Q and R can together do in 1 day = 1/4
Amount of work R can do in 1 day = 1/4 - (1/16 + 1/12) = 3/16 – 1/12 = 5/48
=> Hence R can do the job on 48/5 days = 9 (3/5) days
Amount of work Q can do in 1 day = 1/12
Amount of work P, Q and R can together do in 1 day = 1/4
Amount of work R can do in 1 day = 1/4 - (1/16 + 1/12) = 3/16 – 1/12 = 5/48
=> Hence R can do the job on 48/5 days = 9 (3/5) days
A is thrice as good as B in work. A is able to finish a job in 60 days less than B. They can finish the work in - days if they work together.A.- a)18 days
- b)22 ½ days
- c)24 days
- d)26 days
- e)20 days
Correct answer is option 'B'. Can you explain this answer?
A is thrice as good as B in work. A is able to finish a job in 60 days less than B. They can finish the work in - days if they work together.A.
a)
18 days
b)
22 ½ days
c)
24 days
d)
26 days
e)
20 days

|
Manoj Joshi answered |
If A completes a work in 1 day, B completes the same work in 3 days
Hence, if the difference is 2 days, B can complete the work in 3 days
=> if the difference is 60 days, B can complete the work in 90 days
=> Amount of work B can do in 1 day= 1/90
Amount of work A can do in 1 day = 3 × (1/90) = 1/30
Amount of work A and B can together do in 1 day = 1/90 + 1/30 = 4/90 = 2/45
=> A and B together can do the work in 45/2 days = 22 ½ days
Hence, if the difference is 2 days, B can complete the work in 3 days
=> if the difference is 60 days, B can complete the work in 90 days
=> Amount of work B can do in 1 day= 1/90
Amount of work A can do in 1 day = 3 × (1/90) = 1/30
Amount of work A and B can together do in 1 day = 1/90 + 1/30 = 4/90 = 2/45
=> A and B together can do the work in 45/2 days = 22 ½ days
If a printer prints 1 word in p seconds, then how many words can it print in ‘q’ seconds where ‘p’ and ‘q’ are positive real numbers?- a)p/60q
- b)q/60p
- c)p/q
- d)q/p
- e)pq
Correct answer is option 'D'. Can you explain this answer?
If a printer prints 1 word in p seconds, then how many words can it print in ‘q’ seconds where ‘p’ and ‘q’ are positive real numbers?
a)
p/60q
b)
q/60p
c)
p/q
d)
q/p
e)
pq

|
Manasa Kulkarni answered |
Solution:
Let us assume that the printer prints x words in q seconds.
Using unitary method, we can say that the printer will print 1 word in p seconds.
Therefore, the printer will print x words in q seconds, which means that the time taken to print x words is q seconds.
Hence, the time taken to print 1 word will be q/x seconds.
We know that the printer prints 1 word in p seconds.
Therefore, the printer will print q/x words in q/x × p seconds.
Simplifying the above expression, we get:
q/x × p = q × (1/x) × p
= q × p/x
= q/p × 1/x
= q/p × (1/60) × 60/x
= q/p × (1/60) × (60/x)
= q/p × (1/60) × p/1
= q/60p
Hence, the number of words that the printer can print in q seconds is q/60p.
Therefore, the correct answer is option D.
Let us assume that the printer prints x words in q seconds.
Using unitary method, we can say that the printer will print 1 word in p seconds.
Therefore, the printer will print x words in q seconds, which means that the time taken to print x words is q seconds.
Hence, the time taken to print 1 word will be q/x seconds.
We know that the printer prints 1 word in p seconds.
Therefore, the printer will print q/x words in q/x × p seconds.
Simplifying the above expression, we get:
q/x × p = q × (1/x) × p
= q × p/x
= q/p × 1/x
= q/p × (1/60) × 60/x
= q/p × (1/60) × (60/x)
= q/p × (1/60) × p/1
= q/60p
Hence, the number of words that the printer can print in q seconds is q/60p.
Therefore, the correct answer is option D.
Machines M and N produce identical widgets but at different constant rates. Machine M takes 10 hours to produce 1000 widgets and Machines M and N together take 6 hours and 40 minutes to produce 2000 widgets. How much time does Machine N take to produce 3000 widgets?- a)3 hours
- b)5 hours
- c)9 hours
- d)10 hours
- e)15 hours
Correct answer is option 'E'. Can you explain this answer?
Machines M and N produce identical widgets but at different constant rates. Machine M takes 10 hours to produce 1000 widgets and Machines M and N together take 6 hours and 40 minutes to produce 2000 widgets. How much time does Machine N take to produce 3000 widgets?
a)
3 hours
b)
5 hours
c)
9 hours
d)
10 hours
e)
15 hours

|
Sanjana Nambiar answered |
Given:
- Let rate of machine N be n widgets per hour and let the rate of Machine M be m widgets per hour
- m ≠ n
- Number of widgets produced by M in 10 hours = 1000
- Number of widgets produced by M and N together in 6 hours 40 minutes = 2000
To Find: Time taken by N to produce 3000 widgets
Approach:
- So, to answer the question, we need to know the value of n
2. We are given the Combined output of M and N in 6 hours 40 minutes. From this piece of information, we can find the combined Rate of M and N
a. Combined Rate of M and N = m + n
b. So, n = (Combined Rate of M and N) – m
c. Therefore, we need to find not only the Combined Rate of M and N, but also the value of m
3. We’re given the output of M alone in 10 hours. From this piece of information, we can find the value of m.
b. So, n = (Combined Rate of M and N) – m
c. Therefore, we need to find not only the Combined Rate of M and N, but also the value of m
3. We’re given the output of M alone in 10 hours. From this piece of information, we can find the value of m.
Working out:
- Finding the Combined Rate of M and N
- Finding n
- n = (300 – 100) widgets per hour = 200 widgets per hour
Looking at the answer choices, we see that the correct answer is Option E
6 men and 8 women can complete a work in 10 days. 26 men and 48 women can finish the same work in 2 days. 15 men and 20 women can do the same work in - days.- a)4 days
- b)6 days
- c)2 days
- d)8 days
- e)5 days
Correct answer is option 'A'. Can you explain this answer?
6 men and 8 women can complete a work in 10 days. 26 men and 48 women can finish the same work in 2 days. 15 men and 20 women can do the same work in - days.
a)
4 days
b)
6 days
c)
2 days
d)
8 days
e)
5 days

|
Saumya Bose answered |
Given Information:
- 6 men and 8 women complete a work in 10 days
- 26 men and 48 women complete the same work in 2 days
Calculating the work rate per person:
- Let the work be represented as W
- The work rate for 6 men and 8 women is W/10
- The work rate for 26 men and 48 women is W/2
Calculating the work rate per man and woman:
- Let the work rate for a man be M and for a woman be W
- From the given information, we can set up the equations:
6M + 8W = W/10
26M + 48W = W/2
Solving the equations:
- Simplifying the first equation, we get 60M + 80W = W
- Simplifying the second equation, we get 52M + 96W = W
- By solving these equations, we find M = 1/60 and W = 1/80
Calculating the work rate for 15 men and 20 women:
- The work rate for 15 men and 20 women is 15M + 20W = 15/60 + 20/80 = 1/4
Calculating the number of days needed:
- Let the number of days needed be D
- The total work is 1, so the work rate for 15 men and 20 women over D days is 1/D
- Setting up the equation, we get 1/4 = 1/D
- Solving for D, we find D = 4 days
Therefore, the work can be completed by 15 men and 20 women in 4 days.
- 6 men and 8 women complete a work in 10 days
- 26 men and 48 women complete the same work in 2 days
Calculating the work rate per person:
- Let the work be represented as W
- The work rate for 6 men and 8 women is W/10
- The work rate for 26 men and 48 women is W/2
Calculating the work rate per man and woman:
- Let the work rate for a man be M and for a woman be W
- From the given information, we can set up the equations:
6M + 8W = W/10
26M + 48W = W/2
Solving the equations:
- Simplifying the first equation, we get 60M + 80W = W
- Simplifying the second equation, we get 52M + 96W = W
- By solving these equations, we find M = 1/60 and W = 1/80
Calculating the work rate for 15 men and 20 women:
- The work rate for 15 men and 20 women is 15M + 20W = 15/60 + 20/80 = 1/4
Calculating the number of days needed:
- Let the number of days needed be D
- The total work is 1, so the work rate for 15 men and 20 women over D days is 1/D
- Setting up the equation, we get 1/4 = 1/D
- Solving for D, we find D = 4 days
Therefore, the work can be completed by 15 men and 20 women in 4 days.
20 men can do a job in 5 days while 10 women can do the same job in 4 days. In how many days can 2 men and 8 women complete the job? Assume the rate of work of all men to be equal and the rate of work of all women to be equal.- a)11/50
- b)9/4
- c)41/11
- d)50/11
- e)5
Correct answer is option 'D'. Can you explain this answer?
20 men can do a job in 5 days while 10 women can do the same job in 4 days. In how many days can 2 men and 8 women complete the job? Assume the rate of work of all men to be equal and the rate of work of all women to be equal.
a)
11/50
b)
9/4
c)
41/11
d)
50/11
e)
5

|
Maya Choudhury answered |
Understanding Work Rates
To solve this problem, we first need to calculate the work rates of men and women.
Work Rate of Men
- 20 men can complete the job in 5 days.
- Total work done = 1 job.
- Work rate of 20 men = 1 job / 5 days = 1/5 job per day.
- Therefore, work rate of 1 man = (1/5) / 20 = 1/100 job per day.
Work Rate of Women
- 10 women can complete the job in 4 days.
- Total work done = 1 job.
- Work rate of 10 women = 1 job / 4 days = 1/4 job per day.
- Therefore, work rate of 1 woman = (1/4) / 10 = 1/40 job per day.
Combined Work Rate of 2 Men and 8 Women
- Work rate of 2 men = 2 * (1/100) = 2/100 = 1/50 job per day.
- Work rate of 8 women = 8 * (1/40) = 8/40 = 1/5 job per day.
Total Work Rate
- Total work rate of 2 men and 8 women = (1/50) + (1/5).
- To add these fractions, we find a common denominator (50).
- (1/5) = (10/50), so total work rate = (1/50) + (10/50) = 11/50 job per day.
Calculating Days to Complete the Job
- If their combined work rate is 11/50 job per day, it will take them:
- Days = 1 job / (11/50) = 50/11 days.
Thus, 2 men and 8 women can complete the job in 50/11 days.
Conclusion
The correct answer is option D: 50/11 days.
To solve this problem, we first need to calculate the work rates of men and women.
Work Rate of Men
- 20 men can complete the job in 5 days.
- Total work done = 1 job.
- Work rate of 20 men = 1 job / 5 days = 1/5 job per day.
- Therefore, work rate of 1 man = (1/5) / 20 = 1/100 job per day.
Work Rate of Women
- 10 women can complete the job in 4 days.
- Total work done = 1 job.
- Work rate of 10 women = 1 job / 4 days = 1/4 job per day.
- Therefore, work rate of 1 woman = (1/4) / 10 = 1/40 job per day.
Combined Work Rate of 2 Men and 8 Women
- Work rate of 2 men = 2 * (1/100) = 2/100 = 1/50 job per day.
- Work rate of 8 women = 8 * (1/40) = 8/40 = 1/5 job per day.
Total Work Rate
- Total work rate of 2 men and 8 women = (1/50) + (1/5).
- To add these fractions, we find a common denominator (50).
- (1/5) = (10/50), so total work rate = (1/50) + (10/50) = 11/50 job per day.
Calculating Days to Complete the Job
- If their combined work rate is 11/50 job per day, it will take them:
- Days = 1 job / (11/50) = 50/11 days.
Thus, 2 men and 8 women can complete the job in 50/11 days.
Conclusion
The correct answer is option D: 50/11 days.
4 identical machines, which operate at the same constant rate, together started manufacturing the batch of an item at 2 PM. Did
they finish the batch before 3.30 PM?
(1) The batch size was between 200 and 210 units, inclusive, of the item
(2) One machine could manufacture between 30 and 50 units, inclusive, of the item in 1 hour- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
Correct answer is option 'E'. Can you explain this answer?
4 identical machines, which operate at the same constant rate, together started manufacturing the batch of an item at 2 PM. Did
they finish the batch before 3.30 PM?
(1) The batch size was between 200 and 210 units, inclusive, of the item
(2) One machine could manufacture between 30 and 50 units, inclusive, of the item in 1 hour
they finish the batch before 3.30 PM?
(1) The batch size was between 200 and 210 units, inclusive, of the item
(2) One machine could manufacture between 30 and 50 units, inclusive, of the item in 1 hour
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
answer the question asked, and additional data specific to the
problem are needed

|
Manoj Joshi answered |
Step 1 & 2: Understand Question and Draw Inference
Given: Number of machines = 4
Let the rate of production for each machine = R units per hour
Let the rate of production for each machine = R units per hour
- So, the number of units produced by 4 machines in 1 hour = 4R
Let the batch size be B units
- Time taken by 4 machines to make 4R units = 1 hour
- So, time taken by 4 machines to make 1 unit = 1 4R hours
- So, the time taken by 4 machines to produce B units =B4R hours
To Find: Did the machines finish the batch before 3:30 PM
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘The batch size was between 200 and 210 units, inclusive
of the item’
of the item’
- So, 200 ≤ B ≤ 210
- However, since we do not know the value of R yet, we cannot answer the question
- Statement 1 is not sufficient
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘One machine could manufacture between 30 and 50 units, inclusive, of the item in 1 hour’
- So, 30 ≤ R ≤ 50
- However, since we do not know the value of B yet, we cannot answer the question
- Statement 2 is not sufficient
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: 200 ≤ B ≤ 210
- From Statement 2: 30 ≤ R ≤ 50
- Therefore, the minimum possible value of
- Thus, by combining the 2 statements, we see that the value of B/R lies between 4 and 7, inclusive
- So, the answer to the question ‘Is Is
may be YES or NO, depending on the particular values of B and R
- So, the 2 statements together are not sufficient to answer the question
Answer: Option E
One smurf and one elf can build a treehouse together in two hours, but the smurf would need the help of two fairies in order to complete the same job in the same amount of time. If one elf and one fairy worked together, it would take them four hours to build the treehouse. Assuming that work rates for smurfs, elves, and fairies remain constant, how many hours would it take one smurf, one elf, and one fairy, working together, to build the treehouse?- a)5/7
- b)1
- c)10/7
- d)12/7
- e)22/7
Correct answer is option 'D'. Can you explain this answer?
One smurf and one elf can build a treehouse together in two hours, but the smurf would need the help of two fairies in order to complete the same job in the same amount of time. If one elf and one fairy worked together, it would take them four hours to build the treehouse. Assuming that work rates for smurfs, elves, and fairies remain constant, how many hours would it take one smurf, one elf, and one fairy, working together, to build the treehouse?
a)
5/7
b)
1
c)
10/7
d)
12/7
e)
22/7

|
Siddharth Pillai answered |
The combined rate of individuals working together is equal to the sum of all the individual working rates.
Let s = rate of a smurf, e = rate of an elf, and f = rate of a fairy. A rate is expressed in terms of treehouses/hour. So for instance, the first equation below says that a smurf and an elf working together can build 1 treehouse per 2 hours, for a rate of 1/2 treehouse per hour.
s + e = 1/2
s + e = 1/2
2) s + 2 f = 1/2
e + f = 1/4
e + f = 1/4
The three equations can be combined by solving the first one for s in terms of e, and the third equation for f in terms of e, and then by substituting both new equations into the middle equation.
1) s = 1/2 – e
2) (1/2 – e) + 2 (1/4 – e) = 1/2
3) f = 1/4 – e
Now, we simply solve equation 2 for e:
(1/2 – e) + 2 (1/4 – e) = 1/2
2/4 – e + 2/4 – 2 e = 2/4
4/4 – 3e = 2/4
-3e = -2/4
e = 2/12
e = 1/6
2) (1/2 – e) + 2 (1/4 – e) = 1/2
3) f = 1/4 – e
Now, we simply solve equation 2 for e:
(1/2 – e) + 2 (1/4 – e) = 1/2
2/4 – e + 2/4 – 2 e = 2/4
4/4 – 3e = 2/4
-3e = -2/4
e = 2/12
e = 1/6
Once we know e, we can solve for s and f:
s = 1/2 – e
s = 1/2 – 1/6
s = 3/6 – 1/6
s = 2/6
s = 1/3
f = 1/4 – e
f = 1/4 – 1/6
f = 3/12 – 2/12
f = 1/12
We add up their individual rates to get a combined rate:
e + s + f =
1/6 + 1/3 + 1/12 =
2/12 + 4/12 + 1/12 = 7/12
s = 1/2 – 1/6
s = 3/6 – 1/6
s = 2/6
s = 1/3
f = 1/4 – e
f = 1/4 – 1/6
f = 3/12 – 2/12
f = 1/12
We add up their individual rates to get a combined rate:
e + s + f =
1/6 + 1/3 + 1/12 =
2/12 + 4/12 + 1/12 = 7/12
Remembering that a rate is expressed in terms of treehouses/hour, this indicates that a smurf, an elf, and a fairy, working together, can produce 7 treehouses per 12 hours. Since we want to know the number of hours per treehouse, we must take the reciprocal of the rate. Therefore we conclude that it takes them 12 hours per 7 treehouses, which is equivalent to 12/7 of an hour per treehouse.
The correct answer is D.
Two machines A and B work at constant rates which are in the ratio of 1:2 respectively. If the two machines work together, they can complete 1/3rd of a job in 3 hours. If machine A starts working on the job and works alone for 18 hours, how many hours would machine B working alone take to complete the remaining work?- a)3.5
- b)4
- c)4.5
- d)5
- e)5.5
Correct answer is option 'C'. Can you explain this answer?
Two machines A and B work at constant rates which are in the ratio of 1:2 respectively. If the two machines work together, they can complete 1/3rd of a job in 3 hours. If machine A starts working on the job and works alone for 18 hours, how many hours would machine B working alone take to complete the remaining work?
a)
3.5
b)
4
c)
4.5
d)
5
e)
5.5

|
Swati Datta answered |
Given:
- Let the rate of machine A be x units of work per hour
- Therefore the rate of machine B = 2x units of ork per hour
- Let the total amount of work to be done be W units
- Time taken by machines A and B working together to complete
- Time taken by machines A and B working together to complete
- Machine A works alone for 18 hours
To Find: Time taken by machine B to complete the remaining work
Approach:
- We know that Work = Rate * Time
c. So, to find the time taken, we either need to find the amount of remaining work and the rate of machine B or the ratio of 
2. For finding the remaining work, we need to find the amount of work done by machine A in 18 hours
- Remaining work = W – work done by machine A in 18 hours
- Work done by machine A in 18 hours = Rate of machine A * 18
- As, rate of machine A is in terms of x, work done by machine A in 18 hours can be expressed in terms of x
- Remaining work = W – work done by machine A in 18 hours
- This will be an expression in terms of W and x. As the rate of machine B is in terms of x, we need to express W also in
- This will be an expression in terms of W and x. As the rate of machine B is in terms of x, we need to express W also in
3. We are given that machines A and B working together take 3 hours to complete W/3 units of work.
- We will use the above relation to express W in terms of x
Working out:
- Machines A and B working together take 3 hours to complete W/3 units of work
2. Amount of work done by machine A working alone for 18 hours = x * 18 = 18x
3. Remaining work = W – 18x = 27x – 18x = 9x
4. Amount of time taken by machine B to complete the remaining work =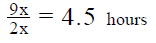
4. Amount of time taken by machine B to complete the remaining work =
Answer : C
An inlet pipe can fill an empty tank in 3 minutes while an outlet pipe can empty this completely filled tank in 6 minutes. If the tank is empty, then in how many minutes would the tank be full when both the inlet and outlet pipes are open?- a)3
- b)4.5
- c)6
- d)7.5
- e)9
Correct answer is option 'C'. Can you explain this answer?
An inlet pipe can fill an empty tank in 3 minutes while an outlet pipe can empty this completely filled tank in 6 minutes. If the tank is empty, then in how many minutes would the tank be full when both the inlet and outlet pipes are open?
a)
3
b)
4.5
c)
6
d)
7.5
e)
9

|
Kirti Roy answered |
Given:
- The inlet pipe can fill an empty tank in 3 minutes.
- The outlet pipe can empty the completely filled tank in 6 minutes.
To find:
- In how many minutes would the tank be full when both the inlet and outlet pipes are open?
Approach:
- Let's assume that the capacity of the tank is 'x'.
- The inlet pipe can fill the entire tank in 3 minutes.
- Therefore, in 1 minute, the inlet pipe can fill 1/3rd of the tank.
- The outlet pipe can empty the entire tank in 6 minutes.
- Therefore, in 1 minute, the outlet pipe can empty 1/6th of the tank.
- When both pipes are open, the net inflow is (1/3 - 1/6) = 1/6th of the tank in 1 minute.
Calculation:
- To fill the entire tank, the net inflow should be equal to the capacity of the tank, which is 'x'.
- So, x/6 = t, where 't' is the time taken to fill the tank.
- Therefore, t = 6x.
Answer:
- The tank will be full in 6 minutes when both the inlet and outlet pipes are open.
- Hence, option 'C' is the correct answer.
- The inlet pipe can fill an empty tank in 3 minutes.
- The outlet pipe can empty the completely filled tank in 6 minutes.
To find:
- In how many minutes would the tank be full when both the inlet and outlet pipes are open?
Approach:
- Let's assume that the capacity of the tank is 'x'.
- The inlet pipe can fill the entire tank in 3 minutes.
- Therefore, in 1 minute, the inlet pipe can fill 1/3rd of the tank.
- The outlet pipe can empty the entire tank in 6 minutes.
- Therefore, in 1 minute, the outlet pipe can empty 1/6th of the tank.
- When both pipes are open, the net inflow is (1/3 - 1/6) = 1/6th of the tank in 1 minute.
Calculation:
- To fill the entire tank, the net inflow should be equal to the capacity of the tank, which is 'x'.
- So, x/6 = t, where 't' is the time taken to fill the tank.
- Therefore, t = 6x.
Answer:
- The tank will be full in 6 minutes when both the inlet and outlet pipes are open.
- Hence, option 'C' is the correct answer.
If 30 machines, each working at the same constant rate, together can produce n/2 units of an item in 15 days, how many machines will be needed to produce 2n units of the item in 45 days?- a)30
- b)40
- c)45
- d)50
- e)60
Correct answer is option 'B'. Can you explain this answer?
If 30 machines, each working at the same constant rate, together can produce n/2 units of an item in 15 days, how many machines will be needed to produce 2n units of the item in 45 days?
a)
30
b)
40
c)
45
d)
50
e)
60

|
Shreya Basu answered |
Given:
- Let the production rate of one machine = r units per day
- Number of machines working = 30
- Number of items produced by 30 machines = n/2 units
- Time taken by 30 machines to produce n/2 items = 15 days
To Find: Number of machines needed to produce 2n units of the item in 45 days
Approach:
- Let the number of machines needed be x
- Production rate of one machine = r units per day
- Production rate of x machines = rx units per day
- We know that Work = Rate * Time
- So, 2n = r * 45 * x
-
- For finding the value of x, we need to either find the values of n and r, or the ratio n/r
-
- As we are given the time taken by 30 machines to produce n/2 items, we can use this information to find the value of n/r.
Working out:
5. So, it will take 40 machines to produce 2n units of the item in 45 days
Answer : B
P, Q and R can do a work in 20, 30 and 60 days respectively. How many days does it need to complete the work if P does the work and he is assisted by Q and R on every third day?- a)10 days
- b)14 days
- c)15 days
- d)9 days
- e)11 days
Correct answer is option 'C'. Can you explain this answer?
P, Q and R can do a work in 20, 30 and 60 days respectively. How many days does it need to complete the work if P does the work and he is assisted by Q and R on every third day?
a)
10 days
b)
14 days
c)
15 days
d)
9 days
e)
11 days

|
Arjun Iyer answered |
Given information:
- P can complete the work in 20 days
- Q can complete the work in 30 days
- R can complete the work in 60 days
Approach:
- Let's calculate the efficiency of each worker
- Then, we can find out how much work is done by P in 3 days and how much work is done by Q and R together in 1 day
- Finally, we can determine the total number of days required to complete the work with this arrangement
Calculations:
- Efficiency of P = 1/20
- Efficiency of Q = 1/30
- Efficiency of R = 1/60
- In 3 days, P completes 3/20 of the work
- In 1 day, Q and R together complete 1/30 + 1/60 = 1/20 of the work
- So, in every 3-day cycle, 3/20 + 1/20 = 1/4 of the work is completed
- Therefore, the work will be completed in 15 days (3-day cycle repeated 5 times)
Conclusion:
The work will be completed in 15 days if P does the work and is assisted by Q and R on every third day.
- P can complete the work in 20 days
- Q can complete the work in 30 days
- R can complete the work in 60 days
Approach:
- Let's calculate the efficiency of each worker
- Then, we can find out how much work is done by P in 3 days and how much work is done by Q and R together in 1 day
- Finally, we can determine the total number of days required to complete the work with this arrangement
Calculations:
- Efficiency of P = 1/20
- Efficiency of Q = 1/30
- Efficiency of R = 1/60
- In 3 days, P completes 3/20 of the work
- In 1 day, Q and R together complete 1/30 + 1/60 = 1/20 of the work
- So, in every 3-day cycle, 3/20 + 1/20 = 1/4 of the work is completed
- Therefore, the work will be completed in 15 days (3-day cycle repeated 5 times)
Conclusion:
The work will be completed in 15 days if P does the work and is assisted by Q and R on every third day.
paint crew gets a rush order to paint 80 houses in a new development. They paint the first y houses at arate of x houses per week. Realizing that they'll be late at this rate, they bring in some more painters andpaint the rest of the houses at the rate of 1.25x houses per week. The total time it takes them to paint all thehouses under this scenario is what fraction of the time it would have taken if they had painted all the housesat their original rate of x houses per week?- a)0.8(80 – y)
- b)0.8 + 0.0025y
- c)80/y – 1.25
- d)80/1.25y
- e)80 – 0.25y
Correct answer is option 'B'. Can you explain this answer?
paint crew gets a rush order to paint 80 houses in a new development. They paint the first y houses at arate of x houses per week. Realizing that they'll be late at this rate, they bring in some more painters andpaint the rest of the houses at the rate of 1.25x houses per week. The total time it takes them to paint all thehouses under this scenario is what fraction of the time it would have taken if they had painted all the housesat their original rate of x houses per week?
a)
0.8(80 – y)
b)
0.8 + 0.0025y
c)
80/y – 1.25
d)
80/1.25y
e)
80 – 0.25y

|
Soumya Iyer answered |
Rate is defined as distance divided by time.
Therefore:
The RATE of machine A =
The RATE of machine B =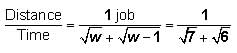 The COMBINED RATE of machine A and machine B =
The COMBINED RATE of machine A and machine B = 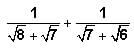
This expression can be simplified by eliminating the roots in the denominators as follows:
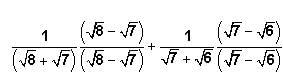
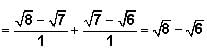
Therefore:
The RATE of machine A =
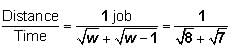
The RATE of machine B =
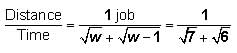 The COMBINED RATE of machine A and machine B =
The COMBINED RATE of machine A and machine B = 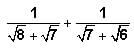
This expression can be simplified by eliminating the roots in the denominators as follows:
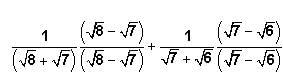
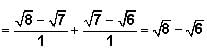
The question asks us for the time, t, that it will take both machines working together to finish one job.
Using the combined rate above and a distance of 1 job, we can solve for t as follows:
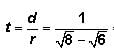
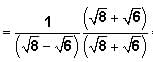
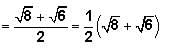
The correct answer is choice B.
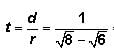
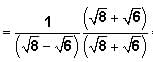
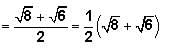
The correct answer is choice B.
Machine A and Machine B can produce 1 widget in 3 hours working together at their respective constant
rates. If Machine A's speed were doubled, the two machines could produce 1 widget in 2 hours working
together at their respective rates. How many hours does it currently take Machine A to produce 1 widget on
its own?- a)1/2
- b)2
- c)3
- d)5
- e)6
Correct answer is option 'E'. Can you explain this answer?
Machine A and Machine B can produce 1 widget in 3 hours working together at their respective constant
rates. If Machine A's speed were doubled, the two machines could produce 1 widget in 2 hours working
together at their respective rates. How many hours does it currently take Machine A to produce 1 widget on
its own?
rates. If Machine A's speed were doubled, the two machines could produce 1 widget in 2 hours working
together at their respective rates. How many hours does it currently take Machine A to produce 1 widget on
its own?
a)
1/2
b)
2
c)
3
d)
5
e)
6

|
Janani Sharma answered |
Let a be the number of hours it takes Machine A to produce 1 widget on its own. Let b be the number of hours it takes Machine B to produce 1 widget on its own.
The question tells us that Machines A and B together can produce 1 widget in 3 hours. Therefore, in 1 hour, the two machines can produce 1/3 of a widget. In 1 hour, Machine A can produce 1/a widgets and Machine B can produce 1/b widgets. Together in 1 hour, they produce 1/a + 1/b = 1/3 widgets.
If Machine A's speed were doubled it would take the two machines 2 hours to
produce 1 widget. When one doubles the speed, one cuts the amount of time it takes in half. Therefore, the amount of time it would take Machine A to produce 1 widget would be a/2. Under these new conditions, in 1 hour Machine A and B could produce 1/(a/2) + 1/b = 1/2 widgets. We now have two unknowns and two different equations. We can solve for a.
The two equations:
2/a + 1/b = 1/2 (Remember, 1/(a/2) = 2/a)
1/a + 1/b = 1/3
2/a + 1/b = 1/2 (Remember, 1/(a/2) = 2/a)
1/a + 1/b = 1/3
Subtract the bottom equation from the top:
2/a – 1/a = 1/2 – 1/3
1/a = 3/6 – 2/6
1/a = 1/6
Therefore, a = 6.
2/a – 1/a = 1/2 – 1/3
1/a = 3/6 – 2/6
1/a = 1/6
Therefore, a = 6.
The correct answer is E.
If John produces n units of an item in t hours, what is the value of n?(1) If John produces 4 more items per hour, he would take 1/4 lesser time to produce n units of the item.
(2) If John increases his rate of production by 25 percent, the time taken by him to produce n items would be 80 percent of the original time.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
Correct answer is option 'E'. Can you explain this answer?
If John produces n units of an item in t hours, what is the value of n?
(1) If John produces 4 more items per hour, he would take 1/4 lesser time to produce n units of the item.
(2) If John increases his rate of production by 25 percent, the time taken by him to produce n items would be 80 percent of the original time.
(2) If John increases his rate of production by 25 percent, the time taken by him to produce n items would be 80 percent of the original time.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
answer the question asked, and additional data specific to the
problem are needed

|
Pranav Mehta answered |
Step 1 & 2: Understand Question and Draw Inference
- Work done = Number of items produced by John = n
- Time taken = Time taken to produce n items = t hours
- Therefore, Rate of work done = Number of items produced in 1 hour = n/t
To Find: Value of n
Step 3 : Analyze Statement 1 independent
(1) If John produces 4 more items per hour, he would take 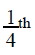 lesser time to produce n units of the item.
lesser time to produce n units of the item.
- Number of items produced = n
- (Number of items produced) = (New Rate)*(New Time)
However, we do not know the value of t, hence we cannot find the value of n.
Insufficient to answer
Step 4 : Analyze Statement 2 independent
(2) If John increases his rate of production by 25 percent, the time taken by him to produce n items would be 80 percent of the original time.
Thus, there is no new information given. Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
1. n = 12t
2. No new information given
2. No new information given
As statement-2 does not provide us any new information, the combination of the statements is insufficient to answer the question.
Answer: E
Operating at their respective constant rates, Photocopying machine B takes 6 minutes more than photocopying machine A to copy x pages. When machines A and B are operated simultaneously, 7x pages can be copied in 20 minutes. In how many minutes can machine A operating alone copy 2x pages?- a)60/7
- b)8
- c)30/7
- d)4
- e)A unique answer cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Operating at their respective constant rates, Photocopying machine B takes 6 minutes more than photocopying machine A to copy x pages. When machines A and B are operated simultaneously, 7x pages can be copied in 20 minutes. In how many minutes can machine A operating alone copy 2x pages?
a)
60/7
b)
8
c)
30/7
d)
4
e)
A unique answer cannot be determined

|
Mainak Chakraborty answered |
Given:
- Time taken by A and B together to copy 7x pages) = 20 minutes
To Find: Time taken by A alone to copy 2x pages
Approach:
2. We’re given the combined output of A and B and the time taken for this output. Using this data, we can find the combined rate of A and B.
Then, we’ll use the equation (Combined Rate of A and B) = (Rate of A) + (Rate of B) to get an equation in terms of a.
Then, we’ll use the equation (Combined Rate of A and B) = (Rate of A) + (Rate of B) to get an equation in terms of a.
Working out:
- When A and B operate simultaneously, 7x pages take 20 minutes
- So, Combined Rate =
pages per minute
- So, Combined Rate =
- The negative root is rejected since time cannot be negative.
- So, a = 4 minutes
- Therefore, Required Time = 2a = 2*4 = 8 minutes
Looking at the answer choices, we see that the correct answer is Option B
A pipe takes 3 hours to fill an empty reservoir to 2/7th of its total capacity. How much time (in hours) more would it take to completely fill the reservoir.- a)3
- b)4.5
- c)6
- d)7.5
- e)9
Correct answer is option 'D'. Can you explain this answer?
A pipe takes 3 hours to fill an empty reservoir to 2/7th of its total capacity. How much time (in hours) more would it take to completely fill the reservoir.
a)
3
b)
4.5
c)
6
d)
7.5
e)
9

|
Kavya Chakraborty answered |
Given:
- Time taken by the pipe to fill the reservoir to 2/7th of its total capacity = 3 hours
To find:
- Time taken to completely fill the reservoir
Approach:
- We can assume that the total capacity of the reservoir is 7x (as 2/7th of the total capacity is filled by the pipe)
- So, the amount of water filled by the pipe in 1 hour = (2x/7)/3 = 2x/21
- Now, to fill the remaining 5x/7th of the reservoir, we need to find the time taken by the pipe
Calculation:
- Let the time taken by the pipe to fill the remaining 5x/7th of the reservoir be t
- Amount of water filled by the pipe in t hours = (2x/21)t
- Total amount of water in the reservoir = 7x
- As the pipe fills 2x/21 amount of water in 1 hour, it will fill 5x/7 amount of water in (5x/7)/(2x/21) = 15/2 hours
- So, the total time taken to fill the reservoir completely = 3 + 15/2 = 21/2 hours
Therefore, the correct answer is option D) 7.5
- Time taken by the pipe to fill the reservoir to 2/7th of its total capacity = 3 hours
To find:
- Time taken to completely fill the reservoir
Approach:
- We can assume that the total capacity of the reservoir is 7x (as 2/7th of the total capacity is filled by the pipe)
- So, the amount of water filled by the pipe in 1 hour = (2x/7)/3 = 2x/21
- Now, to fill the remaining 5x/7th of the reservoir, we need to find the time taken by the pipe
Calculation:
- Let the time taken by the pipe to fill the remaining 5x/7th of the reservoir be t
- Amount of water filled by the pipe in t hours = (2x/21)t
- Total amount of water in the reservoir = 7x
- As the pipe fills 2x/21 amount of water in 1 hour, it will fill 5x/7 amount of water in (5x/7)/(2x/21) = 15/2 hours
- So, the total time taken to fill the reservoir completely = 3 + 15/2 = 21/2 hours
Therefore, the correct answer is option D) 7.5
P is able to do a piece of work in 15 days and Q can do the same work in 20 days. If they can work together for 4 days, what is the fraction of work left?- a)8/15
- b)7/15
- c)11/15
- d)2/11
- e)7/11
Correct answer is option 'A'. Can you explain this answer?
P is able to do a piece of work in 15 days and Q can do the same work in 20 days. If they can work together for 4 days, what is the fraction of work left?
a)
8/15
b)
7/15
c)
11/15
d)
2/11
e)
7/11

|
Prashanth Chawla answered |
Amount of work P can do in 1 day = 1/15
Amount of work Q can do in 1 day = 1/20
Amount of work P and Q can do in 1 day = 1/15 + 1/20 = 7/60
Amount of work P and Q can together do in 4 days = 4 × (7/60) = 7/15
Fraction of work left = 1 – 7/15= 8/15
Amount of work Q can do in 1 day = 1/20
Amount of work P and Q can do in 1 day = 1/15 + 1/20 = 7/60
Amount of work P and Q can together do in 4 days = 4 × (7/60) = 7/15
Fraction of work left = 1 – 7/15= 8/15
At a food processing and packaging plant, identical packets of confectionary items are prepared at a constant rate by a packaging machine. Each packet contains 3 chocolates, 4 candied nuts and 2 chewing gums. The production rate of chocolates, candied nuts and chewing gums at the plant is 750, 975 and 575 units per hour respectively. All the produced items are immediately sent to a common quality checking machine that can process 3000 units of confectionary items per hour. 20 percent each of chocolates, candied nuts and chewing gums fail the quality check. The remaining items are sent to the packaging plant without any holdup or delay. Which of the following can represent the number of packets of confectionary items prepared by the packaging machine in one hour?I. 195
II. 230
III. 280- a)I only
- b)II only
- c)III only
- d)I and II only
- e)I, II and III
Correct answer is option 'A'. Can you explain this answer?
At a food processing and packaging plant, identical packets of confectionary items are prepared at a constant rate by a packaging machine. Each packet contains 3 chocolates, 4 candied nuts and 2 chewing gums. The production rate of chocolates, candied nuts and chewing gums at the plant is 750, 975 and 575 units per hour respectively. All the produced items are immediately sent to a common quality checking machine that can process 3000 units of confectionary items per hour. 20 percent each of chocolates, candied nuts and chewing gums fail the quality check. The remaining items are sent to the packaging plant without any holdup or delay. Which of the following can represent the number of packets of confectionary items prepared by the packaging machine in one hour?
I. 195
II. 230
III. 280
II. 230
III. 280
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
I, II and III

|
Manoj Joshi answered |
Given:
- Contents of 1 packet:
- Chocolates = 3
- Candied Nuts = 4
- Chewing Gums = 2
- The production rate (number of units produced per hour) is as under:
- The maximum units that the quality checking machine can process in 1 hour = 3000
- Since the total number of items produced per hour is only 2300 (less than 3000), this means, there is no holdup/ delay at the quality checking machine. The machine is able to immediately process each produced item.
- 20% each of Chocolates, Candied Nuts and Chewing Gums fail the test This means, only 80% of the produced Chocolates, Candied Nuts and Chewing Gums go to the packaging plant.
To Find: Can the number of packets prepared by the packaging machine in 1 hour be {195, 230, 280}?
Approach:
- To answer the question, we first need to understand what are the constraints on the number of packets prepared by the packaging machine in 1 hour.
- Constraint 1 – The processing capacity of the packaging machine. For example, say the packaging machine is only able to prepare 100 packets per hour.
- Constraint 2 – The number of Chocolates, Candied Nuts and Chewing Gums available to the packaging machine per hour.
- For example, say the packaging machine has the capacity to prepare 10,000 packets per hour but only 30 chocolates come into the packaging machine in one hour. This means, the packaging machine can only produce 10 packets in one hour (since each packet must contain 3 chocolates). This will be the case if the number of Candied Nuts and Chewing Gums is not a limiting factor.
- Now assume a further scenario where only 30 chocolates, 8 candied nuts and 10 chewing gums come into the packaging machine per hour. In this case, the packaging machine can only produce 2 packets per hour (since each packet must contain 4 candied nuts). The number of candied nuts proved to a limiting factor in this scenario.
- So, our approach will be to first find the number of Chocolates, Candied Nuts and Chewing Gums available to the packaging machine per hour (as inferred in the Given section, this number is equal to 80% of the respective production rates of these 3 items)
- Next, we’ll find which of these 3 items acts as a limiting factor, and will find the number of packets that are produced per hour in the case of the limiting factor.
Working out:
- So, each hour the packaging machine gets 600 Chocolates, 780 Candied Nuts and 460 Chewing Gums.
- Once again, remember that each packet contains 3 Chocolates, 4 Candied Nuts and 2 Chewing Gums.
- So, the maximum number of packets that can be packaged in 1 hour =
- Note that Candied Nuts acted as a limiting factor in the number of packets produced per hour.
- So, given the current production (and quality check failing) rates of Chocolates, Candied Nuts and Chewing Gums, the maximum number of packets that can be produced per hour is 195.
- The production will be 195 packets per hour if the processing capacity of the packaging machine is not the limiting factor (that is, Constraint 1 doesn’t come into play, as in the example we considered above where the machine was even capable of packaging 10,000 packets per hour but was limited in its actual output by the number of Chocolates, Candied Nuts and Chewing Gums that were available to it per hour)
- However, if the processing capacity of the packaging machine is the limiting factor, then the actual number of packets produced will be less than 195.
- For example, say the packaging machine can only process 50 packets in 1 hour. Then, even though it is getting enough Chocolates, Candied Nuts and Chewing Gums to be able to pack 195 packets in one hour, it will only be able to pack 50 packets in 1 hour (resulting in a huge stockpiling of Chocolates, Candied Nuts and Chewing Gums at the site of the packaging machine!)
- Thus, the number of packets produced per hour will be less than or equal to 195.
- Out of the 3 given values, the only value possible is Value 1 (195)
Looking at the answer choices, we see that the correct answer is Option A
Transmitting data at the same constant rate, 12 identical cables can transmit x bits of digital information per minute. How many bits of information can be transmitted by 27 such cables in 25 seconds?- a)15x/16
- b)16x/15
- c)45x/4
- d)225x/16
- e)225x/4
Correct answer is option 'A'. Can you explain this answer?
Transmitting data at the same constant rate, 12 identical cables can transmit x bits of digital information per minute. How many bits of information can be transmitted by 27 such cables in 25 seconds?
a)
15x/16
b)
16x/15
c)
45x/4
d)
225x/16
e)
225x/4

|
Tarun Khanna answered |
Given:
- Rate of transmission of 12 identical cables = x bits per minute
- Rate of transmission is constant
To Find: Number of bits (in terms of x) transmitted by 27 identical cables in 25 seconds
Approach:
- Required number of bits = 27*(Number of bits transmitted by 1 cable in 25 seconds)
- = 27*(Number of bits transmitted by 1 cable in 1 second) *25
- So, to answer the question, we need to find the number of bits transmitted by 1 cable in 1 second
Working out:
- Finding the number of bits transmitted by 1 cable in 1 second
- Finding the Required value
Looking at the answer choices, we see that the correct answer is Option A
The water from outlet A, flowing at a constant rate, can fill a rectangular swimming pool in 12 hours while the water from outlet B, flowing at a constant rate, can fill the same swimming pool in 18 hours. On a day when the pool was empty, outlet A was opened at 7 AM and outlet B was opened at 10 AM. Outlet A was closed at 2 PM and outlet B was closed at 4 PM. If there was no water flow from outlet A between 10:30 AM to 11:30 AM because of maintenance work, the height of the water in the pool at 4 PM was approximately what percentage of the depth of the pool?- a)55%
- b)67%
- c)75%
- d)83%
- e)93%
Correct answer is option 'D'. Can you explain this answer?
The water from outlet A, flowing at a constant rate, can fill a rectangular swimming pool in 12 hours while the water from outlet B, flowing at a constant rate, can fill the same swimming pool in 18 hours. On a day when the pool was empty, outlet A was opened at 7 AM and outlet B was opened at 10 AM. Outlet A was closed at 2 PM and outlet B was closed at 4 PM. If there was no water flow from outlet A between 10:30 AM to 11:30 AM because of maintenance work, the height of the water in the pool at 4 PM was approximately what percentage of the depth of the pool?
a)
55%
b)
67%
c)
75%
d)
83%
e)
93%

|
Manoj Joshi answered |
Given:
- Outlet A can fill a swimming pool in 12 hours
- Outlet B can fill the same swimming pool in 18 hours
- Outlet A was opened at 7 AM
- Outlet A was closed at 2 PM
- No water flow between 10:30 AM -11:30 AM, i.e. 1 hour
- Outlet B was opened at 10 AM
- Outlet B was closed at 4 PM
To Find: Percentage of swimming pool that is filled?
Approach:
b. As outlet A working alone can fill the entire swimming pool in 12 hours, we can write the volume of swimming pool = Rate of outlet
A * 11
A * 11
e. As outlet B working alone can fill the entire swimming pool in 18 hours, we can write the volume of swimming pool = Rate of outlet
A * 18
A * 18
2. As, we are given the time for which outlets A and B were open, we can find the percentage of swimming pool filled by outlet A and B
Working out:
- Outlet A
a. Time at which outlet A was opened = 7 AM
b. Time for which outlet A was closed = 2 PM
c. However, outlet did not work for 1 hour between 10:30 AM - 11:30 AM
d. Hence outlet A worked for 7 – 1 = 6 hours
e. So, percentage of swimming pool filled by outlet A in 6 hours = 6/12 = 50% of the swimming pool
b. Time for which outlet A was closed = 2 PM
c. However, outlet did not work for 1 hour between 10:30 AM - 11:30 AM
d. Hence outlet A worked for 7 – 1 = 6 hours
e. So, percentage of swimming pool filled by outlet A in 6 hours = 6/12 = 50% of the swimming pool
2. Outlet B
a. Time at which outlet B was opened = 10 AM
b. Time for which outlet B was closed = 4 PM
c. Time for which outlet B worked = 4 PM – 10 AM = 6 hours
d. So, percentage of swimming pool filled by outlet B in 6 hours = 6/18 = 33% of the swimming pool
3. Therefore, outlet A and B working for 6 hours each can fill (50% +33%) = 83% of the entire swimming pool
a. Time at which outlet B was opened = 10 AM
b. Time for which outlet B was closed = 4 PM
c. Time for which outlet B worked = 4 PM – 10 AM = 6 hours
d. So, percentage of swimming pool filled by outlet B in 6 hours = 6/18 = 33% of the swimming pool
3. Therefore, outlet A and B working for 6 hours each can fill (50% +33%) = 83% of the entire swimming pool
Answer : D
A container is completely filled with a sugar solution composed of water and sugar syrup in the ratio of 7:3. The container has 2 holes covered with filters such that from one of the holes only sugar syrup can flow out and from the other hole only water can flow out. The rates of water outflow and sugar syrup outflow from their respective holes are x cubic centimeters per hour and y cubic centimeters per half an hour respectively, such that x:y = 5:1. If the water from the solution can be drained out completely in 14 hours from the hole, how much time in hours would it take the container to be empty if both the holes are opened simultaneously?- a)14
- b)15
- c)29
- d)30
- e)44
Correct answer is option 'B'. Can you explain this answer?
A container is completely filled with a sugar solution composed of water and sugar syrup in the ratio of 7:3. The container has 2 holes covered with filters such that from one of the holes only sugar syrup can flow out and from the other hole only water can flow out. The rates of water outflow and sugar syrup outflow from their respective holes are x cubic centimeters per hour and y cubic centimeters per half an hour respectively, such that x:y = 5:1. If the water from the solution can be drained out completely in 14 hours from the hole, how much time in hours would it take the container to be empty if both the holes are opened simultaneously?
a)
14
b)
15
c)
29
d)
30
e)
44

|
Shreya Basu answered |
Given:
- Let the volume of the container be S liters
- Since the container is completely filled with the sugar solution, the volume of sugar solution will also be S liters
- Volume of water = 0.7S
- Volume of sugar syrup = 0.3S
- Rate of water outflow = x cubic centimeters per hour
- Water can be drained out completely in 14 hours
- Rate of sugar syrup outflow = y cubic centimeters per half an hour
- Rate of sugar syrup outflow = 2y cubic centimeters per hour x: y = 5:1
To Find: Time taken for container to be empty, if both the holes are opened simultaneously?
Approach:
- As both the holes are opened simultaneously, the time taken to empty the container = Max( Time taken for sugar syrup to drain completely, Time taken for water to drain completely)
- So, we need to find the individual time taken for both water and sugar syrup to drain out completely
- As we are given the time taken for water to drain out completely, we need to find the time taken for sugar syrup to drain out completely
- Time taken for sugar syrup to drain completely =
- So, we need to find either the values of S and y or the ratio S/Y
- Now, we are given that x : y = 5: 1, so if we can find the ratio of S/X, we can find the ratio of S/Y
- Also, since we know that water can be drained out completely in 14 hours, we can calculate the ratio of S/X by using
Working out:
4. So, let’s compare the time taken for water and sugar syrup to drain out completely
a. Time taken for water to drain out completely = 14 hours
b. Time taken for sugar syrup to drain out completely = 15 hours
5. Hence, the time taken for the container to be empty = Max( 14, 15) = 15 hours
Therefore, the container would be completely empty in 15 hours
a. Time taken for water to drain out completely = 14 hours
b. Time taken for sugar syrup to drain out completely = 15 hours
5. Hence, the time taken for the container to be empty = Max( 14, 15) = 15 hours
Therefore, the container would be completely empty in 15 hours
Answer B
If it takes 3 identical printers, working at the same rate, 2 minutes to print 9 binders, how many minutes will it take 6 of the same printers to print 54 binders?- a)
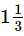
- b)
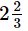
- c)3
- d)
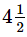
- e)6
Correct answer is option 'E'. Can you explain this answer?
If it takes 3 identical printers, working at the same rate, 2 minutes to print 9 binders, how many minutes will it take 6 of the same printers to print 54 binders?
a)
b)
c)
3
d)
e)
6

|
Prashanth Chawla answered |
Step 1: Question statement and Inferences
The question asks for the number of minutes required for 6 identical printers to print 54 binders given that 3 printers take 2 minutes to print 9 binders. You can infer that the rate of printing does not change.
Step 2: Finding required values
Number of binders printed by 3 printers in 2 minutes = 9
Number of binders printed by 3 printers in 1 minute = 9/2
Number of binders printed by 1 printer in 1 minute = 3/2
Number of binders printed by 6 printers in 1 minute = 3/2 × 6
Number of binders printed by 6 printers in x minutes = 9x
Step 3: Calculating the final answer
Put 9x = 54
x = 6
Thus 6 printers will take 6 minutes to print 54 binders.
Answer: Option (E)
On the first day of the launch of an anticipated electronic item, a queue formed outside an exclusive electronics store that sold the item. At the time the store opened, the queue had 60 people in it and throughout the day, a new person joined the queue every 3 minutes. That day, the store served, only the people in the queue, at a constant service rate of 30 people per hour. If no person re-joined the queue upon getting served once, how many people were in the queue 4 hours after the store opened?- a)20
- b)40
- c)60
- d)80
- e)100
Correct answer is option 'A'. Can you explain this answer?
On the first day of the launch of an anticipated electronic item, a queue formed outside an exclusive electronics store that sold the item. At the time the store opened, the queue had 60 people in it and throughout the day, a new person joined the queue every 3 minutes. That day, the store served, only the people in the queue, at a constant service rate of 30 people per hour. If no person re-joined the queue upon getting served once, how many people were in the queue 4 hours after the store opened?
a)
20
b)
40
c)
60
d)
80
e)
100

|
Shreya Basu answered |
Given:
- Number of people in the queue when the store opened = 60
- 1 person joins the queue every 3 minutes
- So, Queue Joining Rate = 1 person per 3 minutes
- Constant service rate = 30 people per hour
- So, 30 people exit the queue each hour
To Find: Number of people in the queue 4 hours after the store opened
Approach:
- Number of people in the queue 4 hours after the store opened = (Number of people in the queue when the store opened) + (Number of people who join the queue in 4 hours) – (Number of people who exit the queue in 4 hours)
- Number of people who join the queue in 4 hours = (Queue Joining Rate, in terms of people per hour)* 4
- (Number of people who exit the queue in 4 hours) = (Service Rate, in terms of people per hour)*4
- We’re already given the number of people in the queue when the store opened and the Service Rate, in terms of people per hour. So, the only piece of information that we need to find is the Queue Joining Rate, in terms of people per hour
Working out:
- Finding Queue Joining Rate, in terms of people per hour
- Number of people who join in 3 minutes = 1
- Number of people who join in 60 minutes =
- So, the Queue Joining Rate = 20 persons per hour
- Finding the Required Value
- Number of people in the queue 4 hours after the store opened = (Number of people in the queue when the store opened) + (Number of people who join the queue in 4 hours) – (Number of people who exit the queue in 4 hours)
- Number of people in the queue 4 hours after the store opened = 60 + 20*4 – 30*4
- = 60 – 10*4
- =60 – 40
- = 20
Looking at the answer choices, we see that the correct answer is Option A
Working alone, Bill can finish his design in 10 days. With Mason’s help, he only takes 4 days to complete his design. At this rate, how many days would it take Mason, working alone, to complete the design? - a)
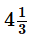
- b)
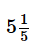
- c)
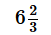
- d)
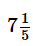
- e)
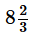
Correct answer is option 'C'. Can you explain this answer?
Working alone, Bill can finish his design in 10 days. With Mason’s help, he only takes 4 days to complete his design. At this rate, how many days would it take Mason, working alone, to complete the design?
a)
b)
c)
d)
e)

|
Avantika Sengupta answered |
Step 1: Question statement and Inferences
The question is asking for the time needed for Mason to complete the job based on the time needed by Bill alone and by Bill and Mason working together.
You can infer that the rates in which they work do not change.
Step 2: Finding required values
Working alone, Bill can complete the design in 10 days.
Let the total amount of work involved in making the design be W
So, work done by Bill in 10 days = W
Work done by Bill in 1 day = W/10
Let Mason working alone take d days to complete W amount of work
So, work done by Mason in d days = W
Work done by Mason in 1 day = W/d
When Bill and Mason work together,
They complete the work in 4 days
This means,
Work done by Bill and Mason in 4 days = W
Work done by Bill and Mason in 1 day = W/4
So,
W/10 + W/d = W/4
1/10 + 1/d = 1/4
Step 3: Calculating the final answer
Solve for Mason’s time. First, subtract from both sides:
1/d = 3/20
Next, cross multiply:
3(d) = 20
Finally, divide both sides by 3:
d = 20/3
It would take Mason, working alone, 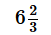 days to complete the design.
days to complete the design.
Answer: Option (C)
An automated manufacturing plant uses robots to manufacture products. A generation-I robot working alone can manufacture a product in 30 hours whereas a generation-II robot working alone can manufacture the same product in 20 hours. If the manager of the plant wants the product manufacturing time to be greater than equal to 5 hours with at least 1 robot each of both generations working together, how many possible combinations of the number of robots of each generation is possible?- a)4
- b)5
- c)6
- d)7
- e)8
Correct answer is option 'E'. Can you explain this answer?
An automated manufacturing plant uses robots to manufacture products. A generation-I robot working alone can manufacture a product in 30 hours whereas a generation-II robot working alone can manufacture the same product in 20 hours. If the manager of the plant wants the product manufacturing time to be greater than equal to 5 hours with at least 1 robot each of both generations working together, how many possible combinations of the number of robots of each generation is possible?
a)
4
b)
5
c)
6
d)
7
e)
8

|
Mainak Chakraborty answered |
Given:
- Generation-I Robot
- Time taken to manufacture a product = 30 hours
- Generation-II Robot
- Time taken to manufacture the product = 20 hours
- To Find: Possible combinations of number of generation-I and II robots such that the product manufacturing time ≥ 5 hours
- Let the number of generation-I robots be x and number of generation-II robots be y
Approach:
- We need to find the possible combination of the values of (x, y).
- As we are given that the time taken for x generation-I and y generation-II robots should be greater than equal to 5 hours, we will formula an inequality in time taken for x generation robots and y generation-II robots to evaluate the possible combination of (x, y)
- As Work = Rate * Time, for finding the time taken by the robots, we would need to find the work done and the rate
- Number of products to be produced = 1
- Now, we know that rate of production of n robots = n * rate of production of 1 robot.
- So, once we find the rate of production of 1 robot for each generation, we can find the rate of production of x generation-I robots and y generation-II robots respectively.
- As we are given the time taken by 1 generation-I robot and 1 generation-II robot to produce 1 product each, we can find the rate of production for robots of both generations.
Working out:
Generation-I
a. Work Done = 1 product
b. Time taken = 30 hours
c. Rate of manufacturing products = products per hour
Generation-II
a. Work Done = 1 product
b. Time taken = 20 hours
c. Rate of manufacturing products = 1/20 products per hour
3. Let’s assume there are x generation-I robots and y generation-II robots working together to produce 1 unit of product
a. So, work done = 1 product
a. Work Done = 1 product
b. Time taken = 30 hours
c. Rate of manufacturing products = products per hour
Generation-II
a. Work Done = 1 product
b. Time taken = 20 hours
c. Rate of manufacturing products = 1/20 products per hour
3. Let’s assume there are x generation-I robots and y generation-II robots working together to produce 1 unit of product
a. So, work done = 1 product
b. Rate of x generation-I robots = 
c. Rate of y generation-II robots = 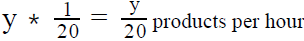
4. As the time taken ≥ 5 hours, we can write
5. So, the possible combinations of {x, y} can be:
a. If y = 1, x = {1,2,3,4} – 4 options
b. If y = 2, x = {1,2,3} – 3 options
c. If x = 1, y = {1,2,3} – 3 options
d. However {x, y} = {1,1} and {1,2} is repeated.
6. So, we have a total of 10 -2 = 8 possible options
a. Please note that we have not considered x, y = 0 as we are given that at-least 1 robot of each generation should be working
a. If y = 1, x = {1,2,3,4} – 4 options
b. If y = 2, x = {1,2,3} – 3 options
c. If x = 1, y = {1,2,3} – 3 options
d. However {x, y} = {1,1} and {1,2} is repeated.
6. So, we have a total of 10 -2 = 8 possible options
a. Please note that we have not considered x, y = 0 as we are given that at-least 1 robot of each generation should be working
Answer : E
Jeff was given a report to complete. In how many days can he complete the report, if his rate of completion is consistent?(1) Jeff can complete 10% of the report in 2 days.(2) After 7 days, there was still 65% of the report to be completed.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
Jeff was given a report to complete. In how many days can he complete the report, if his rate of completion is consistent?
(1) Jeff can complete 10% of the report in 2 days.
(2) After 7 days, there was still 65% of the report to be completed.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Prashanth Chawla answered |
Steps 1 & 2: Understand Question and Draw Inferences
The question asks for the number of days it will take Jeff to complete the report. You need to know the portion of the report, whether as a fraction or a percent, that Jeff can complete in a single day.
We are also given that he completes the same percent of his report every day.
Step 3: Analyze Statement 1
(1) Jeff can complete 10% of the report in 2 days.
If Jeff completes 10% of the report in 2 days, then he completes 5% in one day. At this rate, it will take Jeff 20 days to complete the report.
Statement 1 is sufficient.
Step 4: Analyze Statement 2
(2) After 7 days, there was still 65% of the report to be completed.
If 65% of the report remains after 7 days, then Jeff has completed 35% during these 7 days. AT this rate, he completes 5% in one day, and it will take him 20 days to complete the report.
Statement 2 is sufficient.
Step 5: Analyze Both Statements Together (if needed)
You get unique answers in steps 3 and 4, so this step is not required
Answer: Option (D)
Adam and Brianna plan to install a new tile floor in a classroom. Adam works at a constant rate of 50 tiles per
hour, and Brianna works at a constant rate of 55 tiles per hour. If the new floor consists of exactly 1400 tiles,
how long will it take Adam and Brianna working together to complete the classroom floor?- a)26 hrs. 44 mins.
- b)26 hrs. 40 mins.
- c)13 hrs. 20 mins.
- d)13 hrs. 18 mins.
- e)12 hrs. 45 mins.
Correct answer is option 'C'. Can you explain this answer?
Adam and Brianna plan to install a new tile floor in a classroom. Adam works at a constant rate of 50 tiles per
hour, and Brianna works at a constant rate of 55 tiles per hour. If the new floor consists of exactly 1400 tiles,
how long will it take Adam and Brianna working together to complete the classroom floor?
hour, and Brianna works at a constant rate of 55 tiles per hour. If the new floor consists of exactly 1400 tiles,
how long will it take Adam and Brianna working together to complete the classroom floor?
a)
26 hrs. 44 mins.
b)
26 hrs. 40 mins.
c)
13 hrs. 20 mins.
d)
13 hrs. 18 mins.
e)
12 hrs. 45 mins.

|
Sharmila Singh answered |
Because Adam and Brianna are working together, add their individual rates to find their combined rate:
50 + 55 = 105 tiles per hour
The question asks how long it will take them to set 1400 tiles.
Time = Work / Rate = 1400 tiles / (105 tiles / hour) = 40/3 hours = 13 and 1/3 hours = 13 hours and 20 minutes
The correct answer is C.
Chapter doubts & questions for Time and Work - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Time and Work - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









