All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Algebra Introduction for GMAT Exam
If a and b are integers such that a > b > 0, what is the minimum value of (a2 + b2) (a+b) (a-b) + 2b4?- a)7
- b)17
- c)27
- d)37
- e)47
Correct answer is option 'B'. Can you explain this answer?
If a and b are integers such that a > b > 0, what is the minimum value of (a2 + b2) (a+b) (a-b) + 2b4?
a)
7
b)
17
c)
27
d)
37
e)
47
|
|
Meera Rana answered |
Solution : (a2+b2)(a+b)(a-b) + 2b4
= (a2+b2)(a2 - b2) + 2b4
= (a4 - b4) + 2b4
= (a2+b2)(a2 - b2) + 2b4
= (a4 - b4) + 2b4
since a> b > 0
set is a =2 b = 1
value = 15+2 = 17
set is a =2 b = 1
value = 15+2 = 17
What is the highest integral value of 'k' for which the quadratic equation x2 - 6x + k = 0 will have two real and distinct roots?- a)9
- b)7
- c)3
- d)8
- e)12
Correct answer is option 'D'. Can you explain this answer?
What is the highest integral value of 'k' for which the quadratic equation x2 - 6x + k = 0 will have two real and distinct roots?
a)
9
b)
7
c)
3
d)
8
e)
12
|
|
Aditya Kumar answered |
Step 1: Nature of Roots of Quadratic Equation Theory
D is called the Discriminant of a quadratic equation.
D = b2 - 4ac for quadratic equations of the form ax2 + bx + c = 0.
If D > 0, roots of such quadratic equations are Real and Distinct
If D = 0, roots of such quadratic equations are Real and Equal
If D < 0, roots of such quadratic equations are Imaginary. i.e., such quadratic equations will NOT have real roots.
In this GMAT sample question in algebra, we have to determine the largest integer value that ‘k’ can take such that the discriminant of the quadratic equation is positive.
D = b2 - 4ac for quadratic equations of the form ax2 + bx + c = 0.
If D > 0, roots of such quadratic equations are Real and Distinct
If D = 0, roots of such quadratic equations are Real and Equal
If D < 0, roots of such quadratic equations are Imaginary. i.e., such quadratic equations will NOT have real roots.
In this GMAT sample question in algebra, we have to determine the largest integer value that ‘k’ can take such that the discriminant of the quadratic equation is positive.
Step 2: Compute maximum value of k that will make the discriminant of the quadratic equation positive
The given quadratic equation is x2 - 6x + k = 0.
In this equation, a = 1, b = -6 and c = k
The value of the discriminant, D = 62 - 4 * 1 * k
We have compute values of 'k' for which D > 0.
i.e., 36 – 4k > 0
Or 36 > 4k or k < 9.
In this equation, a = 1, b = -6 and c = k
The value of the discriminant, D = 62 - 4 * 1 * k
We have compute values of 'k' for which D > 0.
i.e., 36 – 4k > 0
Or 36 > 4k or k < 9.
The question is "What is the highest integer value that k can take?"
If k < 9, the highest integer value that k can take is 8.
If k < 9, the highest integer value that k can take is 8.
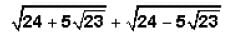 lies between:
lies between:- a)4 & 5
- b)5 & 6
- c)6 & 7
- d)7 & 8
- e)8 & 9
Correct answer is option 'D'. Can you explain this answer?
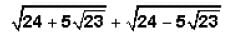 lies between:
lies between:a)
4 & 5
b)
5 & 6
c)
6 & 7
d)
7 & 8
e)
8 & 9
|
|
Anaya Patel answered |
In order to rid the expression of square roots, let's first square the entire expression. We are allowed to do this as long as we remember to "unsquare" whatever solution we get at that end.
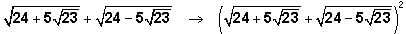
Notice that the new expression is of the form where
where
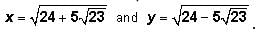
Recall that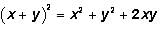 This is one of the GMAT's favorite expressions.
This is one of the GMAT's favorite expressions.
Returning to our expression:
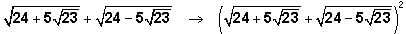
Notice that the new expression is of the form
 where
where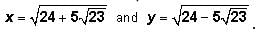
Recall that
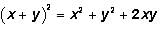 This is one of the GMAT's favorite expressions.
This is one of the GMAT's favorite expressions.Returning to our expression:


Notice that x2 + y2 neatly simplifies to 48. This leaves only the 2xy expression left to simplify.
In order to simplify
 recall that
recall that 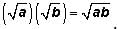
Thus,
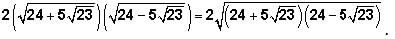
Notice that the expression under the square root sign is of the form
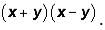 And recall that
And recall that 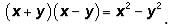 This is another one of the GMAT's favorite expressions. Returning to our expression:
This is another one of the GMAT's favorite expressions. Returning to our expression: 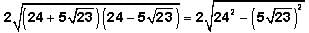
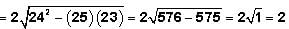
Finally then:
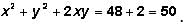
But now we must remember to "unsquare" (or take the square root of) our answer:
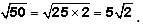
If x, y, z are non-zero numbers and x + xy2 = z3, then which of the following is NOT equal to 1?- a)
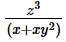
- b)
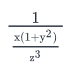
- c)
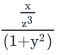
- d)
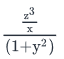
- e)

Correct answer is option 'C'. Can you explain this answer?
If x, y, z are non-zero numbers and x + xy2 = z3, then which of the following is NOT equal to 1?
a)
b)
c)
d)
e)
|
|
Aditya Kumar answered |
Given equation is
x+xy2 = z3
This can be rewritten as:
x(1+y2) = z3 …………….. (I)
We need to find the option statement whose value is not equal to 1.
Now let us look at each option.
Option A:
This is same as
From (I), we know that the numerator and denominator of Expression A are equal.
Therefore the value of Expression A is 1.
Option B:
This can be rewritten as:
We already saw in the previous option that this is equal to 1.
Option C:
This can be rewritten as:
From I, we can rewrite this as:
It is given that y is a non-zero number. Therefore, the value of (1+y2) is always greater than 1.
So, Expression C cannot be equal to 1.
Option D:
This can be rewritten as:
From options A and B, we already know that this expression is equal to 1.
Option E:
We already know that this expression is equal to 1.
Correct Answer: C
What is the value of the expression 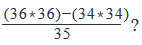
- a)3
- b)3.5
- c)4
- d)4.5
- e)5
Correct answer is 'C'. Can you explain this answer?
What is the value of the expression
a)
3
b)
3.5
c)
4
d)
4.5
e)
5

|
Cstoppers Instructors answered |
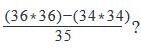
= [(1296)-(1156)]/35
= 140/35
= 4
Solve 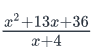 when x =1/4 ?
when x =1/4 ?- a)35/17
- b)37/17
- c)35/4
- d)37/4
- e)39/4
Correct answer is option 'D'. Can you explain this answer?
Solve 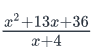 when x =1/4 ?
when x =1/4 ?
a)
35/17
b)
37/17
c)
35/4
d)
37/4
e)
39/4
|
|
Yash Patel answered |
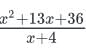 where x =1/4
where x =1/4= [ (1/4)2 + 13(1/4) + 36 ] / (1/4) + 4
= [ 1/16 + 13/4 + 36 ] / 17/4
= [ ( 1 + 52 + 576) /16 ] x 4/16
= 629/16 x 4/17
= 37/4
Three years back, a father was 24 years older than his son. At present the father is 5 times as old as the son. How old will the son be three years from now?- a)12 years
- b)6 years
- c)3 years
- d)9 years
- e)27 years
Correct answer is option 'D'. Can you explain this answer?
Three years back, a father was 24 years older than his son. At present the father is 5 times as old as the son. How old will the son be three years from now?
a)
12 years
b)
6 years
c)
3 years
d)
9 years
e)
27 years

|
Jatin Kapoor answered |
Let the age of the son 3 years back be 'x' years.
Information 1: Three years back, a father was 24 years older than his son.
Therefore, the age of the father 3 years back was (x + 24).
Information 1: Three years back, a father was 24 years older than his son.
Therefore, the age of the father 3 years back was (x + 24).
If the age of the son 3 years back was 'x' years, the present age of the son is x + 3.
Present age of father = x + 24 + 3
Present age of father = x + 24 + 3
Information 2: The father is at present 5 times as old as the son.
i.e., (x + 24 + 3) = 5(x + 3)
Or x + 27 = 5x + 15
Or 4x = 12 or x = 3.
i.e., (x + 24 + 3) = 5(x + 3)
Or x + 27 = 5x + 15
Or 4x = 12 or x = 3.
Step 2 of solving this GMAT Algebra Word Problem: From unknown to the answer
x was the age of the son 3 years back.
Therefore, the son was 3 years old 3 years back.
x was the age of the son 3 years back.
Therefore, the son was 3 years old 3 years back.
The question is "How old will the son be three years from now?"
If the son was 3 years old, 3 years back, the son is 6 years old now.
Hence, he will be 9 years old three years from now.
If the son was 3 years old, 3 years back, the son is 6 years old now.
Hence, he will be 9 years old three years from now.
Choice D is the correct answer.
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?- a)3
- b)6
- c)5
- d)4
- e)Infinitely many
Correct answer is option 'C'. Can you explain this answer?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
a)
3
b)
6
c)
5
d)
4
e)
Infinitely many

|
Prateek Gupta answered |
Understanding the Equation
The equation given is:
5x + 4|y| = 55.
We need to find integer values of (x, y) such that x > 0.
Rearranging the Equation
We can rearrange the equation to isolate |y|:
4|y| = 55 - 5x
|y| = (55 - 5x) / 4.
Constraints on x
Since x must be a positive integer, we should determine the values of x that keep |y| non-negative:
55 - 5x ≥ 0
This leads to:
x ≤ 11.
Thus, x can take on integer values from 1 to 11 (inclusive).
Calculating Possible Values of y
Next, we calculate |y| for each integer value of x from 1 to 11:
- For each x, |y| = (55 - 5x) / 4 must also be an integer.
- This implies that 55 - 5x must be divisible by 4.
Checking Integer Values
Now, let's check the values of x:
- x = 1: |y| = 12.
- x = 2: |y| = 11.
- x = 3: |y| = 10.
- x = 4: |y| = 9.
- x = 5: |y| = 8.
- x = 6: |y| = 7.
- x = 7: |y| = 6.
- x = 8: |y| = 5.
- x = 9: |y| = 4.
- x = 10: |y| = 3.
- x = 11: |y| = 2.
Total Solutions for y
For each of these values of |y| (12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2), there are two corresponding integer values for y: y and -y. Therefore, the total number of integer pairs (x, y) is:
- 11 values of x * 2 = 22 possible pairs.
However, we need to ensure we count unique values that yield valid solutions, leading to 5 unique integer values for y when x is positive.
Final Answer
Thus, the total integer values of (x, y) that satisfy the equation is 5. Therefore, the correct answer is option 'C'.
The equation given is:
5x + 4|y| = 55.
We need to find integer values of (x, y) such that x > 0.
Rearranging the Equation
We can rearrange the equation to isolate |y|:
4|y| = 55 - 5x
|y| = (55 - 5x) / 4.
Constraints on x
Since x must be a positive integer, we should determine the values of x that keep |y| non-negative:
55 - 5x ≥ 0
This leads to:
x ≤ 11.
Thus, x can take on integer values from 1 to 11 (inclusive).
Calculating Possible Values of y
Next, we calculate |y| for each integer value of x from 1 to 11:
- For each x, |y| = (55 - 5x) / 4 must also be an integer.
- This implies that 55 - 5x must be divisible by 4.
Checking Integer Values
Now, let's check the values of x:
- x = 1: |y| = 12.
- x = 2: |y| = 11.
- x = 3: |y| = 10.
- x = 4: |y| = 9.
- x = 5: |y| = 8.
- x = 6: |y| = 7.
- x = 7: |y| = 6.
- x = 8: |y| = 5.
- x = 9: |y| = 4.
- x = 10: |y| = 3.
- x = 11: |y| = 2.
Total Solutions for y
For each of these values of |y| (12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2), there are two corresponding integer values for y: y and -y. Therefore, the total number of integer pairs (x, y) is:
- 11 values of x * 2 = 22 possible pairs.
However, we need to ensure we count unique values that yield valid solutions, leading to 5 unique integer values for y when x is positive.
Final Answer
Thus, the total integer values of (x, y) that satisfy the equation is 5. Therefore, the correct answer is option 'C'.
The basic one-way air fare for a child aged between 3 and 10 years costs half the regular fare for an adult plus a reservation charge that is the same on the child's ticket as on the adult's ticket. One reserved ticket for an adult costs $216 and the cost of a reserved ticket for an adult and a child (aged between 3 and 10) costs $327. What is the basic fare for the journey for an adult?- a)$111
- b)$52.5
- c)$210
- d)$58.5
- e)$6
Correct answer is option 'C'. Can you explain this answer?
The basic one-way air fare for a child aged between 3 and 10 years costs half the regular fare for an adult plus a reservation charge that is the same on the child's ticket as on the adult's ticket. One reserved ticket for an adult costs $216 and the cost of a reserved ticket for an adult and a child (aged between 3 and 10) costs $327. What is the basic fare for the journey for an adult?
a)
$111
b)
$52.5
c)
$210
d)
$58.5
e)
$6

|
Malavika Choudhury answered |
Step 1 : Assign variables and frame equations
Let the basic fare for the child be $X.
Let the basic fare for the child be $X.
Information 1: Basic one-way air fare of a child costs half the regular fare for an adult.
Therefore, the basic fare for an adult = 2(basic one-way airfare for a child) = $2X.
Therefore, the basic fare for an adult = 2(basic one-way airfare for a child) = $2X.
Information 2: Reservation charge is the same on the child's ticket as on the adult's ticket.
Let the reservation charge per ticket be $Y
A child's ticket will cost (Basic fare + Reservation charges) = X + Y
Hence, an adult ticket will cost (Basic fare + Reservation charges) = 2X + Y.
Information 3: One reserved ticket for an adult costs $216. So, 2X + Y = $216 .... (1)
Information 4: The cost of a reserved ticket for an adult and a child (aged between 3 and 10) is $327.
So, the ticket for an adult and a child will cost (2X + Y) + (X + Y) = 3X + 2Y = $327 .... (2)
Let the reservation charge per ticket be $Y
A child's ticket will cost (Basic fare + Reservation charges) = X + Y
Hence, an adult ticket will cost (Basic fare + Reservation charges) = 2X + Y.
Information 3: One reserved ticket for an adult costs $216. So, 2X + Y = $216 .... (1)
Information 4: The cost of a reserved ticket for an adult and a child (aged between 3 and 10) is $327.
So, the ticket for an adult and a child will cost (2X + Y) + (X + Y) = 3X + 2Y = $327 .... (2)
Step 2 of solving this GMAT Algebra Question: Solve the simultaneous equations and determine basic fare for an adult.
Multiply equation (1) by 2: 4X + 2Y = 432 .... (3)
Subtract equation (2) from equation (3):
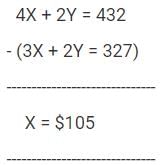
The question is "What is the basic fare for an adult?"
The basic fare of an adult ticket = 2X = 2*105 = $210
Multiply equation (1) by 2: 4X + 2Y = 432 .... (3)
Subtract equation (2) from equation (3):
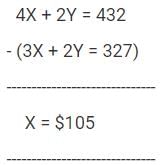
The question is "What is the basic fare for an adult?"
The basic fare of an adult ticket = 2X = 2*105 = $210
Choice C is the correct answer.
A poultry farm has only chickens and pigs. When the manager of the poultry counted the heads of the stock in the farm, the number totaled up to 200. However, when the number of legs was counted, the number totaled up to 540. How many more chickens were there in the farm? Note: In the farm, each pig had 4 legs and each chicken had 2 legs.- a)70
- b)120
- c)60
- d)130
- e)80
Correct answer is option 'C'. Can you explain this answer?
A poultry farm has only chickens and pigs. When the manager of the poultry counted the heads of the stock in the farm, the number totaled up to 200. However, when the number of legs was counted, the number totaled up to 540. How many more chickens were there in the farm? Note: In the farm, each pig had 4 legs and each chicken had 2 legs.
a)
70
b)
120
c)
60
d)
130
e)
80

|
Tejas Gupta answered |
Step 1 : Assign Variables and Frame Equations
Let the number of chickens in the farm be 'x'.
Let the number of pigs in the farm be 'y'.
Let the number of chickens in the farm be 'x'.
Let the number of pigs in the farm be 'y'.
Each pig or each chicken has one head.
Therefore, number of heads will be the same as the sum of the chickens and pigs in the farm.
The count of the heads in the farm is 200. So, the sum of the number of chickens and pigs is 200.
So, x + y = 200 .... (1)
Therefore, number of heads will be the same as the sum of the chickens and pigs in the farm.
The count of the heads in the farm is 200. So, the sum of the number of chickens and pigs is 200.
So, x + y = 200 .... (1)
Each chicken has 2 legs and each pig has 4 legs
'x' chickens will therefore, have 2x legs and 'y' pigs will have 4y legs.
The count of the legs in the farm is 540. So, the sum of the number of legs of chickens and the number of legs of pigs is 540.
Therefore, 2x + 4y = 540 .... (2)
'x' chickens will therefore, have 2x legs and 'y' pigs will have 4y legs.
The count of the legs in the farm is 540. So, the sum of the number of legs of chickens and the number of legs of pigs is 540.
Therefore, 2x + 4y = 540 .... (2)
Step 2 of solving this GMAT Linear Equations Question: Solve the system of linear equations
Multiply equation (1) by 2. We get 2x + 2y = 400 .... (3)
Subtract equation (3) from equation (2).
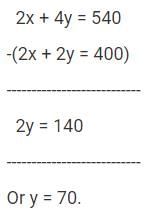
Multiply equation (1) by 2. We get 2x + 2y = 400 .... (3)
Subtract equation (3) from equation (2).
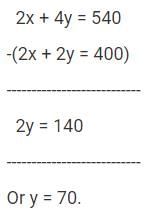
Substitute 'y' as 70 in equation (1).
70 + y = 200. So, x = 130
70 + y = 200. So, x = 130
'x' is the number of chickens in the farm. 'y' is the number of pigs in the farm. So, the farm has 130 chickens and 70 pigs.
Note:The question is "How many more chickens were there in the farm?"
The farm has 130 chickens and 70 pigs. So, the farm has (130 - 70) = 60 more chickens
The farm has 130 chickens and 70 pigs. So, the farm has (130 - 70) = 60 more chickens
A, B, C, D, E, F, G, and H are all integers, listed in order of increasing size. When these numbers are arranged on a number line, the distance between any two consecutive numbers is constant. If G and H are equal to 512 and 513, respectively, what is the value of A?- a)-24(512)
- b)-23(512)
- c)-24(56)
- d)23(512)
- e)24(512)
Correct answer is option 'B'. Can you explain this answer?
A, B, C, D, E, F, G, and H are all integers, listed in order of increasing size. When these numbers are arranged on a number line, the distance between any two consecutive numbers is constant. If G and H are equal to 512 and 513, respectively, what is the value of A?
a)
-24(512)
b)
-23(512)
c)
-24(56)
d)
23(512)
e)
24(512)

|
Srestha Basu answered |
Understanding the problem:
In this problem, we are given that the numbers A, B, C, D, E, F, G, and H are integers listed in increasing order and have a constant distance between them on the number line. We are also told that G = 512 and H = 513.
Solution:
- Let's assume the constant difference between each consecutive number is x.
- Since G = 512 and H = 513, the difference between G and H is 513 - 512 = 1, which is equal to x.
- Therefore, x = 1.
- Now, since the numbers are in increasing order, the value of A will be 512 - 23(1) = 512 - 23 = 512 - 23 = 489.
- So, the value of A is 489.
Therefore, the correct answer is option B (-23(512)).
In this problem, we are given that the numbers A, B, C, D, E, F, G, and H are integers listed in increasing order and have a constant distance between them on the number line. We are also told that G = 512 and H = 513.
Solution:
- Let's assume the constant difference between each consecutive number is x.
- Since G = 512 and H = 513, the difference between G and H is 513 - 512 = 1, which is equal to x.
- Therefore, x = 1.
- Now, since the numbers are in increasing order, the value of A will be 512 - 23(1) = 512 - 23 = 512 - 23 = 489.
- So, the value of A is 489.
Therefore, the correct answer is option B (-23(512)).
y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?- a)-32
- b)-256
- c)-255
- d)-257
- e)0
Correct answer is option 'D'. Can you explain this answer?
y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?
a)
-32
b)
-256
c)
-255
d)
-257
e)
0

|
Sandeep Mehra answered |
Understanding the Quadratic Equation
The equation given is y = x^2 + bx + 256. This is a standard form of a quadratic equation where the roots (x-intercepts) are denoted by (h, 0) and (k, 0).
Roots and Coefficients Relationship
For a quadratic equation of the form y = ax^2 + bx + c, the sum and product of the roots can be expressed as:
- Sum of roots (h + k) = -b/a
- Product of roots (hk) = c/a
In our case, a = 1 and c = 256.
Finding Values from Roots
Using the relationships:
- Product of roots: hk = 256
- Sum of roots: h + k = -b
We need to find integer pairs (h, k) such that their product equals 256.
Identifying Integer Pairs
The integer pairs (h, k) that multiply to 256 include:
- 1 and 256
- 2 and 128
- 4 and 64
- 8 and 32
- 16 and 16
- Negative pairs like (-1, -256) and so forth.
Calculating Values of b
Now we calculate the corresponding values of b for these pairs:
- For (1, 256): b = -(1 + 256) = -257
- For (2, 128): b = -(2 + 128) = -130
- For (4, 64): b = -(4 + 64) = -68
- For (8, 32): b = -(8 + 32) = -40
- For (16, 16): b = -(16 + 16) = -32
The least value among these is -257.
Conclusion
Thus, the least value of b that satisfies the conditions of the problem is:
-257
This corresponds to option 'D'.
The equation given is y = x^2 + bx + 256. This is a standard form of a quadratic equation where the roots (x-intercepts) are denoted by (h, 0) and (k, 0).
Roots and Coefficients Relationship
For a quadratic equation of the form y = ax^2 + bx + c, the sum and product of the roots can be expressed as:
- Sum of roots (h + k) = -b/a
- Product of roots (hk) = c/a
In our case, a = 1 and c = 256.
Finding Values from Roots
Using the relationships:
- Product of roots: hk = 256
- Sum of roots: h + k = -b
We need to find integer pairs (h, k) such that their product equals 256.
Identifying Integer Pairs
The integer pairs (h, k) that multiply to 256 include:
- 1 and 256
- 2 and 128
- 4 and 64
- 8 and 32
- 16 and 16
- Negative pairs like (-1, -256) and so forth.
Calculating Values of b
Now we calculate the corresponding values of b for these pairs:
- For (1, 256): b = -(1 + 256) = -257
- For (2, 128): b = -(2 + 128) = -130
- For (4, 64): b = -(4 + 64) = -68
- For (8, 32): b = -(8 + 32) = -40
- For (16, 16): b = -(16 + 16) = -32
The least value among these is -257.
Conclusion
Thus, the least value of b that satisfies the conditions of the problem is:
-257
This corresponds to option 'D'.
If (22x+1)(32y-1) = 8x27y, then x + y =- a)-3
- b)-1
- c)0
- d)1
- e)3
Correct answer is option 'C'. Can you explain this answer?
If (22x+1)(32y-1) = 8x27y, then x + y =
a)
-3
b)
-1
c)
0
d)
1
e)
3

|
Ujwal Iyer answered |
Let's rewrite the right side of the equation in base 2 and base 3: (22x+1)(32y-1) = (23)x(33)y. This can be rewritten as: (22x+1)(32y-1) = 23x33y Since both bases on either side of the equation are prime, we can set the exponents of each respective base equal to one another: 2x + 1 = 3x , so x = 1 2y – 1 = 3y, so y = -1 Therefore, x + y = 1 + (-1) = 0.
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?- a)3
- b)12
- c)6
- d)24
- e)8
Correct answer is option 'B'. Can you explain this answer?
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?
a)
3
b)
12
c)
6
d)
24
e)
8

|
Tanishq Yadav answered |
In quadratic equations of the form 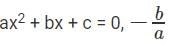 represents the sum of the roots of the quadratic equation and c/a
represents the sum of the roots of the quadratic equation and c/a
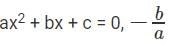 represents the sum of the roots of the quadratic equation and c/a
represents the sum of the roots of the quadratic equation and c/a represents the product of the roots of the quadratic equation.
In the equation given a = 1, b = b and c = 72
So, the product of roots of the quadratic equation = 72/1 = 72
And the sum of roots of this quadratic equation= -b/1 = -b
We have been asked to find the number of values that 'b' can take.
If we list all possible combinations for the roots of the quadratic equation, we can find out the number of values the sum of the roots of the quadratic equation can take.
Consequently, we will be able to find the number of values that 'b' can take.
If we list all possible combinations for the roots of the quadratic equation, we can find out the number of values the sum of the roots of the quadratic equation can take.
Consequently, we will be able to find the number of values that 'b' can take.
The question states that the roots are integers.
If the roots are r1 and r2, then r1 * r2 = 72, where both r1 and r2 are integers.
Possible combinations of integers whose product equal 72 are : (1, 72), (2, 36), (3, 24), (4, 18), (6, 12) and (8, 9) where both r1 and r2 are positive. 6 combinations.
If the roots are r1 and r2, then r1 * r2 = 72, where both r1 and r2 are integers.
Possible combinations of integers whose product equal 72 are : (1, 72), (2, 36), (3, 24), (4, 18), (6, 12) and (8, 9) where both r1 and r2 are positive. 6 combinations.
For each of these combinations, both r1 and r2 could be negative and their product will still be 72.
i.e., r1 and r2 can take the following values too : (-1, -72), (-2, -36), (-3, -24), (-4, -18), (-6, -12) and (-8, -9). 6 combinations.
i.e., r1 and r2 can take the following values too : (-1, -72), (-2, -36), (-3, -24), (-4, -18), (-6, -12) and (-8, -9). 6 combinations.
Therefore, 12 combinations are possible where the product of r1 and r2 is 72.
Hence, 'b' will take 12 possible values.
Hence, 'b' will take 12 possible values.
The three-digit positive integer x has the hundreds, tens, and units digits of a, b, and c, respectively. The three-digit positive integer y has the hundreds, tens, and units digits of k, l , and m, respectively. If (2a)(3b)(5c) = 12(2k)(3l)(5m), what is the value of x – y?- a)21
- b)200
- c)210
- d)300
- e)310
Correct answer is option 'C'. Can you explain this answer?
The three-digit positive integer x has the hundreds, tens, and units digits of a, b, and c, respectively. The three-digit positive integer y has the hundreds, tens, and units digits of k, l , and m, respectively. If (2a)(3b)(5c) = 12(2k)(3l)(5m), what is the value of x – y?
a)
21
b)
200
c)
210
d)
300
e)
310

|
Tanishq Yadav answered |
First, let us simplify the exponential equation:
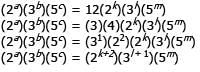
When the bases on both sides of an equation are equal and the bases are prime numbers, the exponents of the respective bases must also be equal: a = k + 2; b = l + 1; and c = m . Now recall that a , b , and c represent the hundreds, tens, and units digits of the three-digit integer x ; similarly, k , l , and m represent the hundreds, tens, and units digits of the three-digit integer y .
Therefore, the hundreds digit of x is 2 greater than the hundreds digit of y ; the tens digit of x is 1 greater than the tens digit of y ; finally, the units digit of x is equal to the units digit of y . Using this information, we can set up our subtraction problem and find the value of (x – y ):
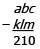
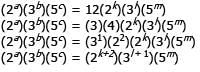
When the bases on both sides of an equation are equal and the bases are prime numbers, the exponents of the respective bases must also be equal: a = k + 2; b = l + 1; and c = m . Now recall that a , b , and c represent the hundreds, tens, and units digits of the three-digit integer x ; similarly, k , l , and m represent the hundreds, tens, and units digits of the three-digit integer y .
Therefore, the hundreds digit of x is 2 greater than the hundreds digit of y ; the tens digit of x is 1 greater than the tens digit of y ; finally, the units digit of x is equal to the units digit of y . Using this information, we can set up our subtraction problem and find the value of (x – y ):
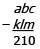
A children's gift store sells gift certificates in denominations of $3 and $5. The store sold 'm' $3 certificates and 'n' $5 certificates worth $93 on a Saturday afternoon. If 'm' and 'n' are natural numbers, how many different values can 'm' take?- a)5
- b)7
- c)6
- d)31
- e)18
Correct answer is option 'C'. Can you explain this answer?
A children's gift store sells gift certificates in denominations of $3 and $5. The store sold 'm' $3 certificates and 'n' $5 certificates worth $93 on a Saturday afternoon. If 'm' and 'n' are natural numbers, how many different values can 'm' take?
a)
5
b)
7
c)
6
d)
31
e)
18

|
Rhea Gupta answered |
Step 1: Understand Key Data
Total value of all certificates sold = $93.
Certificates sold were in denominations of $3 and $5.
Both 'm' and 'n' are natural numbers.
Approach to solve this GMAT Algebra Word Problem
The value of all certificates sold, 93 is divisible by 3.
So, a maximum of 31 $3 certificates and no $5 certificates could have been sold.
However, the question states that both 'm' and 'n' are natural numbers.
Hence, at least 1 $5 certificate should have been sold.
Certificates sold were in denominations of $3 and $5.
Both 'm' and 'n' are natural numbers.
Approach to solve this GMAT Algebra Word Problem
The value of all certificates sold, 93 is divisible by 3.
So, a maximum of 31 $3 certificates and no $5 certificates could have been sold.
However, the question states that both 'm' and 'n' are natural numbers.
Hence, at least 1 $5 certificate should have been sold.
Let us reduce the number of $3 certificates from theoretical maximum count of 31 by say 'x' and correspondingly increase $5 certificates by 'y'.
Evidently, 3x = 5y because the value of $3 certificates reduced should be the same as the value of $5 certificates increased.
Evidently, 3x = 5y because the value of $3 certificates reduced should be the same as the value of $5 certificates increased.
It means that x has to be a multiple of 5 and y has to be a multiple of 3.
Or $3 certificates reduce in steps of 5 certificates.
Or $3 certificates reduce in steps of 5 certificates.
Step 2 of solving this GMAT Algebra Question: List down possible values for 'm' and 'n'
The following combinations are possible.
The following combinations are possible.
m = 26, n = 3
m = 21, n = 6
m = 16, n = 9
m = 11, n = 12
m = 6, n = 15
m = 1, n = 18
The question is "How many different values can 'm' take?"
Hence, m can take 6 values.
m = 21, n = 6
m = 16, n = 9
m = 11, n = 12
m = 6, n = 15
m = 1, n = 18
The question is "How many different values can 'm' take?"
Hence, m can take 6 values.
Choice C is the correct answer.
For what values of 'k' will the pair of equations 3x + 4y = 12 and kx + 12y = 30 NOT have a unique solution?- a)9
- b)12
- c)3
- d)7.5
- e)2.5
Correct answer is option 'A'. Can you explain this answer?
For what values of 'k' will the pair of equations 3x + 4y = 12 and kx + 12y = 30 NOT have a unique solution?
a)
9
b)
12
c)
3
d)
7.5
e)
2.5

|
Rutuja Banerjee answered |
A system of linear equations ax + by + c = 0 and dx + ey + g = 0 will have a unique solution if the two lines represented by the equations ax + by + c = 0 and dx + ey + g = 0 intersect at a point.
i.e., if the two lines are neither parallel nor coincident.
Essentially, the slopes of the two lines should be different.
i.e., if the two lines are neither parallel nor coincident.
Essentially, the slopes of the two lines should be different.
What does that translate into?
ax + by + c = 0 and dx + ey + g = 0 will intersect at one point if their slopes are different.
Express both the equations in the standardized y = mx + c format, where 'm' is the slope of the line and 'c' is the y-intercept.
ax + by + c = 0 and dx + ey + g = 0 will intersect at one point if their slopes are different.
Express both the equations in the standardized y = mx + c format, where 'm' is the slope of the line and 'c' is the y-intercept.
ax + by + c = 0 can be written as 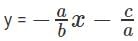
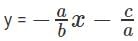
And dx + ey + g = 0 can be written as


Slope of the first line is -a/b and that of the second line is -d/e
For a unique solution, the slopes of the lines should be different.
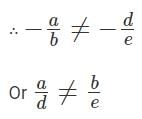
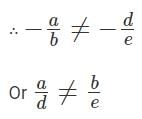
Condition for the equations to NOT have a unique solution
The slopes should be equal
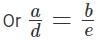
Apply the condition in the given equations to find k
In the question given above, a = 3, b = 4, d = k and e = 12.
Therefore,
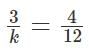
The slopes should be equal
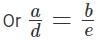
Apply the condition in the given equations to find k
In the question given above, a = 3, b = 4, d = k and e = 12.
Therefore,
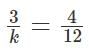
Or 'k' should be equal to 9 for the system of linear equations to NOT have a unique solution.
The question is "What is the value of k?
When k = 9, the system of equations will represent a pair of parallel lines (their y-intercepts are different). So, there will be NO solution to this system of linear equations in two variables.
Choice A is the correct answer.
When k = 9, the system of equations will represent a pair of parallel lines (their y-intercepts are different). So, there will be NO solution to this system of linear equations in two variables.
Choice A is the correct answer.
For what value of 'm' will the quadratic equation x2 - mx + 4 = 0 have real and equal roots?- a)16
- b)8
- c)2
- d)-4
- e)Choice (B) and (C)
Correct answer is option 'D'. Can you explain this answer?
For what value of 'm' will the quadratic equation x2 - mx + 4 = 0 have real and equal roots?
a)
16
b)
8
c)
2
d)
-4
e)
Choice (B) and (C)

|
Palak Saha answered |
Understanding Quadratic Equations
A quadratic equation in the form ax² + bx + c = 0 has real and equal roots when its discriminant (D) is equal to zero. The discriminant is calculated using the formula:
D = b² - 4ac
In this case, the equation is x² - mx + 4 = 0. Here, a = 1, b = -m, and c = 4.
Finding the Discriminant
To find the condition for real and equal roots:
- Substitute a, b, and c into the discriminant formula:
D = (-m)² - 4(1)(4)
- This simplifies to:
D = m² - 16
Setting the Discriminant to Zero
For the roots to be real and equal, we set the discriminant equal to zero:
m² - 16 = 0
Solving for m
Now, solve for m:
- Rearranging gives:
m² = 16
- Taking the square root of both sides results in:
m = ±4
Identifying the Correct Option
From the values obtained (m = 4 and m = -4), we can see that:
- The possible values of m are 4 and -4.
- The question specifies the correct option as 'D', which corresponds to -4.
Therefore, the value of m that will ensure the quadratic equation x² - mx + 4 = 0 has real and equal roots is indeed -4.
A quadratic equation in the form ax² + bx + c = 0 has real and equal roots when its discriminant (D) is equal to zero. The discriminant is calculated using the formula:
D = b² - 4ac
In this case, the equation is x² - mx + 4 = 0. Here, a = 1, b = -m, and c = 4.
Finding the Discriminant
To find the condition for real and equal roots:
- Substitute a, b, and c into the discriminant formula:
D = (-m)² - 4(1)(4)
- This simplifies to:
D = m² - 16
Setting the Discriminant to Zero
For the roots to be real and equal, we set the discriminant equal to zero:
m² - 16 = 0
Solving for m
Now, solve for m:
- Rearranging gives:
m² = 16
- Taking the square root of both sides results in:
m = ±4
Identifying the Correct Option
From the values obtained (m = 4 and m = -4), we can see that:
- The possible values of m are 4 and -4.
- The question specifies the correct option as 'D', which corresponds to -4.
Therefore, the value of m that will ensure the quadratic equation x² - mx + 4 = 0 has real and equal roots is indeed -4.
What is the sum of the squares of x2 and y2?(1) x8 – y8 = 6(2) x4 – y4 = 2- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
What is the sum of the squares of x2 and y2?
(1) x8 – y8 = 6
(2) x4 – y4 = 2
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Arya Yadav answered |
Steps 1 & 2: Understand Question and Draw Inferences
We need to find the sum of the squares of x2 and y2.
Square of x2 = (x2)2 = x4
Square of y2 = (y2)2 = y4
Therefore we need to find the value of the expression x4 + y4
Step 3: Analyze Statement 1
Statement (1) says:
x8 – y8 = 6
We know that: x8 – y8 = (x4 + y4)(x4 – y4 )
[Formula used: (a2 - b2) = (a + b)(a - b)
This means that,(x4 + y4)(x4 – y4 ) = 6 ……………… (I)
However, we don’t know the value of the expression (x4 – y4 )
Therefore statement 1 alone is not sufficient to arrive at a unique answer
Step 4: Analyze Statement 2
Statement (2) says:
(x4 – y4 ) = 2 ……………………(II)
However, this alone doesn’t help us in finding the value of (x4 + y4)
Therefore statement 2 alone is not sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
Now let us look at both the statements together.
Using (II) in (I), we get:
(x4 + y4) * 2 = 6
(x4 + y4) = 3
Statement (1) and statement (2) together are sufficient to arrive at a unique answer.
Correct Answer: C
What is the value of  where a ≠0?(i) a = 8(ii) b = 16a
where a ≠0?(i) a = 8(ii) b = 16a- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
What is the value of  where a ≠0?
where a ≠0?
(i) a = 8
(ii) b = 16a
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
EduRev GMAT answered |
Step 1: Simplify the Given Expression
We need to find the value of the expression:
((a - b)² - (a² + b²) + 4ab) / a²
Let's simplify the numerator first:
(a² - 2ab + b²) - (a² + b²) + 4ab
a² - 2ab + b² - a² - b² + 4ab = 2ab
- Expand (a - b)²: a² - 2ab + b²
- Substitute back into the expression:
- Simplify the terms:
Now, the expression simplifies to:
2ab / a² = 2b / a
Step 2: Analyze Each Statement
- Statement (1): a = 8
Substitute a = 8 into the simplified expression:2b / 8 = b / 4Here, we still don't know the value of b. Therefore, Statement (1) alone is insufficient. - Statement (2): b = 16a
Substitute b = 16a into the simplified expression:2 * 16a / a = 32a / a = 32Since a ≠ 0, the a terms cancel out, and we get a definite value of 32. Therefore, Statement (2) alone is sufficient.
Step 3: Evaluate Combined Statements
While combining both statements would provide consistent values, it's unnecessary because Statement (2) alone already gives us a definitive answer.
Final Determination:
- Statement (1) Alone: Insufficient.
- Statement (2) Alone: Sufficient.
- Both Statements Together: Sufficient but redundant.
Therefore, the correct option is:
b) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
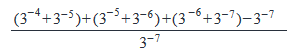 is what multiple of 17?
is what multiple of 17?- a)1
- b)2Update Question
- c)3
- d)4
- e)11
Correct answer is option 'C'. Can you explain this answer?
is what multiple of 17?
a)
1
b)
2Update Question
c)
3
d)
4
e)
11

|
Arya Yadav answered |
Step 1: Question statement and Inferences
Set up the fraction without the brackets so you can simplify it.
Step 2 & 3: Simplifying the fraction and calculating the final answer
Turn the bottom negative exponent into a fraction:
Multiply the numerator and denominator with 37:
(3−4+3−5+3−5+3−6+3−6)×37
Distribute the 37 among the other exponents:
(33+32+32+31+31)
Simplify the remaining numbers:
(27+9+9+3+3)
51
51 = 17 * 3
Answer: Option (C)
Find the value of the expression: 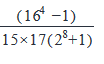
- a)1/15
- b)1
- c)15
- d)255
- e)1023
Correct answer is option 'B'. Can you explain this answer?
Find the value of the expression: 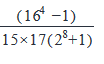
a)
1/15
b)
1
c)
15
d)
255
e)
1023

|
Sounak Iyer answered |
Step 1: Question statement and Inferences
This question is based on the concept that n2 – 1 = (n – 1)(n + 1)
Step 2 & 3: Finding required values and calculating the final answer
Apply the n2 – 1 concept to the numerator:
Apply the n2 – 1 concept again to the 162 – 1: = (16-1)(16+1)=15*17
Cancel the 15 × 17 from top and bottom:
Convert 16 to 24 :
Convert (24)2 to 28 :
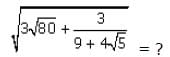
- a)2√3√5
- b)3
- c)3√3
- d)9+4√5
- e)3+2√5
Correct answer is option 'C'. Can you explain this answer?
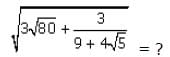
a)
2√3√5
b)
3
c)
3√3
d)
9+4√5
e)
3+2√5

|
Isha Sen answered |
A radical expression in a denominator is considered non-standard. To eliminate a radical in the denominator, we can multiply both the numerator and the denominator by the conjugate of that denominator.
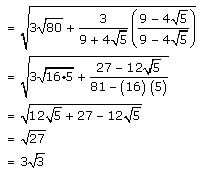
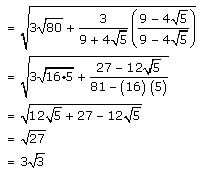
A salesman’s monthly wage is calculated as follows:He gets paid $80 for every deal that he makes and gets a deduction of $30 for every deal that he fails to make. If he gets paid a wage of S in a month and attempts a total of D number of deals in the month, how many deals does he fail to make?- a)
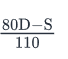
- b)
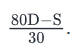
- c)
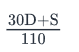
- d)
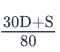
- e)
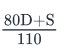
Correct answer is option 'A'. Can you explain this answer?
A salesman’s monthly wage is calculated as follows:
He gets paid $80 for every deal that he makes and gets a deduction of $30 for every deal that he fails to make. If he gets paid a wage of S in a month and attempts a total of D number of deals in the month, how many deals does he fail to make?
a)
b)
c)
d)
e)
|
|
Ruseau Samuels answered |
If a is the correct answer, aren't we considering failed deals twice in it?
For how many real values of x is this expression equal to zero? 
- a)0
- b)1
- c)2
- d)4
- e)6
Correct answer is option 'C'. Can you explain this answer?
For how many real values of x is this expression equal to zero?
a)
0
b)
1
c)
2
d)
4
e)
6

|
Aditya Gupta answered |
Step 1: Question statement and Inferences
The fraction is equal to zero when the numerator is equal to zero.
Step 2 & 3: Simplifying the fraction and calculating the final answer
For the fraction to equal zero, (x2 + x4 -x6) has to equal 1 to subtract with the 1 on its left:
The only way that (x2 + x4 -x6) can equal 1 is if x = 1 or –1. There are two possible values of x: 1 and –1.
Note that x cannot equal 2 or –2, making the denominator equal 0. This would result in a non-real number, which is not equal to 0.
Answer: Option (C)
If one of the roots of the quadratic equation x2 + mx + 24 = 0 is 1.5, then what is the value of m?- a)-22.5
- b)16
- c)-10.5
- d)-17.5
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
If one of the roots of the quadratic equation x2 + mx + 24 = 0 is 1.5, then what is the value of m?
a)
-22.5
b)
16
c)
-10.5
d)
-17.5
e)
Cannot be determined

|
Sankar Desai answered |
If 1.5 is a root of the quadratic equation, substituting x = 1.5 in the equation will satisfy the equation.
The given quadratic equation is x2 + mx + 24 = 0
Substitute x = 1.5 in the above equation because 1.5 is a root of the equation.
(1.5)2 + 1.5m + 24 = 0
2.25 + 1.5m + 24 = 0
Substitute x = 1.5 in the above equation because 1.5 is a root of the equation.
(1.5)2 + 1.5m + 24 = 0
2.25 + 1.5m + 24 = 0
1.5m = -26.25 Or 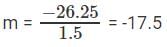
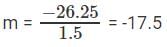
If (a + b)2 = x and (a – b)2 = y, then what is the value of 2ab in terms of x and y?- a)
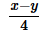
- b)
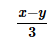
- c)
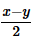
- d)
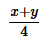
- e)
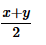
Correct answer is option 'C'. Can you explain this answer?
If (a + b)2 = x and (a – b)2 = y, then what is the value of 2ab in terms of x and y?
a)
b)
c)
d)
e)

|
Malavika Choudhury answered |
Step 1: Question statement and Inferences
I:
(a + b)2 = x
a2 + b2 + 2ab = x
Similarly,
II:
(a – b)2 = y
a2 + b2 – 2ab = y
Step 2:Finding required values
If we subtract y from x, we have
x – y = (a2 + b2 + 2ab) – (a2 + b2 -2ab) = 4ab
We have eliminated a2 and b2. We are very close to the answer.
Step 3: Calculating the final answer
The question requires us to find the expression for 2ab. We have already obtained the expression for 4ab.
Lets divide both sides by 2,
What is the highest integral value of 'k' for which the quadratic equation x2 - 6x + k = 0 will have two real and distinct roots?- a)9
- b)7
- c)3
- d)8
- e)12
Correct answer is option 'D'. Can you explain this answer?
What is the highest integral value of 'k' for which the quadratic equation x2 - 6x + k = 0 will have two real and distinct roots?
a)
9
b)
7
c)
3
d)
8
e)
12

|
Nilotpal Sen answered |
Step 1:
Nature of Roots of Quadratic Equation Theory
D is called the Discriminant of a quadratic equation.
D = b2 - 4ac for quadratic equations of the form ax2 + bx + c = 0.
If D > 0, roots of such quadratic equations are Real and Distinct
If D = 0, roots of such quadratic equations are Real and Equal
If D < 0, roots of such quadratic equations are Imaginary. i.e., such quadratic equations will NOT have real roots.
In this GMAT sample question in algebra, we have to determine the largest integer value that ‘k’ can take such that the discriminant of the quadratic equation is positive.
D = b2 - 4ac for quadratic equations of the form ax2 + bx + c = 0.
If D > 0, roots of such quadratic equations are Real and Distinct
If D = 0, roots of such quadratic equations are Real and Equal
If D < 0, roots of such quadratic equations are Imaginary. i.e., such quadratic equations will NOT have real roots.
In this GMAT sample question in algebra, we have to determine the largest integer value that ‘k’ can take such that the discriminant of the quadratic equation is positive.
Step 2:
Compute maximum value of k that will make the discriminant of the quadratic equation positive
The given quadratic equation is x2 - 6x + k = 0.
In this equation, a = 1, b = -6 and c = k
The value of the discriminant, D = 62 - 4 * 1 * k
We have compute values of 'k' for which D > 0.
i.e., 36 – 4k > 0
Or 36 > 4k or k < 9.
The given quadratic equation is x2 - 6x + k = 0.
In this equation, a = 1, b = -6 and c = k
The value of the discriminant, D = 62 - 4 * 1 * k
We have compute values of 'k' for which D > 0.
i.e., 36 – 4k > 0
Or 36 > 4k or k < 9.
The question is "What is the highest integer value that k can take?"
If k < 9, the highest integer value that k can take is 8.
If k < 9, the highest integer value that k can take is 8.
Choice D is the correct answer.
The cost C and revenue R of a product depend on the number of units x produced. The equations are: - C=5000+20x
- R=50x
Find the number of units x that must be produced for the company to break even (i.e., where revenue equals cost).- a)167
- b)210
- c)165
- d)170
- e)200
Correct answer is option 'A'. Can you explain this answer?
The cost C and revenue R of a product depend on the number of units x produced. The equations are:
- C=5000+20x
- R=50x
Find the number of units x that must be produced for the company to break even (i.e., where revenue equals cost).
a)
167
b)
210
c)
165
d)
170
e)
200

|
EduRev GMAT answered |
- To find the break-even point, set C=R
- 5000+20x=50x
- Rearrange terms:
- 5000=30x
- hence, x = 166.66 = 167 units.
 , where x ≠ -1 and x ≠ 1If x is replaced with - 1/x in the expression P, the expression Q is obtained. Which of the following is the correct relationship between P and Q?
, where x ≠ -1 and x ≠ 1If x is replaced with - 1/x in the expression P, the expression Q is obtained. Which of the following is the correct relationship between P and Q?- a)PQ = 1
- b)PQ = -1
- c)P/Q=1
- d)P/Q=−1
- e)P/Q2=1
Correct answer is option 'B'. Can you explain this answer?
If x is replaced with - 1/x in the expression P, the expression Q is obtained. Which of the following is the correct relationship between P and Q?
a)
PQ = 1
b)
PQ = -1
c)
P/Q=1
d)
P/Q=−1
e)
P/Q2=1

|
Aditya Sharma answered |
Step 1: Question statement and Inferences
We have to replace x everywhere in the given expression for P with −1/x
Step 2: Finding required values
Replacing x with −1/x
, we get Q.
Multiplying the numerator and the denominator with -1, we have
Multiplying the numerator and the denominator with x3, we have
Step 3: Calculating the final answer
Notice the similarity between P and Q.
Are P and 1/Q equal? No.
How about - 1/Q ?
In other words, PQ = -1
Answer: Option (B)
If 274x + 2 × 162-2x × 36x × 96 – 2x = 1, then what is the value of x?- a)-9
- b)-6
- c)3
- d)6
- e)9
Correct answer is option 'A'. Can you explain this answer?
If 274x + 2 × 162-2x × 36x × 96 – 2x = 1, then what is the value of x?
a)
-9
b)
-6
c)
3
d)
6
e)
9

|
Abhishek Choudhury answered |
An effective strategy for problems involving exponents is to break the bases of all the exponents into prime factors. This technique will allow us to combine like terms:
274x + 2 × 162-2x × 36x × 96 – 2x = 1 (33)4x + 2 × (2 × 34)-2x × (22 × 32)x × (32)6 – 2x = 1
312x + 6 × 2-2x × 3-8x × 22x × 32x × 312 – 4x = 1
2-2x + 2x × 312x + 6 – 8x + 2x + 12 – 4x = 1
20 × 3 2x + 18 = 1
3 2x + 18 = 1
3 2x + 18 = 30
2x + 18 = 0
2x = -18
x = -9
274x + 2 × 162-2x × 36x × 96 – 2x = 1 (33)4x + 2 × (2 × 34)-2x × (22 × 32)x × (32)6 – 2x = 1
312x + 6 × 2-2x × 3-8x × 22x × 32x × 312 – 4x = 1
2-2x + 2x × 312x + 6 – 8x + 2x + 12 – 4x = 1
20 × 3 2x + 18 = 1
3 2x + 18 = 1
3 2x + 18 = 30
2x + 18 = 0
2x = -18
x = -9
If b≠0 and (a/b) +3 = {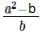 }, then 2b =
}, then 2b =- a)
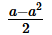
- b)0
- c)
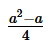
- d)1
- e)
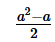
Correct answer is option 'E'. Can you explain this answer?
If b≠0 and (a/b) +3 = {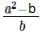 }, then 2b =
}, then 2b =
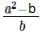 }, then 2b =
}, then 2b =a)
b)
0
c)
d)
1
e)

|
Niti Choudhury answered |
We need to find the value of 2b.
Given equation is:

(We can safely cancel b from both sides since it is given that b≠0)
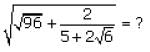 lies between:
lies between:- a)1 & 2
- b)2 & 3
- c)3 & 4
- d)4 & 5
- e)5 & 6
Correct answer is option 'C'. Can you explain this answer?
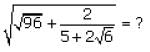 lies between:
lies between:a)
1 & 2
b)
2 & 3
c)
3 & 4
d)
4 & 5
e)
5 & 6

|
Tejas Gupta answered |
The first culprit in this expression is the radical in the denominator. Radicals in the denominator are dealt with by multiplying the fraction with an expression that is equal to 1 but contains a “canceling radical” in both the numerator and denominator.
For example,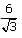 is simplified by multiplying by
is simplified by multiplying by 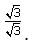
In the case of a complex radical, such as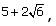 we multiply by the conjugate,
we multiply by the conjugate,  as follows:
as follows:

Simplifying radicals in the denominator with conjugate radical expressions is very useful on challenging GMAT radical questions.
For example,
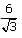 is simplified by multiplying by
is simplified by multiplying by 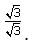
In the case of a complex radical, such as
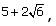 we multiply by the conjugate,
we multiply by the conjugate,  as follows:
as follows:
Simplifying radicals in the denominator with conjugate radical expressions is very useful on challenging GMAT radical questions.
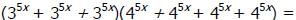
- a)125x+1
- b)315x + 420x
- c)255x
- d)735x
- e)255x+1
Correct answer is option 'A'. Can you explain this answer?
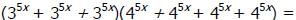
a)
125x+1
b)
315x + 420x
c)
255x
d)
735x
e)
255x+1

|
Malavika Choudhury answered |
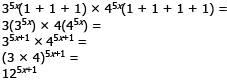
Remember that when you multiply different bases raised to the SAME exponent, the product is simply the product of the bases raised to their common exponent.
If y >2, and 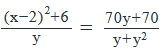 which of the following could be the value of 2x + 3?
which of the following could be the value of 2x + 3? - a)-9
- b)-6
- c)0
- d)10
- e)17
Correct answer is option 'A'. Can you explain this answer?
If y >2, and 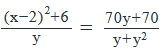 which of the following could be the value of 2x + 3?
which of the following could be the value of 2x + 3?
a)
-9
b)
-6
c)
0
d)
10
e)
17

|
Aditya Gupta answered |
Given equation is:
(Let’s call the above equation as I)
We need to find the value of 2x + 3
On the RHS of I, notice that:
- The numerator: 70y+70=70(y+1)
- The denominator: y+y2=y(1+y)
Therefore I can written as:
Observe that you can cancel the common term in the numerator and denominator.
Similarly, you can cancel the common term in the denominator of LHS and the denominator of RHS.
(Note that it is given that y>2 and therefore neither y nor y+1 can be zero. So we can safely cancel these terms out.)
(x−2)2+6=70
- (x−2)2=64
- (x−2)=±8
Case 1:
(x - 2) = 8
- x = 10
- 2x + 3 = 23
Case 2:
(x - 2) = -8
- x = -6
- 2x + 3 = -9
In the given options, -9 is given.
Correct Answer: A
Chapter doubts & questions for Algebra Introduction - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Algebra Introduction - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup










