All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Two-Part Analysis for GMAT Exam
Mike is considering job offers from two competing firms. Acme Anvils offers an annual salary of $50,000 with a guaranteed increase of 5% every year. Retro Rockets offers an annual salary of $60,000 with a $3,000 increase each year. Find the salary Mike can expect to earn after 20 years with each company.
- a)$97,500, $117,000
- b)$126,348, $117,000
- c)$126,348, $121,750
- d)$151,617, $117,000
- e)$126,348, $132,665
Correct answer is option 'B'. Can you explain this answer?
Mike is considering job offers from two competing firms. Acme Anvils offers an annual salary of $50,000 with a guaranteed increase of 5% every year. Retro Rockets offers an annual salary of $60,000 with a $3,000 increase each year. Find the salary Mike can expect to earn after 20 years with each company.

a)
$97,500, $117,000
b)
$126,348, $117,000
c)
$126,348, $121,750
d)
$151,617, $117,000
e)
$126,348, $132,665

|
EduRev GMAT answered |
If Mike accepts the offer from Acme Anvils, his year 20 salary will reflect 19 increases of 5% and will be $50,000 × 1.0519 = $126,347.51. If he takes the job with Retro Rockets, he will have received 19 raises of $3,000 each, and his salary will be $60,000 + 19 × $3,000 = $117,000.
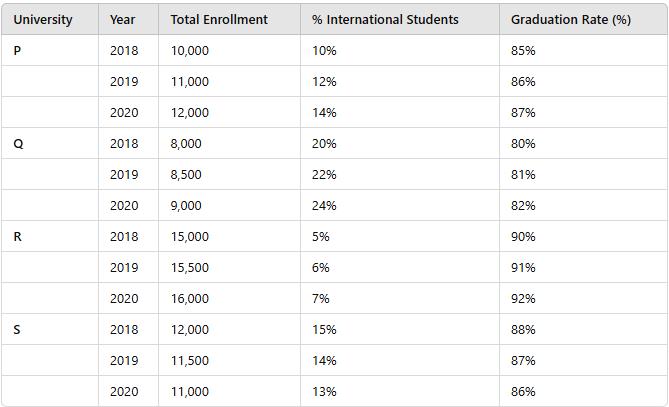
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).
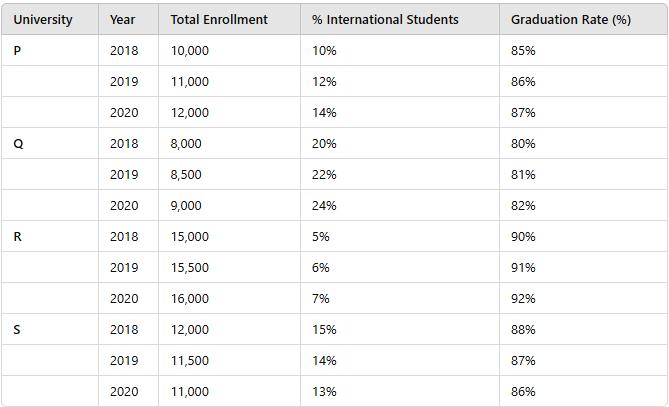 What was the percentage increase in total enrollment for University P from 2018 to 2020?
What was the percentage increase in total enrollment for University P from 2018 to 2020?- a)15%
- b)20%
- c)25%
- d)30%
Correct answer is option 'B'. Can you explain this answer?
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).

What was the percentage increase in total enrollment for University P from 2018 to 2020?
a)
15%
b)
20%
c)
25%
d)
30%

|
EduRev GMAT answered |
Calculate the percentage increase in enrollment for University P:
Percentage Increase = [(12,000 - 10,000) / 10,000] × 100% = (2,000 / 10,000) × 100% = 20%
Percentage Increase = [(12,000 - 10,000) / 10,000] × 100% = (2,000 / 10,000) × 100% = 20%
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).
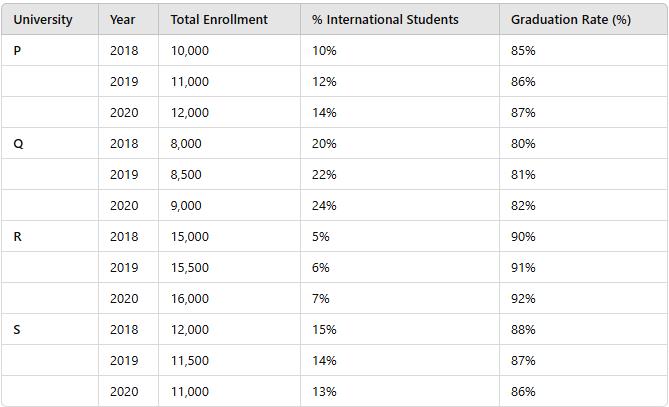 Which university had the highest average graduation rate over the three years?
Which university had the highest average graduation rate over the three years?- a)University P
- b)University Q
- c)University R
- d)University S
Correct answer is option 'C'. Can you explain this answer?
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).

Which university had the highest average graduation rate over the three years?
a)
University P
b)
University Q
c)
University R
d)
University S

|
EduRev GMAT answered |
Calculate the average graduation rate for each university:
University P: (85% + 86% + 87%) / 3 ≈ 86%
University Q: (80% + 81% + 82%) / 3 ≈ 81%
University R: (90% + 91% + 92%) / 3 ≈ 91%
University S: (88% + 87% + 86%) / 3 ≈ 87%
Conclusion:
University R had the highest average graduation rate of 91%.
University P: (85% + 86% + 87%) / 3 ≈ 86%
University Q: (80% + 81% + 82%) / 3 ≈ 81%
University R: (90% + 91% + 92%) / 3 ≈ 91%
University S: (88% + 87% + 86%) / 3 ≈ 87%
Conclusion:
University R had the highest average graduation rate of 91%.
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).
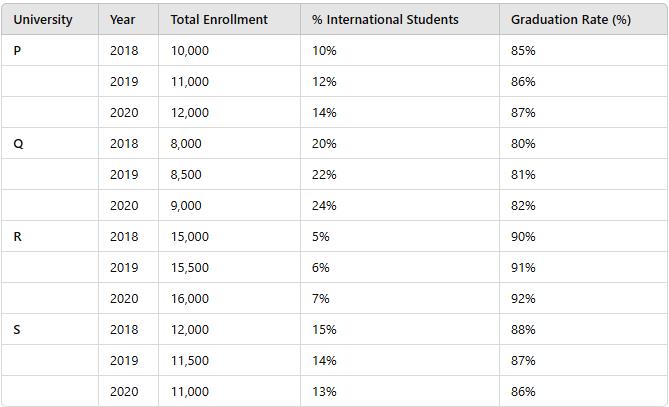 In 2020, which university had the highest number of international students?
In 2020, which university had the highest number of international students?- a)University P
- b)University Q
- c)University R
- d)University S
Correct answer is option 'B'. Can you explain this answer?
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).

In 2020, which university had the highest number of international students?
a)
University P
b)
University Q
c)
University R
d)
University S

|
EduRev GMAT answered |
Calculate the number of international students in 2020 for each university:
- University P: 12,000 × 14% = 1,680 students
- University Q: 9,000 × 24% = 2,160 students
- University R: 16,000 × 7% = 1,120 students
- University S: 11,000 × 13% = 1,430 students
Registrants for a conference were asked to choose a room for single or double occupancy and to reserve seating for lunches only or for lunches and dinners. A total of 1,250 people registered for the conference, and 250 of those requested single-occupancy rooms. Two hundred people reserved lunch-only seating, and 50 declined all meal service. Find the number of dinners that will be needed and the total number of rooms reserved.
- a)1000, 750
- b)1250, 750
- c)500, 250
- d)750, 1250
- e)1000, 500
Correct answer is option 'A'. Can you explain this answer?
Registrants for a conference were asked to choose a room for single or double occupancy and to reserve seating for lunches only or for lunches and dinners. A total of 1,250 people registered for the conference, and 250 of those requested single-occupancy rooms. Two hundred people reserved lunch-only seating, and 50 declined all meal service. Find the number of dinners that will be needed and the total number of rooms reserved.


a)
1000, 750
b)
1250, 750
c)
500, 250
d)
750, 1250
e)
1000, 500

|
EduRev GMAT answered |
The conference organizers need 250 single rooms, and the remaining 1,000 people can be housed in 500 double rooms, so a total of 750 rooms will be needed. For meals, 50 of the 1,250 attendees declined all meals, and 200 more chose only lunches, so 1,250 – 50 – 200 = 1,000 people reserved dinner seating.
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).
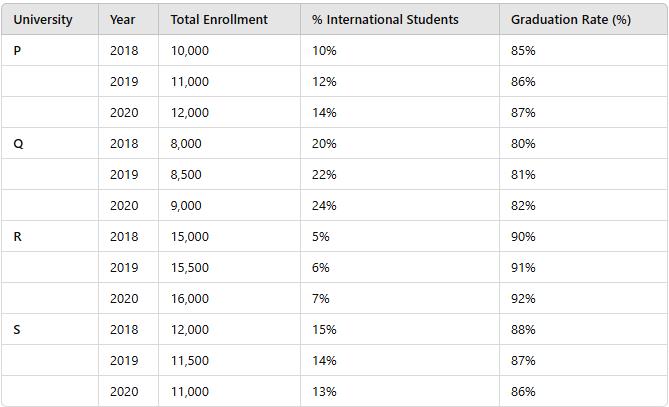 Which university had the greatest total number of graduates in 2019?
Which university had the greatest total number of graduates in 2019?- a)University P
- b)University Q
- c)University R
- d)University S
Correct answer is option 'C'. Can you explain this answer?
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).

Which university had the greatest total number of graduates in 2019?
a)
University P
b)
University Q
c)
University R
d)
University S

|
EduRev GMAT answered |
Calculate the number of graduates in 2019:
- University P: 11,000 × 86% = 9,460 graduates
- University Q: 8,500 × 81% = 6,885 graduates
- University R: 15,500 × 91% = 14,105 graduates
- University S: 11,500 × 87% = 10,005 graduates
Conclusion:
University R had the greatest number of graduates with 14,105.
University R had the greatest number of graduates with 14,105.
Marcel is taking a trip, driving at a constant speed of X miles per hour for the first 2 hours of his trip, and at a constant speed of Y miles per hour after the first 2 hours.In terms of X and Y, select the expression that represents Marcel’s average speed if he drives for a total of 5 hours, and select the expression that represents Marcel’s average speed if he drives for a total of 5X miles. Make only one selection in each column.
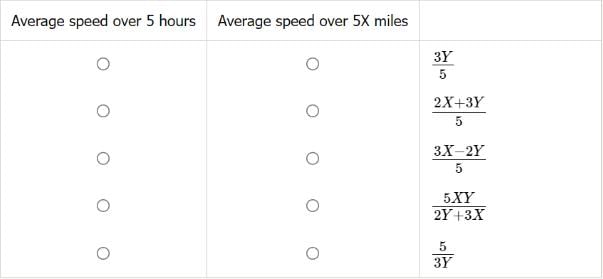
- a)1st option, 4th option
- b)2nd option, 4th option
- c)2nd option, 5th option
- d)3rd option, 5th option
- e)2nd option, 1st option
Correct answer is option 'B'. Can you explain this answer?
Marcel is taking a trip, driving at a constant speed of X miles per hour for the first 2 hours of his trip, and at a constant speed of Y miles per hour after the first 2 hours.
In terms of X and Y, select the expression that represents Marcel’s average speed if he drives for a total of 5 hours, and select the expression that represents Marcel’s average speed if he drives for a total of 5X miles. Make only one selection in each column.


a)
1st option, 4th option
b)
2nd option, 4th option
c)
2nd option, 5th option
d)
3rd option, 5th option
e)
2nd option, 1st option

|
EduRev GMAT answered |
The first question is easier to answer. If Marcel drives for 5 hours, then he goes at a constant speed of X for 2 hours and at a constant speed of Y for the remaining 3 hours. Thus, his average speed is
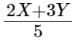
Now, if Marcel travels a total of 5X miles, then over the first 2 hours he covers 2X miles, so he has 3X miles left to travel at a speed of Y miles per hour:
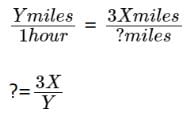
Therefore, in total his trip lasts
2 + 3X/Yhours.
You can now find his average speed for the trip:
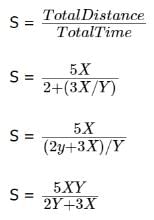
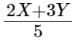
Now, if Marcel travels a total of 5X miles, then over the first 2 hours he covers 2X miles, so he has 3X miles left to travel at a speed of Y miles per hour:
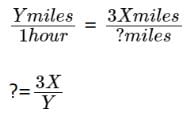
Therefore, in total his trip lasts
2 + 3X/Yhours.
You can now find his average speed for the trip:
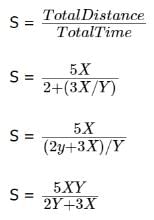
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).
 In which university did the percentage of international students decrease over the three years?
In which university did the percentage of international students decrease over the three years?- a)University P
- b)University Q
- c)University R
- d)University S
Correct answer is option 'D'. Can you explain this answer?
The following table presents data for four universities (P, Q, R, S) over the years 2018 to 2020. The data includes Total Enrollment, Percentage of International Students (%), and Graduation Rate (%).

In which university did the percentage of international students decrease over the three years?
a)
University P
b)
University Q
c)
University R
d)
University S

|
EduRev GMAT answered |
Observe the percentage of international students over the years for University S:
- 2018: 15%
- 2019: 14%
- 2020: 13%
Conclusion:
University S experienced a decrease in the percentage of international students.
University S experienced a decrease in the percentage of international students.
Light The Stage, a stage lighting equipment rental company, charges $x for the first four weeks that a lighting instrument is rented, and $y per week for each week after that. The company 1564 Theatre Group has budgeted $2,000 to spend on the rental of lighting instruments from Light TheStage for its upcoming production.
In the table, indicate which expression corresponds to the maximum number of weeks per instrument for which 1564 Theatre Group can rent 10 instruments given its budget, as well as which expression corresponds to the maximum number of instruments 1564 Theatre Group can rent for a total of 10 weeks per instrument given its budget. Make only two selections, one in each column.
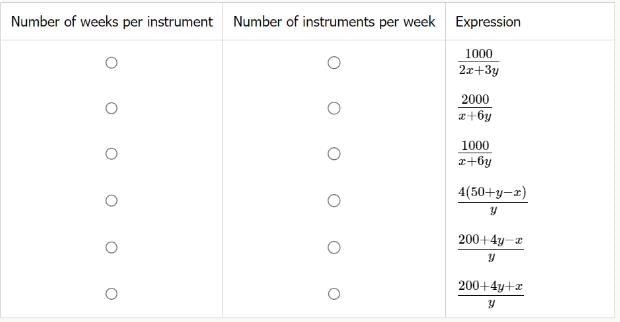
- a)Option 3, Option 2
- b)Option 1, Option 3
- c)Option 4, Option 3
- d)Option 5, Option 2
- e)Option 4, Option 2
Correct answer is option 'D'. Can you explain this answer?
Light The Stage, a stage lighting equipment rental company, charges $x for the first four weeks that a lighting instrument is rented, and $y per week for each week after that. The company 1564 Theatre Group has budgeted $2,000 to spend on the rental of lighting instruments from Light TheStage for its upcoming production.
In the table, indicate which expression corresponds to the maximum number of weeks per instrument for which 1564 Theatre Group can rent 10 instruments given its budget, as well as which expression corresponds to the maximum number of instruments 1564 Theatre Group can rent for a total of 10 weeks per instrument given its budget. Make only two selections, one in each column.


a)
Option 3, Option 2
b)
Option 1, Option 3
c)
Option 4, Option 3
d)
Option 5, Option 2
e)
Option 4, Option 2

|
EduRev GMAT answered |
Step 1: Preview the task.
A quick glance at the answer table tells you that this is a quantitative question. Additionally, all answer choices are algebraic expressions in x and y, so you will have to set up some sort of equation and solve for an unknown quantity.
A quick glance at the answer table tells you that this is a quantitative question. Additionally, all answer choices are algebraic expressions in x and y, so you will have to set up some sort of equation and solve for an unknown quantity.
Step 2: Read the prompt.
You have a vendor, a customer, the customer’s budget, and the vendor’s rental prices. Two absolute values are given (the theater’s lighting rental budget and the 4 weeks of the initial rental rate) and two variables for the two rental rates. Circle back to the tasks you have to perform. Note that they are similar but independent of each other. You will have to set up two algebraic expressions, one for each column, and solve the first one for the number of weeks per instrument, and the second one for the number of instruments per week.
Step 3: Proceed to solving, one column at a time.
Column 1: Let W be the maximum number of weeks that 1564 Theatre Group rents each of the 10 instruments. Then W – 4 is the maximum number of weeks per instrument during which 1564 Theatre Group pays $y per instrument (since for the first 4 weeks it pays $x per instrument—and remember, that’s $x in total for each instrument for the first 4 weeks, not $x per week). The total cost per instrument, then, is x + y(W − 4). The theater company is renting 10 instruments, so its total cost is 10[x + y(W − 4)]
Equate this expression to $2,000 and solve for W:
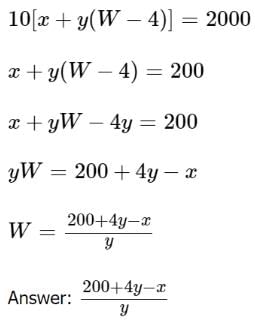
Column 2: Follow the same process you did for column 1. If 1564 Theatre Group is renting each instrument for 10 weeks, then it is paying $x for the first four weeks and $y per week for the remaining 6 weeks. Thus, it is paying
X + 6y in total for each instrument. Let I be the maximum number of instruments the theater company rents. Then, its total cost is I(x + 6y)
Equate this expression to $2,000 and solve for I:
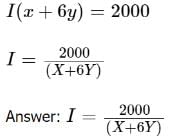
Column 1: Let W be the maximum number of weeks that 1564 Theatre Group rents each of the 10 instruments. Then W – 4 is the maximum number of weeks per instrument during which 1564 Theatre Group pays $y per instrument (since for the first 4 weeks it pays $x per instrument—and remember, that’s $x in total for each instrument for the first 4 weeks, not $x per week). The total cost per instrument, then, is x + y(W − 4). The theater company is renting 10 instruments, so its total cost is 10[x + y(W − 4)]
Equate this expression to $2,000 and solve for W:
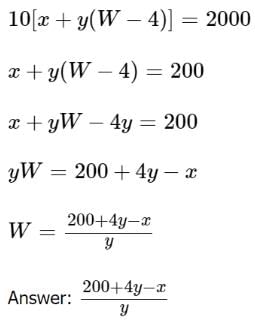
Column 2: Follow the same process you did for column 1. If 1564 Theatre Group is renting each instrument for 10 weeks, then it is paying $x for the first four weeks and $y per week for the remaining 6 weeks. Thus, it is paying
X + 6y in total for each instrument. Let I be the maximum number of instruments the theater company rents. Then, its total cost is I(x + 6y)
Equate this expression to $2,000 and solve for I:
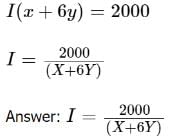
During a lottery, several lots are to be selected. A is the event that a certain subset of these lots is selected, and B is the event that another subset of these lots is selected, such that: - the probability of event A occurring is 2/5.
- the probability of event B occurring is 4/5.
- the probability of the union of events A and B occurring is 1.
- the intersection of events A and B is an event with four desirable outcomes.
In the following table, identify the total number of lots and the number of desirable outcomes in event B. Make only one selection in each column.
- a)15, 20
- b)20, 19
- c)20, 16
- d)16, 18
- e)19, 16
Correct answer is option 'C'. Can you explain this answer?
During a lottery, several lots are to be selected. A is the event that a certain subset of these lots is selected, and B is the event that another subset of these lots is selected, such that:
- the probability of event A occurring is 2/5.
- the probability of event B occurring is 4/5.
- the probability of the union of events A and B occurring is 1.
- the intersection of events A and B is an event with four desirable outcomes.
In the following table, identify the total number of lots and the number of desirable outcomes in event B. Make only one selection in each column.


a)
15, 20
b)
20, 19
c)
20, 16
d)
16, 18
e)
19, 16

|
EduRev GMAT answered |
The probability of the union of events A and B occurring equals the probability of event A occurring, plus the probability of event B occurring, minus the probability of the intersection of events A and B occurring. You know the value of all of these probabilities except the last one. The probability of the intersection of events A and B equals the number of desirable outcomes in the intersection of A and B, which is 4, over the number of total outcomes in the lottery—let’s call that t. Thus, you have:
P (AUB) = P (A) + P (B) - P (A∩B)
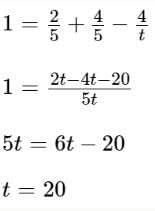
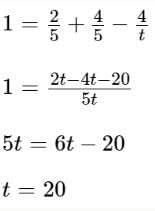
So the correct answer in the first column = the total number of lots is 20.
Next, let the number of desirable outcomes in event B be b. In that case, you have:
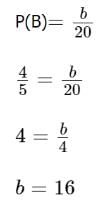
So the correct answer in the second column is: the number of desirable outcomes in event B is 16.
Next, let the number of desirable outcomes in event B be b. In that case, you have:
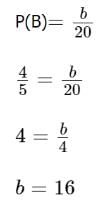
So the correct answer in the second column is: the number of desirable outcomes in event B is 16.
Chapter doubts & questions for Two-Part Analysis - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Two-Part Analysis - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









