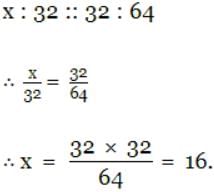All Exams >
Class 6 >
Class 6 All Subjects (Old NCERT) >
All Questions
All questions of Ratio and Proportion for Class 6 Exam
If 2, 3, 28 and x are in proportion then find the value of x.- a)42
- b)28
- c)56
- d)14
Correct answer is option 'A'. Can you explain this answer?
If 2, 3, 28 and x are in proportion then find the value of x.
a)
42
b)
28
c)
56
d)
14
|
Ishan Choudhury answered |
Let present age of father be 7x and that of son is 2x
after 10 years, their ages will be 7x+10 and 2x+10 respectively
so ratio will be
(7x+10)/(2x+10) = 9/4
28x+40 = 18x+90
10x = 50
x = 5
so present age of father is 7x =
35 years
If 12, 14; 9 and x are in proportion then find the value of x.
- a)21
- b)9
- c)10.5
- d)105
Correct answer is option 'C'. Can you explain this answer?
If 12, 14; 9 and x are in proportion then find the value of x.
a)
21
b)
9
c)
10.5
d)
105
|
Varun Kapoor answered |
12/14 = 9/x
12x=9x14
x=9x14/12
x=21/2
x=10.5
12x=9x14
x=9x14/12
x=21/2
x=10.5
If 5, 30, 3 and x are in proportion then find the value of x.
- a)24
- b)6
- c)18
- d)15
Correct answer is option 'C'. Can you explain this answer?
If 5, 30, 3 and x are in proportion then find the value of x.
a)
24
b)
6
c)
18
d)
15
|
EduRev Class 6 answered |
As they are in Proportion
so 5/30=3/x
1/6=3/x
so cross multiply
x=18
so 5/30=3/x
1/6=3/x
so cross multiply
x=18
If 8, 18, 18 and x in proportion then find the value of x.
- a)40.5
- b)18
- c)405
- d)81
Correct answer is option 'A'. Can you explain this answer?
If 8, 18, 18 and x in proportion then find the value of x.
a)
40.5
b)
18
c)
405
d)
81
|
|
Varun Kapoor answered |
8/18 :: 18/x
By cross multiply, we get
8x = 324
x = 40.5
The length and width of a tape are 2 m and 28 cm. What is their ratio?
- a)100:14
- b)7:50
- c)50:7
- d)1:8
Correct answer is option 'C'. Can you explain this answer?
The length and width of a tape are 2 m and 28 cm. What is their ratio?
a)
100:14
b)
7:50
c)
50:7
d)
1:8
|
|
EduRev Class 6 answered |
2m = 2x100 cm = 200 cm
28 cm
200:28
50:7
28 cm
200:28
50:7
If x, 30,24 and 16 are in proportion then find the value of x.- a)45
- b)60
- c)15
- d)80
Correct answer is option 'A'. Can you explain this answer?
If x, 30,24 and 16 are in proportion then find the value of x.
a)
45
b)
60
c)
15
d)
80
|
Mahesh Chavan answered |
Given: x, 30, 24, 16 are in proportion.
To find: The value of x.
Solution:
The given numbers are in proportion. This means that the ratio of any two consecutive numbers is equal to the ratio of the other two consecutive numbers.
Therefore, we can write:
x/30 = 24/16
Cross-multiplying, we get:
16x = 30 × 24
Simplifying, we get:
16x = 720
Dividing both sides by 16, we get:
x = 45
Therefore, the value of x is 45.
Hence, option A is the correct answer.
To find: The value of x.
Solution:
The given numbers are in proportion. This means that the ratio of any two consecutive numbers is equal to the ratio of the other two consecutive numbers.
Therefore, we can write:
x/30 = 24/16
Cross-multiplying, we get:
16x = 30 × 24
Simplifying, we get:
16x = 720
Dividing both sides by 16, we get:
x = 45
Therefore, the value of x is 45.
Hence, option A is the correct answer.
A car travels 90 km in 5/2 hours. Find the distance covered in 3 hours with the same speed.- a)81 km
- b)99 km
- c)108 km
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A car travels 90 km in 5/2 hours. Find the distance covered in 3 hours with the same speed.
a)
81 km
b)
99 km
c)
108 km
d)
None of these
|
Athira Basak answered |
Speed = distance /time
Speed = 90/(5/2)
= 36 km/hr
Now as speed remains same
36 = distance / 2
Distance = 72km
In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year?- a)it is 5:1
- b)it is 1:5
- c)it is 1:4
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year?
a)
it is 5:1
b)
it is 1:5
c)
it is 1:4
d)
None of these
|
Gayatri Chavan answered |
Given:
Number of holidays in a year = 73.
To do:
We have to find the ratio of the number of holidays to the number of days in one year.
Solution:
Number of days in a year = 365.
Therefore,
The ratio of the number of holidays to the number of days in one year = 73:365 = 1:5.
What is the new ratio obtained by adding 4 to the antecedent and 2 to the consequent of the ratio 3:8?
- a)5:12
- b)10:7
- c)12:5
- d)7:10
Correct answer is option 'D'. Can you explain this answer?
What is the new ratio obtained by adding 4 to the antecedent and 2 to the consequent of the ratio 3:8?
a)
5:12
b)
10:7
c)
12:5
d)
7:10
|
Priyanka Mukherjee answered |
Given ratio is 3:8.
To obtain the new ratio, we need to add 4 to the antecedent and 2 to the consequent.
Adding 4 to the antecedent of 3, we get 7.
Adding 2 to the consequent of 8, we get 10.
Therefore, the new ratio is 7:10.
Hence, the correct answer is option D.
To obtain the new ratio, we need to add 4 to the antecedent and 2 to the consequent.
Adding 4 to the antecedent of 3, we get 7.
Adding 2 to the consequent of 8, we get 10.
Therefore, the new ratio is 7:10.
Hence, the correct answer is option D.
If 18, 16, 99 and x are in proportion then find the value of x.- a)88
- b)32
- c)99
- d)64
Correct answer is option 'A'. Can you explain this answer?
If 18, 16, 99 and x are in proportion then find the value of x.
a)
88
b)
32
c)
99
d)
64
|
|
Mansi Yadav answered |
18/16 = 9/8
99/88 = 9/8
9/8 : 9/8
, That is why A (88) is correct
99/88 = 9/8
9/8 : 9/8
, That is why A (88) is correct
If 9, 18, x and 8 are in proportion then find the value of x.
- a)2
- b)4
- c)3
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If 9, 18, x and 8 are in proportion then find the value of x.
a)
2
b)
4
c)
3
d)
None of these
|
Neha Mehta answered |
Given: 9, 18, x, 8 are in proportion
To find: value of x
Solution:
We know that when four numbers are in proportion, the product of the extremes is equal to the product of the means.
So, we can write:
9 × 8 = 18 × x
72 = 18x
4 = x
Therefore, the value of x is 4.
Hence, option B is the correct answer.
To find: value of x
Solution:
We know that when four numbers are in proportion, the product of the extremes is equal to the product of the means.
So, we can write:
9 × 8 = 18 × x
72 = 18x
4 = x
Therefore, the value of x is 4.
Hence, option B is the correct answer.
In the word GEOMETRY, what is the ratio of number of consonants to the number of vowels?- a)4:7
- b)5:3
- c)5:6
- d)6:5
Correct answer is option 'B'. Can you explain this answer?
In the word GEOMETRY, what is the ratio of number of consonants to the number of vowels?
a)
4:7
b)
5:3
c)
5:6
d)
6:5
|
Arjun Desai answered |
As there is 3 vowel in it i.e,E,O,E
And 5 consonants i.e, G,M,T,R,Y
So ratio of vowels is to consonants is 3/5
In a cricket coaching camp, 1200 children are trained out of which 900 are selected for various matches. What is the ratio of non-selected children to the total number of children?- a)300:120
- b)4:1
- c)1:4
- d)120:300
Correct answer is option 'C'. Can you explain this answer?
In a cricket coaching camp, 1200 children are trained out of which 900 are selected for various matches. What is the ratio of non-selected children to the total number of children?
a)
300:120
b)
4:1
c)
1:4
d)
120:300
|
Rakesh Singh answered |
Yes correct answer is C that is 1:4
What are the extremes of the proportion 9:3::36:12?- a)9, 3
- b)36, 12
- c)3, 36
- d)9, 12
Correct answer is option 'D'. Can you explain this answer?
What are the extremes of the proportion 9:3::36:12?
a)
9, 3
b)
36, 12
c)
3, 36
d)
9, 12
|
Manasa Saha answered |
To solve this proportion, we need to determine the relationship between the first pair of numbers and apply the same relationship to the second pair of numbers.
In the given proportion, 9:3 and 36:12, we can see that both pairs have a ratio of 3:1. This means that for every 3 in the first pair, there is 1 in the second pair.
To find the extremes of the proportion, we need to identify the first and last numbers in each pair. In the first pair, the first number is 9 and the last number is 3. In the second pair, the first number is 36 and the last number is 12.
Therefore, the extremes of the proportion are 9 and 12.
Hence, the correct answer is option D) 9, 12.
In the given proportion, 9:3 and 36:12, we can see that both pairs have a ratio of 3:1. This means that for every 3 in the first pair, there is 1 in the second pair.
To find the extremes of the proportion, we need to identify the first and last numbers in each pair. In the first pair, the first number is 9 and the last number is 3. In the second pair, the first number is 36 and the last number is 12.
Therefore, the extremes of the proportion are 9 and 12.
Hence, the correct answer is option D) 9, 12.
If x, 24 and 30,16 are in proportion, then find the value of x.- a)30
- b)45
- c)15
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If x, 24 and 30,16 are in proportion, then find the value of x.
a)
30
b)
45
c)
15
d)
None of these
|
|
Aathmika Shree answered |
Hngvyytvtffvyhgbhgbyhyhy fog and all that but the way he looks in his
The ratios 6:3 and 5 :15 are given. Which of the following is true about them?- a)The given ratios are not in proportion
- b)The given ratios are equal
- c)The given ratios are equivalent
- d)The given ratios are in proportion
Correct answer is option 'A'. Can you explain this answer?
The ratios 6:3 and 5 :15 are given. Which of the following is true about them?
a)
The given ratios are not in proportion
b)
The given ratios are equal
c)
The given ratios are equivalent
d)
The given ratios are in proportion
|
Sanky Bhim answered |
-when two ratios are same they are said to be in proportion.
- suppose we write the two ratios like this ---> 6:3::5:15 ( :: means same as )
- but 6:3 is not same as 5:15
- to check it we know product of extremes = product of means
- 6 * 15 = 90
-3* 5 = 15
- 90 is not equal to 15 hence the given ratios are not in proportion .
The mean proportion of 9 and 16 is- a)16
- b)9
- c)12
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The mean proportion of 9 and 16 is
a)
16
b)
9
c)
12
d)
None of these
|
|
Arjun Desai answered |
Let mean proportion be x.
9/x = x/16
x^2 = 9 x 16 = 144
x = 12
What is the simplest form of the ratio 144:28?- a)28:4
- b)36: 7
- c)7:36
- d)1:2
Correct answer is option 'B'. Can you explain this answer?
What is the simplest form of the ratio 144:28?
a)
28:4
b)
36: 7
c)
7:36
d)
1:2
|
Anoushka Sharma answered |
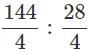(Since H.C.F. of 144 and 28=4)There are 45 persons working in an office. If the number of females is 25 and the remaining are males, find the ratio of the number of females to number of males.- a)it is 1:5
- b)it is 1:4
- c)it is 4:5
- d)it is 5:4
Correct answer is option 'D'. Can you explain this answer?
There are 45 persons working in an office. If the number of females is 25 and the remaining are males, find the ratio of the number of females to number of males.
a)
it is 1:5
b)
it is 1:4
c)
it is 4:5
d)
it is 5:4
|
garima sharma answered |
Answer will be 5:4
The ratio of lemons to number of cups of water to be mixed to prepare lemon juice is 3 :5. For 12 lemons what is the number of cups of water required?- a)10
- b)15
- c)20
- d)25
Correct answer is option 'C'. Can you explain this answer?
The ratio of lemons to number of cups of water to be mixed to prepare lemon juice is 3 :5. For 12 lemons what is the number of cups of water required?
a)
10
b)
15
c)
20
d)
25
|
Nandita Choudhary answered |
Number of players in a cricket team = 11 Wicketkeeper = 1
∴ Ratio =11:1
∴ Ratio =11:1
The ratio of number of boys to number of girls in a tutorial is 2:3. If there are 180 girls, what is the number of boys?
- a)36
- b)60
- c)120
- d)100
Correct answer is option 'C'. Can you explain this answer?
The ratio of number of boys to number of girls in a tutorial is 2:3. If there are 180 girls, what is the number of boys?
a)
36
b)
60
c)
120
d)
100
|
Uday Gupta answered |
Ratio of number of boys to number of girls = 2:3
Number of girls = 180
Let the number of boys be x.
⇒ 2/3 = x/180 [∵ they are equivalent ratios]
⇒ 3x = 2×180
⇒ x = 360/3
⇒ x = 120
∴ Number of boys are 120.
Number of girls = 180
Let the number of boys be x.
⇒ 2/3 = x/180 [∵ they are equivalent ratios]
⇒ 3x = 2×180
⇒ x = 360/3
⇒ x = 120
∴ Number of boys are 120.
Find the ratio of 81 to 108.- a)it is 1:4
- b)it is 4:3
- c)it is 3:4
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Find the ratio of 81 to 108.
a)
it is 1:4
b)
it is 4:3
c)
it is 3:4
d)
None of these
|
Saikat Rane answered |
Ratio refers to the quantitative relationship between two amounts or values. It is expressed in the form of a:b, where a and b are the two values being compared.
To find the ratio of 81 to 108, we need to divide both numbers by their greatest common factor, which is 27.
81 ÷ 27 = 3
108 ÷ 27 = 4
Therefore, the ratio of 81 to 108 is 3:4.
Option C, "it is 3:4", is the correct answer.
To find the ratio of 81 to 108, we need to divide both numbers by their greatest common factor, which is 27.
81 ÷ 27 = 3
108 ÷ 27 = 4
Therefore, the ratio of 81 to 108 is 3:4.
Option C, "it is 3:4", is the correct answer.
Length of a room is 30 m and its breadth is 20 m. Find the ratio of length of the room to the breadth of the room.- a)it is 2:3
- b)it is 3:2
- c)it is 1:3
- d)it is 1:2
Correct answer is option 'B'. Can you explain this answer?
Length of a room is 30 m and its breadth is 20 m. Find the ratio of length of the room to the breadth of the room.
a)
it is 2:3
b)
it is 3:2
c)
it is 1:3
d)
it is 1:2
|
|
Jay Goyal answered |
To find the ratio of length to breadth, we need to divide the length of the room by the breadth of the room.
Given:
Length of the room = 30 m
Breadth of the room = 20 m
To find the ratio of length to breadth, we divide the length by the breadth:
Ratio = Length / Breadth
Let's calculate:
Ratio = 30 m / 20 m
Simplifying the division, we get:
Ratio = 3/2
Thus, the ratio of length to breadth is 3:2, which corresponds to option B.
Explanation:
The ratio of length to breadth represents the relationship between the length and breadth of the room. In this case, the length is 30 m and the breadth is 20 m. When we divide the length by the breadth, we get a ratio of 3/2. This means that for every 3 units of length, there are 2 units of breadth. So, the ratio of length to breadth is 3:2.
Given:
Length of the room = 30 m
Breadth of the room = 20 m
To find the ratio of length to breadth, we divide the length by the breadth:
Ratio = Length / Breadth
Let's calculate:
Ratio = 30 m / 20 m
Simplifying the division, we get:
Ratio = 3/2
Thus, the ratio of length to breadth is 3:2, which corresponds to option B.
Explanation:
The ratio of length to breadth represents the relationship between the length and breadth of the room. In this case, the length is 30 m and the breadth is 20 m. When we divide the length by the breadth, we get a ratio of 3/2. This means that for every 3 units of length, there are 2 units of breadth. So, the ratio of length to breadth is 3:2.
What is the value of x in 12:3: :x:1?- a)1/4
- b)1
- c)4
- d)5
Correct answer is option 'C'. Can you explain this answer?
What is the value of x in 12:3: :x:1?
a)
1/4
b)
1
c)
4
d)
5
|
Sagar Mehta answered |
12:3::x:1 ⇒3x =12 ⇒ x = 12/3 = 4
Find the mean proportion of 25:10::10:4.- a)25
- b)10
- c)4
- d)100
Correct answer is option 'B'. Can you explain this answer?
Find the mean proportion of 25:10::10:4.
a)
25
b)
10
c)
4
d)
100
|
Dr Manju Sen answered |
- The problem involves finding the mean proportion between two pairs of numbers in a proportion: 25:10 and 10:4.
- In a proportion (a:b::c:d), the mean proportion or geometric mean is the middle term (b) when (a:b = b:c).
- Here, the numbers 25, 10, 10, and 4 form the proportion (25:10::10:4).
- The mean proportion is 10, as it is the common term between the two ratios.
- In a proportion (a:b::c:d), the mean proportion or geometric mean is the middle term (b) when (a:b = b:c).
- Here, the numbers 25, 10, 10, and 4 form the proportion (25:10::10:4).
- The mean proportion is 10, as it is the common term between the two ratios.
If 14, 16, x and 24 are in proportion then find the value of x.- a)10.5
- b)21
- c)5
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If 14, 16, x and 24 are in proportion then find the value of x.
a)
10.5
b)
21
c)
5
d)
None of these
|
Praveen Kumar answered |
To find the value of x in the proportion 14 : 16 = x : 24, use cross-multiplication:
14 × 24 = 16 × x
336 = 16x
Divide both sides by 16:
x = 21
14 × 24 = 16 × x
336 = 16x
Divide both sides by 16:
x = 21
There are 45 persons working in an office. If the number of females is 25 and the remaining are males, find the ratio of the number of males to number of females.- a)it is 1:5
- b)it is 5:4
- c)it is 4:5
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
There are 45 persons working in an office. If the number of females is 25 and the remaining are males, find the ratio of the number of males to number of females.
a)
it is 1:5
b)
it is 5:4
c)
it is 4:5
d)
None of these
|
|
Kshitij Singh answered |
See,number of employees=45number of
If x : y : : y : z, identify the correct statement from among the following.
- a)xy = yz
- b)y2 = xz
- c)xyz = x
- d)zy = x
Correct answer is option 'B'. Can you explain this answer?
If x : y : : y : z, identify the correct statement from among the following.
a)
xy = yz
b)
y2 = xz
c)
xyz = x
d)
zy = x
|
|
Sagar Mehta answered |
x:y::y:z
x/y=y/z now cross multiply
y2=xz
⇒y2=xz
x/y=y/z now cross multiply
y2=xz
⇒y2=xz
Identify the ratio of 4 seconds and 1/4 minute from the following.- a)4 : 15
- b)1 : 4
- c)15 : 4
- d)1 : 16
Correct answer is option 'A'. Can you explain this answer?
Identify the ratio of 4 seconds and 1/4 minute from the following.
a)
4 : 15
b)
1 : 4
c)
15 : 4
d)
1 : 16
|
Shiksha Academy answered |
We are asked to identify the ratio of 4 seconds and 1/4 minute. Let's break it down:
1 minute = 60 seconds, so:
1/4 minute = 1/4 × 60 = 15 seconds
Now, the ratio of 4 seconds to 15 seconds is:
Ratio = 4 : 15
In a cricket team what is the ratio of total number of players to the number of wicket keepers?- a)1:11
- b)11:1
- c)16:1
- d)10:1
Correct answer is option 'B'. Can you explain this answer?
In a cricket team what is the ratio of total number of players to the number of wicket keepers?
a)
1:11
b)
11:1
c)
16:1
d)
10:1
|
|
Prasad Kulkarni answered |
In a cricket team, the ratio of the total number of players to the number of wicket keepers is 11:1. This means that for every 11 players in the team, there is only 1 wicket keeper. Let's understand this in more detail.
Understanding the Roles in a Cricket Team:
Cricket is a team sport played between two teams, with each team consisting of multiple players. In a cricket team, there are various roles and positions that players take up. One of the important positions is that of a wicket keeper.
What is a Wicket Keeper?
A wicket keeper is a player who stands behind the stumps (the set of three wooden sticks called wickets) to catch the ball and try to dismiss the batsman. The wicket keeper plays a crucial role in the team as they are responsible for catching the ball when the batsman misses it or edges it.
The Ratio of Players to Wicket Keepers:
In a cricket team, there are typically 11 players on the field at any given time. These players can have various roles such as batsmen, bowlers, and fielders. However, there is only one wicket keeper who stands behind the stumps.
Therefore, the ratio of the total number of players to the number of wicket keepers is 11:1. This means that for every 11 players in the team, there is only 1 wicket keeper.
Example:
Let's consider an example to illustrate this. Suppose we have a cricket team with a total of 22 players. In this case, the ratio of the total number of players to the number of wicket keepers would be 22:2, which can be simplified to 11:1. This means that in a team of 22 players, there would be 2 wicket keepers.
Conclusion:
In summary, the ratio of the total number of players to the number of wicket keepers in a cricket team is 11:1. This ratio implies that for every 11 players, there is only 1 wicket keeper. It is important to have a wicket keeper in the team as they play a crucial role in catching the ball and trying to dismiss the batsman.
Understanding the Roles in a Cricket Team:
Cricket is a team sport played between two teams, with each team consisting of multiple players. In a cricket team, there are various roles and positions that players take up. One of the important positions is that of a wicket keeper.
What is a Wicket Keeper?
A wicket keeper is a player who stands behind the stumps (the set of three wooden sticks called wickets) to catch the ball and try to dismiss the batsman. The wicket keeper plays a crucial role in the team as they are responsible for catching the ball when the batsman misses it or edges it.
The Ratio of Players to Wicket Keepers:
In a cricket team, there are typically 11 players on the field at any given time. These players can have various roles such as batsmen, bowlers, and fielders. However, there is only one wicket keeper who stands behind the stumps.
Therefore, the ratio of the total number of players to the number of wicket keepers is 11:1. This means that for every 11 players in the team, there is only 1 wicket keeper.
Example:
Let's consider an example to illustrate this. Suppose we have a cricket team with a total of 22 players. In this case, the ratio of the total number of players to the number of wicket keepers would be 22:2, which can be simplified to 11:1. This means that in a team of 22 players, there would be 2 wicket keepers.
Conclusion:
In summary, the ratio of the total number of players to the number of wicket keepers in a cricket team is 11:1. This ratio implies that for every 11 players, there is only 1 wicket keeper. It is important to have a wicket keeper in the team as they play a crucial role in catching the ball and trying to dismiss the batsman.
What is the condition for two ratios to be equal?
- a)Product of means is equal to antecedents
- b)Product of extremes is equal to consequents
- c)Antecedents are equal to consequents
- d)Product of means is equal to product of extremes
Correct answer is option 'D'. Can you explain this answer?
What is the condition for two ratios to be equal?
a)
Product of means is equal to antecedents
b)
Product of extremes is equal to consequents
c)
Antecedents are equal to consequents
d)
Product of means is equal to product of extremes
|
|
Maya Deshpande answered |
Ratios:
A ratio is a comparison of two quantities. It is expressed in the form of a fraction or using a colon (:). For example, if we have two quantities A and B, the ratio of A to B can be written as A/B or A:B.
Equality of Ratios:
Two ratios are said to be equal if they represent the same comparison between quantities. In other words, the two ratios have the same value.
Conditions for Ratios to be Equal:
To determine if two ratios are equal, we can use different methods. However, the most common condition for two ratios to be equal is when the product of the means is equal to the product of the extremes.
Explanation:
Let's consider two ratios, A/B and C/D. According to the condition for equality of ratios, we have the following equation:
(A/B) = (C/D)
To check if the condition holds true, we can cross multiply the terms:
A * D = B * C
If the product of the means (B * C) is equal to the product of the extremes (A * D), then the two ratios are equal.
Example:
Let's take an example to understand this concept better. Consider the ratios 2/3 and 4/6. We can check if they are equal using the condition mentioned above:
Product of means = (3 * 4) = 12
Product of extremes = (2 * 6) = 12
Since the product of the means is equal to the product of the extremes (12 = 12), the two ratios are equal.
Conclusion:
In summary, two ratios are equal if the product of the means is equal to the product of the extremes. This condition allows us to determine if two ratios represent the same comparison between quantities.
A ratio is a comparison of two quantities. It is expressed in the form of a fraction or using a colon (:). For example, if we have two quantities A and B, the ratio of A to B can be written as A/B or A:B.
Equality of Ratios:
Two ratios are said to be equal if they represent the same comparison between quantities. In other words, the two ratios have the same value.
Conditions for Ratios to be Equal:
To determine if two ratios are equal, we can use different methods. However, the most common condition for two ratios to be equal is when the product of the means is equal to the product of the extremes.
Explanation:
Let's consider two ratios, A/B and C/D. According to the condition for equality of ratios, we have the following equation:
(A/B) = (C/D)
To check if the condition holds true, we can cross multiply the terms:
A * D = B * C
If the product of the means (B * C) is equal to the product of the extremes (A * D), then the two ratios are equal.
Example:
Let's take an example to understand this concept better. Consider the ratios 2/3 and 4/6. We can check if they are equal using the condition mentioned above:
Product of means = (3 * 4) = 12
Product of extremes = (2 * 6) = 12
Since the product of the means is equal to the product of the extremes (12 = 12), the two ratios are equal.
Conclusion:
In summary, two ratios are equal if the product of the means is equal to the product of the extremes. This condition allows us to determine if two ratios represent the same comparison between quantities.
Which of the following is a proportion?- a)3,27,9,9
- b)5,11,15,44
- c)3,5,15,25
- d)4,3,36,18
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a proportion?
a)
3,27,9,9
b)
5,11,15,44
c)
3,5,15,25
d)
4,3,36,18
|
Arshiya Sen answered |
In a proportion, product of extremes is equal to product of means.
Chapter doubts & questions for Ratio and Proportion - Class 6 All Subjects (Old NCERT) 2025 is part of Class 6 exam preparation. The chapters have been prepared according to the Class 6 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Ratio and Proportion - Class 6 All Subjects (Old NCERT) in English & Hindi are available as part of Class 6 exam.
Download more important topics, notes, lectures and mock test series for Class 6 Exam by signing up for free.
Class 6 All Subjects (Old NCERT)
297 videos|1066 docs|204 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup