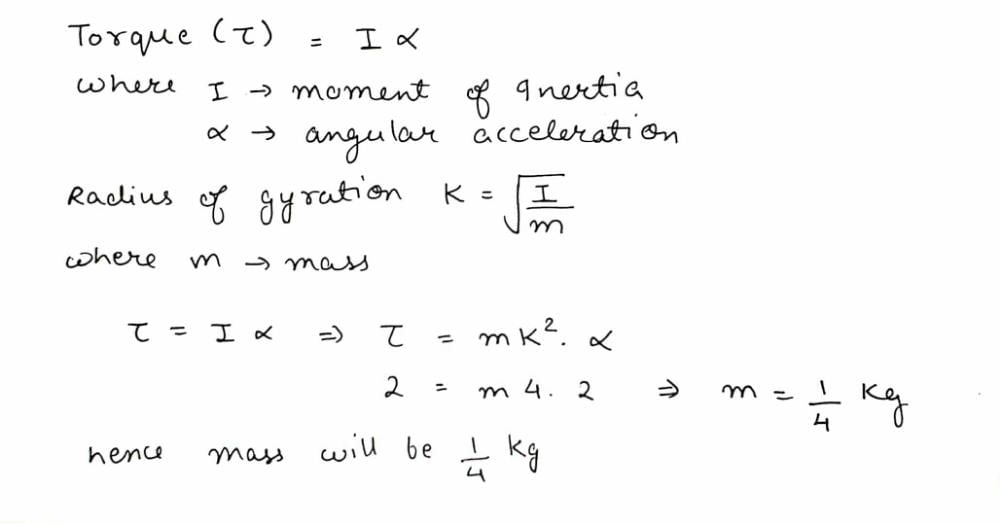All questions of Rotational Dynamics for Grade 9 Exam
The centre of mass of a body is locateda)outside the systemb)inside or outside the systemc)inside the systemd)at the centre of systemCorrect answer is option 'B'. Can you explain this answer?
|
|
Suresh Iyer answered |
Example
(i) Centre of mass of a uniform rod lies at its geometrical centre which lies within the rod
(ii) Centre of mass of a uniform ring lies at its geometrical centre which lies outside the ring.
Can you explain the answer of this question below:Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
- A:
10 m/s
- B:
5 m/s
- C:
15 m/s
- D:
20 m/s
The answer is a.
Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
10 m/s
5 m/s
15 m/s
20 m/s

|
EduRev JEE answered |
Velocity of lighter block (v1) = 0m/s
Velocity of centre of mass,
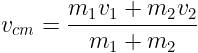
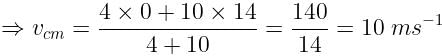
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
- a)Is zero
- b)Remains constant
- c)Goes on increasing
- d)Goes on decreasing
Correct answer is option 'B'. Can you explain this answer?
|
|
Krishna Iyer answered |
L = mv×y
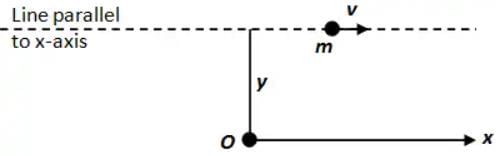
⇒ L = constant
There are two objects of masses 1 kg and 2 kg located at (1, 2) and (-1, 3) respectively. The coordinates of the centre of mass are- a)( 2, -1 )
- b)( 8/3 ,-1/3 )
- c)( -1/3 , 8/3 )
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
|
|
Riya Banerjee answered |
Body B has mass of 2kg and location (-1,3)
(1+2) xc = (1 * 1) + (2 * -1)
xc = -1/3
mcyc = m1y1 + m2y2
(1 + 2) yc = (1 * 2) + (2 * 3)
yc= 8/3
The moment of inertia of two spheres of equal masses is equal. If one of the spheres is solid of radius  m and the other is a hollow sphere. What is the radius of the hollow sphere?
m and the other is a hollow sphere. What is the radius of the hollow sphere?- a)5 m
- b)√3 m
- c)3√3 m
- d)3 m
Correct answer is option 'C'. Can you explain this answer?
 m and the other is a hollow sphere. What is the radius of the hollow sphere?
m and the other is a hollow sphere. What is the radius of the hollow sphere?

|
Sushil Kumar answered |
moment of inertia of hollow sphere Ih =2/3MR2
given mass of solid sphere =√45 kg.
Is=Ih
2MR2/5=2MR2/3
given their masses are equal 2 (√45)2/5= 2 R2/3
45/5=R2/3
9=R2/3
9×3=R2
27=R2
√27=R
√3×9=R
3√3 m=R.
A right triangular plate ABC of mass m is free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is : 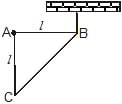
- a)

- b)
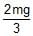
- c)
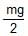
- d)mg
Correct answer is option 'B'. Can you explain this answer?

|
Crafty Classes answered |
Force of magnitude mg is acting downwards at its COM.
Moment balance around B gives:
mg(2L/3)−FA(L)=0
(Moment= × =rFsin(θ)=F(rsin(θ))=Fr⊥)
∴FA=2mg/3
The motion of a potter’s wheel is an example of
- a)rolling motion
- b)rotatory motion
- c)translatory motion
- d)precessional motion
Correct answer is option 'B'. Can you explain this answer?
|
|
Anjali Iyer answered |
The centre of mass of a system of particles does not depend on
- a)masses of the particles
- b)forces on the particles
- c)relative distances between the particles
- d)position of the particles
Correct answer is option 'B'. Can you explain this answer?
|
|
Neha Joshi answered |
If a shell at rest explodes then the centre of mass of the fragments
- a)remains at rest
- b)Moves along a parabolic path
- c)Moves along a straight line
- d)moves along an elliptical path
Correct answer is option 'A'. Can you explain this answer?
|
|
Gaurav Kumar answered |
Two rings have their moment of inertia in the ratio 2:1 and their diameters are in the ratio 2:1. The ratio of their masses will be:- a)1:2
- b)2:1
- c)1:4
- d)1:1
Correct answer is option 'A'. Can you explain this answer?
|
|
Suresh Reddy answered |
Where m is mass of the ring and r is its radius
When we have ratio of I = 2:1
And ratio of r = 2:1
We get ratio of r2 = 4:1
Thus to make this ratio 2:1 , that ratio of masses must be 1:2
If a man of mass M jumps to the ground from height h and his centre of mass moves a distance x in the time taken by him to hit the ground, the average force acting on him is (assuming his retardation to be constant during his impact with the ground)- a)
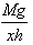
- b)
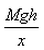
- c)
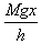
- d)
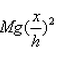
Correct answer is option 'B'. Can you explain this answer?
|
|
Neha Joshi answered |
Work done = Change in potential energy
⇒ Fx = Mgh
⇒ F =
In the pulley system shown, if radii of the bigger and smaller pulley are 2 m and 1 m respectively and the acceleration of block ‘A’ is 5 m/s2 in the downward direction , then the acceleration of block B will be :
- a)0 m / s2
- b)5 m / s2
- c) 10 m / s2
- d) 5 / 2 m / s2
Correct answer is option 'D'. Can you explain this answer?
|
|
Anjali Sharma answered |
⇒α1=α2⇒a1/ r1=a2/ r2 because α=a/r
⇒a1/1=5/2(Given, a2=5m/s2)
⇒a1=5/2 m/s2
Therefore, D is the correct option.
There are two circular iron discs A and B having masses in the ratio 1:2 and diameter in the ratio 2:1. The ratio of their moment of inertia is- a)4:1
- b)1:3
- c)2:1
- d)8:1
Correct answer is option 'C'. Can you explain this answer?
|
|
Preeti Iyer answered |
Mass of A=1,
Mass of B=2.
diameter if A=2,
diameter if B=1.
radius (r) of A=d/2=2/2=1.
radius (r) of B=d/2=1/2.
we know ,
moment of inertia of disc=MR2/2.
moment of inertia (I)of A/moment of inertia (I)of B=MR2/2/MR2/2.
(I) of A/(I) of B=1×12/2/2×(1/2)2/2.
=1×1/2/2×(1/4)/2.
=1/2/(1/2)/2.
=1/2/1/4.
=4/2.
=2/1.
When external forces acting on a body are zero, then its centre of mass- a)remains stationary
- b)moves with uniform velocity
- c)either remains stationary or moves with uniform velocity
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
|
|
Naina Sharma answered |
A homogeneous cubical brick lies motionless on a rough inclined surface. The half of the brick which applies greater pressure on the plane is : 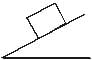
- a) Left half
- b)Right half
- c)Both applies equal pressure
- d)The answer depend upon coefficient of friction
Correct answer is option 'A'. Can you explain this answer?

|
Mohit Rajpoot answered |
mgcosx acts perpendicular to flow of the object.
The pressure of right half comes on left half hence left half has maximum pressure.
There are some passengers inside a stationary railway compartment. The centre of masses of the compartment itself(without the passengers) is C1, while the centre of mass of the compartment plus passengers’ system is C2. if the passengers moves about inside the compartment
- a)both C1 and C2 will move with respect to the ground
- b)neither C1 nor C2 will move with respect to the ground
- c)C1 will move but C2 will be stationary with respect to the ground
- d)C2 will move but C1 will be stationary with respect to the ground
Correct answer is option 'C'. Can you explain this answer?
|
|
Lavanya Menon answered |
Can you explain the answer of this question below:The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by 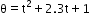 . The linear velocity of the particle
. The linear velocity of the particle
- A:
1.84 m/s
- B:
1.80 m/s
- C:
1.82 m/s
- D:
1.88 m/s
The answer is a.
The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by 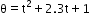 . The linear velocity of the particle
. The linear velocity of the particle
1.84 m/s
1.80 m/s
1.82 m/s
1.88 m/s

|
Knowledge Hub answered |
So, as we know,
After differentiating angular velocity with respect to t,
Linear velocity=2t+2.3=ω
Now,
Velocity=r x ω(where r is 0.8m)
=0.8x2.3
=1.84m/s
A solid sphere and a hollow sphere of the same mass have the same moments of inertia about their respective diameters, the ratio of their radii is- a)(5)1/2 : (3)1/2
- b) (3)1/2 : (5)1/2
- c)3 : 2
- d)2 : 3
Correct answer is option 'A'. Can you explain this answer?
|
|
Gaurav Kumar answered |
moment of inertia of hollow sphere IH=2/3mHRH2 As per question Is=IH
Now,
2/5msRs2=2/3mHRH2
as the masses are equal the ratio of their radii will be
Rs2 /RH2 =2/3/2/5=√5/3=(5)1/2: (3)1/2
A disc of radius b and mass m rolls down an inclined plane of vertical height h. the translational speed when it reaches the bottom of the plane will be - a)
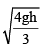
- b)
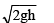
- c)
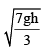
- d)
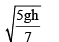
Correct answer is option 'A'. Can you explain this answer?
|
|
Preeti Iyer answered |
As the KE at the top point is zero and let say KE at bottom is ½ mv2 + ½ Iw2
Where m is its mass, I is its moment of inertia, I = ½ mr2
Where r is its radius, v is its gained translational speed and w is its gained angular speed.
w = v/r
Hence equating PE and KE gives
mgh = ½ mv2 + ½ Iw2
That is mgh = ½ mv2 + ½ mr2.(v/r)2
We get mgh = ½ mv2 + ¼ mv2
Thus we get v = √gh/3
A uniform rod of length L and mass M is bent to make a reactangle PQRS such that QR/PQ = 1/2 Moment of inertia of the rectangle about the side QR can be expressed as :
- a)
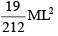
- b)
- c)
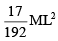
- d)
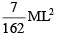
Correct answer is option 'D'. Can you explain this answer?

|
Sushil Kumar answered |
A rigid body is one
- a)the sum of distances of all particles from the axis remains constant
- b)in which the distance between all pairs of particles remains fixed
- c)whose centre of mass follows a parabolic path
- d)that deforms and comes back to its original shape after getting deformed
Correct answer is option 'B'. Can you explain this answer?
|
|
Krishna Iyer answered |
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4 kg m2.- a)12 kg m2
- b)3 kg m2
- c)6 kg m2
- d)9 kg m2
Correct answer is option 'C'. Can you explain this answer?
|
|
Naina Sharma answered |
MR2/2 = 4, MR2 = 8 then substitute in (1) you will get I = 12, this is for tangent perpendicular to plane then divide by 2 you will get tangent along the plane
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is- a)4 unit
- b)6 unit
- c)8 unit
- d)10 unit
Correct answer is option 'D'. Can you explain this answer?
|
|
Krishna Iyer answered |
MI of a disc about its diameter = mr2/4 = 2
And also MI about a point on its rim = mr2/4 + mr2
= 5mr2/4
= 5 x 2 = 10
A CD accelerates uniformly from rest to 200 spins per minute in 8 seconds. If the rate of change of speed is constant, determine the instantaneous acceleration in rad/s2 .- a)200.2 π rad/s2
- b)25 rad/ s2
- c)20.9 rad/ s2
- d)2.6 rad/ s2
Correct answer is option 'D'. Can you explain this answer?
|
|
Varun Kapoor answered |
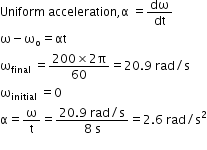
The moment of inertia and rotational kinetic energy of a fly wheel are 20kg-m2 and 1000 joule respectively. Its angular frequency per minute would be -- a)600/π
- b)25/π2
- c)5/π
- d)300/π
Correct answer is option 'D'. Can you explain this answer?
|
|
Riya Banerjee answered |
Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
- a) 3 ml2
- b) ml2
- c) 2 ml2
- d) √3 ml2
Correct answer is option 'A'. Can you explain this answer?
|
|
Raghav Bansal answered |
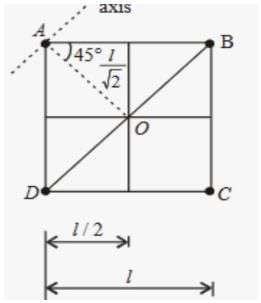
IA=0 (on the Axis .)
IB=ID=mr2
=m(l/√2)2
=ml2/2
IC=m(√2l)2
IC=2ml2
I=IA+IB+IC+ID
I=0+ml2/2+ml2/2+2ml2
I=3ml2
An automobile engine develops 100H.P. when rotating at a speed of 1800 rad/min. The torque it delivers is- a)3.33 W-s
- b)200W-s
- c)248.7 W-s
- d)2487 W-s
Correct answer is option 'D'. Can you explain this answer?

|
Manish Aggarwal answered |
Two rings of radius R and nR made up of same material have the ratio of moment of inertia about an axis passing through centre is 1 : 8. The value of n is- a)2
- b)2√2
- c)4
- d)1/2
Correct answer is option 'A'. Can you explain this answer?

|
Naman Flora answered |
If three balls of same radius are placed touching each other on a horizontal surface such that they will form an equilateral triangle, when their centers are joined. What will be the position of the centre of mass of the system?- a)At the point of intersection of the medians.
- b)At the line joining the centers of any two balls.
- c)At the centre of one of the ball.
- d)At the horizontal surface.
Correct answer is option 'A'. Can you explain this answer?
|
|
Neha Joshi answered |
When a shell was following a parabolic path in the air, it explodes somewhere in its flight. The centre of mass of fragments will continue to move in- a)any direction
- b)horizontal direction
- c)same parabolic path
- d)vertical direction
Correct answer is option 'C'. Can you explain this answer?
|
|
Riya Banerjee answered |
A mixer grinder rotates clockwise, its angular velocity will be :- a)zero
- b)negative
- c)uniform but not zero
- d)positive
Correct answer is option 'B'. Can you explain this answer?
|
|
Ashish Roy answered |
A mixer grinder is a device that is used for grinding and mixing various ingredients. It consists of a motor and a set of blades that rotate at high speeds to perform the grinding and mixing tasks. When the mixer grinder is turned on, the motor starts rotating the blades in a clockwise direction.
**Angular Velocity:**
Angular velocity is a measure of how quickly an object rotates or moves around a central point. It is defined as the rate of change of angular displacement with respect to time. The direction of the angular velocity is determined by the direction of rotation. In the case of a mixer grinder rotating clockwise, the angular velocity will be negative.
**Direction of Angular Velocity:**
The direction of angular velocity is determined by the right-hand rule. According to the right-hand rule, if the fingers of the right hand curl in the direction of rotation, the thumb will point in the direction of the angular velocity vector. In the case of a mixer grinder rotating clockwise, the fingers of the right hand curl in the clockwise direction, and the thumb points in the opposite direction, which is counterclockwise or negative.
**Significance of Negative Angular Velocity:**
A negative angular velocity indicates that the object is rotating in the opposite direction compared to the conventional positive direction. In the case of a mixer grinder, a negative angular velocity means that the blades are rotating counterclockwise when viewed from above. This counterclockwise rotation is necessary for the blades to effectively grind and mix the ingredients.
**Conclusion:**
In conclusion, a mixer grinder rotates clockwise, which means its angular velocity will be negative. The negative angular velocity indicates that the blades are rotating counterclockwise when viewed from above, allowing them to efficiently perform the grinding and mixing tasks.
A thin rod of length 4 l , mass 4 m is bent at the points as shown in the fig. What is the moment of inertia of the rod about the axis passing through point O and perpendicular to the plane of the paper : 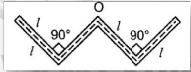
- a)ml2/3
- b)10ml2/3
- c)ml2/12
- d)ml2/24
Correct answer is option 'B'. Can you explain this answer?
|
|
Krishna Iyer answered |
so mass C = m
and length of AB = BO=OC= CD = l
WE, know moment of Inertia of a rod about to end = ml2/3
So, moment of Inertia of AB, BO, OC, CD about B, O, O, C respectively = ml2/3
From parallel axis theorem
Moment of Inertia of AB about O.
=ml2/3+ml2=4ml2/3
Similarly od CD about O =4ml2/3
SO moment of Inertia Rod about O
=ml2/3+ml2/3+4ml2/3+4ml2/3
=10ml2/3
Fig shows a flywheel of radius 10 cm. Its moment of inertia about the rotation axis is 0.4 kg m2. A massless string passes over the flywheel and a mass 2 kg is attached at its lower end. Angular acceleration of the mass in rad/s2 is nearly. 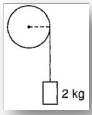
- a)4.8 rad/s2
- b)6.2 rad/s2
- c) 3.2 rad/s2
- d) 9.6 rad/s2
Correct answer is option 'A'. Can you explain this answer?

|
Mohit Rajpoot answered |
I took g = 10 but if g = 9.8 is taken then we get the exact answer.
Can you explain the answer of this question below:An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
- A:
y = +5 cm
- B:
y = +20 cm
- C:
y = -20 cm
- D:
y = -5 cm
The answer is d.
An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
y = +5 cm
y = +20 cm
y = -20 cm
y = -5 cm

|
Ambition Institute answered |
⇒ net external force during this process is 0 i.e. center mass will not change.
Let positon of larger fragment be y.
⇒ (m/4 * 15) + (3m/4 * y) = 0
⇒ y = - 5 cm
An inclined plane makes an angle of 30o with the horizontal. A ring rolling down this inclinedplane from rest without slipping has a linear acceleration equal to :- a)2g/3
- b)g/2
- c)g/3
- d)g/4
Correct answer is option 'D'. Can you explain this answer?
|
|
Neha Joshi answered |
Where I is body's moment of inertia. Here, I = mR2
Thus just by putting the values to the formula we get
a = g.sin 30° / 2
= g/4
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction m . A horizontal force F is applied on the prism as shown in the fig. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is :
- a)
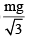
- b)
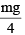
- c)
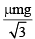
- d)

Correct answer is option 'A'. Can you explain this answer?
|
|
Rajesh Gupta answered |

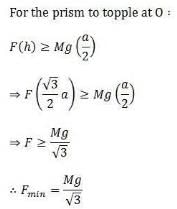
If the net force acting on the system of particles is zero, then which of the following may vary
- a)moment of inertia
- b)Kinetic energy of the system
- c)velocity of centre of mass
- d)position of centre of mass
Correct answer is option 'D'. Can you explain this answer?
|
|
Suresh Kumar answered |
A child sits stationary at one end of long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs about on the trolley in the forward direction with speed u. The centre of mass of the system (child + trolley) will move with speed- a)v
- b)zero
- c)u + v
- d)v/u
Correct answer is option 'A'. Can you explain this answer?
|
|
Preeti Iyer answered |
Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be 
- a)
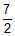 PQ2
PQ2 - b)
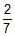 PQ2
PQ2 - c)
 PQ2
PQ2 - d)
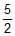 PQ2
PQ2
Correct answer is option 'A'. Can you explain this answer?

|
Lohit Matani answered |
(MOI)1 = MOI about diameter + PQ2
MOI about diameter = ½ PQ2
(MOI)1 = 3/2 PQ2
Similarly, (MOI)2 = 3/2 PQ2
(MOI)3 = ½ PQ2
Total MOI = 7/2 PQ2
A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total length of the rod AB = 3m. To keep the rod in equilibrium a force of 6N should act in the following manner :- a)Downwards at any point between A and B.
- b) Downwards at mid point of AB.
- c)Downwards at a point C such that AC = 1m.
- d) Downwards at a point D such that BD = 1m.
Correct answer is option 'D'. Can you explain this answer?
|
|
Riya Banerjee answered |
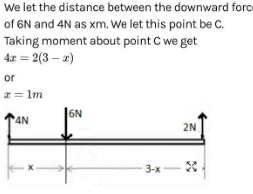
The moment of inertia of a body depends upon -- a) mass only
- b) angular velocity only
- c)distribution of particles only
- d)mass and distribution of mass about the axis
Correct answer is option 'D'. Can you explain this answer?
|
|
Preeti Iyer answered |
An object comprises of a uniform ring of radius R and its uniform chord AB (not necessarily made of the same material) as shown. Which of the following can not be the centre of mass of the object.
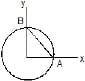
- a) (R/3, R/3)
- b) (R/3, R/2)
- c)(R/4, R/4)
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
|
|
Raghav Bansal answered |
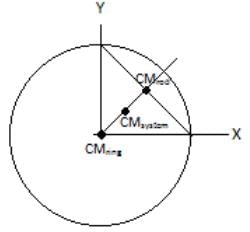
Since the points must have symmetric coordinates so B is the answer.
A wheel starting with angular velocity of 10 radian/sec acquires angular velocity of 100 radian/sec in 15 seconds. If moment of inertia is 10kg-m2, then applied torque (in newton-metre) is- a)900
- b)100
- c)90
- d)60
Correct answer is option 'D'. Can you explain this answer?
|
|
Gaurav Kumar answered |
Hence, τ = 60
Consider the following statementsAssertion (A) : The moment of inertia of a rigid body reduces to its minimum value as compared to any other parallel axis when the axis of rotation passes through its centre of mass.Reason (R) : The weight of a rigid body always acts through its centre of mass in uniform gravitational field. Of these statements :- a)both A and R are true and R is the correct explanation of A
- b) both A and R are true but R is not a correct explanation of A
- c)A is true but R is false
- d) A is false but R is true
Correct answer is option 'B'. Can you explain this answer?
|
|
Neha Joshi answered |
On applying a constant torque on a body- a) Linear velocity may be increases
- b)Angular velocity may be increases
- c)It will rotate with constant angular velocity
- d)It will move with constant velocity
Correct answer is option 'A'. Can you explain this answer?
|
|
Geetika Shah answered |
Chapter doubts & questions for Rotational Dynamics - Physics 2025 is part of Grade 9 exam preparation. The chapters have been prepared according to the Grade 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Physics
307 videos|482 docs|202 tests
|

Contact Support
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|