All Exams >
JEE >
SRMJEEE Subject Wise & Full Length Mock Tests 2026 >
All Questions
All questions of Section wise Tests: Maths for JEE Exam
Equation of the circle having diameters 2x - 3y = 5 and 3x - 4y = 7 and radius 8 is- a)x2 + y2 - 2x + 2y - 62 = 0
- b)x2 + y2 + 2x + 2y - 2 = 0
- c)x2 + y2 + 2x - 2y - 62 = 0
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Equation of the circle having diameters 2x - 3y = 5 and 3x - 4y = 7 and radius 8 is
a)
x2 + y2 - 2x + 2y - 62 = 0
b)
x2 + y2 + 2x + 2y - 2 = 0
c)
x2 + y2 + 2x - 2y - 62 = 0
d)
none of these
|
Subham Goyal answered |
Finding the Center of the Circle
To find the equation of the circle, we first need to find its center. We can do this by finding the intersection of the two diameters.
- Rewrite both equations in slope-intercept form:
2x - 3y = 5 --> y = (2/3)x - 5/3
3x - 4y = 7 --> y = (3/4)x - 7/4
- Find the midpoint of each diameter. This is the center of the circle.
Midpoint of first diameter:
( (0 + 5)/2 , (0 + 0)/2 ) = (5/2, 0)
Midpoint of second diameter:
( (0 + 7)/2 , (0 + 0)/2 ) = (7/2, 0)
- Equate the x-coordinates of the two midpoints and solve for y.
5/2 = 7/2 + m --> m = -1
- The center of the circle is at (5/2, -1).
Finding the Equation of the Circle
Now that we have the center of the circle, we can use the radius of 8 to write the equation in standard form.
- The standard form of the equation of a circle is (x - h)^2 + (y - k)^2 = r^2, where (h,k) is the center of the circle and r is the radius.
- Substituting (5/2, -1) for (h,k) and 8 for r, we get:
(x - 5/2)^2 + (y + 1)^2 = 64
- Expanding and simplifying, we get:
x^2 - 5x + 25/4 + y^2 + 2y + 1 = 64
x^2 + y^2 - 5x + 2y - 62 = 0
- Therefore, the equation of the circle is x^2 + y^2 - 5x + 2y - 62 = 0, which is option A.
To find the equation of the circle, we first need to find its center. We can do this by finding the intersection of the two diameters.
- Rewrite both equations in slope-intercept form:
2x - 3y = 5 --> y = (2/3)x - 5/3
3x - 4y = 7 --> y = (3/4)x - 7/4
- Find the midpoint of each diameter. This is the center of the circle.
Midpoint of first diameter:
( (0 + 5)/2 , (0 + 0)/2 ) = (5/2, 0)
Midpoint of second diameter:
( (0 + 7)/2 , (0 + 0)/2 ) = (7/2, 0)
- Equate the x-coordinates of the two midpoints and solve for y.
5/2 = 7/2 + m --> m = -1
- The center of the circle is at (5/2, -1).
Finding the Equation of the Circle
Now that we have the center of the circle, we can use the radius of 8 to write the equation in standard form.
- The standard form of the equation of a circle is (x - h)^2 + (y - k)^2 = r^2, where (h,k) is the center of the circle and r is the radius.
- Substituting (5/2, -1) for (h,k) and 8 for r, we get:
(x - 5/2)^2 + (y + 1)^2 = 64
- Expanding and simplifying, we get:
x^2 - 5x + 25/4 + y^2 + 2y + 1 = 64
x^2 + y^2 - 5x + 2y - 62 = 0
- Therefore, the equation of the circle is x^2 + y^2 - 5x + 2y - 62 = 0, which is option A.
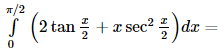
- a)π
- b)π 2
- c)2 π 3
- d)π 6
Correct answer is option 'A'. Can you explain this answer?
a)
π
b)
π 2
c)
2 π 3
d)
π 6
|
Vikash Yadav answered |
Now, just apply the limits....
U get the answer as Pi.
Option A
A and B are two independent events. P( A and B) = 1/6 and the probability that neither of them occur is 1/3 . Find the probability occurrence of A?- a)1 4
- b)1 3
- c)1 5
- d)1 8
Correct answer is option 'B'. Can you explain this answer?
A and B are two independent events. P( A and B) = 1/6 and the probability that neither of them occur is 1/3 . Find the probability occurrence of A?
a)
1 4
b)
1 3
c)
1 5
d)
1 8
|
Ankit Chaudhary answered |
Let P(A) = X and P(B) = Y;
So, P(A’) = 1 - X and P(B’) = 1 - Y
P(A and B) = P(A) x P(B) = XY = 1/6
Probability that neither of them occurs = P(A’) x P(B’) = (1 - X) x (1 - Y) = 1/3
Solving the resulting quadratic equation, we get X = 1/3 or 1/2 that is the probability of occurrence of A
So, P(A’) = 1 - X and P(B’) = 1 - Y
P(A and B) = P(A) x P(B) = XY = 1/6
Probability that neither of them occurs = P(A’) x P(B’) = (1 - X) x (1 - Y) = 1/3
Solving the resulting quadratic equation, we get X = 1/3 or 1/2 that is the probability of occurrence of A
Number of divisors of n = 38808 (except 1 and n) is- a)70
- b)68
- c)72
- d)74
Correct answer is option 'A'. Can you explain this answer?
Number of divisors of n = 38808 (except 1 and n) is
a)
70
b)
68
c)
72
d)
74
|
Priyanka Kulkarni answered |
Factorizing the given number, we have
38808 = 23 . 32 . 72 . 11
Therefore the total number of divisors
= (3 + 1) (2 + 1) (1 + 1) - 1 = 71
But this includes the division by the number itself
Hence, the required number of divisors
= 71 - 1 = 70
38808 = 23 . 32 . 72 . 11
Therefore the total number of divisors
= (3 + 1) (2 + 1) (1 + 1) - 1 = 71
But this includes the division by the number itself
Hence, the required number of divisors
= 71 - 1 = 70
Chapter doubts & questions for Section wise Tests: Maths - SRMJEEE Subject Wise & Full Length Mock Tests 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Section wise Tests: Maths - SRMJEEE Subject Wise & Full Length Mock Tests 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
SRMJEEE Subject Wise & Full Length Mock Tests 2026
1 videos|4 docs|90 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily