Explore Exams
Login Signup
Sign in Open App

All questions of Percentages for Civil Engineering (CE) Exam

Clear all your doubts with EduRev

There are three galleries in a coal mine. On the first day, two galleries are operative and after some time, the third gallery is made operative. With this, the output of the mine became half as large again. What is the capacity of the second gallery as a percentage of the first, if it is given that a four-month output of the first and the third galleries was the same as the annual output of the second gallery?
  • a)
    60% ​
  • b)
    64%
  • c)
    65%  
  • d)
    70%
Correct answer is option 'A'. Can you explain this answer?

Tanishq Sengupta answered
The third gallery making the capacity ‘half as large again’ means an increase of 50%.
Further, it is given that: 4(first + third) = 12 (second) In order to get to the correct answer, try to fit in the options into this situation.
(Note here that the question is asking you to find the capacity of the second gallery as a percentage of the first.)
If we assume option (a) as correct – 70% the following solution follows:
If the second is 70, then first is 100 and the first + second is 170. Then third will be 85 (50% of first + second).
Then the equation:
4 X (100 + 85) should be equal to 12 X 70
But this is not true.
Through trial and error, you can see that the third option fits correctly.
4 X (100 + 80) = 12 X 60.
Hence, it is the correct answer.

Sailesh is working as a sales executive with a reputed FMCG Company in Hyderabad. As per the Company’s policy, Sailesh gets a commission of 6% on all sales upto Rs. 1,00,000 and 5% on all sales in excess of this amount. If Sailesh remits Rs. 2,65,000 to the FMCG company after deducting his commission, his total sales were worth:
  • a)
    Rs. 2,80,000
  • b)
    Rs. 2,90,526
  • c)
    Rs. 2,21,054
  • d)
    Rs. 1,20,000
Correct answer is option 'A'. Can you explain this answer?

EduRev CLAT answered
Let total sales be ‘x’
The commission that Sailesh will get is x – 265000
He gets 6% on sales upto 100000 and 5% on sales greater than that.
Calculating his commission on total sales:
0.06*100000 + 0.05(x-100000)
Equating,
0.05x + 1000 = x – 265000
0.95x = 266000
x= 280000
Hence, his sales were worth 280,000

What percentage of numbers from 1 to 70 have 1 or 9 in the unit's digit?
  • a)
    1
  • b)
    14
  • c)
    20
  • d)
    21
Correct answer is 'C'. Can you explain this answer?

Gowri Chakraborty answered
Clearly, the numbers which have 1 or 9 in the unit's digit, have squares that end in the digit 1. Such numbers from 1 to 70 are 1, 9, 11, 19, 21, 29, 31, 39, 41, 49, 51, 59, 61, 69.
Number of such number =14
 Required percentage = (14/70 * 100)% = 20%

What percentage of numbers from 1 to 70 have 1 or 9 in the unit's digit?
  • a)
    1
  • b)
    14
  • c)
    20
  • d)
    21
Correct answer is option 'C'. Can you explain this answer?

Nitya Reddy answered
Clearly, the numbers which have 1 or 9 in the unit's digit, have squares that end in the digit 1. Such numbers from 1 to 70 are 1, 9, 11, 19, 21, 29, 31, 39, 41, 49, 51, 59, 61, 69.
Number of such number =14

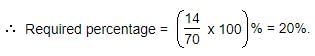
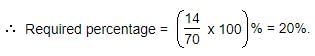
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for Percentages under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. Two students appeared at an examination. One of them secured 9 marks more than the other and his marks was 56% of the sum of their marks. The marks obtained by them are:
  • a)
    39, 30
  • b)
    41, 32
  • c)
    42, 33
  • d)
    43, 34
Correct answer is option 'C'. Can you explain this answer?

Raghavendra Sharma answered
Let their marks be (x+9) and x.
Then, x+9 = 56/100(x + 9 +x)
=> 25(x+9)
=> 14 (2x + 9)
=> 3x = 99
=> x = 33.
So, their marks are 42 and 33

The population of a village has increased annually at the rate of 20%. If at the end of 3 years it is 21600, the population in the beginning of the first year?
  • a)
    10000
  • b)
    12500
  • c)
    15000
  • d)
    17500
Correct answer is option 'B'. Can you explain this answer?

Bayshore Academy answered
  • The population increases by 20% annually, meaning it multiplies by 1.20 each year.
  • After 3 years, the population is 21600.
  • Using the compound growth formula P=P0(1+r)t, where P = 21600, r = 0.20, and t = 3, we calculate the initial population P0.
  • Solving 21600=P0 x (1.20)3, we find P0 = 12500.
  • The initial population is therefore 12500.

The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is
  • a)
    65
  • b)
    50
  • c)
    60
  • d)
    35
Correct answer is option 'A'. Can you explain this answer?

Riverdale Learning Institute answered
Let the number of girls be 2x and number of boys be x.
Girls getting admission = 0.6x
Boys getting admission = 0.45x
Number of students not getting admission = 3x – 0.6x -0.45x = 1.95x
Percentage = (1.95x/3x) * 100 = 65%

In an examination 70% candidates passed in prelims and 55% candidates passed in Mains. If 62% candidates passed in both these subjects, then what per cent of candidates failed in both the exams?
  • a)
    37%
  • b)
    26%
  • c)
    43%
  • d)
    15%
  • e)
    None of these
Correct answer is option 'A'. Can you explain this answer?

Rajeev Kumar answered
Answer – 1.37% Explanation : Students passed in Prelims = 70% Students passed in Mains = 55% Students passed in both  = 62% No of students passed in at least one subject = (70+55)-62 = 63%. students failed in both subjects = 100-63 = 37%.

Fresh fruits contain 75% while dry fruits contain 20% water. If the weight of dry fruits is 300 kg, what was its total weight when it was fresh?
  • a)
    900kg
  • b)
    850kg
  • c)
    920kg
  • d)
    960kg
Correct answer is option 'D'. Can you explain this answer?

Engineers Adda answered
Quantity of water in 300 kg dry fruits, = (20 /100) *300 = 60 kg
Quantity of fruit alone= 300-60 =240 kg
25 kg fruit piece in 100 kg fresh fruits
For 240 = (100 *240)/25 = 960 kg.

The number of seats in a cinema hall is decreased by 8% and also the price of the ticket is increased by 4 percent. What is the effect on the revenue collected?
  • a)
    increase 4.32%
  • b)
    decrease 4.32%
  • c)
    increase 3.32 percent
  • d)
    decrease 3.32%
Correct answer is option 'B'. Can you explain this answer?

EduRev GATE answered
Let initially seats are 100 and price of each seat is 100, so total initial revenue = 10000
now, seats are 92 and price of each seat = 104, so total revenue = 92*104 = 9568
so percent change in revenue = (432/10000)*100 = 4.32 decrease

Alisha goes to a supermarket and bought things worth rupees 60, out of which 40 paise went on sales tax. If the tax rate is 10 percent, then what was the cost of tax free items?
  • a)
    54.60
  • b)
    55.60
  • c)
    56.60
  • d)
    57.60
Correct answer is option 'B'. Can you explain this answer?

Niharika Basu answered
Calculation of Tax-Free Items Cost:
Explanation:
- Total cost of items = Rs. 60
- Sales tax = 40 paise
- Tax rate = 10%

Step 1: Calculate the total tax amount
- Tax rate = 10%
- Total cost of items = Rs. 60
- Tax amount = 10% of Rs. 60 = Rs. 6

Step 2: Convert the tax amount to paise
- 1 Rupee = 100 paise
- Rs. 6 = 6 * 100 = 600 paise

Step 3: Calculate the tax-free items cost
- Total cost of items = Rs. 60 = 6000 paise
- Sales tax = 40 paise
- Total tax amount = 600 paise
- Cost of tax-free items = Total cost of items - Total tax amount
- Cost of tax-free items = 6000 paise - 600 paise = 5400 paise = Rs. 54
Therefore, the cost of the tax-free items is Rs. 54.60, which is option 'B'.

The tank-full petrol in Arun’s motor-cycle last for 10 days. If he starts using 25% more every day, how many days will the tank-full petrol last?
  • a)
    4
  • b)
    6
  • c)
    8
  • d)
    10
Correct answer is option 'C'. Can you explain this answer?

Engineers Adda answered
Assume – Arun’s motorcycle uses 1L per day and therefore tank’s Capacity = 10L.
25% increased per day= 1+(25/100) = 5/4 ie. 1.25L per day
Days = 10/1.25 = 8

Weights of two friends A and B are in the ratio of 1:2. A’s weight increases by 20% and the total weight of A and B together becomes 60 kg, with an increase of 30%. By what percent the weight of B increase?
  • a)
    30%
  • b)
    35%
  • c)
    40%
  • d)
    45%
Correct answer is option 'B'. Can you explain this answer?

Telecom Tuners answered
weight of A is x and weight of B is 2x
given that 60 kg weight is the 30% percent increase of the original weight, so
(130/100)*W = 60, W = 600/13 kg (W = original weight)
X + 2x = 600/13, x = 200/13
So weight of A = 200/13 and of B = 400/13
(120/100)*(200/13) + [(100 + a)/100]*(400/13) = 60
Solve for a. We will get a = 35%

Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is
  • a)
    70
  • b)
     80
  • c)
    60 
  • d)
     75
Correct answer is option 'A'. Can you explain this answer?

Naveen Banerjee answered
To solve this problem, let's break it down into steps:

Step 1: Find Meena's score before the review
Meena scores 40% in the examination. Let's assume the total marks in the examination are 'x'. So her score before the review is 40% of x, which is 0.4x.

Step 2: Find Meena's score after the review
After the review, her score is increased by 50%. So her new score after the review is 0.4x + 0.5(0.4x) = 0.4x + 0.2x = 0.6x.

Step 3: Find the passing score
We know that after the review, Meena fails by 35 marks. So her post-review score is less than the passing score by 35 marks. Let's assume the passing score is 'p'. Therefore, 0.6x = p - 35.

Step 4: Find Meena's score after the further increase
Meena's score after the further increase is 20% more than her post-review score. So her new score after the further increase is 0.6x + 0.2(0.6x) = 0.6x + 0.12x = 0.72x.

Step 5: Find the passing score after the further increase
We know that her post-review score after the further increase is 7 marks more than the passing score. So the passing score after the further increase is p + 7.

Step 6: Set up an equation
Now, we can set up an equation based on the information from steps 3 and 5:
0.72x = (p + 7)

Step 7: Solve the equation
From step 3, we know that 0.6x = p - 35. We can substitute this value of p from step 3 into the equation in step 6:
0.72x = (0.6x + 7) - 35
0.72x - 0.6x = -28
0.12x = -28
x = -28 / 0.12
x = -280 / 12
x = -70 / 3

Step 8: Find the passing percentage
To find the percentage score needed for passing the examination, we need to find the passing score as a percentage of the total marks. The passing score is p = 0.6x + 35.
Substituting the value of x from step 7, we get:
p = 0.6(-70/3) + 35
p = -42 + 35
p = -7

Since the passing score cannot be negative, we need to consider the absolute value of p, which is 7. Therefore, the passing score is 7 out of -70/3, which is approximately 10%.

So, the percentage score needed for passing the examination is 10%. None of the given options (a, b, c, d) match the correct answer.

Traders A and B buy two goods for Rs. 1000 and Rs. 2000 respectively. Trader A marks his goods up by x%, while trader B marks his goods up by 2x% and offers a discount of x%. If both make the same non-zero profit, find x.
  • a)
    25%
  • b)
    12.5%
  • c)
    37.5%
  • d)
    40%
Correct answer is option 'A'. Can you explain this answer?

Sonal Nambiar answered
Understanding the Problem
Traders A and B purchase goods for Rs. 1000 and Rs. 2000, respectively. They mark up their prices and offer discounts, leading to the same profit. We need to determine the value of x.
Trader A's Calculation
- Cost Price (CP): Rs. 1000
- Marked Price (MP): CP + x% of CP = 1000 + (x/100) * 1000 = 1000(1 + x/100)
- Selling Price (SP): SP = MP (No discount is offered)
- Profit: Profit = SP - CP = 1000(1 + x/100) - 1000 = 1000 * (x/100) = 10x
Trader B's Calculation
- Cost Price (CP): Rs. 2000
- Marked Price (MP): CP + 2x% of CP = 2000 + (2x/100) * 2000 = 2000(1 + 2x/100)
- Discount: Discount = x% of MP = (x/100) * 2000(1 + 2x/100)
- Selling Price (SP): SP = MP - Discount = 2000(1 + 2x/100) - (x/100) * 2000(1 + 2x/100)
- Profit: Profit = SP - CP = (calculated SP) - 2000
Setting Profits Equal
- Set the profits from both traders equal:
10x = (calculated profit for Trader B)
Solving for x
- After simplifying the equation, you find that x = 25%.
Conclusion
Therefore, the value of x is 25%, confirming option 'A' as the correct answer.

Deepika went to a fruit shop with a certain amount of money. She retains 15% of her money for auto fare. She can buy either 40 apples or 70 oranges with that remaining amount. If she buys 35 oranges, how many more apples she can buy?
  • a)
    35
  • b)
    40
  • c)
    15
  • d)
    20
Correct answer is option 'D'. Can you explain this answer?

Gate Funda answered
Assume Total amount = Rs.100
Auto fare= 15% of Total amount i.e Rs.15
Now the amount is Rs.85
Price of 70 oranges = Rs.85
Price of 35 oranges = (85/70)*35 = Rs. 42.50
Remaining amount to buy apples is =Rs. 42.50
Price of 40 apples = Rs.85
Price of X apples = Rs.42.50
X=(85/42.5)*40 = 20 Apples

40% of the women are above 30 years of age and 80 percent of the women are less than or equal to 50 years of age. 20 percent of all women play basketball. If 30 percent of the women above the age of 50 plays basketball, what percent of players are less than or equal to 50 years?
  • a)
    50%
  • b)
    60%
  • c)
    70%
  • d)
    80%
Correct answer is option 'C'. Can you explain this answer?

EduRev GATE answered
take total women =100
Women less than or equal to 50 years = 80 and women above 50 years = 20
20 = women plays basketball
30% of the women above 50 plays basketball = 6
So remaining 14 women who plays basketball are less than or equal to 50 years
So (14/20)*100 = 70%

The price of a car is Rs. 4,50,000. It was insured to 80% of its price. The car was damaged completely in an accident and the insurance company paid 90% of the insurance. What was the difference between the price of the car and the amount received?
  • a)
    Rs.1,76,375
  • b)
    Rs.3,24,000
  • c)
    Rs.1,82,150
  • d)
    Rs.1,26,000
Correct answer is option 'D'. Can you explain this answer?

Dishani Bose answered
Understanding the Car Insurance Calculation
To determine the difference between the price of the car and the amount received from the insurance company, we can break down the problem step by step.
Step 1: Determine the Insured Amount
- The price of the car = Rs. 4,50,000
- The car was insured for 80% of its price.
Calculation:
- Insured Amount = 80% of 4,50,000
= 0.80 * 4,50,000
= Rs. 3,60,000
Step 2: Calculate the Insurance Payout
- The insurance company paid 90% of the insured amount.
Calculation:
- Amount Received = 90% of Insured Amount
= 0.90 * 3,60,000
= Rs. 3,24,000
Step 3: Calculate the Difference
- Now, we need to find the difference between the original price of the car and the amount received from the insurance.
Calculation:
- Difference = Price of Car - Amount Received
= 4,50,000 - 3,24,000
= Rs. 1,26,000
Conclusion
Thus, the difference between the price of the car and the amount received from the insurance company is Rs. 1,26,000. Therefore, the correct answer is option 'D'.

In a class, 60% of the students are boys and in an examination, 80% of the girls scored more than 40 marks(Maximum Marks:150). If 60% of the total students scored more than 40 marks in the same exam, what is the fraction of the boys who scored 40 marks or less.
  • a)
    8/15
  • b)
    7/15
  • c)
    4/5
  • d)
    1/5
Correct answer is option 'A'. Can you explain this answer?

Engineers Adda answered
Assume Total no of students = 100
60% of the students are boys. so Boys=60,Girls=40
No. of girls who scored more than 40 marks = 80% of girls = 80% of 40 = 32.
No. of students who scored more than 40 marks = 60% of Total Students = 60
Therefore No. of boys who scored more than 40 marks = 60-32=28
No. of boys who scored less= Total boys – Boys(scored more) = 60-28=32
Fraction=(scored less)/Total boys = 32/60 =8/15

In an examination, 50% of the students passed in Science and  75% passed in Social, while 20% students failed in both the subjects. If 270 students passed in both subjects, find the total number of students who appeared in the exam?
  • a)
    400
  • b)
    540
  • c)
    600
  • d)
    750
Correct answer is option 'C'. Can you explain this answer?

Gate Gurus answered
passed in science = 50%
passed in social = 75%
20% students failed in both the subjects and 80% passed in at least one subject
No of students passed in both subjects = 50+75−x=80  x=45% 45% of x = 270  x = 270*100/45 = 600
Total number of students =600

A man spends 60% of his income. His income is increased by 20% and his expenditure also increases by 10%. Find the percentage decrease/increase in his savings?
  • a)
    35% increase
  • b)
    15% increase
  • c)
    20% decrease
  • d)
    10% decrease
Correct answer is option 'A'. Can you explain this answer?

Harsh Kulkarni answered
Initial Setup
- Let the man's original income be 100 units.
- Therefore, his original expenditure is 60% of his income, which is 60 units.
- His initial savings would be: 100 - 60 = 40 units.
Income Increase
- The man's income increases by 20%.
- New income = 100 + (20% of 100) = 100 + 20 = 120 units.
Expenditure Increase
- His expenditure increases by 10% of the original expenditure.
- New expenditure = 60 + (10% of 60) = 60 + 6 = 66 units.
New Savings Calculation
- The new savings would be: New Income - New Expenditure = 120 - 66 = 54 units.
Change in Savings
- The original savings were 40 units, and the new savings are 54 units.
- The change in savings = New Savings - Original Savings = 54 - 40 = 14 units.
Percentage Increase in Savings
- To find the percentage increase in savings:
- Percentage Increase = (Change in Savings / Original Savings) * 100
- Percentage Increase = (14 / 40) * 100 = 35%.
Conclusion
- The percentage increase in his savings is 35%.
- Thus, the correct answer is option 'A': 35% increase.

In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
  • a)
    62
  • b)
    55
  • c)
    66
  • d)
    59
Correct answer is option 'C'. Can you explain this answer?

S.S Career Academy answered
Let ‘x’ be the strength of group G. Based on the information, 0.65x constitutes of literate people {the rest 0.35x = illiterate}
Of this 0.65x , 75% are old people =(0.75)0.65x old literates.
The total number of old people in group G is 0.72x  {72% of the total}.
Thus, the total number of old people who are illiterate = 0.72x - 0.4875x = 0.2325x.
This is 
≈ 66& of the total number of illiterates.
Hence, Option C is the correct answer.

Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
  • a)
    55
  • b)
    60
  • c)
    54
  • d)
    50
Correct answer is option 'D'. Can you explain this answer?

Upsc Rank Holders answered
Let the CP of the each toy be “x”. CP of 12 toys will be “12x”. Now the shopkeeper made a 10% profit on CP. This means that
12x(1.1)= 2112 or x=160 . Hence the CP of each toy is ₹160.
Now let the SP of each toy be “m”. Now he sold 8 toys at 20% discount. This means that 8m(0.8) or 6.4m
He sold 4 toys at an additional 25% discount. 4m(0.8)(0.75)=2.4m  Now 6.4m+2.4m=8.8m=2112 or m=240
Hence CP= 160 and SP=240. Hence profit percentage is 50%.

The ratio of number of male and female journalists in a newspaper office is 5:4. The newspaper has two sections, political and sports. If 30 percent of the male journalists and 40 percent of the female journalists are covering political news, what percentage of the journalists (approx.) in the newspaper is currently involved in sports reporting?
  • a)
    60 percent
  • b)
    65 percent
  • c)
    70 percent
  • d)
    None of the above
Correct answer is option 'B'. Can you explain this answer?

Riverdale Learning Institute answered
The ratio of number of male and female journalists in a newspaper office is 5:4.
The newspaper has two sections, political and sports.
If 30 percent of the male journalists and 40 percent of the female journalists are covering political news, what percentage of the journalists (approx.) in the newspaper is currently involved in sports reporting?
Let ‘9x’ be the number of total journalists in the office.
Then, we can say that the number of male and female journalists are ‘5x’ and ‘4x’ respectively.
It is given that 30 percent of the male journalists and 40 percent of the female journalists are covering political news. Hence, total number of journalists who are covering political news = 0.3*5x + 0.4*4x = 3.1x
Therefore, the total number journalists who are covering sports news = 9x – 3.1x = 5.9x.
Hence, the percentage of the journalists in the newspaper is currently involved in sports reporting = 5.9x/9x x 100 ≈ 
65 percent. Therefore, option B is the correct answer.

In a class of 500 students  ,65%  are boys. 20% of the girls and 40% of the boys failed the exam.Find the of students in the school passed the exam?
  • a)
    335
  • b)
    270
  • c)
    400
  • d)
    362
Correct answer is option 'A'. Can you explain this answer?

Gate Funda answered
Total students are 100% = 500
Boys = 65% of 500 = 325,
Girls = 35% =35*500/100 =175
Girls failed in the exam= 175*80/100 = 140
Boys failed in the exam =40/100x 325 = 195
Total = 140+195 = 335

The ratio of the number of boys and girls in a school is 3:2. If 20% of the boys and 25% of the girls are scholarship holders, the percentage of the students who are not scholarship holders is:
  • a)
    30%
  • b)
    60%
  • c)
    75%
  • d)
    78%
Correct answer is option 'D'. Can you explain this answer?

Telecom Tuners answered
Consider Total no of students = 100
Ratio is 3:2 i.e Boys=60 and Girls=40
20% of boys who get scholarship = 60*20/100=12%
25% of girls who get scholarship = 40*25/100 =10%
Therefore % of students who do not get scholarship =100-(12+10) = 78%

Chapter doubts & questions for Percentages - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Percentages - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam. Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.

6 Months Preparation for GATE Civil Engg

488 videos|1261 docs|878 tests

Top Courses Civil Engineering (CE)

© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup