All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of System of Forces for Civil Engineering (CE) Exam
There are two types of loading. The uniformly distributed and the non-uniformly distributed that is the one having two different values at corners.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'D'. Can you explain this answer?
There are two types of loading. The uniformly distributed and the non-uniformly distributed that is the one having two different values at corners.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too

|
Kritika Shah answered |
The two forms of the loading are the uniformly distributed and the non-uniformly distributed that is the one having two different values at corners. The uniform distributed load is not having two different values of the load per unit meter on the corner.
Which of the following is true?- a)Total moment of various forces acting on the body is the vector sum of all moments in 3D
- b)Total moment of various forces acting on the body is the algebraic sum of all moments in 3D
- c)Total moment of various forces acting on the body is always zero in any dimension
- d)Total moment of various forces acting on the body is the vector sum of all moments which is perpendicular to each other forces whatever be the dimensions
Correct answer is option 'A'. Can you explain this answer?
Which of the following is true?
a)
Total moment of various forces acting on the body is the vector sum of all moments in 3D
b)
Total moment of various forces acting on the body is the algebraic sum of all moments in 3D
c)
Total moment of various forces acting on the body is always zero in any dimension
d)
Total moment of various forces acting on the body is the vector sum of all moments which is perpendicular to each other forces whatever be the dimensions

|
Jaya Yadav answered |
When we consider about the dimensions we need to be careful.The moment is the vector quantity. Thus the value of the total moment caused by various forces acting on the body is the vector sum of all the vectors. Also the moments are not perpendicular to each other, unless it is specified.
The calculation of the moment about the axis and the moment about any point by a force applied on the body are different from each other.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The calculation of the moment about the axis and the moment about any point by a force applied on the body are different from each other.
a)
True
b)
False
|
|
Anjali Shah answered |
The calculation of the moment about the axis and the moment about any point by a force applied on the body are different from each other. It is because both of the calculations require different formulas. And both of the formulas have different inputs, which is obviously different.
Which of the following is correct w.r.t the moment (M) of the force (F) acting on the body at a distance L from the axis of the rotation?- a)M=FLsinθ
- b)M=FLcosθ
- c)M=F.Lsinθ
- d)M=FxLsinθ
Correct answer is option 'A'. Can you explain this answer?
Which of the following is correct w.r.t the moment (M) of the force (F) acting on the body at a distance L from the axis of the rotation?
a)
M=FLsinθ
b)
M=FLcosθ
c)
M=F.Lsinθ
d)
M=FxLsinθ
|
|
Aditya Deshmukh answered |
The moment of the force about the axis of rotation by the application of the force on the body is given by the cross product of both. If the force not perpendicular to the axis, and making angle θ then cosine form of angle is used. As usually used in the cross product.
If a vector is multiplied by a scalar:- a)Then its magnitude is increased by the square root of that scalar’s magnitude
- b)Then its magnitude is increased by the square of that scalar’s magnitude
- c)Then its magnitude is increased by amount of that scalar’s magnitude
- d)You cannot multiply the vector with a scalar
Correct answer is option 'C'. Can you explain this answer?
If a vector is multiplied by a scalar:
a)
Then its magnitude is increased by the square root of that scalar’s magnitude
b)
Then its magnitude is increased by the square of that scalar’s magnitude
c)
Then its magnitude is increased by amount of that scalar’s magnitude
d)
You cannot multiply the vector with a scalar
|
|
Anjali Sengupta answered |
If a vector is multiplied by a scalar then its magnitude is increased by amount of that scalar’s magnitude. When multiplied by a negative scalar it going to change the directional sense of the vector.
What is the direction of the resultant vector if two vectors having equal length is placed in the Cartesian plane at origin as, one being parallel to and heading towards positive x-axis and the other making 165 degree with it and heading in the opposite direction of that of the first one?
- a)It is either in the 1st quadrant or in 2nd quadrant
- b)It is either in the 1st quadrant or in 3rd quadrant
- c)It is either in the 1st quadrant or in 4th quadrant
- d)Only in the 1st quadrant
Correct answer is option 'C'. Can you explain this answer?
What is the direction of the resultant vector if two vectors having equal length is placed in the Cartesian plane at origin as, one being parallel to and heading towards positive x-axis and the other making 165 degree with it and heading in the opposite direction of that of the first one?
a)
It is either in the 1st quadrant or in 2nd quadrant
b)
It is either in the 1st quadrant or in 3rd quadrant
c)
It is either in the 1st quadrant or in 4th quadrant
d)
Only in the 1st quadrant

|
Swara Dasgupta answered |
If one is heading towards positive X-axis and the other is in the other direction opposite to the first one, with both having the same length and having an angle between them being obtuse, means that the direction is to be in the direction of either 1st quadrant or in the 4th quadrant.
Force vector R is having a______________- a)Length of R and a specific direction
- b)Length of R
- c)A specific direction
- d)Length of magnitude equal to square root of R and a specific direction
Correct answer is option 'A'. Can you explain this answer?
Force vector R is having a______________
a)
Length of R and a specific direction
b)
Length of R
c)
A specific direction
d)
Length of magnitude equal to square root of R and a specific direction
|
|
Dishani Desai answered |
As it is a force vector, it means it is going to have a direction and a magnitude. The magnitude is not the square root of R, R is just the magnitude of the vector given.
A force vector with magnitude R and making an angle α with the x-axis is having its component along x-axis and y-axis as:- a)Rcosine (α) and Rsine(α)
- b)Rcosine (180-α) and Rsine(α)
- c)Rcosine (180-α) and Rsine(180+α)
- d)Rcosine (α) and Rsine(180+α)
Correct answer is option 'A'. Can you explain this answer?
A force vector with magnitude R and making an angle α with the x-axis is having its component along x-axis and y-axis as:
a)
Rcosine (α) and Rsine(α)
b)
Rcosine (180-α) and Rsine(α)
c)
Rcosine (180-α) and Rsine(180+α)
d)
Rcosine (α) and Rsine(180+α)
|
|
Sanskriti Basu answered |
The component along x-axis is the cosine component of the vector. And the y-axis component of the vector is sine component, if the angle is being made with the x-axis. And 180- α for some of the trigonometric function may change their sign.
The moment axis is in the direction perpendicular to the plane of the force and the distance.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The moment axis is in the direction perpendicular to the plane of the force and the distance.
a)
True
b)
False

|
Anirban Khanna answered |
The moment axis is always perpendicular to the planes of the force and the distance of the axis and the point of action of the force on the body. This means that the moment is the cross product of the force and the distance between the axis and the point of action of the force.
If the non-Uniform loading is of the type of parabola then?- a)The net load will not be formed as all the forces will be cancelled
- b)The net force will act the centre of the parabola
- c)The net force will act on the base of the loading horizontally
- d)The net force will act at the centroid of the parabola
Correct answer is option 'D'. Can you explain this answer?
If the non-Uniform loading is of the type of parabola then?
a)
The net load will not be formed as all the forces will be cancelled
b)
The net force will act the centre of the parabola
c)
The net force will act on the base of the loading horizontally
d)
The net force will act at the centroid of the parabola
|
|
Kirti Bose answered |
The net force will act at the centroid of the parabola. Whether it be a parabola or the cubic curve the centroid is the only point at which the net force act. Force can’t be acted horizontally if the loading is vertical. Hence whatever be the shape of the loading, the centroid is the point of action of net force.
The magnitude of the resultant of the two vectors is always_____________- a)Greater than one of the vector’s magnitude
- b)Smaller than one of the vector’s magnitude
- c)Depends on the angle between them
- d)Axis we choose to calculate the magnitude
Correct answer is option 'C'. Can you explain this answer?
The magnitude of the resultant of the two vectors is always_____________
a)
Greater than one of the vector’s magnitude
b)
Smaller than one of the vector’s magnitude
c)
Depends on the angle between them
d)
Axis we choose to calculate the magnitude
|
|
Sinjini Bose answered |
Yes, the magnitude of the resultant of the two vectors always depends on the angle between them. It might be greater or smaller than one of the vector’s length. For perfectly saying, it does depends upon the angle between them.
Which of the following statement is true?- a)A scalar is any physical quantity that can be completely specified by its magnitude
- b)A vector is any positive or negative physical quantity that can be completely specified by its magnitude
- c)A scalar is any physical quantity that requires both a magnitude and a direction for its complete description
- d)A scalar is any physical quantity that can be completely specified by its direction
Correct answer is option 'A'. Can you explain this answer?
Which of the following statement is true?
a)
A scalar is any physical quantity that can be completely specified by its magnitude
b)
A vector is any positive or negative physical quantity that can be completely specified by its magnitude
c)
A scalar is any physical quantity that requires both a magnitude and a direction for its complete description
d)
A scalar is any physical quantity that can be completely specified by its direction

|
Sravya Rane answered |
A scalar is any positive or negative physical quantity that can be completely specified by its magnitude. Examples of scalar quantities include length, mass, time, etc.
What is multiplication law?- a)A.B =B.A
- b)a(A.B) = A.(aB)
- c)A.(B+D) = (A.B) + (A.D)
- d)a(A.B) = AxB
Correct answer is option 'B'. Can you explain this answer?
What is multiplication law?
a)
A.B =B.A
b)
a(A.B) = A.(aB)
c)
A.(B+D) = (A.B) + (A.D)
d)
a(A.B) = AxB
|
|
Gopal Choudhury answered |
For three vectors A, B and D the various laws are. Communitive law: A.B =B.A. While distributive law is A.(B+D) = (A.B) + (A.D). And multiplication law is a(A.B) = A.(aB).
For two vectors A and B, what is A.B (if they have angle α between them)?- a)|A||B| cosα
- b)|A||B|
- c)√(|A||B|) cosα
- d)|A||B| sinα
Correct answer is option 'A'. Can you explain this answer?
For two vectors A and B, what is A.B (if they have angle α between them)?
a)
|A||B| cosα
b)
|A||B|
c)
√(|A||B|) cosα
d)
|A||B| sinα
|
|
Divyansh Goyal answered |
If A and B are two vectors and θ is the angle between them, A.B represents the dot product of A and B. The dot product of two vectors is defined as:
A.B = |A| |B| cos(θ),
where |A| and |B| represent the magnitudes of vectors A and B, respectively.
A.B = |A| |B| cos(θ),
where |A| and |B| represent the magnitudes of vectors A and B, respectively.
Which statement is true? (For three vectors P, Q and R)- a)Associative law for cross product: (PxQ)xS = Px(QxS)
- b)Associative law for cross product: (PxQ)xS ≠ Px(QxS)
- c)Associative law for cross product: (PxQ)xS > Px(QxS)
- d)Associative law for cross product: (PxQ)xS < Px(QxS)
Correct answer is option 'B'. Can you explain this answer?
Which statement is true? (For three vectors P, Q and R)
a)
Associative law for cross product: (PxQ)xS = Px(QxS)
b)
Associative law for cross product: (PxQ)xS ≠ Px(QxS)
c)
Associative law for cross product: (PxQ)xS > Px(QxS)
d)
Associative law for cross product: (PxQ)xS < Px(QxS)
|
|
Shreya Kulkarni answered |
= Qx(PxS)c)Associative law for cross product: (PxQ)xS = (PxS)xQ
Determine the magnitude of the resultant force acting on the shaft shown from left.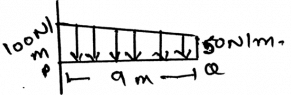
- a)640N
- b)675N
- c)620N
- d)610N
Correct answer is option 'B'. Can you explain this answer?
Determine the magnitude of the resultant force acting on the shaft shown from left.
a)
640N
b)
675N
c)
620N
d)
610N
|
|
Akshara Rane answered |
The net force will act at the centroid of the parabola. Whether it be a parabola or the cubic curve the centroid is the only point at which the net force act. Force can’t be acted horizontally if the loading is vertical. Hence whatever be the shape of the loading, the centroid is the point of action of net force.
The resultant force acting, of the uniformly distributed loading is dependent on:- a)Area
- b)Vertical distance
- c)Length of the supports
- d)The distance of the supports between them
Correct answer is option 'A'. Can you explain this answer?
The resultant force acting, of the uniformly distributed loading is dependent on:
a)
Area
b)
Vertical distance
c)
Length of the supports
d)
The distance of the supports between them
|
|
Gopal Choudhury answered |
The resultant force acting, of the uniformly distributed loading is dependent on the area that the distribution is covering. The more the area the more is the force. That is the more is the tension created over the structure on which loading is kept. Hence the answer.
M = ∑(rxF) represents what?- a)The total distance of the point of contact of the and the axis of rotation
- b)The total moment of the forces
- c)The total force acting on the body
- d)The equation is wrong, it must be Fxr
Correct answer is option 'B'. Can you explain this answer?
M = ∑(rxF) represents what?
a)
The total distance of the point of contact of the and the axis of rotation
b)
The total moment of the forces
c)
The total force acting on the body
d)
The equation is wrong, it must be Fxr
|
|
Anshul Sharma answered |
The given equation represents the total moment of the forces which are acting on the body. That is the summation of all the rxF. Where the r is the distance of the axis from the point of action of the force on the body. And thus this is the total summation of the moments of all the forces acting on the body.
The axis vector in the calculation of the moment along the axis of rotation is the axis which is collinear with the force vector.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
The axis vector in the calculation of the moment along the axis of rotation is the axis which is collinear with the force vector.
a)
True
b)
False
|
|
Anjali Shah answered |
The axis of the rotation cannot be collinear with the force vector. If it does so then the rotation of body is not possible. That is the moment of the force is zero. Which means no rotation being given by the force along the axis of rotation of the body.
What does FLsinθ means/represents for the moment (M) of the force (F) acting on the body at a distance L from the axis of the rotation?- a)The direction vector of the moment
- b)Unit vector of the moment vector
- c)The magnitude of the moment caused by the force on the body
- d)The perpendicular distance of the force from the axis of rotation
Correct answer is option 'C'. Can you explain this answer?
What does FLsinθ means/represents for the moment (M) of the force (F) acting on the body at a distance L from the axis of the rotation?
a)
The direction vector of the moment
b)
Unit vector of the moment vector
c)
The magnitude of the moment caused by the force on the body
d)
The perpendicular distance of the force from the axis of rotation
|
|
Kalyan Chakraborty answered |
The moment of the force about the axis of rotation by the application of the force on the body is given by the cross product of both. If the force not perpendicular to the axis, and making angle θ then cosine form of angle is used. Thus, FLsinθ represents the magnitude of the moment.
What if the moment of the force calculated about the axis is negative?- a)It means that the force is applied in the opposite direction as imagined
- b)It means that the direction of the motion is in the opposite sense as imagined
- c)It means that the radius vector is in the opposite sense as imagined
- d)Such calculation means that the calculations are wrongly done
Correct answer is option 'B'. Can you explain this answer?
What if the moment of the force calculated about the axis is negative?
a)
It means that the force is applied in the opposite direction as imagined
b)
It means that the direction of the motion is in the opposite sense as imagined
c)
It means that the radius vector is in the opposite sense as imagined
d)
Such calculation means that the calculations are wrongly done
|
|
Dipika Kulkarni answered |
Explanation:
Opposite Sense of Motion:
- When the moment of the force calculated about the axis is negative, it indicates that the direction of the motion is in the opposite sense as imagined.
- This means that the force applied tends to cause a rotational motion in the opposite direction to what was initially assumed.
- In simple terms, the negative sign signifies that the rotation caused by the force is opposite to the anticipated direction.
Example:
- For instance, if a force is applied in a clockwise direction but the calculated moment is negative, it implies that the actual motion induced by the force is counterclockwise.
Importance of Understanding:
- It is crucial to interpret the sign of the calculated moment correctly in engineering applications to ensure the accurate prediction of motion and behavior of the system.
- Incorrect interpretation can lead to errors in analysis, design, and decision-making processes.
In conclusion, when the moment of the force about the axis is negative, it signifies that the direction of the motion induced by the force is opposite to the assumed sense. This understanding is essential for accurate engineering calculations and predictions.
Opposite Sense of Motion:
- When the moment of the force calculated about the axis is negative, it indicates that the direction of the motion is in the opposite sense as imagined.
- This means that the force applied tends to cause a rotational motion in the opposite direction to what was initially assumed.
- In simple terms, the negative sign signifies that the rotation caused by the force is opposite to the anticipated direction.
Example:
- For instance, if a force is applied in a clockwise direction but the calculated moment is negative, it implies that the actual motion induced by the force is counterclockwise.
Importance of Understanding:
- It is crucial to interpret the sign of the calculated moment correctly in engineering applications to ensure the accurate prediction of motion and behavior of the system.
- Incorrect interpretation can lead to errors in analysis, design, and decision-making processes.
In conclusion, when the moment of the force about the axis is negative, it signifies that the direction of the motion induced by the force is opposite to the assumed sense. This understanding is essential for accurate engineering calculations and predictions.
Which of the following is correct? (For A representing the vector representation of the axis of rotation, r the radius vector and F the force vector)- a)A.(rxF)
- b)Ax(rxF)
- c)A.(r.F)
- d)Fx(r.F)
Correct answer is option 'A'. Can you explain this answer?
Which of the following is correct? (For A representing the vector representation of the axis of rotation, r the radius vector and F the force vector)
a)
A.(rxF)
b)
Ax(rxF)
c)
A.(r.F)
d)
Fx(r.F)
|
|
Suyash Patel answered |
The correct form of the equation is given by A.(rxF). Where A represents the vector representation of the axis of rotation, r the radius vector and F the force vector. This is usually done for determining the moment of the force about the axis. That is if body is being rotated by the force about an axis.
The simplification of the forces on the axis is done as __________- a)A particular system of rule is followed
- b)No simplification of the forces is possible
- c)The forces are already simplified and don’t need simplification
- d)The forces are very tentative quantity on terms of simplification and hence no simplification possible
Correct answer is option 'A'. Can you explain this answer?
The simplification of the forces on the axis is done as __________
a)
A particular system of rule is followed
b)
No simplification of the forces is possible
c)
The forces are already simplified and don’t need simplification
d)
The forces are very tentative quantity on terms of simplification and hence no simplification possible
|
|
Avantika Sen answered |
A particular system of the rules is followed that is if the upward direction is taken as positive then the downward direction is taken as negative. This is same as done with the couple in the 2D. That is the forces can be easily simplified. If taken in the vector form then the task is even easier.
In case of forces, a couple means- a)Two unequal forces acting at two points
- b)Two equal and like parallel forces acting at two points
- c)Two equal and perpendicular forces acting at two points
- d)Two equal and opposite forces acting at two points
Correct answer is option 'D'. Can you explain this answer?
In case of forces, a couple means
a)
Two unequal forces acting at two points
b)
Two equal and like parallel forces acting at two points
c)
Two equal and perpendicular forces acting at two points
d)
Two equal and opposite forces acting at two points
|
|
Avinash Sharma answered |
Couple: When the pair of equal parallel forces that are opposite in direction applied on a body then it rotates of tries to rotate about a point or axis is called a couple.
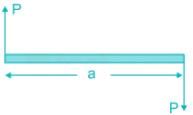
Moment of a couple or couple (C) = P × a
Characteristics of a couple: A couple (whether clockwise or anticlockwise) has the following characteristics:

Moment of a couple or couple (C) = P × a
Characteristics of a couple: A couple (whether clockwise or anticlockwise) has the following characteristics:
- The algebraic sum of the forces, constituting the couple, is zero.
- The algebraic sum of the moments of the forces, constituting the couple, about any point is the same, and equal to the moment of the couple itself.
- A couple cannot be balanced by a single force. But it can be balanced only by a couple of opposite sense.
- Any no. of co-planer couples can be reduced to a single couple, whose magnitude will be equal to the algebraic sum of the moments of all the couples.
Torque (τ): It is a physical quantity, similar to force that causes the rotational motion. It is the cross product of the force with the perpendicular distance between the axis of rotation and the point of application of the force with the force.
⇒ τ = r × F = r F sin θ
Where r = distance from point of application of force (in meter), f = force (in Newton), and θ = angle between
Also, Torque (τ) = r × f = r × F
Where r = component of the distance in the direction perpendicular to the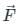
F = component of the force in the direction perpendicular to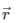
⇒ τ = r × F = r F sin θ
Where r = distance from point of application of force (in meter), f = force (in Newton), and θ = angle between
Also, Torque (τ) = r × f = r × F
Where r = component of the distance in the direction perpendicular to the
F = component of the force in the direction perpendicular to
If you are getting to know about the direction of the moment caused by the force applied on the body by using your wrist and curling it in the direction of the rotation then which of the following is not right?
- a)The thumb represents the direction of the moment
- b)The thumb represents the direction of the force
- c)The fingers represents the direction of the force
- d)The direction in which you curl your wrist is towards the direction of the distance from point of contact of force to the axis of rotation.
Correct answer is option 'B'. Can you explain this answer?
If you are getting to know about the direction of the moment caused by the force applied on the body by using your wrist and curling it in the direction of the rotation then which of the following is not right?
a)
The thumb represents the direction of the moment
b)
The thumb represents the direction of the force
c)
The fingers represents the direction of the force
d)
The direction in which you curl your wrist is towards the direction of the distance from point of contact of force to the axis of rotation.
|
|
Arshiya Dey answered |
The curled hand represents various thing. The direction of the moment axis is given by the thumb. The direction of the force is given by the fingers. As we place the fingers on the force and curl towards the rotational direction of the body about the axis.
Which is true for two vector A = A1i + A2j + A3k and B = B1i + B2j + B3k?- a)A.B = A1B1 + A2B2 + A3B3
- b)AxB = A1B1 + A2B2 + A3B3
- c)A.B = A1B2 + A2B3 + A3B1
- d)AxB = A1B2 + A2B3 + A3B1
Correct answer is option 'A'. Can you explain this answer?
Which is true for two vector A = A1i + A2j + A3k and B = B1i + B2j + B3k?
a)
A.B = A1B1 + A2B2 + A3B3
b)
AxB = A1B1 + A2B2 + A3B3
c)
A.B = A1B2 + A2B3 + A3B1
d)
AxB = A1B2 + A2B3 + A3B1
|
|
Devansh Sengupta answered |
The multiplication of x, y and z components with their respective same component give a scalar, equal to 1, i.e. i.i = 1 and j.j = 1, while jxj =0. This is the basic principle of the vector algebra which needs to apply wherever needed.
The moment axis, force and the perpendicular distance in the moment of the force calculation is lying in____________- a)Two planes perpendicular to each other
- b)A single plane in the direction of the force
- c)A single plane in the direction of the perpendicular distance
- d)A single line in the direction of the force
Correct answer is option 'A'. Can you explain this answer?
The moment axis, force and the perpendicular distance in the moment of the force calculation is lying in____________
a)
Two planes perpendicular to each other
b)
A single plane in the direction of the force
c)
A single plane in the direction of the perpendicular distance
d)
A single line in the direction of the force
|
|
Jyoti Deshpande answered |
The moment axis, force and the perpendicular distance is lying in the three dimensional Cartesian. It doesn’t lye on the single plane. It also doesn’t lye in a single line. Nor in the direction of the force. Thus they all lye in the planes which are perpendicular to each other.
The difference between the two types of loading namely uniformly distributed and the non-uniformly distributed loading is that:- a)The latter has the involvement of the integration for the calculation of the net force
- b)The former has the involvement of the integration for the calculation of the net force
- c)The latter has the involvement of the differentiation for the calculation of the net force
- d)The former has the involvement of the differentiation for the calculation of the net force
Correct answer is option 'A'. Can you explain this answer?
The difference between the two types of loading namely uniformly distributed and the non-uniformly distributed loading is that:
a)
The latter has the involvement of the integration for the calculation of the net force
b)
The former has the involvement of the integration for the calculation of the net force
c)
The latter has the involvement of the differentiation for the calculation of the net force
d)
The former has the involvement of the differentiation for the calculation of the net force
|
|
Sanskriti Chakraborty answered |
The non-uniformly distributed loading is using the integration for getting the net force given by it. And the former only need the area or the linear distance of the loading. That is when the distance is multiplied by the uniformly distributed load the net force is obtained. But that is not so with the non-uniform one.
If a car is moving forward, what is the direction of the moment of the moment caused by the rotation of the tires?- a)It is heading inwards, i.e. the direction is towards inside of the car
- b)It is heading outwards, i.e. the direction is towards outside of the car
- c)It is heading forward, i.e. the direction is towards the forward direction of the motion of the car
- d)It is heading backward, i.e. the direction is towards back side of the motion of the car
Correct answer is option 'A'. Can you explain this answer?
If a car is moving forward, what is the direction of the moment of the moment caused by the rotation of the tires?
a)
It is heading inwards, i.e. the direction is towards inside of the car
b)
It is heading outwards, i.e. the direction is towards outside of the car
c)
It is heading forward, i.e. the direction is towards the forward direction of the motion of the car
d)
It is heading backward, i.e. the direction is towards back side of the motion of the car
|
|
Disha Nambiar answered |
When you curl your wrist in the direction in which the tires are moving then you will find that the thumb is pointing outwards. That is outwards the body of the car. This phenomena is also observed in rainy seasons. When cars travel on the roads, the water is thrown outside from the tires, due to moment.
Moments can be added like scalars that is it can be added algebraically with proper signs.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Moments can be added like scalars that is it can be added algebraically with proper signs.
a)
True
b)
False
|
|
Disha Nambiar answered |
The moments in the 2D can be added algebraically just like the scalar quantities. But the need is that the signs must be taken into the consideration. As if clockwise is positive, so anti clockwise is negative. And the result can be negative too. That is counter clockwise direction.
Determine the location of the resultant force acting on the shaft shown from left. The length is 2m.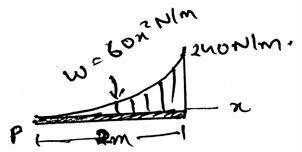
- a)1.5m
- b)0.5m
- c)0.7m
- d)1.8m
Correct answer is option 'A'. Can you explain this answer?
Determine the location of the resultant force acting on the shaft shown from left. The length is 2m.
a)
1.5m
b)
0.5m
c)
0.7m
d)
1.8m
|
|
Stuti Bajaj answered |
The net force will act at the centroid of the parabola. Whether it be a parabola or the cubic curve the centroid is the only point at which the net force act. Force can’t be acted horizontally if the loading is vertical. Hence whatever be the shape of the loading, the centroid is the point of action of net force.
Which of the following is correct in the determination of the moment direction by curling of wrist?- a)The thumb represents the direction of the force
- b)The thumb represents the direction of the moment
- c)The fingers represents the direction of the force
- d)The direction in which you curl your wrist is towards the direction of the distance from point of contact of force to the axis of rotation.
Correct answer is option 'B'. Can you explain this answer?
Which of the following is correct in the determination of the moment direction by curling of wrist?
a)
The thumb represents the direction of the force
b)
The thumb represents the direction of the moment
c)
The fingers represents the direction of the force
d)
The direction in which you curl your wrist is towards the direction of the distance from point of contact of force to the axis of rotation.

|
Sahana Dey answered |
The curled hand represents various thing. The direction of the moment axis is given by the thumb. The direction of the force is given by the fingers. As we place the fingers on the force and curl towards the rotational direction of the body about the axis.
The resultant couple moment is ____________ sum of various couples acting on the body.- a)Vector
- b)Scalar
- c)Scalar Triple
- d)Dot
Correct answer is option 'A'. Can you explain this answer?
The resultant couple moment is ____________ sum of various couples acting on the body.
a)
Vector
b)
Scalar
c)
Scalar Triple
d)
Dot
|
|
Sanskriti Basu answered |
As we know that the moment is vector quantity, their summation requires vector math. The couple moment is also the same. That is they are also the vectors, and requires vector math. Thus the resultant couple moment is the vector sum of the various couples acting in the body.
What if the perpendicular distance from the axis is infinity?- a)The rotation is not possible
- b)The rotation is possible but the moment generated is very less
- c)The force applied will be very much high for even a small rotation
- d)No rotation unless the contact is being broken
Correct answer is option 'C'. Can you explain this answer?
What if the perpendicular distance from the axis is infinity?
a)
The rotation is not possible
b)
The rotation is possible but the moment generated is very less
c)
The force applied will be very much high for even a small rotation
d)
No rotation unless the contact is being broken
|
|
Aniket Saini answered |
The long distance means a huge force which one needs to apply. Because distance increased will also increase the resistance inertia which will obviously increase the force required for the rotation. Though we know that the larger the distance the small is the force applied for rotation. But inertia must be taken into the considerations some times.
We can express the force in the Cartesian form.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
We can express the force in the Cartesian form.
a)
True
b)
False
|
|
Soumya Basak answered |
Yes, we can prepare the moment in the Cartesian form. As the moment in the 3D is the vector. Which can be easily made in the form of Cartesian coordinates. Also it can be seen that the moment is the cross product of the force and the distance, hence the moment is in vector form.
The ___________ forces do not cause the rotation.- a)Non-concurrent
- b)Concurrent
- c)Parallel
- d)Non-Parallel
Correct answer is option 'B'. Can you explain this answer?
The ___________ forces do not cause the rotation.
a)
Non-concurrent
b)
Concurrent
c)
Parallel
d)
Non-Parallel
|
|
Samarth Chaudhary answered |
The concurrent forces are the which are somewhere touching the axis of rotation. If any of the force is touching that axis, that force is not considered, or is insufficient to cause a rotation. If a force is concurrent then the perpendicular distance of the force from the line of axis is zero, thus no rotation. As we know rotation is caused by moment.
The resultant force is equal to the _______ of all the forces.- a)Sum
- b)Product
- c)Subtraction
- d)Division
Correct answer is option 'A'. Can you explain this answer?
The resultant force is equal to the _______ of all the forces.
a)
Sum
b)
Product
c)
Subtraction
d)
Division
|
|
Sanskriti Basu answered |
As the simplification means addition and the subtraction of the forces. This results in the simplification of the forces and thus gives us a single force. It is in a particular direction. But if one is considering the direction with the magnitude of the force, we can say that the resultant is the sum of all the forces.
In the equation A.(rxF) the r is heading from ______________ and ending at _____________- a)Axis of rotation, Force vector
- b)Axis of rotation, Force vector’s point of action on the body
- c)Force vector, Axis of rotation
- d)Force vector’s point of action on the body, Axis of rotation
Correct answer is option 'B'. Can you explain this answer?
In the equation A.(rxF) the r is heading from ______________ and ending at _____________
a)
Axis of rotation, Force vector
b)
Axis of rotation, Force vector’s point of action on the body
c)
Force vector, Axis of rotation
d)
Force vector’s point of action on the body, Axis of rotation
|
|
Saranya Saha answered |
It is the radius vector. The radius vector is always from the axis of rotation to the point of action of the force on the body. Which means that the radius vector is not on any point on the force vector. Rather it ending at the point on the force vector, where it is being in contact of the body.
Determine the magnitude of the force F = 300j parallel to the direction of AB?
- a)155N
- b)257.1N
- c)200N
- d)175N
Correct answer is option 'B'. Can you explain this answer?
Determine the magnitude of the force F = 300j parallel to the direction of AB?
a)
155N
b)
257.1N
c)
200N
d)
175N

|
Pranavi Gupta answered |
Force component in the direction parallel to the AB is given by unit vector 0.286i + 0.857j + 0.429k. Now (300j).(0.286i + 0.857j + 0.429k) = 257.1N. Just try to resolve the force into it’s particular components.
What is the dot product of two vectors which are having magnitude equal to unity and are making an angle of 45°?- a)0.707
- b)-0.707
- c)1.414
- d)-1.414
Correct answer is option 'A'. Can you explain this answer?
What is the dot product of two vectors which are having magnitude equal to unity and are making an angle of 45°?
a)
0.707
b)
-0.707
c)
1.414
d)
-1.414

|
Asha Nambiar answered |
°
The dot product of two vectors is given by the product of their magnitudes and the cosine of the angle between them.
Let's assume the two vectors as a and b.
Magnitude of vector a = 1
Magnitude of vector b = 1
Angle between them = 45°
Therefore, the dot product of vectors a and b can be calculated as:
a · b = |a| |b| cos θ
a · b = (1)(1) cos 45°
a · b = (1)(1) (1/√2)
a · b = 1/√2
Hence, the dot product of two vectors having magnitude equal to unity and making an angle of 45° is 1/√2.
The dot product of two vectors is given by the product of their magnitudes and the cosine of the angle between them.
Let's assume the two vectors as a and b.
Magnitude of vector a = 1
Magnitude of vector b = 1
Angle between them = 45°
Therefore, the dot product of vectors a and b can be calculated as:
a · b = |a| |b| cos θ
a · b = (1)(1) cos 45°
a · b = (1)(1) (1/√2)
a · b = 1/√2
Hence, the dot product of two vectors having magnitude equal to unity and making an angle of 45° is 1/√2.
Which among the following is the distributive law for the cross product of three vectors?- a)Px(Q+S) = (PxQ) + (PxS)
- b)Px(QxS) = (PxQ) + (PxS)
- c)Px(QxS) = (PxQ) x (PxS)
- d)Px(Q+S) = (PxQ) + (QxS)
Correct answer is option 'A'. Can you explain this answer?
Which among the following is the distributive law for the cross product of three vectors?
a)
Px(Q+S) = (PxQ) + (PxS)
b)
Px(QxS) = (PxQ) + (PxS)
c)
Px(QxS) = (PxQ) x (PxS)
d)
Px(Q+S) = (PxQ) + (QxS)
|
|
Sahil Majumdar answered |
The distributive law works just like the simple multiplication of the constant before the brackets. That is in the equation Px(Q+S) = (PxQ) + (PxS), P is crossed by Q and S both. This is simple as, if we first add the two vectors and then do the cross product or we first do the cross product and the do the sum.
α = cos-1(A.B/AB). What is the range of α?- a)0˚<α<90˚
- b)0˚<α<180˚
- c)90˚<α<180C
- d)0˚<α<45˚
Correct answer is option 'B'. Can you explain this answer?
α = cos-1(A.B/AB). What is the range of α?
a)
0˚<α<90˚
b)
0˚<α<180˚
c)
90˚<α<180C
d)
0˚<α<45˚
|
|
Sparsh Chakraborty answered |
The term "digital divide" refers to the gap between individuals, households, businesses, and communities that have access to digital technologies and those that do not. It encompasses both the physical access to technology, such as computers and the internet, as well as the skills and knowledge necessary to use these technologies effectively.
The digital divide can exist within a country, with certain segments of the population having greater access to digital resources than others. It can also exist on a global scale, with some countries or regions being more technologically advanced than others. This divide can have significant social, economic, and educational implications, as those without access to digital technologies may be left behind in terms of job opportunities, educational resources, and access to information.
Efforts to bridge the digital divide include initiatives to increase internet connectivity in rural and underserved areas, provide affordable or free devices and internet access to low-income individuals and families, and provide digital literacy training to help individuals develop the skills needed to fully participate in the digital world.
The digital divide can exist within a country, with certain segments of the population having greater access to digital resources than others. It can also exist on a global scale, with some countries or regions being more technologically advanced than others. This divide can have significant social, economic, and educational implications, as those without access to digital technologies may be left behind in terms of job opportunities, educational resources, and access to information.
Efforts to bridge the digital divide include initiatives to increase internet connectivity in rural and underserved areas, provide affordable or free devices and internet access to low-income individuals and families, and provide digital literacy training to help individuals develop the skills needed to fully participate in the digital world.
Which of them is not correct?- a)j x j = 0
- b)j x k = i
- c)j x i = k
- d)j x i = -k
Correct answer is option 'C'. Can you explain this answer?
Which of them is not correct?
a)
j x j = 0
b)
j x k = i
c)
j x i = k
d)
j x i = -k
|
|
Mahi Kaur answered |
As asked, the one which is not correct is the third one. The product is containing the cosine function, and the angle which is going to be inserted in the function is the angle between the vectors. Thus if the angle is 90, then the cross will be zero.
Commutative law is valid for the cross product of two vectors. (Commutative law: PxQ = QxP; for two vectors P and Q)- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Commutative law is valid for the cross product of two vectors. (Commutative law: PxQ = QxP; for two vectors P and Q)
a)
True
b)
False
|
|
Divyansh Goyal answered |
The Commutative Law and the Cross Product of Vectors
The commutative law states that for any two elements, the order of the operation does not affect the result. In the case of vectors, this means that the order in which we perform the cross product should not affect the outcome. However, the correct answer to the given question is option 'B' - False. Let's understand why.
Explanation:
1. The Cross Product:
The cross product is an operation that combines two vectors to produce a third vector that is perpendicular to both of the original vectors. It is denoted by the symbol '×' and is defined as:
P × Q = ||P|| ||Q|| sin(θ) n
where P and Q are the vectors being crossed, ||P|| and ||Q|| are their magnitudes, θ is the angle between them, and n is a unit vector perpendicular to the plane formed by P and Q.
2. Commutative Law:
The commutative law states that for any two elements, the order of the operation does not affect the result. In mathematical terms, it can be written as:
a × b = b × a
This law holds true for many mathematical operations, such as addition and multiplication. However, it does not hold true for the cross product of vectors.
3. Non-Commutativity of Cross Product:
The cross product of vectors is not commutative, which means that changing the order of the vectors being crossed will result in a different outcome.
To see this, let's consider two vectors P and Q. The cross product of P and Q is given by:
P × Q = ||P|| ||Q|| sin(θ) n
Now, if we switch the order and calculate the cross product of Q and P, we get:
Q × P = ||Q|| ||P|| sin(θ') n'
Here, θ' is the angle between Q and P, and n' is a unit vector perpendicular to the plane formed by Q and P.
Since the angles and magnitudes may be different for P and Q, the resulting cross products will also be different. Thus, the commutative law does not hold for the cross product of vectors.
Conclusion:
In conclusion, the commutative law is not valid for the cross product of two vectors. The order of the vectors being crossed affects the outcome, and switching the order will result in a different cross product.
The commutative law states that for any two elements, the order of the operation does not affect the result. In the case of vectors, this means that the order in which we perform the cross product should not affect the outcome. However, the correct answer to the given question is option 'B' - False. Let's understand why.
Explanation:
1. The Cross Product:
The cross product is an operation that combines two vectors to produce a third vector that is perpendicular to both of the original vectors. It is denoted by the symbol '×' and is defined as:
P × Q = ||P|| ||Q|| sin(θ) n
where P and Q are the vectors being crossed, ||P|| and ||Q|| are their magnitudes, θ is the angle between them, and n is a unit vector perpendicular to the plane formed by P and Q.
2. Commutative Law:
The commutative law states that for any two elements, the order of the operation does not affect the result. In mathematical terms, it can be written as:
a × b = b × a
This law holds true for many mathematical operations, such as addition and multiplication. However, it does not hold true for the cross product of vectors.
3. Non-Commutativity of Cross Product:
The cross product of vectors is not commutative, which means that changing the order of the vectors being crossed will result in a different outcome.
To see this, let's consider two vectors P and Q. The cross product of P and Q is given by:
P × Q = ||P|| ||Q|| sin(θ) n
Now, if we switch the order and calculate the cross product of Q and P, we get:
Q × P = ||Q|| ||P|| sin(θ') n'
Here, θ' is the angle between Q and P, and n' is a unit vector perpendicular to the plane formed by Q and P.
Since the angles and magnitudes may be different for P and Q, the resulting cross products will also be different. Thus, the commutative law does not hold for the cross product of vectors.
Conclusion:
In conclusion, the commutative law is not valid for the cross product of two vectors. The order of the vectors being crossed affects the outcome, and switching the order will result in a different cross product.
Couple is having a combination of two forces. They are different in magnitude.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Couple is having a combination of two forces. They are different in magnitude.
a)
True
b)
False
|
|
Pankaj Joshi answered |
The couple is a combination of two forces of same magnitude. They are acting in the same sense of rotation. That is they are acting in the opposite direction, but giving the body a rotation in the same direction. Whether it may be in clockwise direction or anti-clockwise.
If the forces acting on the couple are in the same direction, that is they are not in the opposite direction as always they are, then?- a)The direction of the forces doesn’t determine the moment
- b)The couple moment will be maximum
- c)The couple is not possible
- d)No change occurs
Correct answer is option 'C'. Can you explain this answer?
If the forces acting on the couple are in the same direction, that is they are not in the opposite direction as always they are, then?
a)
The direction of the forces doesn’t determine the moment
b)
The couple moment will be maximum
c)
The couple is not possible
d)
No change occurs
|
|
Meera Bose answered |
B) The direction of the forces does not matter for the couple's effect. The couple moment will still be the same.
A man is travelling in the car. He is driving the car. If he is taking a turn in the road. He is applying force to the steering wheel by holding the wheel with his both hands. The steering wheel is facing a moment of force.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
A man is travelling in the car. He is driving the car. If he is taking a turn in the road. He is applying force to the steering wheel by holding the wheel with his both hands. The steering wheel is facing a moment of force.
a)
True
b)
False
|
|
Aman Ghosh answered |
Explanation:
The correct answer is option B: False. The statement is incorrect because taking a turn in the road does not involve applying a moment of force to the steering wheel.
Steering Wheel and Force:
The steering wheel is a component of a car's steering system that allows the driver to control the direction of the vehicle. It is connected to the front wheels through a series of linkages and mechanisms. When the driver turns the steering wheel, it causes the front wheels to change their orientation, which in turn changes the direction of the car.
Force and Moment of Force:
Force is a vector quantity that is defined as a push or pull that can cause an object with mass to accelerate or change its state of motion. It is measured in newtons (N). A moment of force, also known as torque, is a measure of the tendency of a force to rotate an object about an axis. It is calculated by multiplying the force applied by the perpendicular distance from the axis of rotation.
Applying Force to the Steering Wheel:
When a driver takes a turn in a car, they apply a force to the steering wheel. However, this force is not a moment of force or torque. Instead, it is a linear force that is applied along the circumference of the steering wheel. The driver uses their hands to push or pull on the steering wheel, causing it to rotate. This rotation is then transmitted to the front wheels, causing them to turn and change the direction of the car.
Conclusion:
In conclusion, when a driver takes a turn in a car, they apply a linear force to the steering wheel, not a moment of force. Therefore, the statement that the steering wheel is facing a moment of force when the driver takes a turn is false.
The correct answer is option B: False. The statement is incorrect because taking a turn in the road does not involve applying a moment of force to the steering wheel.
Steering Wheel and Force:
The steering wheel is a component of a car's steering system that allows the driver to control the direction of the vehicle. It is connected to the front wheels through a series of linkages and mechanisms. When the driver turns the steering wheel, it causes the front wheels to change their orientation, which in turn changes the direction of the car.
Force and Moment of Force:
Force is a vector quantity that is defined as a push or pull that can cause an object with mass to accelerate or change its state of motion. It is measured in newtons (N). A moment of force, also known as torque, is a measure of the tendency of a force to rotate an object about an axis. It is calculated by multiplying the force applied by the perpendicular distance from the axis of rotation.
Applying Force to the Steering Wheel:
When a driver takes a turn in a car, they apply a force to the steering wheel. However, this force is not a moment of force or torque. Instead, it is a linear force that is applied along the circumference of the steering wheel. The driver uses their hands to push or pull on the steering wheel, causing it to rotate. This rotation is then transmitted to the front wheels, causing them to turn and change the direction of the car.
Conclusion:
In conclusion, when a driver takes a turn in a car, they apply a linear force to the steering wheel, not a moment of force. Therefore, the statement that the steering wheel is facing a moment of force when the driver takes a turn is false.
The moment axis is in the direction parallel to the plane of the force and the distance.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
The moment axis is in the direction parallel to the plane of the force and the distance.
a)
True
b)
False
|
|
Raj Kumar answered |
The moment axis is always perpendicular to the planes of the force and the distance of the axis and the point of action of the force on the body. This means that the moment is the cross product of the force and the distance between the axis and the point of action of the force.
Determine the moment about the point P.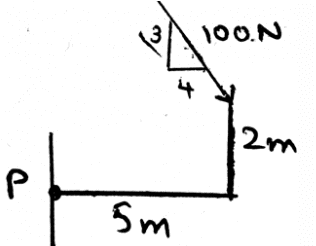
- a)460Nm
- b)500Nm
- c)705Nm
- d)0Nm
Correct answer is option 'A'. Can you explain this answer?
Determine the moment about the point P.
a)
460Nm
b)
500Nm
c)
705Nm
d)
0Nm
|
|
Sinjini Bose answered |
As we know that the moment is the cross product of the force and the distance between the point of contact of the force and the point about which moment needs to be calculated. Thus forming the distance vector and then crossing it with the force will give us the answer. Remember force also needs to be in the vector form for doing the cross product.
Chapter doubts & questions for System of Forces - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of System of Forces - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup