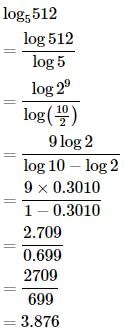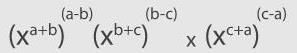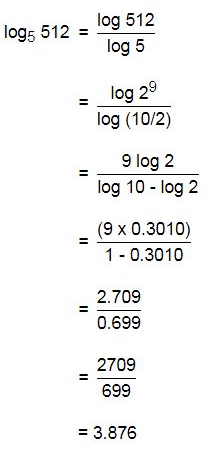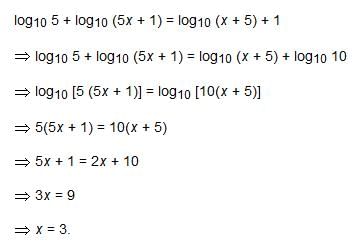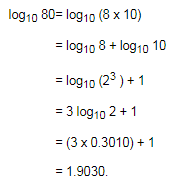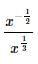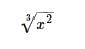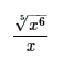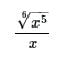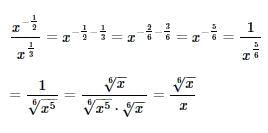All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Powers, Exponents and Logarithms for Computer Science Engineering (CSE) Exam
What is the value of 225 + 225?- a)226
- b)250
- c)425
- d)450
- e)2625
Correct answer is option 'A'. Can you explain this answer?
What is the value of 225 + 225?
a)
226
b)
250
c)
425
d)
4
50
e)
2625

|
Anihegde1502 answered |
Take 2raise to25 common thjs ib bracket there will be (1+1)i.e 2raise to25 *2 thus power will get add 25+1 i.e 26 hence ans is option A
If ‘x’ and ‘y’ are non-negative integers, what is the value of x + y?(1) x4 is even, where x is a prime number.(2) xy is odd.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
If ‘x’ and ‘y’ are non-negative integers, what is the value of x + y?
(1) x4 is even, where x is a prime number.
(2) xy is odd.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
BT Educators answered |
(1) x = 2, y is unknown. Insufficient
(2) x and y unknown. Insufficient
(1)+(2) only possibility x=2, y=0; Sufficient
C is correct
(2) x and y unknown. Insufficient
(1)+(2) only possibility x=2, y=0; Sufficient
C is correct
If a, b and x are integers such that 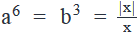 , what is the value of a - b
, what is the value of a - b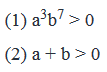
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If a, b and x are integers such that 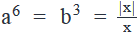 , what is the value of a - b
, what is the value of a - b
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Anaya Patel answered |
Steps 1 & 2: Understand Question and Draw Inferences
- As a6 is always positive,a6 = 1, i.e. a = 1 or -1
- So, we can reject the value of Possible values of a – b
- If a = 1 and b = 1, a – b = 0
- If a = -1 and b = 1, a- b = -2
- So, we need to find the unique value of a to find the value of a – b.Step 3: Analyze Statement 1 independently(1) a3 b7 > 0
- Rewriting a3b7 as ab(a2b6)
- Therefore, ab(a2b6)>0
- We know that a2b6 is always > 0 (even power of any number is always positive)
- So, for ab(a2b6)> 0
- ab > 0
- This tells us that a and b have same signs.
- Since b > 0, therefore a will also be greater than 0, so the value of a = 1.
- a – b = 1 -1 = 0
- Sufficient to answerStep 4: Analyze Statement 2 independently(2) a + b > 0
- If a = 1 and b = 1, a + b = 2 > 0
- If a = -1 and b = 1, a + b = 0, is not greater than zero
- Hence, we have a unique answer, where a =1 and b = 1Thus a – b = 1 – 1 = 0.Sufficient to answer.Step 5: Analyze Both Statements Together (if needed)As we have a unique answer from steps 3 and 4, this step is not required.Answer: D
James deposited $1,000 each in two investment schemes X and Y. Scheme X doubles the invested amount every 7 years and scheme Y doubles the invested amount every 14 years. If James withdraws $500 from scheme X at the end of every 7th year, how many years will it take for the total amount invested in schemes X and Y to amount more than $40,000?
- a)14
- b)28
- c)42
- d)56
- e)70
Correct answer is option 'C'. Can you explain this answer?
James deposited $1,000 each in two investment schemes X and Y. Scheme X doubles the invested amount every 7 years and scheme Y doubles the invested amount every 14 years. If James withdraws $500 from scheme X at the end of every 7th year, how many years will it take for the total amount invested in schemes X and Y to amount more than $40,000?
a)
14
b)
28
c)
42
d)
56
e)
70

|
Wizius Careers answered |
Given
- Scheme X doubles the invested amount every 7 years
- James deposited $1000 in scheme X
- James withdraws $500 from scheme X after the end of every 7 years
- Scheme Y doubles the invested amount after every 14 years
- James deposited $1,000 in scheme Y
To Find: Number of years it will take total amount deposited in schemes X and Y to grow to > $40,000?
Approach
- For finding the number of years it will take the deposits in schemes X and Y to grow to more than $40,000, we need to find the amount in both the schemes X and Y after every 7 years.(As amount in scheme X doubles after every 7 years, we will need to calculate the amount at the end of every 7 years and not at the end of 14 years).
- Scheme X
- As the amount invested in scheme X doubles every 7 years, we will need to calculate the amount in scheme X after every interval of 7 years
- However, we will need to make sure that we subtract $500 at each interval of 7 years from the final amount
- Scheme Y
- As the amount invested in scheme Y doubles after every 14 years, we will need to calculate the amount in scheme Y after every interval of 14 years.
- At each interval, we will calculate the sum of amounts in scheme X and Y to check if it exceeds $40,000.
Working Out
- Amount at the end of year 7 in scheme X = $1000 * 2 = $2000
- However James withdrew $500 at the end of 7th year, So, the amount remaining will be $2000 – $500 = $1500
- The same logic has been applied in calculating the amounts at the end of every 7 year interval
- Amount at the end of year 14 in scheme Y = $1000 * 2 = $2000
- The same logic has been applied in calculating the amounts at the end of every 14 years interval.
- The same logic has been applied in calculating the amounts at the end of every 14 years interval.
- We can see that the total amount in schemes X and Y exceed $40,000 by the end of the year 42.
Answer: C
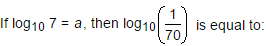
- a)- (1 + a)
- b)(1 + a)-1
- c)
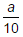
- d)
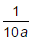
Correct answer is option 'A'. Can you explain this answer?
a)
- (1 + a)
b)
(1 + a)-1
c)
d)
|
|
Dia Mehta answered |
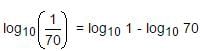
⇒ - log10 (7 x 10)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
The value of 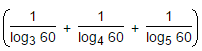 is:
is: - a)0
- b)1
- c)5
- d)60
Correct answer is option 'B'. Can you explain this answer?
The value of 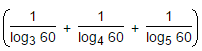 is:
is:
a)
0
b)
1
c)
5
d)
60
|
|
Shalini Patel answered |
Given expression = 1/log60 3 + 1/log60 4 + 1/log60 5
= log60 (3 x 4 x 5)
= log60 60
= 1.
= log60 (3 x 4 x 5)
= log60 60
= 1.
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.- a)15
- b)14
- c)13
- d)12
Correct answer is option 'A'. Can you explain this answer?
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.
a)
15
b)
14
c)
13
d)
12

|
Ishani Rane answered |
log(648)^5
= 5 log(648)
= 5 log(81 x 8)
= 5[log(81) + log(8)]
=5 [log(34) + log(23)]
=5[4log(3) + 3log(2)]
= 5[4 x 0.4771 + 3 x 0.30103]
= 5(1.9084 + 0.90309)
= 5 x 2.81149
approx. = 14.05
ie, log(648)^5 = 14.05 (approx.)
ie, its characteristic = 14
Hence, number of digits in (648)5 = 14+1 = 15
If Z is a positive integer such that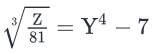
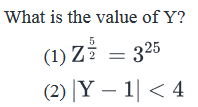
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If Z is a positive integer such that
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Meera Rana answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
- Z is a positive integer
- Z = 81(Y4 – 7)3 . . . (1)
We need to find the value of Y.
Step 3: Analyze Statement 1 independently
- Squaring both sides:
- Z5 = 350
- Taking 5th root on both sides:
- Z = 310 . . . (2)
- Put (2) in (1):
- 310 = 34(Y4 – 7)3
- 36 = (Y4 – 7)3
- Taking the cube-root on both sides:
- 32 = Y4 – 7
- Y4 = 9 + 7 = 16
- Y4 = 24 = (-2)4
- Y = 2 or -2
Not sufficient to determine a unique value of Y.
Step 4: Analyze Statement 2 independently
(2) |Y-1| < 4
- Distance of Y from 1 on the number line is less than 4 units
- -3 < Y < 5
Multiple values of Y possible. Not sufficient.
Step 5: Analyze Both Statements Together (if needed)
- From St. 1, Y = 2 or – 2
- From St. 2, -3 < Y < 5
- This inequality is satisfied by both 2 and -2
So, even after combining both statements, we have 2 possible values of Y
Since we couldn’t find a unique value of Y, the correct answer. Is Option E.
Which of the following statements is not correct?
- a)log10 10 = 1
- b)log (2 + 3) = log (2 x 3)
- c)log10 1 = 0
- d)log (1 + 2 + 3) = log 1 + log 2 + log 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not correct?
a)
log10 10 = 1
b)
log (2 + 3) = log (2 x 3)
c)
log10 1 = 0
d)
log (1 + 2 + 3) = log 1 + log 2 + log 3

|
Prince Chaudhary answered |
According to logarithm rule . option B is never correct
If log 27 = 1.431, then the value of log 9 is:- a)0.934
- b)0.945
- c)0.954
- d)0.958
Correct answer is option 'C'. Can you explain this answer?
If log 27 = 1.431, then the value of log 9 is:
a)
0.934
b)
0.945
c)
0.954
d)
0.958

|
Gowri Chakraborty answered |
Log 27 = 1.431
log (33 ) = 1.431
3 log 3 = 1.431
log 3 = 0.477
log 9 = log(32 ) = 2 log 3 = (2 x 0.477) = 0.954.
Find the value of 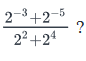
- a)1/256
- b)1/128
- c)1/64
- d)1/32
- e)1/16
Correct answer is option 'B'. Can you explain this answer?
Find the value of 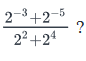
a)
1/256
b)
1/128
c)
1/64
d)
1/32
e)
1/16
|
|
Catalyst Learningacademy answered |
We want to evaluate:
(2-3 + 2-5) / (22 + 24).
Step 1. Compute the numerator: 2-3 = 1 / 23 = 1 / 8
2-5 = 1 / 25 = 1 / 32
2-5 = 1 / 25 = 1 / 32
Hence, 2-3 + 2-5 = (1/8) + (1/32) = (4/32) + (1/32) = 5/32.
Step 2. Compute the denominator: 22 = 4
24 = 16
So, 22 + 24 = 4 + 16 = 20.
24 = 16
So, 22 + 24 = 4 + 16 = 20.
Step 3. Combine numerator and denominator: (5/32) / 20 = (5/32) × (1/20) = 5 / (32 × 20) = 5/640 = 1/128.
Thus, the value of the given expression is 1/128.
if log 2 = 0.30103, the number of digits in 2128 is- a)38
- b)39
- c)40
- d)41
Correct answer is option 'B'. Can you explain this answer?
if log 2 = 0.30103, the number of digits in 2128 is
a)
38
b)
39
c)
40
d)
41

|
Milan Nair answered |
log(2128) = 128log(2) = 128 × 0.30103 ≈ 38.4
ie, its characteristic = 38
Hence, number of digits in 2128 = 38+1 = 39
ie, its characteristic = 38
Hence, number of digits in 2128 = 38+1 = 39
If n is a positive integer greater than 2, what is the greatest prime factor of 3n + 3n + 3n – 3n-2?- a)3
- b)5
- c)7
- d)11
- e)13
Correct answer is option 'E'. Can you explain this answer?
If n is a positive integer greater than 2, what is the greatest prime factor of 3n + 3n + 3n – 3n-2?
a)
3
b)
5
c)
7
d)
11
e)
13

|
Arnab Kumar answered |
Solution:
Firstly, we can simplify the given expression by combining the exponents:
3n 3n 3n 3n-2 = 33n-2 * 33n = 36n
Now, to find the greatest prime factor of 36n, we can factorize it into prime factors:
36n = 2^2 * 3^2 * n
The greatest prime factor of 36n would be the largest prime factor of n. Since n is greater than 2, we know that it is either a prime number or a composite number with prime factors.
To find the greatest prime factor of n, we can start by dividing n by 2 repeatedly until we get an odd number. For example, if n is 60, we can divide it by 2 three times to get 15:
60 ÷ 2 = 30
30 ÷ 2 = 15
Now, we can check if 15 is a prime number or if it has any other prime factors. We can do this by dividing 15 by the smallest prime numbers, which are 2, 3, 5, 7, 11, 13, etc.
15 ÷ 3 = 5
Since 5 is a prime number, it is the greatest prime factor of n. Therefore, the greatest prime factor of 36n is 13, which is the largest prime factor of 3.
Firstly, we can simplify the given expression by combining the exponents:
3n 3n 3n 3n-2 = 33n-2 * 33n = 36n
Now, to find the greatest prime factor of 36n, we can factorize it into prime factors:
36n = 2^2 * 3^2 * n
The greatest prime factor of 36n would be the largest prime factor of n. Since n is greater than 2, we know that it is either a prime number or a composite number with prime factors.
To find the greatest prime factor of n, we can start by dividing n by 2 repeatedly until we get an odd number. For example, if n is 60, we can divide it by 2 three times to get 15:
60 ÷ 2 = 30
30 ÷ 2 = 15
Now, we can check if 15 is a prime number or if it has any other prime factors. We can do this by dividing 15 by the smallest prime numbers, which are 2, 3, 5, 7, 11, 13, etc.
15 ÷ 3 = 5
Since 5 is a prime number, it is the greatest prime factor of n. Therefore, the greatest prime factor of 36n is 13, which is the largest prime factor of 3.
If log(64)= 1.806, log(16) = ?- a) 1.204
- b)0.903
- c)1.806
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If log(64)= 1.806, log(16) = ?
a)
1.204
b)
0.903
c)
1.806
d)
None of these

|
Gowri Chakraborty answered |
log(64)= 1.806
=> log(4^3) = 1.806
=> 3log(4) = 1.806
⇒log(4) = 1.806/3
log(16) = log (4^2) = 2log(4) = 2*1.806/3 = 2*0.062 = 1.204
Find the value of n that satisfies the equation 2(-3)4n = 18(27)n+2- a)3
- b)4
- c)6
- d)8
- e)22
Correct answer is option 'D'. Can you explain this answer?
Find the value of n that satisfies the equation 2(-3)4n = 18(27)n+2
a)
3
b)
4
c)
6
d)
8
e)
22

|
Mrinalini Dasgupta answered |
We need to find the value of n, given 2(−34n)=18(27)n+2
(Cancelling 2 on both sides. Also making use of the fact that 32k = (-3)2k)
If 3p+3p+3p=3q, what is p in terms of q?- a)q-1
- b)q/3
- c)3q
- d)q+1
- e)q/6
Correct answer is option 'A'. Can you explain this answer?
If 3p+3p+3p=3q, what is p in terms of q?
a)
q-1
b)
q/3
c)
3q
d)
q+1
e)
q/6

|
Siddharth Pillai answered |
We have 3p+3p+3p=3∗3p=3p+1=3q.
So p+1=q, and p=q−1.
Find the value of positive integer P that lies between 1 and 30 and is a perfect square.(1) P has at least one Prime factor(2) The cube of P is less than 300- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
Find the value of positive integer P that lies between 1 and 30 and is a perfect square.
(1) P has at least one Prime factor
(2) The cube of P is less than 300
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Saumya Shah answered |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1): P has at least one Prime factor
This statement tells us that P has at least one prime factor. Since a perfect square is a number that can be expressed as the product of two equal integers, we can conclude that P must have at least one prime factor that repeats.
To find a perfect square between 1 and 30, we can list the squares of all the positive integers less than or equal to the square root of 30 (which is approximately 5.5). The perfect squares between 1 and 30 are: 1, 4, 9, 16, and 25.
From this list, we can see that all the perfect squares have at least one prime factor. Therefore, statement (1) alone is sufficient to find the value of P.
Statement (2) ALONE is not sufficient.
Statement (2): The cube of P is less than 300
This statement tells us that the cube of P is less than 300. However, it does not provide any information about the prime factors or whether P is a perfect square.
Let's analyze the possible values of P using statement (2):
- If P is 1, 1^3 = 1, which is less than 300.
- If P is 2, 2^3 = 8, which is less than 300.
- If P is 3, 3^3 = 27, which is less than 300.
- If P is 4, 4^3 = 64, which is less than 300.
- If P is 5, 5^3 = 125, which is less than 300.
- If P is 6, 6^3 = 216, which is less than 300.
From this analysis, we can see that there are multiple possible values of P that satisfy statement (2), and not all of them are perfect squares. Therefore, statement (2) alone is not sufficient to find the value of P.
Conclusion:
Statement (1) alone is sufficient to find the value of P, as all the perfect squares between 1 and 30 have at least one prime factor. However, statement (2) alone is not sufficient, as it does not provide any information about the prime factors or whether P is a perfect square. Therefore, the correct answer is option (a) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1): P has at least one Prime factor
This statement tells us that P has at least one prime factor. Since a perfect square is a number that can be expressed as the product of two equal integers, we can conclude that P must have at least one prime factor that repeats.
To find a perfect square between 1 and 30, we can list the squares of all the positive integers less than or equal to the square root of 30 (which is approximately 5.5). The perfect squares between 1 and 30 are: 1, 4, 9, 16, and 25.
From this list, we can see that all the perfect squares have at least one prime factor. Therefore, statement (1) alone is sufficient to find the value of P.
Statement (2) ALONE is not sufficient.
Statement (2): The cube of P is less than 300
This statement tells us that the cube of P is less than 300. However, it does not provide any information about the prime factors or whether P is a perfect square.
Let's analyze the possible values of P using statement (2):
- If P is 1, 1^3 = 1, which is less than 300.
- If P is 2, 2^3 = 8, which is less than 300.
- If P is 3, 3^3 = 27, which is less than 300.
- If P is 4, 4^3 = 64, which is less than 300.
- If P is 5, 5^3 = 125, which is less than 300.
- If P is 6, 6^3 = 216, which is less than 300.
From this analysis, we can see that there are multiple possible values of P that satisfy statement (2), and not all of them are perfect squares. Therefore, statement (2) alone is not sufficient to find the value of P.
Conclusion:
Statement (1) alone is sufficient to find the value of P, as all the perfect squares between 1 and 30 have at least one prime factor. However, statement (2) alone is not sufficient, as it does not provide any information about the prime factors or whether P is a perfect square. Therefore, the correct answer is option (a) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
What is the maximum possible power of 4 in the number that is obtained when the product of the first 15 positive integers is subtracted from the product of the first 20 positive integers?- a)0
- b)3
- c)5
- d)7
- e)8
Correct answer is option 'C'. Can you explain this answer?
What is the maximum possible power of 4 in the number that is obtained when the product of the first 15 positive integers is subtracted from the product of the first 20 positive integers?
a)
0
b)
3
c)
5
d)
7
e)
8

|
Akshay Khanna answered |
To solve this problem, we need to find the maximum possible power of 4 in the difference between the product of the first 20 positive integers and the product of the first 15 positive integers.
Let's start by finding the product of the first 20 positive integers:
1 * 2 * 3 * ... * 18 * 19 * 20 = 2432902008176640000
Now let's find the product of the first 15 positive integers:
1 * 2 * 3 * ... * 13 * 14 * 15 = 1307674368000
To find the difference, we subtract the product of the first 15 positive integers from the product of the first 20 positive integers:
2432902008176640000 - 1307674368000 = 2432902006868972000
Now we need to find the maximum possible power of 4 in this difference. To do that, we need to find how many times we can divide the difference by 4 without getting a fraction.
Let's divide the difference by 4:
2432902006868972000 ÷ 4 = 608225501717243000
We can divide the result by 4 again:
608225501717243000 ÷ 4 = 152056375429310750
And once more:
152056375429310750 ÷ 4 = 38014093857327687.5
At this point, we can see that we have reached a fraction, so we can no longer divide by 4. Therefore, the maximum possible power of 4 in the difference is 3.
Therefore, the correct answer is option 'C', 5.
Let's start by finding the product of the first 20 positive integers:
1 * 2 * 3 * ... * 18 * 19 * 20 = 2432902008176640000
Now let's find the product of the first 15 positive integers:
1 * 2 * 3 * ... * 13 * 14 * 15 = 1307674368000
To find the difference, we subtract the product of the first 15 positive integers from the product of the first 20 positive integers:
2432902008176640000 - 1307674368000 = 2432902006868972000
Now we need to find the maximum possible power of 4 in this difference. To do that, we need to find how many times we can divide the difference by 4 without getting a fraction.
Let's divide the difference by 4:
2432902006868972000 ÷ 4 = 608225501717243000
We can divide the result by 4 again:
608225501717243000 ÷ 4 = 152056375429310750
And once more:
152056375429310750 ÷ 4 = 38014093857327687.5
At this point, we can see that we have reached a fraction, so we can no longer divide by 4. Therefore, the maximum possible power of 4 in the difference is 3.
Therefore, the correct answer is option 'C', 5.
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?- a)4.31
- b)3.88
- c)3.91
- d)2.97
Correct answer is option 'A'. Can you explain this answer?
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?
a)
4.31
b)
3.88
c)
3.91
d)
2.97

|
Gowri Chakraborty answered |
log 5 1024= log1024/log5 = log ( 2^10)/log(10/2)=10log(2)/log10−log2
=10*0.3010/1−0.3010 = 3.01/0.699 = 3010/699 = 4.31
What is the remainder obtained when 1010 + 105 – 24 is divided by 36?- a)5
- b)6
- c)12
- d)16
- e)32
Correct answer is option 'E'. Can you explain this answer?
What is the remainder obtained when 1010 + 105 – 24 is divided by 36?
a)
5
b)
6
c)
12
d)
16
e)
32

|
Sandeep Mehra answered |
To find the remainder when 1010, 105, and 24 are divided by 36, we can perform the division and observe the remainder.
Dividing 1010 by 36:
When we divide 1010 by 36, we get a quotient of 28 and a remainder of 22.
Dividing 105 by 36:
When we divide 105 by 36, we get a quotient of 2 and a remainder of 33.
Dividing 24 by 36:
When we divide 24 by 36, we get a quotient of 0 and a remainder of 24.
Now, let's perform the division again but with the remainders.
Dividing 22 by 36:
When we divide 22 by 36, we get a quotient of 0 and a remainder of 22.
Dividing 33 by 36:
When we divide 33 by 36, we get a quotient of 0 and a remainder of 33.
Dividing 24 by 36:
When we divide 24 by 36, we get a quotient of 0 and a remainder of 24.
Summing the remainders:
To find the remainder when the sum of the three numbers is divided by 36, we sum the remainders obtained in each division: 22 + 33 + 24 = 79.
Reducing the remainder:
Since the remainder obtained (79) is greater than the divisor (36), we need to reduce it. We can do this by repeatedly subtracting the divisor until we obtain a remainder less than the divisor.
79 - 36 = 43
43 - 36 = 7
The remainder after reducing is 7.
Therefore, the remainder obtained when 1010, 105, and 24 are divided by 36 is 7.
Hence, the correct answer is option E.
Dividing 1010 by 36:
When we divide 1010 by 36, we get a quotient of 28 and a remainder of 22.
Dividing 105 by 36:
When we divide 105 by 36, we get a quotient of 2 and a remainder of 33.
Dividing 24 by 36:
When we divide 24 by 36, we get a quotient of 0 and a remainder of 24.
Now, let's perform the division again but with the remainders.
Dividing 22 by 36:
When we divide 22 by 36, we get a quotient of 0 and a remainder of 22.
Dividing 33 by 36:
When we divide 33 by 36, we get a quotient of 0 and a remainder of 33.
Dividing 24 by 36:
When we divide 24 by 36, we get a quotient of 0 and a remainder of 24.
Summing the remainders:
To find the remainder when the sum of the three numbers is divided by 36, we sum the remainders obtained in each division: 22 + 33 + 24 = 79.
Reducing the remainder:
Since the remainder obtained (79) is greater than the divisor (36), we need to reduce it. We can do this by repeatedly subtracting the divisor until we obtain a remainder less than the divisor.
79 - 36 = 43
43 - 36 = 7
The remainder after reducing is 7.
Therefore, the remainder obtained when 1010, 105, and 24 are divided by 36 is 7.
Hence, the correct answer is option E.
What are the last two digits, in order, of 6789 ?Possible Answers:- a)36
- b)16
- c)56
- d)96
- e)76
Correct answer is option 'D'. Can you explain this answer?
What are the last two digits, in order, of 6789 ?
Possible Answers:
a)
36
b)
16
c)
56
d)
96
e)
76

|
Ankita Chauhan answered |
To find the last two digits of a large number, we need to consider the remainder when the number is divided by 100.
In this case, we are asked to find the last two digits of 6789.
Remainder when divided by 100:
To find the remainder when 6789 is divided by 100, we can use the concept of modular arithmetic. We can rewrite 6789 as (6700 + 89) since 6700 is a multiple of 100.
The remainder when 6700 is divided by 100 is 0, so we only need to consider the remainder when 89 is divided by 100.
Finding the remainder when 89 is divided by 100:
To find the remainder when 89 is divided by 100, we can divide 89 by 100 and observe the remainder.
89 ÷ 100 = 0 remainder 89
Therefore, the remainder when 89 is divided by 100 is 89.
Determining the last two digits:
Since the remainder when 89 is divided by 100 is 89, the last two digits of 6789 are also 89.
Therefore, the correct answer is option 'D' (96).
In this case, we are asked to find the last two digits of 6789.
Remainder when divided by 100:
To find the remainder when 6789 is divided by 100, we can use the concept of modular arithmetic. We can rewrite 6789 as (6700 + 89) since 6700 is a multiple of 100.
The remainder when 6700 is divided by 100 is 0, so we only need to consider the remainder when 89 is divided by 100.
Finding the remainder when 89 is divided by 100:
To find the remainder when 89 is divided by 100, we can divide 89 by 100 and observe the remainder.
89 ÷ 100 = 0 remainder 89
Therefore, the remainder when 89 is divided by 100 is 89.
Determining the last two digits:
Since the remainder when 89 is divided by 100 is 89, the last two digits of 6789 are also 89.
Therefore, the correct answer is option 'D' (96).
If log10 2 = 0.3010, then log2 10 is equal to:- a)
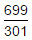
- b)
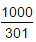
- c)0.3010
- d)0.6990
Correct answer is 'B'. Can you explain this answer?
If log10 2 = 0.3010, then log2 10 is equal to:
a)
b)
c)
0.3010
d)
0.6990

|
Aman Jha answered |
Log10 2=1/log2 10 therefore 0.3010=1/log2 10 log2 10=1/0.3010 so log2 10 = 1000/301
Which of the following statements is not correct?- a)log10 10 = 1
- b)log (2 + 3) = log (2 x 3)
- c)log10 1 = 0
- d)log (1 + 2 + 3) = log 1 + log 2 + log 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not correct?
a)
log10 10 = 1
b)
log (2 + 3) = log (2 x 3)
c)
log10 1 = 0
d)
log (1 + 2 + 3) = log 1 + log 2 + log 3

|
Bank Exams India answered |
- Since loga a = 1, so log10 10 = 1.
- log (2 + 3) = log 5 and log (2 x 3) = log 6 = log 2 + log 3
∴ log (2 + 3) ≠ log (2 x 3) - Since loga 1 = 0. so logio 1 = 0.
- log (1 + 2 + 3) = log 6
log (1 x 2 x 3) = log 1 + log 2 + log 3=log (6).
So. option (b) is incorrect.
Z=2a×5b×7cA positive integer Z can be expressed in terms of its prime factors as above, where a, b and c are positive integers. Is 3|a−b|<9?(1) Z is divisible by 40 but not by 50(2) Za−b=26×52×74- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Z=2a×5b×7c
A positive integer Z can be expressed in terms of its prime factors as above, where a, b and c are positive integers. Is 3|a−b|<9?
(1) Z is divisible by 40 but not by 50
(2) Za−b=26×52×74
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Devansh Shah answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
Step 3: Analyze Statement 1 independently
(1) Z is divisible by 40 but not by 50
- 40 = 23*5
- 50 = 2*52
- The power of 2 in Z is at least 3
- a ≥ 3
- The power of 5 in Z is 1.
- b = 1
- Therefore, a – b ≥ 3 – 1
a – b ≥ 2
So, answer to the asked question is: NO
Statement 1 is sufficient to answer the question.
Step 4: Analyze Statement 2 independently
- Equating the powers of a base on both sides of the equation:
- a(a - b) = 6. . . (1)
- b(a - b) = 2. . . (2)
- Dividing (1) by (2)
- The minimum value of b is 1 (b is a positive integer)
- So, minimum value of a – b = 2
Thus, the answer to the asked question is: NO
Statement 2 is sufficient to answer the question.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at unique answers in Steps 3 and 4, this step is not required
Answer: Option D
If x is a positive integer less than 100 such that x is divisible by 2y, where y is a positive integer, what is the value of y?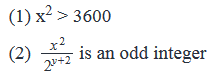
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If x is a positive integer less than 100 such that x is divisible by 2y, where y is a positive integer, what is the value of y?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Abhishek Choudhury answered |
Steps 1 & 2: Understand Question and Draw Inferences
- x is an integer such that 0 < x < 100
- x is divisible by 2y, where y is a positive integer
- Since y > 0, this means 2 is definitely a prime factor 2
- Since x is a positive integer, we can write the Prime-factorized form of x as:
- are integers > 0, z ≥ y and are prime numbers other than 2.
- As x < 100, 2z < 100
- So, z = { 1, 2, 3, 4, 5, 6} as 27 = 128 > 100
- Since x is completely divisible by 2y, z ≥ y. So, y can take any value of z, i.e. 1 ≤ y ≤ 6
- To Find: Unique value of y
Step 3: Analyze Statement 1 independently
- As x is a positive integer, x < -60 is not possible.
- So, x > 60, i.e. 60 < x < 100.
However, we do not know if 2 is the only prime factor or x. So, we cannot find a unique value of y.
- For example, if 2 is the only prime factor of x, then y can have only 1 value: 6
- But if x has other prime factors, then multiple values of y are possible. For example, x could be 22*3*7 (y = 2) or 23*11 (y = 3) etc.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
- Using the prime factorized expression of x, we can write:
- Since the integer resulting from this division is odd, the powers of 2 in the numerator and the denominator should cancel out each other.
- Hence 22z = 2y+2
- z=y/2+1 ….(1). So, y must be even as z is an integer
- Also, from our discussion in Steps 1 and 2, we know that z ≥ y
- Substituting (1) in the above inequality, we get:
Using (2), along with the inference that y must be even, we have y = 2 as the only possible option.
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step 4, this step is not required.
Answer: B
If 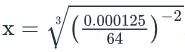 , what is the value of x?
, what is the value of x?- a)6400
- b)8000
- c)12500
- d)15625
- e)22500
Correct answer is option 'A'. Can you explain this answer?
If 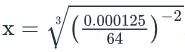 , what is the value of x?
, what is the value of x?
a)
6400
b)
8000
c)
12500
d)
15625
e)
22500

|
Arya Yadav answered |
Given:
To find: Value of x
Working Out:
Looking at the answer choices, we see that the correct answer is Option A
Is the sum of xy and yx positive?(1) xy > 0(2) x + y > 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Is the sum of xy and yx positive?
(1) xy > 0
(2) x + y > 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Sahana Mehta answered |
Steps 1 & 2: Understand Question and Draw Inferences
To Find: If xy + yx > 0
Step 3: Analyze Statement 1 independently
(1) xy > 0
- Tells that x and y are of the same sign. Two cases arise:
- x, y > 0
- In this case xy, yx > 0. So, xy + yx > 0
- x, y < 0
- In this case, xy + yx may or may not be positive, depending on the values of x and y. Following cases can arise:
- Both x, y are even → In this case xy,yx > 0. So, xy+yx > 0
- Both x and y are odd → In this case xy,yx < 0. So, xy+yx < 0
- x is even and y is odd → In this case xy < 0, yx > 0. Cannot comment on the value of xy+yx
- x is odd and y is even → In this case xy < 0, yx > 0. Cannot comment on the value of xy+yx
- x, y > 0
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) x + y > 0
- Considering the constraint x + y > 0, following cases are possible:
- x, y > 0. So, x + y > 0. In this case, xy, yx > 0. So, xy + yx > 0
- x < 0, y > 0 and |y| > |x|. So, x + y > 0. In this case xy + yx may or may not be positive.
- If y is odd, then xy < 0 , yx > 0 as y is positive. In this case, we cannot comment on the value of xy + yx
- If y is even , then xy > 0 , yx > 0 as y is positive. In this case, xy + yx > 0
- x > 0, y < 0 and |x| > |y|. So, x + y > 0. In this case xy + yx may or may not be positive.
Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1, xy > 0
- From Statement 2, x + y > 0
Statement-1 tells us that x and y have the same signs. Following cases are possible:
- If x & y > 0, xy > 0 and x + y > 0. In this case xy + yx > 0
- If x & y < 0, x+ y < 0. Not possible. (If x & y both are negative, the x + y cannot be > 0)
The only possible case is when x, y > 0 and hence xy + yx > 0
Sufficient to answer.
Answer: C
Which of the following is equal to 4log3−2log6 ?- a)log9−log4
- b)0
- c)log4−log9
- d)log3−log2
- e)log2−log3
Correct answer is option 'A'. Can you explain this answer?
Which of the following is equal to 4log3−2log6 ?
a)
log9−log4
b)
0
c)
log4−log9
d)
log3−log2
e)
log2−log3

|
Jhanvi Saha answered |
4log3−2log6
=log(34)−log(62)
=log81−log36
=log81/36
=log9/4
=log 9− log 4
Simplify:

- a)60 x12
- b)x60
- c)x12
- d)12x
- e)60x
Correct answer is option 'B'. Can you explain this answer?
Simplify:


a)
60 x12
b)
x60
c)
x12
d)
12x
e)
60x

|
Avantika Sengupta answered |
Apply the power of a power principle twice by multiplying exponents:
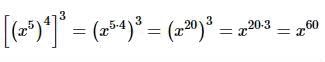
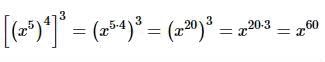
Which of the following is equal to log8+log5−log4 ?- a)2 log 5
- b)log 9
- c)2
- d)1
- e)0
Correct answer is option 'D'. Can you explain this answer?
Which of the following is equal to log8+log5−log4 ?
a)
2 log 5
b)
log 9
c)
2
d)
1
e)
0

|
Krithika Datta answered |
log8+log5−log4
=log(8⋅5)−log4
=log40−log4
=log(40÷4)
=log10=1
=log(8⋅5)−log4
=log40−log4
=log(40÷4)
=log10=1
if, 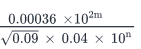 = 3 x 107 , then 4m - 2n =
= 3 x 107 , then 4m - 2n =- a)9
- b)10
- c)14
- d)16
- e)18
Correct answer is option 'E'. Can you explain this answer?
if, 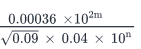 = 3 x 107 , then 4m - 2n =
= 3 x 107 , then 4m - 2n =
a)
9
b)
10
c)
14
d)
16
e)
18

|
Soumya Iyer answered |
We need to find the value of 4m – 2n.
Given expression:
Therefore, 4m -2n =2 * (2m -n) =18
Correct Answer: E
If x and y are non-zero numbers, what is the value of y?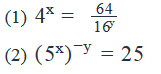
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If x and y are non-zero numbers, what is the value of y?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Arka Basu answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: x ≠ 0, y ≠ 0
To find: y = ?
Step 3: Analyze Statement 1 independently
Equating the powers of 2 on both sides:
2x = 6 – 4y
x + 2y = 3
1 Linear Equation with 2 unknowns. Not sufficient to find a unique value of y.
Step 4: Analyze Statement 2 independently
Not sufficient to find a unique value of y.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: x + 2y = 3 . . . (1)
- From Statement 2: xy = -2
Substituting (2) in (1):
- This quadratic equation gives 2 values of y
- The only constraint on y: y ≠ 0
- Since 0 is not a root of the above quadratic equation, this constraint doesn’t help eliminate one of the two roots of y
- Thus, 2 values of y are obtained from the combination of the two statements
Not sufficient to obtain a unique value of y.
Answer: Option E
Simplify the given expression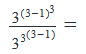
- a)1/9
- b)1/3
- c)1
- d)3
- e)9
Correct answer is option 'B'. Can you explain this answer?
Simplify the given expression
a)
1/9
b)
1/3
c)
1
d)
3
e)
9

|
Gitanjali Kumar answered |
Correct Answer: Option B
Positive integer P lies between 1 and 30. What is the value of P?(1) P has at least two prime factors(2) The cube of P is less than 300- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
Positive integer P lies between 1 and 30. What is the value of P?
(1) P has at least two prime factors
(2) The cube of P is less than 300
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Soumya Iyer answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given that P is a positive integer and that 1 < P < 30.
We need to find the value of P
Step 3: Analyze Statement 1
Given that P has at least two prime factors.
- P is a composite number with two or more prime factors.
However, there are more than one composite number between 1 and 30. The possible values of P are:
Clearly, Statement (1) doesn’t lead us to a unique value of P.
Not Sufficient.
Step 4: Analyze Statement 2
Statement 2 says that the cube of P is less than 300.
Let us list out the cubes of natural numbers.
There are 5 natural numbers between 1 and 30 whose cubes are less than 300.
Statement 2 alone is not sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1,
Possible values of P: 6, 10, 14, 15, 21, 22, 26
From Statement 2,
Possible values of P: 2, 3, 4, 5, 6
By combining the two statements, we get:
P = 6
Therefore statement 1 and statement 2 combined are sufficient to arrive at a unique answer.
Correct Answer: C
The half-life of a radioactive element is defined as the amount of time required for the amount of the element to decrease by half. If the half-life of an element is 3 years, how long will it take for the element to be reduced to one-eighth of its original amount?- a)3 years
- b)9 years
- c)21 years
- d)24 years
- e)27 years
Correct answer is option 'B'. Can you explain this answer?
The half-life of a radioactive element is defined as the amount of time required for the amount of the element to decrease by half. If the half-life of an element is 3 years, how long will it take for the element to be reduced to one-eighth of its original amount?
a)
3 years
b)
9 years
c)
21 years
d)
24 years
e)
27 years

|
Mrinalini Dasgupta answered |
Let us first understand the given information.
The question states the following about half-life:
- Half-life is defined as the time taken for the mass of a radioactive substance to reduce to half.
The interesting thing to notice here is that the Half-life apparently is not dependent on the initial mass of the radioactive substance.
In other words, if a particular radioactive substance’s half-life is 2 years, then the time taken by it
- To reduce from 1000 kg to 500 kg is 2 years
- To reduce from 500 kg to 250 kg is 2 years
- To reduce from 250 kg to 125 kg is 2 years and so on.
This makes it easier for us to calculate the time taken by the radioactive substance to decay because we will be simply counting the number of half-lives taken.
We need to find the approximate time taken for a X grams block of the radioactive element to reduce to about X/8 grams.
As we noted earlier,
In 1 half-life, the amount of element left = ½ * X
In 2 half-lives, the amount of element left = ½ * ½ * X = (½)2 * X
Let’s say the number of half-lives taken = n.
Then in n half-lives, the amount of element left = (½)n * X
Given that the mass left is 1/8 th of the original amount.
Therefore amount of element left = X/8
This gives us (½)n * X = X/8
- (½)n = 1/8
- (½)n = (½)3
- n = 3
Therefore the time taken = 3 half-lives = 3*3 = 9 years.
Correct Answer: B
Is xy ≥ 1 if both x and y are non-zero integers?(1) y = -x(2) y = 2k where k is a non-zero integer- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
Is xy ≥ 1 if both x and y are non-zero integers?
(1) y = -x
(2) y = 2k where k is a non-zero integer
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Athul Joshi answered |
Step 1: Question statement and Inferences
xy ≥ 1 if one of two things is true. This is when
- x and y are both positive (23), or
- x is negative and y is positive and even
Note, a negative y does not helps us since any integer raised to a negative power cannot be greater than 1. Hence lets figure out if x and y fulfill one of the two criteria above.
Step 3: Analyze Statement 1
1) y = -x
Statement 1 says that y and x are of opposite signs.
Let’s say that x = 2
This means, y = -2
So xy = 2-2 = ¼ which is less than 1
Let’s now consider the case x = -2
This means, y = 2
So, xy = (-2)2 = 4, which is greater than 1
Thus, we realize that Statement 1 does not lead us to a definitive answer. So, Statement 1 is NOT SUFFICIENT
Step 4: Analyze Statement 2
y = 2k where k is a non-zero integer
We are given that k cannot be equal to zero.
Can k be a negative integer?
The answer is No. Because if k were to be a negative integer, then y would become a fraction (For example, say k = -3. Then y =2-3 = 1/8)
But, we are given that y is an integer.
This is only possible if k is a positive integer.
Thus, k can have only positive values and y is a positive multiple of 2.
x may be a positive or a negative integer, but when it is raised to an even power, the result is always going to be positive.
If x = -1 or 1, then the value of xy will be equal to 1. For any other allowed value of x (remember: x = 0 is not allowed), the value of xy will be greater than 1.
Statement 2 is SUFFICIENT
Answer: Option (B)
If 22 x 83 = 2 x 4z, what is the value of z?- a)2
- b)4
- c)5
- d)7
- e)10
Correct answer is option 'C'. Can you explain this answer?
If 22 x 83 = 2 x 4z, what is the value of z?
a)
2
b)
4
c)
5
d)
7
e)
10

|
Isha Sen answered |
Given 22 x 83 = 2 x 4z
⇒ 22 x 23.3 = 2 x 22z
⇒ 211 = 21+2z
⇒ 11 = 1 + 2z
⇒10 = 2z
⇒ z = 5
Chapter doubts & questions for Powers, Exponents and Logarithms - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Powers, Exponents and Logarithms - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
453 videos|1305 docs|700 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily