All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Stacks & Queues for Computer Science Engineering (CSE) Exam
Consider the following C program: #include <stdio.h>#define EOF -1void push (int); /* push the argument on the stack */int pop (void); /* pop the top of the stack */void flagError ();int main (){ int c, m, n, r; while ((c = getchar ()) != EOF){ if (isdigit (c) ) push (c);else if ((c == '+') || (c == '*')){ m = pop ();n = pop ();r = (c == '+') ? n + m : n*m;push (r);}
else if (c != ' ') flagError ();}
printf("% c", pop ());}What is the output of the program for the following input?5 2 * 3 3 2 + * +- a)15
- b)25
- c)30
- d)150
Correct answer is option 'B'. Can you explain this answer?
Consider the following C program:
#include <stdio.h>
#define EOF -1
void push (int); /* push the argument on the stack */
int pop (void); /* pop the top of the stack */
void flagError ();
int main ()
{ int c, m, n, r;
while ((c = getchar ()) != EOF)
{ if (isdigit (c) )
push (c);
else if ((c == '+') || (c == '*'))
{ m = pop ();
n = pop ();
r = (c == '+') ? n + m : n*m;
push (r);
}
else if (c != ' ')
else if (c != ' ')
flagError ();
}
printf("% c", pop ());
printf("% c", pop ());
}
What is the output of the program for the following input?
5 2 * 3 3 2 + * +
a)
15
b)
25
c)
30
d)
150
|
|
Yash Patel answered |
B) 25
let first part
5 ----push
2------push
push------5*2=10. (pops 5 and 2)
let first part
5 ----push
2------push
push------5*2=10. (pops 5 and 2)
push 3
push 3
push 2
push 3+2 = 5 (pops 2 and 3)
push 5*3 = 15 (pops (5 and 3)
push 15 + 10 = 25 (pops (15 and 10)
push 3
push 2
push 3+2 = 5 (pops 2 and 3)
push 5*3 = 15 (pops (5 and 3)
push 15 + 10 = 25 (pops (15 and 10)
In stack, memory allocation and deallocation is performed in ________.- a)Last-in-first-out (LIFO) manner
- b)First-in-first-out (FIFO) manner
- c)First-in-last-out (FILO) manner
- d)Random manner
Correct answer is option 'A'. Can you explain this answer?
In stack, memory allocation and deallocation is performed in ________.
a)
Last-in-first-out (LIFO) manner
b)
First-in-first-out (FIFO) manner
c)
First-in-last-out (FILO) manner
d)
Random manner

|
EduRev GATE answered |
A stack is a linear data type that acts as a collection of elements. A stack is a linear data structure that operates memory allocation and deallocation on the Last-In-First-Out (LIFO) principle. In linear data structures, the elements are accessed in sequential order but it is not compulsory to store all elements sequentially. It has two main operations:
- Push, which adds a new element to the collection, and
- Pop, which removes the most recently added element that hasn't been removed yet.
Hence the correct answer is Last-in-first-out (LIFO) manner.
Which of the following is the postfix equivalent of (9 - 5) + 2 ?- a)-95 + 2
- b)95 + 2-
- c)95 - 2+
- d)+-952
Correct answer is option 'C'. Can you explain this answer?
Which of the following is the postfix equivalent of (9 - 5) + 2 ?
a)
-95 + 2
b)
95 + 2-
c)
95 - 2+
d)
+-952

|
EduRev GATE answered |
The given data:
Infix: (9 - 5) + 2
Postfix: 95-2+
Postfix: 95-2+
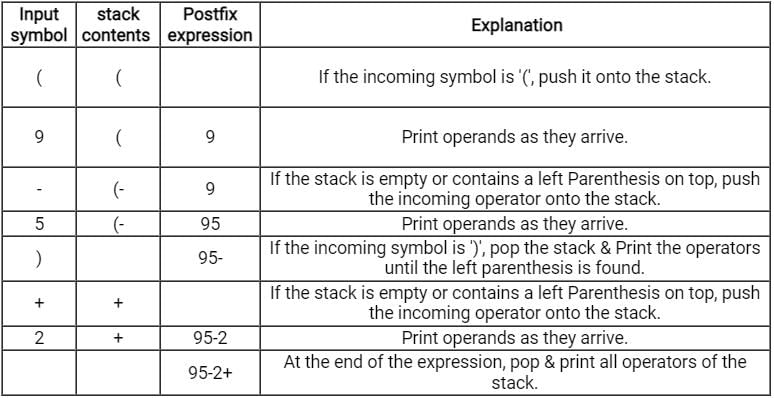
Hence the correct answer is 95-2+.
The result evaluating the postfix expression 10 5 + 60 6/* 8 - is- a)284
- b)213
- c)142
- d)71
Correct answer is option 'C'. Can you explain this answer?
The result evaluating the postfix expression 10 5 + 60 6/* 8 - is
a)
284
b)
213
c)
142
d)
71
|
|
Baishali Reddy answered |
10 5 + 60 6 / * 8 -

Result is 142.

Result is 142.
A stack A has 4 entries as following sequence a,b,c,d and stack B is empty. An entry popped out of stack A can be printed or pushed to stack B. An entry popped out of stack B can only be printed.
Then the number of possible permutations that the entries can be printed will be ?
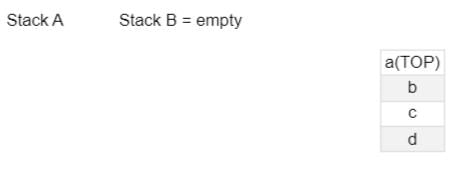
- a)24
- b)12
- c)21
- d)14
Correct answer is option 'D'. Can you explain this answer?
A stack A has 4 entries as following sequence a,b,c,d and stack B is empty. An entry popped out of stack A can be printed or pushed to stack B. An entry popped out of stack B can only be printed.
Then the number of possible permutations that the entries can be printed will be ?
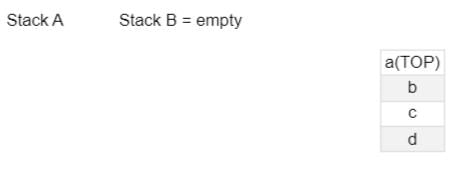
a)
24
b)
12
c)
21
d)
14
|
|
Prateek Khanna answered |
permutations which start with D:
to print D first , all a,b,c must be pushed on to stack before popping D and the only arrangement possible = D C B A
permutations start with C:
you need to push a and b from stack A to stack B , now print C
content of stack B= b a (from top to bottom)
content of stack A = d
permutations possible = 3!/2! = 3 = they are c d b a, c b d a, c b a d --> 3 permutations here
permutations starting with b :
to print b first, a will be pushed onto stack B
content of stack B= a
content of stack A= c d
you can bring these out in (3! -1) as (d a c) is not possible--> 5 possible
permutations starting with a:
fix ab
a b _ _
in this a b c d or a b dc
fix ac
a c _ _
a c b d or a c d b
fix ad
a d _ _
a d c b
total 5
total = 1+3+5+5= 14
to print D first , all a,b,c must be pushed on to stack before popping D and the only arrangement possible = D C B A
permutations start with C:
you need to push a and b from stack A to stack B , now print C
content of stack B= b a (from top to bottom)
content of stack A = d
permutations possible = 3!/2! = 3 = they are c d b a, c b d a, c b a d --> 3 permutations here
permutations starting with b :
to print b first, a will be pushed onto stack B
content of stack B= a
content of stack A= c d
you can bring these out in (3! -1) as (d a c) is not possible--> 5 possible
permutations starting with a:
fix ab
a b _ _
in this a b c d or a b dc
fix ac
a c _ _
a c b d or a c d b
fix ad
a d _ _
a d c b
total 5
total = 1+3+5+5= 14
How many stacks are needed to implement a queue. Consider the situation where no other data structure like arrays, linked list is available to you.- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
How many stacks are needed to implement a queue. Consider the situation where no other data structure like arrays, linked list is available to you.
a)
1
b)
2
c)
3
d)
4

|
Crack Gate answered |
- A queue operates on a First In, First Out (FIFO) principle, while a stack works on a Last In, First Out (LIFO) principle.
- By using two stacks, we can simulate the FIFO behavior of a queue.
thus option B is correct
What all is true about Stack data structure? (More than one option is correct)- a)Last IN First OUT
- b)Minimum 2 queues are required to implement a stack
- c)First IN First OUT
- d)Does not have a fixed size.
Correct answer is option 'A,B,D'. Can you explain this answer?
What all is true about Stack data structure? (More than one option is correct)
a)
Last IN First OUT
b)
Minimum 2 queues are required to implement a stack
c)
First IN First OUT
d)
Does not have a fixed size.
|
|
Ananya Kumari answered |
What all is true about stack data structure? ( more than one option is correct)
last in first out ,
maximum 2 queues are required to implement a stack
does not have a fixed size
Correct is ABD is right ans
last in first out ,
maximum 2 queues are required to implement a stack
does not have a fixed size
Correct is ABD is right ans
The result evaluating the postfix expression 10 5 + 60 6 / * 8 − is- a)284
- b)213
- c)142
- d)71
Correct answer is option 'C'. Can you explain this answer?
The result evaluating the postfix expression 10 5 + 60 6 / * 8 − is
a)
284
b)
213
c)
142
d)
71

|
EduRev GATE answered |
Postfix expression 10 5 + 60 6 / * 8 −
PUSH: 10 and 5(TOS)
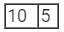
Add: 10 + 5 = 15
PUSH: 15 60 6 (TOS)
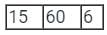

Add: 10 + 5 = 15
PUSH: 15 60 6 (TOS)

Divide: 60/6 = 10
PUSH: 10

PUSH: 10

Multiply: 15 × 10 = 150
PUSH: 150 and 8

PUSH: 150 and 8

Subtract: 150 - 8 = 142
Diagram:
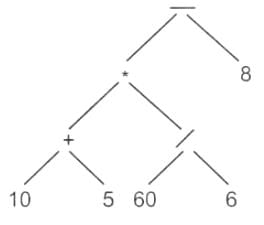
Evaluate Infix notation:
(((10 + 5) * (60 / 6)) - 8) = ((15 * 10) - 8) = 150 - 8 = 142
Suppose a circular queue of capacity (n - 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are- a)full: (REAR+1) mod n == FRONTempty: REAR == FRONT$
- b)full: (REAR+1) mod n == FRONTempty: (FRONT+1) mod n == REAR
- c)full: REAR == FRONTempty: (REAR+1) mod n == FRONT
- d)full: (FRONT+1) mod n == REARempty: REAR == FRONT
Correct answer is option 'A'. Can you explain this answer?
Suppose a circular queue of capacity (n - 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are
a)
full: (REAR+1) mod n == FRONT
empty: REAR == FRONT$
b)
full: (REAR+1) mod n == FRONT
empty: (FRONT+1) mod n == REAR
c)
full: REAR == FRONT
empty: (REAR+1) mod n == FRONT
d)
full: (FRONT+1) mod n == REAR
empty: REAR == FRONT

|
Sagnik Sen answered |
In a circular queue implementation using an array of size n, the queue is considered full when there is only one empty space left in the array. This means that if the next element is inserted at the current REAR position, it will wrap around to the FRONT position, and there will be no space for additional elements.
The condition to detect a full queue is:
(REAR + 1) mod n == FRONT
Here, (REAR + 1) calculates the next position in the array after the current REAR position, and mod n ensures that the position wraps around within the range of the array. If this calculated next position is equal to the current FRONT position, it means the queue is full because there is only one empty space left.
Similarly, the condition to detect an empty queue is:
REAR == FRONT
If the REAR and FRONT indices are equal, it means there are no elements in the queue, and it is empty.
Therefore, the correct answer is option 'A' – full: (REAR + 1) mod n == FRONT, empty: REAR == FRONT.
Suppose you are given an implementation of a queue of integers. The operations that can be performed on the queue are:i. isEmpty (Q) — returns true if the queue is empty, false otherwise.ii. delete (Q) — deletes the element at the front of the queue and returns its value.iii. insert (Q, i) — inserts the integer i at the rear of the queue.Consider the following function:void f (queue Q) {int i ;if (!isEmpty(Q)) { i = delete(Q);f(Q);insert(Q, i);}
}What operation is performed by the above function f ?- a)Leaves the queue Q unchanged
- b)Reverses the order of the elements in the queue Q
- c)Deletes the element at the front of the queue Q and inserts it at the rear keeping the other elements in the same order
- d)Empties the queue Q
Correct answer is option 'B'. Can you explain this answer?
Suppose you are given an implementation of a queue of integers. The operations that can be performed on the queue are:
i. isEmpty (Q) — returns true if the queue is empty, false otherwise.
ii. delete (Q) — deletes the element at the front of the queue and returns its value.
iii. insert (Q, i) — inserts the integer i at the rear of the queue.
Consider the following function:
void f (queue Q) {
int i ;
if (!isEmpty(Q)) {
i = delete(Q);
f(Q);
insert(Q, i);
}
}
}
What operation is performed by the above function f ?
a)
Leaves the queue Q unchanged
b)
Reverses the order of the elements in the queue Q
c)
Deletes the element at the front of the queue Q and inserts it at the rear keeping the other elements in the same order
d)
Empties the queue Q
|
|
Mira Choudhary answered |
insert() will inserts the value in just reverse order.
Consider the following statements:
i. First-in-first-out types of computations are efficiently supported by STACKS.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
- a)(ii) and (iii) are true
- b)(i) and (ii) are true
- c)(iii) and (iv) are true
- d)(ii) and (iv) are true
Correct answer is option 'A'. Can you explain this answer?
Consider the following statements:
i. First-in-first-out types of computations are efficiently supported by STACKS.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
a)
(ii) and (iii) are true
b)
(i) and (ii) are true
c)
(iii) and (iv) are true
d)
(ii) and (iv) are true

|
S V Sravan Kumar Kandreg answered |
Obviously we already know that LIFO data structure is STACK and FIFO data structure is QUEUE.We have these two statements as wrong in both (i) and (iv).So we have only option A as these two statements are wrong.Hence,by knowing just these two basic points,we can find correct answer I.e.,A.(ii) and (iii) are true. : )
A recursive problem like tower of hanoi can be rewritten without recursion using:- a)stack
- b)priority queue
- c)graph
- d)cycles
Correct answer is option 'A'. Can you explain this answer?
A recursive problem like tower of hanoi can be rewritten without recursion using:
a)
stack
b)
priority queue
c)
graph
d)
cycles
|
|
Sudhir Patel answered |
A recursive problem like the Tower of Hanoi can be rewritten using system stack or user-defined stack
Recurrence relation of tower of Hanoi: T(n) = 2T(n - 1) + 1
Recurrence relation of tower of Hanoi: T(n) = 2T(n - 1) + 1
Following is C like pseudo code of a function that takes a Queue as an argument, and uses a stack S to do processing.void fun(Queue *Q)
{
Stack S; // Say it creates an empty stack S // Run while Q is not empty
while (!isEmpty(Q))
{
// deQueue an item from Q and push the dequeued item to S
push(&S, deQueue(Q));
} // Run while Stack S is not empty
while (!isEmpty(&S))
{
// Pop an item from S and enqueue the poppped item to Q
enQueue(Q, pop(&S));
}
}
Q.
What does the above function do in general?- a)Removes the last from Q
- b)Keeps the Q same as it was before the call
- c)Makes Q empty
- d)Reverses the Q
Correct answer is option 'D'. Can you explain this answer?
Following is C like pseudo code of a function that takes a Queue as an argument, and uses a stack S to do processing.
void fun(Queue *Q)
{
Stack S; // Say it creates an empty stack S
{
Stack S; // Say it creates an empty stack S
// Run while Q is not empty
while (!isEmpty(Q))
{
// deQueue an item from Q and push the dequeued item to S
push(&S, deQueue(Q));
}
while (!isEmpty(Q))
{
// deQueue an item from Q and push the dequeued item to S
push(&S, deQueue(Q));
}
// Run while Stack S is not empty
while (!isEmpty(&S))
{
// Pop an item from S and enqueue the poppped item to Q
enQueue(Q, pop(&S));
}
}
Q.
What does the above function do in general?
while (!isEmpty(&S))
{
// Pop an item from S and enqueue the poppped item to Q
enQueue(Q, pop(&S));
}
}
Q.
What does the above function do in general?
a)
Removes the last from Q
b)
Keeps the Q same as it was before the call
c)
Makes Q empty
d)
Reverses the Q
|
|
Maulik Pillai answered |
The function takes a queue Q as an argument. It dequeues all items of Q and pushes them to a stack S. Then pops all items of S and enqueues the items back to Q. Since stack is LIFO order, all items of queue are reversed.
Let's break down the code to understand its functionality:
1. The function fun takes a Queue Q as an argument and creates an empty Stack S.
2. It enters a loop that runs as long as the Queue Q is not empty. Inside the loop:
● An item is dequeued (removed) from the front of the Queue Q.
● The dequeued item is then pushed (added) onto the Stack S.
3. After the first loop completes, the Queue Q becomes empty, and the Stack S contains all the items from the original Queue in reverse order.
4. Another loop begins, running as long as the Stack S is not empty. Inside this loop:
● An item is popped (removed) from the top of the Stack S.
● The popped item is enqueued (added) to the rear of the Queue Q.
5. After the second loop completes, the Queue Q contains all the items that were originally in Q, but they are now in reversed order. This is why the function reverses the Queue.
Therefore, the correct answer is option 'D': The function reverses the Queue.
An implementation of a queue Q, using two stacks S1 and S2, is given below: void insert (Q, x) { push (S1, x);}void delete (Q) {if (stack-empty(S2)) thenif (stack-empty(S1)) then {print(“Q is empty”);return;}else while (!(stack-empty(S1))){x=pop(S1);push(S2,x);}
x=pop(S2);}let n insert and m(≤ n)delete operations be performed in an arbitrary order on an empty queue Q. Let x and y be the number of push and pop operations performed respectively in the process. Which one of the following is true for all m and n?- a)n + m ≤ x < 2n and 2m ≤ y ≤ n+m
- b)n+ m≤x < 2n and 2m ≤ y ≤ 2n
- c)2m≤ x < 2n and 2m ≤y ≤n+m
- d)2m≤x <2n and 2m≤y≤2n
Correct answer is option 'A'. Can you explain this answer?
An implementation of a queue Q, using two stacks S1 and S2, is given below:
void insert (Q, x) {
push (S1, x);
}
void delete (Q) {
if (stack-empty(S2)) then
if (stack-empty(S1)) then {
print(“Q is empty”);
return;
}
else while (!(stack-empty(S1))){
x=pop(S1);
push(S2,x);
}
x=pop(S2);
x=pop(S2);
}
let n insert and m(≤ n)delete operations be performed in an arbitrary order on an empty queue Q. Let x and y be the number of push and pop operations performed respectively in the process. Which one of the following is true for all m and n?
a)
n + m ≤ x < 2n and 2m ≤ y ≤ n+m
b)
n+ m≤x < 2n and 2m ≤ y ≤ 2n
c)
2m≤ x < 2n and 2m ≤y ≤n+m
d)
2m≤x <2n and 2m≤y≤2n
|
|
Saikat Basu answered |
Answer is (a)
The order in which insert and delete operations are performed matters here.
The best case: Insert and delete operations are performed alternatively. In every delete operation, 2 pop and 1 push
operations are performed. So, total m+ n push (n push for insert() and m push for delete()) operations and 2m pop operations are performed.
The worst case: First n elements are inserted and then m elements are deleted. In first delete operation, n + 1 pop operations and n push operation are performed. Other than first, in all delete operations, 1 pop operation is performed. So, total m + n pop operations and 2n push operations are performed (n push for insert() and m push for delete())
The order in which insert and delete operations are performed matters here.
The best case: Insert and delete operations are performed alternatively. In every delete operation, 2 pop and 1 push
operations are performed. So, total m+ n push (n push for insert() and m push for delete()) operations and 2m pop operations are performed.
The worst case: First n elements are inserted and then m elements are deleted. In first delete operation, n + 1 pop operations and n push operation are performed. Other than first, in all delete operations, 1 pop operation is performed. So, total m + n pop operations and 2n push operations are performed (n push for insert() and m push for delete())
A function f defined on stacks of integers satisfies the following properties. f(∅) = 0 and f (push (S, i)) = max (f(S), 0) + i for all stacks S and integers i. If a stack S contains the integers 2, -3, 2, -1, 2 in order from bottom to top, what is f(S)?- a)6
- b)4
- c)3
- d)2
Correct answer is option 'C'. Can you explain this answer?
A function f defined on stacks of integers satisfies the following properties. f(∅) = 0 and f (push (S, i)) = max (f(S), 0) + i for all stacks S and integers i.
If a stack S contains the integers 2, -3, 2, -1, 2 in order from bottom to top, what is f(S)?
a)
6
b)
4
c)
3
d)
2
|
|
Mainak Kulkarni answered |
i Element to be pushed
Initial State f(φ) = 0 For Empty Stack F(S) is 0.
Then we push each element ( )one by one and calculate f(s)for each insertion as given
Is the function to compute F(s) for each insertions
1. INSERT 2 into Stack
Similarly ,
The value of F(s) after inserting all elements into stack is 3
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented as INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in- a)non-increasing order
- b)non-decreasing order
- c)strictly increasing order
- d)strictly decreasing order
Correct answer is option 'D'. Can you explain this answer?
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented as INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in
a)
non-increasing order
b)
non-decreasing order
c)
strictly increasing order
d)
strictly decreasing order
|
|
Akshay Singh answered |
Implementing stack using priority queue require first element inserted in stack will be deleted at last, and to implement it using deletemin() operation of queue will require first element inserted in queue must have highest priority.
So the keys must be in strictly decreasing order.
So the keys must be in strictly decreasing order.
Suppose a circular queue of capacity (n – 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operation are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are- a)Full: (REAR+1) mod n == FRONT, empty: REAR == FRONT
- b)Full: (REAR+1) mod n == FRONT, empty: (FRONT+1) mod n == REAR
- c)Full: REAR == FRONT, empty: (REAR+1) mod n == FRONT
- d)Full: (FRONT+1) mod n == REAR, empty: REAR == FRONT
Correct answer is option 'A'. Can you explain this answer?
Suppose a circular queue of capacity (n – 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operation are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are
a)
Full: (REAR+1) mod n == FRONT, empty: REAR == FRONT
b)
Full: (REAR+1) mod n == FRONT, empty: (FRONT+1) mod n == REAR
c)
Full: REAR == FRONT, empty: (REAR+1) mod n == FRONT
d)
Full: (FRONT+1) mod n == REAR, empty: REAR == FRONT
|
|
Ipsita Dasgupta answered |
Suppose we start filling the queue.
Let the maxQueueSize ( Capacity of the Queue) is 4.
So the size of the array which is used to implement this circular queue is 5, which is n.
So the size of the array which is used to implement this circular queue is 5, which is n.
In the begining when the queue is empty, FRONT and REAR point to 0 index in the array.
REAR represents insertion at the REAR index.
FRONT represents deletion from the FRONT index.
FRONT represents deletion from the FRONT index.
enqueue("a"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 1)
enqueue("b"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 2)
enqueue("c"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 3)
enqueue("d"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 4)
enqueue("b"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 2)
enqueue("c"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 3)
enqueue("d"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 4)
An n x n array v is defined as follows: v[i, j] = i - j for all i, j, 1 < i < n, 1 < j < n.The sum of the elements of the array v is - a)0
- b)n -1
- c)n2 - 3n + 2
- d)n2(n + 1)/2
Correct answer is option 'A'. Can you explain this answer?
An n x n array v is defined as follows: v[i, j] = i - j for all i, j, 1 < i < n, 1 < j < n.The sum of the elements of the array v is
a)
0
b)
n -1
c)
n2 - 3n + 2
d)
n2(n + 1)/2
|
|
Shubham Das answered |
Array is
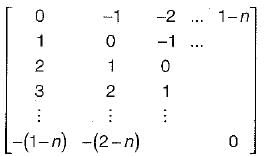
Sum = 0 + 1 + 2 + ... + (-1) + (-2) + ... = 0.
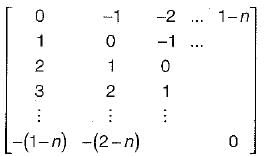
Sum = 0 + 1 + 2 + ... + (-1) + (-2) + ... = 0.
An item that is read as input can be either pushed to a stack and later popped and printed, or printed directly. Which of the following will be the output if the input is the sequence of items -1, 2, 3, 4, 5?
- a)3, 4, 5, 1, 2
- b)3, 4, 5, 2, 1
- c)1, 5, 2, 3, 4
- d)5, 4, 3, 1, 2
Correct answer is option 'B'. Can you explain this answer?
An item that is read as input can be either pushed to a stack and later popped and printed, or printed directly. Which of the following will be the output if the input is the sequence of items -1, 2, 3, 4, 5?
a)
3, 4, 5, 1, 2
b)
3, 4, 5, 2, 1
c)
1, 5, 2, 3, 4
d)
5, 4, 3, 1, 2
|
|
Anoushka Dey answered |
The item can be pushed to stack and later popped and printed, or printed directly. 1, 2, 3, 4, 5 is the input then (a) is not possible because once pushed 1 is printed after 2. Similarly (c) and (d) are also not possible.
We can obtain the sequence by performing the operations in the manner given below.
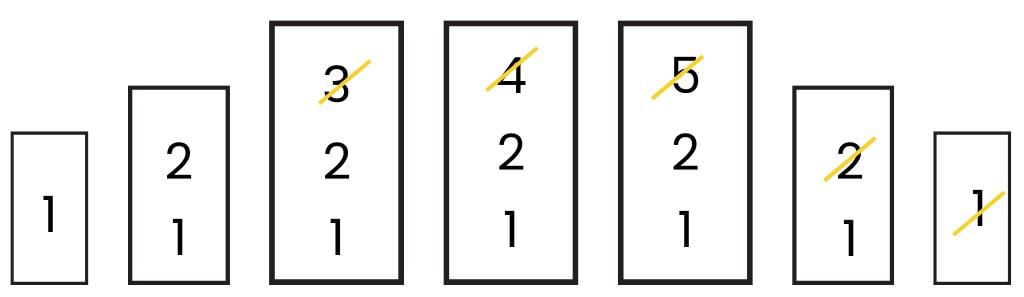
The sequence obtained will be 3,4,5,2,1.
Hence, (b) is the output.
Which of the following expressions accesses the (i, j)th entry of a (m x n) matrix stored in column major form?- a)n x (i - 1) + j
- b)m x (j - 1) + i
- c)m x (n - j) + j
- d)n x (m - i) + j
Correct answer is option 'B'. Can you explain this answer?
Which of the following expressions accesses the (i, j)th entry of a (m x n) matrix stored in column major form?
a)
n x (i - 1) + j
b)
m x (j - 1) + i
c)
m x (n - j) + j
d)
n x (m - i) + j
|
|
Anshu Mehta answered |
(i, j) entries in column major order of size (m x n).
Assume starting address is 1 so, m x (j - 1) + i
Assume starting address is 1 so, m x (j - 1) + i
Consider the following operation along with Enqueue and Dequeue operations on queues, where k is a global parameter.MultiDequeue(Q){ m = kwhile (Q is not empty) and (m > 0) {Dequeue(Q)m = m – 1}}What is the worst case time complexity of a sequence of n queue operations on an initially empty queue?- a)
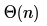
- b)
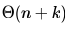
- c)
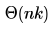
- d)
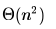
Correct answer is option 'A'. Can you explain this answer?
Consider the following operation along with Enqueue and Dequeue operations on queues, where k is a global parameter.
MultiDequeue(Q){
m = k
while (Q is not empty) and (m > 0) {
Dequeue(Q)
m = m – 1
}
}
What is the worst case time complexity of a sequence of n queue operations on an initially empty queue?
a)
b)
c)
d)
|
|
Saumya Basu answered |
There are three possible operations on queue- Enqueue, Dequeue and MultiDequeue. MultiDequeue is calling Dequeue multiple times based on a global variable k. Since, the queue is initially empty, whatever be the order of these operations, there cannot be more no. of Dequeue operations than Enqueue operations. Hence, the total no. operations will be n only.
A stack is implemented with an array of ‘A [0..N – 1]’ and a variable ‘pos’. The push and pop operations are defined by the following code.push(x) A[pos] ← x
pos ← pos – 1end pushpop( ) pos ← pos + 1
return A[pos]end popQ. Which of the following will initialize an empty stack with capacity N for the above implementation?- a)pos ← -1
- b)pos ← 0
- c)pos ← 1
- d)pos ← N - 1
Correct answer is option 'D'. Can you explain this answer?
A stack is implemented with an array of ‘A [0..N – 1]’ and a variable ‘pos’. The push and pop operations are defined by the following code.
push(x)
A[pos] ← x
pos ← pos – 1
pos ← pos – 1
end push
pop( )
pos ← pos + 1
return A[pos]
return A[pos]
end pop
Q. Which of the following will initialize an empty stack with capacity N for the above implementation?
a)
pos ← -1
b)
pos ← 0
c)
pos ← 1
d)
pos ← N - 1
|
|
Sudhir Patel answered |
For example, if we take an array with N = 4 to represent our stack. It will be A [0, 1, 2, 3].
Now, in order to push four elements, say x, y, z, w
- First we will push at x index 3 which is 4 – 1
- Then, we will decrement pos and push y at index 2 and so on.
Note that, the pop operation is also behaving inversely here.
- In usual stack, pop would decrement value of pos.
In our case, pop is incrementing the value of pos.
A priority queue Q is used to implement a stack S that stores characters. PUSH(C) is implemented as INSERT(Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in- a)Non-increasing order
- b)Non-decreasing order
- c)strictly increasing order
- d)strictly decreasing order
Correct answer is option 'D'. Can you explain this answer?
A priority queue Q is used to implement a stack S that stores characters. PUSH(C) is implemented as INSERT(Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in
a)
Non-increasing order
b)
Non-decreasing order
c)
strictly increasing order
d)
strictly decreasing order
|
|
Advait Shah answered |
Explanation:
The priority queue Q is used to implement a stack S, where PUSH operation is implemented as INSERT(Q, C, K) and POP operation is implemented as DELETEMIN(Q). The key K is an integer chosen by the implementation.
To understand why the correct answer is option 'D' (strictly decreasing order), let's look at the PUSH and POP operations in more detail.
PUSH Operation:
- The PUSH operation is implemented as INSERT(Q, C, K) where C is the character to be pushed onto the stack and K is the key chosen by the implementation.
- When a character is pushed onto the stack, it is added to the priority queue Q with an appropriate key.
- In order to implement the stack behavior, the key K should be chosen in such a way that the characters are sorted in decreasing order based on their keys.
- This ensures that the character with the highest priority (i.e., the character on top of the stack) has the lowest key value.
POP Operation:
- The POP operation is implemented as DELETEMIN(Q) where the character with the lowest key value is removed from the priority queue Q.
- Since the characters are stored in the priority queue Q with decreasing key values, the character with the lowest key value will be the character on top of the stack.
- Therefore, the POP operation effectively removes the character on top of the stack.
Why strictly decreasing order is the correct choice?
- If the keys chosen were in non-increasing order, it would mean that characters with the same key value can be popped in any order, which would violate the stack property of last-in, first-out (LIFO).
- If the keys chosen were in non-decreasing order, it would mean that characters with the same key value can be popped in any order, which would again violate the stack property of LIFO.
- If the keys chosen were in strictly increasing order, it would mean that the character with the lowest key value would not be on top of the stack, which would make the POP operation incorrect.
Conclusion:
- Choosing the keys in strictly decreasing order ensures that the priority queue Q behaves as a stack, where the character with the highest priority (i.e., the character on top of the stack) has the lowest key value.
- This allows the PUSH and POP operations to correctly implement the stack behavior.
The priority queue Q is used to implement a stack S, where PUSH operation is implemented as INSERT(Q, C, K) and POP operation is implemented as DELETEMIN(Q). The key K is an integer chosen by the implementation.
To understand why the correct answer is option 'D' (strictly decreasing order), let's look at the PUSH and POP operations in more detail.
PUSH Operation:
- The PUSH operation is implemented as INSERT(Q, C, K) where C is the character to be pushed onto the stack and K is the key chosen by the implementation.
- When a character is pushed onto the stack, it is added to the priority queue Q with an appropriate key.
- In order to implement the stack behavior, the key K should be chosen in such a way that the characters are sorted in decreasing order based on their keys.
- This ensures that the character with the highest priority (i.e., the character on top of the stack) has the lowest key value.
POP Operation:
- The POP operation is implemented as DELETEMIN(Q) where the character with the lowest key value is removed from the priority queue Q.
- Since the characters are stored in the priority queue Q with decreasing key values, the character with the lowest key value will be the character on top of the stack.
- Therefore, the POP operation effectively removes the character on top of the stack.
Why strictly decreasing order is the correct choice?
- If the keys chosen were in non-increasing order, it would mean that characters with the same key value can be popped in any order, which would violate the stack property of last-in, first-out (LIFO).
- If the keys chosen were in non-decreasing order, it would mean that characters with the same key value can be popped in any order, which would again violate the stack property of LIFO.
- If the keys chosen were in strictly increasing order, it would mean that the character with the lowest key value would not be on top of the stack, which would make the POP operation incorrect.
Conclusion:
- Choosing the keys in strictly decreasing order ensures that the priority queue Q behaves as a stack, where the character with the highest priority (i.e., the character on top of the stack) has the lowest key value.
- This allows the PUSH and POP operations to correctly implement the stack behavior.
The five items: A, B, C, D, and E are pushed in a stack, one after other starting from A. The stack is popped four items and each element is inserted in a queue. The two elements are deleted from the queue and pushed back on the stack. Now one item is popped from the stack. The popped item is- a) A
- b) B
- c) C
- d) D
Correct answer is option 'D'. Can you explain this answer?
The five items: A, B, C, D, and E are pushed in a stack, one after other starting from A. The stack is popped four items and each element is inserted in a queue. The two elements are deleted from the queue and pushed back on the stack. Now one item is popped from the stack. The popped item is
a)
A
b)
B
c)
C
d)
D
|
|
Varun Sen answered |
Explanation:
The given problem involves operations on a stack and a queue. Let's go step by step to understand the solution.
Step 1:
The items A, B, C, D, and E are pushed onto the stack one after another in the order A, B, C, D, E.
Stack: E -> D -> C -> B -> A
Step 2:
The stack is popped four times, and each popped element is inserted into a queue.
Queue: A -> B -> C -> D
Step 3:
The two elements are deleted from the queue, which means the first two elements from the front of the queue are removed.
Queue: C -> D
Step 4:
The two deleted elements, C and D, are pushed back onto the stack. Since the last element pushed onto the stack will be at the top, the order of insertion will be D followed by C.
Stack: C -> D -> E -> B -> A
Step 5:
Now, one item is popped from the stack. As per the order of insertion, the topmost element of the stack is popped.
Popped Item: C
Therefore, the correct answer is option D.
Summary:
- The items A, B, C, D, and E are pushed onto the stack in the order A, B, C, D, E.
- The stack is popped four times, and each popped element is inserted into a queue.
- The two elements, C and D, are deleted from the queue.
- The two deleted elements, C and D, are pushed back onto the stack in the order D, C.
- One item is popped from the stack, resulting in the popped item being C.
The given problem involves operations on a stack and a queue. Let's go step by step to understand the solution.
Step 1:
The items A, B, C, D, and E are pushed onto the stack one after another in the order A, B, C, D, E.
Stack: E -> D -> C -> B -> A
Step 2:
The stack is popped four times, and each popped element is inserted into a queue.
Queue: A -> B -> C -> D
Step 3:
The two elements are deleted from the queue, which means the first two elements from the front of the queue are removed.
Queue: C -> D
Step 4:
The two deleted elements, C and D, are pushed back onto the stack. Since the last element pushed onto the stack will be at the top, the order of insertion will be D followed by C.
Stack: C -> D -> E -> B -> A
Step 5:
Now, one item is popped from the stack. As per the order of insertion, the topmost element of the stack is popped.
Popped Item: C
Therefore, the correct answer is option D.
Summary:
- The items A, B, C, D, and E are pushed onto the stack in the order A, B, C, D, E.
- The stack is popped four times, and each popped element is inserted into a queue.
- The two elements, C and D, are deleted from the queue.
- The two deleted elements, C and D, are pushed back onto the stack in the order D, C.
- One item is popped from the stack, resulting in the popped item being C.
Which of the following permutations can be obtained in the output (in the same order) using a stack assuming that the input is the sequence 1,2, 3, 4, 5 in that order?- a)3, 4, 5, 1,2
- b)3, 4, 5, 2, 1
- c)1,5, 2, 3, 4
- d)5, 4, 3, 1, 2
Correct answer is option 'B'. Can you explain this answer?
Which of the following permutations can be obtained in the output (in the same order) using a stack assuming that the input is the sequence 1,2, 3, 4, 5 in that order?
a)
3, 4, 5, 1,2
b)
3, 4, 5, 2, 1
c)
1,5, 2, 3, 4
d)
5, 4, 3, 1, 2
|
|
Anisha Ahuja answered |
PUSH one by one element into Stack and POP accordingly desired output. Only second option can satisfy.
Stack A has the entries a, b, c (with a on top). Stack B is empty. An entry popped out of stack A can be printed immediately or pushed to stack B. An entry popped out of the stack B can be only be printed. In this arrangement, which of the following permutations of a, b, c are not possible?- a)b a c
- b)b c a
- c)c a b
- d)a b c
Correct answer is option 'C'. Can you explain this answer?
Stack A has the entries a, b, c (with a on top). Stack B is empty. An entry popped out of stack A can be printed immediately or pushed to stack B. An entry popped out of the stack B can be only be printed. In this arrangement, which of the following permutations of a, b, c are not possible?
a)
b a c
b)
b c a
c)
c a b
d)
a b c
|
|
Saptarshi Saha answered |
Possible and Impossible Permutations of Stack A and B
Possible permutations:
- a b c: Pop a, push to B, pop b, push to B, pop c, print
- a c b: Pop a, push to B, pop c, print, pop b, print
- b a c: Pop b, print, pop a, push to B, pop c, print
- b c a: Pop b, print, pop c, push to B, pop a, print
- c b a: Pop c, push to B, pop b, push to B, pop a, print
Impossible permutation:
- c a b: Pop c, push to B, pop a, push to B, pop b. This permutation is impossible because stack B only allows for printing, not pushing. Therefore, once an entry is pushed to stack B, it cannot be popped again to be printed.
Possible permutations:
- a b c: Pop a, push to B, pop b, push to B, pop c, print
- a c b: Pop a, push to B, pop c, print, pop b, print
- b a c: Pop b, print, pop a, push to B, pop c, print
- b c a: Pop b, print, pop c, push to B, pop a, print
- c b a: Pop c, push to B, pop b, push to B, pop a, print
Impossible permutation:
- c a b: Pop c, push to B, pop a, push to B, pop b. This permutation is impossible because stack B only allows for printing, not pushing. Therefore, once an entry is pushed to stack B, it cannot be popped again to be printed.
Suppose a stack implementation supports an instruction REVERSE, which reverses the order of elements on the stack, in addition to the PUSH and POP instructions. Which one of the following statements is TRUE with respect to this modified stack? .- a)A queue cannot be implemented using this stack.
- b)A queue can be implemented where ENQUEUE takes a single instruction and DEQUEUE takes a sequence of two instructions.
- c)A queue can be implemented where ENQUEUE takes a sequence of three instructions and DFQUEUE takes a single instruction.
- d)A queue can be implemented where both ENQUEUE and DEQUEUE take a single instruction each.
Correct answer is option 'C'. Can you explain this answer?
Suppose a stack implementation supports an instruction REVERSE, which reverses the order of elements on the stack, in addition to the PUSH and POP instructions. Which one of the following statements is TRUE with respect to this modified stack? .
a)
A queue cannot be implemented using this stack.
b)
A queue can be implemented where ENQUEUE takes a single instruction and DEQUEUE takes a sequence of two instructions.
c)
A queue can be implemented where ENQUEUE takes a sequence of three instructions and DFQUEUE takes a single instruction.
d)
A queue can be implemented where both ENQUEUE and DEQUEUE take a single instruction each.
|
|
Sonal Nair answered |
Consider an queue with elements inserted in same order as element present in queue.
Now to implement stack same as queue:
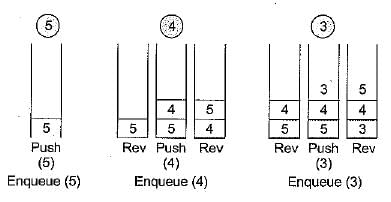
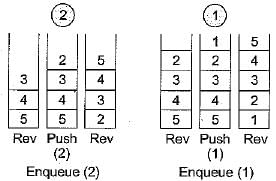
A queue can be implemented where ENQUEUE takes a sequence of three instructions and DEQUEUE takes a single instruction.

Now to implement stack same as queue:


A queue can be implemented where ENQUEUE takes a sequence of three instructions and DEQUEUE takes a single instruction.
Consider the following pseudocode that uses a stackdeclare a stack of characters
while ( there are more characters in the word to read )
{
read a character
push the character on the stack
}
while ( the stack is not empty )
{
pop a character off the stack
write the character to the screen
}
What is output for input “geeksquiz”?- a)geeksquizgeeksquiz
- b)ziuqskeeg
- c)geeksquiz
- d)ziuqskeegziuqskeeg
Correct answer is option 'B'. Can you explain this answer?
Consider the following pseudocode that uses a stack
declare a stack of characters
while ( there are more characters in the word to read )
{
read a character
push the character on the stack
}
while ( the stack is not empty )
{
pop a character off the stack
write the character to the screen
}
What is output for input “geeksquiz”?
while ( there are more characters in the word to read )
{
read a character
push the character on the stack
}
while ( the stack is not empty )
{
pop a character off the stack
write the character to the screen
}
What is output for input “geeksquiz”?
a)
geeksquizgeeksquiz
b)
ziuqskeeg
c)
geeksquiz
d)
ziuqskeegziuqskeeg
|
|
Aarav Malik answered |
Explanation:
Input: "geeksquiz"
- The characters are read one by one from left to right and pushed onto the stack.
- Once all characters are pushed onto the stack, they are popped out and written to the screen in reverse order.
Output: "ziuqskeeg"
- The characters are popped from the stack in LIFO (Last In First Out) order, resulting in the reversed order of the input word.
- Therefore, the output for the input "geeksquiz" is "ziuqskeeg".
What is the value of the postfix expression 6 3 2 4 + – *?- a)1
- b)40
- c)74
- d)-18
Correct answer is option 'D'. Can you explain this answer?
What is the value of the postfix expression 6 3 2 4 + – *?
a)
1
b)
40
c)
74
d)
-18
|
|
Kiran Mehta answered |
The value of the postfix expression "6 3 2 4" cannot be determined as there are no operators present to perform any calculations. In postfix notation, operators are placed after the operands.
Which of the following is not the application of stack?- a)A parentheses balancing program
- b)Tracking of local variables at run time
- c)Compiler Syntax Analyzer
- d)Data Transfer between two asynchronous process
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not the application of stack?
a)
A parentheses balancing program
b)
Tracking of local variables at run time
c)
Compiler Syntax Analyzer
d)
Data Transfer between two asynchronous process
|
|
Sankar Iyer answered |
Explanation:
Stack is a data structure that follows the Last-In-First-Out (LIFO) principle. The element that is added last will be removed first. Stack is used in various applications such as:
a) A parentheses balancing program: This program checks whether the given expression has balanced parentheses or not. It uses stack to store opening parentheses and pops them out when a closing parenthesis is encountered.
b) Tracking of local variables at run time: When a function is called, its local variables are stored in a stack frame. When the function returns, the stack frame is popped out and the variables are destroyed. This way, stack is used to track local variables at run time.
c) Compiler Syntax Analyzer: Compiler uses stack to parse the syntax of a program. It reads the tokens of the program and pushes them onto the stack. When it encounters a production rule, it pops the tokens from the stack and replaces them with a non-terminal symbol.
d) Data Transfer between two asynchronous process: This is not the application of stack. Data transfer between two asynchronous processes can be done using message queues, pipes or sockets.
Therefore, the correct answer is option 'D'.
Stack is a data structure that follows the Last-In-First-Out (LIFO) principle. The element that is added last will be removed first. Stack is used in various applications such as:
a) A parentheses balancing program: This program checks whether the given expression has balanced parentheses or not. It uses stack to store opening parentheses and pops them out when a closing parenthesis is encountered.
b) Tracking of local variables at run time: When a function is called, its local variables are stored in a stack frame. When the function returns, the stack frame is popped out and the variables are destroyed. This way, stack is used to track local variables at run time.
c) Compiler Syntax Analyzer: Compiler uses stack to parse the syntax of a program. It reads the tokens of the program and pushes them onto the stack. When it encounters a production rule, it pops the tokens from the stack and replaces them with a non-terminal symbol.
d) Data Transfer between two asynchronous process: This is not the application of stack. Data transfer between two asynchronous processes can be done using message queues, pipes or sockets.
Therefore, the correct answer is option 'D'.
Consider the usual algorithm for determining whether a sequence of parentheses is balanced. The maximum number of parentheses that appear on the stack AT ANY ONE TIME when the algorithm analyzes: (()(())(()))?- a)1
- b)2
- c)3
- d)4 or more
Correct answer is option 'C'. Can you explain this answer?
Consider the usual algorithm for determining whether a sequence of parentheses is balanced. The maximum number of parentheses that appear on the stack AT ANY ONE TIME when the algorithm analyzes: (()(())(()))?
a)
1
b)
2
c)
3
d)
4 or more
|
|
Shubham Chawla answered |
Algorithm for determining balanced parentheses
To understand why the answer is option 'C', we first need to understand the algorithm for determining whether a sequence of parentheses is balanced. The algorithm is as follows:
1. Initialize an empty stack.
2. Scan the expression from left to right.
3. If the current character is a starting bracket (‘(‘ or ‘{‘ or ‘[‘), push it to the stack.
4. If the current character is a closing bracket (‘)’ or ‘}’ or ‘]’), then pop from the stack and check if the popped bracket is a matching starting bracket or not.
5. If the bracket is not a matching starting bracket, then the expression is not balanced.
6. After complete traversal, if there is some starting bracket left in the stack, then the expression is not balanced.
Maximum number of parentheses on the stack
Now, let's analyze the sequence of parentheses given in the question: (()(()())(()))
1. The first character is ‘(‘, so we push it to the stack. Stack: (.
2. The second character is ‘(‘, so we push it to the stack. Stack: ((.
3. The third character is ‘)’, so we pop the top element from the stack. Stack: (.
4. The fourth character is ‘(‘, so we push it to the stack. Stack: (().
5. The fifth character is ‘(‘, so we push it to the stack. Stack: (().
6. The sixth character is ‘)’, so we pop the top element from the stack. Stack: (.
7. The seventh character is ‘(‘, so we push it to the stack. Stack: ((.
8. The eighth character is ‘)’, so we pop the top element from the stack. Stack: (.
9. The ninth character is ‘)’, so we pop the top element from the stack. Stack: empty.
10. The tenth character is ‘(‘, so we push it to the stack. Stack: (.
11. The eleventh character is ‘)’, so we pop the top element from the stack. Stack: empty.
12. The twelfth character is ‘)’, so we pop the top element from the stack. Stack: empty.
So, the maximum number of parentheses that appear on the stack AT ANY ONE TIME is 3, which occurs when we are analyzing the subsequence ‘(()())’.
Therefore, the correct answer is option 'C', which is 3.
To understand why the answer is option 'C', we first need to understand the algorithm for determining whether a sequence of parentheses is balanced. The algorithm is as follows:
1. Initialize an empty stack.
2. Scan the expression from left to right.
3. If the current character is a starting bracket (‘(‘ or ‘{‘ or ‘[‘), push it to the stack.
4. If the current character is a closing bracket (‘)’ or ‘}’ or ‘]’), then pop from the stack and check if the popped bracket is a matching starting bracket or not.
5. If the bracket is not a matching starting bracket, then the expression is not balanced.
6. After complete traversal, if there is some starting bracket left in the stack, then the expression is not balanced.
Maximum number of parentheses on the stack
Now, let's analyze the sequence of parentheses given in the question: (()(()())(()))
1. The first character is ‘(‘, so we push it to the stack. Stack: (.
2. The second character is ‘(‘, so we push it to the stack. Stack: ((.
3. The third character is ‘)’, so we pop the top element from the stack. Stack: (.
4. The fourth character is ‘(‘, so we push it to the stack. Stack: (().
5. The fifth character is ‘(‘, so we push it to the stack. Stack: (().
6. The sixth character is ‘)’, so we pop the top element from the stack. Stack: (.
7. The seventh character is ‘(‘, so we push it to the stack. Stack: ((.
8. The eighth character is ‘)’, so we pop the top element from the stack. Stack: (.
9. The ninth character is ‘)’, so we pop the top element from the stack. Stack: empty.
10. The tenth character is ‘(‘, so we push it to the stack. Stack: (.
11. The eleventh character is ‘)’, so we pop the top element from the stack. Stack: empty.
12. The twelfth character is ‘)’, so we pop the top element from the stack. Stack: empty.
So, the maximum number of parentheses that appear on the stack AT ANY ONE TIME is 3, which occurs when we are analyzing the subsequence ‘(()())’.
Therefore, the correct answer is option 'C', which is 3.
Consider the usual algorithm for determining whether a sequence of parentheses is balanced. Suppose that you run the algorithm on a sequence that contains 2 left parentheses and 3 right parentheses (in some order). The maximum number of parentheses that appear on the stack AT ANY ONE TIME during the computation?- a)1
- b)2
- c)3
- d)4 or more
Correct answer is option 'B'. Can you explain this answer?
Consider the usual algorithm for determining whether a sequence of parentheses is balanced. Suppose that you run the algorithm on a sequence that contains 2 left parentheses and 3 right parentheses (in some order). The maximum number of parentheses that appear on the stack AT ANY ONE TIME during the computation?
a)
1
b)
2
c)
3
d)
4 or more
|
|
Atharva Kulkarni answered |
Explanation:
The algorithm for determining whether a sequence of parentheses is balanced is as follows:
1. Start with an empty stack.
2. For each parenthesis in the sequence:
a. If it is a left parenthesis, push it onto the stack.
b. If it is a right parenthesis, pop the top element from the stack. If the popped element is not a left parenthesis or the stack is empty, then the sequence is not balanced.
3. After processing all parentheses, if the stack is not empty, then the sequence is not balanced.
Now, let's consider a sequence that contains 2 left parentheses and 3 right parentheses. The possible orders of these parentheses are:
1. ()()() - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
2. (()()) - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
3. (())() - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
4. ()(()) - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
5. ((())) - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
6. )()()( - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 1.
7. ()())( - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 2.
8. ()(() - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 2.
9. ((()) - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 3.
10. )((() - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 2.
From the above analysis, we can see that the maximum number of parentheses on the stack at any one time is 2. Therefore, the correct answer is option B.
The algorithm for determining whether a sequence of parentheses is balanced is as follows:
1. Start with an empty stack.
2. For each parenthesis in the sequence:
a. If it is a left parenthesis, push it onto the stack.
b. If it is a right parenthesis, pop the top element from the stack. If the popped element is not a left parenthesis or the stack is empty, then the sequence is not balanced.
3. After processing all parentheses, if the stack is not empty, then the sequence is not balanced.
Now, let's consider a sequence that contains 2 left parentheses and 3 right parentheses. The possible orders of these parentheses are:
1. ()()() - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
2. (()()) - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
3. (())() - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
4. ()(()) - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
5. ((())) - This sequence is balanced and the maximum number of parentheses on the stack at any one time is 2.
6. )()()( - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 1.
7. ()())( - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 2.
8. ()(() - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 2.
9. ((()) - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 3.
10. )((() - This sequence is not balanced and the maximum number of parentheses on the stack at any one time is 2.
From the above analysis, we can see that the maximum number of parentheses on the stack at any one time is 2. Therefore, the correct answer is option B.
The seven elements A, B, C, D, E, F and G are pushed onto a stack in reverse order, i.e., starting from G. The stack is popped five times and each element is inserted into a queue.Two elements are deleted from the queue and pushed back onto the stack. Now, one element is popped from the stack. The popped item is ________.- a) A
- b) B
- c) F
- d) G
Correct answer is option 'B'. Can you explain this answer?
The seven elements A, B, C, D, E, F and G are pushed onto a stack in reverse order, i.e., starting from G. The stack is popped five times and each element is inserted into a queue.Two elements are deleted from the queue and pushed back onto the stack. Now, one element is popped from the stack. The popped item is ________.
a)
A
b)
B
c)
F
d)
G
|
|
Nisha Ahuja answered |
Explanation:
The given problem involves using a stack and a queue to manipulate a set of elements. Let's break down the steps to understand the solution.
Step 1: Pushing elements onto the stack
The seven elements A, B, C, D, E, F, and G are pushed onto the stack in reverse order, starting from G. This means G is pushed first, followed by F, E, D, C, B, and A.
Step 2: Popping elements from the stack and inserting into the queue
The stack is popped five times, and each popped element is inserted into a queue. This means that the elements are transferred from the stack to the queue in the order they were pushed onto the stack, i.e., A, B, C, D, and E.
Step 3: Deleting two elements from the queue and pushing back onto the stack
Two elements are deleted from the queue. Since the elements were transferred from the stack to the queue in the same order, the first two elements in the queue would be A and B. These elements are then pushed back onto the stack, so the stack now contains A and B at the top, followed by F, G, E, D, and C.
Step 4: Popping one element from the stack
Now, one element is popped from the stack. Since the last two elements pushed onto the stack were A and B, and the stack follows the Last-In-First-Out (LIFO) principle, the element popped from the stack would be B. Therefore, the correct answer is option 'B'.
In summary, the correct answer is option 'B' because after pushing and popping elements onto the stack and transferring them to a queue, the last two elements pushed back onto the stack were A and B, and the element popped from the stack would be the topmost element, which is B.
The given problem involves using a stack and a queue to manipulate a set of elements. Let's break down the steps to understand the solution.
Step 1: Pushing elements onto the stack
The seven elements A, B, C, D, E, F, and G are pushed onto the stack in reverse order, starting from G. This means G is pushed first, followed by F, E, D, C, B, and A.
Step 2: Popping elements from the stack and inserting into the queue
The stack is popped five times, and each popped element is inserted into a queue. This means that the elements are transferred from the stack to the queue in the order they were pushed onto the stack, i.e., A, B, C, D, and E.
Step 3: Deleting two elements from the queue and pushing back onto the stack
Two elements are deleted from the queue. Since the elements were transferred from the stack to the queue in the same order, the first two elements in the queue would be A and B. These elements are then pushed back onto the stack, so the stack now contains A and B at the top, followed by F, G, E, D, and C.
Step 4: Popping one element from the stack
Now, one element is popped from the stack. Since the last two elements pushed onto the stack were A and B, and the stack follows the Last-In-First-Out (LIFO) principle, the element popped from the stack would be B. Therefore, the correct answer is option 'B'.
In summary, the correct answer is option 'B' because after pushing and popping elements onto the stack and transferring them to a queue, the last two elements pushed back onto the stack were A and B, and the element popped from the stack would be the topmost element, which is B.
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in- a)Non-increasing order
- b)Non-decreasing order
- c)Strictly increasing order
- d)Strictly decreasing order
Correct answer is option 'D'. Can you explain this answer?
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in
a)
Non-increasing order
b)
Non-decreasing order
c)
Strictly increasing order
d)
Strictly decreasing order
|
|
Krithika Gupta answered |
In stack last element will be deleted first but according to question, it should be wprk like queue. So last element deleted at last, for that we give lower priority to last element. So all elements should be in strictly decreasing order.
The following postfix expression with single digit operands is evaluated using a stack:8 2 3 ^ / 2 3 * + 5 1 * -
Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are:- a)6, 1
- b)5, 7
- c)3, 2
- d)1, 5
Correct answer is option 'A'. Can you explain this answer?
The following postfix expression with single digit operands is evaluated using a stack:
8 2 3 ^ / 2 3 * + 5 1 * -
Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are:
Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are:
a)
6, 1
b)
5, 7
c)
3, 2
d)
1, 5
|
|
Tanishq Chakraborty answered |
Answer:
To evaluate this postfix expression, we will use a stack to keep track of the intermediate results. Let's go step by step to understand the process:
1. Push 8, 2, and 3 onto the stack:
Stack: [8, 2, 3]
2. Evaluate the exponentiation operation ^:
2 ^ 3 = 8
Replace the top two elements on the stack with the result:
Stack: [8, 8]
3. Evaluate the division operation /:
8 / 8 = 1
Replace the top two elements on the stack with the result:
Stack: [1]
4. Push 2 and 3 onto the stack:
Stack: [1, 2, 3]
5. Evaluate the multiplication operation *:
2 * 3 = 6
Replace the top two elements on the stack with the result:
Stack: [1, 6]
6. Push 5 and 1 onto the stack:
Stack: [1, 6, 5, 1]
7. Evaluate the multiplication operation *:
5 * 1 = 5
Replace the top two elements on the stack with the result:
Stack: [1, 6, 5]
8. Evaluate the subtraction operation -:
6 - 5 = 1
Replace the top two elements on the stack with the result:
Stack: [1, 1]
After the first * operation is evaluated, the top two elements on the stack are 1 and 6. Therefore, the correct answer is option 'A': 6, 1.
To evaluate this postfix expression, we will use a stack to keep track of the intermediate results. Let's go step by step to understand the process:
1. Push 8, 2, and 3 onto the stack:
Stack: [8, 2, 3]
2. Evaluate the exponentiation operation ^:
2 ^ 3 = 8
Replace the top two elements on the stack with the result:
Stack: [8, 8]
3. Evaluate the division operation /:
8 / 8 = 1
Replace the top two elements on the stack with the result:
Stack: [1]
4. Push 2 and 3 onto the stack:
Stack: [1, 2, 3]
5. Evaluate the multiplication operation *:
2 * 3 = 6
Replace the top two elements on the stack with the result:
Stack: [1, 6]
6. Push 5 and 1 onto the stack:
Stack: [1, 6, 5, 1]
7. Evaluate the multiplication operation *:
5 * 1 = 5
Replace the top two elements on the stack with the result:
Stack: [1, 6, 5]
8. Evaluate the subtraction operation -:
6 - 5 = 1
Replace the top two elements on the stack with the result:
Stack: [1, 1]
After the first * operation is evaluated, the top two elements on the stack are 1 and 6. Therefore, the correct answer is option 'A': 6, 1.
The queue data structure is to be realized by using stack. The number of stacks needed would be- a)It cannot be implemented
- b)2 stacks
- c)4 stacks
- d)1 stack
Correct answer is option 'B'. Can you explain this answer?
The queue data structure is to be realized by using stack. The number of stacks needed would be
a)
It cannot be implemented
b)
2 stacks
c)
4 stacks
d)
1 stack
|
|
Sudhir Patel answered |
Method 1 (efficient push):
- push:
- enqueue in queue1
- pop:
- while the size of queue1 is bigger than 1, pipe dequeued items from queue1 into queue2
- dequeue and return the last item of queue1, then switch the names of queue1 and queue2
Method 2 (efficient pop):
- push:
- enqueue in queue2
- enqueue all items of queue1 in queue2, then switch the names of queue1 and queue2
- pop:
- deqeue from queue1
Stacks cannot be used to- a)Evaluate an arithmetic expression in postfix form.
- b)Implement recursion.
- c)Convert a given arithmetic expression in infix form to its equivalent postfix form.
- d)Allocate resources (like CPU) by the operating system.
Correct answer is option 'D'. Can you explain this answer?
Stacks cannot be used to
a)
Evaluate an arithmetic expression in postfix form.
b)
Implement recursion.
c)
Convert a given arithmetic expression in infix form to its equivalent postfix form.
d)
Allocate resources (like CPU) by the operating system.
|
|
Prateek Khanna answered |
Stacks are used to evaluate postfix expressions, to store data in case of recursion and to convert infix forms to postfix forms.
However, resource allocation can’t be done using stack. Scheduling algorithms are used for allocation of CPU time
However, resource allocation can’t be done using stack. Scheduling algorithms are used for allocation of CPU time
In a circularly linked list organization, insertion of a record involves the modification of- a)No pointer
- b)1 pointer
- c)2 pointers
- d)3 pointers
Correct answer is option 'C'. Can you explain this answer?
In a circularly linked list organization, insertion of a record involves the modification of
a)
No pointer
b)
1 pointer
c)
2 pointers
d)
3 pointers
|
|
Nitin Datta answered |
For insertion/deletion of a record in circularly linked list involves 2 pointer.
But for reverse the linked list, it involves 3 pointer.
But for reverse the linked list, it involves 3 pointer.
The concatenation of two lists is to be performed in O(1) time. Which of the following implementations of a list could be used?
- a)Singly linked list
- b)Doubly linked list
- c)Circular doubly linked list
- d)Array implementation of list
Correct answer is option 'C'. Can you explain this answer?
The concatenation of two lists is to be performed in O(1) time. Which of the following implementations of a list could be used?
a)
Singly linked list
b)
Doubly linked list
c)
Circular doubly linked list
d)
Array implementation of list
|
|
Milan Rane answered |
Concatenation of Two Lists in O(1) Time
To perform concatenation of two lists in O(1) time, we need a data structure that supports constant time insertion and deletion at both ends of the list. Let's analyze each option given in the question:
a) Singly linked list: In a singly linked list, we can insert or delete a node at the beginning of the list in O(1) time, but we need to traverse the entire list to insert or delete a node at the end of the list, which takes O(n) time. Therefore, concatenation of two singly linked lists takes O(n) time.
b) Doubly linked list: In a doubly linked list, we can insert or delete a node at both ends of the list in O(1) time. Therefore, concatenation of two doubly linked lists takes O(1) time if we maintain a pointer to the last node of the first list and a pointer to the first node of the second list.
c) Circular doubly linked list: A circular doubly linked list is similar to a doubly linked list, but the last node points to the first node, forming a circular structure. This means that we can maintain a pointer to the last node of the first list and a pointer to the first node of the second list without any extra overhead. Therefore, concatenation of two circular doubly linked lists takes O(1) time.
d) Array implementation of list: In an array implementation of a list, we need to allocate a new array and copy the elements of both lists to the new array, which takes O(n) time. Therefore, concatenation of two arrays takes O(n) time.
Conclusion
The correct option for concatenation of two lists in O(1) time is a circular doubly linked list as it supports constant time insertion and deletion at both ends of the list, and maintains a circular structure to concatenate two lists without any extra overhead.
To perform concatenation of two lists in O(1) time, we need a data structure that supports constant time insertion and deletion at both ends of the list. Let's analyze each option given in the question:
a) Singly linked list: In a singly linked list, we can insert or delete a node at the beginning of the list in O(1) time, but we need to traverse the entire list to insert or delete a node at the end of the list, which takes O(n) time. Therefore, concatenation of two singly linked lists takes O(n) time.
b) Doubly linked list: In a doubly linked list, we can insert or delete a node at both ends of the list in O(1) time. Therefore, concatenation of two doubly linked lists takes O(1) time if we maintain a pointer to the last node of the first list and a pointer to the first node of the second list.
c) Circular doubly linked list: A circular doubly linked list is similar to a doubly linked list, but the last node points to the first node, forming a circular structure. This means that we can maintain a pointer to the last node of the first list and a pointer to the first node of the second list without any extra overhead. Therefore, concatenation of two circular doubly linked lists takes O(1) time.
d) Array implementation of list: In an array implementation of a list, we need to allocate a new array and copy the elements of both lists to the new array, which takes O(n) time. Therefore, concatenation of two arrays takes O(n) time.
Conclusion
The correct option for concatenation of two lists in O(1) time is a circular doubly linked list as it supports constant time insertion and deletion at both ends of the list, and maintains a circular structure to concatenate two lists without any extra overhead.
Let A be a two-dimensional array declared as follows:
A : array [1 ... 10] [1... 15] of integer;
Assuming that each integer takes one memory location. The array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element A [i] [j] ?- a)15i + j + 84
- b)15j + i + 84
- c)10i + j + 89
- d)10j + i + 89
Correct answer is option 'A'. Can you explain this answer?
Let A be a two-dimensional array declared as follows:
A : array [1 ... 10] [1... 15] of integer;
Assuming that each integer takes one memory location. The array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element A [i] [j] ?
A : array [1 ... 10] [1... 15] of integer;
Assuming that each integer takes one memory location. The array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element A [i] [j] ?
a)
15i + j + 84
b)
15j + i + 84
c)
10i + j + 89
d)
10j + i + 89
|
|
Amrutha Singh answered |
Let r be number of elements in a row. Address of the element A[i] [j]
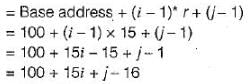
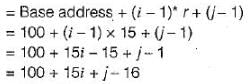
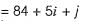
Let S be a stack of size n ≥1. Starting with the empty stack, suppose we push the first n natural numbers in sequence, and then perform n pop operations. Assume that Push and Pop operations take X seconds each, and Y seconds elapse between the end of one such stack operation and the start of the next operation. For m ≥1, define the stack-life of m as the time elapsed from the end of Push(m) to the start of the pop operation that removes m from S. The average stack-life of an element of this stack is- a)n(X+Y)
- b)3Y+2X
- c)n(X+Y)-X
- d)Y+2X
Correct answer is option 'C'. Can you explain this answer?
Let S be a stack of size n ≥1. Starting with the empty stack, suppose we push the first n natural numbers in sequence, and then perform n pop operations. Assume that Push and Pop operations take X seconds each, and Y seconds elapse between the end of one such stack operation and the start of the next operation. For m ≥1, define the stack-life of m as the time elapsed from the end of Push(m) to the start of the pop operation that removes m from S. The average stack-life of an element of this stack is
a)
n(X+Y)
b)
3Y+2X
c)
n(X+Y)-X
d)
Y+2X
|
|
Sagnik Singh answered |
let us represent stack-life of ith element as S(i). The ith element will be in stack till (n-i) elements are pushed and popped. Plus one more Y for the time interval between the push of ith element and the i+1th element. So,
A program attempts to generate as many permutations as possible of the string, 'abcd' by pushing the characters in the same order onto a stack, but it may pop off the top character at any time. Which one of the following strings CANNOT be generated using this program?- a)abcd
- b)dcba
- c)cbad
- d)cabd
Correct answer is option 'D'. Can you explain this answer?
A program attempts to generate as many permutations as possible of the string, 'abcd' by pushing the characters in the same order onto a stack, but it may pop off the top character at any time. Which one of the following strings CANNOT be generated using this program?
a)
abcd
b)
dcba
c)
cbad
d)
cabd
|
|
Shivam Dasgupta answered |
A. push a & pop a, push b & pop b, push c & pop c, and finally push d and pop d
sequence of popped elements will come to abcd
B. first push abcd, and after that pop one by one sequence of popped elements will come to dcba
C. push abc, and after that pop one by one sequence of popped elements will come to cba, now push d and pop d, final
sequence comes to cbad
D. this sequence is not possible because 'a' can not be pooped before 'b' any how
sequence of popped elements will come to abcd
B. first push abcd, and after that pop one by one sequence of popped elements will come to dcba
C. push abc, and after that pop one by one sequence of popped elements will come to cba, now push d and pop d, final
sequence comes to cbad
D. this sequence is not possible because 'a' can not be pooped before 'b' any how
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:The following sequence of operations is performed on a stack:PUSH (10), PUSH (20), POP, PUSH (10), PUSH (20), POP, POP, POP, PUSH (20), POPThe sequence of values popped out is- a)20,10,20,10,20
- b)20,20,10,10,20
- c)10,20,20,10,20
- d)20,20,10,20,10
Correct answer is option 'B'. Can you explain this answer?
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:
The following sequence of operations is performed on a stack:
PUSH (10), PUSH (20), POP, PUSH (10), PUSH (20), POP, POP, POP, PUSH (20), POP
The sequence of values popped out is
a)
20,10,20,10,20
b)
20,20,10,10,20
c)
10,20,20,10,20
d)
20,20,10,20,10
|
|
Sagnik Singh answered |
Lets try something different when you read the word pop then delete the last pushed element and print it ..now delete the push word which we have already executed ..now go on from left to right and do the same
So, Output will be 20, 20, 10, 10, 20
So, Output will be 20, 20, 10, 10, 20
Which of the following permutations can be obtained in the output (in the same order) using a stack assuming that the input is the sequence 1,2,3,4,5 in that order?- a)3, 4, 5, 1, 2
- b)3, 4, 5, 2, 1
- c)1, 5, 2, 3, 4
- d)5, 4, 3, 1, 2
Correct answer is option 'B'. Can you explain this answer?
Which of the following permutations can be obtained in the output (in the same order) using a stack assuming that the input is the sequence 1,2,3,4,5 in that order?
a)
3, 4, 5, 1, 2
b)
3, 4, 5, 2, 1
c)
1, 5, 2, 3, 4
d)
5, 4, 3, 1, 2
|
|
Preethi Iyer answered |
push 1 push 2 push 3 pop 3 push 4 pop 4 push 5 pop 5 pop 2 pop 1 then o/p is 3,4,5,2,1 option b
Which one of the following is an application of Queue Data Structure?- a)When a resource is shared among multiple consumers.
- b)When data is transferred asynchronously (data not necessarily received at same rate as sent) between two processes
- c)Load Balancing
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is an application of Queue Data Structure?
a)
When a resource is shared among multiple consumers.
b)
When data is transferred asynchronously (data not necessarily received at same rate as sent) between two processes
c)
Load Balancing
d)
All of the above

|
Arshiya Mehta answered |
All of the given options (a, b, c, and d) are applications of the Queue data structure.
A queue is a linear data structure that stores data in a first-in-first-out (FIFO) order. It is a useful data structure for implementing certain algorithms and solving certain problems, such as the following:
When a resource is shared among multiple consumers (option a): A queue can be used to manage access to a shared resource, such as a printer or a network connection. Multiple consumers can add requests to the queue, and the resource can be allocated to the requests in the order they were added to the queue.
When data is transferred asynchronously between two processes (option b): A queue can be used to store data that is transferred between two processes, such as a producer and a consumer. The producer can add data to the queue, and the consumer can retrieve the data from the queue in the order it was added. This allows the two processes to operate independently and at their own pace, without the need for synchronization.
Load balancing (option c): A queue can be used to distribute workload among multiple servers or processors in a load-balancing algorithm. Multiple tasks can be added to the queue, and the servers or processors can take tasks from the queue in the order they were added. This allows the workload to be distributed evenly among the servers or processors, improving the overall performance and scalability of the system.
Therefore, the correct answer is option D, as all of the given options (a, b, c, and d) are applications of the Queue data structure.
A Priority-Queue is implemented as a Max-Heap. Initially, it has 5 elements. The level-order traversal of the heap is given below: 10, 8, 5, 3, 2 Two new elements ”1‘ and ”7‘ are inserted in the heap in that order. The level-order traversal of the heap after the insertion of the elements is:- a)10, 8, 7, 5, 3, 2, 1
- b)10, 8, 7, 2, 3, 1, 5
- c)10, 8, 7, 1, 2, 3, 5
- d)10, 8, 7, 3, 2, 1, 5
Correct answer is option 'D'. Can you explain this answer?
A Priority-Queue is implemented as a Max-Heap. Initially, it has 5 elements. The level-order traversal of the heap is given below: 10, 8, 5, 3, 2 Two new elements ”1‘ and ”7‘ are inserted in the heap in that order. The level-order traversal of the heap after the insertion of the elements is:
a)
10, 8, 7, 5, 3, 2, 1
b)
10, 8, 7, 2, 3, 1, 5
c)
10, 8, 7, 1, 2, 3, 5
d)
10, 8, 7, 3, 2, 1, 5

|
Prasenjit Malik answered |
Initially heap has 10, 8, 5, 3, 2
10
/ \
8 5
/ \
3 2
After insertion of 1
10
/ \
8 5
/ \ /
3 2 1
No need to heapify as 5 is greater than 1.
After insertion of 7
10
/ \
8 5
/ \ / \
3 2 1 7
Heapify 5 as 7 is greater than 5
10
/ \
8 7
/ \ / \
3 2 1 5
No need to heapify any further as 10 is
greater than 7
A program P reads in 500 integers in the range (0,100) representing the scores of 500 students.If prints the frequency of each score above 50, what would be the best way for P to store the frequencies?- a)An array of 50 numbers
- b)An array of 100 numbers
- c)An array of 500 numbers
- d)A dynamically allocated array of 550 numbers
Correct answer is option 'A'. Can you explain this answer?
A program P reads in 500 integers in the range (0,100) representing the scores of 500 students.If prints the frequency of each score above 50, what would be the best way for P to store the frequencies?
a)
An array of 50 numbers
b)
An array of 100 numbers
c)
An array of 500 numbers
d)
A dynamically allocated array of 550 numbers
|
|
Kunal Sen answered |
Best way to store the frequencies
To determine the best way to store the frequencies of each score above 50, we need to consider the requirements of the program and the size of the input data.
Program requirements:
- The program needs to store the frequencies of each score above 50.
- The scores are in the range (0,100).
- There are 500 students.
Size of input data:
- There are 500 integers representing the scores of the students.
- The scores are in the range (0,100).
Based on the above information, the best way to store the frequencies would be an array of 50 numbers. Here's why:
Explanation:
1. The program needs to store the frequencies of each score above 50. Since the scores are in the range (0,100), the possible scores above 50 are 51, 52, ..., 100. There are 50 possible scores above 50.
2. Storing the frequencies in an array allows for efficient and direct access to each frequency based on the score. The index of the array represents the score, and the value at that index represents the frequency.
3. An array of 50 numbers is sufficient to store the frequencies of each score above 50. Since there are no scores above 100, there is no need to allocate additional space for scores that do not exist.
4. Using an array of 100 numbers would be wasteful as it would allocate extra space for scores that are not present in the input data.
5. Using an array of 500 numbers would not be efficient as it would allocate more space than necessary. It would also be confusing to map the index of the array to the corresponding score.
6. Using a dynamically allocated array of 550 numbers would also allocate more space than necessary. Additionally, dynamic allocation introduces complexity and overhead that is not required for this problem.
Therefore, the best way to store the frequencies of each score above 50 would be an array of 50 numbers.
To determine the best way to store the frequencies of each score above 50, we need to consider the requirements of the program and the size of the input data.
Program requirements:
- The program needs to store the frequencies of each score above 50.
- The scores are in the range (0,100).
- There are 500 students.
Size of input data:
- There are 500 integers representing the scores of the students.
- The scores are in the range (0,100).
Based on the above information, the best way to store the frequencies would be an array of 50 numbers. Here's why:
Explanation:
1. The program needs to store the frequencies of each score above 50. Since the scores are in the range (0,100), the possible scores above 50 are 51, 52, ..., 100. There are 50 possible scores above 50.
2. Storing the frequencies in an array allows for efficient and direct access to each frequency based on the score. The index of the array represents the score, and the value at that index represents the frequency.
3. An array of 50 numbers is sufficient to store the frequencies of each score above 50. Since there are no scores above 100, there is no need to allocate additional space for scores that do not exist.
4. Using an array of 100 numbers would be wasteful as it would allocate extra space for scores that are not present in the input data.
5. Using an array of 500 numbers would not be efficient as it would allocate more space than necessary. It would also be confusing to map the index of the array to the corresponding score.
6. Using a dynamically allocated array of 550 numbers would also allocate more space than necessary. Additionally, dynamic allocation introduces complexity and overhead that is not required for this problem.
Therefore, the best way to store the frequencies of each score above 50 would be an array of 50 numbers.
A single array A[1..MAXSIZE] is used to implement two stacks. The two stacks grow from opposite ends of the array. Variables top1 and top2 (topl< top 2) point to the location of the topmost element in each of the stacks. If the space is to be used efficiently, the condition for “stack full” is- a)(top1 = MAXSIZE/2) and (top2 = MAXSIZE/2+1)
- b)top1 + top2 = MAXSIZE
- c)(top1= MAXSIZE/2) or (top2 = MAXSIZE)
- d)top1= top2 -1
Correct answer is option 'D'. Can you explain this answer?
A single array A[1..MAXSIZE] is used to implement two stacks. The two stacks grow from opposite ends of the array. Variables top1 and top2 (topl< top 2) point to the location of the topmost element in each of the stacks. If the space is to be used efficiently, the condition for “stack full” is
a)
(top1 = MAXSIZE/2) and (top2 = MAXSIZE/2+1)
b)
top1 + top2 = MAXSIZE
c)
(top1= MAXSIZE/2) or (top2 = MAXSIZE)
d)
top1= top2 -1
|
|
Kritika Sengupta answered |
And top2) are used to indicate the top elements of both stacks. Explain how this array can be used to implement two stacks and discuss the time complexity of the operations.
To implement two stacks using a single array, we can allocate the first half of the array to one stack and the second half to the other stack. For example, if the array size is MAXSIZE, we can allocate the first MAXSIZE/2 elements to the first stack and the remaining MAXSIZE/2 elements to the second stack.
To keep track of the top elements of both stacks, we can use two variables top1 and top2. top1 will initially point to the first element of the first stack, and top2 will initially point to the last element of the second stack. As elements are pushed onto or popped from either stack, these variables will be updated accordingly.
To push an element onto the first stack, we can increment top1 and store the element at A[top1]. Similarly, to push an element onto the second stack, we can decrement top2 and store the element at A[top2].
To pop an element from the first stack, we can read the element at A[top1] and then decrement top1. Similarly, to pop an element from the second stack, we can read the element at A[top2] and then increment top2.
The time complexity of these operations depends on the implementation. If we use a simple array with no additional data structures, the time complexity of push and pop operations will be O(1) as they involve simple array access and update operations.
However, if we want to ensure that both stacks have equal size and avoid overflow or underflow, we can use additional data structures such as a counter or a flag to keep track of the number of elements in each stack. This will increase the time complexity of push and pop operations to O(2) or O(3) as we may need to update the counter or flag in addition to the array access and update operations.
To implement two stacks using a single array, we can allocate the first half of the array to one stack and the second half to the other stack. For example, if the array size is MAXSIZE, we can allocate the first MAXSIZE/2 elements to the first stack and the remaining MAXSIZE/2 elements to the second stack.
To keep track of the top elements of both stacks, we can use two variables top1 and top2. top1 will initially point to the first element of the first stack, and top2 will initially point to the last element of the second stack. As elements are pushed onto or popped from either stack, these variables will be updated accordingly.
To push an element onto the first stack, we can increment top1 and store the element at A[top1]. Similarly, to push an element onto the second stack, we can decrement top2 and store the element at A[top2].
To pop an element from the first stack, we can read the element at A[top1] and then decrement top1. Similarly, to pop an element from the second stack, we can read the element at A[top2] and then increment top2.
The time complexity of these operations depends on the implementation. If we use a simple array with no additional data structures, the time complexity of push and pop operations will be O(1) as they involve simple array access and update operations.
However, if we want to ensure that both stacks have equal size and avoid overflow or underflow, we can use additional data structures such as a counter or a flag to keep track of the number of elements in each stack. This will increase the time complexity of push and pop operations to O(2) or O(3) as we may need to update the counter or flag in addition to the array access and update operations.
Chapter doubts & questions for Stacks & Queues - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Stacks & Queues - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
459 videos|1398 docs|786 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup










