All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Divide & Conquer for Computer Science Engineering (CSE) Exam
Consider the problem of computing min-max in an unsorted array where min and max are minimum and maximum elements of array. Algorithm A1 can compute min-max in a1 comparisons without divide and conquer. Algorithm A2 can compute min-max in a2 comparisons by scanning the array linearly. What could be the relation between a1 and a2 considering the worst case scenarios?- a)a1 < a2
- b)a1 > a2
- c)a1 = a2
- d)Depends on the input
Correct answer is option 'B'. Can you explain this answer?
Consider the problem of computing min-max in an unsorted array where min and max are minimum and maximum elements of array. Algorithm A1 can compute min-max in a1 comparisons without divide and conquer. Algorithm A2 can compute min-max in a2 comparisons by scanning the array linearly. What could be the relation between a1 and a2 considering the worst case scenarios?
a)
a1 < a2
b)
a1 > a2
c)
a1 = a2
d)
Depends on the input

|
Cstoppers Instructors answered |
When Divide and Conquer is used to find the minimum-maximum element in an array, Recurrence relation for the number of comparisons is
T(n) = 2T(n/2) + 2 where 2 is for comparing the minimums as well the maximums of the left and right subarrays
On solving, T(n) = 1.5n - 2.
While doing linear scan, it would take 2*(n-1) comparisons in the worst case to find both minimum as well maximum in one pass.
T(n) = 2T(n/2) + 2 where 2 is for comparing the minimums as well the maximums of the left and right subarrays
On solving, T(n) = 1.5n - 2.
While doing linear scan, it would take 2*(n-1) comparisons in the worst case to find both minimum as well maximum in one pass.
You have to sort 1 GB of data with only 100 MB of available main memory. Which sorting technique will be most appropriate?- a)Heap sort
- b)Merge sort
- c)Quick sort
- d)Insertion sort
Correct answer is option 'B'. Can you explain this answer?
You have to sort 1 GB of data with only 100 MB of available main memory. Which sorting technique will be most appropriate?
a)
Heap sort
b)
Merge sort
c)
Quick sort
d)
Insertion sort
|
|
Arnab Sengupta answered |
Merge Sort
Merge sort is the most appropriate sorting technique for sorting 1 GB of data with only 100 MB of available main memory because it is an efficient external sorting algorithm that can handle large amounts of data with limited memory.
Explanation:
- Divide and Conquer: Merge sort follows the divide-and-conquer approach, where it divides the data into smaller chunks, sorts them individually, and then merges them back together. This allows it to efficiently handle large datasets.
- Memory Efficiency: In merge sort, the data is divided into smaller chunks that can fit into the available memory. This makes it suitable for situations where the entire dataset cannot be loaded into memory at once.
- External Sorting: Merge sort is commonly used for external sorting, where data is too large to fit into main memory. It efficiently utilizes disk I/O operations to merge sorted sublists.
- Stable Sorting: Merge sort is a stable sorting algorithm, meaning that it preserves the relative order of equal elements. This is important when dealing with large datasets where data integrity is crucial.
Therefore, when sorting 1 GB of data with only 100 MB of available main memory, merge sort is the most appropriate choice due to its efficiency, memory handling capabilities, and stability.
Merge sort is the most appropriate sorting technique for sorting 1 GB of data with only 100 MB of available main memory because it is an efficient external sorting algorithm that can handle large amounts of data with limited memory.
Explanation:
- Divide and Conquer: Merge sort follows the divide-and-conquer approach, where it divides the data into smaller chunks, sorts them individually, and then merges them back together. This allows it to efficiently handle large datasets.
- Memory Efficiency: In merge sort, the data is divided into smaller chunks that can fit into the available memory. This makes it suitable for situations where the entire dataset cannot be loaded into memory at once.
- External Sorting: Merge sort is commonly used for external sorting, where data is too large to fit into main memory. It efficiently utilizes disk I/O operations to merge sorted sublists.
- Stable Sorting: Merge sort is a stable sorting algorithm, meaning that it preserves the relative order of equal elements. This is important when dealing with large datasets where data integrity is crucial.
Therefore, when sorting 1 GB of data with only 100 MB of available main memory, merge sort is the most appropriate choice due to its efficiency, memory handling capabilities, and stability.
Which sorting algorithm will take least time when all elements of input array are identical? Consider typical implementations of sorting algorithms.- a)Insertion Sort
- b)Heap Sort
- c)Merge Sort
- d)Selection Sort
Correct answer is option 'A'. Can you explain this answer?
Which sorting algorithm will take least time when all elements of input array are identical? Consider typical implementations of sorting algorithms.
a)
Insertion Sort
b)
Heap Sort
c)
Merge Sort
d)
Selection Sort
|
|
Anshika Kaur answered |
Insertion Sort is the sorting algorithm that will take the least time when all elements of the input array are identical. Here's why:
Explanation:
- Insertion Sort:
- In Insertion Sort, the algorithm checks each element in the array and moves it to its correct position by comparing it with elements on its left side.
- When all elements are identical, there is no need to move any elements around as they are already in the correct order.
- This results in the best-case time complexity of O(n) for Insertion Sort when all elements are the same, making it the most efficient choice in this scenario.
- Heap Sort, Merge Sort, and Selection Sort:
- Heap Sort, Merge Sort, and Selection Sort have worst-case time complexities of O(n log n), O(n log n), and O(n^2) respectively, regardless of the input array being identical or not.
- These algorithms involve more comparisons and movements of elements, which are unnecessary when all elements are the same.
Therefore, in the case where all elements of the input array are identical, Insertion Sort is the most efficient sorting algorithm due to its linear time complexity.
Explanation:
- Insertion Sort:
- In Insertion Sort, the algorithm checks each element in the array and moves it to its correct position by comparing it with elements on its left side.
- When all elements are identical, there is no need to move any elements around as they are already in the correct order.
- This results in the best-case time complexity of O(n) for Insertion Sort when all elements are the same, making it the most efficient choice in this scenario.
- Heap Sort, Merge Sort, and Selection Sort:
- Heap Sort, Merge Sort, and Selection Sort have worst-case time complexities of O(n log n), O(n log n), and O(n^2) respectively, regardless of the input array being identical or not.
- These algorithms involve more comparisons and movements of elements, which are unnecessary when all elements are the same.
Therefore, in the case where all elements of the input array are identical, Insertion Sort is the most efficient sorting algorithm due to its linear time complexity.
Following algorithm (s) can be used to sort n integers in the range [1 ... n3] in O(n) time?- a)Heap sort
- b)Quick sort
- c)Merge sort
- d)Radix sort
Correct answer is option 'D'. Can you explain this answer?
Following algorithm (s) can be used to sort n integers in the range [1 ... n3] in O(n) time?
a)
Heap sort
b)
Quick sort
c)
Merge sort
d)
Radix sort
|
|
Ameya Goyal answered |
Radix sort is a non-comparative integer sorting algorithm that sorts data with integer keys by grouping keys which share same position and value. So it take O(n) time.
You are asked to sort 15 randomly generated numbers. You should prefer- a)Bubble sort
- b)Selection sort
- c)Insertion sort
- d)Heap sort
Correct answer is option 'C'. Can you explain this answer?
You are asked to sort 15 randomly generated numbers. You should prefer
a)
Bubble sort
b)
Selection sort
c)
Insertion sort
d)
Heap sort
|
|
Aditi Gupta answered |
In-order traversal of a Binary Search Tree lists the nodes in ascending order.
Which of the following statements is true?
1. As the number of entries in the hash table increases, the number of collisions increases.
2. Recursive program are efficient.
3. The worst time complexity of quick sort is O(n2).
4. Binary search implemented using a linked list is efficient- a)1 and 2
- b)2 and 3
- c)1 and 4
- d)1 and 3
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is true?
1. As the number of entries in the hash table increases, the number of collisions increases.
2. Recursive program are efficient.
3. The worst time complexity of quick sort is O(n2).
4. Binary search implemented using a linked list is efficient
1. As the number of entries in the hash table increases, the number of collisions increases.
2. Recursive program are efficient.
3. The worst time complexity of quick sort is O(n2).
4. Binary search implemented using a linked list is efficient
a)
1 and 2
b)
2 and 3
c)
1 and 4
d)
1 and 3
|
|
Sagnik Singh answered |
Recursive programs take more time than the equivalent non-recursive version and so not efficient. This is because of the function call overhead.
In binary search, since every time the current list is probed at the middle, random access is preferred. Since linked list does not support random access, binary search implemented this way is inefficient.
In binary search, since every time the current list is probed at the middle, random access is preferred. Since linked list does not support random access, binary search implemented this way is inefficient.
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?- a)O(n)
- b)(nlogn)
- c)0(n2)
- d)0(n!)
Correct answer is option 'C'. Can you explain this answer?
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
a)
O(n)
b)
(nlogn)
c)
0(n2)
d)
0(n!)
|
|
Subhankar Chawla answered |
Randomized quick sort worst case time complexity = O (n2).
For merging two sorted lists of sizes m and n into a sorted list of size m + n, we required comparisons of- a)O(m)
- b)O(n)
- c)O(m + n)
- d)O(logm + logn)
Correct answer is option 'C'. Can you explain this answer?
For merging two sorted lists of sizes m and n into a sorted list of size m + n, we required comparisons of
a)
O(m)
b)
O(n)
c)
O(m + n)
d)
O(logm + logn)
|
|
Kunal Chaudhary answered |
The number of comparisons required in the worst case is O(m + n).
The way a card game player arranges his cards as he picks them up one by one, is an example of- a)Bubble sort
- b)Selection sort
- c)Insertion sort
- d)Merge sort
Correct answer is option 'C'. Can you explain this answer?
The way a card game player arranges his cards as he picks them up one by one, is an example of
a)
Bubble sort
b)
Selection sort
c)
Insertion sort
d)
Merge sort
|
|
Dishani Basu answered |
It is done only by insertion sort because in insertion sort we compare the one card to another all inserted card.
Merge sort uses- a)Divide and conquer strategy
- b)Backtracking approach
- c)Heuristic search
- d)Greedy approach
Correct answer is option 'A'. Can you explain this answer?
Merge sort uses
a)
Divide and conquer strategy
b)
Backtracking approach
c)
Heuristic search
d)
Greedy approach
|
|
Rohit Mukherjee answered |
A merge sort is comparisbn based sorting algorithm and divide-and-conquer algorithm.
Consider a situation where swap operation is very costly. Which of the following sorting algorithms should be preferred so that the number of swap operations are minimized in general?- a)Heap Sort
- b)Selection Sort
- c)Insertion Sort
- d)Merge Sort
Correct answer is option 'B'. Can you explain this answer?
Consider a situation where swap operation is very costly. Which of the following sorting algorithms should be preferred so that the number of swap operations are minimized in general?
a)
Heap Sort
b)
Selection Sort
c)
Insertion Sort
d)
Merge Sort
|
|
Tanishq Chakraborty answered |
Selection Sort
Selection Sort is the preferred sorting algorithm when swap operations are very costly because it minimizes the number of swaps required. Here's why:
How Selection Sort works:
- Selection Sort works by repeatedly finding the minimum element from the unsorted part of the array and placing it at the beginning.
- It divides the array into two parts: sorted and unsorted. Initially, the sorted part is empty, and the unsorted part contains the entire array.
- In each iteration, it finds the minimum element from the unsorted part and swaps it with the first element of the unsorted part.
Minimizing swap operations:
- Selection Sort minimizes the number of swap operations because it performs a swap only when it finds the minimum element.
- It does not swap elements multiple times within the same iteration, unlike other sorting algorithms like Insertion Sort or Bubble Sort.
- Since swap operations are costly, Selection Sort can be more efficient in terms of reducing the total number of swaps required.
Comparison with other sorting algorithms:
- Heap Sort, Merge Sort, and Quick Sort are not as efficient in minimizing swap operations because they involve frequent swapping of elements to maintain the heap property or merge partitions.
- Insertion Sort, while also reducing the number of swaps compared to other algorithms, still requires more swaps than Selection Sort in general.
Conclusion:
- In scenarios where swap operations are costly, Selection Sort should be preferred over other sorting algorithms to minimize the total number of swaps and improve efficiency.
Selection Sort is the preferred sorting algorithm when swap operations are very costly because it minimizes the number of swaps required. Here's why:
How Selection Sort works:
- Selection Sort works by repeatedly finding the minimum element from the unsorted part of the array and placing it at the beginning.
- It divides the array into two parts: sorted and unsorted. Initially, the sorted part is empty, and the unsorted part contains the entire array.
- In each iteration, it finds the minimum element from the unsorted part and swaps it with the first element of the unsorted part.
Minimizing swap operations:
- Selection Sort minimizes the number of swap operations because it performs a swap only when it finds the minimum element.
- It does not swap elements multiple times within the same iteration, unlike other sorting algorithms like Insertion Sort or Bubble Sort.
- Since swap operations are costly, Selection Sort can be more efficient in terms of reducing the total number of swaps required.
Comparison with other sorting algorithms:
- Heap Sort, Merge Sort, and Quick Sort are not as efficient in minimizing swap operations because they involve frequent swapping of elements to maintain the heap property or merge partitions.
- Insertion Sort, while also reducing the number of swaps compared to other algorithms, still requires more swaps than Selection Sort in general.
Conclusion:
- In scenarios where swap operations are costly, Selection Sort should be preferred over other sorting algorithms to minimize the total number of swaps and improve efficiency.
If one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20,47, 15,8,9,4,40,30, 12, 17
Then the order of these elements after second pass of the algorithm is- a)8, 9, 15, 20, 47, 4, 12, 17, 30, 40
- b)8, 15, 20, 47, 4, 9, 30, 40, 12, 17
- c)15, 20, 47, 4, 8, 9, 12, 30, 40, 17
- d)4, 8, 9, 15, 20, 47, 12,17, 30, 40
Correct answer is option 'B'. Can you explain this answer?
If one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20,47, 15,8,9,4,40,30, 12, 17
Then the order of these elements after second pass of the algorithm is
20,47, 15,8,9,4,40,30, 12, 17
Then the order of these elements after second pass of the algorithm is
a)
8, 9, 15, 20, 47, 4, 12, 17, 30, 40
b)
8, 15, 20, 47, 4, 9, 30, 40, 12, 17
c)
15, 20, 47, 4, 8, 9, 12, 30, 40, 17
d)
4, 8, 9, 15, 20, 47, 12,17, 30, 40
|
|
Rajat Sharma answered |
Given: 20, 47, 15, 8, 9, 4, 40, 30, 12, 17
2-way merge sort so group of 2 is taken at once.
2nd pass:
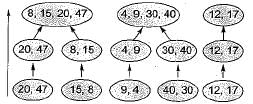
The order of elements after second pass of the algorithm is 8, 15, 20, 47, 4, 9, 30, 40, 12, 17.
2-way merge sort so group of 2 is taken at once.
2nd pass:

The order of elements after second pass of the algorithm is 8, 15, 20, 47, 4, 9, 30, 40, 12, 17.
A list of n strings, each of length n, is sorted into lexicographic order using the merge sort algorithm. The worst case running time of this computation is- a)O(n log n)
- b)O(n2logn)
- c)O(n2 + logn)
- d)O(n2)
Correct answer is option 'B'. Can you explain this answer?
A list of n strings, each of length n, is sorted into lexicographic order using the merge sort algorithm. The worst case running time of this computation is
a)
O(n log n)
b)
O(n2logn)
c)
O(n2 + logn)
d)
O(n2)
|
|
Anshika Kaur answered |
The recurrence tree for merge sort will have height n and O (n2) work will be done at each level of the recurrence tree (Each level involves ncomparisons and a comparison takes O(n) time in worst case). So time complexity of this merge sort will be O(n2 logn).
What is the best sorting algorithm to use for the elements in array are more than 1 million in general?- a)Merge sort
- b)Bubble sort
- c)Quick sort
- d)Insertion sort
Correct answer is option 'C'. Can you explain this answer?
What is the best sorting algorithm to use for the elements in array are more than 1 million in general?
a)
Merge sort
b)
Bubble sort
c)
Quick sort
d)
Insertion sort
|
|
Ravi Singh answered |
Most practical implementations of Quick Sort use randomized version. The randomized version has expected time complexity of O(nLogn). The worst case is possible in randomized version also, but worst case doesn’t occur for a particular pattern (like sorted array) and randomized Quick Sort works well in practice. Quick Sort is also a cache friendly sorting algorithm as it has good locality of reference when used for arrays. Quick Sort is also tail recursive, therefore tail call optimizations is done.
Which of the following algorithms exhibits the unnatural behaviour that, minimum number of comparisons are needed if the list to be sorted is in the reverse order and maximum number of comparisons are needed if they are already in sorted order?- a)Heap sort
- b)Radix sort
- c)Binary insertion sort
- d)There can’t be any such sorting method
Correct answer is option 'C'. Can you explain this answer?
Which of the following algorithms exhibits the unnatural behaviour that, minimum number of comparisons are needed if the list to be sorted is in the reverse order and maximum number of comparisons are needed if they are already in sorted order?
a)
Heap sort
b)
Radix sort
c)
Binary insertion sort
d)
There can’t be any such sorting method
|
|
Ujwal Roy answered |
Binary insertion sort take minimum comparison if the list to be sorted is in reverse order and maximum number of comparison if they already in sorted order.
Pick the correct statements:- a)Sequential file organization is not suitable for batch processing.
- b)Sequential file organization is suitable for interactive processing.
- c)Indexed sequential file organization supports both batch and interactive processing.
- d)Relative file can’t be accessed sequentially.
Correct answer is option 'C'. Can you explain this answer?
Pick the correct statements:
a)
Sequential file organization is not suitable for batch processing.
b)
Sequential file organization is suitable for interactive processing.
c)
Indexed sequential file organization supports both batch and interactive processing.
d)
Relative file can’t be accessed sequentially.
|
|
Divya Kaur answered |
Sequential to be organization suitable for batch processing and not suitable for interactive processing.
The average number of comparisons performed by the merge sort algorithm, in merging two sorted lists of length 2 is- a)8/3
- b)8/5
- c)11/7
- d)11/6
Correct answer is option 'A'. Can you explain this answer?
The average number of comparisons performed by the merge sort algorithm, in merging two sorted lists of length 2 is
a)
8/3
b)
8/5
c)
11/7
d)
11/6
|
|
Kunal Gupta answered |
Size sorted list has size 2, So, number of comparison is between min (2,2) to (2 + 2 - 1) = 3 So, 2, 3, 3 are number of comparisons.
So average number of comparison

So average number of comparison

A sorting technique that guarantees, that records with the same primary key occurs, in the same order in the sorted list as in the original unsorted list is said to be- a)Stable
- b)Consistent
- c)External
- d)Linear
Correct answer is option 'A'. Can you explain this answer?
A sorting technique that guarantees, that records with the same primary key occurs, in the same order in the sorted list as in the original unsorted list is said to be
a)
Stable
b)
Consistent
c)
External
d)
Linear
|
|
Snehal Desai answered |
A sorting algorithm is said to be stable sorting algorithm if two objects /records with equal primary key appears in the same order in the sorted list as in the original unsorted list.
Quicksort is run on two inputs shown below to sort in ascending order:
(i) 1 , 2 , 3 .... n .
(ii) n, n - 1, n - 2 , .... 2, 1Let C1, and C2 be the number of comparisons made for the inputs (i) and (ii) respectively. Then,- a)C1 < C2
- b)C1 > C2
- c)C1 = C2
- d)We cannot say anything for arbitrary n
Correct answer is option 'C'. Can you explain this answer?
Quicksort is run on two inputs shown below to sort in ascending order:
(i) 1 , 2 , 3 .... n .
(ii) n, n - 1, n - 2 , .... 2, 1
(i) 1 , 2 , 3 .... n .
(ii) n, n - 1, n - 2 , .... 2, 1
Let C1, and C2 be the number of comparisons made for the inputs (i) and (ii) respectively. Then,
a)
C1 < C2
b)
C1 > C2
c)
C1 = C2
d)
We cannot say anything for arbitrary n
|
|
Ayush Mehta answered |
Both of given cases are Quicksort Worst cases problem, so comparisons are equal.
Assume that a mergesort algorithm in the worst case takes 30 seconds for an input of size 64. Which of the following most closely approximates the maximum input size of a problem that can be solved in 6 minutes?- a)256
- b)512
- c)1024
- d)2048
Correct answer is option 'B'. Can you explain this answer?
Assume that a mergesort algorithm in the worst case takes 30 seconds for an input of size 64. Which of the following most closely approximates the maximum input size of a problem that can be solved in 6 minutes?
a)
256
b)
512
c)
1024
d)
2048
|
|
Sanya Agarwal answered |
Time complexity of merge sort is θ(nLogn)
c*64Log64 is 30
c*64*6 is 30
c is 5/64
c*64*6 is 30
c is 5/64
For time 6 minutes
5/64*nLogn = 6*60
nLogn = 72*64 = 512 * 9
n = 512.
You want to check whether a given set of items is sorted. Which of the following sorting methods will be the most efficient if it is already is sorted order?- a)Bubble sort
- b)Selection sort
- c)Insertion sort
- d)Merge sort
Correct answer is option 'A,C'. Can you explain this answer?
You want to check whether a given set of items is sorted. Which of the following sorting methods will be the most efficient if it is already is sorted order?
a)
Bubble sort
b)
Selection sort
c)
Insertion sort
d)
Merge sort
|
|
Vaishnavi Kaur answered |
if we want to check if given input is sort or not then one pass of bubble sort and n pass of insertion sort with each has work of O(1) are best i.e.take O(n) time.
Which of the following sorting methods will be the best if number of swappings done, is the only measure of efficiency?
a) Bubble sortb) Insertion sortc) Selection sortd) QuicksortCorrect answer is option 'C'. Can you explain this answer?
|
|
Rajveer Chatterjee answered |
If number of swapping is the measure of efficiency of algorithm the selection sort is best since it cannot take swap more than O(n).
Which one of the following statements is false?- a)Optimal binary search tree construction can be performed efficiently using dynamic programming.
- b)Breadth-first search cannot be used to find connected components of a graph.
- c)Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed.
- d)Depth-first search can be used to find connected components of a graph.
Correct answer is option 'B'. Can you explain this answer?
Which one of the following statements is false?
a)
Optimal binary search tree construction can be performed efficiently using dynamic programming.
b)
Breadth-first search cannot be used to find connected components of a graph.
c)
Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed.
d)
Depth-first search can be used to find connected components of a graph.
|
|
Avantika Shah answered |
Connected components of a graph can be computed in linear time by using either breadth- first search or depth-first search.
Given two sorted list of size m and n respectively. The number of comparisons needed the worst case by the merge sort algorithm will be- a)m x n
- b)maximum of m and n
- c)minimum of m and n
- d)m + n - 1
Correct answer is option 'D'. Can you explain this answer?
Given two sorted list of size m and n respectively. The number of comparisons needed the worst case by the merge sort algorithm will be
a)
m x n
b)
maximum of m and n
c)
minimum of m and n
d)
m + n - 1
|
|
Ravi Singh answered |
To merge two lists of size m and n, we need to do m+n-1 comparisons in worst case. Since we need to merge 2 at a time, the optimal strategy would be to take smallest size lists first. The reason for picking smallest two items is to carry minimum items for repetition in merging. So, option (D) is correct.
Which of the following also called "diminishing interment sort"?- a)Quick sort
- b)Heap sort
- c)Merge sort
- d)Shell sort
Correct answer is option 'D'. Can you explain this answer?
Which of the following also called "diminishing interment sort"?
a)
Quick sort
b)
Heap sort
c)
Merge sort
d)
Shell sort
|
|
Abhijeet Unni answered |
The shell sort sometimes called the “diminishing increment sort" improves on the insertion sort by breaking the original list into a number of smaller sub list each of which is sorted using an insertion sort.
Consider the polynomial p(x) = a0 + a1x + a2x^2 +a3x^3, where ai != 0, for all i. The minimum number of multiplications needed to evaluate p on an input x is:- a)3
- b)4
- c)6
- d)9
Correct answer is option 'A'. Can you explain this answer?
Consider the polynomial p(x) = a0 + a1x + a2x^2 +a3x^3, where ai != 0, for all i. The minimum number of multiplications needed to evaluate p on an input x is:
a)
3
b)
4
c)
6
d)
9
|
|
Sanya Agarwal answered |
Multiplications can be minimized using following order for evaluation of the given expression. p(x) = a0 + x(a1 + x(a2 + a3x))
Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n(≥ 2) numbers? In the recurrence equations given in the options below, c is a constant.- a)T(n)= 2T{nl2) + cn
- b)T (n )= T ( n - 1 ) + T(1) + cn
- c)T( n ) = 2 T( n - 1) + cn
- d)T(n)= T(n/2) + cn
Correct answer is option 'B'. Can you explain this answer?
Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n(≥ 2) numbers? In the recurrence equations given in the options below, c is a constant.
a)
T(n)= 2T{nl2) + cn
b)
T (n )= T ( n - 1 ) + T(1) + cn
c)
T( n ) = 2 T( n - 1) + cn
d)
T(n)= T(n/2) + cn
|
|
Rohan Patel answered |
The correct recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n elements is:
T(n) = T(n-1) + T(0) + O(n)
This equation represents the time complexity of the algorithm when the pivot chosen is always the smallest or largest element in the partition, leading to unbalanced partitions. In this case, the algorithm essentially reduces the problem size by one for each recursive call, resulting in a worst-case time complexity of O(n^2).
T(n) = T(n-1) + T(0) + O(n)
This equation represents the time complexity of the algorithm when the pivot chosen is always the smallest or largest element in the partition, leading to unbalanced partitions. In this case, the algorithm essentially reduces the problem size by one for each recursive call, resulting in a worst-case time complexity of O(n^2).
Choose the false statements:- a)Internal sorting is used if the number of items to be sorted is very large.
- b)External sorting is used if the number of items to be sorted is very large.
- c)External sorting needs auxiliary storage.
- d)Internal sorting do not needs auxiliary storage.
Correct answer is option 'A'. Can you explain this answer?
Choose the false statements:
a)
Internal sorting is used if the number of items to be sorted is very large.
b)
External sorting is used if the number of items to be sorted is very large.
c)
External sorting needs auxiliary storage.
d)
Internal sorting do not needs auxiliary storage.
|
|
Pranab Banerjee answered |
Internal sorting is such a process that takes place entirely within the main memory of a computer. This is only possible whenever data items, to be sorted, is small enough to be accommodated in main memory. Hence, internal sorting do not need auxiliary storage.
External sorting is just opposite to interval sorting and used when input data, to be sorted, is very large. Hence, external sorting need auxiliary storage.
External sorting is just opposite to interval sorting and used when input data, to be sorted, is very large. Hence, external sorting need auxiliary storage.
Of the following sorting algorithms, which has a running time that is least dependent on the initial ordering of the input?- a)Merge Sort
- b)Insertion Sort
- c)Selection Sort
- d)Quick Sort
Correct answer is option 'A'. Can you explain this answer?
Of the following sorting algorithms, which has a running time that is least dependent on the initial ordering of the input?
a)
Merge Sort
b)
Insertion Sort
c)
Selection Sort
d)
Quick Sort
|
|
Sanya Agarwal answered |
In Insertion sort if the array is already sorted then it takes O(n) and if it is reverse sorted then it takes O(n2) to sort the array. In Quick sort, if the array is already sorted or if it is reverse sorted then it takes O(n2).The best and worst case performance of Selection is O(n2) only. But if the array is already sorted then less swaps take place. In merge sort, time complexity is O(nlogn) for all the cases and performance is affected least on the the order of input sequence. So, option (A) is correct.
Which of the following algorithm design technique is used in the quick sort algorithm?- a)Dynamic programming
- b)Backtracking
- c)Divide and conquer
- d)Greedy method
Correct answer is option 'C'. Can you explain this answer?
Which of the following algorithm design technique is used in the quick sort algorithm?
a)
Dynamic programming
b)
Backtracking
c)
Divide and conquer
d)
Greedy method
|
|
Krithika Gupta answered |
Quick sort algorithm uses divide and conquer technique. It divides the data set every time on pivot element and keep on sorting each data set recursively.
Consider a situation where you don't have function to calculate power (pow() function in C) and you need to calculate x^n where x can be any number and n is a positive integer. What can be the best possible time complexity of your power function?- a)O(n)
- b)O(nLogn)
- c)O(LogLogn)
- d)O(Logn)
Correct answer is option 'D'. Can you explain this answer?
Consider a situation where you don't have function to calculate power (pow() function in C) and you need to calculate x^n where x can be any number and n is a positive integer. What can be the best possible time complexity of your power function?
a)
O(n)
b)
O(nLogn)
c)
O(LogLogn)
d)
O(Logn)
|
|
Ravi Singh answered |
We can calculate power using divide and conquer in O(Logn) time.
Which of the following sorting methods sorts a given set of items that is already in sorted order or in reverse sorted order with equal speed?- a)Heap sort
- b)Quick sort
- c)Insertion sort
- d)Selection sor
Correct answer is option 'B'. Can you explain this answer?
Which of the following sorting methods sorts a given set of items that is already in sorted order or in reverse sorted order with equal speed?
a)
Heap sort
b)
Quick sort
c)
Insertion sort
d)
Selection sor
|
|
Surbhi Kaur answered |
Quick sort has two worst cases, when input is in either ascending or descending order, it takes same time O(n2).
A sorting technique is called stable if- a)It takes 0(nlog n) time
- b)It maintains the relative order of occurrence of non-distinct elements
- c)It uses divide and conquer paradigm
- d)It takes O(n) space
Correct answer is option 'B'. Can you explain this answer?
A sorting technique is called stable if
a)
It takes 0(nlog n) time
b)
It maintains the relative order of occurrence of non-distinct elements
c)
It uses divide and conquer paradigm
d)
It takes O(n) space
|
|
Vaibhav Choudhary answered |
A sorting algorithm is called stable if it keeps elements with equal keys in the same relative order in the output as they were in the input.
For example in the following input the two 4’s are indistinguishable. 1,4a, 3, 4b, 2 and so the output of a stable sorting algorithm must be:
1, 2, 3, 4a, 4b
Bubble sort, merge sort, counting sort, insertion sort are stable sorting algorithms.
For example in the following input the two 4’s are indistinguishable. 1,4a, 3, 4b, 2 and so the output of a stable sorting algorithm must be:
1, 2, 3, 4a, 4b
Bubble sort, merge sort, counting sort, insertion sort are stable sorting algorithms.
In a modified merge sort, the input array is splitted at a position one-third of the length(N) of the array. Which of the following is the tightest upper bound on time complexity of this modified Merge Sort.- a)N(logN base 3)
- b)N(logN base 2/3)
- c)N(logN base 1/3)
- d)N(logN base 3/2)
Correct answer is option 'D'. Can you explain this answer?
In a modified merge sort, the input array is splitted at a position one-third of the length(N) of the array. Which of the following is the tightest upper bound on time complexity of this modified Merge Sort.
a)
N(logN base 3)
b)
N(logN base 2/3)
c)
N(logN base 1/3)
d)
N(logN base 3/2)
|
|
Ravi Singh answered |
The time complexity is given by: T(N) = T(N/3) + T(2N/3) + N Solving the above recurrence relation gives, T(N) = N(logN base 3/2)
Which of the following sorting algorithms has the lowest worst-case complexity?- a)Merge Sort
- b)Bubble Sort
- c)Quick Sort
- d)Selection Sort
Correct answer is option 'A'. Can you explain this answer?
Which of the following sorting algorithms has the lowest worst-case complexity?
a)
Merge Sort
b)
Bubble Sort
c)
Quick Sort
d)
Selection Sort
|
|
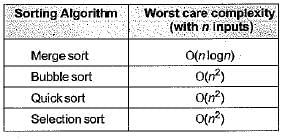
Ravi Singh answered |
Worst case complexities for the above sorting algorithms are as follows: Merge Sort — nLogn Bubble Sort — n^2 Quick Sort — n^2 Selection Sort — n^2
As part of the maintenance work, you are entrusted with the work of rearranging the library books in a shelf in proper order, at the end of each day. The ideal choice will be- a)Bubble sort
- b)Insertion sort
- c)Selection sort
- d)Heap sort
Correct answer is option 'B'. Can you explain this answer?
As part of the maintenance work, you are entrusted with the work of rearranging the library books in a shelf in proper order, at the end of each day. The ideal choice will be
a)
Bubble sort
b)
Insertion sort
c)
Selection sort
d)
Heap sort
|
|
Arnab Kapoor answered |
Rearranging the library books in a shelf in proper order is same as arranging cards. So insertion sort should be preferred.
What are the worst-case complexities of insertion and deletion of a key in a binary search tree?- a)
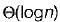 for both insertion and deletion
for both insertion and deletion - b)
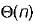 for both insertion and deletion
for both insertion and deletion - c)
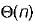 for insertion and
for insertion and 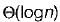 for deletion
for deletion - d)
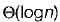 for insertion and
for insertion and 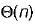 for deletion
for deletion
Correct answer is option 'B'. Can you explain this answer?
What are the worst-case complexities of insertion and deletion of a key in a binary search tree?
a)
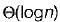 for both insertion and deletion
for both insertion and deletionb)
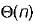 for both insertion and deletion
for both insertion and deletionc)
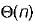 for insertion and
for insertion and 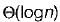 for deletion
for deletiond)
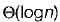 for insertion and
for insertion and 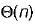 for deletion
for deletion|
|
Gaurav Verma answered |
In worst case the BST may be Skewed BST. This case occurs when we insert the elements in increasing order or decreasing order. Example: Consider we insert elements, in the order 1, 12, 39, 43, 50......
The BST would be
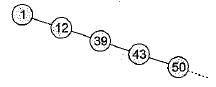
To find ‘n’ is the worst case we may have to traverse to bottom of tree which takes O(n) time.
Hence for both insertion and deletion worst case goes to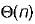
The BST would be

To find ‘n’ is the worst case we may have to traverse to bottom of tree which takes O(n) time.
Hence for both insertion and deletion worst case goes to
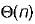
Consider the following array. Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order?
Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order?- a)Selection sort
- b)Mergesort
- c)Insertion sort
- d)Quicksort using the last element as pivot
Correct answer is option 'C'. Can you explain this answer?
Consider the following array.

Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order?
a)
Selection sort
b)
Mergesort
c)
Insertion sort
d)
Quicksort using the last element as pivot
|
|
Ravi Singh answered |
Since, given array is almost sorted in ascending order, so Insertion sort will give its best case with time complexity of order O(n).
Which of the following is not a stable sorting algorithm in its typical implementation.- a)Insertion Sort
- b)Merge Sort
- c)Quick Sort
- d)Bubble Sort
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a stable sorting algorithm in its typical implementation.
a)
Insertion Sort
b)
Merge Sort
c)
Quick Sort
d)
Bubble Sort
|
|
Sanya Agarwal answered |
Quick Sort, Heap Sort etc., can be made stable by also taking the position of the elements into consideration. This change may be done in a way which does not compromise a lot on the performance and takes some extra space
In the following C function, let n ≥ m.
int gcd(n, m)
{
if (n% m = - 0} return m;
n = n% m;
return gcd (m, n);
}
How many recursive calls are made by this function?- a)
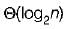
- b)
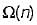
- c)
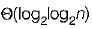
- d)
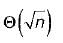
Correct answer is option 'A'. Can you explain this answer?
In the following C function, let n ≥ m.
int gcd(n, m)
{
if (n% m = - 0} return m;
n = n% m;
return gcd (m, n);
}
How many recursive calls are made by this function?
int gcd(n, m)
{
if (n% m = - 0} return m;
n = n% m;
return gcd (m, n);
}
How many recursive calls are made by this function?
a)
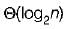
b)
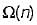
c)
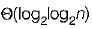
d)
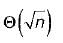
|
|
Rajveer Sharma answered |
Let, T(m, n) be the total number of steps.
So, T(m, 0) = 0, T{m, n) = T{n, m m o d n ) on average
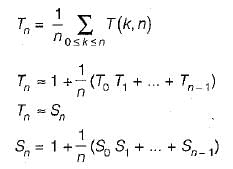
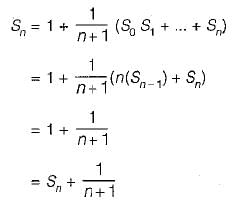
So, T(m, 0) = 0, T{m, n) = T{n, m m o d n ) on average
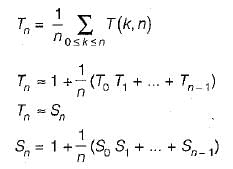
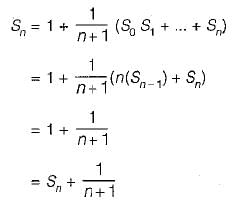
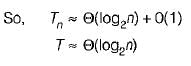
A binary search tree contains the values 1, 2, 3, 4, 5, 6, 7 and 8. The tree is traversed in preorder and the values are printed out. Which of the following sequences is a valid output?
- a)5 3 1 2 4 7 8 6
- b)5 3 1 2 6 4 9 7
- c)5 3 2 4 1 6 7 8
- d)5 3 1 2 4 7 6 8
Correct answer is option 'D'. Can you explain this answer?
A binary search tree contains the values 1, 2, 3, 4, 5, 6, 7 and 8. The tree is traversed in preorder and the values are printed out. Which of the following sequences is a valid output?
a)
5 3 1 2 4 7 8 6
b)
5 3 1 2 6 4 9 7
c)
5 3 2 4 1 6 7 8
d)
5 3 1 2 4 7 6 8
|
|
Navya Menon answered |
Preorder is root, left, right.
- So, option (b) can’t be a valid output. Since, 5 being the root and [312] a left sub-tree and [6487] being a right sub tree. But, 4 < 5, so not possible.
- In option (a), considering 5 as root, [786] becomes the right sub tree. Further, 7 being the root 6 can’t be apart of right sub-tree.
- Similarly, we can shown (c) can’t be a valid output.
- So, (d) can be the only possible valid output.
A list of n string, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is- a)O (n log n)
- b)O (n2 log n)
- c)O (n2 + log n)
- d)O (n2)
Correct answer is option 'B'. Can you explain this answer?
A list of n string, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is
a)
O (n log n)
b)
O (n2 log n)
c)
O (n2 + log n)
d)
O (n2)
|
|
Ravi Singh answered |
The recurrence tree for merge sort will have height Log(n). And O(n2) work will be done at each level of the recurrence tree (Each level involves n comparisons and a comparison takes O(n) time in worst case). So time complexity of this Merge Sort will be O (n2 log n).
The recurrence relation that arises in relation with the complexity of binary search is- a)
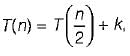 k is a constant
k is a constant - b)
 k is a constant
k is a constant - c)

- d)
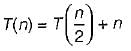
Correct answer is option 'A'. Can you explain this answer?
The recurrence relation that arises in relation with the complexity of binary search is
a)
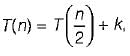 k is a constant
k is a constantb)
 k is a constant
k is a constantc)

d)
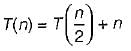
|
|
Krish Datta answered |
Binary search only half of the array.
So,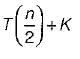
So,
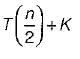
The worst case running time to search for an element in a balanced binary search tree with n 2n elements is- a)
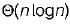
- b)
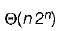
- c)
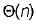
- d)
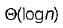
Correct answer is option 'C'. Can you explain this answer?
The worst case running time to search for an element in a balanced binary search tree with n 2n elements is
a)
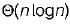
b)
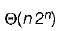
c)
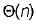
d)
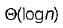
|
|
Mansi Shah answered |
We know that in balanced BST there are log2n levels in both worst as well as best case where ‘n’ is number of elements
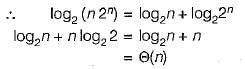
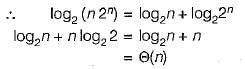
Which one of the following is the tightest upper bound that represents the time complexity of inserting an object into a binary search tree of n nodes?- a)O(1)
- b)O(logn)
- c)O(n)
- d)O(n logn)
Correct answer is option 'C'. Can you explain this answer?
Which one of the following is the tightest upper bound that represents the time complexity of inserting an object into a binary search tree of n nodes?
a)
O(1)
b)
O(logn)
c)
O(n)
d)
O(n logn)
|
|
Aarav Malik answered |
In the worst case length of binary search tree can be O(n).
So insertion of an object will take O(n) time in worst case.
So insertion of an object will take O(n) time in worst case.
Which of the following data structures is generally used to implement priority queue?- a)Table
- b)Stack
- c)Graph
- d)Heap tree
Correct answer is option 'D'. Can you explain this answer?
Which of the following data structures is generally used to implement priority queue?
a)
Table
b)
Stack
c)
Graph
d)
Heap tree

|
Crack Gate answered |
Priority queue can be implemented using an array, a linked list, a heap data structure. Among these data structures, heap data structure provides an efficient implementation of priority queues. In a normal queue, queue is implemented based on FIFO but in priority queue nodes are removed based on the priority.
Time complexity of priority queue using binary heap or binary search tree :
Time complexity of priority queue using binary heap or binary search tree :
- Insert operation takes : O( log n )
- Delete operation takes : O (log n )
Consider a list of recursive algorithms and a list of recurrence relations as shown below. Each recurrence relation corresponds to exactly one algorithm and is used to derive the time complexity of the algorithm.List-I (Recursive Algorithm)
P. Binary search
Q. Merge sort
R. Quicksort
S. Tower of Hanoi
List-li (Recurrence Relation)
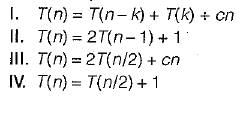
Which of the following is the correct match between the algorithms and their recurrence relations?

- a)a
- b)b
- c)c
- d)d
Correct answer is option 'B'. Can you explain this answer?
Consider a list of recursive algorithms and a list of recurrence relations as shown below. Each recurrence relation corresponds to exactly one algorithm and is used to derive the time complexity of the algorithm.
List-I (Recursive Algorithm)
P. Binary search
Q. Merge sort
R. Quicksort
S. Tower of Hanoi
List-li (Recurrence Relation)
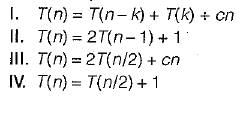
Which of the following is the correct match between the algorithms and their recurrence relations?

P. Binary search
Q. Merge sort
R. Quicksort
S. Tower of Hanoi
List-li (Recurrence Relation)
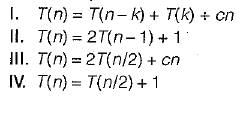
Which of the following is the correct match between the algorithms and their recurrence relations?

a)
a
b)
b
c)
c
d)
d
|
|
Arka Dasgupta answered |
Binary search : T(n) = T(n/2) + 1
Merge sort : T(n) = 2T(n/2) + cn
Quick sort : T(n) = T(n - k) + T(k) + cn
Merge sort : T(n) = 2T(n/2) + cn
Quick sort : T(n) = T(n - k) + T(k) + cn
Tower of Hanoi : T(n) = 2T(n - 1) + 1
In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?- a)
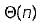
- b)
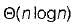
- c)
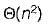
- d)
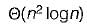
Correct answer is option 'B'. Can you explain this answer?
In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?
a)
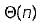
b)
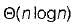
c)
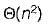
d)
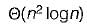
|
|
Kavya Mukherjee answered |
The relation T(n) = T(n/4) + T(3n/4) + n The pivot element is selected in such a way that it will divide the array into 1/4th and 3/4th always solving this relation give 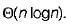
Chapter doubts & questions for Divide & Conquer - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Divide & Conquer - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
453 videos|1305 docs|700 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

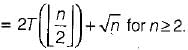 Which of the following statements is true?
Which of the following statements is true?