All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Relational Algebra for Computer Science Engineering (CSE) Exam
Which of the following statements is correct with respect to entity integrity?- a)Entity integrity constraints specify that primary key values can be composite. .
- b)Entity, integrity constraints are specified on individual relations.
- c)Entity integrity constraints are specified between weak entities.
- d)When entity integrity rules are enforced, a tuple in one relation that refers to another relation must refer to an existing tuple.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is correct with respect to entity integrity?
a)
Entity integrity constraints specify that primary key values can be composite. .
b)
Entity, integrity constraints are specified on individual relations.
c)
Entity integrity constraints are specified between weak entities.
d)
When entity integrity rules are enforced, a tuple in one relation that refers to another relation must refer to an existing tuple.
|
|
Ashutosh Mukherjee answered |
According to entity integrity primary key of relation should not contain null values.
What is the method of specifying a primary key in a schema description?- a)By writing it in bold letters
- b)By underlining it using a dashed line
- c)By writing it in capital letters
- d)By underlining it using a bold line
Correct answer is option 'D'. Can you explain this answer?
What is the method of specifying a primary key in a schema description?
a)
By writing it in bold letters
b)
By underlining it using a dashed line
c)
By writing it in capital letters
d)
By underlining it using a bold line
|
|
Sudhir Patel answered |
We can specify a primary key in schema description by underlining the respective attribute with a bold line.
Which of the given tuple calculus expressions can be used to find first name and last name of all the employees whose salary is above $15000 from the relation EMPLOYEE?- a){t.Fname, t.Lname | EMPLOYEE(t) OR t.Salary > 15000}
- b){t.Fname, t.Lname | t.Salary > 15000}
- c){t.Fname, t.Lname | EMPLOYEE(t) AND t.Salary > 15000}
- d){t.Fname, t.Lname, EMPLOYEE(t) | t.Salary > 15000}
Correct answer is option 'C'. Can you explain this answer?
Which of the given tuple calculus expressions can be used to find first name and last name of all the employees whose salary is above $15000 from the relation EMPLOYEE?
a)
{t.Fname, t.Lname | EMPLOYEE(t) OR t.Salary > 15000}
b)
{t.Fname, t.Lname | t.Salary > 15000}
c)
{t.Fname, t.Lname | EMPLOYEE(t) AND t.Salary > 15000}
d)
{t.Fname, t.Lname, EMPLOYEE(t) | t.Salary > 15000}
|
|
Sudhir Patel answered |
The condition EMPLOYEE(t) specifies that the range relation of tuple variable t is EMPLOYEE. First name and last name of EMPLOYEE tuple t that satisfies the condition t.Salary > 15000 will be retrieved.
{t.Fname, t.Lname | EMPLOYEE(t) AND t.Salary > 15000} is the correct expression.
In relational databases, the natural join of two tables is:- a)Combination of Union and filtered Cartesian product.
- b)Combination of projection and filtered Cartesian product.
- c)Combination of selection and filtered Cartesian product
- d)Cartesian product always
Correct answer is option 'B'. Can you explain this answer?
In relational databases, the natural join of two tables is:
a)
Combination of Union and filtered Cartesian product.
b)
Combination of projection and filtered Cartesian product.
c)
Combination of selection and filtered Cartesian product
d)
Cartesian product always
|
|
Sudhir Patel answered |
Natural join is used to join two relations having any number of attributes. It is denoted by a symbol ( ⨝). It is the combination of projection and filtered cartesian product. It optimizes the query as the cartesian product gives unnecessary results and set union and set intersection operations are application only on those relations that have an equal number of attributes with the same data types.
Example: Given two relation employee and departments.
Employee:
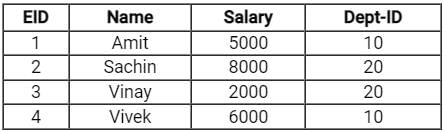
Department:

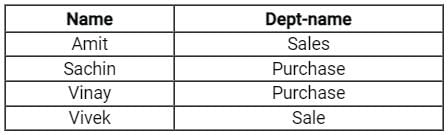
Query: Find the name of all employees from Employee with their respective Department names using natural join :
The result will be:

Relational Algebra is a __________ query language that takes two relations as input and produces another relation as an output of the query.- a)Relational
- b)Structural
- c)Procedural
- d)Fundamental
Correct answer is option 'C'. Can you explain this answer?
Relational Algebra is a __________ query language that takes two relations as input and produces another relation as an output of the query.
a)
Relational
b)
Structural
c)
Procedural
d)
Fundamental
|
|
Garima Bose answered |
Relational Algebra is a Procedural query language that takes two relations as input and produces another relation as an output of the query.
What is Relational Algebra?
Relational Algebra is a procedural query language that is used to operate on relational databases. It provides a set of operations that can be performed on relations or tables to retrieve desired information. Relational Algebra is a theoretical foundation for relational databases and is used as a basis for the design and implementation of relational database management systems (RDBMS).
Types of Query Languages
There are different types of query languages used in database systems, including:
1. Relational: Relational Algebra is a type of relational query language that operates on relations.
2. Structural: Structural query languages focus on the structure of the query rather than the specific operations performed on the data.
3. Procedural: Procedural query languages specify the step-by-step procedure to be followed to obtain the desired results.
4. Fundamental: Fundamental query languages are the basic languages used to interact with databases.
Characteristics of Relational Algebra
Relational Algebra has the following characteristics:
1. Set-oriented: Relational Algebra treats relations as sets of tuples and performs set operations such as union, intersection, and difference.
2. Closed: The result of any operation in Relational Algebra is always a relation.
3. Procedural: Relational Algebra specifies the order in which operations are executed to obtain the desired results.
4. Formal: Relational Algebra is based on a formal system of rules and principles.
Relational Algebra Operations
Relational Algebra provides several operations to manipulate relations. Some of the commonly used operations include:
1. Selection: Selects rows from a relation that satisfy a given condition.
2. Projection: Selects specific columns from a relation.
3. Union: Combines two relations to form a new relation that includes all tuples from both relations.
4. Intersection: Retrieves tuples that are common to two relations.
5. Difference: Retrieves tuples from one relation that are not present in another relation.
6. Join: Combines tuples from two relations based on a common attribute.
Conclusion
Relational Algebra is a procedural query language used to operate on relational databases. It takes two relations as input and produces another relation as the output of the query. Relational Algebra provides a set of operations to manipulate relations and retrieve desired information from databases. It is an essential component of relational database management systems and forms the foundation for designing and implementing database systems.
What is Relational Algebra?
Relational Algebra is a procedural query language that is used to operate on relational databases. It provides a set of operations that can be performed on relations or tables to retrieve desired information. Relational Algebra is a theoretical foundation for relational databases and is used as a basis for the design and implementation of relational database management systems (RDBMS).
Types of Query Languages
There are different types of query languages used in database systems, including:
1. Relational: Relational Algebra is a type of relational query language that operates on relations.
2. Structural: Structural query languages focus on the structure of the query rather than the specific operations performed on the data.
3. Procedural: Procedural query languages specify the step-by-step procedure to be followed to obtain the desired results.
4. Fundamental: Fundamental query languages are the basic languages used to interact with databases.
Characteristics of Relational Algebra
Relational Algebra has the following characteristics:
1. Set-oriented: Relational Algebra treats relations as sets of tuples and performs set operations such as union, intersection, and difference.
2. Closed: The result of any operation in Relational Algebra is always a relation.
3. Procedural: Relational Algebra specifies the order in which operations are executed to obtain the desired results.
4. Formal: Relational Algebra is based on a formal system of rules and principles.
Relational Algebra Operations
Relational Algebra provides several operations to manipulate relations. Some of the commonly used operations include:
1. Selection: Selects rows from a relation that satisfy a given condition.
2. Projection: Selects specific columns from a relation.
3. Union: Combines two relations to form a new relation that includes all tuples from both relations.
4. Intersection: Retrieves tuples that are common to two relations.
5. Difference: Retrieves tuples from one relation that are not present in another relation.
6. Join: Combines tuples from two relations based on a common attribute.
Conclusion
Relational Algebra is a procedural query language used to operate on relational databases. It takes two relations as input and produces another relation as the output of the query. Relational Algebra provides a set of operations to manipulate relations and retrieve desired information from databases. It is an essential component of relational database management systems and forms the foundation for designing and implementing database systems.
Choose the correct statements:- a)Relational algebra and relational calculus are both procedural query languages.
- b)Relational algebra and relational calculus are both non-procedural query languages.
- c)Relational algebra is a procedural query language and relational calculus is a nonprocedural query language.
- d)Relational algebra is a non-procedural query language and relational calculus is a procedural query language.
Correct answer is option 'C'. Can you explain this answer?
Choose the correct statements:
a)
Relational algebra and relational calculus are both procedural query languages.
b)
Relational algebra and relational calculus are both non-procedural query languages.
c)
Relational algebra is a procedural query language and relational calculus is a nonprocedural query language.
d)
Relational algebra is a non-procedural query language and relational calculus is a procedural query language.
|
|
Avantika Menon answered |
Relation algebra is procedural query language while relational calculus is non-procedural query language.
A relation (from the relational database model) consists of a set of tuples, which implies that- a)Relational model supports multi-valued attributes whose values can be represented in sets.
- b)For any two tuples, the values associated with all of their attributes may be the same.
- c)For any two tuples, the value associated with one or more of their attributes must differ.
- d)All tuples in a particular relation may have different attributes.
Correct answer is option 'C'. Can you explain this answer?
A relation (from the relational database model) consists of a set of tuples, which implies that
a)
Relational model supports multi-valued attributes whose values can be represented in sets.
b)
For any two tuples, the values associated with all of their attributes may be the same.
c)
For any two tuples, the value associated with one or more of their attributes must differ.
d)
All tuples in a particular relation may have different attributes.
|
|
Baishali Dasgupta answered |
Explanation:
Relational database model is based on the concept of relations or tables. A relation consists of a set of tuples, where each tuple represents a single entity or object in the real world. Each tuple has a set of attributes or fields, which represent the properties or characteristics of that entity. The values of these attributes are stored in the corresponding columns of the table.
Let us now understand the given options one by one:
a) Relational model supports multi-valued attributes whose values can be represented in sets.
This statement is incorrect. Relational model does not support multi-valued attributes. Each attribute in a relation can have only a single value. However, we can represent multiple values of an attribute by creating a separate table and establishing a relationship between the two tables.
b) For any two tuples, the values associated with all of their attributes may be the same.
This statement is also incorrect. In a relation, each tuple represents a unique entity, and therefore, the values associated with all of their attributes cannot be the same. There must be at least one attribute whose value differs between the two tuples.
c) For any two tuples, the value associated with one or more of their attributes must differ.
This statement is correct. As explained above, each tuple in a relation represents a unique entity, and therefore, the values associated with all of their attributes cannot be the same. There must be at least one attribute whose value differs between the two tuples.
d) All tuples in a particular relation may have different attributes.
This statement is also incorrect. In a relation, all tuples must have the same set of attributes, although some attributes may have null values in some tuples.
Therefore, the correct answer is option 'C', which states that for any two tuples, the value associated with one or more of their attributes must differ.
Relational database model is based on the concept of relations or tables. A relation consists of a set of tuples, where each tuple represents a single entity or object in the real world. Each tuple has a set of attributes or fields, which represent the properties or characteristics of that entity. The values of these attributes are stored in the corresponding columns of the table.
Let us now understand the given options one by one:
a) Relational model supports multi-valued attributes whose values can be represented in sets.
This statement is incorrect. Relational model does not support multi-valued attributes. Each attribute in a relation can have only a single value. However, we can represent multiple values of an attribute by creating a separate table and establishing a relationship between the two tables.
b) For any two tuples, the values associated with all of their attributes may be the same.
This statement is also incorrect. In a relation, each tuple represents a unique entity, and therefore, the values associated with all of their attributes cannot be the same. There must be at least one attribute whose value differs between the two tuples.
c) For any two tuples, the value associated with one or more of their attributes must differ.
This statement is correct. As explained above, each tuple in a relation represents a unique entity, and therefore, the values associated with all of their attributes cannot be the same. There must be at least one attribute whose value differs between the two tuples.
d) All tuples in a particular relation may have different attributes.
This statement is also incorrect. In a relation, all tuples must have the same set of attributes, although some attributes may have null values in some tuples.
Therefore, the correct answer is option 'C', which states that for any two tuples, the value associated with one or more of their attributes must differ.
The assignment operator is denoted by- a)->
- b)<-
- c)=
- d)==
Correct answer is option 'B'. Can you explain this answer?
The assignment operator is denoted by
a)
->
b)
<-
c)
=
d)
==
|
|
Aman Menon answered |
The assignment operator is denoted by "=" in most programming languages, including C, C++, Java, and Python.
A Tuple Relational Calculus query is expressed as ________.- a){ P( ) | T)
- b){ T | p(T) }
- c){ T | P() | T}
- d){ p(T) | T }
Correct answer is option 'B'. Can you explain this answer?
A Tuple Relational Calculus query is expressed as ________.
a)
{ P( ) | T)
b)
{ T | p(T) }
c)
{ T | P() | T}
d)
{ p(T) | T }
|
|
Avantika Shah answered |
The correct answer is option 'B': { T | p(T) }.
Tuple Relational Calculus is a non-procedural query language that specifies the desired result without specifying the method to obtain it. It is based on mathematical logic and allows users to specify what data they want to retrieve from a database, rather than how to retrieve it.
When expressing a query in Tuple Relational Calculus, the format is as follows:
{ | }
Explanation:
- The curly braces {} indicate that it is a query in Tuple Relational Calculus.
- The represent the attributes or columns of the relation that we want to retrieve.
- The vertical bar | separates the attributes from the condition.
- The specifies the condition or predicate that must be satisfied for a tuple to be included in the result.
In this case, the query is expressed as { T | p(T) }:
- T represents the attributes or columns of the relation that we want to retrieve.
- p(T) represents the condition or predicate that must be satisfied for a tuple to be included in the result.
So, the query { T | p(T) } means that we want to retrieve all tuples (rows) from the relation where the condition p(T) is true.
By selecting option 'B': { T | p(T) }, we are expressing the query in the correct format of Tuple Relational Calculus.
Tuple Relational Calculus is a non-procedural query language that specifies the desired result without specifying the method to obtain it. It is based on mathematical logic and allows users to specify what data they want to retrieve from a database, rather than how to retrieve it.
When expressing a query in Tuple Relational Calculus, the format is as follows:
{
Explanation:
- The curly braces {} indicate that it is a query in Tuple Relational Calculus.
- The
- The vertical bar | separates the attributes from the condition.
- The
In this case, the query is expressed as { T | p(T) }:
- T represents the attributes or columns of the relation that we want to retrieve.
- p(T) represents the condition or predicate that must be satisfied for a tuple to be included in the result.
So, the query { T | p(T) } means that we want to retrieve all tuples (rows) from the relation where the condition p(T) is true.
By selecting option 'B': { T | p(T) }, we are expressing the query in the correct format of Tuple Relational Calculus.
Which of the following is used to denote the selection operation in relational algebra?- a)Pi (Greek)
- b)Sigma (Greek)
- c)Lambda (Greek)
- d)Omega (Greek)
Correct answer is option 'B'. Can you explain this answer?
Which of the following is used to denote the selection operation in relational algebra?
a)
Pi (Greek)
b)
Sigma (Greek)
c)
Lambda (Greek)
d)
Omega (Greek)
|
|
Sudhir Patel answered |
The select operation selects tuples that satisfy a given predicate.
Which of the following is a unary operation?
- a)Join
- b)Cartesian Product
- c)Intersection
- d)Projection
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a unary operation?
a)
Join
b)
Cartesian Product
c)
Intersection
d)
Projection
|
|
Shubham Chawla answered |
Unary Operation
A unary operation is an operation that takes only one operand or input. In other words, it is an operation that works with a single element or entity. Unary operations are commonly used in various fields, including mathematics, computer science, and logic.
Examples of Unary Operations:
1. Increment and decrement operators: In programming languages like C, C++, and Java, the increment (++) and decrement (--) operators are unary operators. They operate on a single variable, increasing or decreasing its value by one.
2. Negation: The negation operator (-) is also a unary operator. It changes the sign of a number. For example, -5 is the negation of 5.
3. Logical negation: In logic, the negation operator (~ or ¬) is a unary operator that negates the truth value of a proposition. For example, if P is true, then ¬P is false.
4. Absolute value: The absolute value function (|x|) is a unary operation that returns the positive magnitude of a number. For example, |−3| is equal to 3.
5. Square root: The square root (√) is another unary operation. It calculates the non-negative square root of a number. For example, √9 is equal to 3.
Unary Operation in the context of the given options:
Among the options given (a) Selection operation, (b) Primitive operation, (c) Projection operation, and (d) Generalized selection, the only option that represents a unary operation is (d) Generalized selection.
Generalized selection is a unary operation in the context of relational algebra, which is a mathematical system used for modeling and manipulating relational databases. It is a unary operation that selects tuples from a relation based on a given condition or predicate. The condition is applied to each tuple individually, and only the tuples that satisfy the condition are included in the result.
In contrast, the other options mentioned are not unary operations:
- Selection operation (a) typically refers to a binary operation where tuples are selected based on a specific condition involving two relations.
- Primitive operation (b) is a generic term and does not specifically denote a unary operation.
- Projection operation (c) is also not a unary operation. It involves selecting specific attributes or columns from a relation while maintaining the integrity of the tuples.
Therefore, the correct answer is option (d) Generalized selection, which represents a unary operation in the given options.
A unary operation is an operation that takes only one operand or input. In other words, it is an operation that works with a single element or entity. Unary operations are commonly used in various fields, including mathematics, computer science, and logic.
Examples of Unary Operations:
1. Increment and decrement operators: In programming languages like C, C++, and Java, the increment (++) and decrement (--) operators are unary operators. They operate on a single variable, increasing or decreasing its value by one.
2. Negation: The negation operator (-) is also a unary operator. It changes the sign of a number. For example, -5 is the negation of 5.
3. Logical negation: In logic, the negation operator (~ or ¬) is a unary operator that negates the truth value of a proposition. For example, if P is true, then ¬P is false.
4. Absolute value: The absolute value function (|x|) is a unary operation that returns the positive magnitude of a number. For example, |−3| is equal to 3.
5. Square root: The square root (√) is another unary operation. It calculates the non-negative square root of a number. For example, √9 is equal to 3.
Unary Operation in the context of the given options:
Among the options given (a) Selection operation, (b) Primitive operation, (c) Projection operation, and (d) Generalized selection, the only option that represents a unary operation is (d) Generalized selection.
Generalized selection is a unary operation in the context of relational algebra, which is a mathematical system used for modeling and manipulating relational databases. It is a unary operation that selects tuples from a relation based on a given condition or predicate. The condition is applied to each tuple individually, and only the tuples that satisfy the condition are included in the result.
In contrast, the other options mentioned are not unary operations:
- Selection operation (a) typically refers to a binary operation where tuples are selected based on a specific condition involving two relations.
- Primitive operation (b) is a generic term and does not specifically denote a unary operation.
- Projection operation (c) is also not a unary operation. It involves selecting specific attributes or columns from a relation while maintaining the integrity of the tuples.
Therefore, the correct answer is option (d) Generalized selection, which represents a unary operation in the given options.
What is a foreign key?- a)A foreign key is a primary key of a relation which is an attribute in another relation
- b)A foreign key is a superkey of a relation which is an attribute in more than one other relations
- c)A foreign key is an attribute of a relation that is a primary key of another relation
- d)A foreign key is the primary key of a relation that does not occur anywhere else in the schema
Correct answer is option 'C'. Can you explain this answer?
What is a foreign key?
a)
A foreign key is a primary key of a relation which is an attribute in another relation
b)
A foreign key is a superkey of a relation which is an attribute in more than one other relations
c)
A foreign key is an attribute of a relation that is a primary key of another relation
d)
A foreign key is the primary key of a relation that does not occur anywhere else in the schema
|
|
Raghav Joshi answered |
What is a Foreign Key?
A foreign key is a crucial concept in relational database management systems that establishes a link between two tables. It plays a significant role in maintaining the integrity of data across different tables.
Definition of a Foreign Key
- A foreign key is an attribute (or a set of attributes) in one table that refers to the primary key of another table.
- This relationship creates a dependency between the two tables, allowing for organized data management.
Key Characteristics
- Reference: The foreign key in one table points to the primary key in another table, establishing a relationship between the two.
- Data Integrity: By enforcing this relationship, foreign keys help maintain referential integrity. This means that records in the referencing table (child table) must correspond to valid records in the referenced table (parent table).
- Examples: For example, in a database of students and courses, a 'Course_ID' in the 'Enrollments' table could serve as a foreign key, linking to the 'Course_ID' primary key in the 'Courses' table.
Why Option C is Correct
- Option C states that "A foreign key is an attribute of a relation that is a primary key of another relation," which accurately describes the relationship foreign keys have with primary keys in different tables.
- This definition aligns perfectly with the purpose and function of foreign keys, making it the correct answer.
Conclusion
Understanding foreign keys is essential for designing relational databases that ensure data integrity and logical relationships between different entities.
A foreign key is a crucial concept in relational database management systems that establishes a link between two tables. It plays a significant role in maintaining the integrity of data across different tables.
Definition of a Foreign Key
- A foreign key is an attribute (or a set of attributes) in one table that refers to the primary key of another table.
- This relationship creates a dependency between the two tables, allowing for organized data management.
Key Characteristics
- Reference: The foreign key in one table points to the primary key in another table, establishing a relationship between the two.
- Data Integrity: By enforcing this relationship, foreign keys help maintain referential integrity. This means that records in the referencing table (child table) must correspond to valid records in the referenced table (parent table).
- Examples: For example, in a database of students and courses, a 'Course_ID' in the 'Enrollments' table could serve as a foreign key, linking to the 'Course_ID' primary key in the 'Courses' table.
Why Option C is Correct
- Option C states that "A foreign key is an attribute of a relation that is a primary key of another relation," which accurately describes the relationship foreign keys have with primary keys in different tables.
- This definition aligns perfectly with the purpose and function of foreign keys, making it the correct answer.
Conclusion
Understanding foreign keys is essential for designing relational databases that ensure data integrity and logical relationships between different entities.
The SQL expression :
SELECT distinct 7.branch_name
FROM branch T, branch S
WHERE T.assets >S.assets and S.branch_city = "PONDICHERRY”
Finds the names of- a)All branches that have greater assets than any branch located in PONDICHERRY.
- b)All branches that have greater assets than all branches located in PONDICHERRY.
- c)The branch that have greater assetin PONDICHERRY.
- d)Any branches that have greater asset than any branch located in PONDICHERRY.
Correct answer is option 'A'. Can you explain this answer?
The SQL expression :
SELECT distinct 7.branch_name
FROM branch T, branch S
WHERE T.assets >S.assets and S.branch_city = "PONDICHERRY”
Finds the names of
SELECT distinct 7.branch_name
FROM branch T, branch S
WHERE T.assets >S.assets and S.branch_city = "PONDICHERRY”
Finds the names of
a)
All branches that have greater assets than any branch located in PONDICHERRY.
b)
All branches that have greater assets than all branches located in PONDICHERRY.
c)
The branch that have greater assetin PONDICHERRY.
d)
Any branches that have greater asset than any branch located in PONDICHERRY.
|
|
Aravind Sengupta answered |
The condition T. assets > S. assets and S. branch_city = “PONDICHERRY” checks for the all those branch-name who have greater assets than any branch located in Pondicherry. The keyword distinct removes the duplicacy of branch_name satisfy the given condition.
What is an Instance of a Database?- a)The logical design of the database system
- b)The entire set of attributes of the Database put together in a single relation
- c)The state of the database system at any given point of time
- d)The initial values inserted into the Database immediately after its creation
Correct answer is option 'C'. Can you explain this answer?
What is an Instance of a Database?
a)
The logical design of the database system
b)
The entire set of attributes of the Database put together in a single relation
c)
The state of the database system at any given point of time
d)
The initial values inserted into the Database immediately after its creation
|
|
Sudhir Patel answered |
The state of the database system at any given point of time is called as an Instance of the database.
What action does ⋈ operator perform in relational algebra- a)Output specified attributes from all rows of the input relation and remove duplicate tuples from the output
- b)Outputs pairs of rows from the two input relations that have the same value on all attributes that have the same name
- c)Output all pairs of rows from the two input relations (regardless of whether or not they have the same values on common attributes)
- d)Return rows of the input relation that satisfy the predicate
Correct answer is option 'A'. Can you explain this answer?
What action does ⋈ operator perform in relational algebra
a)
Output specified attributes from all rows of the input relation and remove duplicate tuples from the output
b)
Outputs pairs of rows from the two input relations that have the same value on all attributes that have the same name
c)
Output all pairs of rows from the two input relations (regardless of whether or not they have the same values on common attributes)
d)
Return rows of the input relation that satisfy the predicate
|
|
Aashna Sen answered |
Explanation:
The action performed by the projection operator in relational algebra is to output specified attributes from all rows of the input relation and remove duplicate tuples from the output.
Projection is one of the fundamental operations in relational algebra and is denoted by the Greek letter π (pi). It allows us to select a subset of attributes from a relation and discard the rest. The result of the projection is a new relation that contains only the selected attributes.
Here is a detailed explanation of the projection operation:
1. Selecting attributes: The projection operator takes a relation as input and specifies a list of attributes that we want to select from that relation. These attributes can be specified using attribute names or by their position in the relation.
2. Outputting rows: The projection operator outputs all the rows from the input relation, but only includes the selected attributes in the output. The order of the attributes in the output relation may be different from the order in the input relation.
3. Removing duplicates: After selecting the specified attributes, the projection operator removes duplicate tuples from the output relation. This means that if there are multiple rows in the input relation that have the same values for the selected attributes, only one of them will appear in the output.
4. Result relation: The result of the projection operation is a new relation that contains only the selected attributes and does not have any duplicate tuples. This result relation can be used as input for further operations in relational algebra.
In summary, the projection operator in relational algebra selects specified attributes from all rows of the input relation and removes duplicate tuples from the output. It is a fundamental operation that allows us to manipulate and analyze data in a relational database.
The action performed by the projection operator in relational algebra is to output specified attributes from all rows of the input relation and remove duplicate tuples from the output.
Projection is one of the fundamental operations in relational algebra and is denoted by the Greek letter π (pi). It allows us to select a subset of attributes from a relation and discard the rest. The result of the projection is a new relation that contains only the selected attributes.
Here is a detailed explanation of the projection operation:
1. Selecting attributes: The projection operator takes a relation as input and specifies a list of attributes that we want to select from that relation. These attributes can be specified using attribute names or by their position in the relation.
2. Outputting rows: The projection operator outputs all the rows from the input relation, but only includes the selected attributes in the output. The order of the attributes in the output relation may be different from the order in the input relation.
3. Removing duplicates: After selecting the specified attributes, the projection operator removes duplicate tuples from the output relation. This means that if there are multiple rows in the input relation that have the same values for the selected attributes, only one of them will appear in the output.
4. Result relation: The result of the projection operation is a new relation that contains only the selected attributes and does not have any duplicate tuples. This result relation can be used as input for further operations in relational algebra.
In summary, the projection operator in relational algebra selects specified attributes from all rows of the input relation and removes duplicate tuples from the output. It is a fundamental operation that allows us to manipulate and analyze data in a relational database.
The following relation records the age of 500 employees of a company, where empNo (Indicating the employee number) is the key:
empAge(empNo, age)Consider the following relational algebra expression:
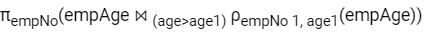
Q. What does the above expression generate?- a)Employee numbers of only those employees whose age is the maximum.
- b)Employee numbers of all employees whose age is not the minimum.
- c)Employee numbers of only those employees whose age is more than the age of exactly one other employee.
- d)Employee numbers of all employees whose age is the minimum.
Correct answer is option 'B'. Can you explain this answer?
The following relation records the age of 500 employees of a company, where empNo (Indicating the employee number) is the key:
empAge(empNo, age)
empAge(empNo, age)
Consider the following relational algebra expression:
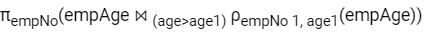
Q. What does the above expression generate?
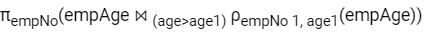
Q. What does the above expression generate?
a)
Employee numbers of only those employees whose age is the maximum.
b)
Employee numbers of all employees whose age is not the minimum.
c)
Employee numbers of only those employees whose age is more than the age of exactly one other employee.
d)
Employee numbers of all employees whose age is the minimum.
|
|
Sudhir Patel answered |
Consider the empAge(empNo, age) Table
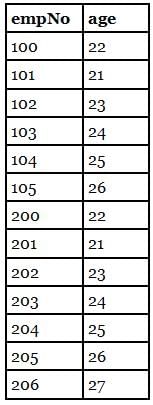
We run the following Query on above Table
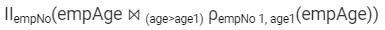
We get Output Table as
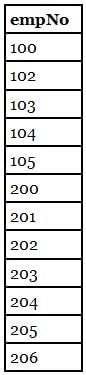
Hence the Output is "Employees whose age greater than at least one employee" or "Employees whose age is no minimum".
Which of the following operations is not part of the five basic set operations in relational algebra?- a)Union
- b)Division
- c)Cartesian Product
- d)Set Difference
Correct answer is option 'B'. Can you explain this answer?
Which of the following operations is not part of the five basic set operations in relational algebra?
a)
Union
b)
Division
c)
Cartesian Product
d)
Set Difference
|
|
Rishabh Sharma answered |
Five primitive operators of Codd’s algebra are the selection, the projection the Cartesian product, the set union and the set difference.
Consider the set of relations given below and the SQL query that follows:
Students: (Roll_number, Name, date_of_birth)
Courses: (Course_number, Course_name, Instructor)
Grades: (RolL_number, Course_number, Grade)
SELECT DISTINCT Name
FROM Students, Courses, Grades
WHERE Students. RolLnumber = Grades.
RolLnumber
ANDCourse.lnstructor = Korth
AND Courses.Course_number =. Grades. Course_number AND Grades.Grade = A
Which of the following sets is computed by the above query?- a)Names of students who have got an A grade in all courses taught by Korth.
- b)Names of students who have got an A grade in all courses.
- c)Names of students who have got an A grade in at least one of the courses taught by Korth.
- d)None of the above.
Correct answer is option 'C'. Can you explain this answer?
Consider the set of relations given below and the SQL query that follows:
Students: (Roll_number, Name, date_of_birth)
Courses: (Course_number, Course_name, Instructor)
Grades: (RolL_number, Course_number, Grade)
SELECT DISTINCT Name
FROM Students, Courses, Grades
WHERE Students. RolLnumber = Grades.
RolLnumber
ANDCourse.lnstructor = Korth
AND Courses.Course_number =. Grades. Course_number AND Grades.Grade = A
Which of the following sets is computed by the above query?
Students: (Roll_number, Name, date_of_birth)
Courses: (Course_number, Course_name, Instructor)
Grades: (RolL_number, Course_number, Grade)
SELECT DISTINCT Name
FROM Students, Courses, Grades
WHERE Students. RolLnumber = Grades.
RolLnumber
ANDCourse.lnstructor = Korth
AND Courses.Course_number =. Grades. Course_number AND Grades.Grade = A
Which of the following sets is computed by the above query?
a)
Names of students who have got an A grade in all courses taught by Korth.
b)
Names of students who have got an A grade in all courses.
c)
Names of students who have got an A grade in at least one of the courses taught by Korth.
d)
None of the above.
|
|
Rishabh Pillai answered |
Explanation:
The given SQL query selects the distinct names of students who have received an A grade in at least one course taught by Korth. Let's break down the query and understand it step by step.
1. FROM Students, Courses, Grades
- This clause specifies the tables from which we are fetching the data: Students, Courses, and Grades.
2. WHERE Students.Roll_number = Grades.Roll_number
- This condition joins the Students and Grades tables based on the Roll_number attribute. It ensures that we only consider the records where the Roll_number matches in both tables.
3. AND Courses.Instructor = 'Korth'
- This condition further filters the joined result by only considering the records where the Instructor attribute of the Courses table is equal to 'Korth'.
4. AND Courses.Course_number = Grades.Course_number
- This condition ensures that we only consider the records where the Course_number matches in both the Courses and Grades tables.
5. AND Grades.Grade = 'A'
- This condition further filters the result by only considering the records where the Grade attribute of the Grades table is equal to 'A'.
6. SELECT DISTINCT Name
- Finally, we select the distinct names from the result obtained after applying the above conditions.
Conclusion:
The query retrieves the distinct names of students who have received an A grade in at least one course taught by Korth. Therefore, option C is the correct answer: "Names of students who have got an A grade in at least one of the courses taught by Korth."
The given SQL query selects the distinct names of students who have received an A grade in at least one course taught by Korth. Let's break down the query and understand it step by step.
1. FROM Students, Courses, Grades
- This clause specifies the tables from which we are fetching the data: Students, Courses, and Grades.
2. WHERE Students.Roll_number = Grades.Roll_number
- This condition joins the Students and Grades tables based on the Roll_number attribute. It ensures that we only consider the records where the Roll_number matches in both tables.
3. AND Courses.Instructor = 'Korth'
- This condition further filters the joined result by only considering the records where the Instructor attribute of the Courses table is equal to 'Korth'.
4. AND Courses.Course_number = Grades.Course_number
- This condition ensures that we only consider the records where the Course_number matches in both the Courses and Grades tables.
5. AND Grades.Grade = 'A'
- This condition further filters the result by only considering the records where the Grade attribute of the Grades table is equal to 'A'.
6. SELECT DISTINCT Name
- Finally, we select the distinct names from the result obtained after applying the above conditions.
Conclusion:
The query retrieves the distinct names of students who have received an A grade in at least one course taught by Korth. Therefore, option C is the correct answer: "Names of students who have got an A grade in at least one of the courses taught by Korth."
Given relations R(w, x) and S(y, z), the result of
SELECT DISTINCT w,x
FROM R, S
Is guaranteed to be same as R, if- a)R has no duplicates and S is non-empty
- b)R and S have no duplicates
- c)S has no duplicates and R is non-empty
- d)R and S have the same number of tuples
Correct answer is option 'A'. Can you explain this answer?
Given relations R(w, x) and S(y, z), the result of
SELECT DISTINCT w,x
FROM R, S
Is guaranteed to be same as R, if
SELECT DISTINCT w,x
FROM R, S
Is guaranteed to be same as R, if
a)
R has no duplicates and S is non-empty
b)
R and S have no duplicates
c)
S has no duplicates and R is non-empty
d)
R and S have the same number of tuples
|
|
Preethi Iyer answered |
The given query
SELECT DISTINCT W, X
FROM R, S
Is guaranteed to be same as R, if R has no duplicates and ‘S’ is non-empty.
Since, if R is having a duplicates, then the tuples selected by SELECT operation of the R and the given query will not be same also if ‘S’ is empty then the given query outputs null.
SELECT DISTINCT W, X
FROM R, S
Is guaranteed to be same as R, if R has no duplicates and ‘S’ is non-empty.
Since, if R is having a duplicates, then the tuples selected by SELECT operation of the R and the given query will not be same also if ‘S’ is empty then the given query outputs null.
Choose the option that correctly explains in words, the function of the following relational algebra expressionσyear≥2009 (book ⋈ borrow)
- a)Selects all tuples from the Cartesian product of book and borrow
- b)Selects all the tuples from the natural join of book and student wherever the year is greater than or equal to 2009
- c)Selects all the tuples from the natural join of book and borrow wherever the year is lesser than 2009
- d)Selects all tuples from the Cartesian product of book and borrow wherever the year is greater than or equal to 2009
Correct answer is option 'B'. Can you explain this answer?
Choose the option that correctly explains in words, the function of the following relational algebra expressionσyear≥2009 (book ⋈ borrow)
a)
Selects all tuples from the Cartesian product of book and borrow
b)
Selects all the tuples from the natural join of book and student wherever the year is greater than or equal to 2009
c)
Selects all the tuples from the natural join of book and borrow wherever the year is lesser than 2009
d)
Selects all tuples from the Cartesian product of book and borrow wherever the year is greater than or equal to 2009
|
|
Nisha Gupta answered |
There is no relational algebra expression provided to analyze and explain.
Which of the following is not outer join?
- a)Left outer join
- b)Right outer join
- c)Full outer join
- d)Natural Join
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not outer join?
a)
Left outer join
b)
Right outer join
c)
Full outer join
d)
Natural Join
|
|
Sanaya Gupta answered |
Explanation:
An outer join is a type of join operation that retrieves matching records from two tables, even if there is no match between the columns being joined. It includes all the rows from one table and the matching rows from the other table.
There are three types of outer joins: left outer join, right outer join, and full outer join.
Left Outer Join:
- A left outer join returns all the rows from the left table (the table specified before the LEFT JOIN keyword), and the matching rows from the right table (the table specified after the ON keyword).
- If there is no match, NULL values are returned for the columns of the right table.
- This type of join is denoted by the keyword "LEFT JOIN" or "LEFT OUTER JOIN".
- Example: SELECT * FROM table1 LEFT JOIN table2 ON table1.column = table2.column;
Right Outer Join:
- A right outer join returns all the rows from the right table (the table specified after the RIGHT JOIN keyword), and the matching rows from the left table (the table specified before the ON keyword).
- If there is no match, NULL values are returned for the columns of the left table.
- This type of join is denoted by the keyword "RIGHT JOIN" or "RIGHT OUTER JOIN".
- Example: SELECT * FROM table1 RIGHT JOIN table2 ON table1.column = table2.column;
Full Outer Join:
- A full outer join returns all the rows from both tables, regardless of whether there is a match or not.
- If there is no match, NULL values are returned for the columns of the table without a match.
- This type of join is denoted by the keyword "FULL JOIN" or "FULL OUTER JOIN".
- Example: SELECT * FROM table1 FULL JOIN table2 ON table1.column = table2.column;
Conclusion:
- The correct answer is option 'D' because all three types of outer joins (left outer join, right outer join, and full outer join) are included in the given options.
- Therefore, none of the options mentioned are not outer joins.
An outer join is a type of join operation that retrieves matching records from two tables, even if there is no match between the columns being joined. It includes all the rows from one table and the matching rows from the other table.
There are three types of outer joins: left outer join, right outer join, and full outer join.
Left Outer Join:
- A left outer join returns all the rows from the left table (the table specified before the LEFT JOIN keyword), and the matching rows from the right table (the table specified after the ON keyword).
- If there is no match, NULL values are returned for the columns of the right table.
- This type of join is denoted by the keyword "LEFT JOIN" or "LEFT OUTER JOIN".
- Example: SELECT * FROM table1 LEFT JOIN table2 ON table1.column = table2.column;
Right Outer Join:
- A right outer join returns all the rows from the right table (the table specified after the RIGHT JOIN keyword), and the matching rows from the left table (the table specified before the ON keyword).
- If there is no match, NULL values are returned for the columns of the left table.
- This type of join is denoted by the keyword "RIGHT JOIN" or "RIGHT OUTER JOIN".
- Example: SELECT * FROM table1 RIGHT JOIN table2 ON table1.column = table2.column;
Full Outer Join:
- A full outer join returns all the rows from both tables, regardless of whether there is a match or not.
- If there is no match, NULL values are returned for the columns of the table without a match.
- This type of join is denoted by the keyword "FULL JOIN" or "FULL OUTER JOIN".
- Example: SELECT * FROM table1 FULL JOIN table2 ON table1.column = table2.column;
Conclusion:
- The correct answer is option 'D' because all three types of outer joins (left outer join, right outer join, and full outer join) are included in the given options.
- Therefore, none of the options mentioned are not outer joins.
Consider the expression t ϵ instructor ∧ ∃ s ϵ department (t [dept_name] = s [dept_name]) the variables t and s are _____ respectively. - a)Free variable and bound variable
- b)Bound variable and free variable
- c)Free variable and free variable
- d)Bound variable and bound variable
Correct answer is option 'A'. Can you explain this answer?
Consider the expression t ϵ instructor ∧ ∃ s ϵ department (t [dept_name] = s [dept_name]) the variables t and s are _____ respectively.
a)
Free variable and bound variable
b)
Bound variable and free variable
c)
Free variable and free variable
d)
Bound variable and bound variable
|
|
Sudhir Patel answered |
- A tuple variable t is bound if it is quantified, meaning that it appears in existential or universal quantifier clause, otherwise it is free. Formally, tuple variable is free or bound as :
- An occurrence of a tuple variable in a formula F that is an atom is free in F.
- An occurrence of a tuple variable t is free or bound in a formula made up of logical connectives – (F1 AND F2), (F1 OR F2), NOT(F1) and NOT(F2)- depending on whether it is free or bound in F1 or F2. In a formula of the form F = (F1 AND F2) or F = (F1 OR F2), a tuple variable may be free in F1 and bound in F2 or vice versa.
- All free occurrences of a tuple variable t in F are bound in F’ of form F’ = (∃ t) F or F’ = (for all t)F
Here, given expression is :
t ϵ instructor ∧ ∃ s ϵ department (t [dept_name] = s [dept_name])
t ϵ instructor ∧ ∃ s ϵ department (t [dept_name] = s [dept_name])
According to above rules:
t is the free variable and s is the bound variable.
t is the free variable and s is the bound variable.
Which of the following statements is FALSE?- a){2, 3, 4} ∈ A and {2, 3} ∈ B implies that {4} ⊆ A - B.
- b){2, 3, 4} ⊆ A implies that 2 ∈ A and {3, 4} ⊆ A
- c)A ∩ B {2, 3, 4} implies that {2, 3, 4} ⊆ A and {2, 3, 4} ⊆ B.
- d)A - B ⊇ {3, 4} and {1, 2} ⊆ B implies that {1, 2, 3, 4} ⊆ A ∪ B
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is FALSE?
a)
{2, 3, 4} ∈ A and {2, 3} ∈ B implies that {4} ⊆ A - B.
b)
{2, 3, 4} ⊆ A implies that 2 ∈ A and {3, 4} ⊆ A
c)
A ∩ B {2, 3, 4} implies that {2, 3, 4} ⊆ A and {2, 3, 4} ⊆ B.
d)
A - B ⊇ {3, 4} and {1, 2} ⊆ B implies that {1, 2, 3, 4} ⊆ A ∪ B
|
|
Manisha Sharma answered |
Understanding the Statements
To determine which statement is false, let's analyze each option carefully.
Statement A
- {2, 3, 4} is a subset of set A, and {2, 3} is a subset of set B.
- This implies that {4} should be a subset of A - B.
- This statement holds true because since {2, 3, 4} is in A and {2, 3} is in B, {4} cannot be in B, thus it must be in A - B.
Statement B
- If {2, 3, 4} is a subset of A, then it implies that 2 is in A and {3, 4} is a subset of A as well.
- This statement is also true, as being a subset guarantees that all elements are included.
Statement C
- The condition A ∩ B = {2, 3, 4} suggests that these elements are common to both A and B.
- However, if {2, 3, 4} is in both A and B, it doesn't necessarily mean that {2, 3, 4} is a subset of A or B; they could contain other elements.
- This statement is false because the conclusion does not logically follow from the premise.
Statement D
- If A - B is a superset of {3, 4} and {1, 2} is a subset of B, it implies that {1, 2, 3, 4} is a subset of A ∪ B.
- This statement is true since the elements {3, 4} are in A but not in B, and {1, 2} is in B.
Conclusion
- The false statement is option C, as the intersection of A and B does not guarantee that the entire set {2, 3, 4} is a subset of both A and B.
To determine which statement is false, let's analyze each option carefully.
Statement A
- {2, 3, 4} is a subset of set A, and {2, 3} is a subset of set B.
- This implies that {4} should be a subset of A - B.
- This statement holds true because since {2, 3, 4} is in A and {2, 3} is in B, {4} cannot be in B, thus it must be in A - B.
Statement B
- If {2, 3, 4} is a subset of A, then it implies that 2 is in A and {3, 4} is a subset of A as well.
- This statement is also true, as being a subset guarantees that all elements are included.
Statement C
- The condition A ∩ B = {2, 3, 4} suggests that these elements are common to both A and B.
- However, if {2, 3, 4} is in both A and B, it doesn't necessarily mean that {2, 3, 4} is a subset of A or B; they could contain other elements.
- This statement is false because the conclusion does not logically follow from the premise.
Statement D
- If A - B is a superset of {3, 4} and {1, 2} is a subset of B, it implies that {1, 2, 3, 4} is a subset of A ∪ B.
- This statement is true since the elements {3, 4} are in A but not in B, and {1, 2} is in B.
Conclusion
- The false statement is option C, as the intersection of A and B does not guarantee that the entire set {2, 3, 4} is a subset of both A and B.
______ operation preserves those tuples that would be lost in____- a)Natural join, outer join
- b)Outer join, natural join
- c)Left outer join, right outer join
- d)Left outer join, natural join
Correct answer is option 'B'. Can you explain this answer?
______ operation preserves those tuples that would be lost in____
a)
Natural join, outer join
b)
Outer join, natural join
c)
Left outer join, right outer join
d)
Left outer join, natural join
|
|
Megha Yadav answered |
Outer Join Preserves Tuples that would be Lost in Natural Join
Definition of Natural Join:
- Natural join combines two tables based on columns with the same name.
- Only the matching tuples between the two tables are included in the result.
Definition of Outer Join:
- Outer join includes all tuples from one table and only matching tuples from the other table.
- It preserves tuples that do not have a match in the other table by filling in null values.
Explanation:
- In a natural join, only the tuples with matching values in the common columns are included in the result.
- Tuples that do not have a match in the other table are excluded from the result, leading to potential data loss.
- On the other hand, an outer join includes all tuples from one table, ensuring that no data is lost.
- By filling in null values for non-matching tuples, the outer join preserves all the data from both tables.
Definition of Natural Join:
- Natural join combines two tables based on columns with the same name.
- Only the matching tuples between the two tables are included in the result.
Definition of Outer Join:
- Outer join includes all tuples from one table and only matching tuples from the other table.
- It preserves tuples that do not have a match in the other table by filling in null values.
Explanation:
- In a natural join, only the tuples with matching values in the common columns are included in the result.
- Tuples that do not have a match in the other table are excluded from the result, leading to potential data loss.
- On the other hand, an outer join includes all tuples from one table, ensuring that no data is lost.
- By filling in null values for non-matching tuples, the outer join preserves all the data from both tables.
If P and Q are predicates and P is the relational algebra expression, then which of the following equivalence are valid ?- a)σP(σQ(e)) = σQ(σP(e))
- b)σP(σQ(e)) = σP ∪ Q(e)
- c)σP(σP(e)) = σP V Q(e)
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If P and Q are predicates and P is the relational algebra expression, then which of the following equivalence are valid ?
a)
σP(σQ(e)) = σQ(σP(e))
b)
σP(σQ(e)) = σP ∪ Q(e)
c)
σP(σP(e)) = σP V Q(e)
d)
None of these

|
Crack Gate answered |
In relational algebra, selection operations can be combined, and the order of these operations does not affect the final result when the operations are based on different predicates combined with a logical AND. Here's a short explanation of each option presented in your question:
- σP(σQ(e)) = σQ(σP(e))
Valid. This shows that the order of applying selection predicates does not matter when you're effectively filtering by both conditions (P AND Q). It's like saying "get me all items that are red (P) and round (Q)" is the same as saying "get me all items that are round (Q) and red (P)." - σP(σQ(e)) = σP ∪ Q(e)
Not Valid. This suggests combining predicates P and Q through selection and then implies a union operation, which doesn't make sense in this context. Selection operations imply an AND relationship, not a UNION, which would correspond to an OR relationship. - σP(σP(e)) = σP V Q(e)
Not Valid. Applying the same predicate P twice is redundant and does not involve predicate Q. Additionally, the expression hints at a logical OR (possibly intended by "V") or another operation not applicable here.
Which of the following is a fundamental operation in relational algebra?- a)Set intersection
- b)Natural join
- c)Assignment
- d)None of the mentioned
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a fundamental operation in relational algebra?
a)
Set intersection
b)
Natural join
c)
Assignment
d)
None of the mentioned
|
|
Preethi Iyer answered |
< b="" />Fundamental Operations in Relational Algebra< />
- Relational algebra is a formal query language used to perform operations on relational databases. It consists of a set of operations that manipulate relations or tables in a database.
< b="" />Set Intersection< />
- Set intersection is not a fundamental operation in relational algebra. It involves finding the common elements between two sets or relations. However, it is not part of the basic operations defined in relational algebra.
< b="" />Natural Join< />
- Natural join is a fundamental operation in relational algebra. It combines two relations based on the equality of their attributes. It returns a new relation that contains all the attributes from both relations, eliminating duplicate attributes, and only including the rows where the values of the common attributes match.
< b="" />Assignment< />
- Assignment is not a fundamental operation in relational algebra. It is a process of assigning values to variables or attributes. In relational algebra, the focus is on manipulating relations rather than assigning values to variables.
< b="" />None of the Mentioned< />
- The correct answer is "None of the mentioned." Set intersection and assignment are not fundamental operations in relational algebra, while natural join is a fundamental operation. Therefore, none of the given options are fully correct.
- The fundamental operations in relational algebra include selection, projection, union, set difference, cartesian product, and rename. These operations allow for querying and manipulating data in a relational database.
- Selection is used to retrieve specific rows from a relation that satisfy a given condition.
- Projection is used to retrieve specific columns from a relation.
- Union combines two relations into a new relation, including all the rows from both relations while eliminating duplicate rows.
- Set difference returns a relation that contains the rows from one relation that do not exist in the other relation.
- Cartesian product returns a relation that combines every row from one relation with every row from another relation.
- Rename is used to change the name of attributes in a relation.
- These fundamental operations in relational algebra form the basis for performing complex queries and data manipulations in relational databases.
- Relational algebra is a formal query language used to perform operations on relational databases. It consists of a set of operations that manipulate relations or tables in a database.
< b="" />Set Intersection< />
- Set intersection is not a fundamental operation in relational algebra. It involves finding the common elements between two sets or relations. However, it is not part of the basic operations defined in relational algebra.
< b="" />Natural Join< />
- Natural join is a fundamental operation in relational algebra. It combines two relations based on the equality of their attributes. It returns a new relation that contains all the attributes from both relations, eliminating duplicate attributes, and only including the rows where the values of the common attributes match.
< b="" />Assignment< />
- Assignment is not a fundamental operation in relational algebra. It is a process of assigning values to variables or attributes. In relational algebra, the focus is on manipulating relations rather than assigning values to variables.
< b="" />None of the Mentioned< />
- The correct answer is "None of the mentioned." Set intersection and assignment are not fundamental operations in relational algebra, while natural join is a fundamental operation. Therefore, none of the given options are fully correct.
- The fundamental operations in relational algebra include selection, projection, union, set difference, cartesian product, and rename. These operations allow for querying and manipulating data in a relational database.
- Selection is used to retrieve specific rows from a relation that satisfy a given condition.
- Projection is used to retrieve specific columns from a relation.
- Union combines two relations into a new relation, including all the rows from both relations while eliminating duplicate rows.
- Set difference returns a relation that contains the rows from one relation that do not exist in the other relation.
- Cartesian product returns a relation that combines every row from one relation with every row from another relation.
- Rename is used to change the name of attributes in a relation.
- These fundamental operations in relational algebra form the basis for performing complex queries and data manipulations in relational databases.
Consider Join of a relation R with a relation S. If R has m tuples and S has n tuples, then maximum and minimum sizes of the Join respectively are- a)m + n and 0
- b)mn and 0
- c)m + n and |m - n|
- d)mn and m + n
Correct answer is option 'B'. Can you explain this answer?
Consider Join of a relation R with a relation S. If R has m tuples and S has n tuples, then maximum and minimum sizes of the Join respectively are
a)
m + n and 0
b)
mn and 0
c)
m + n and |m - n|
d)
mn and m + n
|
|
Sudhir Patel answered |
Consider an example, suppose there is two tables Employee(Eid, Ename) consists of 5 tuples and department(Eid, Did) consists of 3 tuples only.
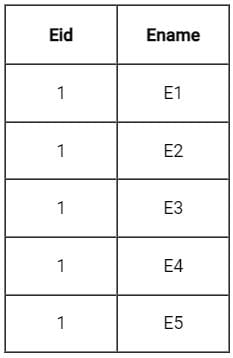
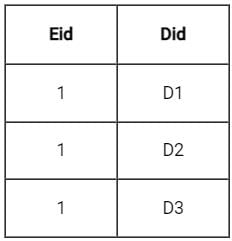
Natural join of employee and department(Employee * Department) gives:
m×n = 5 × 3 = 15
Therefore maximum size is m × n
m×n = 5 × 3 = 15
Therefore maximum size is m × n
Minimum size:
When Both the relations have a common attribute but no tuple in both relations match.
∴ minimum size = 0.
When Both the relations have a common attribute but no tuple in both relations match.
∴ minimum size = 0.
Joining a table with itself is called- a)Self Join
- b)Equi Join
- c)Outer Join
- d)Join
Correct answer is option 'A'. Can you explain this answer?
Joining a table with itself is called
a)
Self Join
b)
Equi Join
c)
Outer Join
d)
Join
|
|
Nilesh Chavan answered |
Understanding Self Join
A self join is a powerful concept in database management that allows a table to be joined with itself. This technique is particularly useful for querying hierarchical data or comparing rows within the same table.
Definition
- A self join involves creating two aliases for the same table, enabling the comparison of rows within that table as if they were from two distinct tables.
Purpose
- Self joins are used to retrieve records that have a relationship with other records in the same table.
- Common use cases include finding employees and their managers within an employee table, or comparing products with similar attributes.
How It Works
- In a self join, the table is referenced twice in the SQL query with different aliases, allowing for comparison of columns.
- The join condition specifies how the records from the two aliases relate to each other, typically using a primary key and a foreign key.
Example
- Consider an "Employees" table with columns: EmployeeID, Name, and ManagerID. A self join can be used to list employees along with their respective managers:
sql
SELECT e1.Name AS Employee, e2.Name AS Manager
FROM Employees e1
JOIN Employees e2 ON e1.ManagerID = e2.EmployeeID;
Conclusion
- Self joins are essential for analyzing and managing data within a single table, allowing for complex queries that reveal relationships and hierarchies.
- Understanding this concept is vital for effective database design and querying in relational databases.
A self join is a powerful concept in database management that allows a table to be joined with itself. This technique is particularly useful for querying hierarchical data or comparing rows within the same table.
Definition
- A self join involves creating two aliases for the same table, enabling the comparison of rows within that table as if they were from two distinct tables.
Purpose
- Self joins are used to retrieve records that have a relationship with other records in the same table.
- Common use cases include finding employees and their managers within an employee table, or comparing products with similar attributes.
How It Works
- In a self join, the table is referenced twice in the SQL query with different aliases, allowing for comparison of columns.
- The join condition specifies how the records from the two aliases relate to each other, typically using a primary key and a foreign key.
Example
- Consider an "Employees" table with columns: EmployeeID, Name, and ManagerID. A self join can be used to list employees along with their respective managers:
sql
SELECT e1.Name AS Employee, e2.Name AS Manager
FROM Employees e1
JOIN Employees e2 ON e1.ManagerID = e2.EmployeeID;
Conclusion
- Self joins are essential for analyzing and managing data within a single table, allowing for complex queries that reveal relationships and hierarchies.
- Understanding this concept is vital for effective database design and querying in relational databases.
Consider the relations r(A, B) and s(B, C), where s.B is a primary key and r.B is a foreign key referencing s.B. Consider the query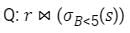
Let LOJ denote the natural left outer-join operation. Assume that r and s contain no null values.Which one of the following queries is NOT equivalent to Q?- a)
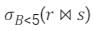
- b)
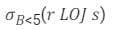
- c)

- d)
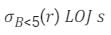
Correct answer is option 'C'. Can you explain this answer?
Consider the relations r(A, B) and s(B, C), where s.B is a primary key and r.B is a foreign key referencing s.B. Consider the query
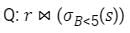
Let LOJ denote the natural left outer-join operation. Assume that r and s contain no null values.
Which one of the following queries is NOT equivalent to Q?
a)
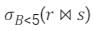
b)
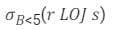
c)

d)
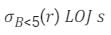
|
|
Sudhir Patel answered |
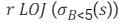 will include record with b> = 5 but other three queries will not.
will include record with b> = 5 but other three queries will not.What does the “x” operator do in relational algebra?- a)Output specified attributes from all rows of the input relation. Remove duplicate tuples from the output
- b)Output pairs of rows from the two input relations that have the same value on all attributes that have the same name
- c)Output all pairs of rows from the two input relations (regardless of whether or not they have the same values on common attributes)
- d)Returns the rows of the input relation that satisfy the predicate
Correct answer is option 'C'. Can you explain this answer?
What does the “x” operator do in relational algebra?
a)
Output specified attributes from all rows of the input relation. Remove duplicate tuples from the output
b)
Output pairs of rows from the two input relations that have the same value on all attributes that have the same name
c)
Output all pairs of rows from the two input relations (regardless of whether or not they have the same values on common attributes)
d)
Returns the rows of the input relation that satisfy the predicate
|
|
Arpita Gupta answered |
Acronym "COVID" stand for?
Consider the following tuple relational calculus:{t | Ǝ s ε instructor (t[name] = s[name] ᴧ Ǝ u ε department (u[dept_name] = s[dept_name] ᴧ u[building] = “Taylor”))}What does the given expression perform?- a)Finds the names of departments in the Taylor building.
- b)Finds the names of all instructors whose department is in the Taylor building.
- c)Finds the names of instructors who do not work in the Taylor building.
- d)Finds the names of all instructors whose department name is Taylor.
Correct answer is option 'B'. Can you explain this answer?
Consider the following tuple relational calculus:
{t | Ǝ s ε instructor (t[name] = s[name]
ᴧ Ǝ u ε department (u[dept_name] = s[dept_name]
ᴧ u[building] = “Taylor”))}
What does the given expression perform?
a)
Finds the names of departments in the Taylor building.
b)
Finds the names of all instructors whose department is in the Taylor building.
c)
Finds the names of instructors who do not work in the Taylor building.
d)
Finds the names of all instructors whose department name is Taylor.
|
|
Sudhir Patel answered |
There are two 'there exists' clauses in the given tuple relational calculus which are connected by and (ᴧ). The tuple variable u is restricted to departments that are located in the Taylor building, while tuple variable s is restricted to instructors whose dept_name matches that of tuple variable u.
Therefore, the given expression finds the names of all instructors whose department is in the Taylor building.
The ___________ operation, denoted by −, allows us to find tuples that are in one relation but are not in another.- a)Union
- b)Set-difference
- c)Difference
- d)Intersection
Correct answer is option 'B'. Can you explain this answer?
The ___________ operation, denoted by −, allows us to find tuples that are in one relation but are not in another.
a)
Union
b)
Set-difference
c)
Difference
d)
Intersection
|
|
Garima Bose answered |
The symbol "+", is a mathematical operation that combines two numbers to produce their sum.
Let R(a, b, c) and S(d, e, f) be two relations in which d is the foreign key of S that refers to the primary key of R. Consider the following four operations R and S
1. Insert into R
2. Insert into S
3. Delete from R
4. Delete from S
Which of the following is true about the referential integrity constraint above?- a)None of 1, 2, 3 or 4 can cause its violation
- b)All of 1, 2, 3 and 4 can cause its violation
- c)Both 1 and 4 can cause its violation
- d)Both 2 and 3 can cause its violation
Correct answer is option 'D'. Can you explain this answer?
Let R(a, b, c) and S(d, e, f) be two relations in which d is the foreign key of S that refers to the primary key of R. Consider the following four operations R and S
1. Insert into R
2. Insert into S
3. Delete from R
4. Delete from S
Which of the following is true about the referential integrity constraint above?
1. Insert into R
2. Insert into S
3. Delete from R
4. Delete from S
Which of the following is true about the referential integrity constraint above?
a)
None of 1, 2, 3 or 4 can cause its violation
b)
All of 1, 2, 3 and 4 can cause its violation
c)
Both 1 and 4 can cause its violation
d)
Both 2 and 3 can cause its violation
|
|
Keerthana Sarkar answered |
Referential integrity constraint: In relational model, two relation are related to each other over the basis of attributes, Every value of referencing attribute must be null or be available in the referenced attribute.
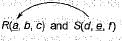
Here d is the foreign key of S that refers to the primary key of R.
1. Insert into R will not cause any violation.
2. Insert into S may cause violation because for each entry in ‘S ’ it must be. in ‘R ’ .
3. Delete from R may cause violation because for the deleted entry in R there may be referenced entry in the reIation S.
4. Delete from S will not cause any violation.
Hence (d) is the correct option.
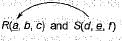
Here d is the foreign key of S that refers to the primary key of R.
1. Insert into R will not cause any violation.
2. Insert into S may cause violation because for each entry in ‘S ’ it must be. in ‘R ’ .
3. Delete from R may cause violation because for the deleted entry in R there may be referenced entry in the reIation S.
4. Delete from S will not cause any violation.
Hence (d) is the correct option.
Which among the following is/are false?I. Relational algebra is more powerful than relational calculus.
II. Relational calculus is more powerful than relational algebra.
III. Relational algebra is as same power as relational calculus.- a)Only II
- b)Only II and III
- c)Only I and II
- d)I, II and III
Correct answer is option 'D'. Can you explain this answer?
Which among the following is/are false?
I. Relational algebra is more powerful than relational calculus.
II. Relational calculus is more powerful than relational algebra.
III. Relational algebra is as same power as relational calculus.
II. Relational calculus is more powerful than relational algebra.
III. Relational algebra is as same power as relational calculus.
a)
Only II
b)
Only II and III
c)
Only I and II
d)
I, II and III
|
|
Sudhir Patel answered |
Every query that can be expressed using a safe relational calculus query can also be expressed as a relational algebra query.
Therefore, relation algebra has the same power as safe relational calculus
Option 4 is correct
Therefore, relation algebra has the same power as safe relational calculus
Option 4 is correct
Confusion Points:
Relational algebra is not having same power as relational calculus unless it is safe relational calculus
Relational algebra is not having same power as relational calculus unless it is safe relational calculus
The employee information in a company is stored in the relation. Assume name is the primary key:
Employee: (name, sex, salary, deptName)
Consider the SQL query;
SELECT deptName
FROM Employee
WHERE sex = M
GROUP By deptName
HAVING avg(salary) > (SELECT avg(salary)
FROM Employee)
It returns the names of the departments in which the average salary. - a)Is more than the average salary in the company.
- b)Of the male employees is more than the average salary of all the male employees in the company.
- c)Of the male employees is more than the average salary of the employees in the same department.
- d)Of the male employees is more than the average salary in the company.
Correct answer is option 'D'. Can you explain this answer?
The employee information in a company is stored in the relation. Assume name is the primary key:
Employee: (name, sex, salary, deptName)
Consider the SQL query;
SELECT deptName
FROM Employee
WHERE sex = M
GROUP By deptName
HAVING avg(salary) > (SELECT avg(salary)
FROM Employee)
It returns the names of the departments in which the average salary.
Employee: (name, sex, salary, deptName)
Consider the SQL query;
SELECT deptName
FROM Employee
WHERE sex = M
GROUP By deptName
HAVING avg(salary) > (SELECT avg(salary)
FROM Employee)
It returns the names of the departments in which the average salary.
a)
Is more than the average salary in the company.
b)
Of the male employees is more than the average salary of all the male employees in the company.
c)
Of the male employees is more than the average salary of the employees in the same department.
d)
Of the male employees is more than the average salary in the company.
|
|
Tarun Saini answered |
The given query first calculates the average salary from the relation Employee, then it selects the department name where employees who have average salary more than the average salary of the company.
State true or false: If a relation consists of a foreign key, then it is called a referenced relation of the foreign key dependency.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
State true or false: If a relation consists of a foreign key, then it is called a referenced relation of the foreign key dependency.
a)
True
b)
False
|
|
Sandeep Majumdar answered |
False
Explanation:
A foreign key is a field in a relation that refers to the primary key of another relation. It establishes a relationship between two relations based on the values of the foreign key and the primary key.
A referenced relation, on the other hand, is a relation that is being referenced by another relation through a foreign key. It is the relation that contains the primary key that is being referred to by the foreign key in another relation.
Foreign Key Dependency:
A foreign key dependency exists when a relation R1 refers to another relation R2 through a foreign key. In this case, R2 is the referenced relation and R1 is the referencing relation.
Example:
Let's consider the following example:
Table Name: Employees
| Employee_ID (Primary Key) | Employee_Name | Department_ID (Foreign Key) |
|---------------------------|---------------|-----------------------------|
| 1 | John | 101 |
| 2 | Jane | 102 |
| 3 | Mark | 101 |
Table Name: Departments
| Department_ID (Primary Key) | Department_Name |
|-----------------------------|-----------------|
| 101 | HR |
| 102 | IT |
In this example, the "Employees" table references the "Departments" table through the "Department_ID" foreign key. The "Departments" table is the referenced relation, and the "Employees" table is the referencing relation.
Conclusion:
In conclusion, a relation that consists of a foreign key is not called a referenced relation of the foreign key dependency. The referenced relation is the relation that is being referred to by the foreign key in another relation.
Explanation:
A foreign key is a field in a relation that refers to the primary key of another relation. It establishes a relationship between two relations based on the values of the foreign key and the primary key.
A referenced relation, on the other hand, is a relation that is being referenced by another relation through a foreign key. It is the relation that contains the primary key that is being referred to by the foreign key in another relation.
Foreign Key Dependency:
A foreign key dependency exists when a relation R1 refers to another relation R2 through a foreign key. In this case, R2 is the referenced relation and R1 is the referencing relation.
Example:
Let's consider the following example:
Table Name: Employees
| Employee_ID (Primary Key) | Employee_Name | Department_ID (Foreign Key) |
|---------------------------|---------------|-----------------------------|
| 1 | John | 101 |
| 2 | Jane | 102 |
| 3 | Mark | 101 |
Table Name: Departments
| Department_ID (Primary Key) | Department_Name |
|-----------------------------|-----------------|
| 101 | HR |
| 102 | IT |
In this example, the "Employees" table references the "Departments" table through the "Department_ID" foreign key. The "Departments" table is the referenced relation, and the "Employees" table is the referencing relation.
Conclusion:
In conclusion, a relation that consists of a foreign key is not called a referenced relation of the foreign key dependency. The referenced relation is the relation that is being referred to by the foreign key in another relation.
Let the following functional dependencies hold for relation R1(A, B, C) and R2(B, D, E)B → A, A → C, the relation R1 contains 35 tuples and relation R2 contains 34 tuples. What is maximum number of tuples possible in natural join R1 and R2?- a)35
- b)36
- c)34
- d)33
Correct answer is option 'C'. Can you explain this answer?
Let the following functional dependencies hold for relation R1(A, B, C) and R2(B, D, E)
B → A, A → C, the relation R1 contains 35 tuples and relation R2 contains 34 tuples. What is maximum number of tuples possible in natural join R1 and R2?
a)
35
b)
36
c)
34
d)
33
|
|
Sudhir Patel answered |
For given relation R1(A, B, C) and R2(B, D, E), functional dependencies are given only for relation R1, not for R2 And the candidate key for R1 is B, so all 35 value must be unique in R1. To get the maximum number of tuples in output, there can be two possibilities.
- All 34 values of B in R2 are the same and there is an entry in R1 that matches with this value. In this case, we get 34 tuples in output.
Example:
Consider an example, suppose there is two tables R1(A, B, C) consists of 5 tuples and R2( B, D, E) consists of 4 tuples only.
Natural join of R1 and R2 (R1 * R2) gives: 4
Branch-scheme = (Branch - name, assets, branch- city)
Customer-scheme = (Customer-name, street, customer- city)
Deposit-scheme = (Branch-name, account-number, customer-name, balance)
Borrow-scheme = (Branch-name, loan-number, customer-name, amount)
Client-scheme = (Customer-name, banker-name)
Which of the following queries finds the clients of banker Agassi and the city they live in?


- a)1 and 3
- b)2 and 3
- c)1 and 4
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Branch-scheme = (Branch - name, assets, branch- city)
Customer-scheme = (Customer-name, street, customer- city)
Deposit-scheme = (Branch-name, account-number, customer-name, balance)
Borrow-scheme = (Branch-name, loan-number, customer-name, amount)
Client-scheme = (Customer-name, banker-name)
Which of the following queries finds the clients of banker Agassi and the city they live in?


Customer-scheme = (Customer-name, street, customer- city)
Deposit-scheme = (Branch-name, account-number, customer-name, balance)
Borrow-scheme = (Branch-name, loan-number, customer-name, amount)
Client-scheme = (Customer-name, banker-name)
Which of the following queries finds the clients of banker Agassi and the city they live in?


a)
1 and 3
b)
2 and 3
c)
1 and 4
d)
None of these
|
|
Anand Chatterjee answered |
Clients of Bankers Agassi can be obtained by using the relation client_scheme while the corresponding customer_city can be obtained -using customer_scheme.
Hence cross product of client and customer must be taken. This can be achieved in two ways.
(i) First taking the Bankers Agassi clients and then checking their name in customer relation and projecting their customer city.
(ii) First taking all the customers and matching them in customer_scheme, then finding out the customers who have the Agassi as the Banker, finally projecting the customer_city of the respective customers.
Hence cross product of client and customer must be taken. This can be achieved in two ways.
(i) First taking the Bankers Agassi clients and then checking their name in customer relation and projecting their customer city.
(ii) First taking all the customers and matching them in customer_scheme, then finding out the customers who have the Agassi as the Banker, finally projecting the customer_city of the respective customers.
A row in a relational database table is also called.- a)Attribute
- b)Instance
- c)Tuple
- d)Field
Correct answer is option 'C'. Can you explain this answer?
A row in a relational database table is also called.
a)
Attribute
b)
Instance
c)
Tuple
d)
Field
|
|
Sudhir Patel answered |
Tuple − A single row of a table, which contains a single record for that relation is called a tuple.
To maintain materialized view in RDBMS, we use -- a)Trigger
- b)Pointer
- c)Clone object
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
To maintain materialized view in RDBMS, we use -
a)
Trigger
b)
Pointer
c)
Clone object
d)
None of the above

|
Machine Experts answered |
Concept:
To maintain materialized view in RDBMS, we use Trigger.
To maintain materialized view in RDBMS, we use Trigger.
Triggers:
Triggers are SQL statements that are run automatically whenever there is a change in the database. Triggers are run in reaction to certain table events (INSERT, UPDATE, or DELETE). These triggers serve to maintain the data's integrity by updating the database's data in a regular manner.
Triggers are SQL statements that are run automatically whenever there is a change in the database. Triggers are run in reaction to certain table events (INSERT, UPDATE, or DELETE). These triggers serve to maintain the data's integrity by updating the database's data in a regular manner.
Syntax:
create trigger Trigger_name
(before | after)
[insert | update | delete]
on [table_name]
[for each row]
[trigger_body]
Pointer and Clone objects are not related to RDBMS and those useful for programming language.
create trigger Trigger_name
(before | after)
[insert | update | delete]
on [table_name]
[for each row]
[trigger_body]
Pointer and Clone objects are not related to RDBMS and those useful for programming language.
Hence the correct answer is Trigger.
Branch-scheme = (Branch - name, assets, branch- city)
Customer-scheme = (Customer-name, street, customer- city)
Deposit-scheme = (Branch-name, account-number, customer-name, balance)
Borrow-scheme = (Branch-name, loan-number, customer-name, amount)
Client-scheme = (Customer-name, banker-name)
Which of the following Domain relational calculus finds all customers who have a loan amount of over 1200?- a)
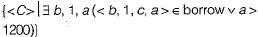
- b)
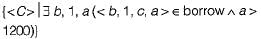
- c)
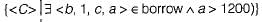
- d)
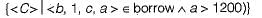
Correct answer is option 'B'. Can you explain this answer?
Branch-scheme = (Branch - name, assets, branch- city)
Customer-scheme = (Customer-name, street, customer- city)
Deposit-scheme = (Branch-name, account-number, customer-name, balance)
Borrow-scheme = (Branch-name, loan-number, customer-name, amount)
Client-scheme = (Customer-name, banker-name)
Which of the following Domain relational calculus finds all customers who have a loan amount of over 1200?
Customer-scheme = (Customer-name, street, customer- city)
Deposit-scheme = (Branch-name, account-number, customer-name, balance)
Borrow-scheme = (Branch-name, loan-number, customer-name, amount)
Client-scheme = (Customer-name, banker-name)
Which of the following Domain relational calculus finds all customers who have a loan amount of over 1200?
a)
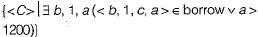
b)
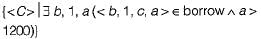
c)
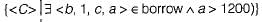
d)
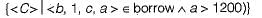
|
|
Sankar Sarkar answered |
All customers who have a lone amount of over 1200


Join Selectivity of a relation R in a natural join with a relation S is the _____- a)Ratio of the distinct attribute values for attribute A participating in the join to the total number of distinct attributes for the same attribute in R.
- b)Ratio of the non-distinct attribute values for attribute A participating in the join to the total number of distinct values for the same attribute in R.
- c)Ratio of the distinct attribute values for attribute A participating in the join to the total number of non-distinct values for the same attribute in R.
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Join Selectivity of a relation R in a natural join with a relation S is the _____
a)
Ratio of the distinct attribute values for attribute A participating in the join to the total number of distinct attributes for the same attribute in R.
b)
Ratio of the non-distinct attribute values for attribute A participating in the join to the total number of distinct values for the same attribute in R.
c)
Ratio of the distinct attribute values for attribute A participating in the join to the total number of non-distinct values for the same attribute in R.
d)
None of the above
|
|
Shubham Sharma answered |
Explanation:
When performing a natural join between two relations, the selectivity of the join refers to the ratio of the distinct attribute values for a particular attribute in the join to the total number of distinct attribute values for the same attribute in one of the relations.
Let's break down the options:
a) Ratio of the distinct attribute values for attribute A participating in the join to the total number of distinct attributes for the same attribute in R.
This option is correct. It correctly describes the selectivity of the relation R in a natural join with relation S.
b) Ratio of the non-distinct attribute values for attribute A participating in the join to the total number of distinct values for the same attribute in R.
This option is not correct. It refers to non-distinct attribute values, which is not what selectivity is measuring.
c) Ratio of the distinct attribute values for attribute A participating in the join to the total number of non-distinct values for the same attribute in R.
This option is not correct. It refers to the total number of non-distinct values, which is not what selectivity is measuring.
d) None of the above.
This option is not correct. Option a is the correct answer.
In summary:
The selectivity of a relation R in a natural join with a relation S is the ratio of the distinct attribute values for attribute A participating in the join to the total number of distinct attributes for the same attribute in R.
When performing a natural join between two relations, the selectivity of the join refers to the ratio of the distinct attribute values for a particular attribute in the join to the total number of distinct attribute values for the same attribute in one of the relations.
Let's break down the options:
a) Ratio of the distinct attribute values for attribute A participating in the join to the total number of distinct attributes for the same attribute in R.
This option is correct. It correctly describes the selectivity of the relation R in a natural join with relation S.
b) Ratio of the non-distinct attribute values for attribute A participating in the join to the total number of distinct values for the same attribute in R.
This option is not correct. It refers to non-distinct attribute values, which is not what selectivity is measuring.
c) Ratio of the distinct attribute values for attribute A participating in the join to the total number of non-distinct values for the same attribute in R.
This option is not correct. It refers to the total number of non-distinct values, which is not what selectivity is measuring.
d) None of the above.
This option is not correct. Option a is the correct answer.
In summary:
The selectivity of a relation R in a natural join with a relation S is the ratio of the distinct attribute values for attribute A participating in the join to the total number of distinct attributes for the same attribute in R.
Consider a database that has the relation schema Random(A, B, C). An instance of the schema Random is as given below.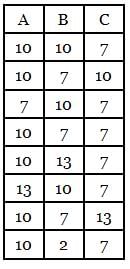 Tuple calculus expression for the above instance is given as {t.B | t ϵ r ∧ (t[A] = 10 ∧ t[C] = 7)}What is the sum of the elements in the output row of the given expression?
Tuple calculus expression for the above instance is given as {t.B | t ϵ r ∧ (t[A] = 10 ∧ t[C] = 7)}What is the sum of the elements in the output row of the given expression?
Correct answer is '32'. Can you explain this answer?
Consider a database that has the relation schema Random(A, B, C). An instance of the schema Random is as given below.

Tuple calculus expression for the above instance is given as {t.B | t ϵ r ∧ (t[A] = 10 ∧ t[C] = 7)}
What is the sum of the elements in the output row of the given expression?

|
Gate Gurus answered |
To solve the given problem, we need to understand the Tuple Relational Calculus (TRC) expression and apply it to the given relation schema. Let's go step-by-step.
- Understanding the TRC Expression:
- The TRC expression given is: {��.��∣��∈��∧(��[��]=10∧��[��]=7)}{t.B∣t∈r∧(t[A]=10∧t[C]=7)}
- This expression means we need to find all tuples ��t in relation ��r where:
- The value of attribute ��A is 10.
- The value of attribute ��C is 7.
- From those tuples, we need to select the value of attribute ��B.
- Analyzing the Relation Schema:
- The relation schema is Random(A, B, C).
- The given instance of the schema Random is:
- A B C
10 10 7
10 7 10
7 10 7
10 7 7
10 13 7
13 10 7
10 7 13
10 2 7
- Applying the TRC Expression to the Relation:
- We need to find all rows where ��=10A=10 and ��=7C=7.
- Let's filter those rows
A B C
10 10 7
10 7 7
10 13 7
10 2 7
10 10 7
10 7 7
10 13 7
10 2 7
Selecting the Attribute ��B:
- From the filtered rows, we extract the values of attribute ��
B
10
7
13
2
10
7
13
2
- Summing the Elements:
- We need to find the sum of these values: 10+7+13+2=3210+7+13+2=32
Therefore, the sum of the elements in the output row of the given expression is 32.
Find the customers having account all branches located in Hyderabad. Use the above relations and find which of the following query is not giving the same.- a){t | ∀ S ϵ Branch (s[city] = “Hyd” ⇒ 4ϵ deposit(4[Bname] = S [Bname] ^ t[cname] = 4 [cname]))}
- b){| ∀m,t,e (7C<(n,t,c) ϵ Branch ∀ t = ‘Hyd’)V → a,b,n ( ϵ Deposit)}
- c)
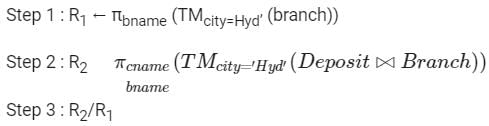
- d)all the above are giving the same result
Correct answer is option 'D'. Can you explain this answer?
Find the customers having account all branches located in Hyderabad. Use the above relations and find which of the following query is not giving the same.
a)
{t | ∀ S ϵ Branch (s[city] = “Hyd” ⇒ 4ϵ deposit
(4[Bname] = S [Bname] ^ t[cname] = 4 [cname]))}
b)
{| ∀m,t,e (7C<(n,t,c) ϵ Branch ∀ t = ‘Hyd’)
V → a,b,n ( ϵ Deposit)}
c)
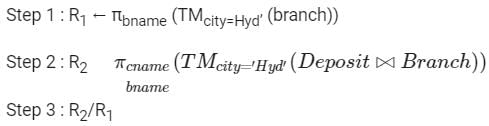
d)
all the above are giving the same result
|
|
Sudhir Patel answered |
Query 1:
It is a Tuple relational calculus query first comparing all tuples with the city is equal to Hyd in deposit table and fetch the customer name when city="Hyd".
It is a Tuple relational calculus query first comparing all tuples with the city is equal to Hyd in deposit table and fetch the customer name when city="Hyd".
Query 2:
It is a Domain relational calculus query first comparing city domain with city equal to Hyd in deposit table and fetch the customer name when city="Hyd".
It is a Domain relational calculus query first comparing city domain with city equal to Hyd in deposit table and fetch the customer name when city="Hyd".
Query 3:
It is a relational algebra query, In the first step fetch all names whose city hyd in the branch table. And the second step joining the deposit and branch and comparing the city equal to 'Hyd' with fetching city_name and branch_name. Finally, division step 2 with step1 will results in customers having account all branches located in Hyderabad.
It is a relational algebra query, In the first step fetch all names whose city hyd in the branch table. And the second step joining the deposit and branch and comparing the city equal to 'Hyd' with fetching city_name and branch_name. Finally, division step 2 with step1 will results in customers having account all branches located in Hyderabad.
Hence the correct answer is all the above are giving the same result.
Consider two database relations R and S having 3 tuples in R and 2 tuples in S. what is the maximum number of tuples that could appear in the natural join of R and S?- a)2
- b)5
- c)3
- d)6
Correct answer is option 'D'. Can you explain this answer?
Consider two database relations R and S having 3 tuples in R and 2 tuples in S. what is the maximum number of tuples that could appear in the natural join of R and S?
a)
2
b)
5
c)
3
d)
6
|
|
Sudhir Patel answered |
Given: two relations R and S having tuples 3 and 2 respectively.
So, their natural join will contain maximum of 3 * 2= 6 tuples.
So, their natural join will contain maximum of 3 * 2= 6 tuples.
Example:
Consider table R (a, b) as ;
Consider table R (a, b) as ;

Relation S(a, c) as :
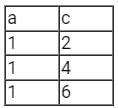

Here, the natural join of R and S will be :

So, it contains total of 6 tuples.
Which of the following uses domain variable that take on values from an attributes domain, rather that values for an entire tuple.?- a)Tuple relational calculus
- b)Relational Algebra
- c)Domain relational calculus
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Which of the following uses domain variable that take on values from an attributes domain, rather that values for an entire tuple.?
a)
Tuple relational calculus
b)
Relational Algebra
c)
Domain relational calculus
d)
None of the above

|
Crack Gate answered |
The question asks for the type of relational calculus that uses domain variables that take on values from an attribute's domain, rather than values for an entire tuple.
From the explanations:
From the explanations:
Tuple Relational Calculus (TRC) uses tuple variables, not domain variables.
Relational Algebra operates on entire relations and does not use domain variables.
Domain Relational Calculus (DRC) specifically uses domain variables that take on values from an attribute’s domain.
Thus, the correct answer is:
Relational Algebra operates on entire relations and does not use domain variables.
Domain Relational Calculus (DRC) specifically uses domain variables that take on values from an attribute’s domain.
Thus, the correct answer is:
C: Domain relational calculus
In a relational database model, cardinality of a relation means - a)The number of tuples
- b)The number of tables
- c)The number of attributes
- d)The number of constraints
Correct answer is option 'A'. Can you explain this answer?
In a relational database model, cardinality of a relation means
a)
The number of tuples
b)
The number of tables
c)
The number of attributes
d)
The number of constraints

|
Gate Gurus answered |
The number of tuples in a relation is known as cardinality
Example:
The number of tuples in the above relation is 4
The cardinality of Employee relation is 4.
Example:

The number of tuples in the above relation is 4
The cardinality of Employee relation is 4.
Let r and s be two relations over the relation schemes R and S respectively, and let A be an attribute in R. Then the relational algebra expression 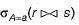 is always equal to
is always equal to - a)σA = a (r)
- b)r
- c)
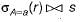
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Let r and s be two relations over the relation schemes R and S respectively, and let A be an attribute in R. Then the relational algebra expression 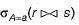 is always equal to
is always equal to
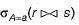 is always equal to
is always equal to a)
σA = a (r)
b)
r
c)
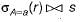
d)
None of these
|
|
Athul Pillai answered |
The relational algebra expression:

Hence (c) is the required option.

Hence (c) is the required option.
Which of the following query transformation (i.e. replacing the LHS expression by the RHS expression) is incorrect? R1 and R2, are relations, C1 C2 are selection conditions and A1 A2 are attributes of R1.- a)
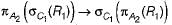
- b)
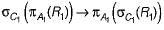
- c)

- d)

Correct answer is option 'D'. Can you explain this answer?
Which of the following query transformation (i.e. replacing the LHS expression by the RHS expression) is incorrect? R1 and R2, are relations, C1 C2 are selection conditions and A1 A2 are attributes of R1.
a)
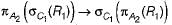
b)
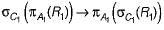
c)

d)

|
|
Akshay Singh answered |
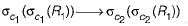
The conditions c1 and c2 may not be same.
Consider the following relational schema pertaining to a students database.
Student: (rollno. name, address)
Enroll: (rollno. courseno. coursename) Where the primary keys are shown underlined. The number of tuples in the Student and the Enroll tables are 120 and 8 respectively. What are the maximum and the minimum number of tuples that can be present in (Student * Enroll), where * denotes natural join?- a)8, 8
- b)120,8
- c)960,120
- d)960,8
Correct answer is option 'A'. Can you explain this answer?
Consider the following relational schema pertaining to a students database.
Student: (rollno. name, address)
Enroll: (rollno. courseno. coursename) Where the primary keys are shown underlined. The number of tuples in the Student and the Enroll tables are 120 and 8 respectively. What are the maximum and the minimum number of tuples that can be present in (Student * Enroll), where * denotes natural join?
Student: (rollno. name, address)
Enroll: (rollno. courseno. coursename) Where the primary keys are shown underlined. The number of tuples in the Student and the Enroll tables are 120 and 8 respectively. What are the maximum and the minimum number of tuples that can be present in (Student * Enroll), where * denotes natural join?
a)
8, 8
b)
120,8
c)
960,120
d)
960,8

|
Gate Gurus answered |
Determining the Maximum and Minimum Number of Tuples in the Natural Join of Student and Enroll Tables
Step 1: Understanding the Given Tables
Student Table: Contains 120 tuples with attributes rollno, name, and address. The primary key is rollno.
Enroll Table: Contains 8 tuples with attributes rollno, courseno, and coursename. The primary key is a combination of rollno and courseno.
Step 1: Understanding the Given Tables
Student Table: Contains 120 tuples with attributes rollno, name, and address. The primary key is rollno.
Enroll Table: Contains 8 tuples with attributes rollno, courseno, and coursename. The primary key is a combination of rollno and courseno.
Step 2: Concept of Natural Join
A natural join between Student and Enroll will match tuples based on the common attribute rollno. This means:
A natural join between Student and Enroll will match tuples based on the common attribute rollno. This means:
Only those tuples from Student that have a matching rollno in Enroll will appear in the result.
The number of tuples in the resulting table depends on how rollno values are distributed between both tables.
The number of tuples in the resulting table depends on how rollno values are distributed between both tables.
Step 3: Finding the Maximum Number of Tuples
The maximum number of tuples occurs when each tuple in the Enroll table has a matching rollno in the Student table.
Since Enroll has only 8 tuples, the maximum number of tuples in the join is 8.
The maximum number of tuples occurs when each tuple in the Enroll table has a matching rollno in the Student table.
Since Enroll has only 8 tuples, the maximum number of tuples in the join is 8.
Step 4: Finding the Minimum Number of Tuples
The minimum number of tuples occurs when all rollno values in Enroll match the same single rollno in Student.
Even in this case, all 8 tuples from Enroll will be present in the join result (since each enroll record must have a matching student).
Therefore, the minimum number of tuples is also 8.
The minimum number of tuples occurs when all rollno values in Enroll match the same single rollno in Student.
Even in this case, all 8 tuples from Enroll will be present in the join result (since each enroll record must have a matching student).
Therefore, the minimum number of tuples is also 8.
Final Answer:
Maximum number of tuples = 8
Minimum number of tuples = 8
Thus, the correct answer is:
8, 8.
Maximum number of tuples = 8
Minimum number of tuples = 8
Thus, the correct answer is:
8, 8.
Chapter doubts & questions for Relational Algebra - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Relational Algebra - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
459 videos|1398 docs|786 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









