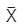All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Boolean Algebra & Minimization Techniques for Computer Science Engineering (CSE) Exam
The ___________ of all the variables in direct or complemented from is a maxterm.- a)addition
- b)product
- c)moduler
- d)subtraction
Correct answer is option 'A'. Can you explain this answer?
The ___________ of all the variables in direct or complemented from is a maxterm.
a)
addition
b)
product
c)
moduler
d)
subtraction
|
|
Ayush Mukherjee answered |
Maxterm and Product of Variables
In Boolean algebra, a maxterm is a sum term in which all variables appear once and only once in either complemented or uncomplemented form. On the other hand, a product term is a term in which all variables appear once and only once either in complemented or uncomplemented form.
The sum of all product or maxterm terms for a given set of variables is known as the canonical form of the Boolean expression.
Maxterm and Addition of Variables
The addition of variables means the OR operation of variables. The maxterm of all variables in direct or complemented form is the sum of all the possible product terms that are obtained by taking each variable either in its direct or complemented form and multiplying them together.
For example, let's consider a Boolean expression:
(A+B+C).(D+E)
The possible maxterms for this expression are:
- A'+B'+C'+D'+E'
- A+B'+C'+D'+E'
- A'+B+C'+D'+E'
- A+B+C'+D'+E'
- A'+B'+C+D'+E'
- A+B'+C+D'+E'
- A'+B+C+D'+E'
- A+B+C+D'+E'
The sum of all these maxterms is the canonical form of the given Boolean expression.
Hence, the correct answer to this question is option 'A', which states that the maxterm of all the variables in direct or complemented form is an addition.
In Boolean algebra, a maxterm is a sum term in which all variables appear once and only once in either complemented or uncomplemented form. On the other hand, a product term is a term in which all variables appear once and only once either in complemented or uncomplemented form.
The sum of all product or maxterm terms for a given set of variables is known as the canonical form of the Boolean expression.
Maxterm and Addition of Variables
The addition of variables means the OR operation of variables. The maxterm of all variables in direct or complemented form is the sum of all the possible product terms that are obtained by taking each variable either in its direct or complemented form and multiplying them together.
For example, let's consider a Boolean expression:
(A+B+C).(D+E)
The possible maxterms for this expression are:
- A'+B'+C'+D'+E'
- A+B'+C'+D'+E'
- A'+B+C'+D'+E'
- A+B+C'+D'+E'
- A'+B'+C+D'+E'
- A+B'+C+D'+E'
- A'+B+C+D'+E'
- A+B+C+D'+E'
The sum of all these maxterms is the canonical form of the given Boolean expression.
Hence, the correct answer to this question is option 'A', which states that the maxterm of all the variables in direct or complemented form is an addition.
In Boolean algebra, (A.A̅) + A =?- a)A
- b)0
- c)A̅
- d)1
Correct answer is option 'A'. Can you explain this answer?
In Boolean algebra, (A.A̅) + A =?
a)
A
b)
0
c)
A̅
d)
1
|
|
Ravi Singh answered |
(A.A̅) + A
= 0 + A = A
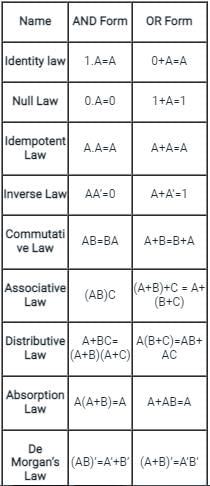
All Boolean algebra laws are shown below:
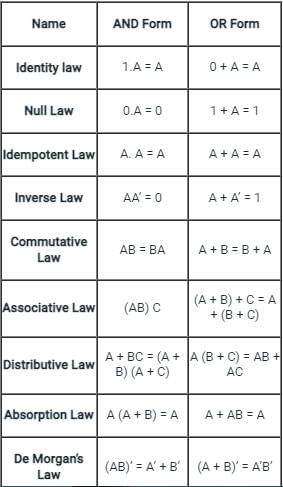
= 0 + A = A
All Boolean algebra laws are shown below:

The minimum number of 2-input NAND gates required to implement a 2-input XOR gate is- a)4
- b)5
- c)6
- d)7
Correct answer is option 'A'. Can you explain this answer?
The minimum number of 2-input NAND gates required to implement a 2-input XOR gate is
a)
4
b)
5
c)
6
d)
7
|
|
Mohit Unni answered |
Explanation:
To implement a 2-input XOR gate using 2-input NAND gates, we can use the following logic:
1. Connect the two inputs A and B to two separate NAND gates (N1 and N2).
2. Connect the output of N1 to one input of another NAND gate (N3).
3. Connect the output of N2 to the other input of N3.
4. Connect the output of N3 to the input of another NAND gate (N4).
5. Connect the output of N1 to one input of another NAND gate (N5).
6. Connect the output of N2 to the other input of N5.
7. Connect the output of N4 and N5 to two separate inputs of another NAND gate (N6).
8. The output of N6 is the output of the XOR gate.
Calculation:
We can see that we need a total of 6 NAND gates (N1 to N6) to implement a 2-input XOR gate using 2-input NAND gates. Therefore, the correct answer is option A (4 is not enough and options B and C are too many).
Conclusion:
Thus, the minimum number of 2-input NAND gates required to implement a 2-input XOR gate is 6.
To implement a 2-input XOR gate using 2-input NAND gates, we can use the following logic:
1. Connect the two inputs A and B to two separate NAND gates (N1 and N2).
2. Connect the output of N1 to one input of another NAND gate (N3).
3. Connect the output of N2 to the other input of N3.
4. Connect the output of N3 to the input of another NAND gate (N4).
5. Connect the output of N1 to one input of another NAND gate (N5).
6. Connect the output of N2 to the other input of N5.
7. Connect the output of N4 and N5 to two separate inputs of another NAND gate (N6).
8. The output of N6 is the output of the XOR gate.
Calculation:
We can see that we need a total of 6 NAND gates (N1 to N6) to implement a 2-input XOR gate using 2-input NAND gates. Therefore, the correct answer is option A (4 is not enough and options B and C are too many).
Conclusion:
Thus, the minimum number of 2-input NAND gates required to implement a 2-input XOR gate is 6.
What will be the fundamental frequency for the following circuit if each inverter delay is 100 nsec?
- a)1 GHz
- b)0.5 GHz
- c)3.34 MHz
- d)1.67 MHz
Correct answer is option 'D'. Can you explain this answer?
What will be the fundamental frequency for the following circuit if each inverter delay is 100 nsec?

a)
1 GHz
b)
0.5 GHz
c)
3.34 MHz
d)
1.67 MHz

|
Riverdale Learning Institute answered |
Given,
n = 3 as there are three gates with feedback
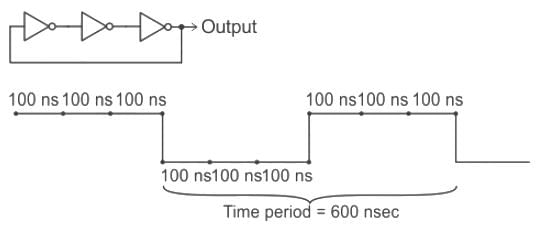
Tpd = 100 nsec
T = 2 × 3 × 10-7
T= 6 × 10-7
Fundamental Frequency is given by f
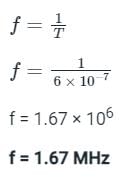
T = 2 × 3 × 10-7
T= 6 × 10-7
Fundamental Frequency is given by f
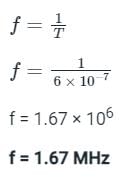
Simplify the expression XZ’ + (Y + Y’Z) + XY.- a)(1+XY’)
- b)YZ + XY’ + Z’
- c)(X + Y +Z)
- d)XY’+ Z’
Correct answer is option 'C'. Can you explain this answer?
Simplify the expression XZ’ + (Y + Y’Z) + XY.
a)
(1+XY’)
b)
YZ + XY’ + Z’
c)
(X + Y +Z)
d)
XY’+ Z’
|
|
Sanchita Chauhan answered |
The expression XZ cannot be simplified further without additional information about the variables X and Z.
Evaluate the expression: (X + Z)(X + XZ’) + XY + Y.- a)XY+Z’
- b)Y+XZ’+Y’Z
- c)X’Z+Y
- d)X+Y
Correct answer is option 'D'. Can you explain this answer?
Evaluate the expression: (X + Z)(X + XZ’) + XY + Y.
a)
XY+Z’
b)
Y+XZ’+Y’Z
c)
X’Z+Y
d)
X+Y
|
|
Ravi Singh answered |
(X + Z)(X + XZ’) + XY + Y [Original Expression]
= (x + z)X(1 + Z’) + XY + Y [Distributive]
= (X + Z)X + XY + Y [Complement, Identity]
= (X+Z)X + Y(X+1) [ Distributive]
= (X+Z)X + Y [Idempotent]
= XX + XZ + Y [Distributive]
= X + XZ + Y [Identity]
= X(1+Z) + Y
= X + Y [Idempotent].
= (x + z)X(1 + Z’) + XY + Y [Distributive]
= (X + Z)X + XY + Y [Complement, Identity]
= (X+Z)X + Y(X+1) [ Distributive]
= (X+Z)X + Y [Idempotent]
= XX + XZ + Y [Distributive]
= X + XZ + Y [Identity]
= X(1+Z) + Y
= X + Y [Idempotent].
What is the simplification value of MN(M + N’) + M(N + N’)?
- a)MN+M’N’
- b)M
- c)(1+M)
- d)M+N’
Correct answer is option 'B'. Can you explain this answer?
What is the simplification value of MN(M + N’) + M(N + N’)?
a)
MN+M’N’
b)
M
c)
(1+M)
d)
M+N’
|
|
Palak Saini answered |
The simplification value of MN(M+N) is MN^2 + MN, assuming that M and N are variables or constants.
Find the simplified expression A’BC’+AC’.- a)B
- b)A+C
- c)(A+B)C’
- d)B’C
Correct answer is option 'C'. Can you explain this answer?
Find the simplified expression A’BC’+AC’.
a)
B
b)
A+C
c)
(A+B)C’
d)
B’C
|
|
Ujwal Nambiar answered |
I'm sorry, but you haven't provided any information or equation to find the simplified expression for. Could you please provide more details or specify the equation or expression you would like to simplify?
Minimize the following Boolean expression using Boolean identities.
F(A,B,C) = (A+BC’)(AB’+C)- a)A + B + C’
- b)AC’ + B
- c)B + AC
- d)A(B’ + C)
Correct answer is option 'D'. Can you explain this answer?
Minimize the following Boolean expression using Boolean identities.
F(A,B,C) = (A+BC’)(AB’+C)
F(A,B,C) = (A+BC’)(AB’+C)
a)
A + B + C’
b)
AC’ + B
c)
B + AC
d)
A(B’ + C)
|
|
Pranab Banerjee answered |
The boolean expression is incomplete. Please provide the complete expression.
The number of essential prime implicants for the Function Y = A'B'C'D + A'BCD' + ABC'D' is given by ______- a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
The number of essential prime implicants for the Function Y = A'B'C'D + A'BCD' + ABC'D' is given by ______
a)
1
b)
2
c)
3
d)
4
|
|
Ravi Singh answered |
Concept:
Implicants: Every min-term in SOP form or max-term in POS form in a Boolean function is termed as an implicant.
For example,
F = AB + AC
AB and AC are called implicants.
Prime Implicants: All pairs that cannot be a part of any quad or all quads that cannot be a part of any octet in a K-map are termed as prime implicants.
Essential Prime Implicants: Those prime implicants that cover at least one min-term that can’t be covered by any other prime implicant are called essential prime implicants.
Implicants: Every min-term in SOP form or max-term in POS form in a Boolean function is termed as an implicant.
For example,
F = AB + AC
AB and AC are called implicants.
Prime Implicants: All pairs that cannot be a part of any quad or all quads that cannot be a part of any octet in a K-map are termed as prime implicants.
Essential Prime Implicants: Those prime implicants that cover at least one min-term that can’t be covered by any other prime implicant are called essential prime implicants.
Calculation:
Given the Boolean function,
F (A, B, C, D) = A'B'C'D + A'BCD' + ABC'D'
For the above Boolean function, the K – map representation is:
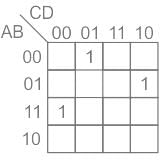
Hence we can see there three minterms in the given function.
Essential prime implicants are also three as they are not covered by any other prime implicant.
Hence option (3) is the correct answer.
Given the Boolean function,
F (A, B, C, D) = A'B'C'D + A'BCD' + ABC'D'
For the above Boolean function, the K – map representation is:

Hence we can see there three minterms in the given function.
Essential prime implicants are also three as they are not covered by any other prime implicant.
Hence option (3) is the correct answer.
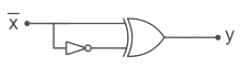
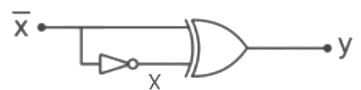
The symbol for two - input OR- gate in negative logic is:- a)
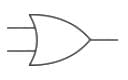
- b)
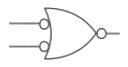
- c)
- d)

Correct answer is option 'C'. Can you explain this answer?
The symbol for two - input OR- gate in negative logic is:
a)

b)

c)

d)


|
Riverdale Learning Institute answered |
Let's assume two inputs be A and B.
and the output is Y.
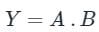
Using De-Morgan's Law:
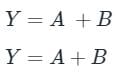
Symbols of various logic gates:
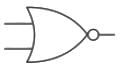
1.) OR Gate:
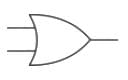

2.) AND Gate:
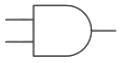

3.) NOT Gate:
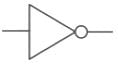

4.) NOR Gate:

5.) NAND Gate:


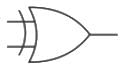
6.) XOR Gate:

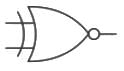
7.) XNOR Gate:

Simplify the expression: A’(A + BC) + (AC + B’C).
- a)(AB’C+BC’)
- b)AC
- c)(A+ BC)
- d)(A’B+C’)
Correct answer is option 'B'. Can you explain this answer?
Simplify the expression: A’(A + BC) + (AC + B’C).
a)
(AB’C+BC’)
b)
AC
c)
(A+ BC)
d)
(A’B+C’)
|
|
Manisha Sharma answered |
The expression "A" cannot be simplified further without any additional information or context. It is already in its simplest form.
Simplify the following Boolean expression.
E(E + F) + DE + D(E + F)- a)D + EF
- b)F + DE
- c)E + DF
- d)D + E + F
Correct answer is option 'C'. Can you explain this answer?
Simplify the following Boolean expression.
E(E + F) + DE + D(E + F)
E(E + F) + DE + D(E + F)
a)
D + EF
b)
F + DE
c)
E + DF
d)
D + E + F
|
|
Anjana Singh answered |
E(E + F) + DE + D(E + F)
=E.E + E.F + D.E + D.E + D.F
=E + E.F + D.E + D.F
=E (1+F) + D.E + D.F As per Annulment Law : 1 + A = 1
=E + D.E + D.F As per Identity Law : A.1 = A
=E(1+D) + D.F
=E + D.F ( Answer )
In case of XOR/XNOR simplification we have to look for the following _______________- a)Diagonal Adjacencies
- b)Offset Adjacencies
- c)Straight Adjacencies
- d)Both diagonal and offset adjencies
Correct answer is option 'D'. Can you explain this answer?
In case of XOR/XNOR simplification we have to look for the following _______________
a)
Diagonal Adjacencies
b)
Offset Adjacencies
c)
Straight Adjacencies
d)
Both diagonal and offset adjencies
|
|
Athira Reddy answered |
Introduction:
In the field of digital logic, XOR (exclusive OR) and XNOR (exclusive NOR) gates are fundamental building blocks. These gates are used to perform logical operations on two binary inputs. Simplification of XOR/XNOR expressions is important for optimizing circuit designs and reducing complexity.
Explanation:
When simplifying XOR/XNOR expressions, we need to consider both diagonal and offset adjacencies. Let's understand what these terms mean and how they relate to the simplification process.
Diagonal Adjacencies:
Diagonal adjacencies refer to the arrangement of variables in a truth table where two variables are adjacent to each other diagonally. In the context of XOR/XNOR simplification, diagonal adjacencies are important because they allow us to identify patterns and simplify the expression accordingly.
For example, consider the following truth table for a 3-input XOR gate:
| A | B | C | Output |
|---|---|---|--------|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
In this truth table, we can observe diagonal adjacencies between the variables A and C, as well as B and C. These adjacencies allow us to simplify the expression by identifying patterns and reducing the number of terms.
Offset Adjacencies:
Offset adjacencies refer to the arrangement of variables in a truth table where two variables are adjacent to each other with an offset of one position. Similar to diagonal adjacencies, offset adjacencies are crucial in simplifying XOR/XNOR expressions.
Continuing with the previous example, we can also observe offset adjacencies between the variables A and B. These adjacencies enable us to simplify the expression by identifying common terms and reducing redundancy.
Importance of Both Diagonal and Offset Adjacencies:
It is important to consider both diagonal and offset adjacencies when simplifying XOR/XNOR expressions because they allow us to identify patterns, reduce the number of terms, and optimize the circuit design. By leveraging these adjacencies, we can simplify complex expressions and improve the efficiency of digital logic circuits.
Conclusion:
When simplifying XOR/XNOR expressions, it is essential to consider both diagonal and offset adjacencies. These adjacencies help in identifying patterns, reducing the number of terms, and optimizing the circuit design. By leveraging these techniques, engineers can simplify complex expressions and improve the efficiency of digital logic circuits.
In the field of digital logic, XOR (exclusive OR) and XNOR (exclusive NOR) gates are fundamental building blocks. These gates are used to perform logical operations on two binary inputs. Simplification of XOR/XNOR expressions is important for optimizing circuit designs and reducing complexity.
Explanation:
When simplifying XOR/XNOR expressions, we need to consider both diagonal and offset adjacencies. Let's understand what these terms mean and how they relate to the simplification process.
Diagonal Adjacencies:
Diagonal adjacencies refer to the arrangement of variables in a truth table where two variables are adjacent to each other diagonally. In the context of XOR/XNOR simplification, diagonal adjacencies are important because they allow us to identify patterns and simplify the expression accordingly.
For example, consider the following truth table for a 3-input XOR gate:
| A | B | C | Output |
|---|---|---|--------|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
In this truth table, we can observe diagonal adjacencies between the variables A and C, as well as B and C. These adjacencies allow us to simplify the expression by identifying patterns and reducing the number of terms.
Offset Adjacencies:
Offset adjacencies refer to the arrangement of variables in a truth table where two variables are adjacent to each other with an offset of one position. Similar to diagonal adjacencies, offset adjacencies are crucial in simplifying XOR/XNOR expressions.
Continuing with the previous example, we can also observe offset adjacencies between the variables A and B. These adjacencies enable us to simplify the expression by identifying common terms and reducing redundancy.
Importance of Both Diagonal and Offset Adjacencies:
It is important to consider both diagonal and offset adjacencies when simplifying XOR/XNOR expressions because they allow us to identify patterns, reduce the number of terms, and optimize the circuit design. By leveraging these adjacencies, we can simplify complex expressions and improve the efficiency of digital logic circuits.
Conclusion:
When simplifying XOR/XNOR expressions, it is essential to consider both diagonal and offset adjacencies. These adjacencies help in identifying patterns, reducing the number of terms, and optimizing the circuit design. By leveraging these techniques, engineers can simplify complex expressions and improve the efficiency of digital logic circuits.
For an n-variable Boolean function, the maximum number of prime implicants is- a)2(n - 1)
- b)n/2
- c)2n
- d)2(n-1)
Correct answer is option 'D'. Can you explain this answer?
For an n-variable Boolean function, the maximum number of prime implicants is
a)
2(n - 1)
b)
n/2
c)
2n
d)
2(n-1)
|
|
Yash Patel answered |
In a n variable Boolean function, the maximum number of prime implicant is given by:
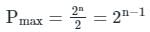
n = 4:

Maximum number of prime applicants = 2n-1 = 24 -1 = 8
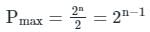
n = 4:

Maximum number of prime applicants = 2n-1 = 24 -1 = 8
______ is also known as Inverter.- a)NOT Gate
- b)OR Gate
- c)NAND Gate
- d)AND Gate
Correct answer is option 'A'. Can you explain this answer?
______ is also known as Inverter.
a)
NOT Gate
b)
OR Gate
c)
NAND Gate
d)
AND Gate
|
|
Ravi Singh answered |
- NOT Gate is also known as Inverter
- The 7404 is a high-speed CMOS Logic Quad NOT Gate.
- The 7404 is also known as Hex inverter.
- The contains Six independent NOT gates in one package. T
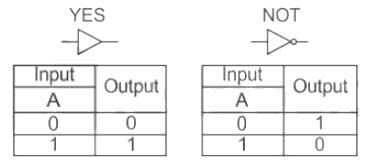
- The NOT gate consists of only one input and one output.
- A NOT gate is used to output the Boolean inverse of the applied input.
- Hence the name ‘Digital Inverter’ or ‘Inverting buffer’. The most commonly used NOT gate IC is 7404.
- The symbol and truth table of NOT gate and a buffer given as
Examine these two statements carefully and select the answers to these items using the code given below:Statement (I): When all inputs of a NAND gate are shorted to get a single input, single output gate, it becomes an inverter.Statement (II): When all inputs of a NAND gate are at logic ‘0’ level, the output is at logic ‘0’ level.- a)Both Statement I and Statement II are individually true and Statement II is the correct explanation of Statement I
- b)Both Statement I and Statement II are individually true but Statement II is not the correct explanation of Statement I
- c)Statement I is true but Statement II is false
- d)Statement I is false but Statement II is true
Correct answer is option 'C'. Can you explain this answer?
Examine these two statements carefully and select the answers to these items using the code given below:
Statement (I): When all inputs of a NAND gate are shorted to get a single input, single output gate, it becomes an inverter.
Statement (II): When all inputs of a NAND gate are at logic ‘0’ level, the output is at logic ‘0’ level.
a)
Both Statement I and Statement II are individually true and Statement II is the correct explanation of Statement I
b)
Both Statement I and Statement II are individually true but Statement II is not the correct explanation of Statement I
c)
Statement I is true but Statement II is false
d)
Statement I is false but Statement II is true

|
Bayshore Academy answered |

Boolean algebra can be used ____________- a)For designing of the digital computers
- b)In building logic symbols
- c)Circuit theory
- d)Building algebraic functions
Correct answer is option 'A'. Can you explain this answer?
Boolean algebra can be used ____________
a)
For designing of the digital computers
b)
In building logic symbols
c)
Circuit theory
d)
Building algebraic functions
|
|
Milan Rane answered |
Boolean algebra is a mathematical structure that deals with variables that can take only two values: true or false, represented as 1 or 0, respectively. It is named after the mathematician George Boole, who first developed this algebraic system in the mid-19th century. Boolean algebra is widely used in various fields, including computer science and digital electronics, due to its ability to represent and manipulate logical statements and operations.
1. For designing of digital computers:
Boolean algebra is extensively used in the design and analysis of digital circuits and systems, including computer architecture and digital logic design. Digital computers are based on binary logic, where information is represented using bits, which can be either 0 or 1. Boolean algebra provides a formalism to express and manipulate logic gates, such as AND, OR, and NOT gates, which are the building blocks of digital circuits. By using Boolean algebra, designers can derive logical expressions and truth tables that describe the behavior of complex digital systems.
2. In building logic symbols:
Logic symbols are graphical representations of logical operations and relationships between variables. Boolean algebra provides a foundation for creating these symbols and defining their behavior. For example, AND and OR gates are represented by specific symbols in circuit diagrams, which are derived from Boolean algebra expressions. Using logic symbols, complex digital systems can be represented visually, making it easier for engineers to understand and analyze their behavior.
3. Circuit theory:
Boolean algebra is closely related to circuit theory, which deals with the analysis and design of electrical circuits. By using Boolean algebra, circuit theorists can express circuit equations and solve them to determine the behavior of electrical systems. Boolean algebra allows for the simplification of complex circuit equations, enabling engineers to optimize circuit designs for efficiency and performance.
4. Building algebraic functions:
Boolean algebra can be used to build algebraic functions that operate on binary variables. These functions can be used for various purposes, such as data manipulation, signal processing, and control systems. Algebraic functions built using Boolean algebra can be expressed as logical expressions and implemented in digital systems using logic gates.
In conclusion, Boolean algebra is a fundamental tool for designing digital computers, building logic symbols, analyzing electrical circuits, and constructing algebraic functions. Its ability to represent and manipulate logical statements and operations makes it an essential concept in the field of computer science and digital electronics.
1. For designing of digital computers:
Boolean algebra is extensively used in the design and analysis of digital circuits and systems, including computer architecture and digital logic design. Digital computers are based on binary logic, where information is represented using bits, which can be either 0 or 1. Boolean algebra provides a formalism to express and manipulate logic gates, such as AND, OR, and NOT gates, which are the building blocks of digital circuits. By using Boolean algebra, designers can derive logical expressions and truth tables that describe the behavior of complex digital systems.
2. In building logic symbols:
Logic symbols are graphical representations of logical operations and relationships between variables. Boolean algebra provides a foundation for creating these symbols and defining their behavior. For example, AND and OR gates are represented by specific symbols in circuit diagrams, which are derived from Boolean algebra expressions. Using logic symbols, complex digital systems can be represented visually, making it easier for engineers to understand and analyze their behavior.
3. Circuit theory:
Boolean algebra is closely related to circuit theory, which deals with the analysis and design of electrical circuits. By using Boolean algebra, circuit theorists can express circuit equations and solve them to determine the behavior of electrical systems. Boolean algebra allows for the simplification of complex circuit equations, enabling engineers to optimize circuit designs for efficiency and performance.
4. Building algebraic functions:
Boolean algebra can be used to build algebraic functions that operate on binary variables. These functions can be used for various purposes, such as data manipulation, signal processing, and control systems. Algebraic functions built using Boolean algebra can be expressed as logical expressions and implemented in digital systems using logic gates.
In conclusion, Boolean algebra is a fundamental tool for designing digital computers, building logic symbols, analyzing electrical circuits, and constructing algebraic functions. Its ability to represent and manipulate logical statements and operations makes it an essential concept in the field of computer science and digital electronics.
What is the definition of Boolean functions?- a)An arithmetic function with k degrees such that f:Y→Yk
- b)A special mathematical function with n degrees such that f:Yn→Y
- c)An algebraic function with n degrees such that f:Xn→X
- d)A polynomial function with k degrees such that f:X2→Xn
Correct answer is option 'B'. Can you explain this answer?
What is the definition of Boolean functions?
a)
An arithmetic function with k degrees such that f:Y→Yk
b)
A special mathematical function with n degrees such that f:Yn→Y
c)
An algebraic function with n degrees such that f:Xn→X
d)
A polynomial function with k degrees such that f:X2→Xn
|
|
Baishali Reddy answered |
-> {0,1}^k -> {0,1}
b)A function that returns a boolean value (either true or false) based on one or more input values.
c)A mathematical function that operates on one or more binary inputs and produces a binary output.
d)A function that takes Boolean values as input and returns a Boolean value as output.
b)A function that returns a boolean value (either true or false) based on one or more input values.
c)A mathematical function that operates on one or more binary inputs and produces a binary output.
d)A function that takes Boolean values as input and returns a Boolean value as output.
If an expression is given that x+x’y’z=x+y’z, find the minimal expression of the function F(x,y,z) = x+x’y’z+yz?- a)y’ + z
- b)xz + y’
- c)x + z
- d)x’ + y
Correct answer is option 'C'. Can you explain this answer?
If an expression is given that x+x’y’z=x+y’z, find the minimal expression of the function F(x,y,z) = x+x’y’z+yz?
a)
y’ + z
b)
xz + y’
c)
x + z
d)
x’ + y
|
|
Shounak Sharma answered |
It seems like the expression "x x" is incomplete or missing the operator or the second operand.
An expression is a combination of variables, constants, and operators that can be evaluated to produce a value. In order to evaluate an expression, it needs to have an operator and at least one operand.
For example, if the expression is "x x + 4", it means that we are multiplying the variable x by itself and then adding 4 to the result.
An expression is a combination of variables, constants, and operators that can be evaluated to produce a value. In order to evaluate an expression, it needs to have an operator and at least one operand.
For example, if the expression is "x x + 4", it means that we are multiplying the variable x by itself and then adding 4 to the result.
Using the transformation method you can realize any POS realization of OR-AND with only.- a)XOR
- b)NAND
- c)AND
- d)NOR
Correct answer is option 'D'. Can you explain this answer?
Using the transformation method you can realize any POS realization of OR-AND with only.
a)
XOR
b)
NAND
c)
AND
d)
NOR
|
|
Disha Mukherjee answered |
POS realization of OR-AND with NOR
POS (Product of Sum) realization is a way to implement logic circuits using AND gates and OR gates. In this method, the output of multiple AND gates is fed to a single OR gate.
To realize a POS realization of OR-AND using only NOR gates, we can use the transformation method. This method involves replacing each OR gate with a combination of NOR gates and each AND gate with a combination of NOR gates and inverters.
Replacing OR gate with NOR gates
To replace an OR gate with NOR gates, we can use the following DeMorgan's theorem:
A + B = (A' * B')'
Using this theorem, we can replace an OR gate with two NOR gates. The first NOR gate will have inverted inputs, and the second NOR gate will have inverted output.
Replacing AND gate with NOR gates and inverters
To replace an AND gate with NOR gates and inverters, we can use the following DeMorgan's theorem:
A * B = (A' + B')'
Using this theorem, we can replace an AND gate with a combination of NOR gates and inverters. The number of NOR gates and inverters depends on the number of inputs in the AND gate.
For example, a 2-input AND gate can be replaced with two inverters and three NOR gates. The first two inverters will invert the inputs, and the three NOR gates will implement the AND function.
Realizing OR-AND with NOR gates
Using the above methods, we can realize any POS realization of OR-AND with only NOR gates. We can replace each OR gate with two NOR gates and each AND gate with a combination of NOR gates and inverters.
For example, a 3-input OR-AND circuit can be realized using only NOR gates as follows:
1. Replace the OR gate with two NOR gates using DeMorgan's theorem.
2. Replace each 3-input AND gate with two inverters and three NOR gates using DeMorgan's theorem.
3. Connect the outputs of all the AND gates to the inputs of the OR gates.
By using this method, we can implement any logic circuit that uses only OR and AND gates using only NOR gates.
POS (Product of Sum) realization is a way to implement logic circuits using AND gates and OR gates. In this method, the output of multiple AND gates is fed to a single OR gate.
To realize a POS realization of OR-AND using only NOR gates, we can use the transformation method. This method involves replacing each OR gate with a combination of NOR gates and each AND gate with a combination of NOR gates and inverters.
Replacing OR gate with NOR gates
To replace an OR gate with NOR gates, we can use the following DeMorgan's theorem:
A + B = (A' * B')'
Using this theorem, we can replace an OR gate with two NOR gates. The first NOR gate will have inverted inputs, and the second NOR gate will have inverted output.
Replacing AND gate with NOR gates and inverters
To replace an AND gate with NOR gates and inverters, we can use the following DeMorgan's theorem:
A * B = (A' + B')'
Using this theorem, we can replace an AND gate with a combination of NOR gates and inverters. The number of NOR gates and inverters depends on the number of inputs in the AND gate.
For example, a 2-input AND gate can be replaced with two inverters and three NOR gates. The first two inverters will invert the inputs, and the three NOR gates will implement the AND function.
Realizing OR-AND with NOR gates
Using the above methods, we can realize any POS realization of OR-AND with only NOR gates. We can replace each OR gate with two NOR gates and each AND gate with a combination of NOR gates and inverters.
For example, a 3-input OR-AND circuit can be realized using only NOR gates as follows:
1. Replace the OR gate with two NOR gates using DeMorgan's theorem.
2. Replace each 3-input AND gate with two inverters and three NOR gates using DeMorgan's theorem.
3. Connect the outputs of all the AND gates to the inputs of the OR gates.
By using this method, we can implement any logic circuit that uses only OR and AND gates using only NOR gates.
Each product term of a group, w’.x.y’ and w.y, represents the ____________ in that group.- a)Input
- b)POS
- c)Sum-of-Minterms
- d)Sum of Maxterms
Correct answer is option 'C'. Can you explain this answer?
Each product term of a group, w’.x.y’ and w.y, represents the ____________ in that group.
a)
Input
b)
POS
c)
Sum-of-Minterms
d)
Sum of Maxterms
|
|
Sudhir Patel answered |
In a minterm, each variable w, x or y appears once either as the variable itself or as the inverse. So, the given expression satisfies the property of Sum of Minterm.
The Boolean expression AB + AC̅ + BC simplifies to- a)BC + AC̅
- b)AB + AC̅ + B
- c)AB + AC̅
- d)AB + BC
Correct answer is option 'A'. Can you explain this answer?
The Boolean expression AB + AC̅ + BC simplifies to
a)
BC + AC̅
b)
AB + AC̅ + B
c)
AB + AC̅
d)
AB + BC
|
|
Ravi Singh answered |
Given Boolean expression is,
F = AB + AC̅ + BC
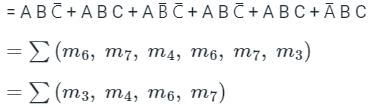
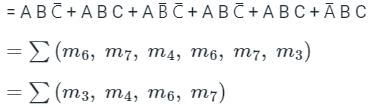
F = BC + AC̅
The minimised form of Boolean logic expression (A’B’C’ + A’BC’ + A’BC + ABC’) can be reduced to
- a)A’C’ + BC’ + A’B
- b)A’C’ + B’C’ + A’B
- c)A’C + BC + A’B
- d)AC + BC’ + AB
Correct answer is option 'A'. Can you explain this answer?
The minimised form of Boolean logic expression (A’B’C’ + A’BC’ + A’BC + ABC’) can be reduced to
a)
A’C’ + BC’ + A’B
b)
A’C’ + B’C’ + A’B
c)
A’C + BC + A’B
d)
AC + BC’ + AB
|
|
Ravi Singh answered |
Given: A′B + ABC′ + BC’ + AB′C′
= A’B + BC’ (1 + A) + AB’C”
= A’B + BC’ + AB’C’
= A’B + BC’ + BC’ + AB’C’
= B(A’ + C’) + C’(A + AB’)
= B(AC)’ + C’ A(1 + B’)
= B(AC)’ + AC’.
= A’B + BC’ (1 + A) + AB’C”
= A’B + BC’ + AB’C’
= A’B + BC’ + BC’ + AB’C’
= B(A’ + C’) + C’(A + AB’)
= B(AC)’ + C’ A(1 + B’)
= B(AC)’ + AC’.
Algebra of logic is termed as ______________
- a)Numerical logic
- b)Arithmetic logic
- c)Boolean algebra
- d)Boolean number
Correct answer is option 'C'. Can you explain this answer?
Algebra of logic is termed as ______________
a)
Numerical logic
b)
Arithmetic logic
c)
Boolean algebra
d)
Boolean number
|
|
Kalyan Menon answered |
Algebra of Logic: Boolean Algebra
Boolean algebra is the algebra of logic, which is a mathematical structure that deals with logical operations and the manipulation of logical values. It is a branch of mathematics that was developed by mathematician and logician George Boole in the mid-19th century.
1. Definition of Boolean Algebra
Boolean algebra is a mathematical structure that consists of a set of elements, a set of binary operations, and a set of axioms or rules that govern the behavior of these operations. The elements of Boolean algebra are called Boolean variables, which can have only two possible values: true (1) or false (0).
2. Operations in Boolean Algebra
Boolean algebra defines several operations that can be performed on Boolean variables. These operations include:
- AND: The AND operation, denoted by the symbol ∧ or ·, takes two Boolean variables and returns true if both variables are true, and false otherwise.
- OR: The OR operation, denoted by the symbol ∨ or +, takes two Boolean variables and returns true if at least one of the variables is true, and false otherwise.
- NOT: The NOT operation, denoted by the symbol ¬ or ', takes a single Boolean variable and returns its opposite value. If the variable is true, NOT returns false, and vice versa.
3. Laws of Boolean Algebra
Boolean algebra is governed by a set of laws, also known as Boolean laws or Boolean identities. These laws are based on the properties of logical operations and help in simplifying complex logical expressions. Some of the fundamental laws of Boolean algebra include:
- Identity laws: These laws state that any Boolean variable combined with a true or false value using the OR or AND operation respectively will result in the same value. For example, A + 1 = 1 and A · 0 = 0.
- Domination laws: These laws state that any Boolean variable combined with a true or false value using the AND or OR operation respectively will result in the same value as the variable itself. For example, A + 0 = A and A · 1 = A.
- De Morgan's laws: These laws state the relationship between the AND and NOT operations, as well as the OR and NOT operations. They state that the negation of an AND operation is equal to the OR operation of the negations of the variables, and the negation of an OR operation is equal to the AND operation of the negations of the variables.
Conclusion
Boolean algebra, also known as the algebra of logic, is a branch of mathematics that deals with logical operations and the manipulation of logical values. It is widely used in computer science and digital electronics for designing and analyzing circuits, as well as in many other fields where logical reasoning is required. Understanding Boolean algebra is essential for working with logical expressions and for solving problems related to logical reasoning.
Boolean algebra is the algebra of logic, which is a mathematical structure that deals with logical operations and the manipulation of logical values. It is a branch of mathematics that was developed by mathematician and logician George Boole in the mid-19th century.
1. Definition of Boolean Algebra
Boolean algebra is a mathematical structure that consists of a set of elements, a set of binary operations, and a set of axioms or rules that govern the behavior of these operations. The elements of Boolean algebra are called Boolean variables, which can have only two possible values: true (1) or false (0).
2. Operations in Boolean Algebra
Boolean algebra defines several operations that can be performed on Boolean variables. These operations include:
- AND: The AND operation, denoted by the symbol ∧ or ·, takes two Boolean variables and returns true if both variables are true, and false otherwise.
- OR: The OR operation, denoted by the symbol ∨ or +, takes two Boolean variables and returns true if at least one of the variables is true, and false otherwise.
- NOT: The NOT operation, denoted by the symbol ¬ or ', takes a single Boolean variable and returns its opposite value. If the variable is true, NOT returns false, and vice versa.
3. Laws of Boolean Algebra
Boolean algebra is governed by a set of laws, also known as Boolean laws or Boolean identities. These laws are based on the properties of logical operations and help in simplifying complex logical expressions. Some of the fundamental laws of Boolean algebra include:
- Identity laws: These laws state that any Boolean variable combined with a true or false value using the OR or AND operation respectively will result in the same value. For example, A + 1 = 1 and A · 0 = 0.
- Domination laws: These laws state that any Boolean variable combined with a true or false value using the AND or OR operation respectively will result in the same value as the variable itself. For example, A + 0 = A and A · 1 = A.
- De Morgan's laws: These laws state the relationship between the AND and NOT operations, as well as the OR and NOT operations. They state that the negation of an AND operation is equal to the OR operation of the negations of the variables, and the negation of an OR operation is equal to the AND operation of the negations of the variables.
Conclusion
Boolean algebra, also known as the algebra of logic, is a branch of mathematics that deals with logical operations and the manipulation of logical values. It is widely used in computer science and digital electronics for designing and analyzing circuits, as well as in many other fields where logical reasoning is required. Understanding Boolean algebra is essential for working with logical expressions and for solving problems related to logical reasoning.
Which of the following is a Simplification law?- a)M.(~M+N) = M.N
- b)M+(N.O) = (M+N)(M+O)
- c)~(M+N) = ~M.~N
- d)M.(N.O) = (M.N).O
Correct answer is option 'A'. Can you explain this answer?
Which of the following is a Simplification law?
a)
M.(~M+N) = M.N
b)
M+(N.O) = (M+N)(M+O)
c)
~(M+N) = ~M.~N
d)
M.(N.O) = (M.N).O
|
|
Atharva Das answered |
Explanation:
The given options are different laws or rules of simplification in Boolean algebra. Boolean algebra is a mathematical structure that deals with binary variables and logical operations. It helps simplify logical expressions and circuits.
The correct option is 'A', which represents the law of absorption. This law states that if we have a logical expression of the form M.(~M N), then it can be simplified to just M.N.
Law of Absorption:
- M.(~M N) = M.N
This law is based on the concept of absorption, where the presence of one variable absorbs or nullifies the effect of the other variable.
Other Options:
Let's briefly explain the other options mentioned:
Option B:
- M (N.O) = (M N)(M O)
This option represents the law of distribution. It states that if we have a logical expression of the form M (N.O), then it can be simplified to (M N)(M O). This law is based on the distributive property.
Option C:
- ~(M N) = ~M.~N
This option represents the law of De Morgan's theorem. It states that the negation of a logical expression can be achieved by negating each individual variable and changing the logical operator. In this case, ~(M N) is equivalent to ~M.~N.
Option D:
- M.(N.O) = (M.N).O
This option represents the law of associativity. It states that the order of operations in a logical expression does not matter. In this case, M.(N.O) is equivalent to (M.N).O.
Conclusion:
Among the given options, option 'A' represents the law of absorption, which simplifies a logical expression by nullifying the effect of one variable. Hence, option 'A' is the correct answer.
The given options are different laws or rules of simplification in Boolean algebra. Boolean algebra is a mathematical structure that deals with binary variables and logical operations. It helps simplify logical expressions and circuits.
The correct option is 'A', which represents the law of absorption. This law states that if we have a logical expression of the form M.(~M N), then it can be simplified to just M.N.
Law of Absorption:
- M.(~M N) = M.N
This law is based on the concept of absorption, where the presence of one variable absorbs or nullifies the effect of the other variable.
Other Options:
Let's briefly explain the other options mentioned:
Option B:
- M (N.O) = (M N)(M O)
This option represents the law of distribution. It states that if we have a logical expression of the form M (N.O), then it can be simplified to (M N)(M O). This law is based on the distributive property.
Option C:
- ~(M N) = ~M.~N
This option represents the law of De Morgan's theorem. It states that the negation of a logical expression can be achieved by negating each individual variable and changing the logical operator. In this case, ~(M N) is equivalent to ~M.~N.
Option D:
- M.(N.O) = (M.N).O
This option represents the law of associativity. It states that the order of operations in a logical expression does not matter. In this case, M.(N.O) is equivalent to (M.N).O.
Conclusion:
Among the given options, option 'A' represents the law of absorption, which simplifies a logical expression by nullifying the effect of one variable. Hence, option 'A' is the correct answer.
There are many situations in logic design in which simplification of logic expression is possible in terms of XOR and _________________ operations.- a)X-NOR
- b)XOR
- c)NOR
- d)NAND
Correct answer is option 'A'. Can you explain this answer?
There are many situations in logic design in which simplification of logic expression is possible in terms of XOR and _________________ operations.
a)
X-NOR
b)
XOR
c)
NOR
d)
NAND
|
|
Sudhir Patel answered |
There are many situations in logic design in which simplification of logic expression is possible in terms of XOR and XNOR operations.
Expression of XOR : AB’ + A’B
Expression of XNOR : AB + A’B’
Expression of XOR : AB’ + A’B
Expression of XNOR : AB + A’B’
Entries known as _______________ mapping.- a)Diagonal
- b)Straight
- c)K
- d)Boolean
Correct answer is option 'A'. Can you explain this answer?
Entries known as _______________ mapping.
a)
Diagonal
b)
Straight
c)
K
d)
Boolean
|
|
Niharika Ahuja answered |
Diagonal Mapping in Computer Science
Definition of Diagonal Mapping
Diagonal mapping is a type of mapping used in computer science in which the elements of an array are mapped diagonally. This mapping technique is used to improve performance and reduce memory usage in certain types of algorithms.
Explanation of Diagonal Mapping
In diagonal mapping, the elements of an array are mapped diagonally, rather than in a straight line or in a K pattern. This means that each element of the array is mapped to a unique location in memory, which can help to reduce memory usage and improve performance.
Applications of Diagonal Mapping
Diagonal mapping is commonly used in a variety of applications in computer science, including:
1. Image processing: Diagonal mapping can be used to improve the performance of image processing algorithms by reducing memory usage and improving processing speed.
2. Data compression: Diagonal mapping can be used to improve the performance of data compression algorithms by reducing the amount of memory required to store compressed data.
3. Pattern recognition: Diagonal mapping can be used to improve the performance of pattern recognition algorithms by reducing the amount of memory required to store pattern data.
Advantages of Diagonal Mapping
Some of the advantages of diagonal mapping include:
1. Improved performance: Diagonal mapping can help to improve the performance of certain types of algorithms by reducing memory usage and improving processing speed.
2. Reduced memory usage: Diagonal mapping can help to reduce the amount of memory required to store data, which can be particularly important in applications where memory usage is a limiting factor.
3. Simplified algorithms: Diagonal mapping can help to simplify algorithms by reducing the amount of data that needs to be processed and stored.
Conclusion
Diagonal mapping is a powerful technique that can be used to improve the performance and reduce memory usage in a variety of applications in computer science. By mapping elements of an array diagonally, this technique can help to simplify algorithms and improve performance, making it a valuable tool for developers and researchers in the field.
Definition of Diagonal Mapping
Diagonal mapping is a type of mapping used in computer science in which the elements of an array are mapped diagonally. This mapping technique is used to improve performance and reduce memory usage in certain types of algorithms.
Explanation of Diagonal Mapping
In diagonal mapping, the elements of an array are mapped diagonally, rather than in a straight line or in a K pattern. This means that each element of the array is mapped to a unique location in memory, which can help to reduce memory usage and improve performance.
Applications of Diagonal Mapping
Diagonal mapping is commonly used in a variety of applications in computer science, including:
1. Image processing: Diagonal mapping can be used to improve the performance of image processing algorithms by reducing memory usage and improving processing speed.
2. Data compression: Diagonal mapping can be used to improve the performance of data compression algorithms by reducing the amount of memory required to store compressed data.
3. Pattern recognition: Diagonal mapping can be used to improve the performance of pattern recognition algorithms by reducing the amount of memory required to store pattern data.
Advantages of Diagonal Mapping
Some of the advantages of diagonal mapping include:
1. Improved performance: Diagonal mapping can help to improve the performance of certain types of algorithms by reducing memory usage and improving processing speed.
2. Reduced memory usage: Diagonal mapping can help to reduce the amount of memory required to store data, which can be particularly important in applications where memory usage is a limiting factor.
3. Simplified algorithms: Diagonal mapping can help to simplify algorithms by reducing the amount of data that needs to be processed and stored.
Conclusion
Diagonal mapping is a powerful technique that can be used to improve the performance and reduce memory usage in a variety of applications in computer science. By mapping elements of an array diagonally, this technique can help to simplify algorithms and improve performance, making it a valuable tool for developers and researchers in the field.
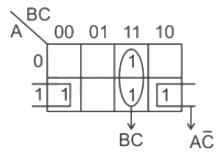
The output of logic circuit given below represents _______ gate.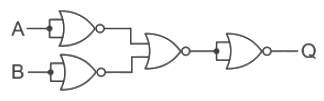
- a)OR
- b)NOR
- c)AND
- d)NAND
Correct answer is option 'D'. Can you explain this answer?
The output of logic circuit given below represents _______ gate.

a)
OR
b)
NOR
c)
AND
d)
NAND

|
Riverdale Learning Institute answered |
Q= AB
Output expression Q is equivalent to NAND gate.
Output expression Q is equivalent to NAND gate.
What are the canonical forms of Boolean Expressions?- a)OR and XOR
- b)NOR and XNOR
- c)MAX and MIN
- d)SOM and POM
Correct answer is option 'D'. Can you explain this answer?
What are the canonical forms of Boolean Expressions?
a)
OR and XOR
b)
NOR and XNOR
c)
MAX and MIN
d)
SOM and POM
|
|
Milan Rane answered |
The correct answer is option 'D': SOM and POM.
To understand why SOM (Sum of Minterms) and POM (Product of Maxterms) are the canonical forms of Boolean expressions, let's first define what these forms represent.
SOM (Sum of Minterms):
- In the SOM form, a Boolean expression is represented as the sum (OR) of its minterms.
- A minterm is a product (AND) of literals (either variables or their complements) that covers all the possible combinations of inputs for which the output is 1.
POM (Product of Maxterms):
- In the POM form, a Boolean expression is represented as the product (AND) of its maxterms.
- A maxterm is a sum (OR) of literals (either variables or their complements) that covers all the possible combinations of inputs for which the output is 0.
Now, let's discuss why SOM and POM are considered canonical forms of Boolean expressions.
1. Completeness:
- SOM and POM forms provide a complete representation of a Boolean function.
- A complete representation means that any Boolean function can be expressed uniquely using either the SOM or POM form.
- This property is essential for simplifying and analyzing Boolean expressions.
2. Uniqueness:
- The SOM and POM forms provide a unique representation for a given Boolean function.
- This means that there is only one way to express a Boolean function using either the SOM or POM form.
- This uniqueness enables standardization and consistency in analyzing and manipulating Boolean expressions.
3. Correspondence to Truth Table:
- The SOM and POM forms directly correspond to the truth table of a Boolean function.
- Each minterm in the SOM form represents a row in the truth table where the output is 1.
- Each maxterm in the POM form represents a row in the truth table where the output is 0.
- This correspondence facilitates the conversion between Boolean expressions and truth tables.
4. Simplification and Optimization:
- The SOM and POM forms can be used to simplify and optimize Boolean expressions.
- By applying Boolean algebra laws and theorems, expressions in SOM or POM form can be simplified to their minimal form.
- The minimal form represents the simplest and most efficient realization of the Boolean function.
In summary, the SOM and POM forms are canonical forms of Boolean expressions because they provide a complete, unique, and correspondence-based representation of Boolean functions. They also enable simplification and optimization, which are crucial in designing efficient digital circuits.
To understand why SOM (Sum of Minterms) and POM (Product of Maxterms) are the canonical forms of Boolean expressions, let's first define what these forms represent.
SOM (Sum of Minterms):
- In the SOM form, a Boolean expression is represented as the sum (OR) of its minterms.
- A minterm is a product (AND) of literals (either variables or their complements) that covers all the possible combinations of inputs for which the output is 1.
POM (Product of Maxterms):
- In the POM form, a Boolean expression is represented as the product (AND) of its maxterms.
- A maxterm is a sum (OR) of literals (either variables or their complements) that covers all the possible combinations of inputs for which the output is 0.
Now, let's discuss why SOM and POM are considered canonical forms of Boolean expressions.
1. Completeness:
- SOM and POM forms provide a complete representation of a Boolean function.
- A complete representation means that any Boolean function can be expressed uniquely using either the SOM or POM form.
- This property is essential for simplifying and analyzing Boolean expressions.
2. Uniqueness:
- The SOM and POM forms provide a unique representation for a given Boolean function.
- This means that there is only one way to express a Boolean function using either the SOM or POM form.
- This uniqueness enables standardization and consistency in analyzing and manipulating Boolean expressions.
3. Correspondence to Truth Table:
- The SOM and POM forms directly correspond to the truth table of a Boolean function.
- Each minterm in the SOM form represents a row in the truth table where the output is 1.
- Each maxterm in the POM form represents a row in the truth table where the output is 0.
- This correspondence facilitates the conversion between Boolean expressions and truth tables.
4. Simplification and Optimization:
- The SOM and POM forms can be used to simplify and optimize Boolean expressions.
- By applying Boolean algebra laws and theorems, expressions in SOM or POM form can be simplified to their minimal form.
- The minimal form represents the simplest and most efficient realization of the Boolean function.
In summary, the SOM and POM forms are canonical forms of Boolean expressions because they provide a complete, unique, and correspondence-based representation of Boolean functions. They also enable simplification and optimization, which are crucial in designing efficient digital circuits.
F(X,Y,Z,M) = X`Y`Z`M`. The degree of the function is ________- a)2
- b)5
- c)4
- d)1
Correct answer is option 'C'. Can you explain this answer?
F(X,Y,Z,M) = X`Y`Z`M`. The degree of the function is ________
a)
2
b)
5
c)
4
d)
1
|
|
Diya Chauhan answered |
The given function F(X, Y, Z, M) is a Boolean function represented using Boolean variables X, Y, Z, and M. The function is defined as F(X, Y, Z, M) = X'Y'Z'M', where ' denotes the complement or negation of the variable.
Degree of a Boolean function refers to the maximum number of literals (variables or their complements) in any term of the function. In other words, it is the highest power of any variable in the function.
To determine the degree of the given function F(X, Y, Z, M) = X'Y'Z'M', we need to find the maximum number of literals in any term. Since each literal corresponds to a variable or its complement, we can count the number of literals in each term.
The function has only one term, X'Y'Z'M', and it contains all the variables X, Y, Z, and M in their complemented form. Therefore, the maximum number of literals in any term is 4.
Hence, the degree of the function F(X, Y, Z, M) = X'Y'Z'M' is 4.
In summary:
- The given function F(X, Y, Z, M) = X'Y'Z'M' represents a Boolean function with four variables.
- The degree of a Boolean function is the maximum number of literals in any term.
- The function has only one term, X'Y'Z'M', and it contains all the variables in their complemented form.
- Therefore, the maximum number of literals in any term is 4.
- Hence, the degree of the function F(X, Y, Z, M) = X'Y'Z'M' is 4.
Degree of a Boolean function refers to the maximum number of literals (variables or their complements) in any term of the function. In other words, it is the highest power of any variable in the function.
To determine the degree of the given function F(X, Y, Z, M) = X'Y'Z'M', we need to find the maximum number of literals in any term. Since each literal corresponds to a variable or its complement, we can count the number of literals in each term.
The function has only one term, X'Y'Z'M', and it contains all the variables X, Y, Z, and M in their complemented form. Therefore, the maximum number of literals in any term is 4.
Hence, the degree of the function F(X, Y, Z, M) = X'Y'Z'M' is 4.
In summary:
- The given function F(X, Y, Z, M) = X'Y'Z'M' represents a Boolean function with four variables.
- The degree of a Boolean function is the maximum number of literals in any term.
- The function has only one term, X'Y'Z'M', and it contains all the variables in their complemented form.
- Therefore, the maximum number of literals in any term is 4.
- Hence, the degree of the function F(X, Y, Z, M) = X'Y'Z'M' is 4.
Which of the following is/are the universal logic gates?- a)OR and NOR
- b)AND
- c)NAND and NOR
- d)NOT
Correct answer is option 'C'. Can you explain this answer?
Which of the following is/are the universal logic gates?
a)
OR and NOR
b)
AND
c)
NAND and NOR
d)
NOT
|
|
Sudhir Patel answered |
NAND and NOR gates are known as the universal logic gates. A universal gate is a gate which can implement any Boolean function without the help of 3 basic gate types.
These logic gates are widely used in _______________ design and therefore are available in IC form.- a)Sampling
- b)Digital
- c)Analog
- d)Systems
Correct answer is option 'B'. Can you explain this answer?
These logic gates are widely used in _______________ design and therefore are available in IC form.
a)
Sampling
b)
Digital
c)
Analog
d)
Systems
|
|
Shalini Chopra answered |
Explanation:
Logic gates are basic building blocks of digital circuits. These gates are used to manipulate binary data. Digital circuits are used in various applications such as computers, smartphones, digital watches, calculators, and many more. Hence, the logic gates are widely used in digital design and are available in IC (Integrated Circuit) form.
Integrated Circuits:
Integrated circuits are miniaturized electronic circuits that are made up of several components such as transistors, diodes, resistors, capacitors, etc. These components are fabricated on a silicon chip and are interconnected using metal wires. ICs are widely used in digital circuits due to their small size, low power consumption, high reliability, and low cost.
Applications of Logic Gates:
Logic gates are used in various digital circuits such as:
- Arithmetic circuits
- Memory circuits
- Control circuits
- Communication circuits
- Digital signal processing circuits
- Microprocessors
Types of Logic Gates:
There are several types of logic gates such as:
- AND gate
- OR gate
- NOT gate
- NAND gate
- NOR gate
- XOR gate
- XNOR gate
Conclusion:
In conclusion, logic gates are widely used in digital design and are available in IC form. These gates are used to manipulate binary data and are the basic building blocks of digital circuits. ICs are widely used due to their small size, low power consumption, high reliability, and low cost. Logic gates are used in various digital circuits such as arithmetic circuits, memory circuits, control circuits, communication circuits, digital signal processing circuits, and microprocessors.
Logic gates are basic building blocks of digital circuits. These gates are used to manipulate binary data. Digital circuits are used in various applications such as computers, smartphones, digital watches, calculators, and many more. Hence, the logic gates are widely used in digital design and are available in IC (Integrated Circuit) form.
Integrated Circuits:
Integrated circuits are miniaturized electronic circuits that are made up of several components such as transistors, diodes, resistors, capacitors, etc. These components are fabricated on a silicon chip and are interconnected using metal wires. ICs are widely used in digital circuits due to their small size, low power consumption, high reliability, and low cost.
Applications of Logic Gates:
Logic gates are used in various digital circuits such as:
- Arithmetic circuits
- Memory circuits
- Control circuits
- Communication circuits
- Digital signal processing circuits
- Microprocessors
Types of Logic Gates:
There are several types of logic gates such as:
- AND gate
- OR gate
- NOT gate
- NAND gate
- NOR gate
- XOR gate
- XNOR gate
Conclusion:
In conclusion, logic gates are widely used in digital design and are available in IC form. These gates are used to manipulate binary data and are the basic building blocks of digital circuits. ICs are widely used due to their small size, low power consumption, high reliability, and low cost. Logic gates are used in various digital circuits such as arithmetic circuits, memory circuits, control circuits, communication circuits, digital signal processing circuits, and microprocessors.
Which of the is sufficient to represent any boolean operation.- a){OR , OR}
- b){XOR}
- c){AND , AND}
- d)2×1 MUX
Correct answer is option 'D'. Can you explain this answer?
Which of the is sufficient to represent any boolean operation.
a)
{OR , OR}
b)
{XOR}
c)
{AND , AND}
d)
2×1 MUX
|
|
Yash Patel answered |
Concept:
- NOR,
- NAND,
- {OR and NOT i.e It behaves like NOR Gate } and
- {AND, NOT, It behaves like NAND Gate}
are the universal gates because they may be used to create any logic gate.
The given option 1, option 2 and option 3 are not sufficient to represent any boolean operation.
Option 1: {OR , OR} behaves like an OR gate. It can not sufficient for the universal gate.
Option 2: {XOR} is a simple XOR gate. It can not sufficient for the universal gate.
Option 3: {AND, AND} behaves like an AND gate. It can not sufficient for the universal gate.
Option 4: 2×1 MUX or 2X1 multiplexer is functionally complete provided we have external 1 and 0 available.
For NOT gate, use x as a select line and use 0 and 1 as inputs.
For AND gate, use y and 0 as inputs and x as select. With {AND, NOT} any other gate can be made.
Hence the correct answer is 2×1 MUX.
The given option 1, option 2 and option 3 are not sufficient to represent any boolean operation.
Option 1: {OR , OR} behaves like an OR gate. It can not sufficient for the universal gate.
Option 2: {XOR} is a simple XOR gate. It can not sufficient for the universal gate.
Option 3: {AND, AND} behaves like an AND gate. It can not sufficient for the universal gate.
Option 4: 2×1 MUX or 2X1 multiplexer is functionally complete provided we have external 1 and 0 available.
For NOT gate, use x as a select line and use 0 and 1 as inputs.
For AND gate, use y and 0 as inputs and x as select. With {AND, NOT} any other gate can be made.
Hence the correct answer is 2×1 MUX.
What will be the simplified Boolean function of the given equation?
F(a, b, c) = ∑(0, 2, 4, 5, 6)- a)c' + ab'
- b)a + b + c
- c)a'b + c
- d)ac' + b
Correct answer is option 'A'. Can you explain this answer?
What will be the simplified Boolean function of the given equation?
F(a, b, c) = ∑(0, 2, 4, 5, 6)
F(a, b, c) = ∑(0, 2, 4, 5, 6)
a)
c' + ab'
b)
a + b + c
c)
a'b + c
d)
ac' + b
|
|
Sanya Agarwal answered |
Concept:
The K-map is a graphical method that provides a systematic method for simplifying and manipulating the Boolean expressions or to convert a truth table to its corresponding logic circuit in a simple, orderly process.
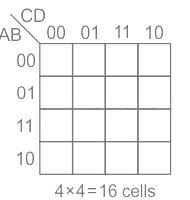
In an 'n' variable K map, there are 2n cells
For 4 variables there will be 24 = 16 cells as shown:
Calculations:
F(a, b, c) = ∑(0, 2, 4, 5, 6)
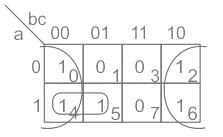
F = c' + ab'
The K-map is a graphical method that provides a systematic method for simplifying and manipulating the Boolean expressions or to convert a truth table to its corresponding logic circuit in a simple, orderly process.
In an 'n' variable K map, there are 2n cells
For 4 variables there will be 24 = 16 cells as shown:

Calculations:
F(a, b, c) = ∑(0, 2, 4, 5, 6)

F = c' + ab'
The following function F= AB'CD' +A'BCD' +AB'C'D+A'BC'D is realized using 2 input EX-OR and AND gates. The number of EX-OR gates and AND Gates required to implement the function respectively are?- a)1,1
- b)1,2
- c)2,1
- d)2,2
Correct answer is option 'C'. Can you explain this answer?
The following function F= AB'CD' +A'BCD' +AB'C'D+A'BC'D is realized using 2 input EX-OR and AND gates. The number of EX-OR gates and AND Gates required to implement the function respectively are?
a)
1,1
b)
1,2
c)
2,1
d)
2,2
|
|
Sanya Agarwal answered |
Concept:
The given data,
F = AB'CD' +A'BCD' +AB'C'D+A'BC'D
F = CD' [ AB' + A'B ] +C'D [AB' + A'B]
F =CD' [A⊕B] + C'D [A⊕B]
F = [A⊕B] [CD' + C'D ]
F = [A⊕B] [C⊕D]
Hence the given function has 2 EX-OR gates and one And gate are required.
Hence the correct answer is 2,1.
The given data,
F = AB'CD' +A'BCD' +AB'C'D+A'BC'D
F = CD' [ AB' + A'B ] +C'D [AB' + A'B]
F =CD' [A⊕B] + C'D [A⊕B]
F = [A⊕B] [CD' + C'D ]
F = [A⊕B] [C⊕D]
Hence the given function has 2 EX-OR gates and one And gate are required.
Hence the correct answer is 2,1.
It should be kept in mind that don’t care terms should be used along with the terms that are present in ___________- a)Minterms
- b)Expressions
- c)K-Map
- d)Latches
Correct answer is option 'A'. Can you explain this answer?
It should be kept in mind that don’t care terms should be used along with the terms that are present in ___________
a)
Minterms
b)
Expressions
c)
K-Map
d)
Latches

|
Athul Das answered |
Every individual has their own thoughts, opinions, and perspectives. What may be important or relevant to one person may not be the same for another.
Additionally, people come from different backgrounds and experiences, which shape their beliefs and values. Therefore, it is essential to consider and respect diverse viewpoints when discussing any topic.
Open-mindedness and empathy are key when engaging in conversations or debates. It is crucial to listen actively, try to understand others' perspectives, and be willing to challenge and expand our own beliefs.
Furthermore, effective communication involves being respectful and maintaining a constructive dialogue. It is important to avoid personal attacks, derogatory language, or dismissive behavior when discussing different points of view.
In conclusion, keeping in mind the diversity of thoughts and opinions, being open-minded and respectful, as well as actively listening and engaging in constructive dialogue are essential for meaningful and productive discussions.
Additionally, people come from different backgrounds and experiences, which shape their beliefs and values. Therefore, it is essential to consider and respect diverse viewpoints when discussing any topic.
Open-mindedness and empathy are key when engaging in conversations or debates. It is crucial to listen actively, try to understand others' perspectives, and be willing to challenge and expand our own beliefs.
Furthermore, effective communication involves being respectful and maintaining a constructive dialogue. It is important to avoid personal attacks, derogatory language, or dismissive behavior when discussing different points of view.
In conclusion, keeping in mind the diversity of thoughts and opinions, being open-minded and respectful, as well as actively listening and engaging in constructive dialogue are essential for meaningful and productive discussions.
Determine the minimised expression of Boolean function
F = X̅ Z̅ + Y̅ Z̅ + Y Z̅ + XYZ- a)X̅ Y̅ + Z
- b)Z̅ + XY
- c)X̅ Y + Z
- d)XYZ
Correct answer is option 'B'. Can you explain this answer?
Determine the minimised expression of Boolean function
F = X̅ Z̅ + Y̅ Z̅ + Y Z̅ + XYZ
F = X̅ Z̅ + Y̅ Z̅ + Y Z̅ + XYZ
a)
X̅ Y̅ + Z
b)
Z̅ + XY
c)
X̅ Y + Z
d)
XYZ
|
|
Ravi Singh answered |
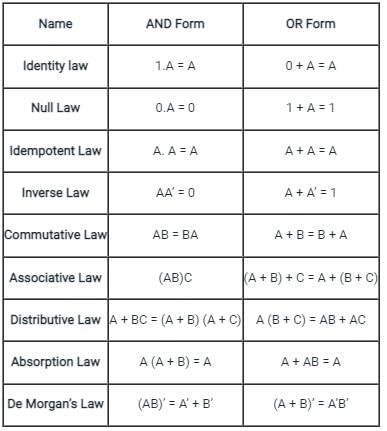
Concept:
All Boolean algebra laws are shown below
Calculation:
F = X̅ Z̅ + Y̅ Z̅ + Y Z̅ + XYZ
= X̅ Z̅ + Z̅ (Y̅ + Y) + XYZ
= X̅ Z̅ + Z̅ + XYZ
= Z̅ (1 + X̅) + XYZ
= Z̅ + XYZ
Now using Distributive Law
= (Z̅ + Z)(Z̅ + XY)
= Z̅ + XY

Calculation:
F = X̅ Z̅ + Y̅ Z̅ + Y Z̅ + XYZ
= X̅ Z̅ + Z̅ (Y̅ + Y) + XYZ
= X̅ Z̅ + Z̅ + XYZ
= Z̅ (1 + X̅) + XYZ
= Z̅ + XYZ
Now using Distributive Law
= (Z̅ + Z)(Z̅ + XY)
= Z̅ + XY
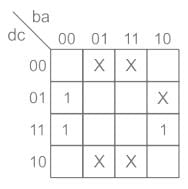
Consider the Karnaugh map given below. Where X represents “don’t care” and blank represents 0.
Assume for all inputs (a, b, c, d), the respective complements (a̅, b̅, c̅, d̅) are also available. The above logic is implemented using 2-input NOR gates only. The minimum number of gates required is ________.
Correct answer is '1'. Can you explain this answer?
Consider the Karnaugh map given below. Where X represents “don’t care” and blank represents 0.

Assume for all inputs (a, b, c, d), the respective complements (a̅, b̅, c̅, d̅) are also available. The above logic is implemented using 2-input NOR gates only. The minimum number of gates required is ________.

Assume for all inputs (a, b, c, d), the respective complements (a̅, b̅, c̅, d̅) are also available. The above logic is implemented using 2-input NOR gates only. The minimum number of gates required is ________.
|
|
Yash Patel answered |
Concept:
Draw the K- map, convert the K-map into a SOP (sum of product) or POS (product of sum) form. While reducing the K-map in these forms, a don’t care will be needed only when with the use of don’t cares we can reduce the term size.
Draw the K- map, convert the K-map into a SOP (sum of product) or POS (product of sum) form. While reducing the K-map in these forms, a don’t care will be needed only when with the use of don’t cares we can reduce the term size.
Diagram: K – Map

From the K-map simplification:
F(a, b, c, d) = a̅.c
Diagram:
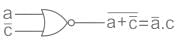
Therefore, only one NOR gate is needed to implement the minimized function

From the K-map simplification:
F(a, b, c, d) = a̅.c
Diagram:
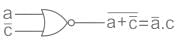
Therefore, only one NOR gate is needed to implement the minimized function
A ________ value is represented by a Boolean expression.- a)Positive
- b)Recursive
- c)Negative
- d)Boolean
Correct answer is option 'D'. Can you explain this answer?
A ________ value is represented by a Boolean expression.
a)
Positive
b)
Recursive
c)
Negative
d)
Boolean
|
|
Palak Shah answered |
Answer:
Boolean Value is represented by a Boolean Expression.
Boolean Value:
A Boolean value is a data type that has one of two possible values, which are typically represented as true and false. Boolean values are used in conditional statements and loops as a way to make decisions based on whether something is true or false.
Boolean Expression:
A Boolean expression is an expression that evaluates to a Boolean value. It consists of operands and operators that are used to test a condition. The operands can be variables, constants, or expressions that evaluate to a value, and the operators can be logical or relational.
Examples of Boolean expressions are:
- x > y
- a == b
- c != d
- x < y="" &&="" a="" /> b
- x == y || a < />
Conclusion:
Therefore, we can say that a Boolean value is represented by a Boolean expression. Boolean expressions are used to test conditions in programming and can have one of two possible values - true or false.
Boolean Value is represented by a Boolean Expression.
Boolean Value:
A Boolean value is a data type that has one of two possible values, which are typically represented as true and false. Boolean values are used in conditional statements and loops as a way to make decisions based on whether something is true or false.
Boolean Expression:
A Boolean expression is an expression that evaluates to a Boolean value. It consists of operands and operators that are used to test a condition. The operands can be variables, constants, or expressions that evaluate to a value, and the operators can be logical or relational.
Examples of Boolean expressions are:
- x > y
- a == b
- c != d
- x < y="" &&="" a="" /> b
- x == y || a < />
Conclusion:
Therefore, we can say that a Boolean value is represented by a Boolean expression. Boolean expressions are used to test conditions in programming and can have one of two possible values - true or false.
The logic gate that provides high output for same inputs ____________- a)NOT
- b)X-NOR
- c)AND
- d)XOR
Correct answer is option 'B'. Can you explain this answer?
The logic gate that provides high output for same inputs ____________
a)
NOT
b)
X-NOR
c)
AND
d)
XOR
|
|
Kaavya Deshpande answered |
The Logic Gate that provides High Output for same inputs is X-NOR gate.
Explanation:
The X-NOR gate is a digital logic gate that outputs a high (1) signal only when its two binary inputs are the same. In other words, it provides a high output when both inputs are either 0 or 1.
Truth Table:
To understand the behavior of the X-NOR gate, let's look at its truth table:
```
| Input A | Input B | Output |
|---------|---------|--------|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
```
From the truth table, we can observe that the X-NOR gate outputs a high (1) signal only when both inputs are the same. When both inputs are 0 or both inputs are 1, the X-NOR gate provides a high output.
Application:
The X-NOR gate is commonly used in various digital circuits and applications, such as:
1. Comparators: X-NOR gates can be used to compare two binary numbers or signals and determine if they are equal.
2. Parity Checkers: X-NOR gates are used to perform parity checks on data to detect errors.
3. Adders: X-NOR gates are used in the construction of adder circuits for binary arithmetic operations.
4. Multiplexers: X-NOR gates are used in multiplexer circuits to select one of multiple input signals based on control inputs.
Conclusion:
The X-NOR gate is the logic gate that provides a high output for the same inputs. It is a fundamental building block of digital logic circuits and finds applications in various fields of computer science and engineering.
Explanation:
The X-NOR gate is a digital logic gate that outputs a high (1) signal only when its two binary inputs are the same. In other words, it provides a high output when both inputs are either 0 or 1.
Truth Table:
To understand the behavior of the X-NOR gate, let's look at its truth table:
```
| Input A | Input B | Output |
|---------|---------|--------|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
```
From the truth table, we can observe that the X-NOR gate outputs a high (1) signal only when both inputs are the same. When both inputs are 0 or both inputs are 1, the X-NOR gate provides a high output.
Application:
The X-NOR gate is commonly used in various digital circuits and applications, such as:
1. Comparators: X-NOR gates can be used to compare two binary numbers or signals and determine if they are equal.
2. Parity Checkers: X-NOR gates are used to perform parity checks on data to detect errors.
3. Adders: X-NOR gates are used in the construction of adder circuits for binary arithmetic operations.
4. Multiplexers: X-NOR gates are used in multiplexer circuits to select one of multiple input signals based on control inputs.
Conclusion:
The X-NOR gate is the logic gate that provides a high output for the same inputs. It is a fundamental building block of digital logic circuits and finds applications in various fields of computer science and engineering.
Product-of-Sums expressions can be implemented using ___________- a)2-level OR-AND logic circuits
- b)2-level NOR logic circuits
- c)2-level XOR logic circuits
- d)Both 2-level OR-AND and NOR logic circuits
Correct answer is option 'D'. Can you explain this answer?
Product-of-Sums expressions can be implemented using ___________
a)
2-level OR-AND logic circuits
b)
2-level NOR logic circuits
c)
2-level XOR logic circuits
d)
Both 2-level OR-AND and NOR logic circuits
|
|
Sudhir Patel answered |
Product-of-Sums expressions can be implemented using 2-level OR-AND & NOR logic circuits.
How many AND and OR gates are required to realise Y = AB + BC + CD?- a)2,3
- b)2,2
- c)B and D
- d)3,1
Correct answer is option 'D'. Can you explain this answer?
How many AND and OR gates are required to realise Y = AB + BC + CD?
a)
2,3
b)
2,2
c)
B and D
d)
3,1

|
Talent Skill Learning answered |
To realise the expression Y = AB + BC + CD, follow these steps to determine the number of AND and OR gates required:
- Each product term (AB, BC, CD) needs an AND gate to combine the variables:
- AB needs 1 AND gate.
- BC needs 1 AND gate.
- CD needs 1 AND gate.
- An OR gate is used to sum the outputs of the AND gates:
- 1 OR gate for combining AB, BC, and CD.
Therefore, you need 3 AND gates and 1 OR gate.
Don’t care conditions can be used for simplifying Boolean expressions in ___________- a)Registers
- b)Terms
- c)K-maps
- d)Latches
Correct answer is option 'C'. Can you explain this answer?
Don’t care conditions can be used for simplifying Boolean expressions in ___________
a)
Registers
b)
Terms
c)
K-maps
d)
Latches
|
|
Sudhir Patel answered |
Don’t care conditions can be used for simplifying Boolean expressions in K-maps which helps in pairing with 1/0.
Identify the logic gate shown in the figure?
- a)XNOR
- b)NAND
- c)NOR
- d)XOR
Correct answer is option 'C'. Can you explain this answer?
Identify the logic gate shown in the figure?

a)
XNOR
b)
NAND
c)
NOR
d)
XOR
|
|
Sanya Agarwal answered |
NOR GATE:
Symbol:
Truth Table:
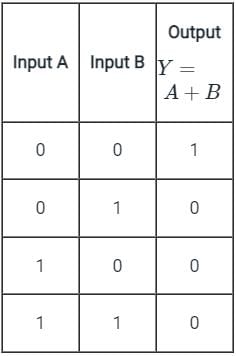
Output equation:
Y=A+B
Output is high only when all inputs are low.
It is a universal gate
Y=A+B
Output is high only when all inputs are low.
It is a universal gate
There are ______ cells in a 4-variable K-map.- a)12
- b)16
- c)18
- d)8
Correct answer is option 'B'. Can you explain this answer?
There are ______ cells in a 4-variable K-map.
a)
12
b)
16
c)
18
d)
8
|
|
Sudhir Patel answered |
There are 16 = (24) cells in a 4-variable K-map.
Solve the following Boolean expression:
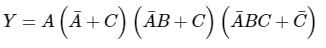
Select the correct option.- a)0
- b)A + B
- c)A̅ + BC
- d)1
Correct answer is option 'A'. Can you explain this answer?
Solve the following Boolean expression:
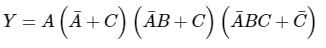
Select the correct option.
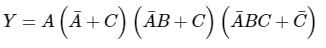
Select the correct option.
a)
0
b)
A + B
c)
A̅ + BC
d)
1
|
|
Sanya Agarwal answered |
Given Y = A (A̅ + C) (A̅B + C) (A̅BC + C̅)
This can be written as:
Y = (A.A̅ + AC) (A̅B + C) (A̅BC + C̅)
Since A.A̅ = 0, the above expression can be written as:
Y = (AC) (A̅B + C) (A̅BC + C̅)
Y = (AC.A̅B + AC.C) (A̅BC + C̅)
With C.C = C, we can write:
Y = (AC) (A̅BC + C̅)
Y = AC.A̅BC + AC.C̅
Y = 0 + 0
Y = 0
This can be written as:
Y = (A.A̅ + AC) (A̅B + C) (A̅BC + C̅)
Since A.A̅ = 0, the above expression can be written as:
Y = (AC) (A̅B + C) (A̅BC + C̅)
Y = (AC.A̅B + AC.C) (A̅BC + C̅)
With C.C = C, we can write:
Y = (AC) (A̅BC + C̅)
Y = AC.A̅BC + AC.C̅
Y = 0 + 0
Y = 0
Find the simplified term Y’ (X’ + Y’) (X + X’Y)?- a)XY’
- b)X’Y
- c)X + Y
- d)X’Y’
Correct answer is option 'A'. Can you explain this answer?
Find the simplified term Y’ (X’ + Y’) (X + X’Y)?
a)
XY’
b)
X’Y
c)
X + Y
d)
X’Y’
|
|
Yash Patel answered |
Given: Y’ (X’ + Y’) (X + X’Y)
= Y’(X’ + Y’)(X + Y)
= (X’Y’ + Y’)(X + Y)
= (XX’Y’ + X’Y’Y + XY’ + YY’)
= XY’.
= Y’(X’ + Y’)(X + Y)
= (X’Y’ + Y’)(X + Y)
= (XX’Y’ + X’Y’Y + XY’ + YY’)
= XY’.
Chapter doubts & questions for Boolean Algebra & Minimization Techniques - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Boolean Algebra & Minimization Techniques - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
453 videos|1305 docs|700 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup