All Exams >
Electrical Engineering (EE) >
6 Months Preparation for GATE Electrical >
All Questions
All questions of Three Phase Circuits (Star-Delta Transformations) for Electrical Engineering (EE) Exam
The value of the 3 resistances when connected in star connection is_________
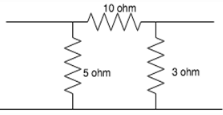
- a)2.32ohm,1.22ohm, 4.54ohm
- b)3.55ohm, 4.33ohm, 5.67ohm
- c)2.78ohm, 1.67ohm, 0.83ohm
- d)4.53ohm, 6.66ohm, 1.23ohm
Correct answer is option 'D'. Can you explain this answer?
The value of the 3 resistances when connected in star connection is_________

a)
2.32ohm,1.22ohm, 4.54ohm
b)
3.55ohm, 4.33ohm, 5.67ohm
c)
2.78ohm, 1.67ohm, 0.83ohm
d)
4.53ohm, 6.66ohm, 1.23ohm
|
|
Gargi Basak answered |
Following the delta to star conversion:
R1=10*5/(10+5+3)
R2=10*3/(10+5+3)
R3=5*3/(10+5+3).
R1=10*5/(10+5+3)
R2=10*3/(10+5+3)
R3=5*3/(10+5+3).
Delta connection is also known as____________- a)Y-connection
- b)Mesh connection
- c)Either Y-connection or mesh connection
- d)Neither Y-connection nor mesh connection
Correct answer is option 'B'. Can you explain this answer?
Delta connection is also known as____________
a)
Y-connection
b)
Mesh connection
c)
Either Y-connection or mesh connection
d)
Neither Y-connection nor mesh connection
|
|
Sanya Agarwal answered |
Delta connection is also known as mean connection because its structure is like a mesh, that is, a closed loop.
Star connection is also known as__________- a)Y-connection
- b)Mesh connection
- c)Either Y-connection or mesh connection
- d)Neither Y-connection nor mesh connection
Correct answer is option 'A'. Can you explain this answer?
Star connection is also known as__________
a)
Y-connection
b)
Mesh connection
c)
Either Y-connection or mesh connection
d)
Neither Y-connection nor mesh connection
|
|
Dipika Basak answered |
The star connection is also known as the Y-connection because its formation is like the letter Y.
Hence Option (A) is correct
For detailed chapter notes on Three Phase Circuits click on the link given below::
If a 6 ohm, 2ohm, and 4ohm resistor is connected in... more delta, find the equivalent star connection.
a)1ohm, 2ohm, 3ohm
b)2ohm, 4ohm, 7ohm
c)5ohm, 4ohm, 2ohm
d)1ohm, 2ohm, 2/3ohm
The correct answer is option 'D'.
Can you explain this answer?
|
|
Shivam Das answered |
Using the delta to star conversion formula:
R1=2*6/(2+6+4)= 1 ohm
R2=2*4/(2+6+4)= 2/3 ohm
R3=4*6/(2+6+4)= 2 ohm
Hence, The Correct Answer is Option D
You can learn more about Delta to Star Conversion by ging through the doc:
R1=2*6/(2+6+4)= 1 ohm
R2=2*4/(2+6+4)= 2/3 ohm
R3=4*6/(2+6+4)= 2 ohm
Hence, The Correct Answer is Option D
You can learn more about Delta to Star Conversion by ging through the doc:
A three-phase balanced delta connected load of (4 + j8) Ω is connected across a 400V, 3 – Ø balanced supply. Determine the phase current IR. Assume the phase sequence to be RYB.- a)44.74 ∠ -63.4⁰A
- b)44.74 ∠ 63.4⁰A
- c)45.74 ∠ -63.4⁰A
- d)45.74 ∠ 63.4⁰A
Correct answer is option 'A'. Can you explain this answer?
A three-phase balanced delta connected load of (4 + j8) Ω is connected across a 400V, 3 – Ø balanced supply. Determine the phase current IR. Assume the phase sequence to be RYB.
a)
44.74 ∠ -63.4⁰A
b)
44.74 ∠ 63.4⁰A
c)
45.74 ∠ -63.4⁰A
d)
45.74 ∠ 63.4⁰A
|
|
Ravi Singh answered |
Taking the line voltage VRY = V∠0⁰ as a reference VRY = 400∠0⁰V, VYB = 400 ∠ -120 ⁰V and VBR = 400∠-240⁰V. Impedance per phase = (4 + j8) Ω = 8.94∠63.4⁰Ω. Phase current IR = (400∠0o)/(8.94∠63.4o )= 44.74 ∠ -63.4⁰A.
If the load impedance is Z∠Ø, the current (IR) is?- a)(V/Z)∠-Ø
- b)(V/Z)∠Ø
- c)(V/Z)∠90-Ø
- d)(V/Z)∠-90+Ø
Correct answer is option 'A'. Can you explain this answer?
If the load impedance is Z∠Ø, the current (IR) is?
a)
(V/Z)∠-Ø
b)
(V/Z)∠Ø
c)
(V/Z)∠90-Ø
d)
(V/Z)∠-90+Ø
|
|
Zoya Sharma answered |
As the load impedance is Z∠Ø, the current flows in the three load impedances and the current flowing in the R impedance is IR = VBR∠0⁰/Z∠Ø = (V/Z)∠-Ø.
If a 4ohm, 3ohm and 2ohm resistor is connected in delta, find the equivalent star connection.- a)8/9ohm, 4/3ohm, 2/3ohm
- b)8/9ohm, 4/3ohm, 7/3ohm
- c)7/9ohm, 4/3ohm, 2/3ohm
- d)8/9ohm, 5/3ohm, 2/3ohm
Correct answer is option 'A'. Can you explain this answer?
If a 4ohm, 3ohm and 2ohm resistor is connected in delta, find the equivalent star connection.
a)
8/9ohm, 4/3ohm, 2/3ohm
b)
8/9ohm, 4/3ohm, 7/3ohm
c)
7/9ohm, 4/3ohm, 2/3ohm
d)
8/9ohm, 5/3ohm, 2/3ohm
|
|
Prasad Verma answered |
Using the delta-star conversion formula:
R1=4*3/(2+3+4)
R2=2*3/(2+3+4)
R3=2*4/(2+3+4).
R1=4*3/(2+3+4)
R2=2*3/(2+3+4)
R3=2*4/(2+3+4).
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the Y phase.- a)1000
- b)2000
- c)3000
- d)4000
Correct answer is option 'B'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the Y phase.
a)
1000
b)
2000
c)
3000
d)
4000
|
|
Ravi Singh answered |
The term power is defined as the product of square of current and the impedance. So the power in the Y phase = 102 x 20 = 2000W.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the line current I1.- a)(-51.96 - j10) A
- b)(-51.96 + j10) A
- c)(51.96 + j10) A
- d)(51.96 - j10) A
Correct answer is option 'C'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the line current I1.
a)
(-51.96 - j10) A
b)
(-51.96 + j10) A
c)
(51.96 + j10) A
d)
(51.96 - j10) A
|
|
Yash Patel answered |
The line current I1 is the difference of IR and IB. So the line current I1 is I1 = IR – IB = (51.96 + j10) A.
Which, among the following is the right expression for converting from delta to star?- a)R1=Ra*Rb/(Ra+Rb+Rc), R2=Rb*Rc/(Ra+Rb+Rc), R3=Rc*Ra/(Ra+Rb+Rc)
- b)R1=Ra/(Ra+Rb+Rc), R2=Rb/(Ra+Rb+Rc), Rc=/(Ra+Rb+Rc)
- c) R1=Ra*Rb*Rc/(Ra+Rb+Rc), R2=Ra*Rb/(Ra+Rb+Rc), R3=Ra/(Ra+Rb+Rc)
- d) R1=Ra*Rb*Rc/(Ra+Rb+Rc), R2=Ra*Rb*Rc/(Ra+Rb+Rc), R3=Ra*Rb*Rc/(Ra+Rb+Rc)
Correct answer is option 'A'. Can you explain this answer?
Which, among the following is the right expression for converting from delta to star?
a)
R1=Ra*Rb/(Ra+Rb+Rc), R2=Rb*Rc/(Ra+Rb+Rc), R3=Rc*Ra/(Ra+Rb+Rc)
b)
R1=Ra/(Ra+Rb+Rc), R2=Rb/(Ra+Rb+Rc), Rc=/(Ra+Rb+Rc)
c)
R1=Ra*Rb*Rc/(Ra+Rb+Rc), R2=Ra*Rb/(Ra+Rb+Rc), R3=Ra/(Ra+Rb+Rc)
d)
R1=Ra*Rb*Rc/(Ra+Rb+Rc), R2=Ra*Rb*Rc/(Ra+Rb+Rc), R3=Ra*Rb*Rc/(Ra+Rb+Rc)
|
|
Rounak Rane answered |
After converting to star, each star connected resistance is equal to the product of the resistances it is connected to and the total sum of the resistances. Hence R1=Ra*Rb/(Ra+Rb+Rc), R2=Rb*Rc/(Ra+Rb+Rc), R3=Rc*Ra/(Ra+Rb+Rc).
Rab is the resistance between the terminals A and B, Rbc between B and C and Rca between C and A. These 3 resistors are connected in star connection. After transforming to delta, the resistance at A will be?- a)Rc+Rb+Rc*Rb/Ra
- b)Rc+Rb+Ra*Rb/Rc
- c)Ra+Rb+Ra*Rc/Rb
- d)Rc+Rb+Rc*Ra/Rb
Correct answer is option 'A'. Can you explain this answer?
Rab is the resistance between the terminals A and B, Rbc between B and C and Rca between C and A. These 3 resistors are connected in star connection. After transforming to delta, the resistance at A will be?
a)
Rc+Rb+Rc*Rb/Ra
b)
Rc+Rb+Ra*Rb/Rc
c)
Ra+Rb+Ra*Rc/Rb
d)
Rc+Rb+Rc*Ra/Rb
|
|
Vaibhav Joshi answered |
After converting to delta, each delta connected resistance is equal to the sum of the two resistances it is connected to+product of the two resistances divided by the remaining resistance. Hence, resistance at A= Ra+Rb+Ra*Rb/Rc.
If a 8/9ohm, 4/3ohm and 2/3ohm resistor is connected in star, find its delta equivalent.- a)4ohm, 3ohm, 2ohm
- b)1ohm, 3ohm, 2ohm
- c)4ohm, 1ohm, 2ohm
- d)4ohm, 3ohm, 1ohm
Correct answer is option 'A'. Can you explain this answer?
If a 8/9ohm, 4/3ohm and 2/3ohm resistor is connected in star, find its delta equivalent.
a)
4ohm, 3ohm, 2ohm
b)
1ohm, 3ohm, 2ohm
c)
4ohm, 1ohm, 2ohm
d)
4ohm, 3ohm, 1ohm
|
|
Saumya Basak answered |
Using the formula for star to delta conversion:
R1=8/9+4/3+(8/9)*(4/3)/(2/3)
R2=8/9+2/3+(8/9)*(2/3)/(4/3)
R3=2/3+4/3+(2/3)*(4/3)/(8/9).
R1=8/9+4/3+(8/9)*(4/3)/(2/3)
R2=8/9+2/3+(8/9)*(2/3)/(4/3)
R3=2/3+4/3+(2/3)*(4/3)/(8/9).
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the B phase.- a)0
- b)1
- c)3
- d)2
Correct answer is option 'A'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the B phase.
a)
0
b)
1
c)
3
d)
2
|
|
Zoya Sharma answered |
The term power is defined as the product of square of current and the impedance. So the power in the B phase = 402 x 0 = 0W.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the R phase.- a)6628
- b)6728
- c)6828
- d)6928
Correct answer is option 'D'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the R phase.
a)
6628
b)
6728
c)
6828
d)
6928
|
|
Zoya Sharma answered |
The term power is defined as the product of square of current and the impedance. So the power in the R phase = 202 x 17.32 = 6928W.
In a balanced three-phase system-delta load, if we assume the line voltage is VRY = V∠0⁰ as a reference phasor. Then the source voltage VYB is?- a)V∠0⁰
- b)V∠-120⁰
- c)V∠120⁰
- d)V∠240⁰
Correct answer is option 'B'. Can you explain this answer?
In a balanced three-phase system-delta load, if we assume the line voltage is VRY = V∠0⁰ as a reference phasor. Then the source voltage VYB is?
a)
V∠0⁰
b)
V∠-120⁰
c)
V∠120⁰
d)
V∠240⁰
|
|
Swati Shah answered |
Phase voltage, then we can use the following formula to calculate the line current:
IL = IR + IY + IB
where IL is the line current, IR is the current flowing through the R phase, IY is the current flowing through the Y phase, and IB is the current flowing through the B phase.
We know that in a delta load, the line voltage is equal to the phase voltage, so we can substitute VRY for VR and get:
IL = IR + IY + IB = VR/R + VY/Y + VB/B
where R, Y, and B are the impedances of the load in the R, Y, and B phases, respectively.
Since the load is balanced, we can assume that R = Y = B = Z, where Z is the impedance of each phase. Therefore, we can simplify the equation to:
IL = (VR + VY + VB)/Z
Since the load is balanced, the phase currents are also equal, so we can use Ohm's Law to calculate the phase currents:
IR = VR/Z, IY = VY/Z, IB = VB/Z
Substituting these values into the equation for the line current, we get:
IL = (IR + IY + IB) = (VR/Z + VY/Z + VB/Z) = (VR + VY + VB)/Z
This confirms that the line current in a balanced three-phase system-delta load is equal to the sum of the phase currents divided by the impedance of each phase.
IL = IR + IY + IB
where IL is the line current, IR is the current flowing through the R phase, IY is the current flowing through the Y phase, and IB is the current flowing through the B phase.
We know that in a delta load, the line voltage is equal to the phase voltage, so we can substitute VRY for VR and get:
IL = IR + IY + IB = VR/R + VY/Y + VB/B
where R, Y, and B are the impedances of the load in the R, Y, and B phases, respectively.
Since the load is balanced, we can assume that R = Y = B = Z, where Z is the impedance of each phase. Therefore, we can simplify the equation to:
IL = (VR + VY + VB)/Z
Since the load is balanced, the phase currents are also equal, so we can use Ohm's Law to calculate the phase currents:
IR = VR/Z, IY = VY/Z, IB = VB/Z
Substituting these values into the equation for the line current, we get:
IL = (IR + IY + IB) = (VR/Z + VY/Z + VB/Z) = (VR + VY + VB)/Z
This confirms that the line current in a balanced three-phase system-delta load is equal to the sum of the phase currents divided by the impedance of each phase.
In wye or star connection _____________ of the three phases are joined together within the alternator.- a)similar ends
- b)opposite ends
- c)one similar end, two opposite ends
- d)one opposite end, two opposite ends
Correct answer is option 'A'. Can you explain this answer?
In wye or star connection _____________ of the three phases are joined together within the alternator.
a)
similar ends
b)
opposite ends
c)
one similar end, two opposite ends
d)
one opposite end, two opposite ends
|
|
Pooja Patel answered |
In wye or star connection, similar ends of the three phases are joined together within the alternator. The common terminal so formed is referred to as the neutral point or neutral terminal.
In a balanced three-phase system-delta load, if we assume the line voltage is VRY = V∠0⁰ as a reference phasor. Then the source voltage VBR is?- a)V∠120⁰
- b)V∠240⁰
- c)V∠-240⁰
- d)V∠-120⁰
Correct answer is option 'C'. Can you explain this answer?
In a balanced three-phase system-delta load, if we assume the line voltage is VRY = V∠0⁰ as a reference phasor. Then the source voltage VBR is?
a)
V∠120⁰
b)
V∠240⁰
c)
V∠-240⁰
d)
V∠-120⁰
|
|
Avik Saha answered |
In a balanced three-phase system-delta load, the line voltage is related to the phase voltage by a factor of √3. Therefore, if we assume the phase voltage is V, then the line voltage will be √3 times the phase voltage.
So, the line voltage can be written as:
Vline = √3 V
If we assume that the phase voltage is VRY, then we can write:
VRY = V
Substituting this into the equation for the line voltage, we get:
Vline = √3 VRY
Therefore, in this case, the line voltage is √3 times the phase voltage, just like in any other balanced three-phase system-delta load.
So, the line voltage can be written as:
Vline = √3 V
If we assume that the phase voltage is VRY, then we can write:
VRY = V
Substituting this into the equation for the line voltage, we get:
Vline = √3 VRY
Therefore, in this case, the line voltage is √3 times the phase voltage, just like in any other balanced three-phase system-delta load.
Which, among the following is the correct expression for star-delta conversion?- a)R1=Ra*Rb/(Ra+Rb+Rc), R2=Rb*Rc/(Ra+Rb+Rc), R3=Rc*Ra/(Ra+Rb+Rc)b)
- b)R1=Ra/(Ra+Rb+Rc), R2=Rb/(Ra+Rb+Rc), Rc=/(Ra+Rb+Rc)
- c)R1=Ra+Rb+Ra*Rb/Rc, R2=Rc+Rb+Rc*Rb/Ra, R3=Ra+Rc+Ra*Rc/Rb
- d)R1=Ra*Rb/Rc, R2=Rc*Rb/Ra, R3=Ra*Rc/Rb
Correct answer is option 'C'. Can you explain this answer?
Which, among the following is the correct expression for star-delta conversion?
a)
R1=Ra*Rb/(Ra+Rb+Rc), R2=Rb*Rc/(Ra+Rb+Rc), R3=Rc*Ra/(Ra+Rb+Rc)b)
b)
R1=Ra/(Ra+Rb+Rc), R2=Rb/(Ra+Rb+Rc), Rc=/(Ra+Rb+Rc)
c)
R1=Ra+Rb+Ra*Rb/Rc, R2=Rc+Rb+Rc*Rb/Ra, R3=Ra+Rc+Ra*Rc/Rb
d)
R1=Ra*Rb/Rc, R2=Rc*Rb/Ra, R3=Ra*Rc/Rb
|
|
Niti Tiwari answered |
After converting to delta, each delta connected resistance is equal to the sum of the two resistance it is connected to+product of the two resistances divided by the remaining resistance. Hence R1=Ra+Rb+Ra*Rb/Rc, R2=Rc+Rb+Rc*Rb/Ra, R3=Ra+Rc+Ra*Rc/Rb.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Determine the phase current IR.- a)(17.32 - j10) A
- b)(-17.32 - j10) A
- c)(17.32 + j10) A
- d)(-17.32 + j10) A
Correct answer is option 'A'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Determine the phase current IR.
a)
(17.32 - j10) A
b)
(-17.32 - j10) A
c)
(17.32 + j10) A
d)
(-17.32 + j10) A
|
|
Mira Mukherjee answered |
Impedances Calculation:
- Given impedances: Z1= 20∠30, Z2= 40∠60, Z3= 10∠-90
- Convert delta impedances to star impedances: Zs = Zd/3
- Zs1 = 20/3∠30, Zs2 = 40/3∠60, Zs3 = 10/3∠-90
Equivalent Star Impedance Calculation:
- Calculate equivalent impedance in star connection: Zs = Zs1 + Zs2 + Zs3
- Zs = (20/3∠30) + (40/3∠60) + (10/3∠-90)
Calculate Phase Current:
- Phase voltage (Vph) = Line voltage (Vline) / √3
- Vph = 400 / √3
- Calculate phase current (I) using Ohm's Law: I = Vph / Zs
Therefore, the phase current IR is 17.32∠-10A which is equivalent to (17.32 - j10) A.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the phase current IB.- a)(34.64 - j20) A
- b)(34.64 + j20) A
- c)(-34.64 + j20) A
- d)(-34.64 - j20) A
Correct answer is option 'D'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the phase current IB.
a)
(34.64 - j20) A
b)
(34.64 + j20) A
c)
(-34.64 + j20) A
d)
(-34.64 - j20) A
|
|
Pooja Patel answered |
The voltage VBR is VBR = 400 ∠ -240⁰V. The impedance Z3 is Z3 = 10 ∠ -90⁰Ω
⇒ IB = (400 ∠ 240o)/(10 ∠ -90o) = (-34.64-j20)A.
⇒ IB = (400 ∠ 240o)/(10 ∠ -90o) = (-34.64-j20)A.
If the system is a three-wire system, the currents flowing towards the load in the three lines must add to ___ at any given instant.- a)1
- b)2
- c)3
- d)zero
Correct answer is option 'D'. Can you explain this answer?
If the system is a three-wire system, the currents flowing towards the load in the three lines must add to ___ at any given instant.
a)
1
b)
2
c)
3
d)
zero
|
|
Rajesh Saha answered |
Explanation:
Three-Wire System:
In a three-wire system, there are three conductors - typically labeled as A, B, and C. These conductors carry the three-phase currents to the load.
Kirchhoff's Current Law (KCL):
According to Kirchhoff's Current Law, the algebraic sum of currents entering a node (or a point) in an electrical circuit is zero. This law is based on the principle of conservation of charge.
Currents in Three-Wire System:
In a three-wire system, the currents flowing towards the load in the three lines must add up to zero at any given instant. This is because the total current entering the load must be equal to the total current leaving the load, according to KCL.
Explanation:
- If the currents flowing towards the load in the three lines do not add up to zero, it would imply a violation of KCL.
- Any imbalance in the currents could lead to issues such as overheating of conductors, voltage fluctuations, and potential damage to the electrical system.
Therefore, in a three-wire system, the currents in the three lines must always sum up to zero at any given instant to ensure the proper functioning and balance of the electrical system.
Three-Wire System:
In a three-wire system, there are three conductors - typically labeled as A, B, and C. These conductors carry the three-phase currents to the load.
Kirchhoff's Current Law (KCL):
According to Kirchhoff's Current Law, the algebraic sum of currents entering a node (or a point) in an electrical circuit is zero. This law is based on the principle of conservation of charge.
Currents in Three-Wire System:
In a three-wire system, the currents flowing towards the load in the three lines must add up to zero at any given instant. This is because the total current entering the load must be equal to the total current leaving the load, according to KCL.
Explanation:
- If the currents flowing towards the load in the three lines do not add up to zero, it would imply a violation of KCL.
- Any imbalance in the currents could lead to issues such as overheating of conductors, voltage fluctuations, and potential damage to the electrical system.
Therefore, in a three-wire system, the currents in the three lines must always sum up to zero at any given instant to ensure the proper functioning and balance of the electrical system.
The voltage between ______________ is called line voltage.- a)line and neutral point
- b)line and reference
- c)line and line
- d)neutral point and reference
Correct answer is option 'C'. Can you explain this answer?
The voltage between ______________ is called line voltage.
a)
line and neutral point
b)
line and reference
c)
line and line
d)
neutral point and reference
|
|
Pooja Patel answered |
The voltage between line and line is called line voltage. And the voltage between line and neutral point is called phase voltage. The currents flowing through the phases are called the phase currents, while those flowing in the lines are called the line currents.
Determine the power (kW) drawn by the load.- a)21
- b)22
- c)23
- d)24
Correct answer is option 'D'. Can you explain this answer?
Determine the power (kW) drawn by the load.
a)
21
b)
22
c)
23
d)
24
|
|
Muskaan Nair answered |
Given, voltage (V) = 230V, current (I) = 105A, power factor (PF) = 0.8
To find the power (P) drawn by the load, we can use the formula:
P = V × I × PF
Substituting the given values, we get:
P = 230V × 105A × 0.8
P = 19320W or 19.32kW
Therefore, the correct answer is option 'D', 24 kW.
To find the power (P) drawn by the load, we can use the formula:
P = V × I × PF
Substituting the given values, we get:
P = 230V × 105A × 0.8
P = 19320W or 19.32kW
Therefore, the correct answer is option 'D', 24 kW.
Find the equivalent resistance between A and B.
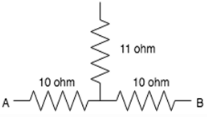
- a)32ohm
- b)31ohm
- c)30ohm
- d)29ohm
Correct answer is option 'D'. Can you explain this answer?
Find the equivalent resistance between A and B.

a)
32ohm
b)
31ohm
c)
30ohm
d)
29ohm
|
|
Sparsh Saini answered |
The equivalent resistance between node 1 and node 3 in the star connected circuit is R=(10×10+10×11+11×10)/11=29ohm.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the phase current IY.- a)(10 - j0) A
- b)(10 + j0) A
- c)(-10 + j0) A
- d)(-10 - j0) A
Correct answer is option 'C'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the phase current IY.
a)
(10 - j0) A
b)
(10 + j0) A
c)
(-10 + j0) A
d)
(-10 - j0) A
|
|
Yash Patel answered |
The voltage VYB is VYB = 400 ∠ -120⁰V. The impedance Z2 is Z2 = 40 ∠ 60⁰Ω
⇒ IY = (400 ∠ -120o)/(40 ∠ 60o)=(-10 + j0)A.
Find the equivalent resistance between X and Y.

- a)3.33 ohm
- b)4.34 ohm
- c)5.65 ohm
- d)2.38 ohm
Correct answer is option 'D'. Can you explain this answer?
Find the equivalent resistance between X and Y.

a)
3.33 ohm
b)
4.34 ohm
c)
5.65 ohm
d)
2.38 ohm
|
|
Ishan Saini answered |
The 3 2ohm resistors are connected in star, changing them to delta, we have R1=R2=R3= 2+2+2*2/2=6 ohm.
The 3 6ohm resistors are connected in parallel to the 10 ohm 5 ohm and 10ohm resistors respectively.
This network can be further reduced to a network consisting of a 3.75ohm and 2.73ohm resistor connected in series whose resultant is intern connected in parallel to the 3.75 ohm resistor.
The 3 6ohm resistors are connected in parallel to the 10 ohm 5 ohm and 10ohm resistors respectively.
This network can be further reduced to a network consisting of a 3.75ohm and 2.73ohm resistor connected in series whose resultant is intern connected in parallel to the 3.75 ohm resistor.
Find the equivalent delta circuit.
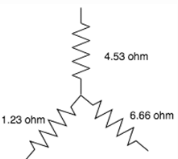
- a)3ohm, 10ohm, 5ohm
- b)3ohm, 10ohm, 15ohm
- c)3ohm, 1ohm, 5ohm
- d)3ohm, 10ohm, 6ohm
Correct answer is option 'A'. Can you explain this answer?
Find the equivalent delta circuit.

a)
3ohm, 10ohm, 5ohm
b)
3ohm, 10ohm, 15ohm
c)
3ohm, 1ohm, 5ohm
d)
3ohm, 10ohm, 6ohm
|
|
Bijoy Mehta answered |
Using the star to delta conversion:
R1=4.53+6.66+4.53*6.66/1.23
R2=4.53+1.23+4.53*1.23/6.66
R3=1.23+6.66+1.23*6.66/4.56.
R1=4.53+6.66+4.53*6.66/1.23
R2=4.53+1.23+4.53*1.23/6.66
R3=1.23+6.66+1.23*6.66/4.56.
If the load impedance is Z∠Ø, the expression obtained for current (IY) is?- a)(V/Z)∠-120+Ø
- b)(V/Z)∠120-Ø
- c)(V/Z)∠120+Ø
- d)(V/Z)∠-120-Ø
Correct answer is option 'D'. Can you explain this answer?
If the load impedance is Z∠Ø, the expression obtained for current (IY) is?
a)
(V/Z)∠-120+Ø
b)
(V/Z)∠120-Ø
c)
(V/Z)∠120+Ø
d)
(V/Z)∠-120-Ø
|
|
Yash Patel answered |
As the load impedance is Z∠Ø, the current flows in the three load impedances and the current flowing in the Y impedance is IY = VYB∠120⁰/Z∠Ø = (V/Z)∠-120-Ø.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the line current I2.- a)(-27.32 + j10) A
- b)(27.32 + j10) A
- c)(-27.32 - j10) A
- d)(27.32 - j10) A
Correct answer is option 'A'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the line current I2.
a)
(-27.32 + j10) A
b)
(27.32 + j10) A
c)
(-27.32 - j10) A
d)
(27.32 - j10) A
|
|
Pooja Patel answered |
The line current I2 is the difference of IY and IR. So the line current I2 is I2 = IY – IR = (-27.32 + j10) A.
Find the current in the circuit.

- a)0.54A
- b)0.65A
- c)0.67A
- d)0.87A
Correct answer is option 'A'. Can you explain this answer?
Find the current in the circuit.

a)
0.54A
b)
0.65A
c)
0.67A
d)
0.87A
|
|
Shivani Saha answered |
The 3 5 ohm resistors are connected in delta. Changing it to star:
R1=R2=R3= 1.67 ohm.
One of the 1.67 ohm resistors are connected in series with the 2 ohm resistor and another 1.67 ohm resistor is connected in series to the 3 ohm resistor.
The resulting network has a 1.67 ohm resistor connected in series with the parallel connection of the 3.67 and 4.67 resistors.
The equivalent resistance is: 3.725A.
I=2/3.725= 0.54A.
R1=R2=R3= 1.67 ohm.
One of the 1.67 ohm resistors are connected in series with the 2 ohm resistor and another 1.67 ohm resistor is connected in series to the 3 ohm resistor.
The resulting network has a 1.67 ohm resistor connected in series with the parallel connection of the 3.67 and 4.67 resistors.
The equivalent resistance is: 3.725A.
I=2/3.725= 0.54A.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the line current I3.- a)(24.646 + j20) A
- b)(-24.646 + j20) A
- c)(-24.646 - j20) A
- d)(24.646 - j20) A
Correct answer is option 'C'. Can you explain this answer?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the line current I3.
a)
(24.646 + j20) A
b)
(-24.646 + j20) A
c)
(-24.646 - j20) A
d)
(24.646 - j20) A
|
|
Ravi Singh answered |
The line current I3 is the difference of IB and IY. So the line current I3 is I3 = IB – IY = (-24.646 - j20) A.
In a delta-connected load, the relation between line voltage and the phase voltage is?- a)line voltage > phase voltage
- b)line voltage < phase voltage
- c)line voltage = phase voltage
- d)line voltage >= phase voltage
Correct answer is option 'C'. Can you explain this answer?
In a delta-connected load, the relation between line voltage and the phase voltage is?
a)
line voltage > phase voltage
b)
line voltage < phase voltage
c)
line voltage = phase voltage
d)
line voltage >= phase voltage
|
|
Yash Patel answered |
In a delta-connected load, the relation between line voltage and the phase voltage is line voltage = phase voltage.
Find the equivalent star network.

- a)2.3ohm, 2.3ohm, 2.3ohm
- b)1.2ohm, 1.2ohm, 1.2ohm
- c)3.3ohm, 3.3ohm, 3.3ohm
- d)4.5ohm, 4.5ohm, 4.5ohm
Correct answer is option 'B'. Can you explain this answer?
Find the equivalent star network.

a)
2.3ohm, 2.3ohm, 2.3ohm
b)
1.2ohm, 1.2ohm, 1.2ohm
c)
3.3ohm, 3.3ohm, 3.3ohm
d)
4.5ohm, 4.5ohm, 4.5ohm
|
|
Devansh Das answered |
The 6 ohm and 9 ohm resistances are connected in parallel. Their equivalent resistances are: 6*9/(9+6)=3.6 ohm.
The 3 3.6 ohm resistors are connected in delta. Converting to star:
R1=R2=R3= 3.6*3.6/(3.6+3.6+3.6)=1.2 ohm.
The 3 3.6 ohm resistors are connected in delta. Converting to star:
R1=R2=R3= 3.6*3.6/(3.6+3.6+3.6)=1.2 ohm.
Chapter doubts & questions for Three Phase Circuits (Star-Delta Transformations) - 6 Months Preparation for GATE Electrical 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Three Phase Circuits (Star-Delta Transformations) - 6 Months Preparation for GATE Electrical in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
6 Months Preparation for GATE Electrical
675 videos|1297 docs|786 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup












