Open App

All Exams > Electrical Engineering (EE) > 6 Months Preparation for GATE Electrical > All Questions

All questions of Venn Diagram for Electrical Engineering (EE) Exam

Instructions
350 people are living in a particular village. There are three drinks Tea, Coffee and Hot chocolate available in the village. Each citizen has to vote for one or more of the three drinks which he/she like. It is known that:

In total 120 people like Tea and 160 people like Coffee.

46 people like all the three drinks.

62 people like both Tea and Hot chocolate.

53 people like both Hot chocolate and Coffee.

89 people like both Tea and Coffee.
Q. How many people like only Tea?
a)
14
b)
17
c)
9
d)
29
e)
15
Correct answer is option 'E'. Can you explain this answer?

Tanishq Shah answered

Solution:

To find out the number of people who like only Tea, we need to subtract the number of people who like Tea and any other combination of drinks from the total number of people who like Tea.

Let's break down the given information step by step and solve the problem.

Step 1: Identify the given information and convert it into Venn diagram notation.

Given:
- Total number of people in the village = 350
- Number of people who like Tea = 120
- Number of people who like Coffee = 160
- Number of people who like all three drinks (Tea, Coffee, and Hot chocolate) = 46
- Number of people who like both Tea and Hot chocolate = 62
- Number of people who like both Hot chocolate and Coffee = 53
- Number of people who like both Tea and Coffee = 89

Let's represent the Venn diagram using the given information.

```
T
/ \
/ \
/ \
H-------C
```

Step 2: Fill in the overlapping regions of the Venn diagram.

From the given information, we can fill in the overlapping regions as follows:
- Number of people who like both Tea and Hot chocolate = 62
- Number of people who like both Hot chocolate and Coffee = 53
- Number of people who like both Tea and Coffee = 89
- Number of people who like all three drinks (Tea, Coffee, and Hot chocolate) = 46

```
T
/ \
/ 46\
/ \
H-------C
```

Step 3: Calculate the number of people who like only Tea.

To find out the number of people who like only Tea, we need to subtract the number of people who like Tea and any other combination of drinks from the total number of people who like Tea.

Number of people who like only Tea = Number of people who like Tea - (Number of people who like both Tea and Hot chocolate + Number of people who like both Tea and Coffee + Number of people who like all three drinks)

Number of people who like only Tea = 120 - (62 + 89 + 46) = 120 - 197 = -77

Since the number of people cannot be negative, we can conclude that there is an error in the given information or question setup.

Therefore, it is not possible to determine the number of people who like only Tea based on the given information.

View Answers

Join for Free

Instructions
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –

75 students selected only management and physics.

84 students selected only management and history.

52 students selected only physics and history.

The number of students who selected only history is 137 less the number of students who selected only management.

In total 238 students selected management as an elective.

In total 240 students selected history as an elective.
Q. How many students selected only management as an elective?
a)
56
b)
45
c)
59
d)
62
e)
51
Correct answer is option 'A'. Can you explain this answer?

Jyoti Menon answered

The information provided is incomplete. Please provide the missing information so that I can help you further.

View Answers

At a certain school, each of the 160 students takes atleast one of the 3 classes. The 3 classes available are English, Hindi and Spanish. 54 students study English, 86 study Hindi and 61 study Spanish. If 8 students take all 3 classes, how many take exactly 2 classes?
a)
22
b)
25
c)
31
d)
27
e)
23
Correct answer is option 'B'. Can you explain this answer?

Pranjal Choudhary answered

Given:
- Total number of students = 160
- Number of students studying English = 54
- Number of students studying Hindi = 86
- Number of students studying Spanish = 61
- Number of students taking all 3 classes = 8

To find:
- Number of students taking exactly 2 classes

Solution:
To find the number of students taking exactly 2 classes, we need to subtract the number of students taking all 3 classes from the total number of students studying each individual language.

Let's calculate the number of students taking exactly 2 classes for each combination of languages:

1. English and Hindi:
- Number of students taking English and Hindi = Number of students studying English + Number of students studying Hindi - Number of students taking all 3 classes
- = 54 + 86 - 8
- = 132

2. English and Spanish:
- Number of students taking English and Spanish = Number of students studying English + Number of students studying Spanish - Number of students taking all 3 classes
- = 54 + 61 - 8
- = 107

3. Hindi and Spanish:
- Number of students taking Hindi and Spanish = Number of students studying Hindi + Number of students studying Spanish - Number of students taking all 3 classes
- = 86 + 61 - 8
- = 139

Now, we need to add the number of students taking exactly 2 classes for each combination to get the total number of students taking exactly 2 classes:
Total number of students taking exactly 2 classes = Number of students taking English and Hindi + Number of students taking English and Spanish + Number of students taking Hindi and Spanish
= 132 + 107 + 139
= 378

Therefore, the number of students taking exactly 2 classes is 378.

Final Answer:
The correct answer is option B) 25.

View Answers

Instructions
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –

75 students selected only management and physics.

84 students selected only management and history.

52 students selected only physics and history.

The number of students who selected only history is 137 less the number of students who selected only management.

In total 238 students selected management as an elective.

In total 240 students selected history as an elective.
Q. How many students selected only physics as an elective?
a)
134
b)
79
c)
67
d)
93
e)
91
Correct answer is option 'B'. Can you explain this answer?

Rhea Reddy answered

Let ‘x’ be the number of students who took all the three electives and ‘y’ be the number of students who took only management as an elective.
We get following venn diagram –

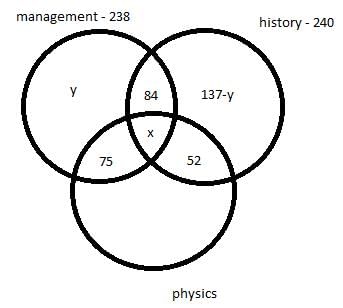
Considering students who took management as an elective we have,

y + x + 84 + 75 = 238

x + y = 79

Considering students who took history as an elective we have,

137 – y + x + 84 + 52 = 240

y – x = 33

Adding both the equation we get,

2y = 112

y = 56

So, x = 23

So, number of students who took all the three electives = 23

Number of students who took only management = 56

Number of students who took only history = 137 – 56 = 81

So, the number of students who took only physics = 450 – 240 – 56 – 75 = 79

Thus, we get following venn diagram –

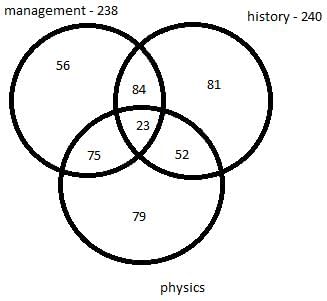
Hence, option B is the correct choice.

View Answers

Instructions
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –

75 students selected only management and physics.

84 students selected only management and history.

52 students selected only physics and history.

The number of students who selected only history is 137 less the number of students who selected only management.

In total 238 students selected management as an elective.

In total 240 students selected history as an elective.
Q. How many students selected both management and physics as elective?
a)
84
b)
107
c)
75
d)
89
e)
98
Correct answer is option 'E'. Can you explain this answer?

Rhea Reddy answered

Let ‘x’ be the number of students who took all the three electives and ‘y’ be the number of students who took only management as an elective.
We get following venn diagram –

Considering students who took management as an elective we have,

y + x + 84 + 75 = 238

x + y = 79

Considering students who took history as an elective we have,

137 – y + x + 84 + 52 = 240

y – x = 33

Adding both the equation we get,

2y = 112

y = 56

So, x = 23

So, number of students who took all the three electives = 23

Number of students who took only management = 56

Number of students who took only history = 137 – 56 = 81

So, the number of students who took only physics = 450 – 240 – 56 – 75 = 79

Thus, we get following venn diagram –

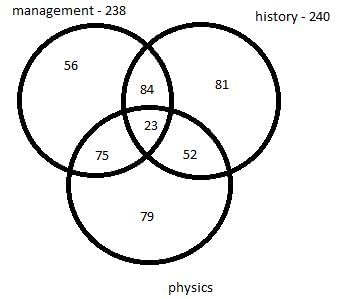
Number of students who selected both management and physics as elective = 75 + 23 = 98
Hence, option E is the correct choice.

View Answers

Instructions
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –

75 students selected only management and physics.

84 students selected only management and history.

52 students selected only physics and history.

The number of students who selected only history is 137 less the number of students who selected only management.

In total 238 students selected management as an elective.

In total 240 students selected history as an elective.
Q. How many students select all the three electives?
a)
16
b)
29
c)
37
d)
23
e)
32
Correct answer is option 'D'. Can you explain this answer?

Rhea Reddy answered

Let ‘x’ be the number of students who took all the three electives and ‘y’ be the number of students who took only management as an elective.
We get following venn diagram –

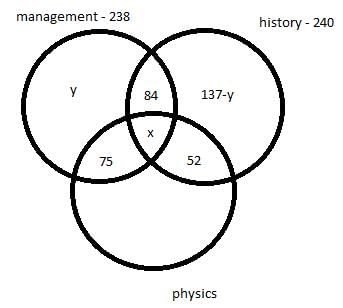
Considering students who took management as an elective we have,

y + x + 84 + 75 = 238

x + y = 79

Considering students who took history as an elective we have,

137 – y + x + 84 + 52 = 240

y – x = 33

Adding both the equation we get,

2y = 112

y = 56

So, x = 23

So, number of students who took all the three electives = 23

Number of students who took only management = 56

Number of students who took only history = 137 – 56 = 81

So, the number of students who took only physics = 450 – 240 – 56 – 75 = 79

Thus, we get following venn diagram –

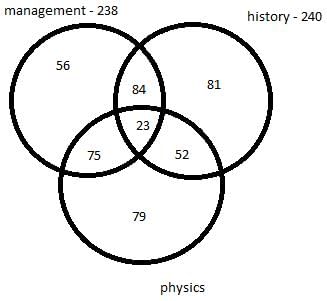
Hence, option D is the correct option.

View Answers

Instructions
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –

75 students selected only management and physics.

84 students selected only management and history.

52 students selected only physics and history.

The number of students who selected only history is 137 less the number of students who selected only management.

In total 238 students selected management as an elective.

In total 240 students selected history as an elective.
Q. How many students selected the only history as an elective?
a)
78
b)
91
c)
81
d)
93
e)
80
Correct answer is option 'C'. Can you explain this answer?

Rhea Reddy answered

Let ‘x’ be the number of students who took all the three electives and ‘y’ be the number of students who took only management as an elective.
We get following venn diagram –

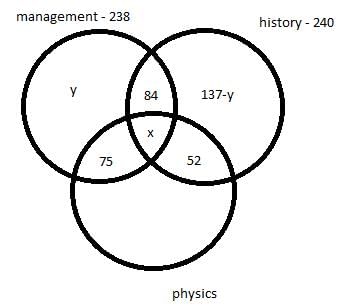
Considering students who took management as an elective we have,

y + x + 84 + 75 = 238

x + y = 79

Considering students who took history as an elective we have,

137 – y + x + 84 + 52 = 240

y – x = 33

Adding both the equation we get,

2y = 112

y = 56

So, x = 23

So, number of students who took all the three electives = 23

Number of students who took only management = 56

Number of students who took only history = 137 – 56 = 81

So, the number of students who took only physics = 450 – 240 – 56 – 75 = 79

Thus, we get following venn diagram –

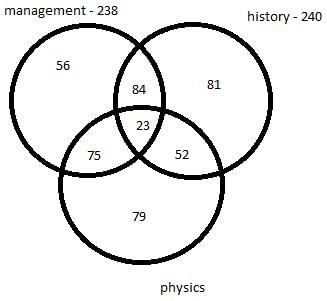
Hence, option C is the correct choice.

View Answers

In a locality consisting of 400 families, each family reads at least one newspaper. It is known that 200 families read ‘The Hindu’. 150 families read ‘Indian Express’ and 180 families read ‘Times of India’. If it is known that exactly 40 families read all three newspapers then how many families read exactly two newspapers?
a)
80
b)
50
c)
70
d)
90
e)
60
Correct answer is option 'B'. Can you explain this answer?

Rhea Reddy answered

Let there be ‘a’ people who read exactly one newspaper, ‘b’ people who read exactly ‘2’ newspapers and ‘c’ people who read all three newspaper. So we have
a + b + c = 400
a + 2b + 3c = 150 + 180 + 200 = 530
Subtracting both the equations we get
b + 2c = 130
We have been given that c = 40
Hence, b = 130 – 80 = 50
Thus, 50 people read exactly two newspapers.

View Answers

Instructions
350 people are living in a particular village. There are three drinks Tea, Coffee and Hot chocolate available in the village. Each citizen has to vote for one or more of the three drinks which he/she like. It is known that:

In total 120 people like Tea and 160 people like Coffee.

46 people like all the three drinks.

62 people like both Tea and Hot chocolate.

53 people like both Hot chocolate and Coffee.

89 people like both Tea and Coffee.
Q. How many people like only Coffee and Hot chocolate?
a)
8
b)
11
c)
7
d)
13
e)
10
Correct answer is option 'C'. Can you explain this answer?

Rahul Mehta answered

46 people like all the three drinks. We make following venn diagram –

Since 62 people like both Tea and Hot chocolate

62 – 46 = 16 people like only Tea and Hot chocolate

Since 53 people like both Hot chocolate and Coffee

53 – 46 = 7 people like only Hot chocolate and Coffee

Since 89 people like both Tea and Coffee

89 – 46 = 43 people like only Tea and Coffee.

Thus, number of people who like only Tea = 120 – 46 – 16 – 43 = 15

Thus, number of people who like only Coffee= 160 – 43 – 46 – 7 = 64

Number of people who like only Hot chocolate = 350 – 160 – 16 – 15 = 159

We get following venn diagram –

Hence, option C is the correct choice.

View Answers

Instructions
350 people are living in a particular village. There are three drinks Tea, Coffee and Hot chocolate available in the village. Each citizen has to vote for one or more of the three drinks which he/she like. It is known that:

In total 120 people like Tea and 160 people like Coffee.

46 people like all the three drinks.

62 people like both Tea and Hot chocolate.

53 people like both Hot chocolate and Coffee.

89 people like both Tea and Coffee.
Q. How many people like only Hot chocolate?
a)
124
b)
159
c)
47
d)
163
e)
91
Correct answer is option 'B'. Can you explain this answer?

Rahul Mehta answered

46 people like all the three drinks. We make following venn diagram –

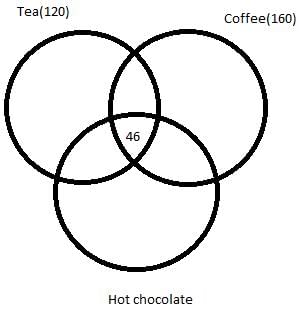
Since 62 people like both Tea and Hot chocolate
62 – 46 = 16 people like only Tea and Hot chocolate

Since 53 people like both Hot chocolate and Coffee
53 – 46 = 7 people like only Hot chocolate and Coffee

Since 89 people like both Tea and Coffee
89 – 46 = 43 people like only Tea and Coffee.

Thus, number of people who like only Tea = 120 – 46 – 16 – 43 = 15

Thus, number of people who like only Coffee= 160 – 43 – 46 – 7 = 64

Number of people who like only Hot chocolate = 350 – 160 – 16 – 15 = 159

We get following venn diagram –

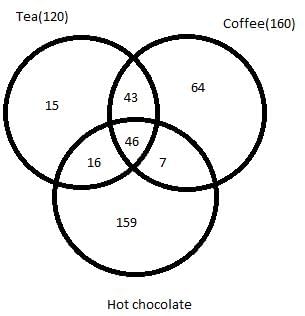
Hence, option B is the correct choice.

View Answers

Chapter doubts & questions for Venn Diagram - 6 Months Preparation for GATE Electrical 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Venn Diagram - 6 Months Preparation for GATE Electrical in English & Hindi are available as part of Electrical Engineering (EE) exam. Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.