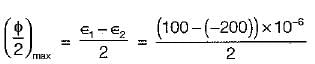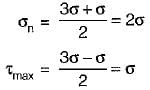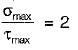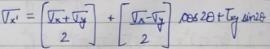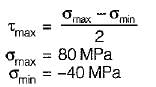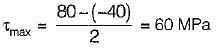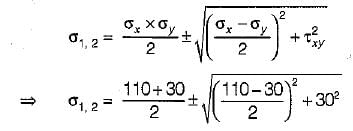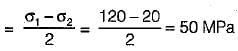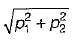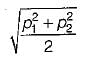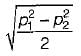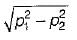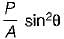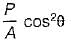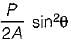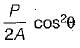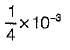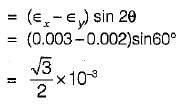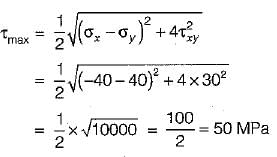All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Principal Stresses & Strains (Mohr's Circle) for Mechanical Engineering Exam
The radius of Mohr’s circle of stress of a strained element is 20 N/mm2 and minor principal tensile stress is 10 N/mm2; The major principal stress is- a)30N/mm2
- b)50 N/mm2
- c)60 N/mm2
- d)100 N/mm2
Correct answer is option 'B'. Can you explain this answer?
The radius of Mohr’s circle of stress of a strained element is 20 N/mm2 and minor principal tensile stress is 10 N/mm2; The major principal stress is
a)
30N/mm2
b)
50 N/mm2
c)
60 N/mm2
d)
100 N/mm2
|
Anand Mehta answered |
Minor principal stress = C - r = 10
Centre of circle (C) = 10 + 20 =30 N/mm2
Major principal stress = C + r = 30 + 20 = 50 N/mm2
Centre of circle (C) = 10 + 20 =30 N/mm2
Major principal stress = C + r = 30 + 20 = 50 N/mm2
A point in a strained body is subjected to a tensile stress of 100 MPa on one plane and a tensile stress of 50 MPa on a plane at right angle to it. If these planes are carrying shear stresses of 50 MPa, then the principal stresses are inclined to the larger normal stress at an angle of- a)tan-1(2)
- b)
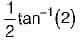
- c)
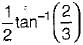
- d)
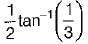
Correct answer is option 'B'. Can you explain this answer?
A point in a strained body is subjected to a tensile stress of 100 MPa on one plane and a tensile stress of 50 MPa on a plane at right angle to it. If these planes are carrying shear stresses of 50 MPa, then the principal stresses are inclined to the larger normal stress at an angle of
a)
tan-1(2)
b)
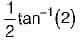
c)
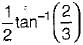
d)
|
|
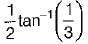
Dhruba Jain answered |
The angle of inclination of principal stress to the larger normal stress is given by,
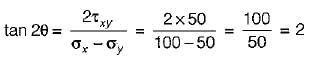
⇒ 2θ = tan-1(2)
∴
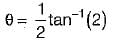
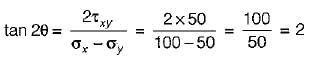
⇒ 2θ = tan-1(2)
∴
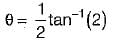
Two planes xyand yz are passing through a point in a strained material. The normal and shear stresses on xy plane are +80 MPa, -30 MPa respectively and normal and shear stresses on plane yz are +30 MPa and +30 MPa respectively. What is the angle between the planes?- a)180°
- b)135°
- c)90°
- d)46°
Correct answer is option 'C'. Can you explain this answer?
Two planes xyand yz are passing through a point in a strained material. The normal and shear stresses on xy plane are +80 MPa, -30 MPa respectively and normal and shear stresses on plane yz are +30 MPa and +30 MPa respectively. What is the angle between the planes?
a)
180°
b)
135°
c)
90°
d)
46°
|
Rithika Kaur answered |
Normal stresses of equal magnitude a, but of opposite signs, act at a point of a strained material in perpendicular direction. What is the magnitude of the stress on a plane inclined at 45° to the applied stresses?- a)2σ
- b)σ/2
- c)σ/4
- d)Zero
Correct answer is option 'D'. Can you explain this answer?
Normal stresses of equal magnitude a, but of opposite signs, act at a point of a strained material in perpendicular direction. What is the magnitude of the stress on a plane inclined at 45° to the applied stresses?
a)
2σ
b)
σ/2
c)
σ/4
d)
Zero
|
|
Garima Kulkarni answered |
Degrees to each of the normal stresses?
The stress on a plane inclined at 45 degrees to each of the normal stresses can be calculated using the formula:
σ = (σx + σy)/2 + (σx - σy)/2cos(2θ)
where σx and σy are the normal stresses and θ is the angle between the plane and the x-axis.
In this case, since the normal stresses have equal magnitude a but opposite signs, we have:
σx = a and σy = -a
Substituting these values into the formula, we get:
σ = (a - a)/2 + (a + a)/2cos(2(45°))
= a/2 + a/2cos(90°)
= a/2
Therefore, the magnitude of the stress on a plane inclined at 45 degrees to each of the normal stresses is equal to half the magnitude of the normal stresses, or a/2.
The stress on a plane inclined at 45 degrees to each of the normal stresses can be calculated using the formula:
σ = (σx + σy)/2 + (σx - σy)/2cos(2θ)
where σx and σy are the normal stresses and θ is the angle between the plane and the x-axis.
In this case, since the normal stresses have equal magnitude a but opposite signs, we have:
σx = a and σy = -a
Substituting these values into the formula, we get:
σ = (a - a)/2 + (a + a)/2cos(2(45°))
= a/2 + a/2cos(90°)
= a/2
Therefore, the magnitude of the stress on a plane inclined at 45 degrees to each of the normal stresses is equal to half the magnitude of the normal stresses, or a/2.
Which of the following formulae is used to calculate tangential stress, when a member is subjected to stress in mutually perpendicular axis and accompanied by shear stress?
- a) [(σx – σy)/2 ]– τ cos 2θ
- b)None of the these
- c) [(σx – σy)/2 ]sin θ – τ cos 2θ
- d)[(σx – σy)/2 ]sin θ – τ2 cos θ
Correct answer is option 'B'. Can you explain this answer?
Which of the following formulae is used to calculate tangential stress, when a member is subjected to stress in mutually perpendicular axis and accompanied by shear stress?
a)
[(σx – σy)/2 ]– τ cos 2θ
b)
None of the these
c)
[(σx – σy)/2 ]sin θ – τ cos 2θ
d)
[(σx – σy)/2 ]sin θ – τ2 cos θ
|
|
Ameya Sen answered |
Σx+σy)/2]+[(σx-σy)/2cos(2θ)+τxysin(2θ)]
b) [(σx+σy)/2]+[(σx-σy)/2sin(2θ)+τxycos(2θ)]
c) [(σx+σy)/2]-[(σx-σy)/2cos(2θ)-τxy*sin(2θ)]
d) [(σx+σy)/2]-[(σx-σy)/2sin(2θ)-τxy*cos(2θ)]
The correct answer is a) [(σx+σy)/2]+[(σx-σy)/2cos(2θ)+τxysin(2θ)].
b) [(σx+σy)/2]+[(σx-σy)/2sin(2θ)+τxycos(2θ)]
c) [(σx+σy)/2]-[(σx-σy)/2cos(2θ)-τxy*sin(2θ)]
d) [(σx+σy)/2]-[(σx-σy)/2sin(2θ)-τxy*cos(2θ)]
The correct answer is a) [(σx+σy)/2]+[(σx-σy)/2cos(2θ)+τxysin(2θ)].
If ∈1 and ∈2 ( ∈1 > ∈2) are the m axim um and minimum strains in the neighbourhood of a point in a stressed material of Young’s modulus E and Poisson’s ratio p, then the maximum principal stress will be given by- a)E∈1
- b)E(∈1 + ∈2)
- c)E(∈1 + μ∈2)/(1-μ2)
- d)E(∈2 + μ∈1)/(1-μ2)
Correct answer is option 'C'. Can you explain this answer?
If ∈1 and ∈2 ( ∈1 > ∈2) are the m axim um and minimum strains in the neighbourhood of a point in a stressed material of Young’s modulus E and Poisson’s ratio p, then the maximum principal stress will be given by
a)
E∈1
b)
E(∈1 + ∈2)
c)
E(∈1 + μ∈2)/(1-μ2)
d)
E(∈2 + μ∈
1
)/(1-μ2)|
|
Manasa Sen answered |
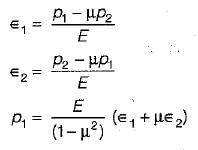
At a point in a strained body carrying two unequal unlike principal stresses p1 and p2 (p1 > p2), the maximum shear stress is given by- a)p1/2
- b)p2/2
- c)(p1 - p2)/2
- d)(p1 + p2)/2
Correct answer is option 'D'. Can you explain this answer?
At a point in a strained body carrying two unequal unlike principal stresses p1 and p2 (p1 > p2), the maximum shear stress is given by
a)
p1/2
b)
p2/2
c)
(p1 - p2)/2
d)
(p1 + p2)/2
|
|
Prashanth Mehra answered |
The maximum shear stress is given by,
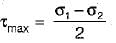
Now, σ1 = +p1
σ2 = -p2
∴
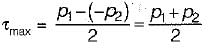
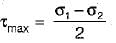
Now, σ1 = +p1
σ2 = -p2
∴
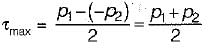
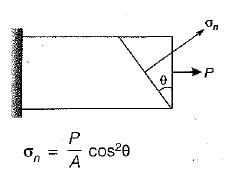
A bar is subjected to a uniaxial tensile stress ‘σ’. The tangential stress on a plane inclined at θ to the bar would be- a)
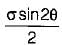
- b)σ sin 2θ
- c)
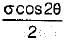
- d)σ cos 2θ
Correct answer is option 'A'. Can you explain this answer?
A bar is subjected to a uniaxial tensile stress ‘σ’. The tangential stress on a plane inclined at θ to the bar would be
a)
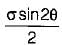
b)
σ sin 2θ
c)
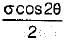
d)
σ cos 2θ
|
|
Srestha Khanna answered |
Normal sress = σ cos2 θ
Tangential Stress = σ sin θ cos θ
Tangential Stress = σ sin θ cos θ
=
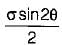
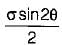
The radius of Mohr’s circle gives the value of- a)minimum normal stress
- b)minimum shear stress
- c)maximum normal stress
- d)maximum shear stress
Correct answer is option 'D'. Can you explain this answer?
The radius of Mohr’s circle gives the value of
a)
minimum normal stress
b)
minimum shear stress
c)
maximum normal stress
d)
maximum shear stress
|
|
Abhay Kapoor answered |
The Concept of Mohr's Circle
Mohr's Circle is a graphical representation used in engineering to determine the state of stress at a point. It illustrates the relationship between normal and shear stresses acting on different planes.
Understanding the Radius of Mohr's Circle
- The radius of Mohr's Circle represents the maximum shear stress at a given point in a material.
- This maximum shear stress occurs on the plane that is oriented at 45 degrees to the principal stress directions.
Key Points about Shear Stress
- Maximum Shear Stress: The maximum shear stress (τ_max) can be calculated directly from the radius of the circle, which is half the distance between the maximum and minimum normal stresses (σ_max and σ_min).
- Implication: The larger the radius, the greater the potential for material failure due to shear.
Relation to Normal Stresses
- While the radius is directly related to shear stress, normal stresses are also represented on the Mohr's Circle, namely the maximum normal stress (σ_max) and minimum normal stress (σ_min).
- However, the primary significance of the radius focuses on shear stress rather than normal stresses.
Conclusion
- Thus, option 'D' (maximum shear stress) is the correct answer. The radius of Mohr's Circle is crucial for understanding how materials will behave under different loading conditions, particularly in predicting failure modes due to shear.
Understanding this concept is essential for civil engineers when designing structures to ensure safety and performance under various stresses.
Mohr's Circle is a graphical representation used in engineering to determine the state of stress at a point. It illustrates the relationship between normal and shear stresses acting on different planes.
Understanding the Radius of Mohr's Circle
- The radius of Mohr's Circle represents the maximum shear stress at a given point in a material.
- This maximum shear stress occurs on the plane that is oriented at 45 degrees to the principal stress directions.
Key Points about Shear Stress
- Maximum Shear Stress: The maximum shear stress (τ_max) can be calculated directly from the radius of the circle, which is half the distance between the maximum and minimum normal stresses (σ_max and σ_min).
- Implication: The larger the radius, the greater the potential for material failure due to shear.
Relation to Normal Stresses
- While the radius is directly related to shear stress, normal stresses are also represented on the Mohr's Circle, namely the maximum normal stress (σ_max) and minimum normal stress (σ_min).
- However, the primary significance of the radius focuses on shear stress rather than normal stresses.
Conclusion
- Thus, option 'D' (maximum shear stress) is the correct answer. The radius of Mohr's Circle is crucial for understanding how materials will behave under different loading conditions, particularly in predicting failure modes due to shear.
Understanding this concept is essential for civil engineers when designing structures to ensure safety and performance under various stresses.
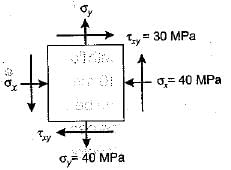
In a plane stress problem there are normal tensile stresses σx and σy accompanied by shear stress τxy at a point along orthogonal Cartesian coordinates x and y respectively. If it is observed that the minimum principal stress on a certain plane is zero the- a)
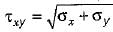
- b)
- c)
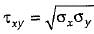
- d)
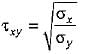
Correct answer is option 'C'. Can you explain this answer?
In a plane stress problem there are normal tensile stresses σx and σy accompanied by shear stress τxy at a point along orthogonal Cartesian coordinates x and y respectively. If it is observed that the minimum principal stress on a certain plane is zero the
a)
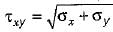
b)
c)
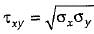
d)
|
|
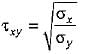
Arya Menon answered |
Principal stresses,
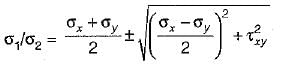
Since minimum principal stress is zero, therefore
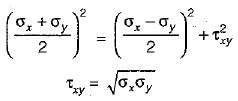
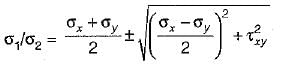
Since minimum principal stress is zero, therefore
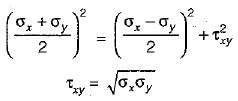
Chapter doubts & questions for Principal Stresses & Strains (Mohr's Circle) - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Principal Stresses & Strains (Mohr's Circle) - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup