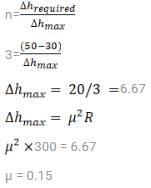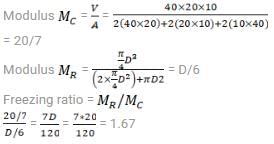All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Practice Tests for Mechanical Engineering Exam
Statements:
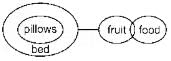
All pillows are beds.
No fruit is pillow.
Some foods are fruits.
Conclusions:
I. At least some foods are pillows.
II. Some beds are definitely fruits.- a)Only Conclusions I follows
- b)Only Conclusions II follows
- c)Either Conclusion I or Conclusions II follows
- d)Neither Conclusions I nor Conclusion II follows
Correct answer is option 'D'. Can you explain this answer?
Statements:
All pillows are beds.
No fruit is pillow.
Some foods are fruits.
Conclusions:
I. At least some foods are pillows.
II. Some beds are definitely fruits.
All pillows are beds.
No fruit is pillow.
Some foods are fruits.
Conclusions:
I. At least some foods are pillows.
II. Some beds are definitely fruits.
a)
Only Conclusions I follows
b)
Only Conclusions II follows
c)
Either Conclusion I or Conclusions II follows
d)
Neither Conclusions I nor Conclusion II follows
|
Gate Funda answered |
Consider the following least possible Venn diagram,
Conclusions:
I. At least some foods are pillows → it’s possible but not definite, hence false.
II. Some beds are definitely fruits → it’s possible but not definite, hence false.
Conclusions:
I. At least some foods are pillows → it’s possible but not definite, hence false.
II. Some beds are definitely fruits → it’s possible but not definite, hence false.
In a certain cooling dehumidification operation, 360 kg/h of air (DBT 35°C & RH 50%) is blown over a cooling coil having apparatus dew point of 5°C, assuming a bypass factor 15% determine outlet conditions of air- a)7°C
- b)12°C
- c) 9.5°C
- d)14°C
Correct answer is option 'C'. Can you explain this answer?
a)
7°C
b)
12°C
c)
9.5°C
d)
14°C
|
Cstoppers Instructors answered |
There are 200 individuals with a skin disorder, 120 had been exposed to the chemical c1, 50 to chemical c2, and 30 to both chemicals c1 and c2. find the number of individuals exposed to chemical c2 but not chemical c1
- a)90
- b)20
- c)140
- d)50
Correct answer is option 'B'. Can you explain this answer?
There are 200 individuals with a skin disorder, 120 had been exposed to the chemical c1, 50 to chemical c2, and 30 to both chemicals c1 and c2. find the number of individuals exposed to chemical c2 but not chemical c1
a)
90
b)
20
c)
140
d)
50
|
Yash Patel answered |
Let U= set of individuals suffering from the skin disorder
A= set of individuals exposed to the chemical c1
B= set of individual exposed to the chemical c2
Then n(u)=200, n(A)=120, n(B)=50 and n(A∩B)=30
Similarly, B=(B−A)∪(A∩B)
∴n(B)=n(B−A)+n(A∩B)
∵n(B−A)∩(A∩B)=φ
∴n(B−A)=n(B)−n(A∩B)
=50−30=20
Hence, 20 individuals exposed to chemical c2 but not to chemical c1
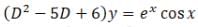is a Partial differential equation whose solution is given by
The value of K is- a)20
- b)1/20
- c)40
- d)1/40
Correct answer is option 'B'. Can you explain this answer?
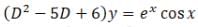is a Partial differential equation whose solution is given byThe value of K is
a)
20
b)
1/20
c)
40
d)
1/40
|
Rhea Reddy answered |
The objective here is to find the Particular integral as Complementary function is already given in the solution.
In spot pulsed laser welding of aluminum plates (density = 2700 
specific heat =896J/kg, melting temperature = 933K, latent heat of melting is 380 kJ/kg) at a temperature of 
Pulse with energy of 0.5 J is focused on to area of 0.05 mm2. If the entire energy is coupled into the material. What will be depth of weld assuming crosssection area of weld as circular and uniform throughout depth and only heat conduction in direction of penetration? - a)5.34 mm
- b) 2.15 mm
- c) 4.23 mm
- d)3.85 mm
Correct answer is option 'D'. Can you explain this answer?
specific heat =896J/kg, melting temperature = 933K, latent heat of melting is 380 kJ/kg) at a temperature of Pulse with energy of 0.5 J is focused on to area of 0.05 mm2. If the entire energy is coupled into the material. What will be depth of weld assuming crosssection area of weld as circular and uniform throughout depth and only heat conduction in direction of penetration? a)
5.34 mm
b)
2.15 mm
c)
4.23 mm
d)
3.85 mm
|
|
Gate Funda answered |
Let depth = d
Volume of weld = Ad
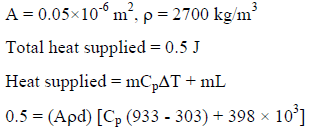
d = 3.84 mm
Volume of weld = Ad
d = 3.84 mm
If amplitude of vibration reduces to 0.25 of its initial value after five oscillations. The longitudinal decrement will be:- a)0.35
- b) 0.33
- c)0.28
- d)0.25
Correct answer is option 'A'. Can you explain this answer?
a)
0.35
b)
0.33
c)
0.28
d)
0.25
|
Pallabi Kulkarni answered |
The given problem involves the concept of longitudinal vibrations. In such vibrations, the displacement of the particles occurs along the same line as the direction of the wave propagation. The amplitude of vibration refers to the maximum displacement from the mean position.
Given:
Amplitude after 5 oscillations = 0.25 times the initial amplitude
To find:
Longitudinal decrement
Let's solve the problem step by step:
Step 1: Understanding the concept of longitudinal decrement
- Longitudinal decrement is a measure of the reduction in amplitude of the longitudinal wave after a certain number of oscillations.
- It is given by the formula:
Decrement = log_e (A_n / A_0)
where A_n is the amplitude after n oscillations, and A_0 is the initial amplitude.
Step 2: Calculating the decrement after 5 oscillations
- Given that the amplitude after 5 oscillations is 0.25 times the initial amplitude, we can substitute the values into the formula.
- Decrement = log_e (0.25 / 1)
Step 3: Evaluating the decrement
- Using logarithmic properties, we can simplify the expression:
Decrement = log_e (0.25) - log_e (1)
Since log_e (1) is zero, the equation becomes:
Decrement = log_e (0.25)
Step 4: Calculating the value of the decrement
- Using a calculator or mathematical software, we can find the value of the logarithm as approximately -1.3863.
Step 5: Interpreting the result
- The obtained value of the decrement (-1.3863) is negative, which means the amplitude is decreasing.
- However, the question asks for the longitudinal decrement, which is always positive.
- Therefore, we take the absolute value of the decrement to obtain the longitudinal decrement.
Final Step: Obtaining the longitudinal decrement
- Longitudinal decrement = | -1.3863 | = 1.3863
Therefore, the correct option is A) 0.35 (rounded to two decimal places), which represents the longitudinal decrement.
Given:
Amplitude after 5 oscillations = 0.25 times the initial amplitude
To find:
Longitudinal decrement
Let's solve the problem step by step:
Step 1: Understanding the concept of longitudinal decrement
- Longitudinal decrement is a measure of the reduction in amplitude of the longitudinal wave after a certain number of oscillations.
- It is given by the formula:
Decrement = log_e (A_n / A_0)
where A_n is the amplitude after n oscillations, and A_0 is the initial amplitude.
Step 2: Calculating the decrement after 5 oscillations
- Given that the amplitude after 5 oscillations is 0.25 times the initial amplitude, we can substitute the values into the formula.
- Decrement = log_e (0.25 / 1)
Step 3: Evaluating the decrement
- Using logarithmic properties, we can simplify the expression:
Decrement = log_e (0.25) - log_e (1)
Since log_e (1) is zero, the equation becomes:
Decrement = log_e (0.25)
Step 4: Calculating the value of the decrement
- Using a calculator or mathematical software, we can find the value of the logarithm as approximately -1.3863.
Step 5: Interpreting the result
- The obtained value of the decrement (-1.3863) is negative, which means the amplitude is decreasing.
- However, the question asks for the longitudinal decrement, which is always positive.
- Therefore, we take the absolute value of the decrement to obtain the longitudinal decrement.
Final Step: Obtaining the longitudinal decrement
- Longitudinal decrement = | -1.3863 | = 1.3863
Therefore, the correct option is A) 0.35 (rounded to two decimal places), which represents the longitudinal decrement.
Amit rows a boat 9 kilometres in 2 hours down-stream and returns upstream in 6 hours. The speed of the boat (in kmph) is:- a)1.5
- b)3
- c)2
- d)1.75
Correct answer is option 'B'. Can you explain this answer?
Amit rows a boat 9 kilometres in 2 hours down-stream and returns upstream in 6 hours. The speed of the boat (in kmph) is:
a)
1.5
b)
3
c)
2
d)
1.75
|
Tanishq Chakraborty answered |
Down-stream rate = 9/2 = 4.5 kmph
Upstream rate = 9/6 = 1.5 kmph
The speed of the boat = (4.5 – 1.5) kmph = 3 kmph
Upstream rate = 9/6 = 1.5 kmph
The speed of the boat = (4.5 – 1.5) kmph = 3 kmph
A shaft of 300 mm diameter is carrying a load of 20 kN at 2000 rpm. A bearing of 450 mm length supporting the shaft. The absolute viscosity of lubricating oil is 0.011 kg/m-s at the operating temperature and diametral clearance of the bearing is 0.30 mm. The power loss in bearing due to friction will be
Correct answer is between '31.5,32.5'. Can you explain this answer?
A shaft of 300 mm diameter is carrying a load of 20 kN at 2000 rpm. A bearing of 450 mm length supporting the shaft. The absolute viscosity of lubricating oil is 0.011 kg/m-s at the operating temperature and diametral clearance of the bearing is 0.30 mm. The power loss in bearing due to friction will be
|
Ashutosh Dasgupta answered |
Given : d = 300 mm = 0.3 m ; W = 20 kN = 20000 N ; N = 2000 r.p.m. ;
l = 450 mm; c = 0.30 mm ; Z = 0.011 kg/m-s
We know that, bearing pressur
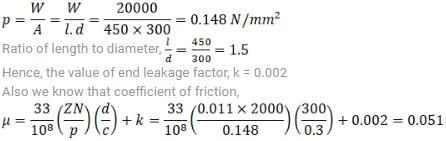
l = 450 mm; c = 0.30 mm ; Z = 0.011 kg/m-s
We know that, bearing pressur
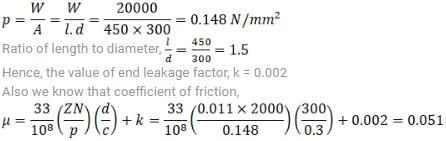
A, B and C shoots to hit a target. If A hits the target 4 times in 5 trials, B hits in 3 times in 4 trials and C hits it 2 times in 3 trials. What is the probability that the target is hit by at least 2 persons?- a)5/6
- b)4/5
- c)3/4
- d)2/3
Correct answer is option 'A'. Can you explain this answer?
a)
5/6
b)
4/5
c)
3/4
d)
2/3
|
Priyanka Tiwari answered |
Understanding the Problem
To solve the problem, we need to calculate the probability that at least 2 out of 3 shooters (A, B, and C) hit the target.
Individual Probabilities
- Probability A hits the target: P(A) = 4/5
- Probability B hits the target: P(B) = 3/4
- Probability C hits the target: P(C) = 2/3
Calculating the Complement
Instead of calculating the probability of at least 2 shooters hitting the target directly, we will find the complement, which is the probability that either 0 or 1 shooter hits the target.
Probability of No Hits
- P(No hits) = P(A misses) * P(B misses) * P(C misses)
- P(A misses) = 1 - P(A) = 1/5
- P(B misses) = 1 - P(B) = 1/4
- P(C misses) = 1 - P(C) = 1/3
Calculating:
P(No hits) = (1/5) * (1/4) * (1/3) = 1/60
Probability of Exactly One Hit
To find the probability of exactly one hit, we consider three cases:
1. A hits, B and C miss.
2. B hits, A and C miss.
3. C hits, A and B miss.
Calculating each case:
1. P(A hits, B misses, C misses) = (4/5) * (1/4) * (1/3) = 1/15
2. P(B hits, A misses, C misses) = (3/4) * (1/5) * (1/3) = 1/20
3. P(C hits, A misses, B misses) = (2/3) * (1/5) * (1/4) = 1/30
Total for exactly one hit:
P(Exactly one hit) = 1/15 + 1/20 + 1/30 = 1/6
Combining Results
Total probability of 0 or 1 hit:
P(0 or 1 hit) = P(No hits) + P(Exactly one hit) = 1/60 + 1/6 = 11/60
Final Probability
Now, we calculate the probability of at least 2 hits:
P(At least 2 hits) = 1 - P(0 or 1 hit) = 1 - 11/60 = 49/60
Upon simplifying, we find that the probability of at least 2 persons hitting the target is:
5/6
Thus, the correct option is a) 5/6.
To solve the problem, we need to calculate the probability that at least 2 out of 3 shooters (A, B, and C) hit the target.
Individual Probabilities
- Probability A hits the target: P(A) = 4/5
- Probability B hits the target: P(B) = 3/4
- Probability C hits the target: P(C) = 2/3
Calculating the Complement
Instead of calculating the probability of at least 2 shooters hitting the target directly, we will find the complement, which is the probability that either 0 or 1 shooter hits the target.
Probability of No Hits
- P(No hits) = P(A misses) * P(B misses) * P(C misses)
- P(A misses) = 1 - P(A) = 1/5
- P(B misses) = 1 - P(B) = 1/4
- P(C misses) = 1 - P(C) = 1/3
Calculating:
P(No hits) = (1/5) * (1/4) * (1/3) = 1/60
Probability of Exactly One Hit
To find the probability of exactly one hit, we consider three cases:
1. A hits, B and C miss.
2. B hits, A and C miss.
3. C hits, A and B miss.
Calculating each case:
1. P(A hits, B misses, C misses) = (4/5) * (1/4) * (1/3) = 1/15
2. P(B hits, A misses, C misses) = (3/4) * (1/5) * (1/3) = 1/20
3. P(C hits, A misses, B misses) = (2/3) * (1/5) * (1/4) = 1/30
Total for exactly one hit:
P(Exactly one hit) = 1/15 + 1/20 + 1/30 = 1/6
Combining Results
Total probability of 0 or 1 hit:
P(0 or 1 hit) = P(No hits) + P(Exactly one hit) = 1/60 + 1/6 = 11/60
Final Probability
Now, we calculate the probability of at least 2 hits:
P(At least 2 hits) = 1 - P(0 or 1 hit) = 1 - 11/60 = 49/60
Upon simplifying, we find that the probability of at least 2 persons hitting the target is:
5/6
Thus, the correct option is a) 5/6.
Match the following:
a) Drop forging i-material is only upset
b) Machine forging ii-repeated hammer blows
c) Press forging iii-carried out manually
d) Upset forging iv-squeezing action
e) Smith forging v-metal gripped & pressure applied at heated end- a)A-i B-ii C-iii D-iv E-v
- b)A-ii B-i C-iv D-v E-iii
- c)A-iv B-ii C-v D-iii E-i
- d)A-iii B-ii C-i D-iv E-v
Correct answer is option 'B'. Can you explain this answer?
Match the following:
a) Drop forging i-material is only upset
b) Machine forging ii-repeated hammer blows
c) Press forging iii-carried out manually
d) Upset forging iv-squeezing action
e) Smith forging v-metal gripped & pressure applied at heated end
a) Drop forging i-material is only upset
b) Machine forging ii-repeated hammer blows
c) Press forging iii-carried out manually
d) Upset forging iv-squeezing action
e) Smith forging v-metal gripped & pressure applied at heated end
a)
A-i B-ii C-iii D-iv E-v
b)
A-ii B-i C-iv D-v E-iii
c)
A-iv B-ii C-v D-iii E-i
d)
A-iii B-ii C-i D-iv E-v
|
Anagha Chopra answered |
In Drop forging repeated hammer blows, for machine forging material is only upset, in press forging squeezing action takes place.
During a certain reversible process, for a closed system, the entropy of system increases by 4 kJ/K. If the process occurs at a constant temperature of 500 K, the heat input to the system will be- a)2000 kJ
- b)1500 kJ
- c) 2500 kJ
- d)1000 kJ
Correct answer is option 'A'. Can you explain this answer?
a)
2000 kJ
b)
1500 kJ
c)
2500 kJ
d)
1000 kJ
|
|
Anjana Mukherjee answered |
500(4)=2000 kJIn a 1:36 scale model test of a spillway, discharge of flow over the model is 6 m3/s. If the velocity of flow over model was found to be 5 knots, then the velocity of flow over prototype in m/s will be- a)30
- b)15.45
- c)9
- d)24.36
Correct answer is option 'B'. Can you explain this answer?
In a 1:36 scale model test of a spillway, discharge of flow over the model is 6 m3/s. If the velocity of flow over model was found to be 5 knots, then the velocity of flow over prototype in m/s will be
a)
30
b)
15.45
c)
9
d)
24.36
|
|
Ritika Joshi answered |
Scale Model Test
In a scale model test, a smaller version of the prototype is built and tested to gather information about the performance and behavior of the full-scale structure. The relationship between the model and the prototype is defined by the scale factor. In this case, the scale factor is 1:36.
Given Information
In the scale model test of a spillway:
- Discharge of flow over the model = 6 m3/s
- Velocity of flow over the model = 5 knots
Finding the Velocity of Flow over Prototype
We need to find the velocity of flow over the prototype, which is the full-scale structure. To do this, we can use the concept of similitude, which states that the ratios of corresponding quantities in the model and prototype should be equal.
Let's consider the velocity of flow over the prototype as Vp and the velocity of flow over the model as Vm.
Using the Discharge Equation
The discharge Q through a cross-section is given by the equation:
Q = A * V
Where:
- Q is the discharge
- A is the cross-sectional area
- V is the velocity
Since the scale factor is 1:36, the cross-sectional area of the model is 1/36 times the cross-sectional area of the prototype:
Am = 1/36 * Ap
Substituting the values:
6 m3/s = (1/36 * Ap) * 5 knots
Converting Knots to m/s
To compare the velocities, we need to convert knots to m/s. 1 knot is equal to 0.5144 m/s.
Substituting the value of velocity in m/s:
6 m3/s = (1/36 * Ap) * 5 * 0.5144 m/s
Simplifying the Equation
Cancelling out the common factors:
6 = (1/36 * Ap) * 2.572
Multiplying both sides by 36:
6 * 36 = Ap * 2.572
Ap = (6 * 36) / 2.572
Ap ≈ 84.36 m2
Calculating the Velocity of Flow over Prototype
Now, let's substitute the value of Ap into the discharge equation for the prototype:
Qp = Ap * Vp
Since the discharge through the model and prototype is the same:
Qp = Qm
Ap * Vp =
In a Bell Coleman cycle, air enters the compressor at a pressure of 2.5 bar at a temperature of 100C. It is then compressed to a pressure of 6.25 bar and then cooled in a cooler to a temperature of 250C in the cooler before being expanded in the expansion cylinder upto a pressure of 2.5 bar. The COP will be ______ .
Correct answer is between '3.1,3.5'. Can you explain this answer?
In a Bell Coleman cycle, air enters the compressor at a pressure of 2.5 bar at a temperature of 100C. It is then compressed to a pressure of 6.25 bar and then cooled in a cooler to a temperature of 250C in the cooler before being expanded in the expansion cylinder upto a pressure of 2.5 bar. The COP will be ______ .
|
|
Yash Patel answered |
Bell Coleman cycle is also known as Reversed Brayton cycle
A gear box of machine is operating under steady state. Input shaft receives 46 kW from prime mover and transmits 30 kW to output shaft, the rest being lost to friction etc. Gear box surface is at an average temperature of 47°C and losses heat to surrounding at 27°C. Find the irreversibility involved.- a)1 kW
- b) 2 kW
- c)3 kW
- d)4 kW
Correct answer is option 'A'. Can you explain this answer?
a)
1 kW
b)
2 kW
c)
3 kW
d)
4 kW
|
|
Swara Gupta answered |
Heat loss due to friction = 46-30 = 16 kW
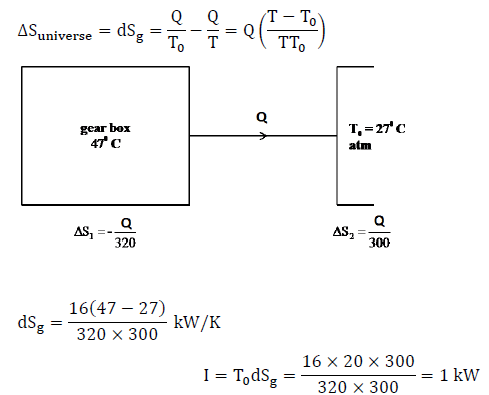
The men's department of a large store employs one tailor for customer fittings. The number of customers requiring fitting appears to follow a Poisson distribution with a mean arrival rate is 24 per hour. Customers fitting time follows an exponential distribution with a mean of 2 minute. The time (minute) a customer is expected to spend in the fitting row is………….- a)6
- b)10
- c)30
- d)16
Correct answer is option 'B'. Can you explain this answer?
a)
6
b)
10
c)
30
d)
16
|
|
Aditi Chakraborty answered |
He always _________ you in his letters- a)Asks around
- b)Asks of
- c)Asks about
- d)Asks to
Correct answer is option 'C'. Can you explain this answer?
a)
Asks around
b)
Asks of
c)
Asks about
d)
Asks to
|
Nilanjan Chawla answered |
He always asks about you in his letters.
- The correct answer is option 'C' - "asks about".
- The phrase "asks about" means to inquire or seek information about someone or something.
- In the given context, the person mentioned in the question is consistently showing interest in knowing about the well-being or current situation of the individual receiving the letters.
- Through his letters, he is making inquiries or seeking updates about the person.
- Let's break down the options and explain why the other options are incorrect:
a) Asks around: This phrase means to inquire or seek information from multiple sources or people. However, in this context, there is no indication that the person is asking others about the individual receiving the letters. Therefore, option 'A' is incorrect.
b) Asks of: This phrase is used to make a request or demand something from someone. It doesn't fit the context of the question, as the person is not asking for anything from the individual receiving the letters. Thus, option 'B' is incorrect.
c) Asks about: This phrase fits perfectly in the context. It implies that the person is consistently inquiring about the well-being or current situation of the individual receiving the letters. Thus, option 'C' is the correct answer.
d) Asks to: This phrase is used to indicate a request or demand made to someone. However, it doesn't fit the context of the question, as there is no indication that the person is making a request or demand from the individual receiving the letters. Therefore, option 'D' is incorrect.
In conclusion, option 'C' - "asks about" is the correct answer as it best fits the context of the question.
An ideal gas of mass 0.5 kg has a pressure of 600 kPa, a temperature of 770C and a volume of 0.08 m3. This gas undergoes an irreversible process to a final pressure of 600 kPa and final volume of 0.12 m3, during which the heat addition and work done on gas are 2 kJ and 30 kJ respectively. The value of Cv of gas is- a)0.718 kJ/kgK
- b)0.365 kJ/kgK
- c)0.319 kJ/kgK
- d)0.638 kJ/kgK
Correct answer is option 'B'. Can you explain this answer?
An ideal gas of mass 0.5 kg has a pressure of 600 kPa, a temperature of 770C and a volume of 0.08 m3. This gas undergoes an irreversible process to a final pressure of 600 kPa and final volume of 0.12 m3, during which the heat addition and work done on gas are 2 kJ and 30 kJ respectively. The value of Cv of gas is
a)
0.718 kJ/kgK
b)
0.365 kJ/kgK
c)
0.319 kJ/kgK
d)
0.638 kJ/kgK
|
Akanksha Bajaj answered |
Given, m =0.5 kg, p1 = p2 =600 kPa, T1 = 770C = 350 K, V1 = 0.08 m3, V2 = 0.12 m3, Q =2 kJ, W = −30 kJ
From ideal gas eqn,
p1V1 = mRT1
From ideal gas eqn,
p1V1 = mRT1
Direction: In the following number series, only one number is wrong. Find out the wrong number.
17 25 34 98 121 339- a)121
- b)98
- c)339
- d)34
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following number series, only one number is wrong. Find out the wrong number.
17 25 34 98 121 339
17 25 34 98 121 339
a)
121
b)
98
c)
339
d)
34
|
|
Bhavya Mukherjee answered |
The pattern followed here is,
⇒ 17 + 23 = 17 + 8 = 25
⇒ 25 + 32 = 25 + 9 = 34
⇒ 34 + 43 = 34 + 64 = 98
⇒ 98 + 52 = 98 + 25 = 123
⇒ 123 + 63 = 123 + 216 = 339
⇒ 17 + 23 = 17 + 8 = 25
⇒ 25 + 32 = 25 + 9 = 34
⇒ 34 + 43 = 34 + 64 = 98
⇒ 98 + 52 = 98 + 25 = 123
⇒ 123 + 63 = 123 + 216 = 339
An air refrigerator of 10 ton capacity operates in Bell Coleman cycle between pressure limits of 1 bar and 4 bar. Air at inlet of compressor is at 1 bar and 253 K. Air at exit of cooler is at 313 K. After air is cooled to 290 K at constant pressure in cooler, it is allowed to expand isentropically to 1 bar in expansion cylinder where temperature limit of cycle. Cold air is then sent to cold chamber to extract heat (Refrigerating effect) determine COP of refrigerator.- a)1.5
- b)2.05
- c) 3.1
- d)3.6
Correct answer is option 'B'. Can you explain this answer?
a)
1.5
b)
2.05
c)
3.1
d)
3.6
|
Akshat Mehta answered |
A boat sails across a river with a velocity of 10 km/hr. If resultant boat velocity is 14 km/hr, then what is the velocity of river water? - a) 17.20 km/hr
- b) 10 km/hr
- c) 9.79 km/hr
- d) 4.88 km/hr
Correct answer is option 'C'. Can you explain this answer?
A boat sails across a river with a velocity of 10 km/hr. If resultant boat velocity is 14 km/hr, then what is the velocity of river water?
a)
17.20 km/hr
b)
10 km/hr
c)
9.79 km/hr
d)
4.88 km/hr
|
|
Simran Saha answered |
Given data:
Speed of the boat in still water (B) = 14 km/hr
Speed of the boat across the river (V) = 10 km/hr
Let the velocity of the river be 'R'.
The velocity of the boat can be resolved into two components:
1. Velocity of the boat in the direction of the river flow (Vr)
2. Velocity of the boat perpendicular to the river flow (Vp)
Hence,
B = Vr + Vp
Given, V = 10 km/hr
As the boat is sailing at an angle to the river flow, the velocity of the boat perpendicular to the river flow is given by:
Vp = V x sinθ
where θ is the angle between the boat's velocity and the river flow.
In this case, θ = 90°, as the boat is sailing perpendicular to the river flow.
Therefore, Vp = V x sin90° = V
Hence, B = Vr + V
Also, given B = 14 km/hr
Substituting the values, we get:
14 = Vr + 10
Vr = 14 - 10 = 4 km/hr
Now, the velocity of the river can be calculated as follows:
Vr = R
4 = R
R = 4 km/hr
Therefore, the velocity of the river water is 4 km/hr, which is option (c).
Speed of the boat in still water (B) = 14 km/hr
Speed of the boat across the river (V) = 10 km/hr
Let the velocity of the river be 'R'.
The velocity of the boat can be resolved into two components:
1. Velocity of the boat in the direction of the river flow (Vr)
2. Velocity of the boat perpendicular to the river flow (Vp)
Hence,
B = Vr + Vp
Given, V = 10 km/hr
As the boat is sailing at an angle to the river flow, the velocity of the boat perpendicular to the river flow is given by:
Vp = V x sinθ
where θ is the angle between the boat's velocity and the river flow.
In this case, θ = 90°, as the boat is sailing perpendicular to the river flow.
Therefore, Vp = V x sin90° = V
Hence, B = Vr + V
Also, given B = 14 km/hr
Substituting the values, we get:
14 = Vr + 10
Vr = 14 - 10 = 4 km/hr
Now, the velocity of the river can be calculated as follows:
Vr = R
4 = R
R = 4 km/hr
Therefore, the velocity of the river water is 4 km/hr, which is option (c).
Water flows through a tube of diameter 25mm at an average velocity 1 m/sec. The properties of water ρ = 1000 kg/m3, μ = 6x 10-4 N-s/m2 , K= 0.625 W/mK, Pr= 4, Given Dittus – Boelter equation, Nu =0.023Re0.8 Prn and constant heat flux Nu = 3.66. What is Nusset number when fluid is cooling?
Correct answer is between '172,174'. Can you explain this answer?
Water flows through a tube of diameter 25mm at an average velocity 1 m/sec. The properties of water ρ = 1000 kg/m3, μ = 6x 10-4 N-s/m2 , K= 0.625 W/mK, Pr= 4, Given Dittus – Boelter equation, Nu =0.023Re0.8 Prn and constant heat flux Nu = 3.66. What is Nusset number when fluid is cooling?
|
Anjana Khanna answered |
Given, Pr = 4, fluid is cooling so, n= 0.3
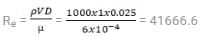
So the flow is turbulent, we have to use Dittus- Boelter equation i.e
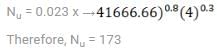
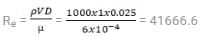
So the flow is turbulent, we have to use Dittus- Boelter equation i.e
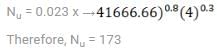
A wooden block (relative density = 0.65) floats above surface of a liquid of relative density of 1.35, contained in a tank. The volume fraction of metallic piece lies above the liquid surface is
Correct answer is '0.519'. Can you explain this answer?
A wooden block (relative density = 0.65) floats above surface of a liquid of relative density of 1.35, contained in a tank. The volume fraction of metallic piece lies above the liquid surface is
|
|
Mira Menon answered |
Let V be total volume of wooden block and V’ is the volume that lies immersed in the liquid.
Using principle of floatation,
Weight of wooden block = weight of the liquid displaced by the immersed portion of the wooden block
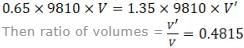
So, the volume fraction of wooden block below the liquid surface = 1 – 0.4815 = 0.5185
Using principle of floatation,
Weight of wooden block = weight of the liquid displaced by the immersed portion of the wooden block
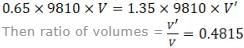
So, the volume fraction of wooden block below the liquid surface = 1 – 0.4815 = 0.5185
Which types of stress strain relationship best describes the behaviour of brittle materials as ceramics and thermosetting plastics?- a)Elastic and perfectly plastic
- b)Elastic and strain hardening
- c)Perfectly elastic
- d)Perfectly plastic
Correct answer is option 'C'. Can you explain this answer?
Which types of stress strain relationship best describes the behaviour of brittle materials as ceramics and thermosetting plastics?
a)
Elastic and perfectly plastic
b)
Elastic and strain hardening
c)
Perfectly elastic
d)
Perfectly plastic
|
Anshika Chopra answered |
Ceramics and thermosetting plastics does not undergo plastic strain since they are brittle materials. The stress strain curve reached to the elastic point and then material fails.
The Mollier diagram of a pure substance is a- a)h-s diagram
- b)T-s diagram
- c)P-h diagram
- d)h-P diagram
Correct answer is option 'A'. Can you explain this answer?
The Mollier diagram of a pure substance is a
a)
h-s diagram
b)
T-s diagram
c)
P-h diagram
d)
h-P diagram
|
|
Rishabh Pillai answered |
The Mollier diagram of a pure substance is a h-s diagram. So, the correct option is (a).
Air enters an insulated diffuser operating at steady state with a pressure of 0.65 bar, temperature of 670C and a velocity of 300 m/s. The inlet area is 0.5 m2. At the exit, the pressure is 1 bar and the area is 0.6 m2. Potential energy changes can be neglected. Assume ideal gas behavior for air. The mass flow rate and temperature of the air at exit is- a)50 kg/s, 350 K
- b)150 kg/s, 355 K
- c)100 kg/s, 355 K
- d)150 kg/s, 350 K
Correct answer is option 'C'. Can you explain this answer?
Air enters an insulated diffuser operating at steady state with a pressure of 0.65 bar, temperature of 670C and a velocity of 300 m/s. The inlet area is 0.5 m2. At the exit, the pressure is 1 bar and the area is 0.6 m2. Potential energy changes can be neglected. Assume ideal gas behavior for air. The mass flow rate and temperature of the air at exit is
a)
50 kg/s, 350 K
b)
150 kg/s, 355 K
c)
100 kg/s, 355 K
d)
150 kg/s, 350 K
|
|
Chirag Chaudhary answered |
P1 = 0.65 bar = 65 kPa
T1 = 670C = 340 K
V1 = 300 m/s
A1 = 0.5 m2
R = 0.287 kJ/kgK
Cp = 1.008 kJ/kgK
P2 = 1 bar = 100 kPa
A2 = 0.6 m2
Given Steady state
Now applying steady flow energy equation between 1 and 2:
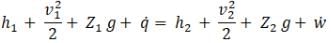
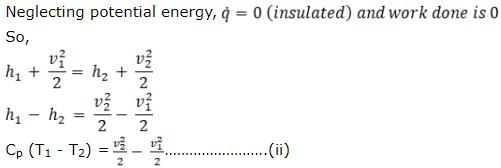
Putting the value of V2 in equation (i), we will get
T1 = 670C = 340 K
V1 = 300 m/s
A1 = 0.5 m2
R = 0.287 kJ/kgK
Cp = 1.008 kJ/kgK
P2 = 1 bar = 100 kPa
A2 = 0.6 m2
Given Steady state
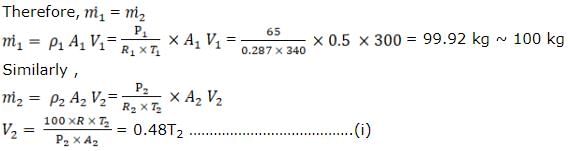
Now applying steady flow energy equation between 1 and 2:
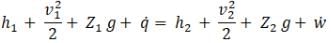
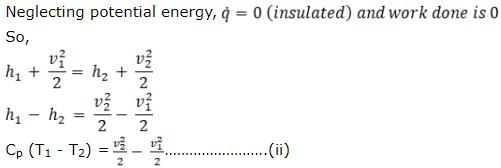
Putting the value of V2 in equation (i), we will get
A helical gear made of plain carbon steel has face width 10 times the normal module. If number of teeth on pinion and gear are 20 and 60 respectively, then what will be the wear strength of helical gear? (Assume mn = 5, BHN = 200 & Ψ = 24o)- a)5751.30 N
- b)5230.19 N
- c)6295.58 N
- d)6891.37 N
Correct answer is option 'C'. Can you explain this answer?
A helical gear made of plain carbon steel has face width 10 times the normal module. If number of teeth on pinion and gear are 20 and 60 respectively, then what will be the wear strength of helical gear? (Assume mn = 5, BHN = 200 & Ψ = 24o)
a)
5751.30 N
b)
5230.19 N
c)
6295.58 N
d)
6891.37 N
|
|
Elisetty Sai answered |
An engine working on OTTO cycle have compression ratio of 5. The maximum and minimum pressure during the cycle are 40 bar and 1 bar respectively. The mean effective pressure of the cycle will be:- a)7 bar
- b) 9.04 bar
- c)7.8 bar
- d)11.2 bar
Correct answer is option 'B'. Can you explain this answer?
a)
7 bar
b)
9.04 bar
c)
7.8 bar
d)
11.2 bar
|
|
Aarav Kulkarni answered |
“Wanted a two bedroom flat in the court area for immediate possession” - An Advertisement.
Assumptions:
I. Flats are available in the court area
II. Some people will respond to the advertisement
III. It is a practice to give such an advertisement- a)All assumptions are implicit
- b)Only assumption II is implicit
- c)Only I and II are implicit
- d)None is implicit
Correct answer is option 'B'. Can you explain this answer?
Assumptions:
I. Flats are available in the court area
II. Some people will respond to the advertisement
III. It is a practice to give such an advertisement
a)
All assumptions are implicit
b)
Only assumption II is implicit
c)
Only I and II are implicit
d)
None is implicit
|
|
Anirudh Banerjee answered |
Assumption I: Flats are available in the court area
This assumption is implicit. The statement in the advertisement clearly mentions that a two-bedroom flat is wanted in the court area. This implies that there are flats available in the court area, otherwise, there would be no point in placing the advertisement.
Assumption II: Some people will respond to the advertisement
This assumption is also implicit. The purpose of placing an advertisement is to attract potential respondents who have a two-bedroom flat available for immediate possession in the court area. The assumption is that there will be individuals who will see the advertisement and respond to it.
Assumption III: It is a practice to give such an advertisement
This assumption is not implicit. The statement in the advertisement does not provide any indication that it is a common practice to give such an advertisement. It could be the first time the advertiser is placing such an advertisement, or it could be a regular practice. The information provided in the statement is not sufficient to make this assumption.
Therefore, only assumptions I and II are implicit in the given advertisement.
This assumption is implicit. The statement in the advertisement clearly mentions that a two-bedroom flat is wanted in the court area. This implies that there are flats available in the court area, otherwise, there would be no point in placing the advertisement.
Assumption II: Some people will respond to the advertisement
This assumption is also implicit. The purpose of placing an advertisement is to attract potential respondents who have a two-bedroom flat available for immediate possession in the court area. The assumption is that there will be individuals who will see the advertisement and respond to it.
Assumption III: It is a practice to give such an advertisement
This assumption is not implicit. The statement in the advertisement does not provide any indication that it is a common practice to give such an advertisement. It could be the first time the advertiser is placing such an advertisement, or it could be a regular practice. The information provided in the statement is not sufficient to make this assumption.
Therefore, only assumptions I and II are implicit in the given advertisement.
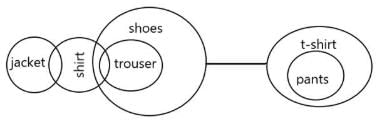
Directions: In each of the questions below, some statements are given followed by some conclusions. You have to consider the statements to be true even if they seem to be at variance with commonly known facts. You have to decide which of the following conclusions logically follows from the given statements. Give answer.
Statements:
Some jacket is shirt.
Some shirts are trouser.
No shoes are t-shirt.
All trousers are shoes.
All pants are t-shirt.
Conclusions:
I. All shirts being t-shirt is a possibility.
II. Some shoes are trouser.
III. Some jackets are t-shirt.
IV. Some shirts being t-shirt is a possibility.- a)Only II and III follow.
- b)Only II and IV follow
- c)Only I follows
- d)All follow
Correct answer is option 'B'. Can you explain this answer?
Directions: In each of the questions below, some statements are given followed by some conclusions. You have to consider the statements to be true even if they seem to be at variance with commonly known facts. You have to decide which of the following conclusions logically follows from the given statements. Give answer.
Statements:
Some jacket is shirt.
Some shirts are trouser.
No shoes are t-shirt.
All trousers are shoes.
All pants are t-shirt.
Conclusions:
I. All shirts being t-shirt is a possibility.
II. Some shoes are trouser.
III. Some jackets are t-shirt.
IV. Some shirts being t-shirt is a possibility.
Statements:
Some jacket is shirt.
Some shirts are trouser.
No shoes are t-shirt.
All trousers are shoes.
All pants are t-shirt.
Conclusions:
I. All shirts being t-shirt is a possibility.
II. Some shoes are trouser.
III. Some jackets are t-shirt.
IV. Some shirts being t-shirt is a possibility.
a)
Only II and III follow.
b)
Only II and IV follow
c)
Only I follows
d)
All follow
|
|
Vaishnavi Chakraborty answered |
Gyroscopic acceleration is due to- a)Change in the direction of linear velocity
- b)Change in the direction of angular velocity
- c)Change in the magnitude of angular velocity analysis
- d)Change in the magnitude of linear velocity
Correct answer is option 'B'. Can you explain this answer?
Gyroscopic acceleration is due to
a)
Change in the direction of linear velocity
b)
Change in the direction of angular velocity
c)
Change in the magnitude of angular velocity analysis
d)
Change in the magnitude of linear velocity
|
Hiral Chakraborty answered |
Gyroscopic acceleration is due to the change in the direction of angular velocity.
So, the correct option is (b).
So, the correct option is (b).
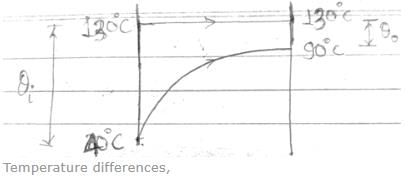
In a certain heat exchanger, cold fluid enters at 40oC and rate of the flow is 1650 kg/hr. The hot fluid is at a temperature of 130oC and cold fluid leaves the heat exchanger at 90oC. Specific heat of the cold fluid is 3.5 kJ/kg-K. If heat transfer area is 0.707 m2, then the overall heat transfer coefficient is- a)1840 W/m2-K
- b)184 W/m2-K
- c)18.4 W/m2-K
- d)2250 W/m2-K
Correct answer is option 'A'. Can you explain this answer?
In a certain heat exchanger, cold fluid enters at 40oC and rate of the flow is 1650 kg/hr. The hot fluid is at a temperature of 130oC and cold fluid leaves the heat exchanger at 90oC. Specific heat of the cold fluid is 3.5 kJ/kg-K. If heat transfer area is 0.707 m2, then the overall heat transfer coefficient is
a)
1840 W/m2-K
b)
184 W/m2-K
c)
18.4 W/m2-K
d)
2250 W/m2-K
|
|
Asha Dey answered |
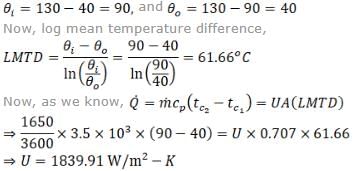
Find the net value of heat flux between two parallel, infinite plates having emissivity of 0.75 and 0.7. The planes are maintained at 450 K and 500 K.- a)734.86 W/m2
- b)692.22 W/m2
- c)1245.5 W/m2
- d)1815.75 W/m2
Correct answer is option 'B'. Can you explain this answer?
Find the net value of heat flux between two parallel, infinite plates having emissivity of 0.75 and 0.7. The planes are maintained at 450 K and 500 K.
a)
734.86 W/m2
b)
692.22 W/m2
c)
1245.5 W/m2
d)
1815.75 W/m2
|
|
Sagnik Unni answered |
The grey body factor is given by,
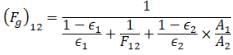
Since infinite long plates can see each other. So, F12 = 1 and A1 = A2 So, the grey body factor will become
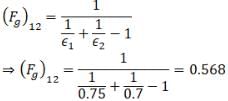
Now, the rate of heat interchange between the plates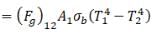
And net heat flux,
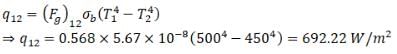
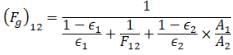
Since infinite long plates can see each other. So, F12 = 1 and A1 = A2 So, the grey body factor will become
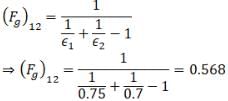
Now, the rate of heat interchange between the plates
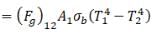
And net heat flux,
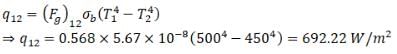
A new flag is to be designed with six vertical stripes using some or all of the colours- yellow, green, blue and red. Then the number of ways this can be done such that no two adjacent stripes have the same colour out is:- a)12×81
- b)16×25
- c) 20×125
- d)24×216
Correct answer is option 'A'. Can you explain this answer?
a)
12×81
b)
16×25
c)
20×125
d)
24×216
|
|
Aarav Chauhan answered |
There are 6 stripes. The 
stripe can be coloured in 4ways, 
in 3, 
in 3 and so on.Thus, total number of ways = 4×3×3×3×3×3=12×81
stripe can be coloured in 4ways, in 3, in 3 and so on.Thus, total number of ways = 4×3×3×3×3×3=12×81
When an ideal gas expands, its temperature- a)Remains constant
- b) Increases
- c)Decreases
- d)May increase or decrease
Correct answer is option 'D'. Can you explain this answer?
a)
Remains constant
b)
Increases
c)
Decreases
d)
May increase or decrease
|
Rahul Chatterjee answered |
The Ideal Gas Law states pV = nRT, where P = The pressure of the gas in Pa, V = Volume of gas in m3, n = Number of moles of gas, R = A constant of about 8.314 and T = Temperature in K. As a gas (like air) expands, the value of V increases and this has the effect of increasing T (The temperature).
Suppose that the reliability of a HIV test is specified as follows: Of people having HIV, 90% of the test detect the disease but 10% go undetected of
people free of HIV, 99% of the test are judged HIV –ve but 1% are diagnosed as showing HIV +ve. From a large population of which only 0.1% have HIV, one person is selected at random, given the HIV test, and the pathologist reports him/her as HIV +ve. What is the probability that the person actually has HIV?- a)0.072
- b)0.095
- c) 0.083
- d)0.12
Correct answer is option 'C'. Can you explain this answer?
people free of HIV, 99% of the test are judged HIV –ve but 1% are diagnosed as showing HIV +ve. From a large population of which only 0.1% have HIV, one person is selected at random, given the HIV test, and the pathologist reports him/her as HIV +ve. What is the probability that the person actually has HIV?
a)
0.072
b)
0.095
c)
0.083
d)
0.12
|
|
Nayanika Yadav answered |
Understanding the Problem
To determine the probability that a person has HIV given a positive test result, we will use Bayes' theorem.
Definitions
- P(HIV): Probability of having HIV = 0.001 (0.1%)
- P(No HIV): Probability of not having HIV = 0.999 (99.9%)
- P(Pos | HIV): Probability of testing positive given HIV = 0.9 (90%)
- P(Pos | No HIV): Probability of testing positive given no HIV = 0.01 (1%)
Calculating the Required Probability
We need to find P(HIV | Pos), the probability of having HIV given a positive test result. According to Bayes' theorem:
P(HIV | Pos) = (P(Pos | HIV) * P(HIV)) / P(Pos)
Calculating P(Pos)
P(Pos) can be calculated as follows:
- P(Pos) = P(Pos | HIV) * P(HIV) + P(Pos | No HIV) * P(No HIV)
- P(Pos) = (0.9 * 0.001) + (0.01 * 0.999)
- P(Pos) = 0.0009 + 0.00999 = 0.01089
Final Calculation
Now substitute back into Bayes' theorem:
P(HIV | Pos) = (0.9 * 0.001) / 0.01089
P(HIV | Pos) ≈ 0.0828
This rounds to approximately 0.083, which corresponds to option 'C'.
Conclusion
Thus, the probability that a person actually has HIV given a positive test result is approximately 0.083.
To determine the probability that a person has HIV given a positive test result, we will use Bayes' theorem.
Definitions
- P(HIV): Probability of having HIV = 0.001 (0.1%)
- P(No HIV): Probability of not having HIV = 0.999 (99.9%)
- P(Pos | HIV): Probability of testing positive given HIV = 0.9 (90%)
- P(Pos | No HIV): Probability of testing positive given no HIV = 0.01 (1%)
Calculating the Required Probability
We need to find P(HIV | Pos), the probability of having HIV given a positive test result. According to Bayes' theorem:
P(HIV | Pos) = (P(Pos | HIV) * P(HIV)) / P(Pos)
Calculating P(Pos)
P(Pos) can be calculated as follows:
- P(Pos) = P(Pos | HIV) * P(HIV) + P(Pos | No HIV) * P(No HIV)
- P(Pos) = (0.9 * 0.001) + (0.01 * 0.999)
- P(Pos) = 0.0009 + 0.00999 = 0.01089
Final Calculation
Now substitute back into Bayes' theorem:
P(HIV | Pos) = (0.9 * 0.001) / 0.01089
P(HIV | Pos) ≈ 0.0828
This rounds to approximately 0.083, which corresponds to option 'C'.
Conclusion
Thus, the probability that a person actually has HIV given a positive test result is approximately 0.083.
In spot welding of two stainless steel sheets, each of 5mm thickness, welding current 15000A is applied for 0.4sec, the heat dissipated to the base metal is 22000J . Assuming that the heat required for melting 2mm3 volume steel is 30J and contact resistance between sheets is 0.0004Ω. The volume (in mm3) of weld nugget is__________.
Correct answer is between '932,934'. Can you explain this answer?
In spot welding of two stainless steel sheets, each of 5mm thickness, welding current 15000A is applied for 0.4sec, the heat dissipated to the base metal is 22000J . Assuming that the heat required for melting 2mm3 volume steel is 30J and contact resistance between sheets is 0.0004Ω. The volume (in mm3) of weld nugget is__________.
|
|
Anushka Mukherjee answered |
Total heat generated = I2RT
= (15000)2 x 0.0004 x 0.4
=36000
Heat required to melt the nugget = 36000 -22000
=14000J
Volume of nugget = 14000/15 = 933.33 mm3
= (15000)2 x 0.0004 x 0.4
=36000
Heat required to melt the nugget = 36000 -22000
=14000J
Volume of nugget = 14000/15 = 933.33 mm3
In a school, 12th class consists of 30% male students of which 30% male students failed in the class. Total 82% students passed in 12th examination out of 900 students. Calculate the total number of female passed students?- a)610
- b)390
- c)489
- d)549
Correct answer is option 'D'. Can you explain this answer?
In a school, 12th class consists of 30% male students of which 30% male students failed in the class. Total 82% students passed in 12th examination out of 900 students. Calculate the total number of female passed students?
a)
610
b)
390
c)
489
d)
549
|
Janhavi Sharma answered |
Short Trick:
Total students = 900
Boys : Girls = 30 % : 70% = 3 : 7
So, exactly Boys : Girls = 270 : 630
Total failed students = 18% of 900 = 162
Failed boys = 30% of 270 = 81
Failed girls = 162 - 81 = 81
Passed female students = 630 - 81 =549
Basic Method:
⇒ Let us consider total number of students be 100x
⇒ ∴ Males students = 30x , female students = 70x
⇒ According to condition given in the problem, of this 30x male students, 70 % male students pass the exam.
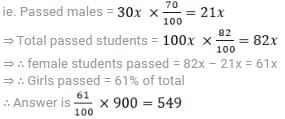
Total students = 900
Boys : Girls = 30 % : 70% = 3 : 7
So, exactly Boys : Girls = 270 : 630
Total failed students = 18% of 900 = 162
Failed boys = 30% of 270 = 81
Failed girls = 162 - 81 = 81
Passed female students = 630 - 81 =549
Basic Method:
⇒ Let us consider total number of students be 100x
⇒ ∴ Males students = 30x , female students = 70x
⇒ According to condition given in the problem, of this 30x male students, 70 % male students pass the exam.
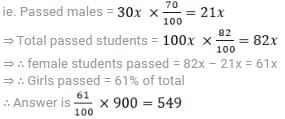
A pelton wheel is required to develop 6 MW when working under a head of 300m. It rotates with a speed of 550rpm. Assuming jet ratio as 10 and overall efficiency as 85%. The diameter of wheel and number of jets respectively are:[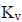
(coefficient of velocity of jet)= 0.98 and 
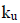(coefficient of peripheral velocity)= 0.46] - a)0.1225m, and 3
- b)1.225m, and 3
- c)0.1225m and 2
- d)1.225m and 2
Correct answer is option 'B'. Can you explain this answer?
(coefficient of velocity of jet)= 0.98 and (coefficient of peripheral velocity)= 0.46] a)
0.1225m, and 3
b)
1.225m, and 3
c)
0.1225m and 2
d)
1.225m and 2
|
Shreya Kulkarni answered |
Velocity of jet,
Tangential [Peripheral] velocity of wheel,
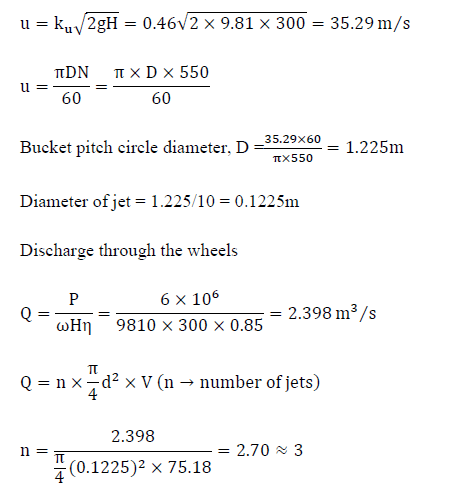
Tangential [Peripheral] velocity of wheel,
Direction: Study the following information carefully and answer the given questions.Seven people, P, Q, R, S, T, W and X sitting in a straight line facing north, not necessarily in the same order. R sits at one of the extreme ends of the line. T has as many people sitting on his right, as on his left. S sits third to the left of X. Q sits on the immediate left of W. Q does not sit at any of the extreme ends of the line.
If all the people are made to sit in alphabetical order from right to left, the positions of how many people will remain unchanged?- a)Five
- b)One
- c)Three
- d)None
Correct answer is option 'B'. Can you explain this answer?
Direction: Study the following information carefully and answer the given questions.
Seven people, P, Q, R, S, T, W and X sitting in a straight line facing north, not necessarily in the same order. R sits at one of the extreme ends of the line. T has as many people sitting on his right, as on his left. S sits third to the left of X. Q sits on the immediate left of W. Q does not sit at any of the extreme ends of the line.
If all the people are made to sit in alphabetical order from right to left, the positions of how many people will remain unchanged?
If all the people are made to sit in alphabetical order from right to left, the positions of how many people will remain unchanged?
a)
Five
b)
One
c)
Three
d)
None
|
|
Kiran Mehta answered |
Hence, only Q's position will remain unchanged.
A simple pendulum of length 5m with a bob of mass 1 kg, is in simple harmonicmotion. As it passes through its mean position, the bob has a speed of 5m/s. The net force on the bob at the mean position is:-- a)Zero
- b)2.5 N
- c) 5N
- d)25N
Correct answer is option 'A'. Can you explain this answer?
a)
Zero
b)
2.5 N
c)
5N
d)
25N
|
|
Rohan Singh answered |
Explanation:
- Given, length of the pendulum, l = 5m
- Mass of the bob, m = 1 kg
- Speed of the bob at mean position, v = 5m/s
- At the mean position, the displacement of the bob is zero and hence the net force on the bob is zero as well.
- At the mean position, the gravitational force acting downward on the bob is balanced by the tension force acting upward on the string.
- As the bob is in simple harmonic motion, the net force acting on the bob at any point is given by F = -kx, where F is the net force, k is the spring constant and x is the displacement from the mean position.
- However, in the case of a pendulum, the restoring force is provided by the weight of the bob and not a spring. The restoring force is given by F = -mg sinθ, where θ is the angle made by the string with the vertical.
- At the mean position, sinθ = 0 and hence the restoring force is zero. Therefore, the net force on the bob at the mean position is zero.
- Hence, option A is the correct answer.
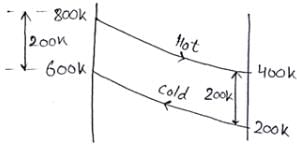
The inlet temperature of hot water is 800K and outlet temperature is 400 K and the inlet temperature of cold water is 200 K, both are flowing at some mass flow rate. Taking counter flow heat exchanger the NTU and LMTD respectively are- a)1.5 and 400 K
- b)2 ad 200 K
- c)0.5 and 200 K
- d)1 and 400 K
Correct answer is option 'B'. Can you explain this answer?
The inlet temperature of hot water is 800K and outlet temperature is 400 K and the inlet temperature of cold water is 200 K, both are flowing at some mass flow rate. Taking counter flow heat exchanger the NTU and LMTD respectively are
a)
1.5 and 400 K
b)
2 ad 200 K
c)
0.5 and 200 K
d)
1 and 400 K
|
Pranavi Tiwari answered |
Here, this is a case of balanced heat exchanger
MhCh =mcCc = C [Both the fluids are water]
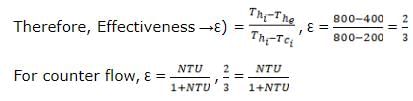
NTU = 2
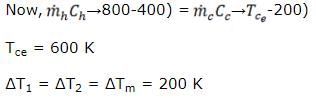
MhCh =mcCc = C [Both the fluids are water]
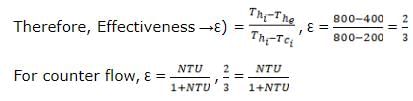
NTU = 2
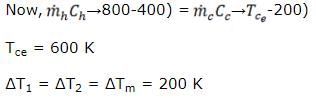
Direction: Two sentences with one blank in each, followed by five alternatives, are given. Choose that option as the answer which can fill both the blanks of both the sentences.
I. Most of our employees get _____ abroad at some stage
II. The aircraft and its crew were ______ missing.- a)announced
- b)arrested
- c)sent
- d)posted
Correct answer is option 'D'. Can you explain this answer?
Direction: Two sentences with one blank in each, followed by five alternatives, are given. Choose that option as the answer which can fill both the blanks of both the sentences.
I. Most of our employees get _____ abroad at some stage
II. The aircraft and its crew were ______ missing.
I. Most of our employees get _____ abroad at some stage
II. The aircraft and its crew were ______ missing.
a)
announced
b)
arrested
c)
sent
d)
posted
|
|
Tanvi Chopra answered |
Post means to send somebody to a place for a period of time as part of their job and to announce something publicly or officially.
Hence, option D is correct.
Hence, option D is correct.
An unsaturated air enters in an insulated chamber at 320C where it flows over a long sheet of water and becomes cooled to 260C, which is adiabatic saturation temperature. The total pressure of the mixture remains constant at 100 kPa. The corresponding pressure to saturation temperature is 3.363 kPa. The humidity ratio at the entry of chamber is (in kg vap/kg dry air)
Given data: Cp of air = 1.005 kJ/kgK
At 320C, hv1 = 2559.9 kJ/kg,
At 260C, hfg2 = 2439.9 kJ/kg, hf2 = 109.1 kJ/kg
Correct answer is between '0.017,0.021'. Can you explain this answer?
An unsaturated air enters in an insulated chamber at 320C where it flows over a long sheet of water and becomes cooled to 260C, which is adiabatic saturation temperature. The total pressure of the mixture remains constant at 100 kPa. The corresponding pressure to saturation temperature is 3.363 kPa. The humidity ratio at the entry of chamber is (in kg vap/kg dry air)
Given data: Cp of air = 1.005 kJ/kgK
At 320C, hv1 = 2559.9 kJ/kg,
At 260C, hfg2 = 2439.9 kJ/kg, hf2 = 109.1 kJ/kg
Given data: Cp of air = 1.005 kJ/kgK
At 320C, hv1 = 2559.9 kJ/kg,
At 260C, hfg2 = 2439.9 kJ/kg, hf2 = 109.1 kJ/kg
|
|
Bhavya Patel answered |
Given, p =100 kPa, ps = 3.363 kPa
Since the system is insulted and no work interaction, so using conservation of energy
ma1ha1 + mv1hv1 + (mv2−mv1) hf2 = ma2ha2 + m2hv2 (i)
ma = mass of dry air (kg)
mv = mass of water vapour (kg)
ha = specific enthalpy of dry air (kJ/kg)
hf = specific enthalpy of liquid water (kJ/kg)
hv = specific enthalpy of water vapour in air (kJ/kg)
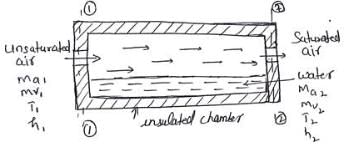
Divide the eqn (i) by ma1, we get
ha1 + W1 hw1 + (W2− W1) hf2 = ha2 + W2hv2 (∵ ma1 = ma2) (ii)
Where, W = specific humidity
Humidity ratio at exit,
(ha1 − ha2) + W2 (hf2 − hv2) = W1 (hf2−hv1)
Cp (T2 – T1) + W2 hfg2 = W1 (hv1−hf2) (∵ hv2 = hg2 and hfg2 = hg2 − hf2)
1.005 × (26−32) + 0.0216×2439.9 = W1 × (2559.9−109.1)
W1 = 0.019 kg vap/kg dry air
Since the system is insulted and no work interaction, so using conservation of energy
ma1ha1 + mv1hv1 + (mv2−mv1) hf2 = ma2ha2 + m2hv2 (i)
ma = mass of dry air (kg)
mv = mass of water vapour (kg)
ha = specific enthalpy of dry air (kJ/kg)
hf = specific enthalpy of liquid water (kJ/kg)
hv = specific enthalpy of water vapour in air (kJ/kg)
Divide the eqn (i) by ma1, we get
ha1 + W1 hw1 + (W2− W1) hf2 = ha2 + W2hv2 (∵ ma1 = ma2) (ii)
Where, W = specific humidity
Humidity ratio at exit,
(ha1 − ha2) + W2 (hf2 − hv2) = W1 (hf2−hv1)
Cp (T2 – T1) + W2 hfg2 = W1 (hv1−hf2) (∵ hv2 = hg2 and hfg2 = hg2 − hf2)
1.005 × (26−32) + 0.0216×2439.9 = W1 × (2559.9−109.1)
W1 = 0.019 kg vap/kg dry air
Find the value of
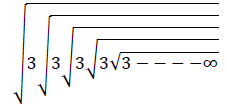
- a)
- b)
- c)
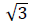
- d)3
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
3
|
Sai Reddy answered |
=y
=3yy(y-3) = 0
y = 3
A milk chilling unit can remove heat from the milk at the rate of 42 MJ/h. The rate of heat leakage into the milk from the surrounding is 4.2 MJ/h. The specific heat of milk above the freezing point is 4.2 kJ/kg K and below the freezing point is 2.1 kJ/kg K. The freezing point of milk is -2 oc and the latent heat is 100 kJ/kg. The time required (in min) for cooling a batch of 100 kg milk from 47 oc to -5 oc is
Correct answer is between '49,50'. Can you explain this answer?
A milk chilling unit can remove heat from the milk at the rate of 42 MJ/h. The rate of heat leakage into the milk from the surrounding is 4.2 MJ/h. The specific heat of milk above the freezing point is 4.2 kJ/kg K and below the freezing point is 2.1 kJ/kg K. The freezing point of milk is -2 oc and the latent heat is 100 kJ/kg. The time required (in min) for cooling a batch of 100 kg milk from 47 oc to -5 oc is
|
Mihir Unni answered |
Suppose the time required is t hrs then
The amount of heat removed
= heat removed to decrease the temperature from 47 oc to -2 oc + latent heat + heat removed to decrease the temperature from -2 oc to -5 oc
(42000 – 4200)t = 100 ×[4.2 × (47+2) + 100 + 2.1× (−2+5)]
t = 0.825 hr = 49.5 min
The amount of heat removed
= heat removed to decrease the temperature from 47 oc to -2 oc + latent heat + heat removed to decrease the temperature from -2 oc to -5 oc
(42000 – 4200)t = 100 ×[4.2 × (47+2) + 100 + 2.1× (−2+5)]
t = 0.825 hr = 49.5 min
A cylindrical pipe is made up of copper having E=120 Gpa and A=110 mm2. This cylindrical tube is covered with an aluminum tube having E=70 Gpa and A=70 mm2. If the two assembly are in parallel and is loaded with a force of 70 KN. Find the deflection of the whole assembly under this loading. Given length of the tube is 500 mm.- a)21 .96 mm
- b)1 .93 mm
- c)2.64 mm
- d)5 .69 mm
Correct answer is option 'B'. Can you explain this answer?
A cylindrical pipe is made up of copper having E=120 Gpa and A=110 mm2. This cylindrical tube is covered with an aluminum tube having E=70 Gpa and A=70 mm2. If the two assembly are in parallel and is loaded with a force of 70 KN. Find the deflection of the whole assembly under this loading. Given length of the tube is 500 mm.
a)
21 .96 mm
b)
1 .93 mm
c)
2.64 mm
d)
5 .69 mm
|
Devansh Sharma answered |
A metric thread of pitch 3mm and diameter 30mm, inspected for its pitch diameter using 2- wire method. The diameter of best size wire in mm is- a)1.44 mm
- b)2.88 mm
- c)1.73 mm
- d)0.72 mm
Correct answer is option 'C'. Can you explain this answer?
A metric thread of pitch 3mm and diameter 30mm, inspected for its pitch diameter using 2- wire method. The diameter of best size wire in mm is
a)
1.44 mm
b)
2.88 mm
c)
1.73 mm
d)
0.72 mm
|
|
Nayanika Sharma answered |
For metric thread included angle is taken 600
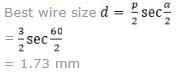
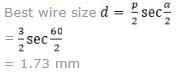
In automobiles, the brakes used in hand braking systems are usually- a)Internal expanding brakes
- b)External contracting brakes
- c)Disc brakes
- d)All of these
Correct answer is option 'B'. Can you explain this answer?
In automobiles, the brakes used in hand braking systems are usually
a)
Internal expanding brakes
b)
External contracting brakes
c)
Disc brakes
d)
All of these
|
|
Ameya Datta answered |
Understanding Hand Braking Systems
Hand braking systems, commonly referred to as parking brakes or emergency brakes, are essential safety features in automobiles. They prevent the vehicle from rolling when parked and provide additional stopping power in emergencies.
Types of Brake Systems
Automobile brake systems can be categorized into several types:
- Internal Expanding Brakes: These brakes expand inside a drum to create friction. They are typically used in rear brakes but are not commonly found in hand braking systems.
- External Contracting Brakes: These brakes work by contracting around an external surface. They are the traditional mechanism used in hand braking systems, especially in older vehicles.
- Disc Brakes: These brakes utilize a rotor and caliper system that clamps down on the rotor to create friction. They are more common in modern vehicles for primary braking but are less common for handbrakes.
Why External Contracting Brakes?
The correct answer to the question is option 'B', External Contracting Brakes, for several reasons:
- Design Efficiency: The design of external contracting brakes allows them to effectively hold the vehicle in place by contracting around the drum or similar component.
- Space Considerations: Hand brakes are typically designed to be compact and efficient. External contracting brakes fit well within these spatial constraints.
- Reliability: These brakes provide reliable performance in holding the vehicle stationary, which is critical for a parking or emergency system.
In summary, while various brake types exist, external contracting brakes are specifically suited for hand braking systems due to their effective design and reliability.
Hand braking systems, commonly referred to as parking brakes or emergency brakes, are essential safety features in automobiles. They prevent the vehicle from rolling when parked and provide additional stopping power in emergencies.
Types of Brake Systems
Automobile brake systems can be categorized into several types:
- Internal Expanding Brakes: These brakes expand inside a drum to create friction. They are typically used in rear brakes but are not commonly found in hand braking systems.
- External Contracting Brakes: These brakes work by contracting around an external surface. They are the traditional mechanism used in hand braking systems, especially in older vehicles.
- Disc Brakes: These brakes utilize a rotor and caliper system that clamps down on the rotor to create friction. They are more common in modern vehicles for primary braking but are less common for handbrakes.
Why External Contracting Brakes?
The correct answer to the question is option 'B', External Contracting Brakes, for several reasons:
- Design Efficiency: The design of external contracting brakes allows them to effectively hold the vehicle in place by contracting around the drum or similar component.
- Space Considerations: Hand brakes are typically designed to be compact and efficient. External contracting brakes fit well within these spatial constraints.
- Reliability: These brakes provide reliable performance in holding the vehicle stationary, which is critical for a parking or emergency system.
In summary, while various brake types exist, external contracting brakes are specifically suited for hand braking systems due to their effective design and reliability.
Chapter doubts & questions for Practice Tests - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Practice Tests - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup