All questions of Programming & Data Structures for Computer Science Engineering (CSE) Exam
#include <stdio.h>
#if X == 3
#define Y 3
#else
#define Y 5
#endif
int main()
{
printf("%d", Y);
return 0;
}What is the output of the above program?- a)3
- b)5
- c)3 or 5 depending on value of X
- d)Compile time error
Correct answer is option 'B'. Can you explain this answer?
#include <stdio.h>
#if X == 3
#define Y 3
#else
#define Y 5
#endif
int main()
{
printf("%d", Y);
return 0;
}
#if X == 3
#define Y 3
#else
#define Y 5
#endif
int main()
{
printf("%d", Y);
return 0;
}
What is the output of the above program?
a)
3
b)
5
c)
3 or 5 depending on value of X
d)
Compile time error

|
Gate Gurus answered |
The output of the given program depends on the value of X.
However, in the given code, the value of X is not explicitly defined, so its value is undefined. If X is not defined or if its value is not explicitly set before the preprocessing phase, it is considered as 0 by default.
Since X is not defined, the #if X == 3 directive evaluates to false, and therefore, the else part of the #if directive is used, setting Y to 5.
So, the output of the program will be:
What are the main applications of tree data structure? 1) Manipulate hierarchical data 2) Make information easy to search (see tree traversal). 3) Manipulate sorted lists of data 4) Router algorithms 5) Form of a multi-stage decision-making, like Chess Game. 6) As a workflow for compositing digital images for visual effects- a)1, 2, 3, 4 and 6
- b)1, 2, 3, 4 and 5
- c)1, 3, 4, 5 and 6
- d)1, 2, 3, 4, 5 and 6
Correct answer is 'D'. Can you explain this answer?
What are the main applications of tree data structure? 1) Manipulate hierarchical data 2) Make information easy to search (see tree traversal). 3) Manipulate sorted lists of data 4) Router algorithms 5) Form of a multi-stage decision-making, like Chess Game. 6) As a workflow for compositing digital images for visual effects
a)
1, 2, 3, 4 and 6
b)
1, 2, 3, 4 and 5
c)
1, 3, 4, 5 and 6
d)
1, 2, 3, 4, 5 and 6
|
|
Atharva Kulkarni answered |
Main Applications of Tree Data Structure:
1. Manipulate Hierarchical Data:
Trees are used to represent hierarchical data, such as file systems or organization charts, where each node represents a folder, file, or employee.
2. Make Information Easy to Search:
Tree traversal algorithms can be used to search for specific data within a tree structure, making it an efficient way to store and retrieve information.
3. Manipulate Sorted Lists of Data:
Binary search trees can be used to manipulate and search sorted lists of data, providing a faster search time than traditional linear searches.
4. Router Algorithms:
Trees are used in computer networking to represent routing algorithms that determine the path of data packets through a network.
5. Multi-Stage Decision Making:
Trees can be used to represent multi-stage decision-making processes, such as in a chess game, where each node represents a possible move and the branches represent subsequent moves.
6. Workflow for Compositing Digital Images:
Trees are used in visual effects to represent the workflow for compositing digital images, where each node represents a stage in the process and the branches represent the steps taken to achieve the final image.
Therefore, the correct answer is D, as all of these applications use tree data structures.
1. Manipulate Hierarchical Data:
Trees are used to represent hierarchical data, such as file systems or organization charts, where each node represents a folder, file, or employee.
2. Make Information Easy to Search:
Tree traversal algorithms can be used to search for specific data within a tree structure, making it an efficient way to store and retrieve information.
3. Manipulate Sorted Lists of Data:
Binary search trees can be used to manipulate and search sorted lists of data, providing a faster search time than traditional linear searches.
4. Router Algorithms:
Trees are used in computer networking to represent routing algorithms that determine the path of data packets through a network.
5. Multi-Stage Decision Making:
Trees can be used to represent multi-stage decision-making processes, such as in a chess game, where each node represents a possible move and the branches represent subsequent moves.
6. Workflow for Compositing Digital Images:
Trees are used in visual effects to represent the workflow for compositing digital images, where each node represents a stage in the process and the branches represent the steps taken to achieve the final image.
Therefore, the correct answer is D, as all of these applications use tree data structures.
Consider the following C program: #include <stdio.h>#define EOF -1void push (int); /* push the argument on the stack */int pop (void); /* pop the top of the stack */void flagError ();int main (){ int c, m, n, r; while ((c = getchar ()) != EOF){ if (isdigit (c) ) push (c);else if ((c == '+') || (c == '*')){ m = pop ();n = pop ();r = (c == '+') ? n + m : n*m;push (r);}
else if (c != ' ') flagError ();}
printf("% c", pop ());}What is the output of the program for the following input?5 2 * 3 3 2 + * +- a)15
- b)25
- c)30
- d)150
Correct answer is option 'B'. Can you explain this answer?
Consider the following C program:
#include <stdio.h>
#define EOF -1
void push (int); /* push the argument on the stack */
int pop (void); /* pop the top of the stack */
void flagError ();
int main ()
{ int c, m, n, r;
while ((c = getchar ()) != EOF)
{ if (isdigit (c) )
push (c);
else if ((c == '+') || (c == '*'))
{ m = pop ();
n = pop ();
r = (c == '+') ? n + m : n*m;
push (r);
}
else if (c != ' ')
else if (c != ' ')
flagError ();
}
printf("% c", pop ());
printf("% c", pop ());
}
What is the output of the program for the following input?
5 2 * 3 3 2 + * +
a)
15
b)
25
c)
30
d)
150
|
|
Yash Patel answered |
B) 25
let first part
5 ----push
2------push
push------5*2=10. (pops 5 and 2)
let first part
5 ----push
2------push
push------5*2=10. (pops 5 and 2)
push 3
push 3
push 2
push 3+2 = 5 (pops 2 and 3)
push 5*3 = 15 (pops (5 and 3)
push 15 + 10 = 25 (pops (15 and 10)
push 3
push 2
push 3+2 = 5 (pops 2 and 3)
push 5*3 = 15 (pops (5 and 3)
push 15 + 10 = 25 (pops (15 and 10)
If arity of operators is fixed, then which of the following notations can be used to parse expressions without parentheses? a) Infix Notation (Inorder traversal of a expression tree) b) Postfix Notation (Postorder traversal of a expression tree) c) Prefix Notation (Preorder traversal of a expression tree)- a)b and c
- b)Only b
- c)a, b and c
- d)None of them
Correct answer is option 'A'. Can you explain this answer?
If arity of operators is fixed, then which of the following notations can be used to parse expressions without parentheses? a) Infix Notation (Inorder traversal of a expression tree) b) Postfix Notation (Postorder traversal of a expression tree) c) Prefix Notation (Preorder traversal of a expression tree)
a)
b and c
b)
Only b
c)
a, b and c
d)
None of them

|
Swara Dasgupta answered |
Consider inorder traversal or infix as
a+b*c+d*e+f+g
its prefix is
++a*bc++*defg
And postfix expression is
abc*++de*f+g++
Here prefix and postfix can be calculated in right way by using algorithms.But inorder can give different values.
Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst-case time complexity of the best-known algorithm to delete the node x from the list ?
- a)O(n)
- b)O(log2 n)
- c)O(log n)
- d)O(1)
Correct answer is option 'A'. Can you explain this answer?
Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst-case time complexity of the best-known algorithm to delete the node x from the list ?
a)
O(n)
b)
O(log2 n)
c)
O(log n)
d)
O(1)
|
|
Soumya Dey answered |

The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a Max Heap. The resultant Max Heap is.- a)
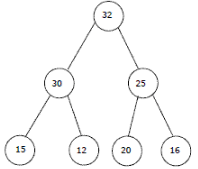
- b)
- c)
- d)
Correct answer is option 'A'. Can you explain this answer?
The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a Max Heap. The resultant Max Heap is.
a)
b)
c)
d)

|
Crack Gate answered |
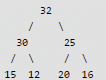
32, 15, 20, 30, 12, 25, 16
After insertion of 32, 15 and 20
After insertion of 32, 15 and 20
After insertion of 30
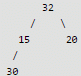
Max Heap property is violated, so 30 is swapped with 15
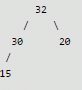
After insertion of 12
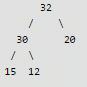
After insertion of 25
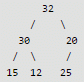
Max Heap property is violated, so 25 is swapped with 20
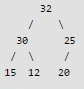
After insertion of 16
Let A be a two dimensional array declared as follows:A: array [1 …. 10] [1 ….. 15] of integer;Assuming that each integer takes one memory location, the array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element 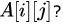
- a)
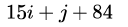
- b)
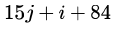
- c)
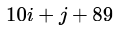
- d)
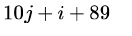
Correct answer is option 'A'. Can you explain this answer?
Let A be a two dimensional array declared as follows:
A: array [1 …. 10] [1 ….. 15] of integer;
Assuming that each integer takes one memory location, the array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element 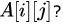
a)
b)
c)
d)

|
Crack Gate answered |
A [ LB1..............UB1,LB2.................UB2 ]
BA = Base address.
C = size of each element.
Row major order.
Loc(a[i][j]) = BA + [ (i-LB1) (UB2 - LB2 + 1) + (j - LB2) ] * C.
Column Major order
Loc(a[i][j]) = BA + [ (j-LB2) (UB1 - LB1 + 1) + (i - LB1) ] * C.
substituting the values. answer is A.
How many distinct binary search trees can be created out of 4 distinct keys?- a)4
- b)14
- c)24
- d)42
Correct answer is option 'B'. Can you explain this answer?
How many distinct binary search trees can be created out of 4 distinct keys?
a)
4
b)
14
c)
24
d)
42
|
|
Rajeev Menon answered |
Number of Binary Search trees for n nodes is given by = (2n)! / n! * (n+1)!
Hence for 4 keys or nodes-
= 8! /4! * 5!
= 14
Hence, 14 distinct binary search trees are possible for 4 keys.
So, the Correct Answer is Option B
So, the Correct Answer is Option B
You can solve many such questions & mock tests by going through the course:
What does the following function do for a given binary tree?int fun(struct node *root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}- a)Counts leaf nodes
- b)Counts internal nodes
- c)Returns height where height is defined as number of edges on the path from root to deepest node
- d)Return diameter where diameter is number of edges on the longest path between any two nodes.
Correct answer is option 'B'. Can you explain this answer?
What does the following function do for a given binary tree?
int fun(struct node *root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}
a)
Counts leaf nodes
b)
Counts internal nodes
c)
Returns height where height is defined as number of edges on the path from root to deepest node
d)
Return diameter where diameter is number of edges on the longest path between any two nodes.
|
|
Sanya Agarwal answered |
The function counts internal nodes. 1) If root is NULL or a leaf node, it returns 0. 2) Otherwise returns, 1 plus count of internal nodes in left subtree, plus count of internal nodes in right subtree.
Which traversal of tree resembles the breadth first search of the graph- a)Preorder
- b)Inorder
- c)Postorder
- d)Level order
Correct answer is option 'D'. Can you explain this answer?
Which traversal of tree resembles the breadth first search of the graph
a)
Preorder
b)
Inorder
c)
Postorder
d)
Level order
|
|
Sanya Agarwal answered |
Breadth first search visits all the neighbors first and then deepens into each neighbor one by one. The level order traversal of the tree also visits nodes on the current level and then goes to the next level.
Level of a node is distance from root to that node. For example, level of root is 1 and levels of left and right children of root is 2. The maximum number of nodes on level i of a binary tree is
In the following answers, the operator '^' indicates power.- a)2^(i-1)
- b)2^i
- c)2^(i+1)
- d)2^[(i+1)/2]
Correct answer is option 'A'. Can you explain this answer?
Level of a node is distance from root to that node. For example, level of root is 1 and levels of left and right children of root is 2. The maximum number of nodes on level i of a binary tree is
In the following answers, the operator '^' indicates power.
In the following answers, the operator '^' indicates power.
a)
2^(i-1)
b)
2^i
c)
2^(i+1)
d)
2^[(i+1)/2]
|
|
Milan Rane answered |
Explanation:
The maximum number of nodes on level i of a binary tree is given by the formula: 2^(i-1)
Proof:
Let's consider the levels of the binary tree from top to bottom. The root node is at level 1, its children are at level 2, their children are at level 3, and so on.
At level 1, there is only one node which is the root node. Therefore, the maximum number of nodes on level 1 is 2^(1-1) = 1.
At level 2, there can be at most two nodes because each node at level 1 can have at most two children. Therefore, the maximum number of nodes on level 2 is 2^(2-1) = 2.
At level 3, each node at level 2 can have at most two children. Therefore, the maximum number of nodes on level 3 is 2^(3-1) = 4.
Similarly, at level i, each node at level i-1 can have at most two children. Therefore, the maximum number of nodes on level i is 2^(i-1).
Hence, the correct answer is option 'A' which is 2^(i-1).
The maximum number of nodes on level i of a binary tree is given by the formula: 2^(i-1)
Proof:
Let's consider the levels of the binary tree from top to bottom. The root node is at level 1, its children are at level 2, their children are at level 3, and so on.
At level 1, there is only one node which is the root node. Therefore, the maximum number of nodes on level 1 is 2^(1-1) = 1.
At level 2, there can be at most two nodes because each node at level 1 can have at most two children. Therefore, the maximum number of nodes on level 2 is 2^(2-1) = 2.
At level 3, each node at level 2 can have at most two children. Therefore, the maximum number of nodes on level 3 is 2^(3-1) = 4.
Similarly, at level i, each node at level i-1 can have at most two children. Therefore, the maximum number of nodes on level i is 2^(i-1).
Hence, the correct answer is option 'A' which is 2^(i-1).
What is the output of the following Java code?public class array
{
public static void main(String args[])
{
int []arr = {1,2,3,4,5};
System.out.println(arr[5]);
}
}- a)4
- b)5
- c)ArrayIndexOutOfBoundsException
- d)InavlidInputException
Correct answer is option 'C'. Can you explain this answer?
What is the output of the following Java code?
public class array
{
public static void main(String args[])
{
int []arr = {1,2,3,4,5};
System.out.println(arr[5]);
}
}
{
public static void main(String args[])
{
int []arr = {1,2,3,4,5};
System.out.println(arr[5]);
}
}
a)
4
b)
5
c)
ArrayIndexOutOfBoundsException
d)
InavlidInputException
|
|
Maitri Dey answered |
**Answer:**
The given Java code will throw an `ArrayIndexOutOfBoundsException` when executed.
**Explanation:**
In Java, arrays are zero-indexed, which means the first element of an array is accessed using the index 0, the second element with index 1, and so on.
In the given code, an array `arr` of size 5 is declared and initialized with the values `{1, 2, 3, 4, 5}`. However, when attempting to access `arr[5]`, we are trying to access the element at index 5, which is outside the valid range of the array.
The valid indices for this array are 0, 1, 2, 3, and 4. Since index 5 does not exist in the array, an `ArrayIndexOutOfBoundsException` is thrown at runtime.
The correct way to access the last element of the array would be to use `arr[arr.length - 1]`. This expression would evaluate to `arr[4]`, which is the value 5 in this case.
Therefore, the output of the given code will be:
```
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: Index 5 out of bounds for length 5
at array.main(array.java:7)
```
So, the correct answer is option **c) ArrayIndexOutOfBoundsException**.
The given Java code will throw an `ArrayIndexOutOfBoundsException` when executed.
**Explanation:**
In Java, arrays are zero-indexed, which means the first element of an array is accessed using the index 0, the second element with index 1, and so on.
In the given code, an array `arr` of size 5 is declared and initialized with the values `{1, 2, 3, 4, 5}`. However, when attempting to access `arr[5]`, we are trying to access the element at index 5, which is outside the valid range of the array.
The valid indices for this array are 0, 1, 2, 3, and 4. Since index 5 does not exist in the array, an `ArrayIndexOutOfBoundsException` is thrown at runtime.
The correct way to access the last element of the array would be to use `arr[arr.length - 1]`. This expression would evaluate to `arr[4]`, which is the value 5 in this case.
Therefore, the output of the given code will be:
```
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: Index 5 out of bounds for length 5
at array.main(array.java:7)
```
So, the correct answer is option **c) ArrayIndexOutOfBoundsException**.
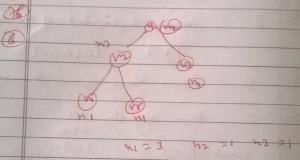
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. n3 can be expressed as- a)n1 + n2 - 1
- b)n1 - 2
- c)[((n1 + n2)/2)]
- d)n2 - 1
Correct answer is option 'B'. Can you explain this answer?
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. n3 can be expressed as
a)
n1 + n2 - 1
b)
n1 - 2
c)
[((n1 + n2)/2)]
d)
n2 - 1
|
|
Maitri Yadav answered |
Consider the following C function:int f(int n){static int i = 1;if(n >= 5) return n;n = n+i; i++;return f(n);}The value returned by f(1) is- a)5
- b)6
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
Consider the following C function:
int f(int n)
{
static int i = 1;
if(n >= 5) return n;
n = n+i;
i++;
return f(n);
}
The value returned by f(1) is
a)
5
b)
6
c)
7
d)
8
|
|
Akshita Khanna answered |
answer is 7.as,
f(1):n=2,i=2
f(2):n=4,i=3
f(4):n=7,i=4
f(7):print(n)===>>> 7<ans>
f(1):n=2,i=2
f(2):n=4,i=3
f(4):n=7,i=4
f(7):print(n)===>>> 7<ans>
A hash table can store a maximum of 10 records. Currently there are records in locations 1, 3, 4, 7, 8, 9, 10. The probability of a new record going into location 2, with a has function resolving collisions by linear probing is- a)0.6
- b)0.1
- c)0.2
- d)0.5
Correct answer is option 'A'. Can you explain this answer?
A hash table can store a maximum of 10 records. Currently there are records in locations 1, 3, 4, 7, 8, 9, 10. The probability of a new record going into location 2, with a has function resolving collisions by linear probing is
a)
0.6
b)
0.1
c)
0.2
d)
0.5
|
|
Maulik Pillai answered |
If the new record hashes onto one of the six locations 7, 8, 9, 10, 1 or 2, the location 2 will receive the new record. The probability is 6/10 (as 10 is the total possible number of locations).
A stack A has 4 entries as following sequence a,b,c,d and stack B is empty. An entry popped out of stack A can be printed or pushed to stack B. An entry popped out of stack B can only be printed.
Then the number of possible permutations that the entries can be printed will be ?
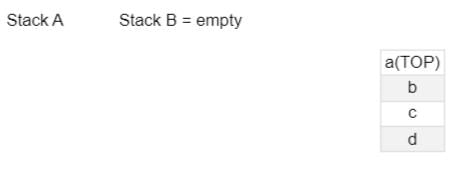
- a)24
- b)12
- c)21
- d)14
Correct answer is option 'D'. Can you explain this answer?
A stack A has 4 entries as following sequence a,b,c,d and stack B is empty. An entry popped out of stack A can be printed or pushed to stack B. An entry popped out of stack B can only be printed.
Then the number of possible permutations that the entries can be printed will be ?
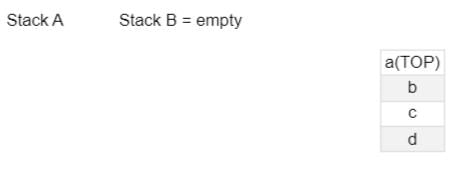
a)
24
b)
12
c)
21
d)
14
|
|
Prateek Khanna answered |
permutations which start with D:
to print D first , all a,b,c must be pushed on to stack before popping D and the only arrangement possible = D C B A
permutations start with C:
you need to push a and b from stack A to stack B , now print C
content of stack B= b a (from top to bottom)
content of stack A = d
permutations possible = 3!/2! = 3 = they are c d b a, c b d a, c b a d --> 3 permutations here
permutations starting with b :
to print b first, a will be pushed onto stack B
content of stack B= a
content of stack A= c d
you can bring these out in (3! -1) as (d a c) is not possible--> 5 possible
permutations starting with a:
fix ab
a b _ _
in this a b c d or a b dc
fix ac
a c _ _
a c b d or a c d b
fix ad
a d _ _
a d c b
total 5
total = 1+3+5+5= 14
to print D first , all a,b,c must be pushed on to stack before popping D and the only arrangement possible = D C B A
permutations start with C:
you need to push a and b from stack A to stack B , now print C
content of stack B= b a (from top to bottom)
content of stack A = d
permutations possible = 3!/2! = 3 = they are c d b a, c b d a, c b a d --> 3 permutations here
permutations starting with b :
to print b first, a will be pushed onto stack B
content of stack B= a
content of stack A= c d
you can bring these out in (3! -1) as (d a c) is not possible--> 5 possible
permutations starting with a:
fix ab
a b _ _
in this a b c d or a b dc
fix ac
a c _ _
a c b d or a c d b
fix ad
a d _ _
a d c b
total 5
total = 1+3+5+5= 14
How many stacks are needed to implement a queue. Consider the situation where no other data structure like arrays, linked list is available to you.- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
How many stacks are needed to implement a queue. Consider the situation where no other data structure like arrays, linked list is available to you.
a)
1
b)
2
c)
3
d)
4

|
Crack Gate answered |
- A queue operates on a First In, First Out (FIFO) principle, while a stack works on a Last In, First Out (LIFO) principle.
- By using two stacks, we can simulate the FIFO behavior of a queue.
thus option B is correct
An array of integers of size n can be converted into a heap by adjusting the heaps rooted at each internal node of the complete binary tree starting at the node ⌊(n - 1) /2⌋, and doing this adjustment up to the root node (root node is at index 0) in the order ⌊(n - 1)/2⌋, ⌊(n - 3)/ 2⌋, ....., 0. The time required to construct a heap in this manner is- a)O(log n)
- b)O(n)
- c)O (n log log n)
- d)O(n log n)
Correct answer is option 'B'. Can you explain this answer?
An array of integers of size n can be converted into a heap by adjusting the heaps rooted at each internal node of the complete binary tree starting at the node ⌊(n - 1) /2⌋, and doing this adjustment up to the root node (root node is at index 0) in the order ⌊(n - 1)/2⌋, ⌊(n - 3)/ 2⌋, ....., 0. The time required to construct a heap in this manner is
a)
O(log n)
b)
O(n)
c)
O (n log log n)
d)
O(n log n)

|
Baishali Bajaj answered |
The above statement is actually algorithm for building a Heap of an input array A.
BUILD-HEAP(A)
heapsize := size(A);
for i := floor(heapsize/2) downto 1
do HEAPIFY(A, i);
end for
END
Upper bound of time complexity is O(n) for above algo
When does the ArrayIndexOutOfBoundsException occur?- a)Compile-time
- b)Run-time
- c)Not an error
- d)Not an exception at all
Correct answer is option 'B'. Can you explain this answer?
When does the ArrayIndexOutOfBoundsException occur?
a)
Compile-time
b)
Run-time
c)
Not an error
d)
Not an exception at all
|
|
Sudhir Patel answered |
ArrayIndexOutOfBoundsException is a run-time exception and the compilation is error-free.
What all is true about Stack data structure? (More than one option is correct)- a)Last IN First OUT
- b)Minimum 2 queues are required to implement a stack
- c)First IN First OUT
- d)Does not have a fixed size.
Correct answer is option 'A,B,D'. Can you explain this answer?
What all is true about Stack data structure? (More than one option is correct)
a)
Last IN First OUT
b)
Minimum 2 queues are required to implement a stack
c)
First IN First OUT
d)
Does not have a fixed size.
|
|
Ananya Kumari answered |
What all is true about stack data structure? ( more than one option is correct)
last in first out ,
maximum 2 queues are required to implement a stack
does not have a fixed size
Correct is ABD is right ans
last in first out ,
maximum 2 queues are required to implement a stack
does not have a fixed size
Correct is ABD is right ans
Postorder traversal of a given binary search tree, T produces the following sequence of keys 10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29 Which one of the following sequences of keys can be the result of an in-order traversal of the tree T? - a)9, 10, 15, 22, 23, 25, 27, 29, 40, 50, 60, 95
- b)9, 10, 15, 22, 40, 50, 60, 95, 23, 25, 27, 29
- c)29, 15, 9, 10, 25, 22, 23, 27, 40, 60, 50, 95
- d)95, 50, 60, 40, 27, 23, 22, 25, 10, 9, 15, 29
Correct answer is option 'A'. Can you explain this answer?
Postorder traversal of a given binary search tree, T produces the following sequence of keys 10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29 Which one of the following sequences of keys can be the result of an in-order traversal of the tree T?
a)
9, 10, 15, 22, 23, 25, 27, 29, 40, 50, 60, 95
b)
9, 10, 15, 22, 40, 50, 60, 95, 23, 25, 27, 29
c)
29, 15, 9, 10, 25, 22, 23, 27, 40, 60, 50, 95
d)
95, 50, 60, 40, 27, 23, 22, 25, 10, 9, 15, 29

|
Saptarshi Nair answered |
Inorder traversal of a BST always gives elements in increasing order. Among all four options, a) is the only increasing order sequence.
What is common in three different types of traversals (Inorder, Preorder and Postorder)?- a)Root is visited before right subtree
- b)Left subtree is always visited before right subtree
- c)Root is visited after left subtree
- d)All of the above
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
What is common in three different types of traversals (Inorder, Preorder and Postorder)?
a)
Root is visited before right subtree
b)
Left subtree is always visited before right subtree
c)
Root is visited after left subtree
d)
All of the above
e)
None of the above
|
|
Sanya Agarwal answered |
The order of inorder traversal is LEFT ROOT RIGHT The order of preorder traversal is ROOT LEFT RIGHT The order of postorder traversal is LEFT RIGHT ROOT In all three traversals, LEFT is traversed before RIGHT
Which of the following traversal outputs the data in sorted order in a BST?- a)Preorder
- b)Inorder
- c)Postorder
- d)Level order
Correct answer is option 'B'. Can you explain this answer?
Which of the following traversal outputs the data in sorted order in a BST?
a)
Preorder
b)
Inorder
c)
Postorder
d)
Level order
|
|
Shraddha Chauhan answered |
Explanation:
In a Binary Search Tree (BST), each node has a key greater than all the keys in its left subtree and smaller than all the keys in its right subtree. Therefore, inorder traversal of a BST visits the nodes in ascending order of their keys.
Inorder Traversal:
Inorder traversal follows the order of Left-Root-Right. It starts from the left subtree, visits the root node, and then the right subtree. This traversal is used to get the elements in sorted order for BST.
Example:
Consider the following BST:
50
/ \
30 70
/ \ / \
20 40 60 80
Inorder traversal of the given tree will output the data in sorted order.
Inorder Traversal: 20 30 40 50 60 70 80
Other Traversals:
Preorder, Postorder, and Level order traversals don't follow the order of keys in a BST.
- Preorder traversal follows the order of Root-Left-Right.
- Postorder traversal follows the order of Left-Right-Root.
- Level order traversal visits the nodes level by level from left to right.
Therefore, inorder traversal is the only traversal that outputs data in sorted order for a BST.
In a Binary Search Tree (BST), each node has a key greater than all the keys in its left subtree and smaller than all the keys in its right subtree. Therefore, inorder traversal of a BST visits the nodes in ascending order of their keys.
Inorder Traversal:
Inorder traversal follows the order of Left-Root-Right. It starts from the left subtree, visits the root node, and then the right subtree. This traversal is used to get the elements in sorted order for BST.
Example:
Consider the following BST:
50
/ \
30 70
/ \ / \
20 40 60 80
Inorder traversal of the given tree will output the data in sorted order.
Inorder Traversal: 20 30 40 50 60 70 80
Other Traversals:
Preorder, Postorder, and Level order traversals don't follow the order of keys in a BST.
- Preorder traversal follows the order of Root-Left-Right.
- Postorder traversal follows the order of Left-Right-Root.
- Level order traversal visits the nodes level by level from left to right.
Therefore, inorder traversal is the only traversal that outputs data in sorted order for a BST.
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i 1]. To be able to store any binary tree on n vertices the minimum size of X should be.
- a) log2n
- b) n
- c) 2n + 1
- d) 2^n — 1
Correct answer is option 'D'. Can you explain this answer?
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i 1]. To be able to store any binary tree on n vertices the minimum size of X should be.
a)
log2nb)
nc)
2n + 1d)
2^n — 1|
|
Neha Choudhury answered |
For a right skewed binary tree, number of nodes will be 2^n – 1. For example, in below binary tree, node ‘A’ will be stored at index 1, ‘B’ at index 3, ‘C’ at index 7 and ‘D’ at index 15.
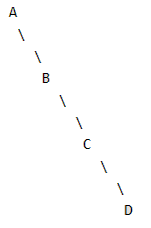
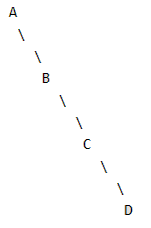
Suppose a circular queue of capacity (n - 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are- a)full: (REAR+1) mod n == FRONTempty: REAR == FRONT$
- b)full: (REAR+1) mod n == FRONTempty: (FRONT+1) mod n == REAR
- c)full: REAR == FRONTempty: (REAR+1) mod n == FRONT
- d)full: (FRONT+1) mod n == REARempty: REAR == FRONT
Correct answer is option 'A'. Can you explain this answer?
Suppose a circular queue of capacity (n - 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are
a)
full: (REAR+1) mod n == FRONT
empty: REAR == FRONT$
b)
full: (REAR+1) mod n == FRONT
empty: (FRONT+1) mod n == REAR
c)
full: REAR == FRONT
empty: (REAR+1) mod n == FRONT
d)
full: (FRONT+1) mod n == REAR
empty: REAR == FRONT

|
Sagnik Sen answered |
In a circular queue implementation using an array of size n, the queue is considered full when there is only one empty space left in the array. This means that if the next element is inserted at the current REAR position, it will wrap around to the FRONT position, and there will be no space for additional elements.
The condition to detect a full queue is:
(REAR + 1) mod n == FRONT
Here, (REAR + 1) calculates the next position in the array after the current REAR position, and mod n ensures that the position wraps around within the range of the array. If this calculated next position is equal to the current FRONT position, it means the queue is full because there is only one empty space left.
Similarly, the condition to detect an empty queue is:
REAR == FRONT
If the REAR and FRONT indices are equal, it means there are no elements in the queue, and it is empty.
Therefore, the correct answer is option 'A' – full: (REAR + 1) mod n == FRONT, empty: REAR == FRONT.
Suppose you are given an implementation of a queue of integers. The operations that can be performed on the queue are:i. isEmpty (Q) — returns true if the queue is empty, false otherwise.ii. delete (Q) — deletes the element at the front of the queue and returns its value.iii. insert (Q, i) — inserts the integer i at the rear of the queue.Consider the following function:void f (queue Q) {int i ;if (!isEmpty(Q)) { i = delete(Q);f(Q);insert(Q, i);}
}What operation is performed by the above function f ?- a)Leaves the queue Q unchanged
- b)Reverses the order of the elements in the queue Q
- c)Deletes the element at the front of the queue Q and inserts it at the rear keeping the other elements in the same order
- d)Empties the queue Q
Correct answer is option 'B'. Can you explain this answer?
Suppose you are given an implementation of a queue of integers. The operations that can be performed on the queue are:
i. isEmpty (Q) — returns true if the queue is empty, false otherwise.
ii. delete (Q) — deletes the element at the front of the queue and returns its value.
iii. insert (Q, i) — inserts the integer i at the rear of the queue.
Consider the following function:
void f (queue Q) {
int i ;
if (!isEmpty(Q)) {
i = delete(Q);
f(Q);
insert(Q, i);
}
}
}
What operation is performed by the above function f ?
a)
Leaves the queue Q unchanged
b)
Reverses the order of the elements in the queue Q
c)
Deletes the element at the front of the queue Q and inserts it at the rear keeping the other elements in the same order
d)
Empties the queue Q
|
|
Mira Choudhary answered |
insert() will inserts the value in just reverse order.
Consider the following statements:
i. First-in-first-out types of computations are efficiently supported by STACKS.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
- a)(ii) and (iii) are true
- b)(i) and (ii) are true
- c)(iii) and (iv) are true
- d)(ii) and (iv) are true
Correct answer is option 'A'. Can you explain this answer?
Consider the following statements:
i. First-in-first-out types of computations are efficiently supported by STACKS.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
a)
(ii) and (iii) are true
b)
(i) and (ii) are true
c)
(iii) and (iv) are true
d)
(ii) and (iv) are true

|
Crack Gate answered |
Let's analyze each statement to determine which ones are true:
i. First-in-first-out types of computations are efficiently supported by STACKS.
- This statement is false. Stacks support Last-in-First-out (LIFO) operations, not FIFO. So, this statement is not true.
- This statement is false. Stacks support Last-in-First-out (LIFO) operations, not FIFO. So, this statement is not true.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.**
- This statement is generally true. Linked lists allow for efficient insertion and deletion operations, which are costly in arrays due to the need to shift elements.
- This statement is generally true. Linked lists allow for efficient insertion and deletion operations, which are costly in arrays due to the need to shift elements.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
- This statement is true. Circular arrays can utilize the entire array space more efficiently and avoid unnecessary shifts compared to a linear array with two indices.
- This statement is true. Circular arrays can utilize the entire array space more efficiently and avoid unnecessary shifts compared to a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
- This statement is false. Last-in-first-out (LIFO) operations are supported by stacks, not queues. Queues support First-in-First-out (FIFO) operations.
- This statement is false. Last-in-first-out (LIFO) operations are supported by stacks, not queues. Queues support First-in-First-out (FIFO) operations.
Conclusion
Based on the analysis:
- Statement ii and iii are true:
- ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
- iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
- ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
- iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
Therefore, the correct answer is:
1. (ii) and (iii) are true
Consider a node X in a Binary Tree. Given that X has two children, let Y be Inorder successor of X. Which of the following is true about Y?- a)Y has no right child
- b)Y has no left child
- c)Y has both children
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Consider a node X in a Binary Tree. Given that X has two children, let Y be Inorder successor of X. Which of the following is true about Y?
a)
Y has no right child
b)
Y has no left child
c)
Y has both children
d)
None of the above

|
Sagarika Patel answered |
Since X has both children, Y must be leftmost node in right child of X.
A binary tree T has 20 leaves. The number of nodes in T having two children is- a)18
- b)19
- c)17
- d)Any number between 10 and 20
Correct answer is option 'B'. Can you explain this answer?
A binary tree T has 20 leaves. The number of nodes in T having two children is
a)
18
b)
19
c)
17
d)
Any number between 10 and 20
|
|
Amar Mukherjee answered |
Sum of all degrees = 2 * |E|. Here considering tree as a k-ary tree :
Sum of degrees of leaves + Sum of degrees for Internal Node except root + Root's degree = 2 * (No. of nodes - 1). Putting values of above terms,
L + (I-1)*(k+1) + k = 2 * (L + I - 1)
L + k*I - k + I -1 + k = 2*L + 2I - 2
L + K*I + I - 1 = 2*L + 2*I - 2
K*I + 1 - I = L
(K-1)*I + 1 = L
Given k = 2, L=20
==> (2-1)*I + 1 = 20
==> I = 19
==> T has 19 internal nodes which are having two children.
L + (I-1)*(k+1) + k = 2 * (L + I - 1)
L + k*I - k + I -1 + k = 2*L + 2I - 2
L + K*I + I - 1 = 2*L + 2*I - 2
K*I + 1 - I = L
(K-1)*I + 1 = L
Given k = 2, L=20
==> (2-1)*I + 1 = 20
==> I = 19
==> T has 19 internal nodes which are having two children.
A circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should point such that both the operations enqueue and dequeue can be performed in constant time?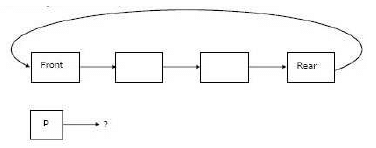
- a)rear node
- b)front node
- c)not possible with a single pointer
- d)node next to front
Correct answer is option 'A'. Can you explain this answer?
A circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should point such that both the operations enqueue and dequeue can be performed in constant time?
a)
rear node
b)
front node
c)
not possible with a single pointer
d)
node next to front
|
|
Aditya Deshmukh answered |
Answer is not “(b) front node”, as we can not get rear from front in O(1), but if p is rear we can implement both enQueue and deQueue in O(1) because from rear we can get front in O(1). Below are sample functions. Note that these functions are just sample are not working. Code to handle base cases is missing.
Following is C like pseudo code of a function that takes a Queue as an argument, and uses a stack S to do processing.void fun(Queue *Q)
{
Stack S; // Say it creates an empty stack S // Run while Q is not empty
while (!isEmpty(Q))
{
// deQueue an item from Q and push the dequeued item to S
push(&S, deQueue(Q));
} // Run while Stack S is not empty
while (!isEmpty(&S))
{
// Pop an item from S and enqueue the poppped item to Q
enQueue(Q, pop(&S));
}
}
Q.
What does the above function do in general?- a)Removes the last from Q
- b)Keeps the Q same as it was before the call
- c)Makes Q empty
- d)Reverses the Q
Correct answer is option 'D'. Can you explain this answer?
Following is C like pseudo code of a function that takes a Queue as an argument, and uses a stack S to do processing.
void fun(Queue *Q)
{
Stack S; // Say it creates an empty stack S
{
Stack S; // Say it creates an empty stack S
// Run while Q is not empty
while (!isEmpty(Q))
{
// deQueue an item from Q and push the dequeued item to S
push(&S, deQueue(Q));
}
while (!isEmpty(Q))
{
// deQueue an item from Q and push the dequeued item to S
push(&S, deQueue(Q));
}
// Run while Stack S is not empty
while (!isEmpty(&S))
{
// Pop an item from S and enqueue the poppped item to Q
enQueue(Q, pop(&S));
}
}
Q.
What does the above function do in general?
while (!isEmpty(&S))
{
// Pop an item from S and enqueue the poppped item to Q
enQueue(Q, pop(&S));
}
}
Q.
What does the above function do in general?
a)
Removes the last from Q
b)
Keeps the Q same as it was before the call
c)
Makes Q empty
d)
Reverses the Q
|
|
Maulik Pillai answered |
The function takes a queue Q as an argument. It dequeues all items of Q and pushes them to a stack S. Then pops all items of S and enqueues the items back to Q. Since stack is LIFO order, all items of queue are reversed.
Let's break down the code to understand its functionality:
1. The function fun takes a Queue Q as an argument and creates an empty Stack S.
2. It enters a loop that runs as long as the Queue Q is not empty. Inside the loop:
● An item is dequeued (removed) from the front of the Queue Q.
● The dequeued item is then pushed (added) onto the Stack S.
3. After the first loop completes, the Queue Q becomes empty, and the Stack S contains all the items from the original Queue in reverse order.
4. Another loop begins, running as long as the Stack S is not empty. Inside this loop:
● An item is popped (removed) from the top of the Stack S.
● The popped item is enqueued (added) to the rear of the Queue Q.
5. After the second loop completes, the Queue Q contains all the items that were originally in Q, but they are now in reversed order. This is why the function reverses the Queue.
Therefore, the correct answer is option 'D': The function reverses the Queue.
An implementation of a queue Q, using two stacks S1 and S2, is given below: void insert (Q, x) { push (S1, x);}void delete (Q) {if (stack-empty(S2)) thenif (stack-empty(S1)) then {print(“Q is empty”);return;}else while (!(stack-empty(S1))){x=pop(S1);push(S2,x);}
x=pop(S2);}let n insert and m(≤ n)delete operations be performed in an arbitrary order on an empty queue Q. Let x and y be the number of push and pop operations performed respectively in the process. Which one of the following is true for all m and n?- a)n + m ≤ x < 2n and 2m ≤ y ≤ n+m
- b)n+ m≤x < 2n and 2m ≤ y ≤ 2n
- c)2m≤ x < 2n and 2m ≤y ≤n+m
- d)2m≤x <2n and 2m≤y≤2n
Correct answer is option 'A'. Can you explain this answer?
An implementation of a queue Q, using two stacks S1 and S2, is given below:
void insert (Q, x) {
push (S1, x);
}
void delete (Q) {
if (stack-empty(S2)) then
if (stack-empty(S1)) then {
print(“Q is empty”);
return;
}
else while (!(stack-empty(S1))){
x=pop(S1);
push(S2,x);
}
x=pop(S2);
x=pop(S2);
}
let n insert and m(≤ n)delete operations be performed in an arbitrary order on an empty queue Q. Let x and y be the number of push and pop operations performed respectively in the process. Which one of the following is true for all m and n?
a)
n + m ≤ x < 2n and 2m ≤ y ≤ n+m
b)
n+ m≤x < 2n and 2m ≤ y ≤ 2n
c)
2m≤ x < 2n and 2m ≤y ≤n+m
d)
2m≤x <2n and 2m≤y≤2n
|
|
Saikat Basu answered |
Answer is (a)
The order in which insert and delete operations are performed matters here.
The best case: Insert and delete operations are performed alternatively. In every delete operation, 2 pop and 1 push
operations are performed. So, total m+ n push (n push for insert() and m push for delete()) operations and 2m pop operations are performed.
The worst case: First n elements are inserted and then m elements are deleted. In first delete operation, n + 1 pop operations and n push operation are performed. Other than first, in all delete operations, 1 pop operation is performed. So, total m + n pop operations and 2n push operations are performed (n push for insert() and m push for delete())
The order in which insert and delete operations are performed matters here.
The best case: Insert and delete operations are performed alternatively. In every delete operation, 2 pop and 1 push
operations are performed. So, total m+ n push (n push for insert() and m push for delete()) operations and 2m pop operations are performed.
The worst case: First n elements are inserted and then m elements are deleted. In first delete operation, n + 1 pop operations and n push operation are performed. Other than first, in all delete operations, 1 pop operation is performed. So, total m + n pop operations and 2n push operations are performed (n push for insert() and m push for delete())
A function f defined on stacks of integers satisfies the following properties. f(∅) = 0 and f (push (S, i)) = max (f(S), 0) + i for all stacks S and integers i. If a stack S contains the integers 2, -3, 2, -1, 2 in order from bottom to top, what is f(S)?- a)6
- b)4
- c)3
- d)2
Correct answer is option 'C'. Can you explain this answer?
A function f defined on stacks of integers satisfies the following properties. f(∅) = 0 and f (push (S, i)) = max (f(S), 0) + i for all stacks S and integers i.
If a stack S contains the integers 2, -3, 2, -1, 2 in order from bottom to top, what is f(S)?
a)
6
b)
4
c)
3
d)
2
|
|
Mainak Kulkarni answered |
i Element to be pushed
Initial State f(φ) = 0 For Empty Stack F(S) is 0.
Then we push each element ( )one by one and calculate f(s)for each insertion as given
Is the function to compute F(s) for each insertions
1. INSERT 2 into Stack
Similarly ,
The value of F(s) after inserting all elements into stack is 3
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented as INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in- a)non-increasing order
- b)non-decreasing order
- c)strictly increasing order
- d)strictly decreasing order
Correct answer is option 'D'. Can you explain this answer?
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented as INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in
a)
non-increasing order
b)
non-decreasing order
c)
strictly increasing order
d)
strictly decreasing order
|
|
Akshay Singh answered |
Implementing stack using priority queue require first element inserted in stack will be deleted at last, and to implement it using deletemin() operation of queue will require first element inserted in queue must have highest priority.
So the keys must be in strictly decreasing order.
So the keys must be in strictly decreasing order.
Suppose a circular queue of capacity (n – 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operation are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are- a)Full: (REAR+1) mod n == FRONT, empty: REAR == FRONT
- b)Full: (REAR+1) mod n == FRONT, empty: (FRONT+1) mod n == REAR
- c)Full: REAR == FRONT, empty: (REAR+1) mod n == FRONT
- d)Full: (FRONT+1) mod n == REAR, empty: REAR == FRONT
Correct answer is option 'A'. Can you explain this answer?
Suppose a circular queue of capacity (n – 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operation are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are
a)
Full: (REAR+1) mod n == FRONT, empty: REAR == FRONT
b)
Full: (REAR+1) mod n == FRONT, empty: (FRONT+1) mod n == REAR
c)
Full: REAR == FRONT, empty: (REAR+1) mod n == FRONT
d)
Full: (FRONT+1) mod n == REAR, empty: REAR == FRONT
|
|
Ipsita Dasgupta answered |
Suppose we start filling the queue.
Let the maxQueueSize ( Capacity of the Queue) is 4.
So the size of the array which is used to implement this circular queue is 5, which is n.
So the size of the array which is used to implement this circular queue is 5, which is n.
In the begining when the queue is empty, FRONT and REAR point to 0 index in the array.
REAR represents insertion at the REAR index.
FRONT represents deletion from the FRONT index.
FRONT represents deletion from the FRONT index.
enqueue("a"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 1)
enqueue("b"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 2)
enqueue("c"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 3)
enqueue("d"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 4)
enqueue("b"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 2)
enqueue("c"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 3)
enqueue("d"); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 4)
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors.
Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?- a)2 * n1 - 3
- b)n2 + 2 * n1 - 2
- c)n3 - n2
- d)n2 + n1 - 2
Correct answer is option 'A'. Can you explain this answer?
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors.
Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?
Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?
a)
2 * n1 - 3
b)
n2 + 2 * n1 - 2
c)
n3 - n2
d)
n2 + n1 - 2
|
|
Rajveer Sharma answered |
With reference to figure of answer of previous question:
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is ________ [This Question was originally a Fill-in-the-blanks Question]- a)15
- b)16
- c)31
- d)32
Correct answer is option 'C'. Can you explain this answer?
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is ________ [This Question was originally a Fill-in-the-blanks Question]
a)
15
b)
16
c)
31
d)
32

|
Arya Kaur answered |
It would be node number 31 for given distance 4. For example if we consider at distance 2, below highlighted node G can be the farthest node at position 7.
Consider the pseudocode given below. The function DoSomething() takes as argument a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation. Each node of the tree is of type treeNode.typedef struct treeNode* treeptr;
struct treeNode
{treeptr leftMostChild, rightSibling;
};int DoSomething (treeptr tree)
{
int value=0;
if (tree != NULL)
{
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild); value = value + DoSomething(tree->rightSibling);
}
return(value);
} Q. When the pointer to the root of a tree is passed as the argument to DoSomething, the value returned by the function corresponds to the- a)number of internal nodes in the tree.
- b)height of the tree.
- c)number of nodes without a right sibling in the tree.
- d)number of leaf nodes in the tree.
Correct answer is option 'D'. Can you explain this answer?
Consider the pseudocode given below. The function DoSomething() takes as argument a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation. Each node of the tree is of type treeNode.
typedef struct treeNode* treeptr;
struct treeNode
{
struct treeNode
{
treeptr leftMostChild, rightSibling;
};
};
int DoSomething (treeptr tree)
{
int value=0;
if (tree != NULL)
{
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild); value = value + DoSomething(tree->rightSibling);
}
return(value);
}
{
int value=0;
if (tree != NULL)
{
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild); value = value + DoSomething(tree->rightSibling);
}
return(value);
}
Q. When the pointer to the root of a tree is passed as the argument to DoSomething, the value returned by the function corresponds to the
a)
number of internal nodes in the tree.
b)
height of the tree.
c)
number of nodes without a right sibling in the tree.
d)
number of leaf nodes in the tree.
|
|
Gauri Banerjee answered |
Explanation:
To understand why the value returned by the function corresponds to the number of leaf nodes in the tree, let's analyze the pseudocode step by step.
The function DoSomething() takes a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation.
Step 1: Initialize a variable "value" to 0.
Step 2: Check if the tree pointer is not NULL. If it is NULL, it means that the tree is empty and there are no nodes. In this case, the function returns 0.
Step 3: If the tree pointer is not NULL, check if the leftMostChild pointer of the current node is NULL. If it is NULL, it means that the current node is a leaf node (a node with no children). In this case, set the value to 1.
Step 4: If the leftMostChild pointer is not NULL, recursively call the DoSomething() function with the leftMostChild pointer as the argument. This will traverse the subtree rooted at the leftMostChild pointer and count the number of leaf nodes in that subtree.
Step 5: After the recursive call, the value variable will hold the number of leaf nodes in the subtree rooted at the leftMostChild pointer.
Step 6: Call the DoSomething() function with the rightSibling pointer as the argument. This will traverse the remaining siblings of the current node and count the number of leaf nodes in each subtree rooted at the siblings.
Step 7: Finally, return the value variable.
Conclusion:
From the above analysis, we can conclude that the value returned by the DoSomething() function corresponds to the number of leaf nodes in the tree. This is because at each recursive call, the function checks whether the current node is a leaf node or not. If it is a leaf node, the value is set to 1. If it is not a leaf node, the function recursively counts the number of leaf nodes in the subtrees rooted at its children. By traversing the entire tree using the leftMostChild-rightSibling representation and counting the number of leaf nodes at each step, the function eventually returns the total number of leaf nodes in the tree.
To understand why the value returned by the function corresponds to the number of leaf nodes in the tree, let's analyze the pseudocode step by step.
The function DoSomething() takes a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation.
Step 1: Initialize a variable "value" to 0.
Step 2: Check if the tree pointer is not NULL. If it is NULL, it means that the tree is empty and there are no nodes. In this case, the function returns 0.
Step 3: If the tree pointer is not NULL, check if the leftMostChild pointer of the current node is NULL. If it is NULL, it means that the current node is a leaf node (a node with no children). In this case, set the value to 1.
Step 4: If the leftMostChild pointer is not NULL, recursively call the DoSomething() function with the leftMostChild pointer as the argument. This will traverse the subtree rooted at the leftMostChild pointer and count the number of leaf nodes in that subtree.
Step 5: After the recursive call, the value variable will hold the number of leaf nodes in the subtree rooted at the leftMostChild pointer.
Step 6: Call the DoSomething() function with the rightSibling pointer as the argument. This will traverse the remaining siblings of the current node and count the number of leaf nodes in each subtree rooted at the siblings.
Step 7: Finally, return the value variable.
Conclusion:
From the above analysis, we can conclude that the value returned by the DoSomething() function corresponds to the number of leaf nodes in the tree. This is because at each recursive call, the function checks whether the current node is a leaf node or not. If it is a leaf node, the value is set to 1. If it is not a leaf node, the function recursively counts the number of leaf nodes in the subtrees rooted at its children. By traversing the entire tree using the leftMostChild-rightSibling representation and counting the number of leaf nodes at each step, the function eventually returns the total number of leaf nodes in the tree.
The numbers 1, 2, .... n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be- a)p
- b)p + 1
- c)n - p
- d)n - p + 1
Correct answer is option 'C'. Can you explain this answer?
The numbers 1, 2, .... n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be
a)
p
b)
p + 1
c)
n - p
d)
n - p + 1
|
|
Srishti Yadav answered |
Binary Search Tree, is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree. There must be no duplicate nodes.
So let us say n=10, p=4. According to BST property the root must be 10-4=6 (considering all unique elements in BST)
And according to BST insertion, root is the first element to be inserted in a BST.
Therefore, the answer is (n-p).
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal, respectively, of a complete binary tree. Which of the following is always true?- a)LASTIN = LASTPOST
- b)LASTIN = LASTPRE
- c)LASTPRE = LASTPOST
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal, respectively, of a complete binary tree. Which of the following is always true?
a)
LASTIN = LASTPOST
b)
LASTIN = LASTPRE
c)
LASTPRE = LASTPOST
d)
None of the above
|
|
Rishabh Menon answered |
Explanation:
In a complete binary tree, the number of nodes is always a power of 2. Let us consider a complete binary tree with 7 nodes numbered from 1 to 7 in level order traversal. The tree looks like:
```
1
/ \
2 3
/ \ / \
4 5 6 7
```
Let us now traverse the tree in inorder, preorder and postorder and observe the values of LASTIN, LASTPRE and LASTPOST.
Inorder traversal: 4 2 5 1 6 3 7
- LASTIN = 7 (last node visited in inorder traversal)
Preorder traversal: 1 2 4 5 3 6 7
- LASTPRE = 7 (last node visited in preorder traversal)
Postorder traversal: 4 5 2 6 7 3 1
- LASTPOST = 7 (last node visited in postorder traversal)
From the above example, we can see that none of the options (a), (b) or (c) are always true.
Conclusion:
Therefore, the correct answer is option (d) None of the above.
In a complete binary tree, the number of nodes is always a power of 2. Let us consider a complete binary tree with 7 nodes numbered from 1 to 7 in level order traversal. The tree looks like:
```
1
/ \
2 3
/ \ / \
4 5 6 7
```
Let us now traverse the tree in inorder, preorder and postorder and observe the values of LASTIN, LASTPRE and LASTPOST.
Inorder traversal: 4 2 5 1 6 3 7
- LASTIN = 7 (last node visited in inorder traversal)
Preorder traversal: 1 2 4 5 3 6 7
- LASTPRE = 7 (last node visited in preorder traversal)
Postorder traversal: 4 5 2 6 7 3 1
- LASTPOST = 7 (last node visited in postorder traversal)
From the above example, we can see that none of the options (a), (b) or (c) are always true.
Conclusion:
Therefore, the correct answer is option (d) None of the above.
An n x n array v is defined as follows: v[i, j] = i - j for all i, j, 1 < i < n, 1 < j < n.The sum of the elements of the array v is - a)0
- b)n -1
- c)n2 - 3n + 2
- d)n2(n + 1)/2
Correct answer is option 'A'. Can you explain this answer?
An n x n array v is defined as follows: v[i, j] = i - j for all i, j, 1 < i < n, 1 < j < n.The sum of the elements of the array v is
a)
0
b)
n -1
c)
n2 - 3n + 2
d)
n2(n + 1)/2
|
|
Shubham Das answered |
Array is
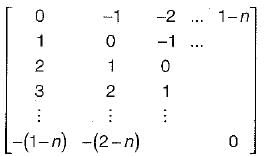
Sum = 0 + 1 + 2 + ... + (-1) + (-2) + ... = 0.
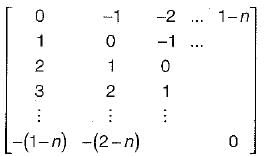
Sum = 0 + 1 + 2 + ... + (-1) + (-2) + ... = 0.
An item that is read as input can be either pushed to a stack and later popped and printed, or printed directly. Which of the following will be the output if the input is the sequence of items -1, 2, 3, 4, 5?
- a)3, 4, 5, 1, 2
- b)3, 4, 5, 2, 1
- c)1, 5, 2, 3, 4
- d)5, 4, 3, 1, 2
Correct answer is option 'B'. Can you explain this answer?
An item that is read as input can be either pushed to a stack and later popped and printed, or printed directly. Which of the following will be the output if the input is the sequence of items -1, 2, 3, 4, 5?
a)
3, 4, 5, 1, 2
b)
3, 4, 5, 2, 1
c)
1, 5, 2, 3, 4
d)
5, 4, 3, 1, 2
|
|
Anoushka Dey answered |
The item can be pushed to stack and later popped and printed, or printed directly. 1, 2, 3, 4, 5 is the input then (a) is not possible because once pushed 1 is printed after 2. Similarly (c) and (d) are also not possible.
We can obtain the sequence by performing the operations in the manner given below.
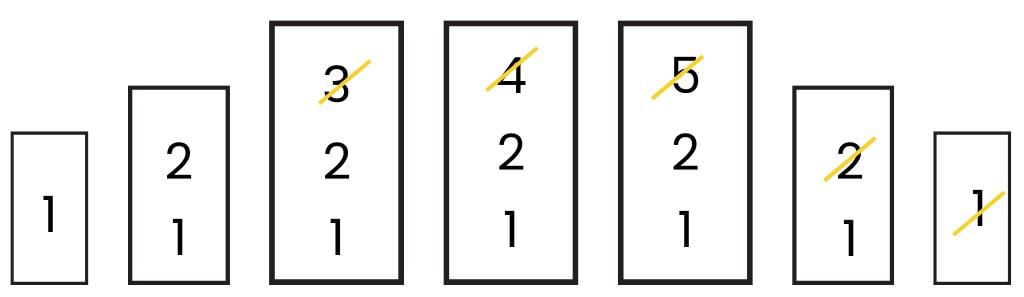
The sequence obtained will be 3,4,5,2,1.
Hence, (b) is the output.
Which of the following expressions accesses the (i, j)th entry of a (m x n) matrix stored in column major form?- a)n x (i - 1) + j
- b)m x (j - 1) + i
- c)m x (n - j) + j
- d)n x (m - i) + j
Correct answer is option 'B'. Can you explain this answer?
Which of the following expressions accesses the (i, j)th entry of a (m x n) matrix stored in column major form?
a)
n x (i - 1) + j
b)
m x (j - 1) + i
c)
m x (n - j) + j
d)
n x (m - i) + j
|
|
Anshu Mehta answered |
(i, j) entries in column major order of size (m x n).
Assume starting address is 1 so, m x (j - 1) + i
Assume starting address is 1 so, m x (j - 1) + i
Consider the following operation along with Enqueue and Dequeue operations on queues, where k is a global parameter.MultiDequeue(Q){ m = kwhile (Q is not empty) and (m > 0) {Dequeue(Q)m = m – 1}}What is the worst case time complexity of a sequence of n queue operations on an initially empty queue?- a)
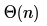
- b)
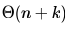
- c)
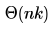
- d)
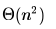
Correct answer is option 'A'. Can you explain this answer?
Consider the following operation along with Enqueue and Dequeue operations on queues, where k is a global parameter.
MultiDequeue(Q){
m = k
while (Q is not empty) and (m > 0) {
Dequeue(Q)
m = m – 1
}
}
What is the worst case time complexity of a sequence of n queue operations on an initially empty queue?
a)
b)
c)
d)
|
|
Saumya Basu answered |
There are three possible operations on queue- Enqueue, Dequeue and MultiDequeue. MultiDequeue is calling Dequeue multiple times based on a global variable k. Since, the queue is initially empty, whatever be the order of these operations, there cannot be more no. of Dequeue operations than Enqueue operations. Hence, the total no. operations will be n only.
Given two max heaps of size n each, what is the minimum possible time complexity to make a one max-heap of size from elements of two max heaps?- a)O(nLogn)
- b)O(nLogLogn)
- c)O(n)
- d)none
Correct answer is option 'C'. Can you explain this answer?
Given two max heaps of size n each, what is the minimum possible time complexity to make a one max-heap of size from elements of two max heaps?
a)
O(nLogn)
b)
O(nLogLogn)
c)
O(n)
d)
none
|
|
Niharika Ahuja answered |
Explanation:
To create a single max heap of size 2n from two max heaps of size n, we need to perform the following steps:
1. Merge the two heaps into a single array of size 2n.
2. Call the heapify function on the merged array to create a max heap.
Time Complexity:
1. Merging two heaps into a single array of size 2n takes O(n) time complexity.
2. Heapify function takes O(n) time complexity.
Therefore, the minimum possible time complexity to make a one max-heap of size from elements of two max heaps is O(n).
Conclusion:
Hence, option 'C' is the correct answer.
To create a single max heap of size 2n from two max heaps of size n, we need to perform the following steps:
1. Merge the two heaps into a single array of size 2n.
2. Call the heapify function on the merged array to create a max heap.
Time Complexity:
1. Merging two heaps into a single array of size 2n takes O(n) time complexity.
2. Heapify function takes O(n) time complexity.
Therefore, the minimum possible time complexity to make a one max-heap of size from elements of two max heaps is O(n).
Conclusion:
Hence, option 'C' is the correct answer.
In a binary tree with n nodes, every node has an odd number of descendants. Every node is considered to be its own descendant. What is the number of nodes in the tree that have exactly one child?- a)0
- b)1
- c)(n-1)/2
- d)n-1
Correct answer is option 'A'. Can you explain this answer?
In a binary tree with n nodes, every node has an odd number of descendants. Every node is considered to be its own descendant. What is the number of nodes in the tree that have exactly one child?
a)
0
b)
1
c)
(n-1)/2
d)
n-1
|
|
Anagha Choudhary answered |
It is mentioned that each node has odd number of descendants including node itself, so all nodes must have even number of descendants 0, 2, 4 so on. Which means each node should have either 0 or 2 children. So there will be no node with 1 child. Hence 0 is answer. Following are few examples.
Such a binary tree is full binary tree (a binary tree where every node has 0 or 2 children).
In a binary max heap containing n numbers, the smallest element can be found in time - a)0(n)
- b)O(logn)
- c)0(loglogn)
- d)0(1)
Correct answer is option 'A'. Can you explain this answer?
In a binary max heap containing n numbers, the smallest element can be found in time
a)
0(n)
b)
O(logn)
c)
0(loglogn)
d)
0(1)
|
|
Palak Khanna answered |
In a max heap, the smallest element is always present at a leaf node. So we need to check for all leaf nodes for the minimum value. Worst case complexity will be O(n)
A complete n-ary tree is a tree in which each node has n children or no children. Let I be the number of internal nodes and L be the number of leaves in a complete n-ary tree. If L = 41, and I = 10, what is the value of n?- a)6
- b)3
- c)4
- d)5
Correct answer is option 'D'. Can you explain this answer?
A complete n-ary tree is a tree in which each node has n children or no children. Let I be the number of internal nodes and L be the number of leaves in a complete n-ary tree. If L = 41, and I = 10, what is the value of n?
a)
6
b)
3
c)
4
d)
5
|
|
Soumya Dey answered |
For an n-ary tree where each node has n children or no children, following relation holds
L = (n-1)*I + 1
Where L is the number of leaf nodes and I is the number of internal nodes. Let us find out the value of n for the given data.
L = 41 , I = 10
41 = 10*(n-1) + 1
(n-1) = 4
n = 5
41 = 10*(n-1) + 1
(n-1) = 4
n = 5
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is- a)Ω(log n)
- b)Ω(n)
- c)Ω(n log n)
- d)Ω(n2)
Correct answer is option 'A'. Can you explain this answer?
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is
a)
Ω(log n)
b)
Ω(n)
c)
Ω(n log n)
d)
Ω(n2)
|
|
Prisha Sharma answered |
The answer to this question is simply max-heapify function. Time complexity of max-heapify is O(Log n) as it recurses at most through height of heap.
// A recursive method to heapify a subtree with root at given index
// This method assumes that the subtrees are already heapified void MinHeap::MaxHeapify(int i)
// This method assumes that the subtrees are already heapified void MinHeap::MaxHeapify(int i)
{
int l = left(i);
int r = right(i);
int largest = i;
if (l < heap_size && harr[l] < harr[i]) largest = l;
if (r < heap_size && harr[r] < harr[smallest]) largest = r;
if (largest != i) { swap(&harr[i], &harr[largest]); MinHeapify(largest);
}
}
int l = left(i);
int r = right(i);
int largest = i;
if (l < heap_size && harr[l] < harr[i]) largest = l;
if (r < heap_size && harr[r] < harr[smallest]) largest = r;
if (largest != i) { swap(&harr[i], &harr[largest]); MinHeapify(largest);
}
}
Chapter doubts & questions for Programming & Data Structures - GATE Computer Science Engineering(CSE) 2026 Mock Test Series 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Programming & Data Structures - GATE Computer Science Engineering(CSE) 2026 Mock Test Series in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup












