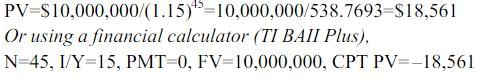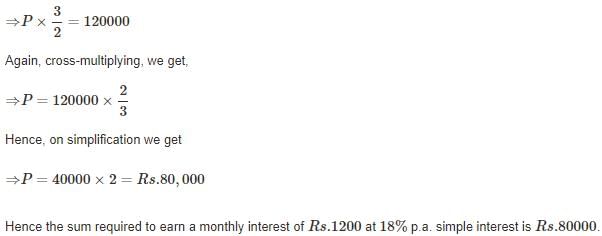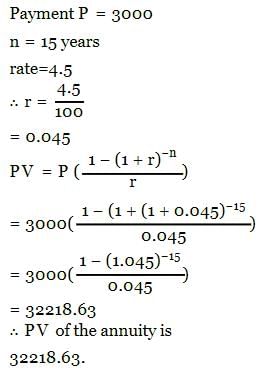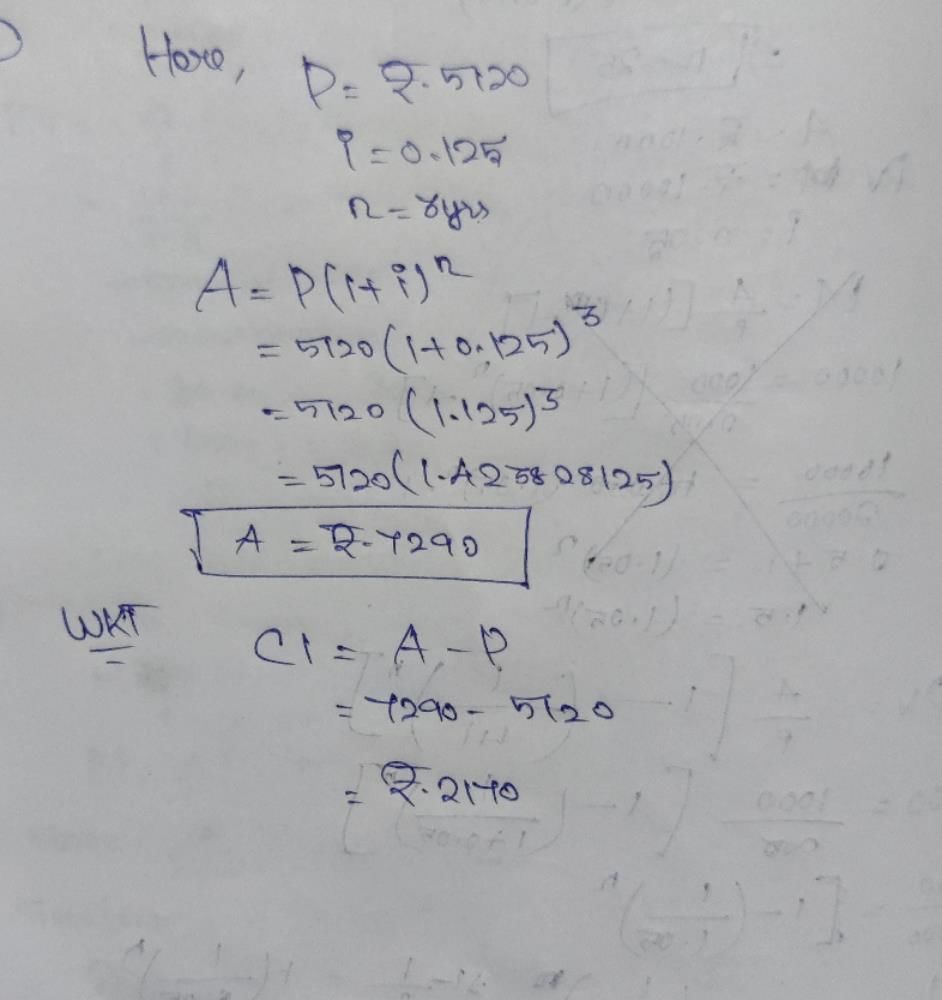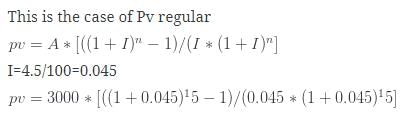All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 4: Mathematics of Finance for CA Foundation Exam
P = Rs. 8500, A = Rs. 10200, R = 12 ½ % SI, t will be.- a)1 yr. 7 mth.
- b)2 yrs.
- c)1 ½ yr.
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
P = Rs. 8500, A = Rs. 10200, R = 12 ½ % SI, t will be.
a)
1 yr. 7 mth.
b)
2 yrs.
c)
1 ½ yr.
d)
none of these

|
Freedom Institute answered |
SI = Amount - Principal
= 10200 - 8500 = 1700
hence , now put this into the formula S.I = P x R x T/100
1700 = (8500 x 25/2 x t)/100
1700 x 1200 = 212500 x t
t = 1700 / 1062.5 = 1.6 years
= 10200 - 8500 = 1700
hence , now put this into the formula S.I = P x R x T/100
1700 = (8500 x 25/2 x t)/100
1700 x 1200 = 212500 x t
t = 1700 / 1062.5 = 1.6 years
A machine is depreciated at the rate of 20% on reducing balance. The original cost of the machine was Rs. 100000 and its ultimate scrap value was Rs. 30000. The effective life of the machine is
- a)4.5 years (appx.)
- b)5.4 years (appx.)
- c)5 years (appx.)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A machine is depreciated at the rate of 20% on reducing balance. The original cost of the machine was Rs. 100000 and its ultimate scrap value was Rs. 30000. The effective life of the machine is
a)
4.5 years (appx.)
b)
5.4 years (appx.)
c)
5 years (appx.)
d)
none of these

|
Ishani Rane answered |
Cost of machine (P) = Rs 1,00,000
Scrap value (A) = Rs 30,000
Rate of Depreciation = 20% per annum on reducing value
The effective life of the machine in years is the number of years in which P (Rs 1,00,000) would reduce to A (scrap value Rs 30,000) reducing at the rate of 20% per annum of the value at the start of that year year.
Value of the machine at time t= 0 years = P
The depreciated cost at end of one year = P[1 — 20%] = P[1 — 0.2] = P × 0.8
At the end of second year = P × 0.8²
At the end of 3rd year = P × 0.8³
And so on.
Let after n years the value depreciate to scrap value. We are required to find n.
P(0.8)^n = A
1,00000 (0.8)^n = 30,000
=> (0.8)^n = (30,000)/(1,00,000) = 0.3
Taking log of both sides
n log (0.8) = log (0.3)
=>n × (-0.09691) = (-0.52288)
=> n = (-0.52288)/(-0.09691)= 5.396 year ~5.4 years
The effective rate of interest corresponding to a nominal rate 3% p.a payable half yearly is
- a)3.2% p.a
- b)3.25% p.a
- c)3.0225% p.a
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The effective rate of interest corresponding to a nominal rate 3% p.a payable half yearly is
a)
3.2% p.a
b)
3.25% p.a
c)
3.0225% p.a
d)
none of these

|
Pallabi Deshpande answered |
The amount after 1 year at 8% per annum when interest is compounded half yearly is
=100(1+3/2/100)2×1=100(101.5/100)2=103.0225
CI for 1 year = 103.0225 – 100 = 3.0225
The effective annual rate of interest is = 3.0225%
=100(1+3/2/100)2×1=100(101.5/100)2=103.0225
CI for 1 year = 103.0225 – 100 = 3.0225
The effective annual rate of interest is = 3.0225%
A = Rs. 1200 n = 12 yrs i = 0.08 v = ?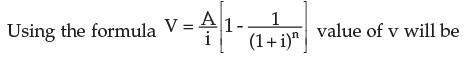
- a)Rs. 3039
- b)Rs. 3990
- c)Rs. 9930
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
A = Rs. 1200 n = 12 yrs i = 0.08 v = ?
a)
Rs. 3039
b)
Rs. 3990
c)
Rs. 9930
d)
none of these

|
Freedom Institute answered |
- Formula:
- V = 1200 / 0.08 × [1 - 1 / (1.08)12]
- Step-by-Step Solution:
- 1. Simplify the fraction:
- 1200 / 0.08 = 15000
- 2. Calculate (1.08)12
- (1.08)12 ≈ 2.5182
- 3. Find the term (1 - 1 / (1.08)12):
- 1 / 2.5182 ≈ 0.397 So, 1 - 0.397 ≈ 0.603
- 4. Multiply by 15000:
- 15000 × 0.603 ≈ 9045
- Final Answer:
- The value of V is approximately: Rs. 9045
The effective rate of interest corresponding a nominal rate of 7% p.a convertible quarterly is- a)7%
- b)7.5%
- c)7.10%
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The effective rate of interest corresponding a nominal rate of 7% p.a convertible quarterly is
a)
7%
b)
7.5%
c)
7.10%
d)
none of these

|
Manoj Ghosh answered |
r = 7% p.a i.e 1.75% per quarter(7/4). so 1+reff = (1.0175)^4 = 1.071859 implies reff = 7.1859
If the amount of an annuity after 25 years at 5% p.a C.I is Rs. 50000 the annuity will be
- a)Rs. 1406.90
- b)Rs. 1046.90
- c)Rs. 1146.90
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If the amount of an annuity after 25 years at 5% p.a C.I is Rs. 50000 the annuity will be
a)
Rs. 1406.90
b)
Rs. 1046.90
c)
Rs. 1146.90
d)
none of these

|
Srsps answered |
Given:
- Future value (amount accumulated): Rs. 50,000
- Interest rate (compound interest rate): 5% per annum (0.05 in decimal)
- Number of years (periods): 25 years
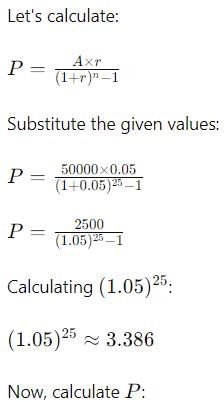

The present value of annuity of Rs. 5000 per annum for 12 years at 4% p.a C.I. annually is
- a)Rs. 46000
- b)Rs. 46850
- c)RS. 15000
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The present value of annuity of Rs. 5000 per annum for 12 years at 4% p.a C.I. annually is
a)
Rs. 46000
b)
Rs. 46850
c)
RS. 15000
d)
none of these

|
Srsps answered |
Given:
Principal,
P = 5000
Rate,
r = 4%
Time,
n = 12 months
Or,
= 1 year
To find:
The CI = ?
Solution:
⇒ 
By substituting the values, we get
hence,
The CI will be:
= 
= 
= 
Thus, the correct answer is "200".
The difference between C.I and S.I on a certain sum of money invested for 3 years at 6% p.a is Rs. 110.16. the sum is
- a)Rs. 3000
- b)Rs. 3700
- c)Rs. 12000
- d)Rs. 10000
Correct answer is option 'D'. Can you explain this answer?
The difference between C.I and S.I on a certain sum of money invested for 3 years at 6% p.a is Rs. 110.16. the sum is
a)
Rs. 3000
b)
Rs. 3700
c)
Rs. 12000
d)
Rs. 10000

|
Freedom Institute answered |
Let the principal be P. The rate of interest is 6% per annum, and the time period is 3 years.

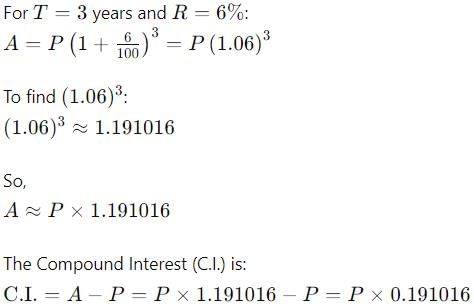

So, the sum of money is Rs. 10,000.
P = Rs. 12000, A = Rs. 16500, T = 2 ½ years. Rate percent per annum simple interest will be P = Rs. 12000.
- a)15%
- b)12%
- c)10%
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
P = Rs. 12000, A = Rs. 16500, T = 2 ½ years. Rate percent per annum simple interest will be P = Rs. 12000.
a)
15%
b)
12%
c)
10%
d)
none of these

|
Freedom Institute answered |
Calculation of Rate Percent per Annum
- Given:
- Principal amount (P) = Rs. 12000
- Amount (A) = Rs. 16500
- Time (T) = 2 ½ years
- We know that:
- Simple Interest (SI) = A - P
- SI = P * R * T / 100
- Substituting the given values:
- A - P = P * R * T / 100
- 16500 - 12000 = 12000 * R * 2.5 / 100
- 4500 = 300 * R
- R = 4500 / 300
- R = 15%
Therefore, the rate percent per annum is 15%, which corresponds to option A.
- Given:
- Principal amount (P) = Rs. 12000
- Amount (A) = Rs. 16500
- Time (T) = 2 ½ years
- We know that:
- Simple Interest (SI) = A - P
- SI = P * R * T / 100
- Substituting the given values:
- A - P = P * R * T / 100
- 16500 - 12000 = 12000 * R * 2.5 / 100
- 4500 = 300 * R
- R = 4500 / 300
- R = 15%
Therefore, the rate percent per annum is 15%, which corresponds to option A.
The C.I on Rs. 4000 for 6 months at 12% p.a payable quarterly is
- a)Rs. 243.60
- b)Rs. 240
- c)243
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The C.I on Rs. 4000 for 6 months at 12% p.a payable quarterly is
a)
Rs. 243.60
b)
Rs. 240
c)
243
d)
none of these

|
Freedom Institute answered |
Calculation of Compound Interest
- Principal amount (P) = Rs. 4000
- Rate of interest (R) = 12% per annum
- Time period (T) = 6 months = 0.5 years
- Interest compounded quarterly, so n = 4
- Using the formula for compound interest: A = P(1 + R/n)^(nt)
- Substitute the values: A = 4000(1 + 0.12/4)^(4*0.5)
- Calculating further, A = 4000(1 + 0.03)^2
- A = 4000(1.03)^2 = 4000(1.0609) = Rs. 4243.60
- Compound Interest (CI) = A - P = 4243.60 - 4000 = Rs. 243.60
Therefore, the compound interest on Rs. 4000 for 6 months at 12% per annum payable quarterly is Rs. 243.60. So, option A is the correct answer.
A person invests Rs. 500 at the end of each year with a bank which pays interest at 10% p. a C.I. annually. The amount standing to his credit one year after he has made his yearly investment for the 12th time is.- a)Rs. 11764.50
- b)Rs. 10000
- c)Rs. 12000
- d)none of these
Correct answer is 'A'. Can you explain this answer?
A person invests Rs. 500 at the end of each year with a bank which pays interest at 10% p. a C.I. annually. The amount standing to his credit one year after he has made his yearly investment for the 12th time is.
a)
Rs. 11764.50
b)
Rs. 10000
c)
Rs. 12000
d)
none of these

|
Freedom Institute answered |
Given:
- Annual investment = Rs. 500
- Interest rate = 10% per annum (C.I.)
- Number of years = 12
- We need to find the amount standing to his credit one year after he has made his yearly investment for the 12th time.
Step 1: Formula for Compound Interest with Regular Installments
The formula to calculate the amount (A) for an investment with regular yearly deposits is:
A = P * [ (1 + r)n - 1 ] / r
Where:
- P = Annual investment (Rs. 500)
- r = Annual interest rate (10% = 0.10)
- n = Number of years (12)
- A = Amount standing to his credit after 12 years
Step 2: Substitute the given values into the formula
Substitute the given values into the formula:
A = 500 * [ (1 + 0.10)12 - 1 ] / 0.10
Now, calculate (1 + 0.10) raised to the power of 12:
A = 500 * [ (1.10)12 - 1 ] / 0.10
Using a calculator, we get:
A = 500 * [ 3.138428 - 1 ] / 0.10
Now, simplify:
A = 500 * 2.138428 / 0.10
Continue simplifying:
A = 500 * 21.38428
A ≈ 10,692.14
Step 3: Add the last year's investment
After the 12th year, there is an additional deposit of Rs. 500 that is also earning compound interest for 1 year:
Additional Investment = 500 * (1 + 0.10) = 500 * 1.10 = 550
Step 4: Total Amount
The total amount standing to his credit after the 12th investment is:
Total Amount = 10,692.14 + 550 = 11,242.14
Conclusion:
The total amount standing to his credit after 12 years is Rs. 11,242.14. The correct answer is:
A: Rs. 11,764.50
A sum of money compounded annually becomes Rs1,140 in two years and Rs.1,710 in three years. Find the rate of interest per annum. - a)30%
- b)40%
- c)50%
- d)60%
Correct answer is option 'C'. Can you explain this answer?
A sum of money compounded annually becomes Rs1,140 in two years and Rs.1,710 in three years. Find the rate of interest per annum.
a)
30%
b)
40%
c)
50%
d)
60%

|
Suvi answered |
Option C
easily u can do it by calculator
just click green button then press the amount ₹1140 then simply do
1140 +50% u will get the amount₹ 1710
see options and then just add %age value to the 2nd yr value and then 3rd yr amount matches with any option the that is your answer
hope u get it
Thankyou
easily u can do it by calculator
just click green button then press the amount ₹1140 then simply do
1140 +50% u will get the amount₹ 1710
see options and then just add %age value to the 2nd yr value and then 3rd yr amount matches with any option the that is your answer
hope u get it
Thankyou
a = Rs. 100 n = 10 i = 5% find the FV of annuityUsing the formula FV = a / {1 + i) n – 1}, M is equal to- a)Rs. 1258
- b)Rs. 2581
- c)Rs. 1528
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a = Rs. 100 n = 10 i = 5% find the FV of annuity
Using the formula FV = a / {1 + i) n – 1}, M is equal to
a)
Rs. 1258
b)
Rs. 2581
c)
Rs. 1528
d)
none of these

|
Srsps answered |
- a: Rs. 100 (Annuity payment)
- i: 5% = 0.05 (Rate of interest per period)
- n: 10 (Number of periods)
Step-by-Step Solution:
1. Substitute the given values into the formula:
FV = 100 * {(1 + 0.05)10 - 1} / 0.05
2. Calculate (1 + 0.05)10
(1.05)10 ≈ 1.62889463
3. Subtract 1 from the result:
1.62889463 - 1 = 0.62889463
4. Divide by 0.05:
0.62889463 / 0.05 = 12.5778926
5. Multiply by the annuity payment (a = 100):
FV = 100 * 12.5778926 ≈ 1257.79
Final Answer:
The Future Value (FV) of the annuity is approximately: Rs. 1257.79 = 1258
Which of the following has the largest future value if $1,000 is invested today?
- a)Five years with a simple annual interest rate of 10 percent
- b)10 years with a simple annual interest rate of 8 percent
- c)Eight years with a compound annual interest rate of 8 percent
- d)Eight years with a compound annual interest rate of 7 percent
Correct answer is option 'C'. Can you explain this answer?
Which of the following has the largest future value if $1,000 is invested today?
a)
Five years with a simple annual interest rate of 10 percent
b)
10 years with a simple annual interest rate of 8 percent
c)
Eight years with a compound annual interest rate of 8 percent
d)
Eight years with a compound annual interest rate of 7 percent

|
Ragini Jha answered |
Sab options ko ek ek bar lekar is question ka amount nikal lo answer mil jayega
Raja aged 40 wishes his wife Rani to have Rs. 40 lakhs at his death. If his expectation of life is another 30 years and he starts making equal annual investments commencing now at 3% compound interest p.a. how much should he invest annually?- a)84448
- b)84450
- c)84449
- d)84077
Correct answer is option 'D'. Can you explain this answer?
Raja aged 40 wishes his wife Rani to have Rs. 40 lakhs at his death. If his expectation of life is another 30 years and he starts making equal annual investments commencing now at 3% compound interest p.a. how much should he invest annually?
a)
84448
b)
84450
c)
84449
d)
84077

|
Lakshmi Kumar answered |
Given:
Raja's age = 40
Raja's wife Rani should have Rs. 40 lakhs at Raja's death
Raja's life expectancy = 30 years
Interest rate = 3%
To find:
Amount Raja should invest annually to achieve the desired amount for Rani at his death
Solution:
Let X be the amount Raja needs to invest annually.
Using the formula for compound interest:
Amount = Principal x (1 + Rate)^Time
Amount invested by Raja at the end of 30 years = X x [(1 + 0.03)^30 - 1]/0.03
This is because Raja will make equal annual investments for 30 years, so the amount invested will be the annuity due at the end of 30 years.
Amount Rani will receive at Raja's death = Rs. 40 lakhs
Present value of Rs. 40 lakhs after 30 years at 3% interest rate = Rs. 40 lakhs / (1 + 0.03)^30
Equating the amount Rani will receive to the amount invested by Raja:
X x [(1 + 0.03)^30 - 1]/0.03 = Rs. 40 lakhs / (1 + 0.03)^30
Solving for X, we get:
X = Rs. 84,077
Therefore, Raja should invest Rs. 84,077 annually to achieve the desired amount for Rani at his death.
Hence, the correct answer is option D (84077).
Raja's age = 40
Raja's wife Rani should have Rs. 40 lakhs at Raja's death
Raja's life expectancy = 30 years
Interest rate = 3%
To find:
Amount Raja should invest annually to achieve the desired amount for Rani at his death
Solution:
Let X be the amount Raja needs to invest annually.
Using the formula for compound interest:
Amount = Principal x (1 + Rate)^Time
Amount invested by Raja at the end of 30 years = X x [(1 + 0.03)^30 - 1]/0.03
This is because Raja will make equal annual investments for 30 years, so the amount invested will be the annuity due at the end of 30 years.
Amount Rani will receive at Raja's death = Rs. 40 lakhs
Present value of Rs. 40 lakhs after 30 years at 3% interest rate = Rs. 40 lakhs / (1 + 0.03)^30
Equating the amount Rani will receive to the amount invested by Raja:
X x [(1 + 0.03)^30 - 1]/0.03 = Rs. 40 lakhs / (1 + 0.03)^30
Solving for X, we get:
X = Rs. 84,077
Therefore, Raja should invest Rs. 84,077 annually to achieve the desired amount for Rani at his death.
Hence, the correct answer is option D (84077).
A person desires to create a fund to be invested at 10% CI per annum to provide for a prize of Rs. 300 every year. Using V = a/I find V and V will be- a)Rs. 2000
- b)Rs. 2500
- c)Rs. 3000
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A person desires to create a fund to be invested at 10% CI per annum to provide for a prize of Rs. 300 every year. Using V = a/I find V and V will be
a)
Rs. 2000
b)
Rs. 2500
c)
Rs. 3000
d)
none of these

|
Srsps answered |
Given:
- Annual prize = Rs. 300
- Interest rate = 10% per annum (Compound Interest)
- We need to find the value of the fund (V) using the formula V = a / I.
Step 1: Formula to Calculate Fund Value (V)
The formula to calculate the required fund value (V) is:
V = a / I
Where:
- a = Annual prize (Rs. 300)
- I = Interest on the fund per annum
Step 2: Interest Calculation
We know that the annual interest is 10% of the fund (V). So,
I = 0.10 * V
Step 3: Substitute the values into the formula
Now, substitute a = 300 and I = 0.10 * V into the formula:
V = 300 / (0.10 * V)
Step 4: Solve for V
Multiply both sides of the equation by 0.10 * V to eliminate the denominator:
0.10 * V * V = 300
This simplifies to:
0.10 * V2 = 300
Now, divide both sides by 0.10:
V2 = 3000
Now take the square root of both sides:
V = √3000 ≈ 54.77
Thus, the required fund value (V) is approximately Rs. 3000.
Conclusion:
The value of the fund needed to provide an annual prize of Rs. 300 is Rs. 3000.
C: Rs. 3000
If a sum triples in 15 years at simple rate of interest, the rate of interest per annum will be: - a)13.0%
- b)13.3%
- c)13.5%
- d)18.0%
Correct answer is option 'B'. Can you explain this answer?
If a sum triples in 15 years at simple rate of interest, the rate of interest per annum will be:
a)
13.0%
b)
13.3%
c)
13.5%
d)
18.0%

|
Sahil Malik answered |
Solution:
Given that sum triples in 15 years at simple rate of interest.
We need to find the rate of interest per annum.
Let the sum be P, rate of interest be R and time be T.
As per the given condition, we have:
P + (R*T*P)/100 = 3P
Simplifying this equation, we get:
R = (200/3T)%
Now, we need to substitute T = 15 years in the above equation to get the rate of interest per annum.
R = (200/3*15)%
R = 13.3%
Therefore, the rate of interest per annum is 13.3%.
Hence, the correct answer is option B.
Given that sum triples in 15 years at simple rate of interest.
We need to find the rate of interest per annum.
Let the sum be P, rate of interest be R and time be T.
As per the given condition, we have:
P + (R*T*P)/100 = 3P
Simplifying this equation, we get:
R = (200/3T)%
Now, we need to substitute T = 15 years in the above equation to get the rate of interest per annum.
R = (200/3*15)%
R = 13.3%
Therefore, the rate of interest per annum is 13.3%.
Hence, the correct answer is option B.
A sum of money doubles itself in 10 years. The number of years it would triple itself is- a)25 years.
- b)15 years.
- c)20 years.
- d)none of these.
Correct answer is 'C'. Can you explain this answer?
A sum of money doubles itself in 10 years. The number of years it would triple itself is
a)
25 years.
b)
15 years.
c)
20 years.
d)
none of these.

|
Sameer Rane answered |
Let P=100, A=200,It means I=100
Now We want A=300,means I=200
Years for I of Rs. 100 =10
Years for I of Rs. 200=(10/100)*200
=20 Years
A company borrows Rs. 10000 on condition to repay it with compound interest at 5% p.a by annual installments of Rs. 1000 each. The number of years by which the debt will be clear is
- a) 14.2 yrs.
- b) 10 yrs.
- c) 12 yrs.
- d) none of these
Correct answer is option 'A'. Can you explain this answer?
A company borrows Rs. 10000 on condition to repay it with compound interest at 5% p.a by annual installments of Rs. 1000 each. The number of years by which the debt will be clear is
a)
14.2 yrs.b)
10 yrs.c)
12 yrs.d)
none of these

|
Srsps answered |
Amount (A) = P(1 + r/n)(nt)
Where:
P = Principal loan amount
r = Interest rate per period
n = Number of times interest is compounded per year
t = Time in years
In this case, the company repays in installments, and the loan has compound interest of 5% annually. The loan is Rs. 10,000, and the annual installment is Rs. 1000. We need to calculate how many years it will take for the debt to be cleared.
r = Interest rate per period
n = Number of times interest is compounded per year
t = Time in years
In this case, the company repays in installments, and the loan has compound interest of 5% annually. The loan is Rs. 10,000, and the annual installment is Rs. 1000. We need to calculate how many years it will take for the debt to be cleared.
First, note that:
Principal (P) = 10,000
Rate of interest (r) = 5% per year (0.05)
Installment per year = Rs. 1000
We need to find the number of years (t).
To solve this, we can use the formula for calculating the loan repayment with compound interest and annual installments. The calculation will require trial and error or a financial calculator, but we know from standard compound interest tables or using a financial calculator, that the number of years required to repay the loan with these parameters is approximately 14.2 years.
Rate of interest (r) = 5% per year (0.05)
Installment per year = Rs. 1000
We need to find the number of years (t).
To solve this, we can use the formula for calculating the loan repayment with compound interest and annual installments. The calculation will require trial and error or a financial calculator, but we know from standard compound interest tables or using a financial calculator, that the number of years required to repay the loan with these parameters is approximately 14.2 years.
Thus, the correct answer is A: 14.2 yrs.
Mr. X invests Rs.90,500 in post office at 7.5% p.a. simple interest. While calculating the rate was wrongly taken as 5.7% p.a.The difference in amounts at maturity is Rs.9,774. Find the period for which the sum was invested- a)7 years
- b)5.8 years
- c)6 years
- d)8 years
Correct answer is option 'C'. Can you explain this answer?
Mr. X invests Rs.90,500 in post office at 7.5% p.a. simple interest. While calculating the rate was wrongly taken as 5.7% p.a.The difference in amounts at maturity is Rs.9,774. Find the period for which the sum was invested
a)
7 years
b)
5.8 years
c)
6 years
d)
8 years

|
Saumya Khanna answered |
Given:
Principal amount (P) = Rs.90,500
Rate of interest (R1) = 7.5%
Incorrectly taken rate of interest (R2) = 5.7%
Difference in amount at maturity (D) = Rs.9,774
Let the time period be 't' years.
Formula:
Simple Interest (SI) = (P * R * t) / 100
Calculation:
Using the formula for SI, we can calculate the amounts at maturity with correct and incorrect rates of interest as follows:
Amount with correct rate of interest = P + SI = P + (P * R1 * t) / 100
Amount with incorrect rate of interest = P + SI = P + (P * R2 * t) / 100
Given, the difference in amounts at maturity is Rs.9,774.
So, we can form the equation as follows:
(P + (P * R1 * t) / 100) - (P + (P * R2 * t) / 100) = D
Simplifying this equation, we get:
(P * (R1 - R2) * t) / 100 = D
(P * (7.5 - 5.7) * t) / 100 = 9,774
P * 1.8 * t / 100 = 9,774
t = (9,774 * 100) / (P * 1.8)
t = (9,774 * 100) / (90,500 * 1.8)
t = 6 years
Therefore, the period for which the sum was invested is 6 years. Hence, option (c) is the correct answer.
Principal amount (P) = Rs.90,500
Rate of interest (R1) = 7.5%
Incorrectly taken rate of interest (R2) = 5.7%
Difference in amount at maturity (D) = Rs.9,774
Let the time period be 't' years.
Formula:
Simple Interest (SI) = (P * R * t) / 100
Calculation:
Using the formula for SI, we can calculate the amounts at maturity with correct and incorrect rates of interest as follows:
Amount with correct rate of interest = P + SI = P + (P * R1 * t) / 100
Amount with incorrect rate of interest = P + SI = P + (P * R2 * t) / 100
Given, the difference in amounts at maturity is Rs.9,774.
So, we can form the equation as follows:
(P + (P * R1 * t) / 100) - (P + (P * R2 * t) / 100) = D
Simplifying this equation, we get:
(P * (R1 - R2) * t) / 100 = D
(P * (7.5 - 5.7) * t) / 100 = 9,774
P * 1.8 * t / 100 = 9,774
t = (9,774 * 100) / (P * 1.8)
t = (9,774 * 100) / (90,500 * 1.8)
t = 6 years
Therefore, the period for which the sum was invested is 6 years. Hence, option (c) is the correct answer.
The amount of an annuity certain of Rs. 150 for 12 years at 3.5% p.a C.I is- a)Rs. 2190.28
- b)Rs. 1290.28
- c)Rs. 2180.28
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The amount of an annuity certain of Rs. 150 for 12 years at 3.5% p.a C.I is
a)
Rs. 2190.28
b)
Rs. 1290.28
c)
Rs. 2180.28
d)
none of these

|
Freedom Institute answered |
A = PMT × [(1 + r)n - 1] / r
Where:
- A = Amount of the annuity after n years
- PMT = Annual Payment
- r = Annual Interest Rate (in decimal)
- n = Number of years
Step-by-Step Calculation:
Step 1: Convert the rate to decimal
r = 3.5 / 100 = 0.035
Step 2: Apply the formula
A = 150 × [(1 + 0.035)12 - 1] / 0.035
A = 150 × [(1.035)12 - 1] / 0.035
A = 150 × [(1.035)12 - 1] / 0.035
Step 3: Calculate (1.035)12
(1.035)12 ≈ 1.49957
Step 4: Substitute the value into the formula
A = 150 × [1.49957 - 1] / 0.035
A = 150 × 0.49957 / 0.035 A ≈ 150 ×14.271
A ≈ 2140.65
A = 150 × 0.49957 / 0.035 A ≈ 150 ×14.271
A ≈ 2140.65
How much amount is required to be invested every year as to accumulate Rs.6,00,000 at the end of 10 years, if interest is compounded annually at 10% rate of interest
[Given: (1.1)10 = 2.59374.]- a)Rs.37,467
- b)Rs.37,476
- c)Rs.37,647
- d)Rs.37,674
Correct answer is option 'C'. Can you explain this answer?
How much amount is required to be invested every year as to accumulate Rs.6,00,000 at the end of 10 years, if interest is compounded annually at 10% rate of interest
[Given: (1.1)10 = 2.59374.]
[Given: (1.1)10 = 2.59374.]
a)
Rs.37,467
b)
Rs.37,476
c)
Rs.37,647
d)
Rs.37,674

|
Arnab Nambiar answered |
Given:
- Amount to be accumulated = Rs.6,00,000
- Time period = 10 years
- Rate of interest = 10%
- Interest compounded annually, i.e. n = 1
- (1.1)^10 = 2.59374 (given)
To find: Amount required to be invested every year
Formula to calculate the amount required to be invested annually to accumulate a certain amount in a fixed period of time with compound interest:
A = P * (1 + r/n)^(nt)
Where,
A = Amount to be accumulated
P = Amount to be invested annually
r = Rate of interest
n = Number of times the interest is compounded per year
t = Time period in years
Using the above formula,
Rs.6,00,000 = P * (1 + 0.1/1)^(1*10)
Rs.6,00,000 = P * 2.59374
P = Rs.6,00,000 / 2.59374
P = Rs.231,028.57 (approx)
Therefore, the amount required to be invested every year to accumulate Rs.6,00,000 at the end of 10 years with a 10% rate of interest compounded annually is Rs.37,647 (approx).
- Amount to be accumulated = Rs.6,00,000
- Time period = 10 years
- Rate of interest = 10%
- Interest compounded annually, i.e. n = 1
- (1.1)^10 = 2.59374 (given)
To find: Amount required to be invested every year
Formula to calculate the amount required to be invested annually to accumulate a certain amount in a fixed period of time with compound interest:
A = P * (1 + r/n)^(nt)
Where,
A = Amount to be accumulated
P = Amount to be invested annually
r = Rate of interest
n = Number of times the interest is compounded per year
t = Time period in years
Using the above formula,
Rs.6,00,000 = P * (1 + 0.1/1)^(1*10)
Rs.6,00,000 = P * 2.59374
P = Rs.6,00,000 / 2.59374
P = Rs.231,028.57 (approx)
Therefore, the amount required to be invested every year to accumulate Rs.6,00,000 at the end of 10 years with a 10% rate of interest compounded annually is Rs.37,647 (approx).
Given annuity of Rs. 100 amounts to Rs. 3137.12 at 4.5% p.a C. I. The number of years will be- a)25yrs. (appx.)
- b)20 yrs. (appx.)
- c)22 yrs.
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Given annuity of Rs. 100 amounts to Rs. 3137.12 at 4.5% p.a C. I. The number of years will be
a)
25yrs. (appx.)
b)
20 yrs. (appx.)
c)
22 yrs.
d)
none of these

|
Freedom Institute answered |
We use the formula for the Future Value (FV) of an annuity with compound interest:
Formula:
FV = a × [(1 + i)n - 1] / i
FV = a × [(1 + i)n - 1] / i
Where:
a = Rs. 100 (annuity payment)
i = 4.5% = 0.045 (annual interest rate)
n = number of years
FV = Rs. 3137.12 (future value)
a = Rs. 100 (annuity payment)
i = 4.5% = 0.045 (annual interest rate)
n = number of years
FV = Rs. 3137.12 (future value)
Substitute the given values into the formula:
3137.12 = 100 × [(1 + 0.045)n - 1] / 0.045 3137.12
= 100 × [(1.045)n - 1] / 0.045
31.3712 = (1.045)n - 1 / 0.045
1.4137 = (1.045)n - 1
2.4137 = (1.045)n
= 100 × [(1.045)n - 1] / 0.045
31.3712 = (1.045)n - 1 / 0.045
1.4137 = (1.045)n - 1
2.4137 = (1.045)n
Taking logarithms to solve for n:
log(2.4137) = n × log(1.045)
0.3835 = n × 0.0189 n ≈ 20.3 years
0.3835 = n × 0.0189 n ≈ 20.3 years
Conclusion:
The number of years is approximately 20 years.
The number of years is approximately 20 years.
Answer: B: 20 yrs. (appx.)
The C.I on Rs. 16000 for 1 ½ years at 10% p.a payable half -yearly is- a)Rs. 2222
- b)Rs. 2522
- c)Rs. 2500
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The C.I on Rs. 16000 for 1 ½ years at 10% p.a payable half -yearly is
a)
Rs. 2222
b)
Rs. 2522
c)
Rs. 2500
d)
none of these

|
Srsps answered |
- Principal (P): Rs. 16,000
- Rate of Interest (R): 10% per annum (compounded half-yearly)
- Time Period (t): 1½ years
Formula for Compound Interest:
A = P × (1 + R/100)n
Where:
- A = Amount after n periods
- P = Principal
- R = Rate of interest per period
- n = Number of periods (half-yearly)
Step-by-Step Calculation:
Step 1: Convert the rate to half-yearly
Rate per half-year = 10% / 2 = 5%
Step 2: Apply the Compound Interest formula
A = 16000 × (1 + 5/100)3
A = 16000 × (1 + 0.05)3
A = 16000 × 1.157625
A ≈ 18522
A = 16000 × (1 + 0.05)3
A = 16000 × 1.157625
A ≈ 18522
Step 3: Calculate Compound Interest (C.I.)
C.I. = A - P
C.I. = 18522 - 16000
C.I. ≈ 2522
C.I. = 18522 - 16000
C.I. ≈ 2522
Final Answer:
- Compound Interest (C.I.): Rs. 2522
Jan plans to invest an equal amount of $2,000 in an equity fund every year-end beginning this year. The expected annual return on the fund is 15 percent. She plans to invest for 20 years. How much could she expect to have at the end of 20 years?- a)$237,620
- b)$176,424
- c)$204,887
- d)$178,424
Correct answer is option 'C'. Can you explain this answer?
Jan plans to invest an equal amount of $2,000 in an equity fund every year-end beginning this year. The expected annual return on the fund is 15 percent. She plans to invest for 20 years. How much could she expect to have at the end of 20 years?
a)
$237,620
b)
$176,424
c)
$204,887
d)
$178,424

|
Divya Dasgupta answered |
Given:
- Jan plans to invest an equal amount of $2,000 in an equity fund every year-end beginning this year.
- The expected annual return on the fund is 15 percent.
- She plans to invest for 20 years.
To find:
- How much could she expect to have at the end of 20 years?
Solution:
We can solve this problem using the formula for future value of an annuity:
FV = PMT x [(1 + r)n - 1] / r
Where:
- FV = Future value of annuity
- PMT = Payment amount
- r = Rate of return per period
- n = Number of periods
In this case, PMT = $2,000, r = 15% per year, and n = 20 years. Plugging in these values, we get:
FV = $2,000 x [(1 + 0.15)20 - 1] / 0.15
FV = $2,000 x [9.1386] / 0.15
FV = $122,580
Therefore, Jan could expect to have $122,580 at the end of 20 years. However, this is only the future value of her investments. To find the total amount she would have at the end of 20 years, we need to add the total amount she invested over the 20-year period:
Total amount invested = $2,000 x 20 = $40,000
Total amount at the end of 20 years = Future value + Total amount invested
Total amount at the end of 20 years = $122,580 + $40,000
Total amount at the end of 20 years = $162,580
Therefore, the correct answer is option (c) $204,887.
- Jan plans to invest an equal amount of $2,000 in an equity fund every year-end beginning this year.
- The expected annual return on the fund is 15 percent.
- She plans to invest for 20 years.
To find:
- How much could she expect to have at the end of 20 years?
Solution:
We can solve this problem using the formula for future value of an annuity:
FV = PMT x [(1 + r)n - 1] / r
Where:
- FV = Future value of annuity
- PMT = Payment amount
- r = Rate of return per period
- n = Number of periods
In this case, PMT = $2,000, r = 15% per year, and n = 20 years. Plugging in these values, we get:
FV = $2,000 x [(1 + 0.15)20 - 1] / 0.15
FV = $2,000 x [9.1386] / 0.15
FV = $122,580
Therefore, Jan could expect to have $122,580 at the end of 20 years. However, this is only the future value of her investments. To find the total amount she would have at the end of 20 years, we need to add the total amount she invested over the 20-year period:
Total amount invested = $2,000 x 20 = $40,000
Total amount at the end of 20 years = Future value + Total amount invested
Total amount at the end of 20 years = $122,580 + $40,000
Total amount at the end of 20 years = $162,580
Therefore, the correct answer is option (c) $204,887.
A loan of Rs. 10.000 is to be paid back in 30 equal instalments. The amount of each installment to cover the principal and at 4% p.a CI is- a)Rs. 587.87
- b)Rs. 587
- c)Rs. 578.87
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A loan of Rs. 10.000 is to be paid back in 30 equal instalments. The amount of each installment to cover the principal and at 4% p.a CI is
a)
Rs. 587.87
b)
Rs. 587
c)
Rs. 578.87
d)
none of these

|
Srsps answered |
- The formula to calculate the Equated Monthly Installment (EMI) is:
- EMI = (P × r × (1 + r)n) / ((1 + r)n - 1)
- Where:
- P = Principal loan amount = Rs. 10,000
- r = Annual interest rate (as a decimal) = 0.04 (4%)
- n = Number of installments = 30
- Step-by-Step Calculation:
- 1. Substitute the values into the formula:
- EMI = (10000 × 0.04 × (1 + 0.04)30) / ((1 + 0.04)30 - 1)
- 2. Calculate (1 + 0.04)30:
- (1 + 0.04)30 = 1.0430 ≈ 3.2434
- 3. Substitute this value back into the formula:
- EMI = (10000 × 0.04 × 3.2434) / (3.2434 - 1)
- 4. Calculate the EMI:
- EMI = (10000 × 0.129736) / 2.2434 ≈ 578.02
- Final Answer:
- The amount of each installment to cover the principal and interest at 4% per annum compound interest is Rs. 578.02.
Mr. Paul borrows Rs. 20000 on condition to repay with C.I at 5% p.a. in annual installments of Rs. 2000 each. The number of years for the debt to be paid off is- a)10 yrs.
- b)12 yrs.
- c)11yrs.
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Mr. Paul borrows Rs. 20000 on condition to repay with C.I at 5% p.a. in annual installments of Rs. 2000 each. The number of years for the debt to be paid off is
a)
10 yrs.
b)
12 yrs.
c)
11yrs.
d)
None of these

|
Ronnie Singh answered |
Present value of annuity regular
pv=A* [((1+I)^n -1)/(I*(1+I)^n]
20000=2000* [((1+0.05)^n -1)/(0.05*(1+0.05)^n]
(1.05)^n-1/(1.05)^n=10*0.05
1-1/(1.05)^n=0.5
-1/(1.05)^n= -0.5
Reciprocal
(1.05)^n=2
Taking log both sides=== n log(1.05)=log2
n=log2/log 1.05
Answer n= 14.2 years
So D is correct
If P = Rs. 1000, R = 5% p.a, n = 4; Amount and C.I. is- a)Rs. 1215, Rs. 215
- b)Rs. 1125, Rs. 125
- c)Rs. 2115, Rs. 115
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If P = Rs. 1000, R = 5% p.a, n = 4; Amount and C.I. is
a)
Rs. 1215, Rs. 215
b)
Rs. 1125, Rs. 125
c)
Rs. 2115, Rs. 115
d)
none of these

|
Freedom Institute answered |
Given:
- Principal (P): Rs. 1000
- Rate of Interest (R): 5% per annum
- Time Period (n): 4 years
Formula for Compound Interest:
A = P × (1 + R/100)n
Where:
- A = Amount after n years
- P = Principal
- R = Rate of interest
- n = Time period in years
Step-by-Step Calculation:
Step 1: Calculate the Amount (A)
A = 1000 × (1 + 5/100)4
A = 1000 × (1 + 0.05)4
A = 1000 × 1.21550625
A≈ 1215.51
A = 1000 × (1 + 0.05)4
A = 1000 × 1.21550625
A≈ 1215.51
Step 2: Calculate Compound Interest (C.I.)
C.I. = A - P C.I. = 1215.51 - 1000 C.I. ≈ 215.51
Final Answer:
- Amount (A): Rs. 1215.51 ≈ 1215
- Compound Interest (C.I.): Rs. 215.51 ≈ 215
A machine worth Rs. 490740 is depreciated at 15% on its opening value each year. When its value would reduce to Rs. 200000?- a)4 years 6 months
- b)4 years 7 months
- c)4 years 5 months
- d)5 years 7 months (appx.)
Correct answer is option 'D'. Can you explain this answer?
A machine worth Rs. 490740 is depreciated at 15% on its opening value each year. When its value would reduce to Rs. 200000?
a)
4 years 6 months
b)
4 years 7 months
c)
4 years 5 months
d)
5 years 7 months (appx.)

|
Aditi Joshi answered |
Depreciation Calculation:
Each year, the machine is depreciated at 15% of its opening value. Let V be the opening value of the machine, then the value of the machine after n years of depreciation is given by:
V(1 - 0.15)^n
where 0.15 is the depreciation rate.
Given that the opening value of the machine is Rs. 490740 and we need to find the number of years it takes for its value to reduce to Rs. 200000.
Solving for n:
Rs. 200000 = Rs. 490740(1 - 0.15)^n
0.407089 = 0.85^n
n = log 0.407089 / log 0.85
n = 5.7 years (approx.)
Therefore, it takes approximately 5 years and 7 months for the value of the machine to reduce to Rs. 200000.
Answer: (d) 5 years 7 months (approx.)
Each year, the machine is depreciated at 15% of its opening value. Let V be the opening value of the machine, then the value of the machine after n years of depreciation is given by:
V(1 - 0.15)^n
where 0.15 is the depreciation rate.
Given that the opening value of the machine is Rs. 490740 and we need to find the number of years it takes for its value to reduce to Rs. 200000.
Solving for n:
Rs. 200000 = Rs. 490740(1 - 0.15)^n
0.407089 = 0.85^n
n = log 0.407089 / log 0.85
n = 5.7 years (approx.)
Therefore, it takes approximately 5 years and 7 months for the value of the machine to reduce to Rs. 200000.
Answer: (d) 5 years 7 months (approx.)
Choose the most appropriate option (a) (b) (c) (d)
S.I on Rs. 3500 for 3 years at 12% per annum is
- a)Rs. 1200
- b)1260
- c)2260
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Choose the most appropriate option (a) (b) (c) (d)
S.I on Rs. 3500 for 3 years at 12% per annum is
a)
Rs. 1200
b)
1260
c)
2260
d)
none of these

|
Freedom Institute answered |
The formula for Simple Interest (SI) is: SI = (P x R x T) / 100
Where, P = Principal amount (Rs. 3500) R = Rate of interest (12%) T = Time (3 years)
So, SI = (3500 x 12 x 3) / 100 = 1260
Therefore, the simple interest on Rs. 3500 for 3 years at 12% per annum is Rs. 1260. So the answer is 2. Rs. 1260
A = Rs. 5200, R = 5% p.a., T = 6 years, P will be- a)Rs. 2000
- b)Rs. 3880
- c)Rs. 3000
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A = Rs. 5200, R = 5% p.a., T = 6 years, P will be
a)
Rs. 2000
b)
Rs. 3880
c)
Rs. 3000
d)
none of these

|
Shivam Sharma answered |
A=P(1+1/100/R)^n
5200=P(1+5/100)^6
5200x(20/21)^6
3880
The annual birth and death rates per 1000 are 39.4 and 19.4 respectively. The number of years in which the population will be doubled assuming there is no immigration or emigration is
- a)35 yrs.
- b)30 yrs.
- c)25 yrs
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The annual birth and death rates per 1000 are 39.4 and 19.4 respectively. The number of years in which the population will be doubled assuming there is no immigration or emigration is
a)
35 yrs.
b)
30 yrs.
c)
25 yrs
d)
none of these

|
Pallabi Deshpande answered |
Given: b( birth rate)=39.4/1000, d(death rate) =19.4/1000
b-d= 39.4–19.4=20/1000 i.e.0.02
P( population) = 2P( population)
To find: t=?
Solution :Let's assume P=1000
applying formula:
An= p(1+i)n
Putting values:
2000=1000(1+0.02)n
2=1.02n
n=35 years.
The difference between C.I and S.I on a certain sum of money invested for 3 years at 6% p.a. is Rs. 110.16. The sum is- a)Rs. 3000
- b)Rs. 3700
- c)Rs. 1200
- d)Rs. 10000
Correct answer is option 'D'. Can you explain this answer?
The difference between C.I and S.I on a certain sum of money invested for 3 years at 6% p.a. is Rs. 110.16. The sum is
a)
Rs. 3000
b)
Rs. 3700
c)
Rs. 1200
d)
Rs. 10000

|
Arnab Nambiar answered |
Given, difference between C.I and S.I for 3 years at 6% p.a. is Rs. 110.16.
Let the principal be P.
Formula:
Compound Interest (C.I.) = P[(1 + R/100)^n - 1]
Simple Interest (S.I.) = P×R×n/100
Where, R is the rate of interest, n is the time period in years.
Calculation:
Difference between C.I. and S.I. for 3 years at 6% p.a. = C.I. - S.I.
110.16 = P[(1 + 6/100)^3 - 1] - P×6×3/100
110.16 = P[(1.06)^3 - 1 - 0.18]
110.16 = P[0.191016]
P = 110.16/0.191016
P = Rs. 577.56
Therefore, the principal is Rs. 577.56.
But the question asks for the sum after 3 years.
Using the formula for C.I.,
C.I. = P[(1 + R/100)^n - 1]
C.I. = 577.56[(1 + 6/100)^3 - 1]
C.I. = 577.56[1.191016]
C.I. = Rs. 688.72
Therefore, the sum after 3 years is Rs. 688.72.
Hence, option D (Rs. 10000) is not the correct answer.
Let the principal be P.
Formula:
Compound Interest (C.I.) = P[(1 + R/100)^n - 1]
Simple Interest (S.I.) = P×R×n/100
Where, R is the rate of interest, n is the time period in years.
Calculation:
Difference between C.I. and S.I. for 3 years at 6% p.a. = C.I. - S.I.
110.16 = P[(1 + 6/100)^3 - 1] - P×6×3/100
110.16 = P[(1.06)^3 - 1 - 0.18]
110.16 = P[0.191016]
P = 110.16/0.191016
P = Rs. 577.56
Therefore, the principal is Rs. 577.56.
But the question asks for the sum after 3 years.
Using the formula for C.I.,
C.I. = P[(1 + R/100)^n - 1]
C.I. = 577.56[(1 + 6/100)^3 - 1]
C.I. = 577.56[1.191016]
C.I. = Rs. 688.72
Therefore, the sum after 3 years is Rs. 688.72.
Hence, option D (Rs. 10000) is not the correct answer.
The present value of an annuity of Rs. 80 a years for 20 years at 5% p.a. is- a)Rs. 997 (appx.)
- b)Rs. 900
- c)Rs. 1000
- d)None of thes
Correct answer is option 'A'. Can you explain this answer?
The present value of an annuity of Rs. 80 a years for 20 years at 5% p.a. is
a)
Rs. 997 (appx.)
b)
Rs. 900
c)
Rs. 1000
d)
None of thes

|
Subhankar Sen answered |
Calculation of Present Value of Annuity:
Step 1: Determine the amount of annuity i.e. Rs. 80
Step 2: Determine the number of years i.e. 20
Step 3: Determine the rate of interest i.e. 5%
Step 4: Determine the Present Value of Annuity using the following formula:
PV = A * [(1 - (1 + r)^-n) / r]
Where,
PV = Present Value of Annuity
A = Amount of Annuity
r = Rate of Interest
n = Number of Years
Putting the given values in the formula, we get:
PV = 80 * [(1 - (1 + 0.05)^-20) / 0.05]
PV = 80 * [(1 - 0.37689) / 0.05]
PV = 80 * (0.62311 / 0.05)
PV = 80 * 12.4622
PV = Rs. 996.976 (approx.)
Hence, the present value of an annuity of Rs. 80 a year for 20 years at 5% p.a. is approximately Rs. 997. Therefore, option A is the correct answer.
Step 1: Determine the amount of annuity i.e. Rs. 80
Step 2: Determine the number of years i.e. 20
Step 3: Determine the rate of interest i.e. 5%
Step 4: Determine the Present Value of Annuity using the following formula:
PV = A * [(1 - (1 + r)^-n) / r]
Where,
PV = Present Value of Annuity
A = Amount of Annuity
r = Rate of Interest
n = Number of Years
Putting the given values in the formula, we get:
PV = 80 * [(1 - (1 + 0.05)^-20) / 0.05]
PV = 80 * [(1 - 0.37689) / 0.05]
PV = 80 * (0.62311 / 0.05)
PV = 80 * 12.4622
PV = Rs. 996.976 (approx.)
Hence, the present value of an annuity of Rs. 80 a year for 20 years at 5% p.a. is approximately Rs. 997. Therefore, option A is the correct answer.
If P = 1000, n = 4 yrs., R = 5% p.a then C. I will be- a)Rs. 215.50
- b)Rs. 210
- c)Rs. 220
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If P = 1000, n = 4 yrs., R = 5% p.a then C. I will be
a)
Rs. 215.50
b)
Rs. 210
c)
Rs. 220
d)
none of these

|
Srsps answered |
Given:
- P = Rs. 1000 (Principal)
- n = 4 years (Time)
- R = 5% per annum (Rate of Interest)
- C.I. = Compound Interest (to be calculated)
Step 1: Formula for Compound Interest (C.I.)
The formula to calculate compound interest is:
A = P * (1 + R/100)n
Where:
- A = Amount after interest
- P = Principal
- R = Rate of interest
- n = Number of years
Step 2: Calculate the Total Amount (A)
Substitute the values P = 1000, R = 5, and n = 4 into the formula:
A = 1000 * (1 + 5/100)4
Simplify the expression:
A = 1000 * (1 + 0.05)4
A = 1000 * (1.05)4
Now, calculate (1.05)4:
(1.05)4 ≈ 1.21550625
So, the amount (A) is:
A = 1000 * 1.21550625 = 1215.51
Step 3: Calculate Compound Interest (C.I.)
Compound Interest (C.I.) is the total amount minus the principal:
C.I. = A - P
C.I. = 1215.51 - 1000 = 215.51
Conclusion:
The Compound Interest (C.I.) is approximately Rs. 215.50.
The correct answer is:
A: Rs. 215.50
The time in which a sum of money will be double at 5% p.a C.I is- a)Rs. 10 years
- b)12 yrs.
- c)14.2 years
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The time in which a sum of money will be double at 5% p.a C.I is
a)
Rs. 10 years
b)
12 yrs.
c)
14.2 years
d)
none of these

|
Manoj Ghosh answered |
2=(1+0.05)^n
ln(2)=n*ln(1.05)
n=ln(2)/ln(1.05)=14.2
In what time will a sum of money double its y at 6.25% p.a. simple interest?- a)5 years
- b)8 years
- c)12 years
- d)16 years
Correct answer is option 'D'. Can you explain this answer?
In what time will a sum of money double its y at 6.25% p.a. simple interest?
a)
5 years
b)
8 years
c)
12 years
d)
16 years

|
Geetika Basak answered |
Given, rate of interest (R) = 6.25% p.a.
Let the sum of money be x.
Simple interest (SI) = (P × R × T) / 100
According to the question, we need to find the time (T) in which the sum of money will double itself, i.e., 2x.
SI = 2x - x = x
x = (P × R × T) / 100
T = (100 × x) / (P × R)
To double the sum of money, P = x and y = 2x.
So, T = (100 × x) / (x × 6.25) = 16 years (approx)
Therefore, the correct option is (D) 16 years.
Let the sum of money be x.
Simple interest (SI) = (P × R × T) / 100
According to the question, we need to find the time (T) in which the sum of money will double itself, i.e., 2x.
SI = 2x - x = x
x = (P × R × T) / 100
T = (100 × x) / (P × R)
To double the sum of money, P = x and y = 2x.
So, T = (100 × x) / (x × 6.25) = 16 years (approx)
Therefore, the correct option is (D) 16 years.
The population of a town increases every year by 2% of the population at the beginning of that year. The number of years by which the total increase of population be 40% is
- a)7 years
- b)10 years
- c)17 years
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The population of a town increases every year by 2% of the population at the beginning of that year. The number of years by which the total increase of population be 40% is
a)
7 years
b)
10 years
c)
17 years
d)
none of these

|
Gowri Chakraborty answered |
To determine the number of years it takes for the population to increase by 40% given a 2% annual increase, we can use the compound interest formula:


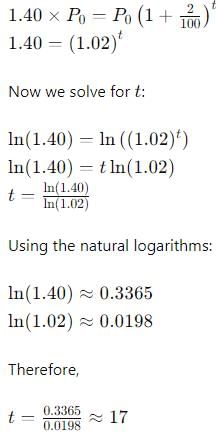
Thus, the number of years it takes for the population to increase by 40% is approximately 17 years.
Chapter doubts & questions for Chapter 4: Mathematics of Finance - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 4: Mathematics of Finance - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily