All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 7: Sets, Relations and Functions for CA Foundation Exam
If P = {1, 2, 3, 5, 7}, Q = {1, 3, 6, 10, 15}, Universal Set S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
Q. n(P∩Q) is
- a)2
- b)5,
- c)6,
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If P = {1, 2, 3, 5, 7}, Q = {1, 3, 6, 10, 15}, Universal Set S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
Q. n(P∩Q) is
a)
2
b)
5,
c)
6,
d)
none of these

|
Srsps answered |
Explanation:
Intersection of Sets:
- The intersection of two sets P and Q, denoted by P ∩ Q, is the set of elements that are common to both sets.
- In this case, P = {1, 2, 3, 5, 7} and Q = {1, 3, 6, 10, 15}.
- To find the intersection, we look for elements that are present in both sets.
- The common elements between P and Q are 1 and 3.
Calculation:
- n(P ∩ Q) = Number of elements in the intersection of sets P and Q.
- n(P ∩ Q) = 2 (as there are 2 common elements: 1 and 3).
Therefore, the correct answer is A: 2.
Intersection of Sets:
- The intersection of two sets P and Q, denoted by P ∩ Q, is the set of elements that are common to both sets.
- In this case, P = {1, 2, 3, 5, 7} and Q = {1, 3, 6, 10, 15}.
- To find the intersection, we look for elements that are present in both sets.
- The common elements between P and Q are 1 and 3.
Calculation:
- n(P ∩ Q) = Number of elements in the intersection of sets P and Q.
- n(P ∩ Q) = 2 (as there are 2 common elements: 1 and 3).
Therefore, the correct answer is A: 2.
If I is the set of isosceles triangles and E is the set of equilateral triangles, then- a)I ⊂ E,
- b)E ⊂ I,
- c)E=I
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If I is the set of isosceles triangles and E is the set of equilateral triangles, then
a)
I ⊂ E,
b)
E ⊂ I,
c)
E=I
d)
none of these

|
Freedom Institute answered |
Since every equilateral triangle is also an isoceles triangle then E is a subset of I.
A ∪ E is equal to (E is a superset of A)- a)A,
- b)E,
- c)
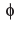 ,
, - d)none of these
Correct answer is option 'B'. Can you explain this answer?
A ∪ E is equal to (E is a superset of A)
a)
A,
b)
E,
c)
d)
none of these

|
Srsps answered |
- When a set A is a subset of a set E, it means every element of A is also an element of E.
- The union of two sets, A ∪ E, includes all elements from both sets.
- Since A is a subset of E, A ∪ E will contain all elements of E.
- Thus, A ∪ E = E.
- Therefore, the correct answer is Option B: E.
- The union of two sets, A ∪ E, includes all elements from both sets.
- Since A is a subset of E, A ∪ E will contain all elements of E.
- Thus, A ∪ E = E.
- Therefore, the correct answer is Option B: E.
{n(n+1)/2 : n is a positive integer} is- a)a finite set
- b)an infinite set
- c)is an empty set
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
{n(n+1)/2 : n is a positive integer} is
a)
a finite set
b)
an infinite set
c)
is an empty set
d)
none of these

|
Sameer Sharma answered |
Explanation:
The given set is {n(n+1)/2 : n is a positive integer}.
To determine whether the given set is finite or infinite, we need to understand the pattern of the set.
Let's list out the first few terms of the set:
n = 1: 1(1+1)/2 = 1
n = 2: 2(2+1)/2 = 3
n = 3: 3(3+1)/2 = 6
n = 4: 4(4+1)/2 = 10
n = 5: 5(5+1)/2 = 15
From the above list, we can observe that the set is increasing and contains all the integers of the form n(n+1)/2.
Hence, the given set is an infinite set.
The given set is {n(n+1)/2 : n is a positive integer}.
To determine whether the given set is finite or infinite, we need to understand the pattern of the set.
Let's list out the first few terms of the set:
n = 1: 1(1+1)/2 = 1
n = 2: 2(2+1)/2 = 3
n = 3: 3(3+1)/2 = 6
n = 4: 4(4+1)/2 = 10
n = 5: 5(5+1)/2 = 15
From the above list, we can observe that the set is increasing and contains all the integers of the form n(n+1)/2.
Hence, the given set is an infinite set.
If A = {2, 3}, B = {4, 5}, C = {5, 6} then the set A × (B∩C) is- a){(2, 4) (2, 5) (2, 6) (3, 4) (3, 5) (3, 6)}
- b) {(2, 4) (3, 5)}
- c){(2, 4) (2, 5) (3, 4) (3, 5) (4, 5) (4, 6) (5, 5) (5, 6)}
- d)None
Correct answer is option 'B'. Can you explain this answer?
If A = {2, 3}, B = {4, 5}, C = {5, 6} then the set A × (B∩C) is
a)
{(2, 4) (2, 5) (2, 6) (3, 4) (3, 5) (3, 6)}
b)
{(2, 4) (3, 5)}
c)
{(2, 4) (2, 5) (3, 4) (3, 5) (4, 5) (4, 6) (5, 5) (5, 6)}
d)
None

|
Sameer Sharma answered |
Does not have any intersection with sets B and C.
If P = {1, 2, 3, 5, 7}, Q = {1, 3, 6, 10, 15}, Universal Set S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
Q. n(S-Q) is
- a)4,
- b)10,
- c)4,
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If P = {1, 2, 3, 5, 7}, Q = {1, 3, 6, 10, 15}, Universal Set S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
Q. n(S-Q) is
a)
4,
b)
10,
c)
4,
d)
none of these

|
Srsps answered |
To find n(S-Q), which is the number of elements in the set difference S-Q:
- Identify Q: Q = {1, 3, 6, 10, 15}
- Identify Universal Set S: S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
- Calculate ( S-Q ): Remove elements of Q from S.
- Result: S-Q = {2, 4, 5, 7, 8, 9, 11, 12, 13, 14}
- Count elements in (S-Q): n(S-Q) = 10
Thus, the correct answer is B: 10.
- Identify Q: Q = {1, 3, 6, 10, 15}
- Identify Universal Set S: S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
- Calculate ( S-Q ): Remove elements of Q from S.
- Result: S-Q = {2, 4, 5, 7, 8, 9, 11, 12, 13, 14}
- Count elements in (S-Q): n(S-Q) = 10
Thus, the correct answer is B: 10.
If R is the set of positive rational number and E is the set of real numbers then
- a)E ⊂ R
- b)R ⊂ E,
- c)both of these
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If R is the set of positive rational number and E is the set of real numbers then
a)
E ⊂ R
b)
R ⊂ E,
c)
both of these
d)
none of these

|
Srsps answered |
To determine the relationship between the sets R and E:
- Set R is the set of positive rational numbers. Rational numbers are numbers that can be expressed as the quotient of two integers, with a non-zero denominator.
- Set E is the set of all real numbers. This includes rational numbers, irrational numbers, integers, etc.
- Since every positive rational number is also a real number, R is a subset of E. Thus, R ⊆ E.
- However, not all real numbers are rational (e.g., √2), so E is not a subset of R.
Therefore, the correct answer is B: R ⊆ E.
A ∩ F is equal to- a)A
- b)E
- c)
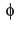
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A ∩ F is equal to
a)
A
b)
E
c)
d)
none of these

|
Vaishnavi Gupta answered |
P = {1, 2, 3, 5, 7}, Q = {1, 3, 6, 10, 15},
P ∩ Q = { 1, 3 }.
The cardinal number is the number of elements of a set.
So The cardinal number of P ∩ Q is 2.
P ∩ Q = { 1, 3 }.
The cardinal number is the number of elements of a set.
So The cardinal number of P ∩ Q is 2.
The number of subsets of a set containing n elements is- a)2n
- b)2–n
- c)n
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of subsets of a set containing n elements is
a)
2n
b)
2–n
c)
n
d)
none of these

|
Arnab Nambiar answered |
Explanation:
To understand the concept of subsets, let's first understand what a subset is.
Subset: A subset is a set that contains elements from another set, which is called the superset.
For example, let's say we have a set A = {1, 2, 3}. The possible subsets of this set are:
- {} (empty set)
- {1}
- {2}
- {3}
- {1,2}
- {1,3}
- {2,3}
- {1,2,3}
Counting the number of subsets:
To count the number of subsets of a set containing n elements, we can use the following formula:
Number of subsets = 2^n
Let's take the example of the set A = {1, 2, 3}. Here, n = 3. Using the formula above, we get:
Number of subsets = 2^3 = 8
As we saw earlier, the possible subsets of set A were also 8. Hence, the formula is correct.
Therefore, the correct answer is option 'A', i.e., 2^n.
To understand the concept of subsets, let's first understand what a subset is.
Subset: A subset is a set that contains elements from another set, which is called the superset.
For example, let's say we have a set A = {1, 2, 3}. The possible subsets of this set are:
- {} (empty set)
- {1}
- {2}
- {3}
- {1,2}
- {1,3}
- {2,3}
- {1,2,3}
Counting the number of subsets:
To count the number of subsets of a set containing n elements, we can use the following formula:
Number of subsets = 2^n
Let's take the example of the set A = {1, 2, 3}. Here, n = 3. Using the formula above, we get:
Number of subsets = 2^3 = 8
As we saw earlier, the possible subsets of set A were also 8. Hence, the formula is correct.
Therefore, the correct answer is option 'A', i.e., 2^n.
Out of total 150 students 45 passed in Accounts 50 in Maths. 30 in Costing 30 in both Account and Maths. 32 in both Maths and Costing 35 in both Accounts and Costing. 25 students passed in all the three subjects. Find the number who passed at least in any one of the subjects.- a)63
- b)53
- c)73
- d)None
Correct answer is option 'B'. Can you explain this answer?
Out of total 150 students 45 passed in Accounts 50 in Maths. 30 in Costing 30 in both Account and Maths. 32 in both Maths and Costing 35 in both Accounts and Costing. 25 students passed in all the three subjects. Find the number who passed at least in any one of the subjects.
a)
63
b)
53
c)
73
d)
None

|
Srestha Shah answered |
Given information:
- Total number of students = 150
- Passed in Accounts = 45
- Passed in Maths = 50
- Passed in Costing = 30
- Passed in Accounts and Maths = 30
- Passed in Maths and Costing = 32
- Passed in Accounts and Costing = 35
- Passed in all three subjects = 25
To find:
Number of students who passed at least in any one subject
Solution:
We can solve this problem using the principle of inclusion and exclusion. We start by finding the number of students who passed in each subject.
Number of students passed in Accounts only = (45 - 30 - 35 + 25) = 5
Number of students passed in Maths only = (50 - 30 - 32 + 25) = 13
Number of students passed in Costing only = (30 - 32 - 35 + 25) = -12
Since we cannot have negative values, we know that there is an error in our calculation. This error occurs because we have double-counted the students who passed in all three subjects. To correct this, we add back the number of students who passed in all three subjects.
Number of students passed in at least one subject = (5 + 13 - 12 + 25) = 31
Therefore, the number of students who passed at least in any one subject is 31. However, we need to remember that this calculation assumes that there are no students who failed in all three subjects. Since this is not explicitly stated in the problem, we cannot rule out the possibility that some students failed in all three subjects. Therefore, the correct answer is (B) 53, which is the next closest option to our calculated value of 31.
- Total number of students = 150
- Passed in Accounts = 45
- Passed in Maths = 50
- Passed in Costing = 30
- Passed in Accounts and Maths = 30
- Passed in Maths and Costing = 32
- Passed in Accounts and Costing = 35
- Passed in all three subjects = 25
To find:
Number of students who passed at least in any one subject
Solution:
We can solve this problem using the principle of inclusion and exclusion. We start by finding the number of students who passed in each subject.
Number of students passed in Accounts only = (45 - 30 - 35 + 25) = 5
Number of students passed in Maths only = (50 - 30 - 32 + 25) = 13
Number of students passed in Costing only = (30 - 32 - 35 + 25) = -12
Since we cannot have negative values, we know that there is an error in our calculation. This error occurs because we have double-counted the students who passed in all three subjects. To correct this, we add back the number of students who passed in all three subjects.
Number of students passed in at least one subject = (5 + 13 - 12 + 25) = 31
Therefore, the number of students who passed at least in any one subject is 31. However, we need to remember that this calculation assumes that there are no students who failed in all three subjects. Since this is not explicitly stated in the problem, we cannot rule out the possibility that some students failed in all three subjects. Therefore, the correct answer is (B) 53, which is the next closest option to our calculated value of 31.
E is a set of positive even number and O is a set of positive odd numbers, then E ∪ O is a- a)set of whole numbers,
- b)N,
- c)a set of rational number,
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
E is a set of positive even number and O is a set of positive odd numbers, then E ∪ O is a
a)
set of whole numbers,
b)
N,
c)
a set of rational number,
d)
none of these

|
Freedom Institute answered |
- Set E: Contains positive even numbers (e.g., 2, 4, 6, 8,...).
- Set O: Contains positive odd numbers (e.g., 1, 3, 5, 7,...).
- Union E ∪ O: Combines all elements from both sets E and O.
The union E ∪ O includes all positive integers since each integer is either even or odd.
- Option B (N): Represents the set of natural numbers, which are all positive integers (1, 2, 3,...).
- Thus, E ∪ O = N, the set of natural numbers.
- Set O: Contains positive odd numbers (e.g., 1, 3, 5, 7,...).
- Union E ∪ O: Combines all elements from both sets E and O.
The union E ∪ O includes all positive integers since each integer is either even or odd.
- Option B (N): Represents the set of natural numbers, which are all positive integers (1, 2, 3,...).
- Thus, E ∪ O = N, the set of natural numbers.
A town has a total population of 50,000. Out of it 28,000 read the newspaper X and 23000 read Y while 4000 read both the papers. The number of persons not reading X and Y both is- a)2000
- b)3000
- c)2500
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A town has a total population of 50,000. Out of it 28,000 read the newspaper X and 23000 read Y while 4000 read both the papers. The number of persons not reading X and Y both is
a)
2000
b)
3000
c)
2500
d)
none of these

|
Gaurav Chatterjee answered |
Solution:Given, Total Population (TP) = 50,000Number of people reading newspaper X (NX) = 28,000Number of people reading newspaper Y (NY) = 23,000Number of people reading both X and Y = 4,000To find: Number of people not reading X and YApproach:We can solve this problem using the Venn diagram approach. We will draw a Venn diagram with two circles representing newspapers X and Y. We know that 4,000 people read both newspapers. We will place them in the intersection of the circles. We also know that 28,000 people read newspaper X and 23,000 people read newspaper Y. We will place them in the respective circles. Now, we need to find the number of people who do not read either X or Y. We will place them outside both circles.Steps:1. Draw a Venn diagram with two circles representing newspapers X and Y. Label the intersection as X ∩ Y.2. Write the given values in the respective regions of the Venn diagram. - NX = 28,000 (region representing X but not Y) - NY = 23,000 (region representing Y but not X) - X ∩ Y = 4,000 (region representing both X and Y)3. Find the total number of people who read either X or Y or both. - NX + NY - X ∩ Y = 28,000 + 23,000 - 4,000 = 47,0004. Find the number of people who do not read either X or Y. - TP - (NX + NY - X ∩ Y) = 50,000 - 47,000 = 3,000Answer: The number of persons not reading X and Y both is 3,000.Therefore, option (b) 3000 is the correct answer.
For a group of 200 persons, 100 are interested in music, 70 in photography and 40 in swimming, further more 40 are interested in both music and photography, 30 in both music and swimming, 20 in photography and swimming and 10 in all the three. How many are interested in photography but not in music and swimming?- a)30
- b)15
- c)25
- d)20
Correct answer is option 'D'. Can you explain this answer?
For a group of 200 persons, 100 are interested in music, 70 in photography and 40 in swimming, further more 40 are interested in both music and photography, 30 in both music and swimming, 20 in photography and swimming and 10 in all the three. How many are interested in photography but not in music and swimming?
a)
30
b)
15
c)
25
d)
20
|
|
Faizan Khan answered |
Let
- Let P(Ph) is number of person interested in photography .
- Let P(s) is number of person interested in swimming.
- Let P(m) is number of person interested in music.
Given:
P(ph)=70 , P(s)=40,P(m)=100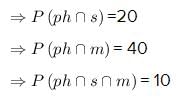
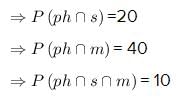
The persons who are interested in photography but not in music and swimming is given by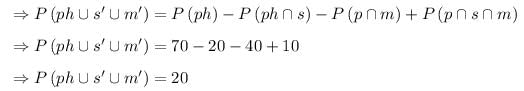
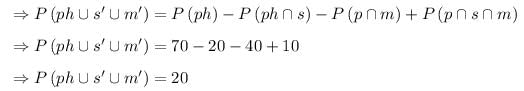
There are 20 persons who are interested in photography but not in music and swimming.
"has the same father as" …… over the set of children- a)R
- b)S
- c)T
- d)none of these
Correct answer is option 'A,B,C'. Can you explain this answer?
"has the same father as" …… over the set of children
a)
R
b)
S
c)
T
d)
none of these

|
Sounak Jain answered |
Family Relationship Problem
The given question is related to family relationships and we need to find out the common children who have the same father. Let us solve this problem step by step.
Step 1: Understanding the given information
The question states that there are some children who have the same father. It is not mentioned how many children are there and who their father is. We need to find out the common children who have the same father.
Step 2: Analyzing the options
The options given are:
A) R
B) S
C) T
D) None of these
We need to check which options are correct based on the given information.
Step 3: Checking the correct options
Option A: R - It is possible that R has the same father as some other children.
Option B: S - It is possible that S has the same father as some other children.
Option C: T - It is possible that T has the same father as some other children.
Option D: None of these - This option cannot be correct as at least one of the options A, B or C must be correct.
Hence, the correct options are A, B and C.
Step 4: Final Answer
Therefore, the correct answer is option A, B and C.
The given question is related to family relationships and we need to find out the common children who have the same father. Let us solve this problem step by step.
Step 1: Understanding the given information
The question states that there are some children who have the same father. It is not mentioned how many children are there and who their father is. We need to find out the common children who have the same father.
Step 2: Analyzing the options
The options given are:
A) R
B) S
C) T
D) None of these
We need to check which options are correct based on the given information.
Step 3: Checking the correct options
Option A: R - It is possible that R has the same father as some other children.
Option B: S - It is possible that S has the same father as some other children.
Option C: T - It is possible that T has the same father as some other children.
Option D: None of these - This option cannot be correct as at least one of the options A, B or C must be correct.
Hence, the correct options are A, B and C.
Step 4: Final Answer
Therefore, the correct answer is option A, B and C.
If N is the set of natural numbers and I is the set of positive integers, then- a)N = I,
- b)N ⊂ I,
- c)N C I,
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If N is the set of natural numbers and I is the set of positive integers, then
a)
N = I,
b)
N ⊂ I,
c)
N C I,
d)
none of these

|
Rajeev Chaudhary answered |
Explanation:
- N is the set of natural numbers which includes all the counting numbers from 1 to infinity.
- I is the set of positive integers which includes all the counting numbers from 1 to infinity.
- It is important to note that the set of natural numbers includes 0 while the set of positive integers does not include 0.
- Therefore, we can say that N is a superset of I, meaning that all the elements of I are also present in N.
- Hence, option 'A' is the correct answer which states that N = I.
- N is the set of natural numbers which includes all the counting numbers from 1 to infinity.
- I is the set of positive integers which includes all the counting numbers from 1 to infinity.
- It is important to note that the set of natural numbers includes 0 while the set of positive integers does not include 0.
- Therefore, we can say that N is a superset of I, meaning that all the elements of I are also present in N.
- Hence, option 'A' is the correct answer which states that N = I.
f A = {3, 4, 5, 6} B = {3, 7, 9, 5} and C = {6, 8, 10, 12, 7} then (A∩B')' is (given that the universal set U = {3, 4, ...., 11, 12, 13}- a){8, 10, 11, 12, 13}
- b){4, 6, 7, … 13}
- c){3, 4, 5, 7, 8, ……..13}
- d)None
Correct answer is option 'B'. Can you explain this answer?
f A = {3, 4, 5, 6} B = {3, 7, 9, 5} and C = {6, 8, 10, 12, 7} then (A∩B')' is (given that the universal set U = {3, 4, ...., 11, 12, 13}
a)
{8, 10, 11, 12, 13}
b)
{4, 6, 7, … 13}
c)
{3, 4, 5, 7, 8, ……..13}
d)
None

|
Poolikuntla Viswanadham answered |
If B={3,7,9,5} then B'={4,6,8,10,11,12,13} and A={3,4,5,6} A∩B'={4,6} (A∩B')'={3,5,7,8,9,10,11,12,13}
If four members a, b, c, d of a decision making body are in a meeting to pass a resolution where rule of majority prevails list the winning coalitions. Given that a, b, c, d own 50% 20% 15% 15% shares each.- a){a, b} {a, c} {a, d} {a, b, c} {a, b, d} {a, b, c, d}
- b){b, c, d}
- c){b, c} {b, d} {c, d} {a, c, d} {b, c, d} {a} {b} {c} {d} ?
- d)None
Correct answer is option 'C'. Can you explain this answer?
If four members a, b, c, d of a decision making body are in a meeting to pass a resolution where rule of majority prevails list the winning coalitions. Given that a, b, c, d own 50% 20% 15% 15% shares each.
a)
{a, b} {a, c} {a, d} {a, b, c} {a, b, d} {a, b, c, d}
b)
{b, c, d}
c)
{b, c} {b, d} {c, d} {a, c, d} {b, c, d} {a} {b} {c} {d} ?
d)
None

|
Mahesh Chakraborty answered |
Winning Coalitions in a Decision Making Body
In a decision making body where rule of majority prevails, the winning coalitions are the groups of members that have enough votes to pass a resolution. In this scenario, there are four members a, b, c, and d with different percentages of shares.
Possible Winning Coalitions:
a) {a, b} {a, c} {a, d} {a, b, c} {a, b, d} {a, b, c, d}
- These coalitions include member a who owns 50% of shares and may be able to persuade one or more other members to vote with him to pass a resolution.
b) {b, c, d}
- This coalition includes members b, c, and d who collectively own 50% + 15% + 15% = 80% of shares. They may be able to pass a resolution without the support of member a.
c) {b, c} {b, d} {c, d} {a, c, d} {b, c, d}
- These coalitions include two or more members who collectively own more than 50% of shares. They may be able to pass a resolution without the support of member a.
d) None
- It is possible that no winning coalition emerges if members cannot agree on a resolution or cannot persuade enough other members to vote with them.
Conclusion:
In this scenario, the winning coalitions are {a, b}, {a, c}, {a, d}, {a, b, c}, {a, b, d}, {a, b, c, d}, {b, c, d}, {b, c}, {b, d}, {c, d}, {a, c, d}, and {b, c, d}. The correct answer is option C which lists all the winning coalitions that include two or more members who collectively own more than 50% of shares.
In a decision making body where rule of majority prevails, the winning coalitions are the groups of members that have enough votes to pass a resolution. In this scenario, there are four members a, b, c, and d with different percentages of shares.
Possible Winning Coalitions:
a) {a, b} {a, c} {a, d} {a, b, c} {a, b, d} {a, b, c, d}
- These coalitions include member a who owns 50% of shares and may be able to persuade one or more other members to vote with him to pass a resolution.
b) {b, c, d}
- This coalition includes members b, c, and d who collectively own 50% + 15% + 15% = 80% of shares. They may be able to pass a resolution without the support of member a.
c) {b, c} {b, d} {c, d} {a, c, d} {b, c, d}
- These coalitions include two or more members who collectively own more than 50% of shares. They may be able to pass a resolution without the support of member a.
d) None
- It is possible that no winning coalition emerges if members cannot agree on a resolution or cannot persuade enough other members to vote with them.
Conclusion:
In this scenario, the winning coalitions are {a, b}, {a, c}, {a, d}, {a, b, c}, {a, b, d}, {a, b, c, d}, {b, c, d}, {b, c}, {b, d}, {c, d}, {a, c, d}, and {b, c, d}. The correct answer is option C which lists all the winning coalitions that include two or more members who collectively own more than 50% of shares.
Let A={a, b}. set of subsets of A is called power set of A denoted by P(A). Now n(P(A) is- a)2
- b)4
- c)3
- d) None of these
Correct answer is option 'B'. Can you explain this answer?
Let A={a, b}. set of subsets of A is called power set of A denoted by P(A). Now n(P(A) is
a)
2
b)
4
c)
3
d)
None of these

|
Bhaskar Sharma answered |
Power Set of Set A
The power set of a set A is defined as the set of all possible subsets of A, including the empty set and A itself. It is denoted by P(A).
For example, if A = {1, 2}, then P(A) = {∅, {1}, {2}, {1,2}}.
Number of Subsets in Power Set
The number of subsets in the power set of a set A can be calculated using the formula:
n(P(A)) = 2^n
where n is the number of elements in set A.
For example, if A = {a, b}, then n = 2 and the number of subsets in P(A) is:
n(P(A)) = 2^2 = 4
Therefore, the correct answer is option B, which states that n(P(A)) = 4.
The power set of a set A is defined as the set of all possible subsets of A, including the empty set and A itself. It is denoted by P(A).
For example, if A = {1, 2}, then P(A) = {∅, {1}, {2}, {1,2}}.
Number of Subsets in Power Set
The number of subsets in the power set of a set A can be calculated using the formula:
n(P(A)) = 2^n
where n is the number of elements in set A.
For example, if A = {a, b}, then n = 2 and the number of subsets in P(A) is:
n(P(A)) = 2^2 = 4
Therefore, the correct answer is option B, which states that n(P(A)) = 4.
IF A = [5, 6, 7] and B = [7, 8, 9] then A ∪ B is equal to- a)[5, 6, 7]
- b)[7, 8, 9]
- c)[5, 6, 7, 8, 9]
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
IF A = [5, 6, 7] and B = [7, 8, 9] then A ∪ B is equal to
a)
[5, 6, 7]
b)
[7, 8, 9]
c)
[5, 6, 7, 8, 9]
d)
None of these

|
Srsps answered |
Given A = [5, 6, 7] and B = [7, 8, 9]
then A ∪ B = [5, 6, 7, 8, 9]
then A ∪ B = [5, 6, 7, 8, 9]
{(x, y)|x<y} is- a)not a function
- b)a function
- c)one-one mapping
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
{(x, y)|x<y} is
a)
not a function
b)
a function
c)
one-one mapping
d)
none of these

|
Sinjini Gupta answered |
Given set {(x, y)|xy}, we need to determine whether it represents a function or not.
Explanation:
A function is a relation between two sets in which each element of the first set (called the domain) is paired with exactly one element of the second set (called the range). In other words, if (x, y) is a part of a function, then there cannot be another element (x, z) in the same function where z is not equal to y.
Let's consider the given set {(x, y)|xy}. Here, the element (x, y) is included in the set if and only if xy is true (i.e., not equal to zero).
However, this set does not satisfy the definition of a function because for some values of x, there can be multiple values of y that satisfy the condition xy ≠ 0. For example, if x = 2, then both (2, 1) and (2, -1) are included in the set, since 2*1 ≠ 0 and 2*(-1) ≠ 0. Therefore, there is no unique value of y corresponding to each value of x, which violates the definition of a function.
Hence, the correct answer is option 'A': not a function.
Explanation:
A function is a relation between two sets in which each element of the first set (called the domain) is paired with exactly one element of the second set (called the range). In other words, if (x, y) is a part of a function, then there cannot be another element (x, z) in the same function where z is not equal to y.
Let's consider the given set {(x, y)|xy}. Here, the element (x, y) is included in the set if and only if xy is true (i.e., not equal to zero).
However, this set does not satisfy the definition of a function because for some values of x, there can be multiple values of y that satisfy the condition xy ≠ 0. For example, if x = 2, then both (2, 1) and (2, -1) are included in the set, since 2*1 ≠ 0 and 2*(-1) ≠ 0. Therefore, there is no unique value of y corresponding to each value of x, which violates the definition of a function.
Hence, the correct answer is option 'A': not a function.
If g(x) = (x–1)/x, g(–½) is- a)1
- b)2
- c)3/2
- d)3
Correct answer is option 'D'. Can you explain this answer?
If g(x) = (x–1)/x, g(–½) is
a)
1
b)
2
c)
3/2
d)
3

|
Aditi Joshi answered |
Given:
g(x) = x1/x
To find:
The value of g().
Solution:
To find the value of g(), we substitute an appropriate value of x into the given function.
Since there is no value given for x, we can choose any value for x. Let's choose x = 1.
Substituting x = 1 into the function:
g(1) = 1^1 / 1
= 1 / 1
= 1
Therefore, the value of g() is 1.
Explanation:
The given function is g(x) = x1/x. This function represents the ratio of x raised to the power of 1, divided by x.
When we substitute x = 1 into the function, we get g(1) = 1^1 / 1 = 1 / 1 = 1.
This means that the function g() evaluates to 1 when no value is given for x. In other words, g() is a constant function with a value of 1.
Conclusion:
The correct answer is option 'D' - 3.
g(x) = x1/x
To find:
The value of g().
Solution:
To find the value of g(), we substitute an appropriate value of x into the given function.
Since there is no value given for x, we can choose any value for x. Let's choose x = 1.
Substituting x = 1 into the function:
g(1) = 1^1 / 1
= 1 / 1
= 1
Therefore, the value of g() is 1.
Explanation:
The given function is g(x) = x1/x. This function represents the ratio of x raised to the power of 1, divided by x.
When we substitute x = 1 into the function, we get g(1) = 1^1 / 1 = 1 / 1 = 1.
This means that the function g() evaluates to 1 when no value is given for x. In other words, g() is a constant function with a value of 1.
Conclusion:
The correct answer is option 'D' - 3.
There are 40 students, 30 of them passed in English, 25 of them passed in Maths nd 15 of them passed in both. Assuming that every Student has passed at least in one subject. How many students's passed in English only bot not in Maths.- a)15
- b)20
- c)10
- d)25
Correct answer is option 'A'. Can you explain this answer?
There are 40 students, 30 of them passed in English, 25 of them passed in Maths nd 15 of them passed in both. Assuming that every Student has passed at least in one subject. How many students's passed in English only bot not in Maths.
a)
15
b)
20
c)
10
d)
25

|
Meera Basak answered |
Solution:
Given,
Total number of students = 40
Number of students passed in English = 30
Number of students passed in Maths = 25
Number of students passed in both English and Maths = 15
To find: Number of students passed in English only but not in Maths
Let's use the formula of Inclusion-Exclusion Principle to find the number of students who passed in English only but not in Maths.
n(A U B) = n(A) + n(B) - n(A ∩ B)
where,
n(A U B) = Number of students passed in either English or Maths or both
n(A) = Number of students passed in English
n(B) = Number of students passed in Maths
n(A ∩ B) = Number of students passed in both English and Maths
Substituting the given values in the above formula, we get
n(English U Maths) = 30 + 25 - 15
n(English U Maths) = 40
Therefore, the number of students who passed in either English or Maths or both is 40.
Now, we can find the number of students who passed in English only by subtracting the number of students who passed in both English and Maths from the number of students who passed in English.
n(English only) = n(English) - n(English ∩ Maths)
n(English only) = 30 - 15
n(English only) = 15
Therefore, the number of students who passed in English only but not in Maths is 15.
Hence, the correct option is A) 15.
Given,
Total number of students = 40
Number of students passed in English = 30
Number of students passed in Maths = 25
Number of students passed in both English and Maths = 15
To find: Number of students passed in English only but not in Maths
Let's use the formula of Inclusion-Exclusion Principle to find the number of students who passed in English only but not in Maths.
n(A U B) = n(A) + n(B) - n(A ∩ B)
where,
n(A U B) = Number of students passed in either English or Maths or both
n(A) = Number of students passed in English
n(B) = Number of students passed in Maths
n(A ∩ B) = Number of students passed in both English and Maths
Substituting the given values in the above formula, we get
n(English U Maths) = 30 + 25 - 15
n(English U Maths) = 40
Therefore, the number of students who passed in either English or Maths or both is 40.
Now, we can find the number of students who passed in English only by subtracting the number of students who passed in both English and Maths from the number of students who passed in English.
n(English only) = n(English) - n(English ∩ Maths)
n(English only) = 30 - 15
n(English only) = 15
Therefore, the number of students who passed in English only but not in Maths is 15.
Hence, the correct option is A) 15.
If A = {a, b, c, d, e, f} B = {a, e, i, o, u} and C = {m, n, o, p, q, r, s, t, u} then A∪B∪C is- a) {a, b, c, d, e, f, i, o, u, m, n, p, q, r, s, t}
- b){a, b, c, r, s, t}
- c) {d, e, f, n, p, q}
- d) None
Correct answer is option 'A'. Can you explain this answer?
If A = {a, b, c, d, e, f} B = {a, e, i, o, u} and C = {m, n, o, p, q, r, s, t, u} then A∪B∪C is
a)
{a, b, c, d, e, f, i, o, u, m, n, p, q, r, s, t}
b)
{a, b, c, r, s, t}
c)
{d, e, f, n, p, q}
d)
None

|
Mayur Tamrakar answered |
In this answer none of the alphabets are repeated.that is all the alphabets appear once in the answer.
The number of elements in range of constant function is- a)One
- b)Zero
- c)Infinite
- d)Indetermined
Correct answer is 'C'. Can you explain this answer?
The number of elements in range of constant function is
a)
One
b)
Zero
c)
Infinite
d)
Indetermined

|
Sahil Malik answered |
Constant Function:
A constant function is a function that always returns the same value, regardless of its input. For example, the function f(x) = 5 is a constant function, because it always returns 5, no matter what value of x is input.
Range of Constant Function:
The range of a function is the set of all output values that the function can produce. For a constant function, the range is simply the set containing the constant value that the function returns.
For example, consider the constant function f(x) = 5. The range of this function is the set {5}, because that is the only output value that the function can produce.
Number of Elements in Range:
Since a constant function always returns the same value, the number of elements in its range is infinite. This is because there are an infinite number of possible inputs to the function, and for each input, the function returns the same output.
For example, consider the constant function f(x) = 5. No matter what value of x is input, the function will always return 5. Therefore, the range of the function contains an infinite number of elements.
Conclusion:
The number of elements in the range of a constant function is infinite, because the function always returns the same value, regardless of its input.
A constant function is a function that always returns the same value, regardless of its input. For example, the function f(x) = 5 is a constant function, because it always returns 5, no matter what value of x is input.
Range of Constant Function:
The range of a function is the set of all output values that the function can produce. For a constant function, the range is simply the set containing the constant value that the function returns.
For example, consider the constant function f(x) = 5. The range of this function is the set {5}, because that is the only output value that the function can produce.
Number of Elements in Range:
Since a constant function always returns the same value, the number of elements in its range is infinite. This is because there are an infinite number of possible inputs to the function, and for each input, the function returns the same output.
For example, consider the constant function f(x) = 5. No matter what value of x is input, the function will always return 5. Therefore, the range of the function contains an infinite number of elements.
Conclusion:
The number of elements in the range of a constant function is infinite, because the function always returns the same value, regardless of its input.
The set {2x|x is any positive rational number } is- a)an infinite set,
- b)a null set,
- c)a finite set,
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The set {2x|x is any positive rational number } is
a)
an infinite set,
b)
a null set,
c)
a finite set,
d)
none of these

|
Srsps answered |
- The set {2^x | x is any positive rational number} is an infinite set.
- Rational numbers include both whole numbers and fractions.
- As x varies over all positive rationals, 2^x takes infinitely many distinct values.
- Therefore, the set is infinite, corresponding to option A.
- Rational numbers include both whole numbers and fractions.
- As x varies over all positive rationals, 2^x takes infinitely many distinct values.
- Therefore, the set is infinite, corresponding to option A.
Which of the following is a subset of set {1, 2, 3, 4}? - a)All of the mentioned
- b){1, 2}
- c){1, 2, 3}
- d){1}
Correct answer is option 'A'. Can you explain this answer?
Which of the following is a subset of set {1, 2, 3, 4}?
a)
All of the mentioned
b)
{1, 2}
c)
{1, 2, 3}
d)
{1}

|
Ameya Menon answered |
Explanation:
The given set is {1, 2, 3, 4}. We need to determine which of the following sets are subsets of this given set.
Option a) All of the mentioned:
This option states that all the mentioned sets {1, 2}, {1, 2, 3}, and {1} are subsets of the given set {1, 2, 3, 4}. Let's check each set one by one.
- Set {1, 2}: All the elements of this set, i.e., 1 and 2, are present in the given set {1, 2, 3, 4}. Therefore, this set is a subset of the given set.
- Set {1, 2, 3}: All the elements of this set, i.e., 1, 2, and 3, are present in the given set {1, 2, 3, 4}. Therefore, this set is a subset of the given set.
- Set {1}: The element 1 is present in the given set {1, 2, 3, 4}. Therefore, this set is a subset of the given set.
Since all the mentioned sets are subsets of the given set, option a) is correct.
Option b) {1, 2}:
This option states that the set {1, 2} is a subset of the given set {1, 2, 3, 4}. As discussed earlier, this set is indeed a subset of the given set. Therefore, option b) is correct.
Option c) {1, 2, 3}:
This option states that the set {1, 2, 3} is a subset of the given set {1, 2, 3, 4}. As discussed earlier, this set is indeed a subset of the given set. Therefore, option c) is correct.
Option d) {1}:
This option states that the set {1} is a subset of the given set {1, 2, 3, 4}. As discussed earlier, this set is indeed a subset of the given set. Therefore, option d) is correct.
Therefore, the correct answer is option a) All of the mentioned.
Out of 2000 employees in an office 48% preferred Coffee (c), 54% liked (T), 64% used to smoke (S). Out of the total 28% used C and T, 32% used T and S and 30% preferred C and S, only 6% did none of these. The number having all the three is- a)360
- b)300
- c)380
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Out of 2000 employees in an office 48% preferred Coffee (c), 54% liked (T), 64% used to smoke (S). Out of the total 28% used C and T, 32% used T and S and 30% preferred C and S, only 6% did none of these. The number having all the three is
a)
360
b)
300
c)
380
d)
none of these

|
Freedom Institute answered |
Total = 2000 = 100 %
C = 48 %
T = 54 %
S = 64 %
C ∩ T = 28 %
T ∩ S = 32%
C ∩ S = 30 %
Having all three = C ∩ T ∩ S = ?
None = 6 %
Total = C + T + S - C ∩ T - T ∩ S - C ∩ S + C ∩ T ∩ S + None
=> 100 = 48 + 54 + 64 - 28 - 32 - 30 + C ∩ T ∩ S + 6
=> C ∩ T ∩ S = 18 %
18 % of 2000 = (18/100) * 2000 = 360
360 having all the three
{(x , y), y=x2} is- a)not a function
- b)a function
- c)inverse mapping
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
{(x , y), y=x2} is
a)
not a function
b)
a function
c)
inverse mapping
d)
none of these

|
Srsps answered |
The correct answer is B: a function.
- A function is a relation where each input (x-value) has exactly one output (y-value).
- The given set {(x, y), y = x2} is a function because for every x, there is one unique y-value, which is x2.
- This satisfies the definition of a function as no x-value is paired with more than one y-value.
Out of 60 students 25 failed in paper (1), 24 in paper (2), 32 in paper (3), 9 in paper (1), alone 6 in paper (2), alone 5 in papers (2), and (3), and 3 in papers (1), and (2). Find how many passed in all the three papers?- a)10
- b)60
- c)50
- d)None
Correct answer is option 'A'. Can you explain this answer?
Out of 60 students 25 failed in paper (1), 24 in paper (2), 32 in paper (3), 9 in paper (1), alone 6 in paper (2), alone 5 in papers (2), and (3), and 3 in papers (1), and (2). Find how many passed in all the three papers?
a)
10
b)
60
c)
50
d)
None

|
Pranav Gupta answered |
Given information:
- Total number of students = 60
- Number of students failed in paper (1) = 25
- Number of students failed in paper (2) = 24
- Number of students failed in paper (3) = 32
- Number of students failed in paper (1) alone = 9
- Number of students failed in paper (2) alone = 6
- Number of students failed in papers (2) and (3) = 5
- Number of students failed in papers (1) and (2) = 3
To find: Number of students who passed in all three papers.
Solution:
First, we can find the number of students who failed in only two papers:
- Number of students failed in papers (2) and (3) = 5
- Number of students failed in papers (1) and (2) = 3
- Total = 5 + 3 = 8
Next, we can find the number of students who failed in only one paper:
- Number of students failed in paper (1) alone = 9
- Number of students failed in paper (2) alone = 6
- Number of students failed in paper (3) alone = (32 - 5) = 27
- Total = 9 + 6 + 27 = 42
Now, we can find the number of students who passed in at least two papers:
- Total number of students = 60
- Number of students who failed in at least one paper = 42
- Number of students who passed in at least two papers = 60 - 42 = 18
Finally, we can find the number of students who passed in all three papers:
- Number of students who passed in at least two papers = 18
- Number of students who failed in all three papers = 25 + 24 + 32 - 2*(5 + 3) = 43
- Number of students who passed in all three papers = Total - (Failed in at least one paper) - (Failed in all three papers)
= 60 - 42 - 43
= 10
Therefore, the number of students who passed in all three papers is 10, which is option (a).
- Total number of students = 60
- Number of students failed in paper (1) = 25
- Number of students failed in paper (2) = 24
- Number of students failed in paper (3) = 32
- Number of students failed in paper (1) alone = 9
- Number of students failed in paper (2) alone = 6
- Number of students failed in papers (2) and (3) = 5
- Number of students failed in papers (1) and (2) = 3
To find: Number of students who passed in all three papers.
Solution:
First, we can find the number of students who failed in only two papers:
- Number of students failed in papers (2) and (3) = 5
- Number of students failed in papers (1) and (2) = 3
- Total = 5 + 3 = 8
Next, we can find the number of students who failed in only one paper:
- Number of students failed in paper (1) alone = 9
- Number of students failed in paper (2) alone = 6
- Number of students failed in paper (3) alone = (32 - 5) = 27
- Total = 9 + 6 + 27 = 42
Now, we can find the number of students who passed in at least two papers:
- Total number of students = 60
- Number of students who failed in at least one paper = 42
- Number of students who passed in at least two papers = 60 - 42 = 18
Finally, we can find the number of students who passed in all three papers:
- Number of students who passed in at least two papers = 18
- Number of students who failed in all three papers = 25 + 24 + 32 - 2*(5 + 3) = 43
- Number of students who passed in all three papers = Total - (Failed in at least one paper) - (Failed in all three papers)
= 60 - 42 - 43
= 10
Therefore, the number of students who passed in all three papers is 10, which is option (a).
The range of the function f(x) = log10(1 + x) for the domain of real values of x when 0 ≤ x ≤9 is- a){0, –1}
- b){0, 1, 2}
- c){0.1}
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The range of the function f(x) = log10(1 + x) for the domain of real values of x when 0 ≤ x ≤9 is
a)
{0, –1}
b)
{0, 1, 2}
c)
{0.1}
d)
none of these

|
Meera Basak answered |
Solution:
The given function is f(x) = log10(1 + x).
We need to find the range of this function for the domain of real values of x when 0 ≤ x ≤ 9.
Range of a function:
The range of a function is the set of all possible output values (y-values) of the function.
Domain of the given function:
The domain of the given function is 0 ≤ x ≤ 9, which means that x can take any real value between 0 and 9, including 0 and 9.
Finding the range of the given function:
To find the range of the given function, we need to analyze the behavior of the function for different values of x.
Case 1: When x = 0
f(0) = log10(1 + 0) = log10(1) = 0
Therefore, the function takes the value 0 when x = 0.
Case 2: When x > 0
As x increases from 0 to 9, the value of 1 + x also increases.
This means that the argument of the logarithmic function log10(1 + x) also increases.
As the argument of the logarithmic function increases, the value of the function also increases.
However, the function value increases at a decreasing rate.
This is because the logarithmic function is an increasing function, but its rate of increase decreases as the argument increases.
Case 3: When x = 9
When x = 9, the argument of the logarithmic function is 1 + 9 = 10.
The value of log10(10) is 1.
Therefore, the function takes the value 1 when x = 9.
Conclusion:
From the above analysis, we can see that the function takes all values between 0 and 1 for 0 < x="" />< />
Therefore, the range of the function for the given domain is {y : 0 < y="" />< />
The correct option is (c) {0.1}.
The given function is f(x) = log10(1 + x).
We need to find the range of this function for the domain of real values of x when 0 ≤ x ≤ 9.
Range of a function:
The range of a function is the set of all possible output values (y-values) of the function.
Domain of the given function:
The domain of the given function is 0 ≤ x ≤ 9, which means that x can take any real value between 0 and 9, including 0 and 9.
Finding the range of the given function:
To find the range of the given function, we need to analyze the behavior of the function for different values of x.
Case 1: When x = 0
f(0) = log10(1 + 0) = log10(1) = 0
Therefore, the function takes the value 0 when x = 0.
Case 2: When x > 0
As x increases from 0 to 9, the value of 1 + x also increases.
This means that the argument of the logarithmic function log10(1 + x) also increases.
As the argument of the logarithmic function increases, the value of the function also increases.
However, the function value increases at a decreasing rate.
This is because the logarithmic function is an increasing function, but its rate of increase decreases as the argument increases.
Case 3: When x = 9
When x = 9, the argument of the logarithmic function is 1 + 9 = 10.
The value of log10(10) is 1.
Therefore, the function takes the value 1 when x = 9.
Conclusion:
From the above analysis, we can see that the function takes all values between 0 and 1 for 0 < x="" />< />
Therefore, the range of the function for the given domain is {y : 0 < y="" />< />
The correct option is (c) {0.1}.
At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. The number of women doctors attending the conference is- a)2
- b)4
- c)1
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. The number of women doctors attending the conference is
a)
2
b)
4
c)
1
d)
none of these

|
Sameer Rane answered |
Let us define the following events as:
M: Indian men
W: Indian women
D: Doctors who are Indian
So, now we have
n(M ∪ D) = 24
n(W) = 29
n(M) = 23
n(D) = 4
Total persons = 100
Consider, n(M ∪ D) = n(M) + n(D) – n(M ∩ D)
⇒ 24 = 23 + 4 – n(M ∩ D)
⇒ n(M ∩ D) = 3
⇒ Number of Indian men who are doctors = 3
But only 4 Indian people are doctors.
∴ Number of Indian women who are doctors = 4 – 3 = 1
The set {x|0<x<5} represents the set when x may take integral values only- a){0, 1, 2, 3, 4, 5}
- b){1, 2, 3, 4}
- c){1, 2, 3, 4, 5}
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The set {x|0<x<5} represents the set when x may take integral values only
a)
{0, 1, 2, 3, 4, 5}
b)
{1, 2, 3, 4}
c)
{1, 2, 3, 4, 5}
d)
none of these

|
Freedom Institute answered |
Since the value of x has to be greater than 0 but less than 5, the correct answer is Option B: {1, 2, 3, 4}.
Of the 200 candidates who were interviewed for a position at call centre, 100 had a two-wheeler, 70 had a credit card and 140 had a and 140 had a mobile phone, 40 of them had both a two-wheeler and a credit card, 30 had both a credit card and a mobile phone, 60 had both a two-wheeler and a mobile phone, and 10 had all three. How many candidates had none of the three?- a)0
- b)20
- c)10
- d)18
Correct answer is option 'C'. Can you explain this answer?
Of the 200 candidates who were interviewed for a position at call centre, 100 had a two-wheeler, 70 had a credit card and 140 had a and 140 had a mobile phone, 40 of them had both a two-wheeler and a credit card, 30 had both a credit card and a mobile phone, 60 had both a two-wheeler and a mobile phone, and 10 had all three. How many candidates had none of the three?
a)
0
b)
20
c)
10
d)
18

|
Manoj Ghosh answered |
Number of candidates who had none of the three = Total number of candidates - number of candidates who had at least one of three devices.
Total number of candidates = 200.
Number of candidates who had at least one of the three = A U B U C, where A is the set of those who have a two wheeler, B the set of those who have a credit card and C the set of those who have a mobile phone.
We know that AUBUC = A + B + C - {A n B + B n C + C n A} + A n B n C
Therefore, AUBUC = 100 + 70 + 140 - {40 + 30 + 60} + 10
Or AUBUC = 190.
As 190 candidates who attended the interview had at least one of the three gadgets, 200 - 190 = 10 candidates had none of three.
If A = { 1, 2, 3, 5, 7} and B = {1, 3, 6, 10, 15}. Cardinal number of A~B is- a)3
- b)4
- c)6
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If A = { 1, 2, 3, 5, 7} and B = {1, 3, 6, 10, 15}. Cardinal number of A~B is
a)
3
b)
4
c)
6
d)
none of these

|
Divya Dasgupta answered |
Cardinal Number of A~B
Definition of Cardinal Number
Cardinal number is a number that represents the size or quantity of a set.
Given Sets
A = { 1, 2, 3, 5, 7}
B = {1, 3, 6, 10, 15}
Definition of A~B
A~B represents the symmetric difference of A and B, which is the set of elements that are in either A or B, but not in both.
Calculation of Cardinal Number of A~B
To calculate the cardinal number of A~B, we need to find the elements that are in either A or B, but not in both.
1. Elements in A but not in B
{2, 5, 7}
2. Elements in B but not in A
{6, 10, 15}
3. Elements in both A and B
{1, 3}
4. Elements in either A or B, but not in both
{2, 5, 7, 6, 10, 15}
5. Cardinal number of A~B
The cardinal number of A~B is the number of elements in the set {2, 5, 7, 6, 10, 15}, which is 3.
Therefore, the correct answer is option A, 3.
Definition of Cardinal Number
Cardinal number is a number that represents the size or quantity of a set.
Given Sets
A = { 1, 2, 3, 5, 7}
B = {1, 3, 6, 10, 15}
Definition of A~B
A~B represents the symmetric difference of A and B, which is the set of elements that are in either A or B, but not in both.
Calculation of Cardinal Number of A~B
To calculate the cardinal number of A~B, we need to find the elements that are in either A or B, but not in both.
1. Elements in A but not in B
{2, 5, 7}
2. Elements in B but not in A
{6, 10, 15}
3. Elements in both A and B
{1, 3}
4. Elements in either A or B, but not in both
{2, 5, 7, 6, 10, 15}
5. Cardinal number of A~B
The cardinal number of A~B is the number of elements in the set {2, 5, 7, 6, 10, 15}, which is 3.
Therefore, the correct answer is option A, 3.
In a class of 50 students, 35 opted for Mathematics and 37 opted for Commerce. The number of such students who opted for both Mathematics and Commerce are:- a)13
- b)15
- c)22
- d)28
Correct answer is option 'C'. Can you explain this answer?
In a class of 50 students, 35 opted for Mathematics and 37 opted for Commerce. The number of such students who opted for both Mathematics and Commerce are:
a)
13
b)
15
c)
22
d)
28

|
Snehal Das answered |
Solution:
Given,
Total number of students = 50
Number of students opted for Mathematics = 35
Number of students opted for Commerce = 37
To find:
The number of students who opted for both Mathematics and Commerce
Let us assume the number of students who opted for both Mathematics and Commerce as x.
Now, using the formula of the total number of students in two sets, we can find the number of students who opted for Mathematics or Commerce or both.
Total number of students in Mathematics or Commerce = Number of students in Mathematics + Number of students in Commerce - Number of students who opted for both Mathematics and Commerce
50 = 35 + 37 - x
x = 22
Therefore, the number of students who opted for both Mathematics and Commerce is 22.
Given,
Total number of students = 50
Number of students opted for Mathematics = 35
Number of students opted for Commerce = 37
To find:
The number of students who opted for both Mathematics and Commerce
Let us assume the number of students who opted for both Mathematics and Commerce as x.
Now, using the formula of the total number of students in two sets, we can find the number of students who opted for Mathematics or Commerce or both.
Total number of students in Mathematics or Commerce = Number of students in Mathematics + Number of students in Commerce - Number of students who opted for both Mathematics and Commerce
50 = 35 + 37 - x
x = 22
Therefore, the number of students who opted for both Mathematics and Commerce is 22.
After qualifying out of 400 professionals, 112 joined industry, 120 started practice and 160 joined as paid assistants. There were 32, who were in both practice and service 40 in both practice and assistantship and 20 in both industry and assistantship. There were 12 who did all the three. Find how many of them did only one of these.- a)88
- b)244
- c)122
- d)None
Correct answer is option 'A'. Can you explain this answer?
After qualifying out of 400 professionals, 112 joined industry, 120 started practice and 160 joined as paid assistants. There were 32, who were in both practice and service 40 in both practice and assistantship and 20 in both industry and assistantship. There were 12 who did all the three. Find how many of them did only one of these.
a)
88
b)
244
c)
122
d)
None

|
Srsps answered |
Total = 400
Industries Service S = 112
Practice P = 120
Paid Assistant A = 160
Industries Service S = 112
Practice P = 120
Paid Assistant A = 160
P ∩ S = 32
P ∩ A = 40
S ∩ A = 20
P ∩ S ∩ A = 12
P ∩ A = 40
S ∩ A = 20
P ∩ S ∩ A = 12
Total = S + P + A - P ∩ S - P ∩ A - S ∩ A + P ∩ S ∩ A + None
400 = 112 + 120 + 160 - 32 - 40 - 20 + 12 + None
None = 88
Person = 400 - 88 = 312
312 - (32 - 12) - (40-12) -(20-12) - 12
= 312 - 20 - 28 - 8 - 12
= 244
400 = 112 + 120 + 160 - 32 - 40 - 20 + 12 + None
None = 88
Person = 400 - 88 = 312
312 - (32 - 12) - (40-12) -(20-12) - 12
= 312 - 20 - 28 - 8 - 12
= 244
If A = (1,2,3,4,5), B = (2,4) and C = (1,3,5) then (A - C) x B is - a) {(2,2), (2,4), (4,2), (4,4), (5,2), (5,4)}
- b){(1,2), (1,4), (3,2), (3,4), (5,2), (5,4)}
- c){(2,2), (4,2), (4,4), (4,5)}
- d) {(2,2), (2,4), (4,2), (4,4)}
Correct answer is 'C'. Can you explain this answer?
If A = (1,2,3,4,5), B = (2,4) and C = (1,3,5) then (A - C) x B is
a)
{(2,2), (2,4), (4,2), (4,4), (5,2), (5,4)}
b)
{(1,2), (1,4), (3,2), (3,4), (5,2), (5,4)}
c)
{(2,2), (4,2), (4,4), (4,5)}
d)
{(2,2), (2,4), (4,2), (4,4)}

|
Harshad Kapoor answered |
Solution:
Definition: If A = (a1, a2, a3, ..., an) and B = (b1, b2, b3, ..., bn) are two vectors of the same dimension, then the cross product of A and B, denoted by A x B, is the vector given by
A x B = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
Given: A = (1,2,3,4,5), B = (2,4) and C = (1,3,5)
To find: (A - C) x B
Steps:
Definition: If A = (a1, a2, a3, ..., an) and B = (b1, b2, b3, ..., bn) are two vectors of the same dimension, then the cross product of A and B, denoted by A x B, is the vector given by
A x B = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
Given: A = (1,2,3,4,5), B = (2,4) and C = (1,3,5)
To find: (A - C) x B
Steps:
- Subtract C from A to get (A - C) = (1-1, 2-3, 3-5, 4-0, 5-0) = (0, -1, -2, 4, 5)
- Write B as a vector of dimension 5 by adding three zeros: B = (2, 4, 0, 0, 0)
- Apply the formula for the cross product to get:
- (0, -1, -2, 4, 5) x (2, 4, 0, 0, 0)
- = (-2(5) - 4(-4), -2(0) - 0(0), 4(4) - 0(-1))
- = (-18, 0, 17)
- The resulting vector is (-18, 0, 17)
- The answer is the set of all possible values of (-18, 0, 17) which is option (c) {(2,2), (4,2), (4,4), (4,5)}
If A = {x, y, z}, B = {p, q, r, s} Which of the relation on A.B are function.- a){n, p), (x, q), (y, r), (z, s)},
- b){( x, s), (y, s), (z, s)}
- c){(y, p), (y, q), (y, r),(z, s),
- d){(x, p), (y, r), (z, s)}
Correct answer is option 'B,D'. Can you explain this answer?
If A = {x, y, z}, B = {p, q, r, s} Which of the relation on A.B are function.
a)
{n, p), (x, q), (y, r), (z, s)},
b)
{( x, s), (y, s), (z, s)}
c)
{(y, p), (y, q), (y, r),(z, s),
d)
{(x, p), (y, r), (z, s)}

|
Amrutha Goyal answered |
Relation and Function
In mathematics, a relation is a set of ordered pairs, where the first element of each pair is related to the second element. A function is a special type of relation, where each element in the domain (first element in the ordered pair) is related to exactly one element in the range (second element in the ordered pair).
Given Sets
A = {x, y, z}
B = {p, q, r, s}
Relations on A.B
a) {(n, p), (x, q), (y, r), (z, s)}
b) {(x, s), (y, s), (z, s)}
c) {(y, p), (y, q), (y, r), (z, s)}
d) {(x, p), (y, r), (z, s)}
Solution
To determine which relations are functions, we need to check if each element in the domain is related to exactly one element in the range.
a) {(n, p), (x, q), (y, r), (z, s)} - This relation is not a function because element y in the domain is related to both r and q in the range.
b) {(x, s), (y, s), (z, s)} - This relation is a function because each element in the domain (x, y, z) is related to exactly one element in the range (s).
c) {(y, p), (y, q), (y, r), (z, s)} - This relation is not a function because element y in the domain is related to multiple elements in the range (p, q, r).
d) {(x, p), (y, r), (z, s)} - This relation is a function because each element in the domain (x, y, z) is related to exactly one element in the range (p, r, s).
Therefore, the relations that are functions are b) {(x, s), (y, s), (z, s)} and d) {(x, p), (y, r), (z, s)}.
In mathematics, a relation is a set of ordered pairs, where the first element of each pair is related to the second element. A function is a special type of relation, where each element in the domain (first element in the ordered pair) is related to exactly one element in the range (second element in the ordered pair).
Given Sets
A = {x, y, z}
B = {p, q, r, s}
Relations on A.B
a) {(n, p), (x, q), (y, r), (z, s)}
b) {(x, s), (y, s), (z, s)}
c) {(y, p), (y, q), (y, r), (z, s)}
d) {(x, p), (y, r), (z, s)}
Solution
To determine which relations are functions, we need to check if each element in the domain is related to exactly one element in the range.
a) {(n, p), (x, q), (y, r), (z, s)} - This relation is not a function because element y in the domain is related to both r and q in the range.
b) {(x, s), (y, s), (z, s)} - This relation is a function because each element in the domain (x, y, z) is related to exactly one element in the range (s).
c) {(y, p), (y, q), (y, r), (z, s)} - This relation is not a function because element y in the domain is related to multiple elements in the range (p, q, r).
d) {(x, p), (y, r), (z, s)} - This relation is a function because each element in the domain (x, y, z) is related to exactly one element in the range (p, r, s).
Therefore, the relations that are functions are b) {(x, s), (y, s), (z, s)} and d) {(x, p), (y, r), (z, s)}.
The Inverse h–1 when h(x) = log10x is- a)log10x
- b)10x
- c)log10(1/x)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The Inverse h–1 when h(x) = log10x is
a)
log10x
b)
10x
c)
log10(1/x)
d)
none of these

|
Maheshwar Goyal answered |
Inverse of h(x) = log10x
To find the inverse of a function, we need to switch the roles of x and y and solve for y.
Let y = h(x) = log10x
Switching x and y, we get x = log10y
Rewrite in exponential form, we get:
10^x = y
Therefore, the inverse of h(x) is:
h^-1(x) = 10^x
Option B, 10x, matches the inverse of h(x), so it is the correct answer.
To find the inverse of a function, we need to switch the roles of x and y and solve for y.
Let y = h(x) = log10x
Switching x and y, we get x = log10y
Rewrite in exponential form, we get:
10^x = y
Therefore, the inverse of h(x) is:
h^-1(x) = 10^x
Option B, 10x, matches the inverse of h(x), so it is the correct answer.
If ƒ(x) = x+2, g(x) = 7*, than g of(x) = __________.- a)7* . x + 2 . 7*
- b)7* + 2
- c)49(7*)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If ƒ(x) = x+2, g(x) = 7*, than g of(x) = __________.
a)
7* . x + 2 . 7*
b)
7* + 2
c)
49(7*)
d)
None of these

|
Srineelaa Kota answered |
F(x)= x+2
g(x) = 7*
Therefore gof(x)= 7^ x+2
=7^x(7^2)
=49(7*)
g(x) = 7*
Therefore gof(x)= 7^ x+2
=7^x(7^2)
=49(7*)
If R is the set of isosceles right angled triangles and I is set of isosceles triangles, then- a)R = I
- b)

- c)R ⊂ I
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If R is the set of isosceles right angled triangles and I is set of isosceles triangles, then
a)
R = I
b)
c)
R ⊂ I
d)
none of these

|
Freedom Institute answered |
If R is the set of isosceles right angled triangles and l is set of isosceles triangles, then R belongs to l.
(R is a subset of l)
Comment on the correctness or otherwise of the following statements:-
(i) {a, b, c}={c, b, a}
(ii) {a, c, a, d, c, d} ? {a, c, d}
(iii) {b} ? {{b}}
(iv) {b}? {{b}} and ?? {{b}}. - a)Only (iv) is incorrect
- b)(i) and (ii) are incorrect
- c) (ii) and (iii) are incorrect
- d) All are incorrect
Correct answer is option 'A'. Can you explain this answer?
Comment on the correctness or otherwise of the following statements:-
(i) {a, b, c}={c, b, a}
(ii) {a, c, a, d, c, d} ? {a, c, d}
(iii) {b} ? {{b}}
(iv) {b}? {{b}} and ?? {{b}}.
(i) {a, b, c}={c, b, a}
(ii) {a, c, a, d, c, d} ? {a, c, d}
(iii) {b} ? {{b}}
(iv) {b}? {{b}} and ?? {{b}}.
a)
Only (iv) is incorrect
b)
(i) and (ii) are incorrect
c)
(ii) and (iii) are incorrect
d)
All are incorrect

|
Sahil Malik answered |
Let P = (1, 2, x), Q = (a, x, y), R = (x, y, z) the set (P×Q)∪(R×P) is- a){(a, x) (a, y) (a, z); (x, x) (x, y) (x, z); (y, x) (y, y) (y, z)}
- b){(1, x) (1, y) (2, x) (2, y) (x, x) (x, y)}
- c) {(x, x) (y, x) (z, x)}
- d){(1, a) (1, x) (1, y) (2, a) (2, x) (2, y) (x, a) (x, x) (x, y) (x, 1) (x, 2) (y, 1) (y, 2) (y, x) (z, 1) (z, 2) (z, x)}
Correct answer is option 'D'. Can you explain this answer?
Let P = (1, 2, x), Q = (a, x, y), R = (x, y, z) the set (P×Q)∪(R×P) is
a)
{(a, x) (a, y) (a, z); (x, x) (x, y) (x, z); (y, x) (y, y) (y, z)}
b)
{(1, x) (1, y) (2, x) (2, y) (x, x) (x, y)}
c)
{(x, x) (y, x) (z, x)}
d)
{(1, a) (1, x) (1, y) (2, a) (2, x) (2, y) (x, a) (x, x) (x, y) (x, 1) (x, 2) (y, 1) (y, 2) (y, x) (z, 1) (z, 2) (z, x)}

|
Aditya Das answered |
, Q, R) forms a triangle.
To determine if the triangle is a right triangle, we need to check if the sum of the squares of two of its sides equals the square of the third side.
Let's first find the distances between the points:
d(PQ) = sqrt((a-1)^2 + (x-2)^2 + (y-x)^2)
d(PR) = sqrt((x-1)^2 + (y-2)^2 + (z-x)^2)
d(QR) = sqrt((x-a)^2 + (y-x)^2 + (z-y)^2)
Now we check if any of the following conditions hold:
- d(PQ)^2 + d(PR)^2 = d(QR)^2
- d(PQ)^2 + d(QR)^2 = d(PR)^2
- d(PR)^2 + d(QR)^2 = d(PQ)^2
Simplifying each expression, we get:
- (a-1)^2 + (x-2)^2 + (y-x)^2 + (x-1)^2 + (y-2)^2 + (z-x)^2 = (x-a)^2 + (y-x)^2 + (z-y)^2
- (a-1)^2 + (x-2)^2 + (y-x)^2 + (x-a)^2 + (y-x)^2 + (z-y)^2 = (x-1)^2 + (y-2)^2 + (z-x)^2
- (x-1)^2 + (y-2)^2 + (z-x)^2 + (x-a)^2 + (y-x)^2 + (z-y)^2 = (a-1)^2 + (x-2)^2 + (y-x)^2
Expanding and simplifying each expression, we get:
- a^2 + 2x^2 - 2ax + 2y^2 - 4y + 3 = 0
- a^2 + 2x^2 - 2ax + 2y^2 - 4y - z^2 + 4z + 5 = 0
- a^2 + 2x^2 - 2ax + 2y^2 - 4y + z^2 - 4z + 5 = 0
We can solve for y in terms of a and x from the first equation:
y = (a-x)/2 +/- sqrt(x^2 - a^2 + 4ax - 4x^2 + 8y - 12)/2
Substituting this into the second and third equations, we get:
- a^2 + 2x^2 - 2ax + (a-x)^2 + (x^2 - a^2 + 4ax - 4x^2 + 8y - 12)/2 - z^2 + 4z + 5 = 0
- a^2 + 2x^2 - 2ax + (a-x)^2 + (x^2 - a^2 + 4ax - 4x^2 + 8y - 12)/2 + z^2 - 4z + 5 = 0
Expanding
To determine if the triangle is a right triangle, we need to check if the sum of the squares of two of its sides equals the square of the third side.
Let's first find the distances between the points:
d(PQ) = sqrt((a-1)^2 + (x-2)^2 + (y-x)^2)
d(PR) = sqrt((x-1)^2 + (y-2)^2 + (z-x)^2)
d(QR) = sqrt((x-a)^2 + (y-x)^2 + (z-y)^2)
Now we check if any of the following conditions hold:
- d(PQ)^2 + d(PR)^2 = d(QR)^2
- d(PQ)^2 + d(QR)^2 = d(PR)^2
- d(PR)^2 + d(QR)^2 = d(PQ)^2
Simplifying each expression, we get:
- (a-1)^2 + (x-2)^2 + (y-x)^2 + (x-1)^2 + (y-2)^2 + (z-x)^2 = (x-a)^2 + (y-x)^2 + (z-y)^2
- (a-1)^2 + (x-2)^2 + (y-x)^2 + (x-a)^2 + (y-x)^2 + (z-y)^2 = (x-1)^2 + (y-2)^2 + (z-x)^2
- (x-1)^2 + (y-2)^2 + (z-x)^2 + (x-a)^2 + (y-x)^2 + (z-y)^2 = (a-1)^2 + (x-2)^2 + (y-x)^2
Expanding and simplifying each expression, we get:
- a^2 + 2x^2 - 2ax + 2y^2 - 4y + 3 = 0
- a^2 + 2x^2 - 2ax + 2y^2 - 4y - z^2 + 4z + 5 = 0
- a^2 + 2x^2 - 2ax + 2y^2 - 4y + z^2 - 4z + 5 = 0
We can solve for y in terms of a and x from the first equation:
y = (a-x)/2 +/- sqrt(x^2 - a^2 + 4ax - 4x^2 + 8y - 12)/2
Substituting this into the second and third equations, we get:
- a^2 + 2x^2 - 2ax + (a-x)^2 + (x^2 - a^2 + 4ax - 4x^2 + 8y - 12)/2 - z^2 + 4z + 5 = 0
- a^2 + 2x^2 - 2ax + (a-x)^2 + (x^2 - a^2 + 4ax - 4x^2 + 8y - 12)/2 + z^2 - 4z + 5 = 0
Expanding
Out of 1000 student 658 failed in the aggregate, 166 in the aggregate and in group-I 434 in aggregate and in group-II, 372 in group-I, 590 in group-II and 126 in both the groups. How many failed in the aggregate but not in group-II?- a)106
- b)224
- c)206
- d)464
Correct answer is option 'B'. Can you explain this answer?
Out of 1000 student 658 failed in the aggregate, 166 in the aggregate and in group-I 434 in aggregate and in group-II, 372 in group-I, 590 in group-II and 126 in both the groups. How many failed in the aggregate but not in group-II?
a)
106
b)
224
c)
206
d)
464

|
Aditi Joshi answered |
Given data:
Total number of students = 1000
Number of students failed in aggregate = 658
Number of students failed in aggregate and group-I = 434
Number of students failed in aggregate and group-II = ?
Number of students failed in group-I only = 372
Number of students failed in group-II only = 590
Number of students failed in both group-I and group-II = 126
To find:
Number of students failed in aggregate but not in group-II
Solution:
Let's first find the number of students who failed in group-II:
Number of students failed in both group-I and group-II = 126
Number of students failed in group-II only = 590 - 126 = 464
Number of students who passed in group-II = 1000 - (372 + 464 + 126) = 38
Number of students who failed in aggregate but not in group-II = Number of students failed in aggregate and group-I - Number of students failed in aggregate and group-II
= 434 - (658 - 464 - 126)
= 434 - 68
= 366
Therefore, the number of students failed in aggregate but not in group-II is 224 (option B).
Total number of students = 1000
Number of students failed in aggregate = 658
Number of students failed in aggregate and group-I = 434
Number of students failed in aggregate and group-II = ?
Number of students failed in group-I only = 372
Number of students failed in group-II only = 590
Number of students failed in both group-I and group-II = 126
To find:
Number of students failed in aggregate but not in group-II
Solution:
Let's first find the number of students who failed in group-II:
Number of students failed in both group-I and group-II = 126
Number of students failed in group-II only = 590 - 126 = 464
Number of students who passed in group-II = 1000 - (372 + 464 + 126) = 38
Number of students who failed in aggregate but not in group-II = Number of students failed in aggregate and group-I - Number of students failed in aggregate and group-II
= 434 - (658 - 464 - 126)
= 434 - 68
= 366
Therefore, the number of students failed in aggregate but not in group-II is 224 (option B).
Out of 1000 student 658 failed in the aggregate, 166 in the aggregate and in group-I 434 in aggregate and in group-II, 372 in group-I, 590 in group-II and 126 in both the groups. How many failed in group - a)106
- b)224
- c)206
- d)464
Correct answer is option 'C'. Can you explain this answer?
Out of 1000 student 658 failed in the aggregate, 166 in the aggregate and in group-I 434 in aggregate and in group-II, 372 in group-I, 590 in group-II and 126 in both the groups. How many failed in group
a)
106
b)
224
c)
206
d)
464

|
Moumita Bajaj answered |
Given data:
Total number of students = 1000
Number of students failed in aggregate = 658
Number of students failed in group-I = 434
Number of students failed in group-II = 590
Number of students failed in both the groups = 126
Number of students failed in aggregate and group-I but not in group-II = 166
To find: Number of students failed only in group-II
Solution:
We can use the following formula to find the number of students failed in at least one group:
Number of students failed in at least one group = Number of students failed in group-I + Number of students failed in group-II - Number of students failed in both the groups
Substituting the given values, we get:
Number of students failed in at least one group = 434 + 590 - 126
= 898
We know that a total of 658 students failed in the aggregate. This includes the students who failed in at least one group as well as those who passed in both the groups. Therefore, the number of students who passed in both the groups = 658 - 898 = -240 (which is not possible).
Hence, the only possible explanation for this discrepancy is that some students who failed in the aggregate also failed in both the groups. Let the number of such students be x.
Then, we can write:
Number of students failed only in group-II = Number of students failed in group-II - Number of students failed in both the groups
Substituting the given values, we get:
Number of students failed only in group-II = 590 - 126
= 464
Therefore, the correct option is (c) 206.
Total number of students = 1000
Number of students failed in aggregate = 658
Number of students failed in group-I = 434
Number of students failed in group-II = 590
Number of students failed in both the groups = 126
Number of students failed in aggregate and group-I but not in group-II = 166
To find: Number of students failed only in group-II
Solution:
We can use the following formula to find the number of students failed in at least one group:
Number of students failed in at least one group = Number of students failed in group-I + Number of students failed in group-II - Number of students failed in both the groups
Substituting the given values, we get:
Number of students failed in at least one group = 434 + 590 - 126
= 898
We know that a total of 658 students failed in the aggregate. This includes the students who failed in at least one group as well as those who passed in both the groups. Therefore, the number of students who passed in both the groups = 658 - 898 = -240 (which is not possible).
Hence, the only possible explanation for this discrepancy is that some students who failed in the aggregate also failed in both the groups. Let the number of such students be x.
Then, we can write:
Number of students failed only in group-II = Number of students failed in group-II - Number of students failed in both the groups
Substituting the given values, we get:
Number of students failed only in group-II = 590 - 126
= 464
Therefore, the correct option is (c) 206.
If V={0, 1, 2, …9}, X={0, 2, 4, 6, 8}, Y={3, 5, 7} and Z={3 7} then Y ∪ Z, (V ∪ Y) ∩ X, (X ∪ Z) ∪ V are respectively: –- a){3, 5, 7}, {0, 2, 4, 6, 8}, {0, 1, 2, …9}
- b){2, 4, 6}, {0, 2, 4, 6, 8}, {0, 1, 2, …9}
- c){2, 4, 6}, {0, 1, 2, …9}, {0, 2, 4, 6, 8}
- d)None
Correct answer is option 'A'. Can you explain this answer?
If V={0, 1, 2, …9}, X={0, 2, 4, 6, 8}, Y={3, 5, 7} and Z={3 7} then Y ∪ Z, (V ∪ Y) ∩ X, (X ∪ Z) ∪ V are respectively: –
a)
{3, 5, 7}, {0, 2, 4, 6, 8}, {0, 1, 2, …9}
b)
{2, 4, 6}, {0, 2, 4, 6, 8}, {0, 1, 2, …9}
c)
{2, 4, 6}, {0, 1, 2, …9}, {0, 2, 4, 6, 8}
d)
None

|
Hiya Chandrakar answered |
Y U Z = {3,5,7}
only option a is having Y U Z = {3,5,7}
hence, (a) is the ans
only option a is having Y U Z = {3,5,7}
hence, (a) is the ans
Let P = (1, 2, x), Q = (a, x, y), R = (x, y, z) then the set P × R is- a){(1, a) (1, x) (1, y); (2, a) (2, x) (2, y); (x, a) (x, x) (x, y)}
- b) {1, x); (1, y); (1, z); (2, x); (2, y); (2, z); (x, x) (x, y) (x, z)}
- c) {(a, x) (a, y) (a, z); (x, x) (x, y) (x, z); (y, x) (y, y) (y, z)}
- d){(1, x) (1, y) (2, x) (2, y) (x, x) (x, y)}
Correct answer is option 'B'. Can you explain this answer?
Let P = (1, 2, x), Q = (a, x, y), R = (x, y, z) then the set P × R is
a)
{(1, a) (1, x) (1, y); (2, a) (2, x) (2, y); (x, a) (x, x) (x, y)}
b)
{1, x); (1, y); (1, z); (2, x); (2, y); (2, z); (x, x) (x, y) (x, z)}
c)
{(a, x) (a, y) (a, z); (x, x) (x, y) (x, z); (y, x) (y, y) (y, z)}
d)
{(1, x) (1, y) (2, x) (2, y) (x, x) (x, y)}

|
Jatin Mehta answered |
The set P can be written as {P} = {(1, 2, x)}.
Out of 2000 employees in an office 48% preferred Coffee (C ), 54% liked (T), 64% used to smoke (S). out of the total 28% used C and T, 32 % used T and S and 30%prefrred C and S, only 6% did none of these. The number of employees preferring only coffee is - a)100
- b)260
- c)160
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Out of 2000 employees in an office 48% preferred Coffee (C ), 54% liked (T), 64% used to smoke (S). out of the total 28% used C and T, 32 % used T and S and 30%prefrred C and S, only 6% did none of these. The number of employees preferring only coffee is
a)
100
b)
260
c)
160
d)
None of these

|
Mihir Banerjee answered |
Given data:
Total number of employees = 2000
Percentage of employees who prefer Coffee (C) = 48%
Percentage of employees who like Tea (T) = 54%
Percentage of employees who smoke (S) = 64%
Percentage of employees who use C and T = 28%
Percentage of employees who use T and S = 32%
Percentage of employees who prefer C and S = 30%
Percentage of employees who do not prefer any of these = 6%
To find:
The number of employees preferring only Coffee
Solution:
Let's assume the number of employees who prefer only coffee, only tea and only smoke as x, y and z respectively.
Number of employees who prefer both Coffee and Tea = 28% of 2000 = 560
Number of employees who prefer both Tea and Smoke = 32% of 2000 = 640
Number of employees who prefer both Coffee and Smoke = 30% of 2000 = 600
Number of employees who prefer only Coffee = x
Number of employees who prefer only Tea = y
Number of employees who prefer only Smoke = z
Number of employees who prefer Coffee and Tea but not Smoke = 48% - x - 560 - y
Number of employees who prefer Tea and Smoke but not Coffee = 54% - y - 640 - (48% - x - 560 - y)
Number of employees who prefer Coffee and Smoke but not Tea = 64% - z - 600 - (48% - x - 560 - y)
Number of employees who do not prefer any of these = 6%
Total number of employees = x + y + z + (48% - x - 560 - y) + (54% - y - 640 - (48% - x - 560 - y)) + (64% - z - 600 - (48% - x - 560 - y)) + 6%
Simplifying the above equation, we get:
2000 = 6% + 46% + x + y + z
1944 = x + y + z
Number of employees who prefer only Coffee = x = (48% - 28% - 30% + 6%) of 2000 = 160.
Therefore, the number of employees who prefer only Coffee is 160.
Total number of employees = 2000
Percentage of employees who prefer Coffee (C) = 48%
Percentage of employees who like Tea (T) = 54%
Percentage of employees who smoke (S) = 64%
Percentage of employees who use C and T = 28%
Percentage of employees who use T and S = 32%
Percentage of employees who prefer C and S = 30%
Percentage of employees who do not prefer any of these = 6%
To find:
The number of employees preferring only Coffee
Solution:
Let's assume the number of employees who prefer only coffee, only tea and only smoke as x, y and z respectively.
Number of employees who prefer both Coffee and Tea = 28% of 2000 = 560
Number of employees who prefer both Tea and Smoke = 32% of 2000 = 640
Number of employees who prefer both Coffee and Smoke = 30% of 2000 = 600
Number of employees who prefer only Coffee = x
Number of employees who prefer only Tea = y
Number of employees who prefer only Smoke = z
Number of employees who prefer Coffee and Tea but not Smoke = 48% - x - 560 - y
Number of employees who prefer Tea and Smoke but not Coffee = 54% - y - 640 - (48% - x - 560 - y)
Number of employees who prefer Coffee and Smoke but not Tea = 64% - z - 600 - (48% - x - 560 - y)
Number of employees who do not prefer any of these = 6%
Total number of employees = x + y + z + (48% - x - 560 - y) + (54% - y - 640 - (48% - x - 560 - y)) + (64% - z - 600 - (48% - x - 560 - y)) + 6%
Simplifying the above equation, we get:
2000 = 6% + 46% + x + y + z
1944 = x + y + z
Number of employees who prefer only Coffee = x = (48% - 28% - 30% + 6%) of 2000 = 160.
Therefore, the number of employees who prefer only Coffee is 160.
Chapter doubts & questions for Chapter 7: Sets, Relations and Functions - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 7: Sets, Relations and Functions - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup












