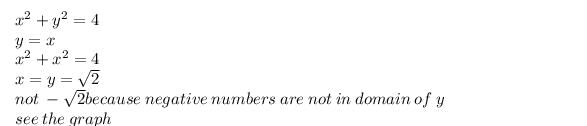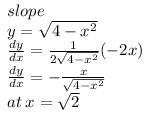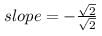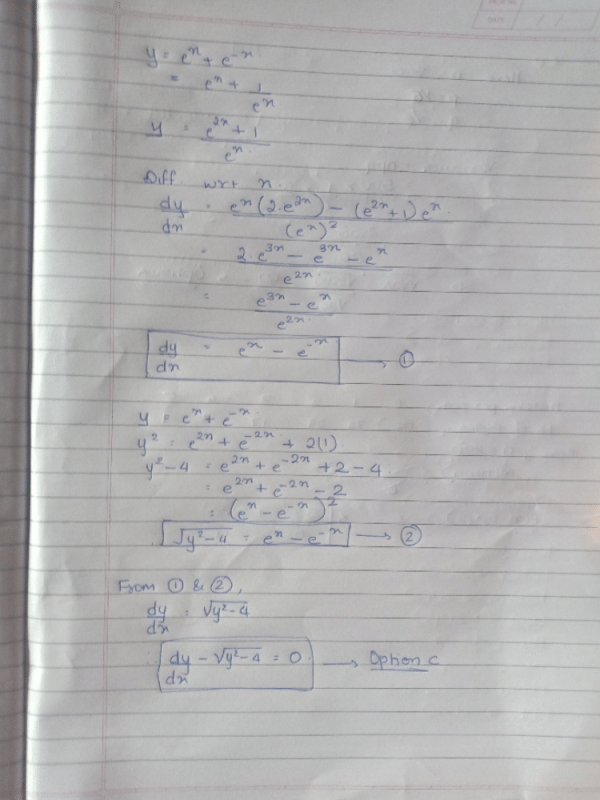All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 8: Basic Applications of Differential and Integral Calculus in Business and Economics for CA Foundation Exam
Choose the most appropriate option (a) (b) (c) or (d)The gradient of the curve y = 2x3 –3x2 – 12x +8 at x = 0 is- a)–12
- b)12
- c)0
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Choose the most appropriate option (a) (b) (c) or (d)
The gradient of the curve y = 2x3 –3x2 – 12x +8 at x = 0 is
a)
–12
b)
12
c)
0
d)
none of these

|
Pallabi Khanna answered |
Finding the Gradient of a Curve
- The gradient of a curve at a particular point is the slope of the tangent to the curve at that point.
- To find the gradient of a curve at a point, we need to differentiate the equation of the curve with respect to x, and then substitute the value of x at the point of interest.
Given Curve and Point
- The given curve is y = 2x^3 - 3x^2 - 12x + 8.
- The point of interest is x = 0.
Differentiating the Curve
- To find the gradient at x = 0, we need to differentiate the curve with respect to x.
- The derivative of y = 2x^3 - 3x^2 - 12x + 8 is:
dy/dx = 6x^2 - 6x - 12
Substituting x = 0
- Now we need to substitute x = 0 in the derivative to find the gradient at x = 0.
- When we substitute x = 0 in the derivative, we get:
dy/dx = 6(0)^2 - 6(0) - 12 = -12
- Therefore, the gradient of the curve y = 2x^3 - 3x^2 - 12x + 8 at x = 0 is -12.
Answer
- The correct option is not given in the question, but option (a) 12 is incorrect.
- The correct answer is option (d) none of these, as the gradient at x = 0 is -12 and not 12.
- The gradient of a curve at a particular point is the slope of the tangent to the curve at that point.
- To find the gradient of a curve at a point, we need to differentiate the equation of the curve with respect to x, and then substitute the value of x at the point of interest.
Given Curve and Point
- The given curve is y = 2x^3 - 3x^2 - 12x + 8.
- The point of interest is x = 0.
Differentiating the Curve
- To find the gradient at x = 0, we need to differentiate the curve with respect to x.
- The derivative of y = 2x^3 - 3x^2 - 12x + 8 is:
dy/dx = 6x^2 - 6x - 12
Substituting x = 0
- Now we need to substitute x = 0 in the derivative to find the gradient at x = 0.
- When we substitute x = 0 in the derivative, we get:
dy/dx = 6(0)^2 - 6(0) - 12 = -12
- Therefore, the gradient of the curve y = 2x^3 - 3x^2 - 12x + 8 at x = 0 is -12.
Answer
- The correct option is not given in the question, but option (a) 12 is incorrect.
- The correct answer is option (d) none of these, as the gradient at x = 0 is -12 and not 12.
If f(x) = 3x2, then F(x) = - a)6x
- b)x3
- c)x3 + C
- d)6x + C
Correct answer is option 'C'. Can you explain this answer?
If f(x) = 3x2, then F(x) =
a)
6x
b)
x3
c)
x3 + C
d)
6x + C

|
Subhankar Sen answered |
Explanation:
The given function is f(x) = 3x^2.
To find its indefinite integral or antiderivative, we need to reverse the process of differentiation by applying the power rule of integration.
Power Rule of Integration:
∫x^n dx = (x^(n+1))/(n+1) + C, where C is the constant of integration.
Using the power rule of integration, we get:
∫f(x) dx = ∫3x^2 dx = 3∫x^2 dx
= 3(x^(2+1))/(2+1) + C
= 3(x^3)/3 + C
= x^3 + C
Therefore, the antiderivative or indefinite integral of f(x) = 3x^2 is F(x) = x^3 + C, where C is the constant of integration.
Hence, the correct answer is option 'C' - x^3.
The given function is f(x) = 3x^2.
To find its indefinite integral or antiderivative, we need to reverse the process of differentiation by applying the power rule of integration.
Power Rule of Integration:
∫x^n dx = (x^(n+1))/(n+1) + C, where C is the constant of integration.
Using the power rule of integration, we get:
∫f(x) dx = ∫3x^2 dx = 3∫x^2 dx
= 3(x^(2+1))/(2+1) + C
= 3(x^3)/3 + C
= x^3 + C
Therefore, the antiderivative or indefinite integral of f(x) = 3x^2 is F(x) = x^3 + C, where C is the constant of integration.
Hence, the correct answer is option 'C' - x^3.
If xy = 1 then y2 + dy/dx is equal to- a)1
- b)0
- c)–1
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If xy = 1 then y2 + dy/dx is equal to
a)
1
b)
0
c)
–1
d)
none of these

|
Talent Skill Learning answered |
- xy = 1
- y = 1/x
- y2 = 1/x2
- dy/dx = -1/ x2
- now , y2 + dy/dx
- 1/x2 - -1/ x2 = 0
If f(x) = xk and f’(1) = 10 the value of k is- a)10
- b)–10
- c)1/10
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If f(x) = xk and f’(1) = 10 the value of k is
a)
10
b)
–10
c)
1/10
d)
none of these

|
Akshay Saini answered |
Solution:
Given, f(x) = xk and f(1) = 10
To find: Value of k
Approach:
We know that f(1) = 1k = 1, as any number to the power of 0 is always 1.
Therefore, f(1) = 1k = 10
So, k = log₁₀10
Using log₁₀10 = 1, we get k = 1.
Therefore, the value of k is 10.
Final Answer: Option A (10)
Given, f(x) = xk and f(1) = 10
To find: Value of k
Approach:
We know that f(1) = 1k = 1, as any number to the power of 0 is always 1.
Therefore, f(1) = 1k = 10
So, k = log₁₀10
Using log₁₀10 = 1, we get k = 1.
Therefore, the value of k is 10.
Final Answer: Option A (10)
The gradient of the curve y + px +qy = 0 at (1, 1) is 1/2. The values of p and q are- a)(–1, 1)
- b)(2, –1)
- c)(1, 2)
- d)none of these
Correct answer is 'A'. Can you explain this answer?
The gradient of the curve y + px +qy = 0 at (1, 1) is 1/2. The values of p and q are
a)
(–1, 1)
b)
(2, –1)
c)
(1, 2)
d)
none of these

|
Arya Roy answered |
+px+qy=0
y+qy=-px
(1+q)y=-px
y=-[p/(1+q)]x
This is a linear function, so has constant gradient at all points on the curve. Hence
-p/(1+q)=1/2
2p=-(1+q)
But there is an issue: you have stated that the curve's gradient is 1/2 at the point (1,1) but the curve does not cross through this point! Regardless of our choices for p and q satisfying the expressions above this paragraph, the equation of the curve will always simplify to y=0.5x, which crosses through the origin (0,0), as well as (1,0.5) and (2,1) - but not (-1,1).
For your curve to pass through (-1,1), we would need to add a constant term, like so:
y+px+qy=1/2
Given x = t + t–1 and y = t – t–1 the value of 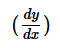 at t = 2 is
at t = 2 is- a)3/5
- b)–3/5
- c)5/3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Given x = t + t–1 and y = t – t–1 the value of 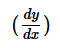 at t = 2 is
at t = 2 is
a)
3/5
b)
–3/5
c)
5/3
d)
none of these

|
Iyyappan Gounder answered |
It's not right answer In my point of view.
The slope of the tangent to the curve y = x2 –x at the point, where the line y = 2 cuts the curve in the Ist quadrant, is- a)2
- b)3
- c)–3
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The slope of the tangent to the curve y = x2 –x at the point, where the line y = 2 cuts the curve in the Ist quadrant, is
a)
2
b)
3
c)
–3
d)
none of these
|
|
Rajat Patel answered |
The point at which line y=2 cut the curve can be found out by
2=x^2-x
x^2-x-2=0
on solving we will get,
x=-1,2
since, the point is in first quadrant, So, x=2
Thus, point is (2,2).
Slope of the curve can be found out by differentiating the the equation of curve with respect to the x.
dy/dx= 2x-1
Now, put the value of x
dy/dx=2(2)-1=4-1=3
Therefore, the slope is 3.
The derivative of x2 log x is- a)1+2log x
- b)x(1 + 2 log x)
- c)2 log x
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The derivative of x2 log x is
a)
1+2log x
b)
x(1 + 2 log x)
c)
2 log x
d)
none of these

|
Jyoti Nair answered |
Derivative of x^2 log x:
We need to use the product rule and chain rule to find the derivative of x^2 log x.
Product rule:
(fg)' = f'g + fg'
Chain rule:
(g(f(x)))' = g'(f(x))f'(x)
Let's apply these rules to the given function:
f(x) = x^2 and g(x) = log x
f'(x) = 2x
g'(x) = 1/x
Using the product rule:
(fg)' = f'g + fg'
= (2x)(log x) + (x^2)(1/x)
= 2x log x + x
Now we simplify this expression:
2x log x + x
= x(2 log x + 1)
Therefore, the derivative of x^2 log x is x(2 log x + 1), which is option B.
We need to use the product rule and chain rule to find the derivative of x^2 log x.
Product rule:
(fg)' = f'g + fg'
Chain rule:
(g(f(x)))' = g'(f(x))f'(x)
Let's apply these rules to the given function:
f(x) = x^2 and g(x) = log x
f'(x) = 2x
g'(x) = 1/x
Using the product rule:
(fg)' = f'g + fg'
= (2x)(log x) + (x^2)(1/x)
= 2x log x + x
Now we simplify this expression:
2x log x + x
= x(2 log x + 1)
Therefore, the derivative of x^2 log x is x(2 log x + 1), which is option B.
If y = 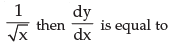
- a)
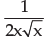
- b)
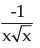
- c)
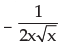
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If y = 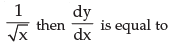
a)
b)
c)
d)
none of these

|
Jayesh Lahoti answered |
Take the derivative of 1/x which is - 1/x*2 and then multiply by the derivative of root x
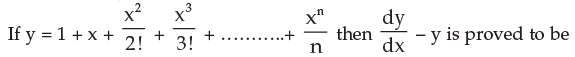
- a)1
- b)–1
- c)0
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
a)
1
b)
–1
c)
0
d)
none of these

|
Tanooj Vulla answered |
Dy/dx = 0+1+2x/2+ 3x²/6+4x³/24+...+(n-1)x^(n-2)/(n-1)(n-2)...3.2.1+nx^(n-1)/n(n-1)...3.2.1
dy/dx = 1+x+x²/2+x³/6+...+ x^(n-2)/(n-2)!+ x^(n-1)/(n-1)!
dy/dx = y
dy/dx-y =0
dy/dx = 1+x+x²/2+x³/6+...+ x^(n-2)/(n-2)!+ x^(n-1)/(n-1)!
dy/dx = y
dy/dx-y =0
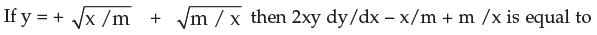
- a)0
- b)1
- c)–1
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
0
b)
1
c)
–1
d)
none of these

|
Bhumi Shah answered |
Ans=(a). 0 but how we will get this ? so plz explain this.
If f(x, y) = x3 + y3 – 3axy = 0, 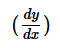 can be found out as
can be found out as- a)
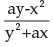
- b)
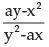
- c)
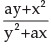
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If f(x, y) = x3 + y3 – 3axy = 0, 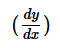 can be found out as
can be found out as
a)
b)
c)
d)
none of these

|
Talent Skill Learning answered |
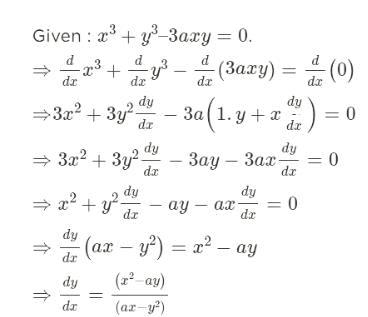
if we take minus common , dy/dx = (ay - x2 )/ (y2 - ax)
If f(x) = x2 – 6x+8 then f ’(5) – f ’(8) is equal to- a)f ’(2)
- b)3f ’(2)
- c)2f ’(2)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If f(x) = x2 – 6x+8 then f ’(5) – f ’(8) is equal to
a)
f ’(2)
b)
3f ’(2)
c)
2f ’(2)
d)
none of these

|
Niharika Joshi answered |
Given function: f(x) = x^2 - 6x + 8
To find: f(5) * f(8)
Solution:
1. Find f(5)
Substituting x = 5 in the given function, we get:
f(5) = (5)^2 - 6(5) + 8
f(5) = 25 - 30 + 8
f(5) = 3
2. Find f(8)
Substituting x = 8 in the given function, we get:
f(8) = (8)^2 - 6(8) + 8
f(8) = 64 - 48 + 8
f(8) = 24
3. Find f(5) * f(8)
f(5) * f(8) = 3 * 24
f(5) * f(8) = 72
4. Check the options
a) f(2) = (2)^2 - 6(2) + 8 = -4
b) 3f(2) = 3[(2)^2 - 6(2) + 8] = 3(-4) = -12
c) 2f(2) = 2[(2)^2 - 6(2) + 8] = 2(-4) = -8
d) None of these options give the value of f(5) * f(8) = 72
Hence, the correct option is (B) 3f(2).
To find: f(5) * f(8)
Solution:
1. Find f(5)
Substituting x = 5 in the given function, we get:
f(5) = (5)^2 - 6(5) + 8
f(5) = 25 - 30 + 8
f(5) = 3
2. Find f(8)
Substituting x = 8 in the given function, we get:
f(8) = (8)^2 - 6(8) + 8
f(8) = 64 - 48 + 8
f(8) = 24
3. Find f(5) * f(8)
f(5) * f(8) = 3 * 24
f(5) * f(8) = 72
4. Check the options
a) f(2) = (2)^2 - 6(2) + 8 = -4
b) 3f(2) = 3[(2)^2 - 6(2) + 8] = 3(-4) = -12
c) 2f(2) = 2[(2)^2 - 6(2) + 8] = 2(-4) = -8
d) None of these options give the value of f(5) * f(8) = 72
Hence, the correct option is (B) 3f(2).
Integration of 3 – 2x – x4 will become- a)– x2 – x5 / 5
- b)3x – x2 – x5 / 5
- c)3x – x2 x5 / 5 +k
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Integration of 3 – 2x – x4 will become
a)
– x2 – x5 / 5
b)
3x – x2 – x5 / 5
c)
3x – x2 x5 / 5 +k
d)
none of these

|
Siddharth Sen answered |
Solution:
The given expression is 3 * 2x * x^4
We can simplify this expression by multiplying the coefficients and adding the exponents of the variables:
3 * 2x * x^4 = 6x^5
Therefore, the integral of 6x^5 is:
∫6x^5 dx = x^6 + C
where C is the constant of integration.
To check if the answer is correct, we can differentiate the result using the power rule of differentiation:
d/dx (x^6 + C) = 6x^5
which is the same as the original expression.
Therefore, the correct answer is option B:
3x + x^2 + x^5/5 + C
The given expression is 3 * 2x * x^4
We can simplify this expression by multiplying the coefficients and adding the exponents of the variables:
3 * 2x * x^4 = 6x^5
Therefore, the integral of 6x^5 is:
∫6x^5 dx = x^6 + C
where C is the constant of integration.
To check if the answer is correct, we can differentiate the result using the power rule of differentiation:
d/dx (x^6 + C) = 6x^5
which is the same as the original expression.
Therefore, the correct answer is option B:
3x + x^2 + x^5/5 + C
If y = x (x –1) (x – 2) then 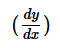 is
is- a)3x2 – 6x +2
- b)6x + 2
- c)3x2 + 2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If y = x (x –1) (x – 2) then 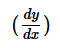 is
is
a)
3x2 – 6x +2
b)
6x + 2
c)
3x2 + 2
d)
none of these

|
Talent Skill Learning answered |
- firstly multiply all three equations
- we get , y = x (x2 - 3x + 2)
- y = x3 - 3x2 + 2x
- dy/dx = 3x2 - 6x + 2
∫ (logx)2 dx and the result is- a)x (logx)2 – 2 x logx + 2x
- b)x (logx)2 – 2x
- c)2x logx – 2x
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
∫ (logx)2 dx and the result is
a)
x (logx)2 – 2 x logx + 2x
b)
x (logx)2 – 2x
c)
2x logx – 2x
d)
none of these

|
Divya Dasgupta answered |
Integration by Parts:
Integration by parts is a technique used to find the integral of a product of two functions. The formula for integration by parts is given by:
∫u dv = uv - ∫v du
Given Integral:
∫(logx)² dx
Let's choose:
u = logx
dv = logx dx
Calculate the differentials:
du = (1/x) dx
v = ∫logx dx = x logx - x
Apply Integration by Parts:
∫(logx)² dx = logx * (x logx - x) - ∫(x logx - x) * (1/x) dx
∫(logx)² dx = x(logx)² - x² - ∫logx dx
∫(logx)² dx = x(logx)² - x² - x logx + x + C
Simplify the Result:
The final result after simplifying the expression is:
x(logx)² - x² - x logx + x + C
Therefore, the correct answer is option D: none of these.
Integration by parts is a technique used to find the integral of a product of two functions. The formula for integration by parts is given by:
∫u dv = uv - ∫v du
Given Integral:
∫(logx)² dx
Let's choose:
u = logx
dv = logx dx
Calculate the differentials:
du = (1/x) dx
v = ∫logx dx = x logx - x
Apply Integration by Parts:
∫(logx)² dx = logx * (x logx - x) - ∫(x logx - x) * (1/x) dx
∫(logx)² dx = x(logx)² - x² - ∫logx dx
∫(logx)² dx = x(logx)² - x² - x logx + x + C
Simplify the Result:
The final result after simplifying the expression is:
x(logx)² - x² - x logx + x + C
Therefore, the correct answer is option D: none of these.
The integral of px3 + qx2 + rk + w/x is equal to- a)px2 + qx + r + k
- b)px3/3 + qx2/2 + rx
- c)3px + 2q – w/x2
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The integral of px3 + qx2 + rk + w/x is equal to
a)
px2 + qx + r + k
b)
px3/3 + qx2/2 + rx
c)
3px + 2q – w/x2
d)
none of these

|
Gaurav Chatterjee answered |
**Explanation:**
In order to find the integral of the given expression, we need to apply the power rule of integration, which states that the integral of x^n with respect to x is equal to (x^(n+1))/(n+1), where n is any real number except -1.
Let's break down the given expression and apply the power rule to each term separately.
1. Integral of px^3 with respect to x:
Using the power rule, we get (px^(3+1))/(3+1) = (px^4)/4.
2. Integral of qx^2 with respect to x:
Using the power rule, we get (qx^(2+1))/(2+1) = (qx^3)/3.
3. Integral of rk with respect to x:
Since rk is a constant, its integral with respect to x is rkx.
4. Integral of w/x with respect to x:
This term can be rewritten as w * (1/x), and since w is also a constant, we can pull it out of the integral:
w * integral of 1/x with respect to x.
The integral of 1/x with respect to x is ln|x|, so the integral becomes w * ln|x|.
Now, let's add up all the integrals we found:
(px^4)/4 + (qx^3)/3 + rkx + w * ln|x|
The given options do not match this result, so none of the options is correct. Therefore, the correct answer is option 'D' (none of these).
It's important to note that in order to find the integral, we need to know the limits of integration or specify that it is an indefinite integral. Without the limits or specifying it as indefinite, we cannot provide a specific numerical result for the integral.
In order to find the integral of the given expression, we need to apply the power rule of integration, which states that the integral of x^n with respect to x is equal to (x^(n+1))/(n+1), where n is any real number except -1.
Let's break down the given expression and apply the power rule to each term separately.
1. Integral of px^3 with respect to x:
Using the power rule, we get (px^(3+1))/(3+1) = (px^4)/4.
2. Integral of qx^2 with respect to x:
Using the power rule, we get (qx^(2+1))/(2+1) = (qx^3)/3.
3. Integral of rk with respect to x:
Since rk is a constant, its integral with respect to x is rkx.
4. Integral of w/x with respect to x:
This term can be rewritten as w * (1/x), and since w is also a constant, we can pull it out of the integral:
w * integral of 1/x with respect to x.
The integral of 1/x with respect to x is ln|x|, so the integral becomes w * ln|x|.
Now, let's add up all the integrals we found:
(px^4)/4 + (qx^3)/3 + rkx + w * ln|x|
The given options do not match this result, so none of the options is correct. Therefore, the correct answer is option 'D' (none of these).
It's important to note that in order to find the integral, we need to know the limits of integration or specify that it is an indefinite integral. Without the limits or specifying it as indefinite, we cannot provide a specific numerical result for the integral.
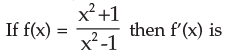
- a)–4x / (x2 – 1)2
- b)4x / (x2 – 1)2
- c)x / (x2 – 1)2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
–4x / (x2 – 1)2
b)
4x / (x2 – 1)2
c)
x / (x2 – 1)2
d)
none of these

|
Talent Skill Learning answered |
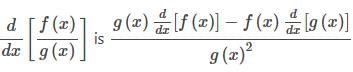
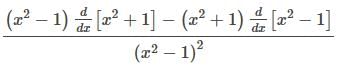
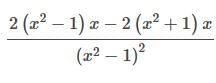
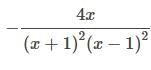
- Hence, option A is correct.
If x3 –2x2 y2 + 5x +y –5 =0 then 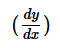 at x = 1, y = 1 is equal to
at x = 1, y = 1 is equal to- a)4/3
- b)– 4/3
- c)3/4
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If x3 –2x2 y2 + 5x +y –5 =0 then 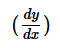 at x = 1, y = 1 is equal to
at x = 1, y = 1 is equal to
a)
4/3
b)
– 4/3
c)
3/4
d)
none of these

|
Talent Skill Learning answered |
On differentiating the above statement , we get
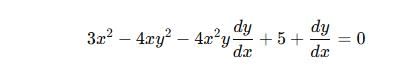
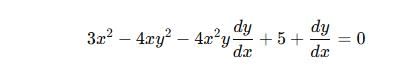
Now we will group the statements with dy/dx and keep the rest aside
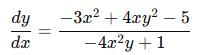
Now putting x = 1 and y= 1, the value of dy/dx becomes
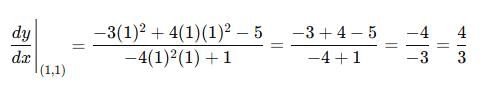
∫ logx dx is equal to- a)x logx
- b)x logx – x2 + k
- c)x logx + k
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
∫ logx dx is equal to
a)
x logx
b)
x logx – x2 + k
c)
x logx + k
d)
none of these

|
Meera Joshi answered |
**Explanation:**
The integral of log(x) with respect to x, denoted as ∫log(x)dx, cannot be expressed in terms of elementary functions (such as polynomials, exponential functions, trigonometric functions, etc.). Therefore, the correct answer is option D, which states "none of these".
To understand why the integral of log(x) cannot be expressed in terms of elementary functions, we need to consider the properties of the logarithm function and the concept of integration.
**Properties of the Logarithm Function:**
1. log(a * b) = log(a) + log(b)
2. log(a / b) = log(a) - log(b)
3. log(a^n) = n * log(a)
**Concept of Integration:**
Integration is the process of finding the antiderivative (or primitive) of a function. The antiderivative of a function F(x) is another function f(x) whose derivative is equal to F(x). In other words, if F'(x) = f(x), then ∫f(x)dx = F(x) + C, where C is the constant of integration.
**Integration of log(x):**
The integral of log(x) with respect to x is denoted as ∫log(x)dx. Since log(x) is not an elementary function, we cannot find its antiderivative using the standard rules of integration (such as power rule, product rule, etc.).
However, we can express the integral of log(x) using a special function called the logarithmic integral (Li(x)). The logarithmic integral is defined as:
Li(x) = ∫[1 / log(t)]dt, where the integral is taken from 2 to x.
Therefore, the integral of log(x) can be expressed as:
∫log(x)dx = Li(x) + C
where C is the constant of integration.
In conclusion, the integral of log(x) cannot be expressed in terms of elementary functions. The correct answer to the given question is option D, "none of these".
The integral of log(x) with respect to x, denoted as ∫log(x)dx, cannot be expressed in terms of elementary functions (such as polynomials, exponential functions, trigonometric functions, etc.). Therefore, the correct answer is option D, which states "none of these".
To understand why the integral of log(x) cannot be expressed in terms of elementary functions, we need to consider the properties of the logarithm function and the concept of integration.
**Properties of the Logarithm Function:**
1. log(a * b) = log(a) + log(b)
2. log(a / b) = log(a) - log(b)
3. log(a^n) = n * log(a)
**Concept of Integration:**
Integration is the process of finding the antiderivative (or primitive) of a function. The antiderivative of a function F(x) is another function f(x) whose derivative is equal to F(x). In other words, if F'(x) = f(x), then ∫f(x)dx = F(x) + C, where C is the constant of integration.
**Integration of log(x):**
The integral of log(x) with respect to x is denoted as ∫log(x)dx. Since log(x) is not an elementary function, we cannot find its antiderivative using the standard rules of integration (such as power rule, product rule, etc.).
However, we can express the integral of log(x) using a special function called the logarithmic integral (Li(x)). The logarithmic integral is defined as:
Li(x) = ∫[1 / log(t)]dt, where the integral is taken from 2 to x.
Therefore, the integral of log(x) can be expressed as:
∫log(x)dx = Li(x) + C
where C is the constant of integration.
In conclusion, the integral of log(x) cannot be expressed in terms of elementary functions. The correct answer to the given question is option D, "none of these".
The differential coefficients of (x2 +1)/x is- a)1 + 1/x2
- b)1 – 1/x2
- c)1/x2
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The differential coefficients of (x2 +1)/x is
a)
1 + 1/x2
b)
1 – 1/x2
c)
1/x2
d)
none of these

|
Mehul Ghoshal answered |
Solution:
We have to find the differential coefficients of (x2 + 1)/x.
To find the differential coefficient, we have to differentiate the given function with respect to x.
Let y = (x2 + 1)/x
Taking the derivative of both sides with respect to x, we get
dy/dx = d/dx [(x2 + 1)/x]
Using the quotient rule of differentiation, we get
dy/dx = [(x2 + 1)d/dx(x) - x d/dx(x2 + 1)]/x2
Simplifying the above expression, we get
dy/dx = [(x2 + 1) - x(2x)]/x2
dy/dx = (1 - x2)/x2
Therefore, the differential coefficient of (x2 + 1)/x is (1 - x2)/x2.
Answer: Option B (1 - x2)/x2.
We have to find the differential coefficients of (x2 + 1)/x.
To find the differential coefficient, we have to differentiate the given function with respect to x.
Let y = (x2 + 1)/x
Taking the derivative of both sides with respect to x, we get
dy/dx = d/dx [(x2 + 1)/x]
Using the quotient rule of differentiation, we get
dy/dx = [(x2 + 1)d/dx(x) - x d/dx(x2 + 1)]/x2
Simplifying the above expression, we get
dy/dx = [(x2 + 1) - x(2x)]/x2
dy/dx = (1 - x2)/x2
Therefore, the differential coefficient of (x2 + 1)/x is (1 - x2)/x2.
Answer: Option B (1 - x2)/x2.
Given f(x) = 4x3 + 3x2 – 2x + 5, ∫ f(x) dx is- a)x4 + x3 – x2 + 5x
- b)x4 + x3 – x2 + 5x + k
- c)12x2 + 6x – 2x2
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Given f(x) = 4x3 + 3x2 – 2x + 5, ∫ f(x) dx is
a)
x4 + x3 – x2 + 5x
b)
x4 + x3 – x2 + 5x + k
c)
12x2 + 6x – 2x2
d)
none of these

|
Rajeev Chaudhary answered |
Solution:
The given function is f(x) = 4x^3 - 3x^2 + 2x + 5
To find f(x) dx, we need to integrate the function with respect to x.
∫f(x) dx = ∫(4x^3 - 3x^2 + 2x + 5) dx
= (4/4)x^4 - (3/3)x^3 + (2/2)x^2 + 5x + C
= x^4 - x^3 + x^2 + 5x + C
where C is the constant of integration.
Therefore, the correct option is (B) x^4 - x^3 + x^2 + 5x + C.
The given function is f(x) = 4x^3 - 3x^2 + 2x + 5
To find f(x) dx, we need to integrate the function with respect to x.
∫f(x) dx = ∫(4x^3 - 3x^2 + 2x + 5) dx
= (4/4)x^4 - (3/3)x^3 + (2/2)x^2 + 5x + C
= x^4 - x^3 + x^2 + 5x + C
where C is the constant of integration.
Therefore, the correct option is (B) x^4 - x^3 + x^2 + 5x + C.
Use method of substitution to integrate the function f(x) = (4x + 5)6 and the answer is- a)1/28 (4x + 5)7 + k
- b)(4x + 5)7/7 + k
- c)(4x + 5)7/7
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Use method of substitution to integrate the function f(x) = (4x + 5)6 and the answer is
a)
1/28 (4x + 5)7 + k
b)
(4x + 5)7/7 + k
c)
(4x + 5)7/7
d)
none of these

|
Tanvi Pillai answered |
To integrate the given function f(x) = (4x - 5)^6, we can use the method of substitution.
Let u = 4x - 5, then du/dx = 4 and dx = du/4.
Substituting these values into the integral, we get:
∫(4x - 5)^6 dx = ∫u^6 (du/4)
= (1/4) ∫u^6 du
= (1/4) [(1/7)u^7 + C]
= (1/28)(4x - 5)^7 + C
Therefore, the correct answer is option A, (4x - 5)^7/28.
Let u = 4x - 5, then du/dx = 4 and dx = du/4.
Substituting these values into the integral, we get:
∫(4x - 5)^6 dx = ∫u^6 (du/4)
= (1/4) ∫u^6 du
= (1/4) [(1/7)u^7 + C]
= (1/28)(4x - 5)^7 + C
Therefore, the correct answer is option A, (4x - 5)^7/28.
The derivative of (x2–1)/x is- a)1 + 1/x2
- b)1 – 1/x2
- c)1/x2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The derivative of (x2–1)/x is
a)
1 + 1/x2
b)
1 – 1/x2
c)
1/x2
d)
none of these
|
|
Asmit Sharma answered |
Denominator wale x ko distribute kro fir 1st term wala ek x cancel hojayega fir derivative lelo
Given x = 2t + 5, y = t2 – 2; 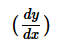 is calculated as
is calculated as - a)t
- b)–1/t
- c)1/t
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Given x = 2t + 5, y = t2 – 2; 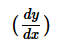 is calculated as
is calculated as
a)
t
b)
–1/t
c)
1/t
d)
none of these

|
Talent Skill Learning answered |
x = 2t + 5
dx/dt = 2
dy/dx = dy/dt / dx/dt
= 2t / 2 = t
dx/dt = 2
dy/dx = dy/dt / dx/dt
= 2t / 2 = t
f(x) = x2/ex then f ’(1) is equal to _____________.- a)– 1/e
- b)1/e
- c)e
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
f(x) = x2/ex then f ’(1) is equal to _____________.
a)
– 1/e
b)
1/e
c)
e
d)
none of these

|
Sanjana Khanna answered |
F(x) = x^2/ex
To find f'(x), we will use the quotient rule.
Let u = x^2 and v = ex.
Then, u' = 2x and v' = ex.
Using the quotient rule, we have:
f'(x) = (u'v - uv') / v^2
= (2x * ex - x^2 * ex) / (ex)^2
= (2xex - x^2ex) / ex^2
= ex(2x - x^2) / ex^2
= (2x - x^2) / ex
Therefore, f'(x) = (2x - x^2) / ex.
To find f'(x), we will use the quotient rule.
Let u = x^2 and v = ex.
Then, u' = 2x and v' = ex.
Using the quotient rule, we have:
f'(x) = (u'v - uv') / v^2
= (2x * ex - x^2 * ex) / (ex)^2
= (2xex - x^2ex) / ex^2
= ex(2x - x^2) / ex^2
= (2x - x^2) / ex
Therefore, f'(x) = (2x - x^2) / ex.
If xy.yx = M, M is constant then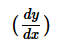 is equal to
is equal to- a)-y/x
- b)
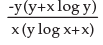
- c)
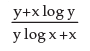
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If xy.yx = M, M is constant then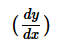 is equal to
is equal to
a)
-y/x
b)
c)
d)
none of these
|
|
Anjali Kumari answered |
Putting log both side
log(x^y into y to power x )is equal to log m
logx^y+log y^x=log m
dy÷dx (y log x+x log y=log m)
and by differentiating these we get
-y(y+x logy)÷x(x+y log x).
log(x^y into y to power x )is equal to log m
logx^y+log y^x=log m
dy÷dx (y log x+x log y=log m)
and by differentiating these we get
-y(y+x logy)÷x(x+y log x).
Can you explain the answer of this question below:For the curve x2 + y2 + 2gx + 2hy = 0, the value of 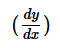 at (0, 0) is
at (0, 0) is
- A:
-g/h
- B:
g/h
- C:
h/g
- D:
none of these
The answer is d.
For the curve x2 + y2 + 2gx + 2hy = 0, the value of at (0, 0) is
-g/h
g/h
h/g
none of these

|
Raghavendra Sharma answered |
x^2+y^2+2gx+2hy=0
2x + 2yy' + 2g + 2hy' = 0
y'(y+h) = -(x+g)
y' = -(x+g)/(y+h)
at (0,0) y' = -g/h
so option D is correct
If y = 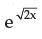 then
then 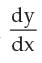 is equal to _____.
is equal to _____.
- a)
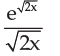
- b)

- c)

- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If y = 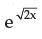 then
then 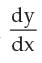 is equal to _____.
is equal to _____.
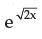 then
then 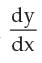 is equal to _____.
is equal to _____.a)
b)
c)

d)
none of these

|
Shubham Kulshrestha Kuls answered |
Yes the correct ans will be a as the derivative of e^√2x but we will take derivative of√2x also which will be √2x^-1/2 hence the ans is e^√2x/ √2x
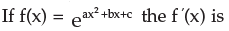
- a)
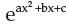
- b)
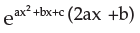
- c)2ax +b
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
a)
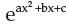
b)
c)
2ax +b
d)
none of these

|
Talent Skill Learning answered |

df/dx = 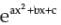 * d/dx(ax2 + bx + c)
* d/dx(ax2 + bx + c)
=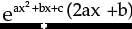
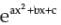 * d/dx(ax2 + bx + c)
* d/dx(ax2 + bx + c)=
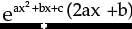
Chapter doubts & questions for Chapter 8: Basic Applications of Differential and Integral Calculus in Business and Economics - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 8: Basic Applications of Differential and Integral Calculus in Business and Economics - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily








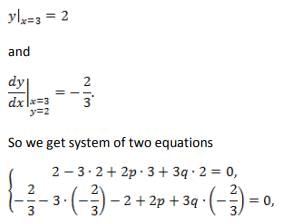
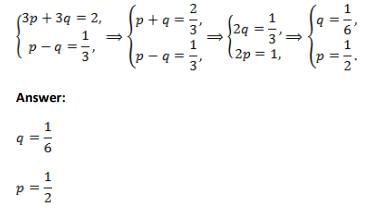
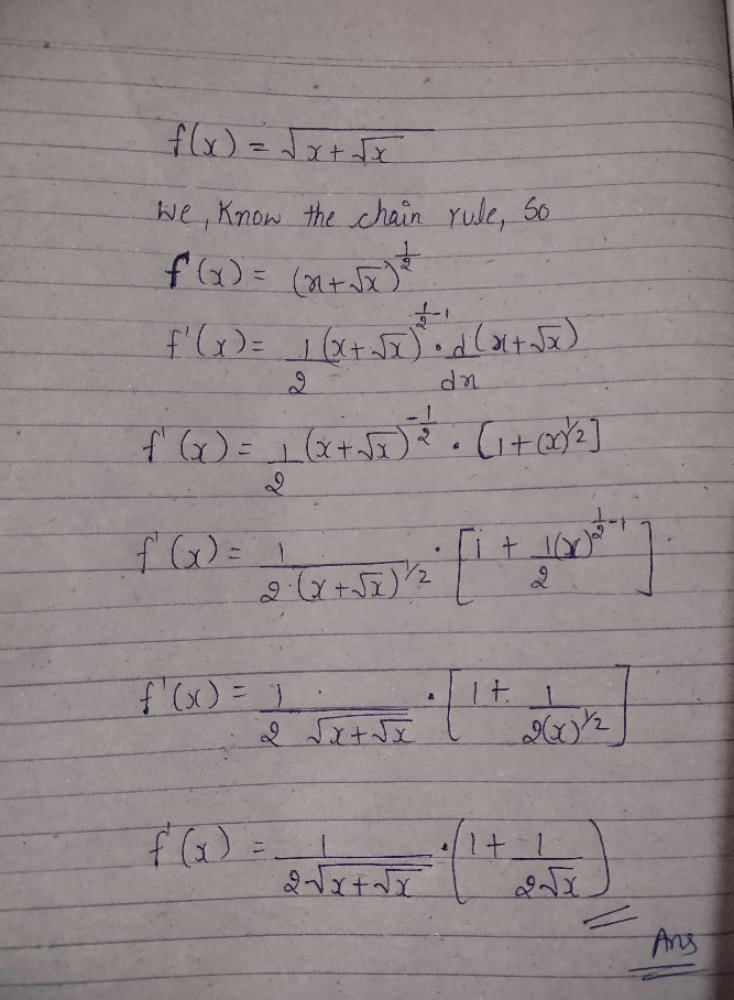

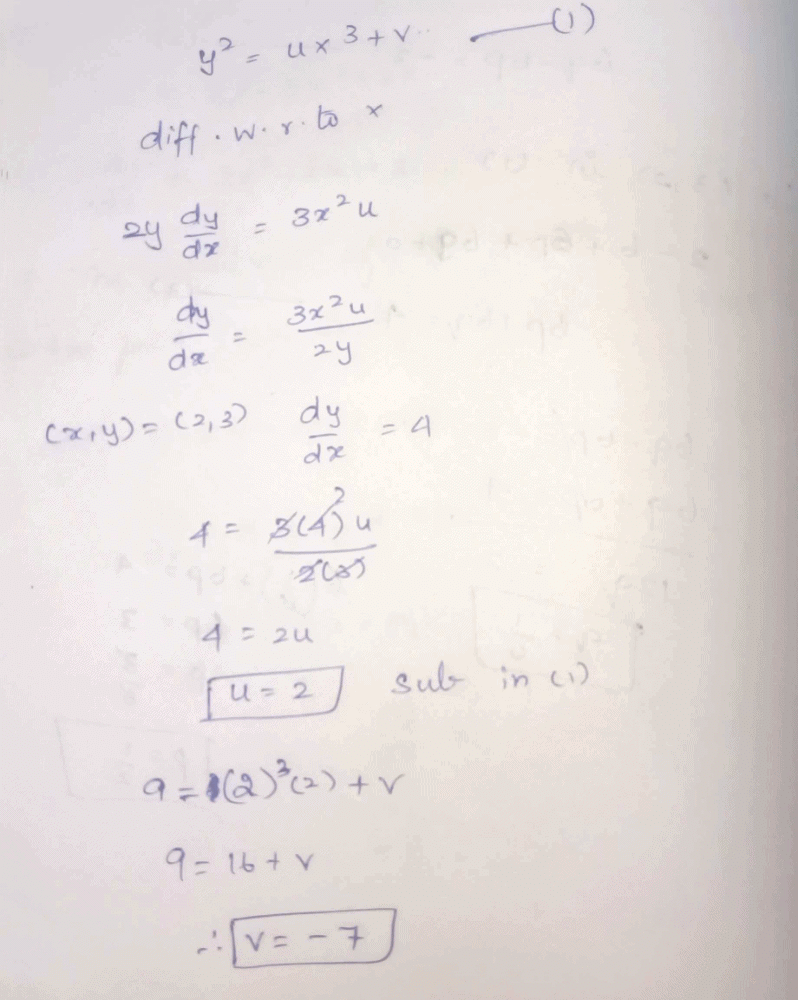
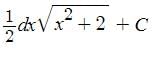



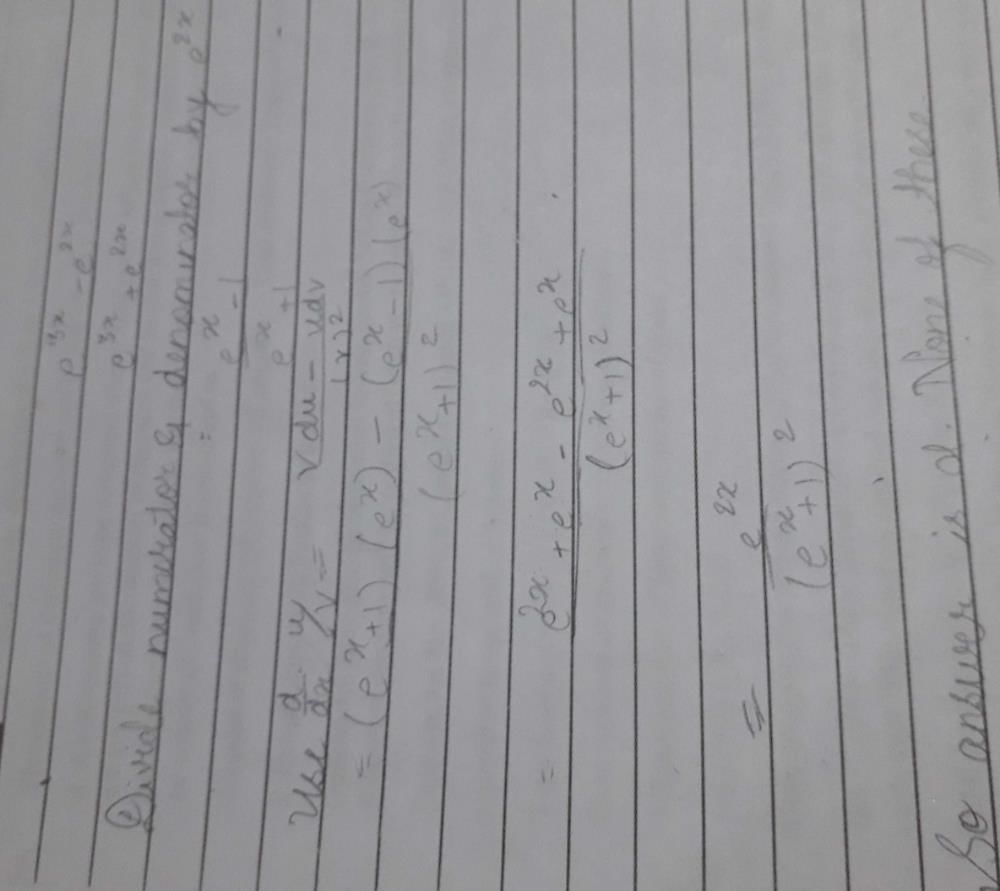




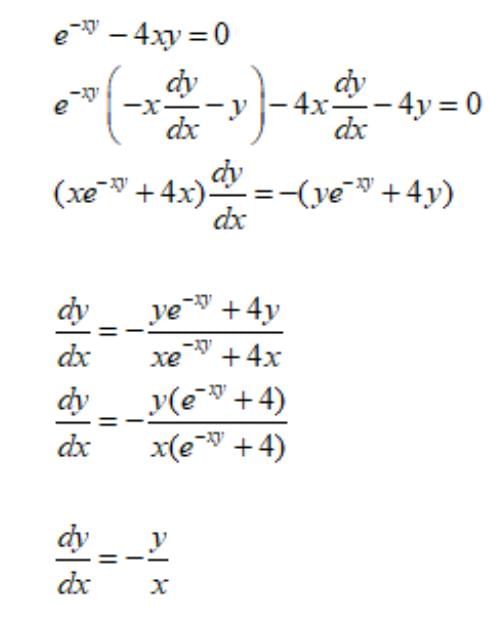



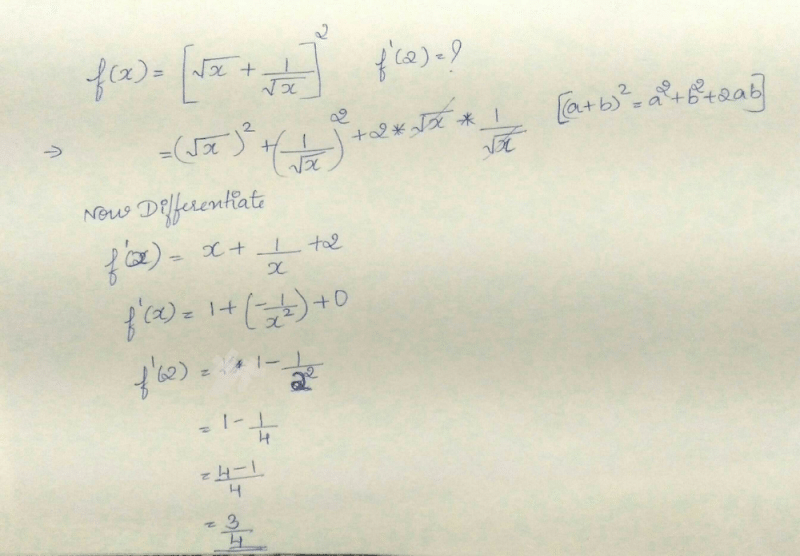
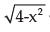 at the point, where the ordinate and the abscissa are equal, is
at the point, where the ordinate and the abscissa are equal, is