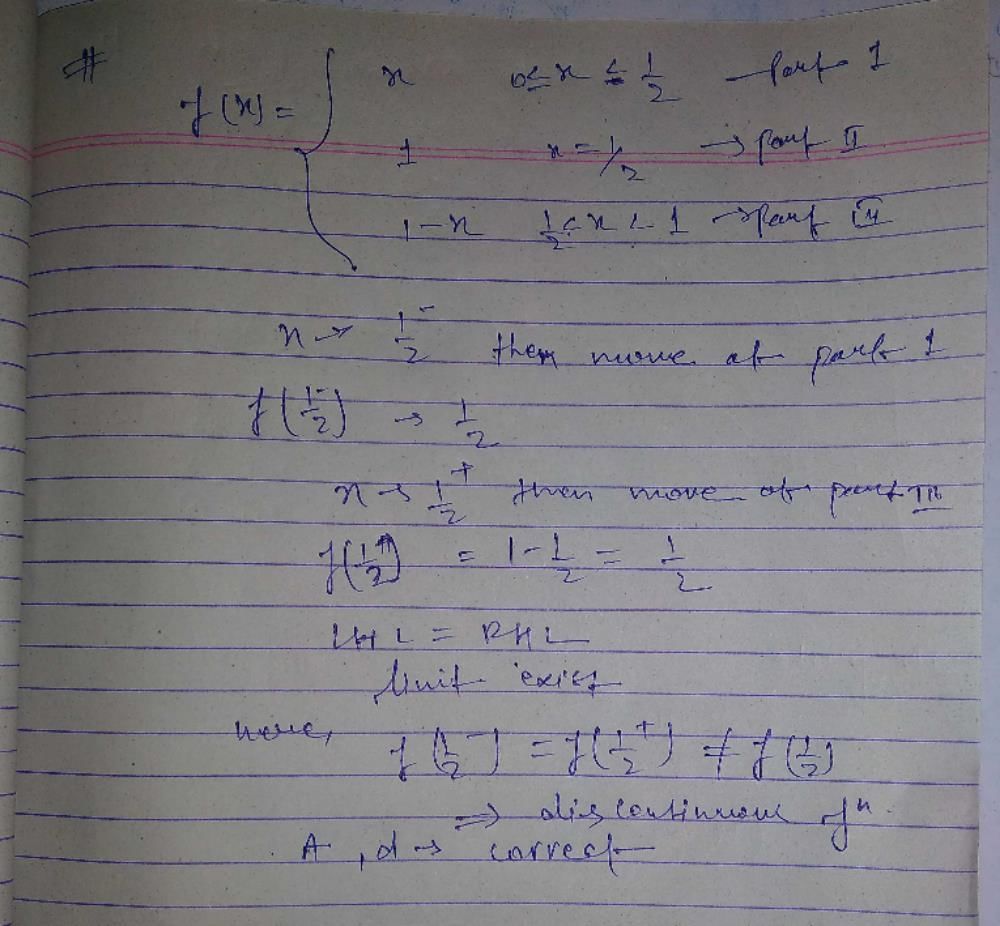All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Limits and Continuity - Intuitive Approach (Old Scheme) for CA Foundation Exam
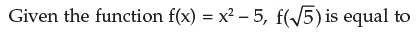
- a)0
- b)5
- c)10
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
0
b)
5
c)
10
d)
none of these

|
Samira Khanna answered |
(√5)square - 5= 5-5=0
f (x) is a continuous function and takes only rational values. If f (0) = 3, then f (2) equals- a)5
- b)0
- c)1
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
f (x) is a continuous function and takes only rational values. If f (0) = 3, then f (2) equals
a)
5
b)
0
c)
1
d)
None of these

|
Shanaya Dasgupta answered |
Solution:
Given, f(x) is a continuous function and takes only rational values. Also, f(0) = 3.
To find: f(2)
Assume that f(x) is a polynomial function of degree n.
Then, f(x) = anxn + an-1xn-1 + … + a1x + a0, where a0, a1, …, an are rational constants.
Since f(x) takes only rational values, all coefficients are rational.
Also, f(0) = a0 = 3.
Now, consider the interval [0,2].
By the intermediate value theorem, f(x) takes all values between f(0) = 3 and f(2) in this interval.
Since f(x) takes only rational values, f(2) must also be rational.
However, there is no polynomial function with rational coefficients that passes through the points (0,3) and (2, irrational).
Therefore, such a function f(x) cannot exist.
Hence, the correct answer is option D, None of these.
Given, f(x) is a continuous function and takes only rational values. Also, f(0) = 3.
To find: f(2)
Assume that f(x) is a polynomial function of degree n.
Then, f(x) = anxn + an-1xn-1 + … + a1x + a0, where a0, a1, …, an are rational constants.
Since f(x) takes only rational values, all coefficients are rational.
Also, f(0) = a0 = 3.
Now, consider the interval [0,2].
By the intermediate value theorem, f(x) takes all values between f(0) = 3 and f(2) in this interval.
Since f(x) takes only rational values, f(2) must also be rational.
However, there is no polynomial function with rational coefficients that passes through the points (0,3) and (2, irrational).
Therefore, such a function f(x) cannot exist.
Hence, the correct answer is option D, None of these.
If f(x) = x2 – x then f( h+1) is equal to- a)f(h)
- b)f(–h)
- c)f(–h + 1)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If f(x) = x2 – x then f( h+1) is equal to
a)
f(h)
b)
f(–h)
c)
f(–h + 1)
d)
none of these

|
Chirag Agrawal answered |
F(h+1) = (h+1)^2 -(h+1)
= h^2 + 2h +1 - h - 1
= h^2 + h
= (-h)^2 - (-h)
= f(-h)
= h^2 + 2h +1 - h - 1
= h^2 + h
= (-h)^2 - (-h)
= f(-h)
If f(x) = 2x2 – 5x + 4 then 2f(x) = f(2x) for- a)x=1
- b)x = – 1
- c)x = ± 1
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If f(x) = 2x2 – 5x + 4 then 2f(x) = f(2x) for
a)
x=1
b)
x = – 1
c)
x = ± 1
d)
none of these

|
Gowri Chakraborty answered |
f(x) = 2x^2–5x+4
2(f(x) = 2(2x^2–5x+4 )= 4x^2–10x+8
f(2x) = 2(2x)^2–5(2x)+4 = 8x^2–10x+4
4x^2–10x+8 = 8x^2–10x+4
8x^2–10x+4 -4x^2+10x-8=0
4x^2–4 = 0
take 4 common so 4(x^2–1=0)
4 = 0 , (x^2–1)=0
4 = 0 is negilisable
(x^2–1 = 0)
x ^2 = 1
Answer (x = +1 , -1 )
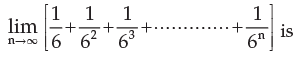
- a)1/5
- b)1/6
- c)– 1/5
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
1/5
b)
1/6
c)
– 1/5
d)
none of these
|
|
Ca Akshita answered |
A/1-r = (1/6)/1-(1/6) = 1/6÷5/6 = 1/5

- a)p
- b)1/p
- c)0
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
a)
p
b)
1/p
c)
0
d)
none of these

|
Priyal Gupta answered |
Limits is not in our course
- a)p/3
- b)p
- c)1/3
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
p/3
b)
p
c)
1/3
d)
none of these

|
Rahul Gill answered |
=(1+px)(3x)÷[(e^3x-1)(3x)]=(1+px)/3x=1/3x+p÷3so the limit does not exist
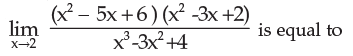
- a)1/3
- b)3
- c)–1/3
- d)none of these
Correct answer is 'C'. Can you explain this answer?
a)
1/3
b)
3
c)
–1/3
d)
none of these

|
Syed Owais answered |
Use L-hoapital rule and substitute x value
The value of the limit when n tends to infinity of the expression 2-n(n2+5n+6)[(n+4)(n+5)]-1 is- a)0
- b)1
- c)-1
- d)None
Correct answer is option 'B'. Can you explain this answer?
The value of the limit when n tends to infinity of the expression 2-n(n2+5n+6)[(n+4)(n+5)]-1 is
a)
0
b)
1
c)
-1
d)
None

|
Disha Joshi answered |
Explanation:
Given expression: 2 - n(n^2 + 5n + 6)[(n+4)(n+5)] - 1
To find the limit of the expression as n tends to infinity, we need to simplify the expression.
Step 1: Expand the expression
2 - n(n^2 + 5n + 6)(n^2 + 9n + 20) - 1
2 - n(n^4 + 9n^3 + 20n^2 + 5n^3 + 45n^2 + 30n + 6n^2 + 54n + 120) - 1
2 - n(n^4 + 14n^3 + 71n^2 + 84n + 120) - 1
2 - n^5 - 14n^4 - 71n^3 - 84n^2 - 120n - 1
Step 2: As n tends to infinity, the higher degree terms dominate the expression
Therefore, the terms with n^5 and n^4 become more significant as n approaches infinity
Step 3: Simplify the expression by neglecting lower degree terms
The expression simplifies to -n^5 as n tends to infinity
Step 4: Take the limit of the simplified expression as n tends to infinity
lim(n->∞) -n^5 = -∞ + 5 = -∞
Therefore, the value of the limit as n tends to infinity of the given expression is -∞, which is equivalent to option 'B' (1).
Given expression: 2 - n(n^2 + 5n + 6)[(n+4)(n+5)] - 1
To find the limit of the expression as n tends to infinity, we need to simplify the expression.
Step 1: Expand the expression
2 - n(n^2 + 5n + 6)(n^2 + 9n + 20) - 1
2 - n(n^4 + 9n^3 + 20n^2 + 5n^3 + 45n^2 + 30n + 6n^2 + 54n + 120) - 1
2 - n(n^4 + 14n^3 + 71n^2 + 84n + 120) - 1
2 - n^5 - 14n^4 - 71n^3 - 84n^2 - 120n - 1
Step 2: As n tends to infinity, the higher degree terms dominate the expression
Therefore, the terms with n^5 and n^4 become more significant as n approaches infinity
Step 3: Simplify the expression by neglecting lower degree terms
The expression simplifies to -n^5 as n tends to infinity
Step 4: Take the limit of the simplified expression as n tends to infinity
lim(n->∞) -n^5 = -∞ + 5 = -∞
Therefore, the value of the limit as n tends to infinity of the given expression is -∞, which is equivalent to option 'B' (1).
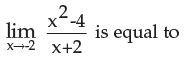
- a)4
- b)–4
- c)does not exist
- d)none of these
Correct answer is 'B'. Can you explain this answer?
a)
4
b)
–4
c)
does not exist
d)
none of these

|
Samraggi Kumar answered |
Lim(( x-2)(x+2))/(x+2)=lim x-2 = -2-2=-4
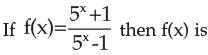
- a)an even function
- b)an odd function
- c)a composite function
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
a)
an even function
b)
an odd function
c)
a composite function
d)
none of these
|
|
Vivek answered |
Replace x by -x and change 5^-x to 1/5^x. take LCM and take out -1 common from the denominator.
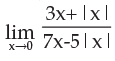
- a)exists
- b)does not exist
- c)1/6
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
exists
b)
does not exist
c)
1/6
d)
none of these

|
Divesh Gupta answered |
L.h.s.= limit x tend to negative zero
= 3x+|x|/7x-5|x|
=3x-x/7x+5x
=2x/12
=1/6
r.h.s.= limit x tend to positive zero
r.h.s. will be =2
l.h.s.does not equal to r.h.s
then option a is answe
= 3x+|x|/7x-5|x|
=3x-x/7x+5x
=2x/12
=1/6
r.h.s.= limit x tend to positive zero
r.h.s. will be =2
l.h.s.does not equal to r.h.s
then option a is answe
The value of the limit when x tends to 2 of the expression (x-2)-1-(x2-3x+2)-1 is- a)1
- b)0
- c)-1
- d)None
Correct answer is option 'A'. Can you explain this answer?
The value of the limit when x tends to 2 of the expression (x-2)-1-(x2-3x+2)-1 is
a)
1
b)
0
c)
-1
d)
None

|
Sameer Basu answered |
The given expression is:
(x-2)-1-(x2-3x 2)-1
Breaking down the expression:
(x-2)-1 can be rewritten as 1/(x-2)
(x2-3x 2)-1 can be rewritten as 1/(x^2-3x+2)
Re-writing the expression:
The given expression can be written as 1/(x-2) - 1/(x^2-3x+2)
Finding the limit:
We are required to find the limit of the expression as x tends to 2.
Approach:
We can find the limit by plugging in the value of x equals to 2 into the expression.
Substituting x = 2:
When we substitute x = 2 in the expression, we get:
1/(2-2) - 1/(2^2-3(2)+2)
= 1/0 - 1/(4-6+2)
= 1/0 - 1/0
Since we have a division by zero in the expression, the limit does not exist.
Conclusion:
The value of the limit when x tends to 2 of the given expression is undefined or does not exist. Therefore, the correct answer is option 'd' (None).
(x-2)-1-(x2-3x 2)-1
Breaking down the expression:
(x-2)-1 can be rewritten as 1/(x-2)
(x2-3x 2)-1 can be rewritten as 1/(x^2-3x+2)
Re-writing the expression:
The given expression can be written as 1/(x-2) - 1/(x^2-3x+2)
Finding the limit:
We are required to find the limit of the expression as x tends to 2.
Approach:
We can find the limit by plugging in the value of x equals to 2 into the expression.
Substituting x = 2:
When we substitute x = 2 in the expression, we get:
1/(2-2) - 1/(2^2-3(2)+2)
= 1/0 - 1/(4-6+2)
= 1/0 - 1/0
Since we have a division by zero in the expression, the limit does not exist.
Conclusion:
The value of the limit when x tends to 2 of the given expression is undefined or does not exist. Therefore, the correct answer is option 'd' (None).
The value of the limit when x tends to zero of the expression (1+n)1/n is- a)e
- b)0
- c)1
- d)-1
Correct answer is option 'A'. Can you explain this answer?
The value of the limit when x tends to zero of the expression (1+n)1/n is
a)
e
b)
0
c)
1
d)
-1

|
Bhaskar Sharma answered |
Explanation:
The expression given is (1+n)^(1/n).
Using the limit definition of e:
We know that the limit as x tends to 0 of (1+x)^(1/x) is equal to e.
Substitute n for x:
When x becomes n in the expression, we get (1+n)^(1/n).
Therefore, the value of the limit when x tends to zero of the expression (1+n)^(1/n) is:
e
The expression given is (1+n)^(1/n).
Using the limit definition of e:
We know that the limit as x tends to 0 of (1+x)^(1/x) is equal to e.
Substitute n for x:
When x becomes n in the expression, we get (1+n)^(1/n).
Therefore, the value of the limit when x tends to zero of the expression (1+n)^(1/n) is:
e
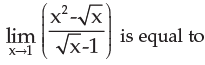
- a)3
- b)–3
- c)1/3
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
3
b)
–3
c)
1/3
d)
none of these

|
User1971744 answered |
Differentiate both num and deno with respect to each other
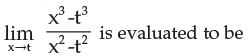
- a) 3/2
- b)2/3t
- c)
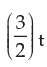
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
a)
3/2
b)
2/3t
c)
d)
none of these

|
Defence Exams answered |
x3 - t3 = (x-t)(x2 + t2 +xt )
x2 - t2 = (x-t)(x + t )
so (x2 + t2 +xt )/(x + t )
(t2 + t2 + txt )/(t + t )
(t2 +t2+t2 )/2t
3t2/2t
3t/2
x2 - t2 = (x-t)(x + t )
so (x2 + t2 +xt )/(x + t )
(t2 + t2 + txt )/(t + t )
(t2 +t2+t2 )/2t
3t2/2t
3t/2
Chapter doubts & questions for Limits and Continuity - Intuitive Approach (Old Scheme) - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Limits and Continuity - Intuitive Approach (Old Scheme) - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
114 videos|169 docs|98 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup