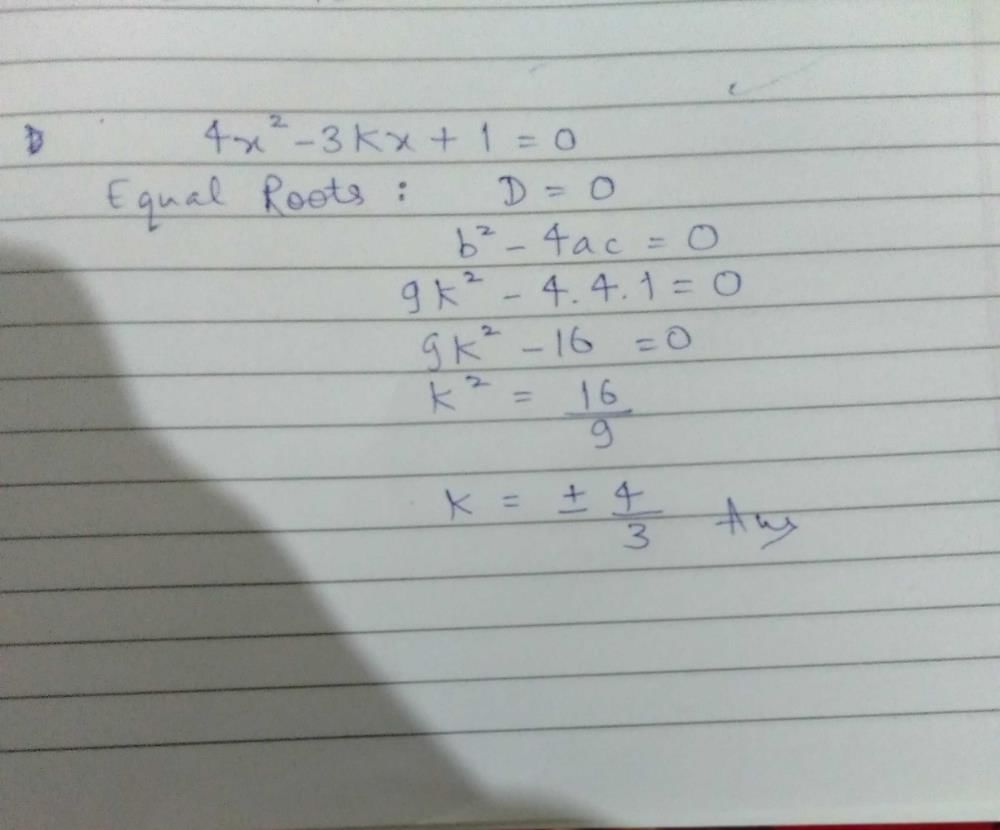All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 2: Equations for CA Foundation Exam
Solve 9x2 = 36- a)±2
- b)±6
- c)±4
- d)2
Correct answer is option 'A'. Can you explain this answer?
Solve 9x2 = 36
a)
±2
b)
±6
c)
±4
d)
2
|
Nilanjan Shah answered |
Solution:
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
A pair of linear equations which has a unique solution x = 2, y = - 3 is
- a)x + y = -1; 2x - 3y = -5
- b)x - 4y - 14 = 0; 5x - y - 13 = 0
- c)2x - y = 1 ; 3x + 2y = 0
- d)2x + 5y = -11; 4x + 10y = -23
Correct answer is option 'B'. Can you explain this answer?
A pair of linear equations which has a unique solution x = 2, y = - 3 is
a)
x + y = -1; 2x - 3y = -5
b)
x - 4y - 14 = 0; 5x - y - 13 = 0
c)
2x - y = 1 ; 3x + 2y = 0
d)
2x + 5y = -11; 4x + 10y = -23
|
Vikram Kapoor answered |
x - 4y -14 = 0
x = 4y+14
putting this in 5x - y -13 = 0
5(4y+14) - y -13 =0
19y = -57
y = -3
putting y = -3 in x = 4y+14
x = 4(-3)+14
x = 2
so option b is correct
If am ≠ bl, then the system of equations, ax + by = c, lx + my = n- a)has a unique solution
- b)has no solution
- c)has infinitely many solutions
- d)may or may not have a solution
Correct answer is option 'A'. Can you explain this answer?
If am ≠ bl, then the system of equations, ax + by = c, lx + my = n
a)
has a unique solution
b)
has no solution
c)
has infinitely many solutions
d)
may or may not have a solution
|
|
Vivek Rana answered |
If am ≠ bl, then the equations ax+by=c, lx+my=n has a unique solution.
Given,
Pair of lines represented by the equations
ax + by = c
lx + my = n
For unique solution
For infinite solutions
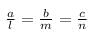
For no solution
Given,
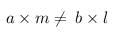
This can be transformed into
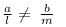
Therefore, If am ≠ bl, then the equations ax+by=c, lx+my=n has a unique solution.
The sum of the digits of a two-digit number is 9. If 27 is added to it, the digit of number get reversed. The number is- a)25
- b)72
- c)63
- d)36
Correct answer is option 'D'. Can you explain this answer?
The sum of the digits of a two-digit number is 9. If 27 is added to it, the digit of number get reversed. The number is
a)
25
b)
72
c)
63
d)
36
|
Avinash Patel answered |
Lets,
First digit number = x
Second digit number = y
Number = (x+10y)
A/Q,
x + y = 9 ...................... (i)
A/Q,
(x+10y) = (10x+y) + 27
x + 10y = 10x + y +27
9x - 9y = 27
9(x - y) = 27
x - y = 27/9
x - y = 3 ......................... (ii)
Equation (i) and (ii) we get,
x = 3
Putting the value of x in eq.(i)
we get,
y = 6
Number = (10x +y)
= 10 x 3 + 6
= 30 + 6
= 36
Find the solution to the following system of linear equations:
x-2y = 6
2x+y = 17- a)(8,1)
- b)(12,3)
- c)(1,2)
- d)(10,2)
Correct answer is option 'A'. Can you explain this answer?
Find the solution to the following system of linear equations:
x-2y = 6
2x+y = 17
x-2y = 6
2x+y = 17
a)
(8,1)
b)
(12,3)
c)
(1,2)
d)
(10,2)
|
Thor Kss answered |
X-2y=6 and 2x+y=17
by eliminating
x-2y=6*2
2x+y=17*1
2x will be cancelled
then y will be 1
and when we value of y in equation 1
we get x=8
by eliminating
x-2y=6*2
2x+y=17*1
2x will be cancelled
then y will be 1
and when we value of y in equation 1
we get x=8
The sum of two numbers is 45 and one is twice the other. What is the smaller number?
- a)30
- b)35
- c)15
- d)25
Correct answer is option 'C'. Can you explain this answer?
The sum of two numbers is 45 and one is twice the other. What is the smaller number?
a)
30
b)
35
c)
15
d)
25
|
Kailash mukherjee answered |
To solve this problem, we can use algebraic equations. Let's assume that the smaller number is x.
Given that one number is twice the other, we can express the larger number in terms of the smaller number as:
Larger number = 2x
And the sum of the two numbers is 45, so we can write the equation:
x + 2x = 45
Simplifying the equation, we have:
3x = 45
Dividing both sides of the equation by 3, we get:
x = 15
Therefore, the smaller number is 15.
So, option C, 15, is the correct answer.
Given that one number is twice the other, we can express the larger number in terms of the smaller number as:
Larger number = 2x
And the sum of the two numbers is 45, so we can write the equation:
x + 2x = 45
Simplifying the equation, we have:
3x = 45
Dividing both sides of the equation by 3, we get:
x = 15
Therefore, the smaller number is 15.
So, option C, 15, is the correct answer.
The pair of equations y = 0 and y = - 7 has- a)one solution
- b)two solutions
- c)infinitely many solutions
- d)no solution
Correct answer is option 'D'. Can you explain this answer?
The pair of equations y = 0 and y = - 7 has
a)
one solution
b)
two solutions
c)
infinitely many solutions
d)
no solution
|
Gaurav Kumar answered |
The equation are y=0 and y=-7
y=0 is on the x-axis and y=-7 is the line parallel to the x-axes at a distance 7 units from y=0
The line will be parallel
if we try to solve these equations we get 0=7 which is absurd.
So the equations are inconsistent.
Therefore there is no solution.
y=0 is on the x-axis and y=-7 is the line parallel to the x-axes at a distance 7 units from y=0
The line will be parallel
if we try to solve these equations we get 0=7 which is absurd.
So the equations are inconsistent.
Therefore there is no solution.
Write the general form of a quadratic polynomia- a)ax2 + bx + c where a, b and c are real numbers
- b)ax2 + bx + c=0
- c)ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
- d)ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
Correct answer is option 'C'. Can you explain this answer?
Write the general form of a quadratic polynomia
a)
ax2 + bx + c where a, b and c are real numbers
b)
ax2 + bx + c=0
c)
ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
d)
ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
|
Krishna Iyer answered |
If the coefficient of x2 is zero , then the equation is not a quadratic equation , its a linear equation. So its necessary condition for the quadratic equation.
Which of the following in not a quadratic equation:- a)(x – 2)2 + 1 = 2x – 3
- b)(x + 2)2 = x3 – 4
- c)x(2x + 3) = x2 + 1
- d)x(x + 1) + 8 = (x + 2) (x – 2)
Correct answer is option 'D'. Can you explain this answer?
Which of the following in not a quadratic equation:
a)
(x – 2)2 + 1 = 2x – 3
b)
(x + 2)2 = x3 – 4
c)
x(2x + 3) = x2 + 1
d)
x(x + 1) + 8 = (x + 2) (x – 2)
|
Rahul Kumar answered |
Option (B) and (D) , both are the correct answers. We have x(x + 1) + 8 = (x + 2) (x – 2)
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
Find the solution to the following system of linear equations: 0.2x + 0.3y = 1.2
0.1x – 0.1y = 0.1- a)(1,2)
- b)(2,3)
- c)(3,2)
- d)(2,1)
Correct answer is option 'C'. Can you explain this answer?
Find the solution to the following system of linear equations: 0.2x + 0.3y = 1.2
0.1x – 0.1y = 0.1
0.1x – 0.1y = 0.1
a)
(1,2)
b)
(2,3)
c)
(3,2)
d)
(2,1)
|
|
Arun Sharma answered |
0.2x + 0.3y = 1.2
2x+3y=12 …..(1)
0.1x – 0.1y = 0.1x-y=1 ….(2)
From (2), x=1+y
Substituting the values of x in (1)
2(1+y)+3y=12
2+2y+3y=12
5y=10
y=2
x=1+2= 3
2x+3y=12 …..(1)
0.1x – 0.1y = 0.1x-y=1 ….(2)
From (2), x=1+y
Substituting the values of x in (1)
2(1+y)+3y=12
2+2y+3y=12
5y=10
y=2
x=1+2= 3
Which of the following points lie on the line 3x+2y=5 ?- a)(1, 1)
- b)(0, 1)
- c)(1, 0)
- d)(2, 1)
Correct answer is option 'A'. Can you explain this answer?
Which of the following points lie on the line 3x+2y=5 ?
a)
(1, 1)
b)
(0, 1)
c)
(1, 0)
d)
(2, 1)
|
|
Krishna Iyer answered |
When we are given only one equation and two variables we assume values for one variable and find the values for the other variable.
3x+2y=5
Let x=1
3*1+2y=5
2y=2
y=1 hence (1,1) lies on the line.
3x+2y=5
Let x=1
3*1+2y=5
2y=2
y=1 hence (1,1) lies on the line.
Can you explain the answer of this question below: If 4 is a root of the equation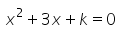 
, then k is
- A:
-28
- B:
-12
- C:
12
- D:
28
The answer is a.
If 4 is a root of the equation , then k is
-28
-12
12
28
|
Vp Classes answered |
4 is the solution , this means that if we put x=4 we get 0. So putting x=4 in the equation x2+3x+k=0 we get 42+3*4+k=0
16+12+k=0 ⇒ k=-28
16+12+k=0 ⇒ k=-28
Solve for x : 6x2 + 40 = 31x- a)
- b)
- c)0,8/3
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Solve for x : 6x2 + 40 = 31x
a)
b)
c)
0,8/3
d)
None of the above
|
|
Nirmal Kumar answered |
6x²-31x+40=0,
a=6,
b=-31,
c=40,
by quadratic formula-->
x=-b±√b²-4ac/2a,
by putting the values of a,b and c, we get,
x=-(-31)±√(-31)²-4(6)(40)/2(6),
=31±√961-960/12,
=31±√1/12,
=31±1/12,
x=30/12or ,32/12,
x=5/2 or, 8/3,
hence , option B is correct
a=6,
b=-31,
c=40,
by quadratic formula-->
x=-b±√b²-4ac/2a,
by putting the values of a,b and c, we get,
x=-(-31)±√(-31)²-4(6)(40)/2(6),
=31±√961-960/12,
=31±√1/12,
=31±1/12,
x=30/12or ,32/12,
x=5/2 or, 8/3,
hence , option B is correct
If x = 1 is a common root of the equation x2 + ax – 3 = 0 and bx2 – 7x + 2 = 0 then ab =
- a)10
- b)-3
- c)6
- d)7
Correct answer is option 'A'. Can you explain this answer?
If x = 1 is a common root of the equation x2 + ax – 3 = 0 and bx2 – 7x + 2 = 0 then ab =
a)
10
b)
-3
c)
6
d)
7
|
Zachary Foster answered |
Given:
- x = 1 is a common root of the equations:
- x² + ax - 3 = 0
- bx² - 7x + 2 = 0
To find:
- The value of ab.
Solution:
Since x = 1 is a root of both equations, we can substitute x = 1 in both equations.
Equation 1:
- 1² + a(1) - 3 = 0
- 1 + a - 3 = 0
- a = 2
Equation 2:
- b(1)² - 7(1) + 2 = 0
- b - 7 + 2 = 0
- b = 5
Therefore, ab = 2 * 5 = 10
So, the value of ab is 10.
The sum of the digits of a two digit number is 12. The number obtained by reversing its digits exceeds the given number by 18. Then the number is_____- a)75
- b)25
- c)52
- d)57
Correct answer is option 'D'. Can you explain this answer?
The sum of the digits of a two digit number is 12. The number obtained by reversing its digits exceeds the given number by 18. Then the number is_____
a)
75
b)
25
c)
52
d)
57
|
Neha Patel answered |
Let us assume x and y are the two digits of the number
Therefore, two-digit number is = 10x + y and the reversed number = 10y + x
Given:
x + y = 12
y = 12 – x (1)
Also given:
10y + x - 10x – y = 18
9y – 9x = 18
y – x = 2 (2)
Substitute the value of y from eqn 1 in eqn 2
12 – x – x = 2
12 – 2x = 2
2x = 10
x = 5
Therefore, y = 12 – x = 12 – 5 = 7
Therefore, the two-digit number is 10x + y = (10*5) + 7 = 57
Find the solution to the following system of linear equations:
2p+3q = 9
p – q = 2
- a)(4,2)
- b)(3,1)
- c)(2,-3)
- d)(-4,1)
Correct answer is option 'B'. Can you explain this answer?
Find the solution to the following system of linear equations:
2p+3q = 9
p – q = 2
2p+3q = 9
p – q = 2
a)
(4,2)
b)
(3,1)
c)
(2,-3)
d)
(-4,1)
|
Clifford Academy answered |
Alright, we have a system of two linear equations with two variables, p and q. Let's write them down:
1) 2p + 3q = 9
2) p - q = 2
Our goal is to find the values of p and q that satisfy both equations. We can use either the substitution method or the elimination method to solve this system. I'll use the substitution method here.
First, we'll solve the second equation for one of the variables. Let's solve for p:
p = q + 2
Now, we'll substitute this expression for p into the first equation:
2(q + 2) + 3q = 9
Distribute the 2:
2q + 4 + 3q = 9
Combine like terms:
5q + 4 = 9
Now, solve for q:
5q = 9 - 4
5q = 5
q = 1
Now that we have the value for q, we can plug it back into the expression for p:
p = q + 2
p = 1 + 2
p = 3
1) 2p + 3q = 9
2) p - q = 2
Our goal is to find the values of p and q that satisfy both equations. We can use either the substitution method or the elimination method to solve this system. I'll use the substitution method here.
First, we'll solve the second equation for one of the variables. Let's solve for p:
p = q + 2
Now, we'll substitute this expression for p into the first equation:
2(q + 2) + 3q = 9
Distribute the 2:
2q + 4 + 3q = 9
Combine like terms:
5q + 4 = 9
Now, solve for q:
5q = 9 - 4
5q = 5
q = 1
Now that we have the value for q, we can plug it back into the expression for p:
p = q + 2
p = 1 + 2
p = 3
The pair of linear equations 2x + 3y = 5 and 4x + 6y = 10 is- a)inconsistent
- b)Both
- c)consistent
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The pair of linear equations 2x + 3y = 5 and 4x + 6y = 10 is
a)
inconsistent
b)
Both
c)
consistent
d)
none of these
|
|
Amit Sharma answered |
a1 / a2 = b1 / b2 = c1 / c2
2/4 = 3/6 = 5/10
1/2 = 1/2 = 1/2
So, a1 / a2 = b1 / b2 = c1 / c2
When these are equal then it is consistent.
Therefore option (C) is correct .
2/4 = 3/6 = 5/10
1/2 = 1/2 = 1/2
So, a1 / a2 = b1 / b2 = c1 / c2
When these are equal then it is consistent.
Therefore option (C) is correct .
If a pair of linear equations has infinitely many solutions, then the lines representing them will be
- a)Parallel
- b)Intersecting lines
- c)Always intersecting
- d)coincident lines
Correct answer is option 'D'. Can you explain this answer?
If a pair of linear equations has infinitely many solutions, then the lines representing them will be
a)
Parallel
b)
Intersecting lines
c)
Always intersecting
d)
coincident lines
|
|
Ananya Das answered |
If two lines i.e. a pair of linear equations, has infinitely many solutions it means lines are overlapping each other i.e. coincident lines.
The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son. The present ages (in years) of the son and the father are, respectively. - a)4 and 24
- b)5 and 30
- c)6 and 36
- d)3 and 24
Correct answer is option 'C'. Can you explain this answer?
The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son. The present ages (in years) of the son and the father are, respectively.
a)
4 and 24
b)
5 and 30
c)
6 and 36
d)
3 and 24
|
|
Ååryañ answered |
The value/s of x when (x – 4) (3x + 2) = 0 ________- a)4, -2/3
- b)-4, – 2/ 3
- c)4, 2/3
- d)-4, 2/3
Correct answer is option 'A'. Can you explain this answer?
The value/s of x when (x – 4) (3x + 2) = 0 ________
a)
4, -2/3
b)
-4, – 2/ 3
c)
4, 2/3
d)
-4, 2/3
|
|
Drishti Kumari answered |
( x - 4 ) ( 3x + 2 ) = 0
x - 4 = 0
x = 4
3x + 2 = 0
3x = -2
x = -2 / 3
Therefore option (A) is correct.
x - 4 = 0
x = 4
3x + 2 = 0
3x = -2
x = -2 / 3
Therefore option (A) is correct.
The nature of the roots of the equation x2 – 5x + 7 = 0 is –- a)No real roots
- b)1 real root
- c)Can't be determined
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The nature of the roots of the equation x2 – 5x + 7 = 0 is –
a)
No real roots
b)
1 real root
c)
Can't be determined
d)
None of these
|
|
Krishna Iyer answered |
Given equation is x2-5x+7=0
We have discriminant as b2-4ac=(-5)2-4*1*7= -3
And x =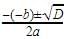
, Since we do not have any real number which is a root of a negative number, the roots are not real.
We have discriminant as b2-4ac=(-5)2-4*1*7= -3
And x =
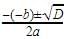, Since we do not have any real number which is a root of a negative number, the roots are not real.
If b2 - 4ac = 0 then The roots of the Quadratic equation ax2 + bx + c = 0 are given by :- a)
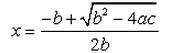
- b)
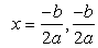
- c)
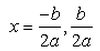
- d)
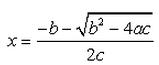
Correct answer is option 'B'. Can you explain this answer?
If b2 - 4ac = 0 then The roots of the Quadratic equation ax2 + bx + c = 0 are given by :
a)
b)
c)
d)
|
Udexy Coaching Center answered |
Formula for finding the roots of a quadratic equation is
So since
b2 - 4ac = 0, putting this value in the equation
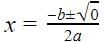
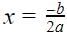So there are repeated roots
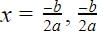
So since
b2 - 4ac = 0, putting this value in the equation
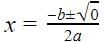
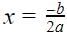So there are repeated roots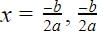Which of the following is not a quadratic equation ?- a)5x + 3y2 = 0
- b)z2 - 2z = 0
- c)3x + 4 - 7x2 = 0
- d)5x2 - 125 = 0
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a quadratic equation ?
a)
5x + 3y2 = 0
b)
z2 - 2z = 0
c)
3x + 4 - 7x2 = 0
d)
5x2 - 125 = 0
|
|
Priyanshu Intelligent answered |
In equation first there are two variables.
That's why it is not a quadratic equation.
That's why it is not a quadratic equation.
The two positive numbers differ by 5 and square of their sum is 169 are
- a)2,4
- b)5,6
- c)4,9
- d)3,7
Correct answer is option 'C'. Can you explain this answer?
The two positive numbers differ by 5 and square of their sum is 169 are
a)
2,4
b)
5,6
c)
4,9
d)
3,7
|
Apoorv khanna answered |
Explanation:
Let the two numbers be x and y, where x is greater than y.
Given, x - y = 5
=> x = y + 5
Also, (x+y)^2 = 169
=> (y+5+y)^2 = 169 (Substituting x = y + 5)
=> (2y+5)^2 = 169
=> 4y^2 + 20y + 25 = 169 (Expanding the square)
=> 4y^2 + 20y - 144 = 0
=> y^2 + 5y - 36 = 0
=> (y + 9)(y - 4) = 0
=> y = -9 or y = 4
Since the numbers are positive, y = 4
Therefore, x = y + 5 = 9
Hence, the two numbers are 4 and 9.
Therefore, option C is the correct answer.
Let the two numbers be x and y, where x is greater than y.
Given, x - y = 5
=> x = y + 5
Also, (x+y)^2 = 169
=> (y+5+y)^2 = 169 (Substituting x = y + 5)
=> (2y+5)^2 = 169
=> 4y^2 + 20y + 25 = 169 (Expanding the square)
=> 4y^2 + 20y - 144 = 0
=> y^2 + 5y - 36 = 0
=> (y + 9)(y - 4) = 0
=> y = -9 or y = 4
Since the numbers are positive, y = 4
Therefore, x = y + 5 = 9
Hence, the two numbers are 4 and 9.
Therefore, option C is the correct answer.
Ruhi’s mother is 26 years older than her. The product of their ages (in years) 3 years from now will be 360. Form a Quadratic equation so as to find Ruhi’s age- a)x 2 + 32 x – 273 = 0
- b)x 2 -32 x – 273=0
- c)x 2 + 32 x + 273 = 0
- d)x 2 – 32 x +273 = 0
Correct answer is option 'A'. Can you explain this answer?
Ruhi’s mother is 26 years older than her. The product of their ages (in years) 3 years from now will be 360. Form a Quadratic equation so as to find Ruhi’s age
a)
x 2 + 32 x – 273 = 0
b)
x 2 -32 x – 273=0
c)
x 2 + 32 x + 273 = 0
d)
x 2 – 32 x +273 = 0
|
|
Amit Sharma answered |
Ruhi’s mother is 26 years older than her
So let Ruhi’s age is x
So mother’s age is x+26
The product of their ages 3 years from now will be 360
So After three years , Ruhi’s age will be x+3
Mother’s age will be x+26+3=x+29
Product of their ages =(x + 3)(x + 29)=360
x2+(3+29)x+87=360
x2+32x-273=0
So let Ruhi’s age is x
So mother’s age is x+26
The product of their ages 3 years from now will be 360
So After three years , Ruhi’s age will be x+3
Mother’s age will be x+26+3=x+29
Product of their ages =(x + 3)(x + 29)=360
x2+(3+29)x+87=360
x2+32x-273=0
The value of x in mx + ny = c; nx – ny = c + 1 is
- a)x = (m + n) / (c + 1)
- b)x = (2c + 1) / (m + n)
- c)x = m + n
- d)x = 2c + 1
Correct answer is option 'B'. Can you explain this answer?
The value of x in mx + ny = c; nx – ny = c + 1 is
a)
x = (m + n) / (c + 1)
b)
x = (2c + 1) / (m + n)
c)
x = m + n
d)
x = 2c + 1
|
|
Mansi desai answered |
To find the value of x in the equation mx + ny = c, we need more information or another equation. The equation nx = 0 does not provide enough information to solve for x.
In elimination method _____________ is an important condition.- a)Equating either of the coefficients
- b)Equating only the y coefficient.
- c)Equating only the x co-efficient.
- d)Equating both the coefficients.
Correct answer is option 'A'. Can you explain this answer?
In elimination method _____________ is an important condition.
a)
Equating either of the coefficients
b)
Equating only the y coefficient.
c)
Equating only the x co-efficient.
d)
Equating both the coefficients.
|
|
Rajiv Gupta answered |
Elimination Method (by Equating Coefficients)
There is another method of eliminating a variable, than often used method i. e --------Suppose you are to solve
23x - 17y + 11=0 ------(1)
and 31x + 13y - 57 = 0 -------(2)
Now expressing x in terms of y would involve division by 23 or 31. Express y in terms of x, it would involve division by 17 or 13. You know that multiplication is more convenient than division, better to convert the division process into a multiplication process.
Multiplying the first equation by 13 viz., coefficient of y in (2), and second by 17 viz., coefficient of y in (1), you will get an equivalent system of equations. The new system has the advantage that y has the same numerical coefficient 17x13 in both the equations. When you add these new equations, the terms containing y would cancel out as these have opposite signs and the same numerical coefficient. Thus, y has been eliminated. Now proceed as before, and solve the system. This method of elimination is also called elimination by equating coefficients for obvious reasons.
Example: Solve the following system of equations using the elimination method by equating coefficients:
11x - 5y + 61 = 0 (1)
3x - 20y - 2 = 0 (2)
Solution: Let us multiply equation (1) by 3 and equation (2) by 11. This gives
33x - 15y + 183 = 0 (3)
and 33x - 220y - 22 = 0 (4)
Subtracting (4) from (3), you will get 205y + 205 = 0
, or y = - 1
Substituting this value of y in equation (2), you will get
3x - 20 * (- 1) - 2 = 0
or 3x = -18
or x = - 6
Thus, the required solution is
x = - 6 and y = -1.
Now you should verify; substitute x = - 6 and y = -1 in the given equations, you will notice both the equations are satisfied. Hence, the solution is correct
The value of q if x = 2 is a solution of 8x2 + qx – 4 = 0 is _____- a)14
- b)-28
- c)-14
- d)28
Correct answer is option 'C'. Can you explain this answer?
The value of q if x = 2 is a solution of 8x2 + qx – 4 = 0 is _____
a)
14
b)
-28
c)
-14
d)
28
|
|
Kuldeep Raj answered |
Let us place 2 in the place of "x" for 8x² + qx - 4 = 0 (According to the question).
8(2)² + q(2) - 4 = 0.
8(4) + 2q - 4 = 0.
32 + 2q - 4 = 0.
Shift (32) to the right side.
2q - 4 = -32.
Shift (-4) to the right side. Then,
2q = -32 + 4.
2q = -28.
q = -28/2.
q = -14.
Therefore, the value of q if x = 2 is a solution of 8x² + qx - 4 = 0 is -14.
Hence, option (c) is correct friend...
8(2)² + q(2) - 4 = 0.
8(4) + 2q - 4 = 0.
32 + 2q - 4 = 0.
Shift (32) to the right side.
2q - 4 = -32.
Shift (-4) to the right side. Then,
2q = -32 + 4.
2q = -28.
q = -28/2.
q = -14.
Therefore, the value of q if x = 2 is a solution of 8x² + qx - 4 = 0 is -14.
Hence, option (c) is correct friend...
The solution of x2 + 4x + 4 = 0 is- a)2
- b)-2
- c)0
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The solution of x2 + 4x + 4 = 0 is
a)
2
b)
-2
c)
0
d)
None of these
|
|
Priyanshu Intelligent answered |
(-2)^2 + 4(-2) + 4
= 4 - 8 + 4
=8-8
=0.
Hence , option b) is the right answer.
= 4 - 8 + 4
=8-8
=0.
Hence , option b) is the right answer.
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Quadratic Equations" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths) Q. Which of the following quadratic expression can be expressed as a product of real linear factors?- a)x2 – 2x + 3
- b)3x2 – √2x – √3
- c)√2x2 – √5x + 3
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Quadratic Equations" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
Q. Which of the following quadratic expression can be expressed as a product of real linear factors?
a)
x2 – 2x + 3
b)
3x2 – √2x – √3
c)
√2x2 – √5x + 3
d)
None of these
|
|
Amit Kumar answered |
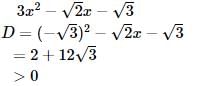
Thus, it can be expressed as product of linear factors.
If one root of a Quadratic equation is m + , then the other root is- a)m – √n
- b)m +√n
- c)Can not be determined
- d)√m + n
Correct answer is option 'A'. Can you explain this answer?
If one root of a Quadratic equation is m + , then the other root is
a)
m – √n
b)
m +√n
c)
Can not be determined
d)
√m + n
|
|
Arun Sharma answered |
In a quadratic equation with rational coefficients has an irrational root α + √β, then it has a conjugate root α - √β.
So if the root is m+ √n the other root will be m- √n
So if the root is m+ √n the other root will be m- √n
The Index of Coincidence for English language is approximately- a)0.068
- b)0.038
- c)0.065
- d)0.048
Correct answer is option 'C'. Can you explain this answer?
The Index of Coincidence for English language is approximately
a)
0.068
b)
0.038
c)
0.065
d)
0.048
|
Hariteja Patnala answered |
Yes actually you said option C is correct it is actually correct but the actual answer is different
actual answer for index of coincide of English language is 0.0 667
index of coincide is a technique to find the probability of the repeating letters in an encrypted text
the index of coincide value is calculated on the basis of the probability of occurrence of a specified letter and the probability of comparing it to the same letter from the second text
so this is my answer for index of coincide of English language is 0.0667 but you have given that C is correct option
actual answer for index of coincide of English language is 0.0 667
index of coincide is a technique to find the probability of the repeating letters in an encrypted text
the index of coincide value is calculated on the basis of the probability of occurrence of a specified letter and the probability of comparing it to the same letter from the second text
so this is my answer for index of coincide of English language is 0.0667 but you have given that C is correct option
A train overtakes two persons who are walking at the rate of 8 kmph and 12 kmph in the same direction in which the train is going, and passes them completely in 9 and 10 seconds respectively. What is the length of the train?- a)200 m
- b) 500 m
- c) 100 m
- d)300 m
Correct answer is option 'C'. Can you explain this answer?
A train overtakes two persons who are walking at the rate of 8 kmph and 12 kmph in the same direction in which the train is going, and passes them completely in 9 and 10 seconds respectively. What is the length of the train?
a)
200 m
b)
500 m
c)
100 m
d)
300 m
|
|
Rajiv Gupta answered |
8 kmph = (8 x 5/18) = 20/9 m/sec
4 kmph = (12 x 5/18 = 10/3 m/sec
18 9
Let the length of the train be x metres and its speed by y m/sec.
Then, [x/(y - 20/9)] = 9 and [x/(y - 10/3)] = 10
Therefore 9y - 20 = x and 10y - 100/3 = x
=> 9y - 20 = 10y - 100/3
solving: y = 40/3
putting value of y in (1):
9 . (40/3) - 20 = x
so, x = 100 m
On solving, we get: x = 100.
Therefore Length of the train is 100 m.
A lending library has a fixed charge for the first two days and an additional charge for each day thereafter. Sunil paid Rs 28 for a book kept for seven days, while Sohail paid Rs 32 for the book he kept for nine days. Find the charge for each extra day.- a)Rs 3
- b)Rs 20
- c)Rs 2
- d)Rs 18
Correct answer is option 'C'. Can you explain this answer?
A lending library has a fixed charge for the first two days and an additional charge for each day thereafter. Sunil paid Rs 28 for a book kept for seven days, while Sohail paid Rs 32 for the book he kept for nine days. Find the charge for each extra day.
a)
Rs 3
b)
Rs 20
c)
Rs 2
d)
Rs 18
|
|
Abhishek Bhai answered |
The roots of x2 – 8x + 12 = 0, are- a)x = 0
- b)no real roots
- c)real and unequal
- d)real and equal
Correct answer is option 'C'. Can you explain this answer?
The roots of x2 – 8x + 12 = 0, are
a)
x = 0
b)
no real roots
c)
real and unequal
d)
real and equal
|
|
Genius answered |
9th standard me kya kr rhe the ?!
If the area of a rectangle is 24 m2 and its perimeter is 20 m, the equation to find its length and breadth would be:
- a)x2 – 10x + 24 = 0
- b)x2 + 1 2x + 24 = 0
- c)x2 – 10x – 24 = 0
- d)x2 + 10x + 28 = 0
Correct answer is option 'A'. Can you explain this answer?
If the area of a rectangle is 24 m2 and its perimeter is 20 m, the equation to find its length and breadth would be:
a)
x2 – 10x + 24 = 0
b)
x2 + 1 2x + 24 = 0
c)
x2 – 10x – 24 = 0
d)
x2 + 10x + 28 = 0
|
|
Aashu Mehra answered |
Perimeter = 2(l+b)=20
l+b=10
lxb=24
so correct option is A
If a,b,c are real and b2-4ac >0 then roots of equation are- a)real roots
- b)real and equal
- c)real and unequal
- d)No real roots
Correct answer is option 'C'. Can you explain this answer?
If a,b,c are real and b2-4ac >0 then roots of equation are
a)
real roots
b)
real and equal
c)
real and unequal
d)
No real roots
|
Ram trivedi answered |
The expression b^2 - 4ac is the discriminant of a quadratic equation of the form ax^2 + bx + c = 0. It determines the nature of the solutions of the equation.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
The condition for equation ax2 + bx + c = 0 to be linear is- a)a > 0, b = 0
- b)a ≠ 0, b = 0
- c)a < 0, b = 0
- d)a = 0, b ≠ 0
Correct answer is option 'D'. Can you explain this answer?
The condition for equation ax2 + bx + c = 0 to be linear is
a)
a > 0, b = 0
b)
a ≠ 0, b = 0
c)
a < 0, b = 0
d)
a = 0, b ≠ 0
|
|
Tanisha answered |
Answer is d...bcoz to make ax^2 +bx+c=0,linear equation.
we need to eliminate ax^2.
So, we will put a=0 ,to make the degree of this equation 1 ...and b should not be equal to 0,bcoz if b will be 0 ,then it will be a constant equation,instead of a linear equation.
we need to eliminate ax^2.
So, we will put a=0 ,to make the degree of this equation 1 ...and b should not be equal to 0,bcoz if b will be 0 ,then it will be a constant equation,instead of a linear equation.
Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.- a)14 and 2
- b)11 and 5
- c)12 and 4
- d)10 and 6
Correct answer is option 'D'. Can you explain this answer?
Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.
a)
14 and 2
b)
11 and 5
c)
12 and 4
d)
10 and 6
|
|
Anjana Khatri answered |
Let x and (16 - x) are two parts of 16 where (16 - x) is longer and x is smaller .
A/C to question,
2 * square of longer = square of smaller + 164
⇒ 2 * (16 - x)^2 = x^2 + 164
⇒ 2 * (256 + x^2 - 32x ) = x^2 + 164
⇒ 512 + 2x^2 - 64x = x^2 + 164
⇒ x^2 - 64x + 512 - 164 = 0
⇒ x^2 - 64x + 348 = 0
⇒x^2 - 58x - 6x + 348 = 0
⇒ x(x - 58) - 6(x - 58) = 0
⇒(x - 6)(x - 58) = 0
⇒ x = 6 and 58
But x ≠ 58 because x < 16
so, x = 6 and 16 - x = 10
Hence, answer is 6 and 10
The sum of areas of two squares is 468m2. If the difference of their perimeters is 24m, then the sides of the two squares are:- a)12m and 18m
- b)24m and 28
- c)6m and 12m
- d)18m and 24m
Correct answer is option 'A'. Can you explain this answer?
The sum of areas of two squares is 468m2. If the difference of their perimeters is 24m, then the sides of the two squares are:
a)
12m and 18m
b)
24m and 28
c)
6m and 12m
d)
18m and 24m
|
|
Rahul Kapoor answered |
Let us say that the sides of the two squares are 'a' and 'b'
Sum of their areas = a^2 + b^2 = 468
Difference of their perimeters = 4a - 4b = 24
=> a - b = 6
=> a = b + 6
So, we get the equation
(b + 6)^2 + b^2 = 468
=> 2b^2 + 12b + 36 = 468
=> b^2 + 6b - 216 = 0
=> b = 12
=> a = 18
The sides of the two squares are 12 and 18.
Find the solution to the following system of linear equations: 2x-y+6=0 4x+5y-16=0- a)(2,-3)
- b)(-1,4)
- c)(2,3)
- d)(1,4)
Correct answer is option 'B'. Can you explain this answer?
Find the solution to the following system of linear equations: 2x-y+6=0 4x+5y-16=0
a)
(2,-3)
b)
(-1,4)
c)
(2,3)
d)
(1,4)
|
Pooja Shah answered |
2x-y+6=0
y=2x+6 ….(1)
4x+5y-16=0
Substituting the values
4x+5(2x+6)-16=0
14x+14=0
x=-1
y=4
y=2x+6 ….(1)
4x+5y-16=0
Substituting the values
4x+5(2x+6)-16=0
14x+14=0
x=-1
y=4
Chapter doubts & questions for Chapter 2: Equations - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 2: Equations - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily