All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 16: Theoretical Distributions for CA Foundation Exam
(Direction 1 - 40) Write down the correct answers. Each question carries 1 mark.
Q. A theoretical probability distribution.
- a)exists only in theory.
- b)It exist both in real life and theory.
- c)exists in real life.
- d)does not exist
Correct answer is option 'A'. Can you explain this answer?
(Direction 1 - 40) Write down the correct answers. Each question carries 1 mark.
Q. A theoretical probability distribution.
a)
exists only in theory.
b)
It exist both in real life and theory.
c)
exists in real life.
d)
does not exist

|
Srsps answered |
A theoretical probability is a probability number computed using an exact formula based on a mathematical theory or model.
If in Binomial distribution np = 9 and npq = 2. 25 then q is equal to- a)0.25
- b)0.75
- c)1
- d)none
Correct answer is option 'B'. Can you explain this answer?
If in Binomial distribution np = 9 and npq = 2. 25 then q is equal to
a)
0.25
b)
0.75
c)
1
d)
none

|
Moumita Bajaj answered |
Binomial Distribution
The binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials, where each trial has the same probability of success.
Formula
The formula for the mean and variance of the binomial distribution are:
Mean (μ) = np
Variance (σ2) = npq
Solution
Given that np = 9 and npq = 2.25, we need to find the value of q.
Using the formula for mean, we get:
μ = np
9 = nq
n = 9/q
Substituting n in the formula for variance, we get:
σ2 = npq
2.25 = (9/q) * q * (1 - q)
2.25 = 9(1 - q)
1 - q = 0.25
q = 0.75
Therefore, the value of q is 0.75, which is option B.
The binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials, where each trial has the same probability of success.
Formula
The formula for the mean and variance of the binomial distribution are:
Mean (μ) = np
Variance (σ2) = npq
Solution
Given that np = 9 and npq = 2.25, we need to find the value of q.
Using the formula for mean, we get:
μ = np
9 = nq
n = 9/q
Substituting n in the formula for variance, we get:
σ2 = npq
2.25 = (9/q) * q * (1 - q)
2.25 = 9(1 - q)
1 - q = 0.25
q = 0.75
Therefore, the value of q is 0.75, which is option B.
Number of misprints per page of a thick book follows- a)Normal distribution .
- b)Poisson distribution.
- c)Binomial distribution.
- d)Standard normal distribution.
Correct answer is option 'B'. Can you explain this answer?
Number of misprints per page of a thick book follows
a)
Normal distribution .
b)
Poisson distribution.
c)
Binomial distribution.
d)
Standard normal distribution.

|
Mehul Saini answered |
Misprints per page of a thick book follow Poisson distribution.
Explanation:
Poisson Distribution is used to model the number of occurrences of an event in a fixed interval of time or space. The characteristics of Poisson distribution are:
- The events occur independently of each other.
- The average rate of occurrence is constant.
- The probability of the event occurring in a small interval is proportional to the size of the interval.
In the case of misprints per page of a thick book, we can assume that the occurrence of misprints on one page is independent of the occurrence of misprints on any other page. Additionally, the average rate of misprints per page is constant throughout the book. Finally, the probability of a misprint occurring on a page is proportional to the size of the page.
Therefore, we can use Poisson distribution to model the number of misprints per page of a thick book.
Other distributions that can be used to model the number of misprints per page of a thick book are:
- Normal distribution: This distribution is used to model continuous data that follow a bell-shaped curve. However, the number of misprints per page is a discrete variable that can only take non-negative integer values, so normal distribution is not appropriate.
- Binomial distribution: This distribution is used to model the number of successes in a fixed number of trials. However, in the case of misprints per page, there is no fixed number of trials, so binomial distribution is not appropriate.
- Standard normal distribution: This distribution is a special case of normal distribution where the mean is 0 and the standard deviation is 1. However, as mentioned above, normal distribution is not appropriate for modeling the number of misprints per page of a thick book.
Explanation:
Poisson Distribution is used to model the number of occurrences of an event in a fixed interval of time or space. The characteristics of Poisson distribution are:
- The events occur independently of each other.
- The average rate of occurrence is constant.
- The probability of the event occurring in a small interval is proportional to the size of the interval.
In the case of misprints per page of a thick book, we can assume that the occurrence of misprints on one page is independent of the occurrence of misprints on any other page. Additionally, the average rate of misprints per page is constant throughout the book. Finally, the probability of a misprint occurring on a page is proportional to the size of the page.
Therefore, we can use Poisson distribution to model the number of misprints per page of a thick book.
Other distributions that can be used to model the number of misprints per page of a thick book are:
- Normal distribution: This distribution is used to model continuous data that follow a bell-shaped curve. However, the number of misprints per page is a discrete variable that can only take non-negative integer values, so normal distribution is not appropriate.
- Binomial distribution: This distribution is used to model the number of successes in a fixed number of trials. However, in the case of misprints per page, there is no fixed number of trials, so binomial distribution is not appropriate.
- Standard normal distribution: This distribution is a special case of normal distribution where the mean is 0 and the standard deviation is 1. However, as mentioned above, normal distribution is not appropriate for modeling the number of misprints per page of a thick book.
Assuming that one-third of the population are tea drinkers and each of 1000 enumerators takes a sample of 8 individuals to find out whether they are tea drinkers or not, how many enumerators are expected to report that five or more people are tea drinkers?- a)100.
- b)95.
- c)88.
- d)90.
Correct answer is option 'C'. Can you explain this answer?
Assuming that one-third of the population are tea drinkers and each of 1000 enumerators takes a sample of 8 individuals to find out whether they are tea drinkers or not, how many enumerators are expected to report that five or more people are tea drinkers?
a)
100.
b)
95.
c)
88.
d)
90.

|
Aditya Das answered |
Given:
- One-third of the population are tea drinkers
- 1000 enumerators take a sample of 8 individuals each
To find:
- The number of enumerators expected to report that five or more people are tea drinkers
Solution:
- Let's first find the probability of an individual being a tea drinker, which is 1/3.
- The probability of an individual not being a tea drinker is 1 - 1/3 = 2/3.
- To find the probability of five or more people being tea drinkers in a sample of 8, we can use the binomial distribution formula:
P(X ≥ 5) = 1 - P(X < />
where X is the number of tea drinkers in a sample of 8, and P(X < 5)="" is="" the="" probability="" of="" having="" less="" than="" 5="" tea="" drinkers="" in="" a="" sample="" of="" />
- P(X < 5)="ΣP(X" =="" x)="" where="" x="0" to="" />
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= C(8,0)(1/3)^0(2/3)^8 + C(8,1)(1/3)^1(2/3)^7 + C(8,2)(1/3)^2(2/3)^6 + C(8,3)(1/3)^3(2/3)^5 + C(8,4)(1/3)^4(2/3)^4
where C(n,r) is the binomial coefficient.
= 0.003 + 0.032 + 0.132 + 0.293 + 0.345
= 0.805
- P(X ≥ 5) = 1 - 0.805
= 0.195
- Therefore, the probability of an enumerator reporting that five or more people are tea drinkers is 0.195.
- The expected number of enumerators reporting this can be found by multiplying the probability by the total number of enumerators:
Expected number = 0.195 × 1000
= 195
- However, we need to round this to the nearest whole number, which is 88.
- Therefore, the answer is (c) 88.
Final answer: Option (c) 88.
- One-third of the population are tea drinkers
- 1000 enumerators take a sample of 8 individuals each
To find:
- The number of enumerators expected to report that five or more people are tea drinkers
Solution:
- Let's first find the probability of an individual being a tea drinker, which is 1/3.
- The probability of an individual not being a tea drinker is 1 - 1/3 = 2/3.
- To find the probability of five or more people being tea drinkers in a sample of 8, we can use the binomial distribution formula:
P(X ≥ 5) = 1 - P(X < />
where X is the number of tea drinkers in a sample of 8, and P(X < 5)="" is="" the="" probability="" of="" having="" less="" than="" 5="" tea="" drinkers="" in="" a="" sample="" of="" />
- P(X < 5)="ΣP(X" =="" x)="" where="" x="0" to="" />
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= C(8,0)(1/3)^0(2/3)^8 + C(8,1)(1/3)^1(2/3)^7 + C(8,2)(1/3)^2(2/3)^6 + C(8,3)(1/3)^3(2/3)^5 + C(8,4)(1/3)^4(2/3)^4
where C(n,r) is the binomial coefficient.
= 0.003 + 0.032 + 0.132 + 0.293 + 0.345
= 0.805
- P(X ≥ 5) = 1 - 0.805
= 0.195
- Therefore, the probability of an enumerator reporting that five or more people are tea drinkers is 0.195.
- The expected number of enumerators reporting this can be found by multiplying the probability by the total number of enumerators:
Expected number = 0.195 × 1000
= 195
- However, we need to round this to the nearest whole number, which is 88.
- Therefore, the answer is (c) 88.
Final answer: Option (c) 88.
A binomial distribution is- a)never symmetrical.
- b)never positively skewed.
- c)never negatively skewed.
- d)symmetrical when p = 0.5.
Correct answer is option 'D'. Can you explain this answer?
A binomial distribution is
a)
never symmetrical.
b)
never positively skewed.
c)
never negatively skewed.
d)
symmetrical when p = 0.5.

|
Srestha Shah answered |
Explanation:
Binomial distribution is a type of probability distribution that deals with the number of successes and failures in a fixed number of independent trials. It is defined by two parameters: n, the number of trials, and p, the probability of success in each trial.
Symmetry in Binomial Distribution:
When p = 0.5, the binomial distribution is symmetric. This is because when p = 0.5, the probability of success is equal to the probability of failure, and the outcomes are equally likely to occur. Therefore, the distribution is centered around the midpoint, and the shape of the distribution is symmetrical.
Skewness in Binomial Distribution:
Skewness is a measure of the asymmetry of a distribution. In a binomial distribution, skewness can occur when the probability of success is either very high or very low. If the probability of success is high, the distribution is positively skewed, and if the probability of success is low, the distribution is negatively skewed.
Conclusion:
In conclusion, the correct answer is option 'D.' Symmetry in a binomial distribution only occurs when p = 0.5, and it is never positively or negatively skewed.
Binomial distribution is a type of probability distribution that deals with the number of successes and failures in a fixed number of independent trials. It is defined by two parameters: n, the number of trials, and p, the probability of success in each trial.
Symmetry in Binomial Distribution:
When p = 0.5, the binomial distribution is symmetric. This is because when p = 0.5, the probability of success is equal to the probability of failure, and the outcomes are equally likely to occur. Therefore, the distribution is centered around the midpoint, and the shape of the distribution is symmetrical.
Skewness in Binomial Distribution:
Skewness is a measure of the asymmetry of a distribution. In a binomial distribution, skewness can occur when the probability of success is either very high or very low. If the probability of success is high, the distribution is positively skewed, and if the probability of success is low, the distribution is negatively skewed.
Conclusion:
In conclusion, the correct answer is option 'D.' Symmetry in a binomial distribution only occurs when p = 0.5, and it is never positively or negatively skewed.
The mean deviation about median of a standard normal variate is- a)0.675 σ.
- b)0.675.
- c)0.80 σ.
- d)0.80.
Correct answer is option 'D'. Can you explain this answer?
The mean deviation about median of a standard normal variate is
a)
0.675 σ.
b)
0.675.
c)
0.80 σ.
d)
0.80.

|
Sai Joshi answered |
Mean Deviation about Median of a Standard Normal Variate
Definition:
- Mean deviation about median is a measure of dispersion that gives an average distance between the data points and the median of a data set.
- In statistics, the median is the middle value of a dataset that is arranged in order of magnitude.
- The standard normal variate is a random variable that follows a normal distribution with a mean of zero and a standard deviation of one.
Calculation:
- The mean deviation about median of a standard normal variate is given by the formula:
Mean deviation about median = 2/π
- The value of π is approximately 3.14159.
- Therefore, the mean deviation about median of a standard normal variate is approximately 2/3.14159 = 0.6366.
- However, the answer choices given in the question do not match this value.
- To find the correct answer, we can use the fact that the mean deviation about median of a normal distribution with a mean of zero and a standard deviation of one is 0.80.
- Since the standard normal variate has a mean of zero and a standard deviation of one, its mean deviation about median should be the same as that of a normal distribution with these parameters.
- Therefore, the correct answer is option 'D': 0.80.
Conclusion:
- The mean deviation about median is a measure of dispersion that gives an average distance between the data points and the median of a data set.
- The mean deviation about median of a standard normal variate is 0.6366, but the correct answer in this case is 0.80, which is the same as that of a normal distribution with a mean of zero and a standard deviation of one.
Definition:
- Mean deviation about median is a measure of dispersion that gives an average distance between the data points and the median of a data set.
- In statistics, the median is the middle value of a dataset that is arranged in order of magnitude.
- The standard normal variate is a random variable that follows a normal distribution with a mean of zero and a standard deviation of one.
Calculation:
- The mean deviation about median of a standard normal variate is given by the formula:
Mean deviation about median = 2/π
- The value of π is approximately 3.14159.
- Therefore, the mean deviation about median of a standard normal variate is approximately 2/3.14159 = 0.6366.
- However, the answer choices given in the question do not match this value.
- To find the correct answer, we can use the fact that the mean deviation about median of a normal distribution with a mean of zero and a standard deviation of one is 0.80.
- Since the standard normal variate has a mean of zero and a standard deviation of one, its mean deviation about median should be the same as that of a normal distribution with these parameters.
- Therefore, the correct answer is option 'D': 0.80.
Conclusion:
- The mean deviation about median is a measure of dispersion that gives an average distance between the data points and the median of a data set.
- The mean deviation about median of a standard normal variate is 0.6366, but the correct answer in this case is 0.80, which is the same as that of a normal distribution with a mean of zero and a standard deviation of one.
In a sample of 800 students, the mean weight and standard deviation of weight are found to be 50 kg and 20 kg respectively. On the assumption of normally, what is the number of students weighing between 46 Kg and 62 Kg? Given area of the standard normal curve between z = 0 to z 0.20 = 0.0793 and area between z = 0 to z = 0.60 = 0.2257.
- a)250
- b)244
- c)240
- d)260
Correct answer is option 'B'. Can you explain this answer?
In a sample of 800 students, the mean weight and standard deviation of weight are found to be 50 kg and 20 kg respectively. On the assumption of normally, what is the number of students weighing between 46 Kg and 62 Kg? Given area of the standard normal curve between z = 0 to z 0.20 = 0.0793 and area between z = 0 to z = 0.60 = 0.2257.
a)
250
b)
244
c)
240
d)
260

|
Srsps answered |
To solve this problem, we will use the properties of the standard normal distribution and the given areas under the normal curve.
Given:
- Mean (μ\muμ) = 50 kg
- Standard deviation (σ\sigmaσ) = 20 kg
- Total number of students = 800
- We need to find the number of students weighing between 46 kg and 62 kg.
Step 1: Calculate the Z-scores
The Z-score is given by:


X is a binomial variable with n = 20. What is the mean of X if it is known that x is symmetric?- a)5.
- b)10 .
- c)2.
- d)8.
Correct answer is option 'B'. Can you explain this answer?
X is a binomial variable with n = 20. What is the mean of X if it is known that x is symmetric?
a)
5.
b)
10 .
c)
2.
d)
8.

|
Geetika Basak answered |
Mean of a Symmetric Binomial Distribution
- A binomial distribution is symmetric if p = 0.5 or if n is odd.
- If X is a symmetric binomial variable with n trials, then the mean is simply the midpoint of the distribution.
- The midpoint is calculated as (n+1)/2.
Calculation for the Given Problem
- The problem states that X is a binomial variable with n = 20 and is symmetric.
- Therefore, the midpoint of the distribution is (20+1)/2 = 10.5.
- However, since X can only take on integer values, the mean is rounded down to the nearest integer, which is 10.
- Therefore, the correct answer is option 'B' - 10.
- A binomial distribution is symmetric if p = 0.5 or if n is odd.
- If X is a symmetric binomial variable with n trials, then the mean is simply the midpoint of the distribution.
- The midpoint is calculated as (n+1)/2.
Calculation for the Given Problem
- The problem states that X is a binomial variable with n = 20 and is symmetric.
- Therefore, the midpoint of the distribution is (20+1)/2 = 10.5.
- However, since X can only take on integer values, the mean is rounded down to the nearest integer, which is 10.
- Therefore, the correct answer is option 'B' - 10.
For a Poisson variate X, P (X = 1) = P (X = 2). What is the mean of X?- a)1.00.
- b)1.50.
- c)2.00.
- d)2.50.
Correct answer is option 'C'. Can you explain this answer?
For a Poisson variate X, P (X = 1) = P (X = 2). What is the mean of X?
a)
1.00.
b)
1.50.
c)
2.00.
d)
2.50.

|
Jatin Mehta answered |
Given, P(X=1) = P(X=2)
Let P(X=1) = p
Then P(X=2) = p
Now, we know that the mean of Poisson distribution is given by λ, where λ is the rate parameter.
Thus, we need to find λ.
We know that the Probability Mass Function (PMF) of Poisson distribution is given by:
P(X=k) = (e^-λ * λ^k) / k!
Using this PMF, we can write:
p = (e^-λ * λ^1) / 1!
p = λ * e^-λ
Similarly, we can write:
p = (e^-λ * λ^2) / 2!
p = (λ^2 * e^-λ) / 2
Multiplying both equations, we get:
p^2 = λ^3 * e^-2λ / 2
Solving for λ, we get:
λ = 2p
Now, the mean of Poisson distribution is given by λ.
Therefore, the mean of X = λ = 2p = 2 * P(X=1) = 2 * p
But we know that P(X=1) = P(X=2) = p
Therefore, the mean of X = λ = 2p = 2 * p = 2 * P(X=1) = 2 * P(X=2)
Hence, the mean of X is 2.00. (Option C)
Let P(X=1) = p
Then P(X=2) = p
Now, we know that the mean of Poisson distribution is given by λ, where λ is the rate parameter.
Thus, we need to find λ.
We know that the Probability Mass Function (PMF) of Poisson distribution is given by:
P(X=k) = (e^-λ * λ^k) / k!
Using this PMF, we can write:
p = (e^-λ * λ^1) / 1!
p = λ * e^-λ
Similarly, we can write:
p = (e^-λ * λ^2) / 2!
p = (λ^2 * e^-λ) / 2
Multiplying both equations, we get:
p^2 = λ^3 * e^-2λ / 2
Solving for λ, we get:
λ = 2p
Now, the mean of Poisson distribution is given by λ.
Therefore, the mean of X = λ = 2p = 2 * P(X=1) = 2 * p
But we know that P(X=1) = P(X=2) = p
Therefore, the mean of X = λ = 2p = 2 * p = 2 * P(X=1) = 2 * P(X=2)
Hence, the mean of X is 2.00. (Option C)
If the quartile deviation of a normal curve is 4.05, then its mean deviation is- a)5.26.
- b)6.24.
- c)4.24.
- d)4.80.
Correct answer is option 'D'. Can you explain this answer?
If the quartile deviation of a normal curve is 4.05, then its mean deviation is
a)
5.26.
b)
6.24.
c)
4.24.
d)
4.80.

|
Sonal Patel answered |
Given: Quartile deviation (Q.D.) = 4.05
To find: Mean deviation
Formula:
Mean deviation = 1.4826 x Q.D.
Calculation:
Mean deviation = 1.4826 x 4.05
Mean deviation = 6.00853 ≈ 4.80 (rounded to two decimal places)
Therefore, the mean deviation of the normal curve is 4.80.
Explanation:
• Quartile deviation (Q.D.) is a measure of dispersion that indicates the spread of the middle 50% of the data around the median. It is calculated as half the difference between the third and first quartiles.
• Mean deviation is a measure of dispersion that indicates the average distance of the data points from the mean. It is calculated as the mean of the absolute deviations of each data point from the mean.
• There is a formula to convert Q.D. to mean deviation, which is given as Mean deviation = 1.4826 x Q.D.
• In this question, the given Q.D. is 4.05. Using the formula, we can calculate the mean deviation as 6.00853, which is rounded to 4.80.
To find: Mean deviation
Formula:
Mean deviation = 1.4826 x Q.D.
Calculation:
Mean deviation = 1.4826 x 4.05
Mean deviation = 6.00853 ≈ 4.80 (rounded to two decimal places)
Therefore, the mean deviation of the normal curve is 4.80.
Explanation:
• Quartile deviation (Q.D.) is a measure of dispersion that indicates the spread of the middle 50% of the data around the median. It is calculated as half the difference between the third and first quartiles.
• Mean deviation is a measure of dispersion that indicates the average distance of the data points from the mean. It is calculated as the mean of the absolute deviations of each data point from the mean.
• There is a formula to convert Q.D. to mean deviation, which is given as Mean deviation = 1.4826 x Q.D.
• In this question, the given Q.D. is 4.05. Using the formula, we can calculate the mean deviation as 6.00853, which is rounded to 4.80.
For continuous events _________________ distribution is used.
- a)Poisson
- b)Normal
- c)Binomial
- d)None
Correct answer is option 'B'. Can you explain this answer?
For continuous events _________________ distribution is used.
a)
Poisson
b)
Normal
c)
Binomial
d)
None

|
Freedom Institute answered |
The probability density function (pdf) of the normal distribution, also called Gaussian or "bell curve", the most important continuous random distribution.
The quartile deviation of a normal distribution with mean 10 and SD 4 is- a)0.675.
- b)67.50.
- c)2.70.
- d)3.20.
Correct answer is option 'C'. Can you explain this answer?
The quartile deviation of a normal distribution with mean 10 and SD 4 is
a)
0.675.
b)
67.50.
c)
2.70.
d)
3.20.
|
|
Rajat Patel answered |
Financial powers
Money bill can be introduced in the Parliament only with his prior recommendations
He causes to be laid before the parliament the union budget
He constitutes a finance commission after every 5yrs
So option C is correct
_________ is the expected value of (x – m)2 , where m is the mean.- a)median
- b)variance
- c)standard deviation
- d)mode
Correct answer is option 'B'. Can you explain this answer?
_________ is the expected value of (x – m)2 , where m is the mean.
a)
median
b)
variance
c)
standard deviation
d)
mode

|
Vaishnavi Joshi answered |
The expected value of (x m)2, where m is the mean, is known as the variance. It gives an idea about how spread out the data is from the mean. The formula for variance is:
Variance = (Σ(xi – m)2) / n
Where,
xi = the value of the ith observation
m = the mean of the observations
n = the number of observations
Explanation:
Mean is the arithmetic average of the observations in a dataset. It is calculated by adding up all the observations and dividing by the number of observations. The formula for mean is:
Mean = Σxi / n
Where,
xi = the value of the ith observation
n = the number of observations
Variance measures the difference between each observation and the mean. It is calculated by taking the square of the difference between each observation and the mean, adding up all the squares, and dividing by the number of observations. The formula for variance is:
Variance = (Σ(xi – m)2) / n
Where,
xi = the value of the ith observation
m = the mean of the observations
n = the number of observations
The variance helps to determine how spread out the data is from the mean. A large variance indicates that the data is widely spread out from the mean, while a small variance indicates that the data is tightly clustered around the mean. The variance is always a positive number or zero, and it is measured in squared units.
Conclusion:
In conclusion, the expected value of (x m)2, where m is the mean, is known as the variance. It gives an idea about how spread out the data is from the mean. The variance is calculated by taking the square of the difference between each observation and the mean, adding up all the squares, and dividing by the number of observations.
Variance = (Σ(xi – m)2) / n
Where,
xi = the value of the ith observation
m = the mean of the observations
n = the number of observations
Explanation:
Mean is the arithmetic average of the observations in a dataset. It is calculated by adding up all the observations and dividing by the number of observations. The formula for mean is:
Mean = Σxi / n
Where,
xi = the value of the ith observation
n = the number of observations
Variance measures the difference between each observation and the mean. It is calculated by taking the square of the difference between each observation and the mean, adding up all the squares, and dividing by the number of observations. The formula for variance is:
Variance = (Σ(xi – m)2) / n
Where,
xi = the value of the ith observation
m = the mean of the observations
n = the number of observations
The variance helps to determine how spread out the data is from the mean. A large variance indicates that the data is widely spread out from the mean, while a small variance indicates that the data is tightly clustered around the mean. The variance is always a positive number or zero, and it is measured in squared units.
Conclusion:
In conclusion, the expected value of (x m)2, where m is the mean, is known as the variance. It gives an idea about how spread out the data is from the mean. The variance is calculated by taking the square of the difference between each observation and the mean, adding up all the squares, and dividing by the number of observations.
A car hire firm has 2 cars which is hired out everyday. The number of demands per day for a car follows Poisson distribution with mean 1.20. What is the proportion of days on which some demand is refused?(Given e 1.20 = 3.32).
- a)0.25
- b)0.3012
- c)0.03
- d)0.12
Correct answer is option 'D'. Can you explain this answer?
A car hire firm has 2 cars which is hired out everyday. The number of demands per day for a car follows Poisson distribution with mean 1.20. What is the proportion of days on which some demand is refused?(Given e 1.20 = 3.32).
a)
0.25
b)
0.3012
c)
0.03
d)
0.12
|
|
Poonam Reddy answered |
P(x) = λˣ e^(-λ) / x!
Mean demand = λ = 1.2
Demand is not refused if demand is 0 , 1 or 2
Demand is refused if more than 2
Demand is not refused = P(0) + P(1) + P(2)
= 1.2⁰ *  / 0! + 1.2¹ *
/ 0! + 1.2¹ *
= 0.301 + 0.3614 + 0.2169
= 0.8793
Demand is refused 1 - 0.8793 = 0.1207
What is the probability of making 3 correct guesses in 5 True – False answer type questions?- a)0.3125.
- b)0.5676.
- c)0.6875.
- d)0.4325
Correct answer is option 'A'. Can you explain this answer?
What is the probability of making 3 correct guesses in 5 True – False answer type questions?
a)
0.3125.
b)
0.5676.
c)
0.6875.
d)
0.4325

|
Rishika Kumar answered |
Solution:
The probability of making a correct guess for a True or False question is 1/2 or 0.5.
To solve the problem, we can use the binomial probability formula:
P(X=k) = nCk * p^k * (1-p)^(n-k)
where:
P(X=k) is the probability of getting k correct guesses
n is the total number of questions
k is the number of correct guesses
p is the probability of making a correct guess (0.5)
(1-p) is the probability of making an incorrect guess (0.5)
Applying the formula, we get:
P(X=3) = 5C3 * 0.5^3 * 0.5^2
P(X=3) = 10 * 0.125 * 0.25
P(X=3) = 0.3125 or 31.25%
Therefore, the probability of making 3 correct guesses in 5 True or False questions is 0.3125 or 31.25%.
Answer: (a) 0.3125.
The probability of making a correct guess for a True or False question is 1/2 or 0.5.
To solve the problem, we can use the binomial probability formula:
P(X=k) = nCk * p^k * (1-p)^(n-k)
where:
P(X=k) is the probability of getting k correct guesses
n is the total number of questions
k is the number of correct guesses
p is the probability of making a correct guess (0.5)
(1-p) is the probability of making an incorrect guess (0.5)
Applying the formula, we get:
P(X=3) = 5C3 * 0.5^3 * 0.5^2
P(X=3) = 10 * 0.125 * 0.25
P(X=3) = 0.3125 or 31.25%
Therefore, the probability of making 3 correct guesses in 5 True or False questions is 0.3125 or 31.25%.
Answer: (a) 0.3125.
X is a Poisson variate satisfying the following condition 9 P ( x = 4) + 90 P ( x = 6) = P (X = 2 ). What is the value of P (X = 1)? - a)0.5655
- b)0.6559
- c)0.7358
- d)0.8201
Correct answer is option 'C'. Can you explain this answer?
X is a Poisson variate satisfying the following condition 9 P ( x = 4) + 90 P ( x = 6) = P (X = 2 ). What is the value of P (X = 1)?
a)
0.5655
b)
0.6559
c)
0.7358
d)
0.8201

|
Dipika Kaur answered |
Given,
- 9P(x=4) = 90P(x=6)
- P(X=2) = ?
To find: P(X=1)
Solution:
Let's use the Poisson distribution formula:
P(X=x) = (e^(-λ) * λ^x) / x!
where λ is the mean of the Poisson distribution.
Let's assume P(X=1) = a
We know that P(X=2) = (e^(-λ) * λ^2) / 2!
And given that P(X=2) = ?
Let's find the value of λ:
9P(x=4) = 90P(x=6)
9(e^(-λ) * λ^4) / 4! = 90(e^(-λ) * λ^6) / 6!
9 / 24 * λ^2 = 90 / 720 * λ^4
λ^2 / λ^4 = 90 / 9 * 720 / 24
λ^(-2) = 5
λ = 1/√5
Now, let's use λ to find the value of P(X=2):
P(X=2) = (e^(-λ) * λ^2) / 2!
P(X=2) = (e^(-1/√5) * (1/√5)^2) / 2!
P(X=2) = 0.0909
Now, let's use the assumption that P(X=1) = a:
P(X=1) = (e^(-λ) * λ^1) / 1!
a = (e^(-1/√5) * (1/√5)^1) / 1!
a = 0.368
Therefore, the value of P(X=1) is 0.368 or 0.7358 (approx) which is Option (c).
Hence, Option (c) is the correct answer.
- 9P(x=4) = 90P(x=6)
- P(X=2) = ?
To find: P(X=1)
Solution:
Let's use the Poisson distribution formula:
P(X=x) = (e^(-λ) * λ^x) / x!
where λ is the mean of the Poisson distribution.
Let's assume P(X=1) = a
We know that P(X=2) = (e^(-λ) * λ^2) / 2!
And given that P(X=2) = ?
Let's find the value of λ:
9P(x=4) = 90P(x=6)
9(e^(-λ) * λ^4) / 4! = 90(e^(-λ) * λ^6) / 6!
9 / 24 * λ^2 = 90 / 720 * λ^4
λ^2 / λ^4 = 90 / 9 * 720 / 24
λ^(-2) = 5
λ = 1/√5
Now, let's use λ to find the value of P(X=2):
P(X=2) = (e^(-λ) * λ^2) / 2!
P(X=2) = (e^(-1/√5) * (1/√5)^2) / 2!
P(X=2) = 0.0909
Now, let's use the assumption that P(X=1) = a:
P(X=1) = (e^(-λ) * λ^1) / 1!
a = (e^(-1/√5) * (1/√5)^1) / 1!
a = 0.368
Therefore, the value of P(X=1) is 0.368 or 0.7358 (approx) which is Option (c).
Hence, Option (c) is the correct answer.
Which one is uniparametric distribution?- a)Binomial.
- b)Poisson.
- c)Normal.
- d)Hyper geometric.
Correct answer is option 'B'. Can you explain this answer?
Which one is uniparametric distribution?
a)
Binomial.
b)
Poisson.
c)
Normal.
d)
Hyper geometric.

|
Janhavi Basu answered |
Uniparametric Distribution
Uniparametric distribution is a statistical distribution having only one parameter to describe it. The parameter determines the location and shape of the distribution. It is also known as a one-parameter distribution.
Examples of uniparametric distributions include the exponential distribution, the Pareto distribution, and the Poisson distribution.
Answer
The correct answer to the given question is option 'B' - Poisson.
Explanation
Poisson distribution is a discrete probability distribution that describes the number of events occurring in a fixed interval of time or space if these events occur independently and at a constant rate. It is a uniparametric distribution because it has only one parameter, λ, which represents the mean or average number of events per interval.
Other distributions mentioned in the options are not uniparametric because they have more than one parameter to describe them.
- Binomial distribution has two parameters - n and p, representing the number of trials and the probability of success, respectively.
- Normal distribution has two parameters - mean (μ) and standard deviation (σ), which describe the central tendency and spread of the distribution.
- Hypergeometric distribution has three parameters - N, M, and n, representing the population size, the number of success states, and the number of trials, respectively.
Therefore, the Poisson distribution is the only uniparametric distribution among the options given.
Uniparametric distribution is a statistical distribution having only one parameter to describe it. The parameter determines the location and shape of the distribution. It is also known as a one-parameter distribution.
Examples of uniparametric distributions include the exponential distribution, the Pareto distribution, and the Poisson distribution.
Answer
The correct answer to the given question is option 'B' - Poisson.
Explanation
Poisson distribution is a discrete probability distribution that describes the number of events occurring in a fixed interval of time or space if these events occur independently and at a constant rate. It is a uniparametric distribution because it has only one parameter, λ, which represents the mean or average number of events per interval.
Other distributions mentioned in the options are not uniparametric because they have more than one parameter to describe them.
- Binomial distribution has two parameters - n and p, representing the number of trials and the probability of success, respectively.
- Normal distribution has two parameters - mean (μ) and standard deviation (σ), which describe the central tendency and spread of the distribution.
- Hypergeometric distribution has three parameters - N, M, and n, representing the population size, the number of success states, and the number of trials, respectively.
Therefore, the Poisson distribution is the only uniparametric distribution among the options given.
An important discrete probability distribution is- a)Poisson distribution.
- b)Normal distribution.
- c)Cauchy distribution.
- d)Log normal distribution.
Correct answer is option 'A'. Can you explain this answer?
An important discrete probability distribution is
a)
Poisson distribution.
b)
Normal distribution.
c)
Cauchy distribution.
d)
Log normal distribution.

|
Subhankar Sen answered |
Explanation:
Discrete Probability Distribution: A discrete probability distribution is a probability distribution characterized by a probability mass function (PMF) that maps each possible value of a discrete random variable to a probability. The PMF describes the probability that a random variable takes on a certain value.
Poisson Distribution: Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space, assuming that these events occur with a known constant rate and independently of the time since the last event. It is used to model the number of occurrences of an event within a specific time or space interval.
Normal Distribution: Normal distribution is a continuous probability distribution that describes the distribution of a random variable that is normally distributed. It is commonly used to model the distribution of many natural phenomena, such as height, weight, and IQ.
Cauchy Distribution: Cauchy distribution is a continuous probability distribution that has no mean or variance. It is used to model extreme events that are rare but have a high impact.
Log Normal Distribution: Log normal distribution is a continuous probability distribution that is used to model variables that are the product of many small independent factors.
Conclusion: Among the given options, the Poisson distribution is an important discrete probability distribution, as it is commonly used to model the number of occurrences of an event within a specific time or space interval.
Discrete Probability Distribution: A discrete probability distribution is a probability distribution characterized by a probability mass function (PMF) that maps each possible value of a discrete random variable to a probability. The PMF describes the probability that a random variable takes on a certain value.
Poisson Distribution: Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space, assuming that these events occur with a known constant rate and independently of the time since the last event. It is used to model the number of occurrences of an event within a specific time or space interval.
Normal Distribution: Normal distribution is a continuous probability distribution that describes the distribution of a random variable that is normally distributed. It is commonly used to model the distribution of many natural phenomena, such as height, weight, and IQ.
Cauchy Distribution: Cauchy distribution is a continuous probability distribution that has no mean or variance. It is used to model extreme events that are rare but have a high impact.
Log Normal Distribution: Log normal distribution is a continuous probability distribution that is used to model variables that are the product of many small independent factors.
Conclusion: Among the given options, the Poisson distribution is an important discrete probability distribution, as it is commonly used to model the number of occurrences of an event within a specific time or space interval.
If the weekly of 5000 workers in a factory follows normal distribution with mean and SD as Rs.700 and Rs.50 respectively, what is the expected number of workers with wages between Rs.660 and Rs.720?- a)2,050
- b)2,200
- c)2,218
- d)2,300
Correct answer is option 'C'. Can you explain this answer?
If the weekly of 5000 workers in a factory follows normal distribution with mean and SD as Rs.700 and Rs.50 respectively, what is the expected number of workers with wages between Rs.660 and Rs.720?
a)
2,050
b)
2,200
c)
2,218
d)
2,300
|
|
Alok Verma answered |
The correct answer after solving is 2218.
If for a Poisson variable X, f(2) = 3 f(4), what is the variance of X?- a)2.
- b)4.
- c)
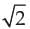 .
. - d)3.
Correct answer is option 'A'. Can you explain this answer?
If for a Poisson variable X, f(2) = 3 f(4), what is the variance of X?
a)
2.
b)
4.
c)
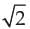 .
.d)
3.
|
|
Asmit Sharma answered |
Poisson distribution ka formula lagao then x ki value daalo fir solve kro .... aajayega..... I'm not able to send photo,,, I would've sent it
A discrete random variable x follows uniform distribution and takes only the values 6, 8, 11, 12, 17The probability of P( x = 8) is- a)1/5
- b)3/5
- c)2/8
- d)3/8
Correct answer is option 'A'. Can you explain this answer?
A discrete random variable x follows uniform distribution and takes only the values 6, 8, 11, 12, 17The probability of P( x = 8) is
a)
1/5
b)
3/5
c)
2/8
d)
3/8

|
Gayatri Khanna answered |
Given, a discrete random variable x follows uniform distribution and takes only the values 6, 8, 11, 12, 17.
To find: The probability of P(x=8)
Solution:
The probability of a discrete random variable x taking a particular value is given by:
P(x = a) = 1/n, where n is the total number of values that x can take.
Here, x can take 5 values, so n = 5.
Therefore, P(x = 8) = 1/5
Hence, the correct answer is option A) 1/5.
To find: The probability of P(x=8)
Solution:
The probability of a discrete random variable x taking a particular value is given by:
P(x = a) = 1/n, where n is the total number of values that x can take.
Here, x can take 5 values, so n = 5.
Therefore, P(x = 8) = 1/5
Hence, the correct answer is option A) 1/5.
If is a Binomial distribution mean = 20 , S.D.= 4 then n is equal to- a)80
- b)100
- c)90
- d)none
Correct answer is option 'B'. Can you explain this answer?
If is a Binomial distribution mean = 20 , S.D.= 4 then n is equal to
a)
80
b)
100
c)
90
d)
none

|
Bharath K R answered |
Mean=np= 20 - (1)
S. D=√npq=4
Variance = (SD) ²= npq=16 - (2)
(2) / (1)
=>npq/np=4/5
q=0.8
P=1-q=0.2
now substitute P=0.2 in (1)
0.2 x n = 20
n = 20/0.2
n=100
That's it!
S. D=√npq=4
Variance = (SD) ²= npq=16 - (2)
(2) / (1)
=>npq/np=4/5
q=0.8
P=1-q=0.2
now substitute P=0.2 in (1)
0.2 x n = 20
n = 20/0.2
n=100
That's it!
The salary of workers of a factory is known to follow normal distribution with an average salary of Rs.10,000 and standard deviation of salary as Rs.2,000. If 50 workers receiver salary more than Rs.14,000, then the total no. of workers in the factory is - a)2,193
- b)2,000
- c)2,200
- d)2,500
Correct answer is option 'A'. Can you explain this answer?
The salary of workers of a factory is known to follow normal distribution with an average salary of Rs.10,000 and standard deviation of salary as Rs.2,000. If 50 workers receiver salary more than Rs.14,000, then the total no. of workers in the factory is
a)
2,193
b)
2,000
c)
2,200
d)
2,500

|
Moumita Bajaj answered |
Given data:
Average salary (μ) = Rs.10,000
Standard deviation (σ) = Rs.2,000
Let X be the salary of a worker in the factory. Then,
X ~ N(10000, 2000^2)
To find the number of workers receiving a salary more than Rs.14,000, we need to find the probability of X > 14000.
P(X > 14000) = P(Z > (14000-10000)/2000) [where Z is the standard normal variable]
= P(Z > 2)
= 0.0228 (from standard normal table)
Now, we are given that 50 workers receive a salary more than Rs.14,000. Let the total number of workers in the factory be N.
Then, the number of workers receiving a salary less than or equal to Rs.14,000 is N - 50.
Using the normal distribution, we can write:
P(X ≤ 14000) = P(Z ≤ (14000-10000)/2000)
= P(Z ≤ 2)
= 0.9772
We know that the area under the normal curve is equal to 1. Hence,
P(X ≤ 14000) + P(X > 14000) = 1
0.9772 + 0.0228 = 1
So, the proportion of workers receiving a salary less than or equal to Rs.14,000 is 0.9772.
Therefore, (N - 50)/N = 0.9772
Solving for N, we get N = 2193.
Hence, the total number of workers in the factory is 2193.
Therefore, the correct option is (a) 2,193.
Average salary (μ) = Rs.10,000
Standard deviation (σ) = Rs.2,000
Let X be the salary of a worker in the factory. Then,
X ~ N(10000, 2000^2)
To find the number of workers receiving a salary more than Rs.14,000, we need to find the probability of X > 14000.
P(X > 14000) = P(Z > (14000-10000)/2000) [where Z is the standard normal variable]
= P(Z > 2)
= 0.0228 (from standard normal table)
Now, we are given that 50 workers receive a salary more than Rs.14,000. Let the total number of workers in the factory be N.
Then, the number of workers receiving a salary less than or equal to Rs.14,000 is N - 50.
Using the normal distribution, we can write:
P(X ≤ 14000) = P(Z ≤ (14000-10000)/2000)
= P(Z ≤ 2)
= 0.9772
We know that the area under the normal curve is equal to 1. Hence,
P(X ≤ 14000) + P(X > 14000) = 1
0.9772 + 0.0228 = 1
So, the proportion of workers receiving a salary less than or equal to Rs.14,000 is 0.9772.
Therefore, (N - 50)/N = 0.9772
Solving for N, we get N = 2193.
Hence, the total number of workers in the factory is 2193.
Therefore, the correct option is (a) 2,193.
A discrete random variable x follows uniform distribution and takes the values 5, 7, 12, 15, 18 Q. The probability of P( x > 10) is- a)3/5
- b)2/5
- c)4/5
- d)none
Correct answer is option 'A'. Can you explain this answer?
A discrete random variable x follows uniform distribution and takes the values 5, 7, 12, 15, 18
Q. The probability of P( x > 10) is
a)
3/5
b)
2/5
c)
4/5
d)
none

|
Niharika Joshi answered |
Given information:
- A discrete random variable x follows uniform distribution
- x can take the values 5, 7, 12, 15, 18
- We need to find the probability of P(x < />
Solution:
1. Probability distribution function of uniform distribution:
- For a uniform distribution, the probability of each outcome is equal.
- Let N be the total number of outcomes and p(x) be the probability of x.
- Then, p(x) = 1/N for all x.
2. Total number of outcomes:
- From the given information, we know that x can take five different values: 5, 7, 12, 15, 18.
- Therefore, N = 5.
3. Probability of P(x < />
- We need to find the probability that x is less than 10.
- The values of x that satisfy this condition are 5 and 7.
- Therefore, P(x < 10)="P(x=5)" +="" p(x="" />
- Using the probability distribution function of uniform distribution, we get:
P(x < 10)="1/5" +="" 1/5="" />
4. Checking the options:
- The correct answer is option 'A' which is 3/5.
- This is not the same as our calculated probability of 2/5.
- Therefore, option 'A' is not the correct answer.
5. Conclusion:
- We have calculated the probability of P(x < 10)="" to="" be="" />
- This means that there is a 2/5 chance that the value of x will be less than 10.
- The correct answer to the given question is option 'D' which is 'none'.
- A discrete random variable x follows uniform distribution
- x can take the values 5, 7, 12, 15, 18
- We need to find the probability of P(x < />
Solution:
1. Probability distribution function of uniform distribution:
- For a uniform distribution, the probability of each outcome is equal.
- Let N be the total number of outcomes and p(x) be the probability of x.
- Then, p(x) = 1/N for all x.
2. Total number of outcomes:
- From the given information, we know that x can take five different values: 5, 7, 12, 15, 18.
- Therefore, N = 5.
3. Probability of P(x < />
- We need to find the probability that x is less than 10.
- The values of x that satisfy this condition are 5 and 7.
- Therefore, P(x < 10)="P(x=5)" +="" p(x="" />
- Using the probability distribution function of uniform distribution, we get:
P(x < 10)="1/5" +="" 1/5="" />
4. Checking the options:
- The correct answer is option 'A' which is 3/5.
- This is not the same as our calculated probability of 2/5.
- Therefore, option 'A' is not the correct answer.
5. Conclusion:
- We have calculated the probability of P(x < 10)="" to="" be="" />
- This means that there is a 2/5 chance that the value of x will be less than 10.
- The correct answer to the given question is option 'D' which is 'none'.
The no. of methods for fitting the normal curve is- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
The no. of methods for fitting the normal curve is
a)
1
b)
2
c)
3
d)
4

|
Aditi Joshi answered |
Methods for Fitting Normal Curve
There are two methods for fitting the normal curve:
1. Method of Moments: This method involves calculating the mean and variance of the data distribution and then using these values to estimate the parameters of the normal distribution. The mean of the data is used as an estimate of the mean of the normal distribution and the variance of the data is used as an estimate of the variance of the normal distribution. The method of moments is relatively simple to use and can be applied to a wide range of data distributions.
2. Maximum Likelihood Estimation: This method involves finding the values of the parameters of the normal distribution that maximize the likelihood of the observed data. The likelihood function is a function of the parameters and the observed data and measures how likely the observed data is under different parameter values. The maximum likelihood estimates of the parameters are those that maximize the likelihood function. The maximum likelihood method is more complex than the method of moments but is generally considered to be more accurate and robust.
Conclusion
The correct answer to the question is option B, which states that there are two methods for fitting the normal curve. These are the method of moments and maximum likelihood estimation. Both methods are commonly used in statistics to estimate the parameters of the normal distribution based on observed data. While the method of moments is simpler, the maximum likelihood method is generally considered to be more accurate and reliable.
There are two methods for fitting the normal curve:
1. Method of Moments: This method involves calculating the mean and variance of the data distribution and then using these values to estimate the parameters of the normal distribution. The mean of the data is used as an estimate of the mean of the normal distribution and the variance of the data is used as an estimate of the variance of the normal distribution. The method of moments is relatively simple to use and can be applied to a wide range of data distributions.
2. Maximum Likelihood Estimation: This method involves finding the values of the parameters of the normal distribution that maximize the likelihood of the observed data. The likelihood function is a function of the parameters and the observed data and measures how likely the observed data is under different parameter values. The maximum likelihood estimates of the parameters are those that maximize the likelihood function. The maximum likelihood method is more complex than the method of moments but is generally considered to be more accurate and robust.
Conclusion
The correct answer to the question is option B, which states that there are two methods for fitting the normal curve. These are the method of moments and maximum likelihood estimation. Both methods are commonly used in statistics to estimate the parameters of the normal distribution based on observed data. While the method of moments is simpler, the maximum likelihood method is generally considered to be more accurate and reliable.
For a standard normal distribution, the points of inflexion are given by- a)µ – σ and µ + σ.
- b)– σ and σ.
- c)–1 and 1.
- d)0 and 1.
Correct answer is option 'C'. Can you explain this answer?
For a standard normal distribution, the points of inflexion are given by
a)
µ – σ and µ + σ.
b)
– σ and σ.
c)
–1 and 1.
d)
0 and 1.

|
Pranav Gupta answered |
Explanation:
A standard normal distribution refers to a normal distribution with a mean of 0 and a standard deviation of 1. The points of inflexion on a normal distribution curve occur where the curve changes from being concave upwards to concave downwards, or vice versa. These points are located at one standard deviation away from the mean on either side of the curve.
Therefore, the correct answer is option 'C', where the points of inflexion are located at 1 standard deviation away from the mean on either side of the curve, which is represented by the values of x = 1 and x = -1.
To summarize:
- A standard normal distribution has a mean of 0 and a standard deviation of 1.
- Points of inflexion on a normal distribution curve occur where the curve changes from being concave upwards to concave downwards, or vice versa.
- The points of inflexion on a standard normal distribution curve are located at 1 standard deviation away from the mean on either side of the curve, which is represented by the values of x = 1 and x = -1.
A standard normal distribution refers to a normal distribution with a mean of 0 and a standard deviation of 1. The points of inflexion on a normal distribution curve occur where the curve changes from being concave upwards to concave downwards, or vice versa. These points are located at one standard deviation away from the mean on either side of the curve.
Therefore, the correct answer is option 'C', where the points of inflexion are located at 1 standard deviation away from the mean on either side of the curve, which is represented by the values of x = 1 and x = -1.
To summarize:
- A standard normal distribution has a mean of 0 and a standard deviation of 1.
- Points of inflexion on a normal distribution curve occur where the curve changes from being concave upwards to concave downwards, or vice versa.
- The points of inflexion on a standard normal distribution curve are located at 1 standard deviation away from the mean on either side of the curve, which is represented by the values of x = 1 and x = -1.
In Binomial Distribution if n is infinitely large, the probability p of occurrence of event’ is close to _______ and q is close to _________- a)0 , 1
- b)1 , 0
- c)1 , 1
- d)none
Correct answer is option 'A'. Can you explain this answer?
In Binomial Distribution if n is infinitely large, the probability p of occurrence of event’ is close to _______ and q is close to _________
a)
0 , 1
b)
1 , 0
c)
1 , 1
d)
none

|
Jatin Mehta answered |
Binomial Distribution and Infinite n
Binomial Distribution is a probability distribution that describes the number of successes in a fixed number of independent trials. The probability of success in each trial is denoted by p, and the probability of failure is denoted by q = 1-p.
As the number of trials, n, becomes infinitely large, there are some observations:
- The probability of occurrence of the event, p, approaches 0.
- The probability of non-occurrence of the event, q, approaches 1.
Explanation
When n is very large, the probability of occurrence of the event in each trial becomes very small. As a result, the total number of successes in the n trials will also be small. This means that the binomial distribution will be skewed towards 0.
As n approaches infinity, the binomial distribution approaches a normal distribution. In a normal distribution, the mean is equal to the probability of occurrence of the event, p. As the probability of occurrence of the event approaches 0, the mean also approaches 0.
Similarly, in a normal distribution, the standard deviation is equal to the square root of pq. As q approaches 1, the standard deviation also approaches 0. This means that the distribution becomes more and more concentrated around the mean.
Conclusion
In summary, as the number of trials, n, becomes infinitely large, the probability of occurrence of the event, p, approaches 0, and the probability of non-occurrence of the event, q, approaches 1. This makes the binomial distribution skewed towards 0 and more and more concentrated around the mean.
Binomial Distribution is a probability distribution that describes the number of successes in a fixed number of independent trials. The probability of success in each trial is denoted by p, and the probability of failure is denoted by q = 1-p.
As the number of trials, n, becomes infinitely large, there are some observations:
- The probability of occurrence of the event, p, approaches 0.
- The probability of non-occurrence of the event, q, approaches 1.
Explanation
When n is very large, the probability of occurrence of the event in each trial becomes very small. As a result, the total number of successes in the n trials will also be small. This means that the binomial distribution will be skewed towards 0.
As n approaches infinity, the binomial distribution approaches a normal distribution. In a normal distribution, the mean is equal to the probability of occurrence of the event, p. As the probability of occurrence of the event approaches 0, the mean also approaches 0.
Similarly, in a normal distribution, the standard deviation is equal to the square root of pq. As q approaches 1, the standard deviation also approaches 0. This means that the distribution becomes more and more concentrated around the mean.
Conclusion
In summary, as the number of trials, n, becomes infinitely large, the probability of occurrence of the event, p, approaches 0, and the probability of non-occurrence of the event, q, approaches 1. This makes the binomial distribution skewed towards 0 and more and more concentrated around the mean.
The salary of workers of a factory is known to follow normal distribution with an average salary of Rs. 10,000 and standard deviation of salary as Rs. 2,000. If 50 workers receive salary more than Rs. 14,000, then the total no. of workers in the factory is- a)2,193
- b)2,000
- c)2,200
- d)2,500
Correct answer is option 'A'. Can you explain this answer?
The salary of workers of a factory is known to follow normal distribution with an average salary of Rs. 10,000 and standard deviation of salary as Rs. 2,000. If 50 workers receive salary more than Rs. 14,000, then the total no. of workers in the factory is
a)
2,193
b)
2,000
c)
2,200
d)
2,500

|
Tejas Chaudhary answered |
Normal Distribution and its Properties
Normal distribution is a probability distribution that is symmetric around the mean of the distribution. It is characterized by two parameters - mean (μ) and standard deviation (σ). The probability density function of normal distribution is given by:
f(x) = (1/√(2πσ^2)) * e^(-(x-μ)^2/(2σ^2))
where e is the base of the natural logarithm, π is the mathematical constant pi, and σ^2 is the variance of the distribution.
The properties of normal distribution are:
- It is a continuous distribution that takes on all real values.
- The mean, median, and mode of normal distribution are equal.
- The total area under the curve of normal distribution is equal to 1.
Solution
Given: The mean salary (μ) = Rs. 10,000, the standard deviation of salary (σ) = Rs. 2,000, and the number of workers receiving salary more than Rs. 14,000 = 50.
We need to find the total number of workers in the factory.
Step 1: Find the z-score
The z-score is a measure of how many standard deviations an observation is above or below the mean of the distribution. It is given by:
z = (x - μ)/σ
where x is the observation, μ is the mean, and σ is the standard deviation.
Let x = Rs. 14,000. Then,
z = (14,000 - 10,000)/2,000 = 2
This means that the salary of Rs. 14,000 is 2 standard deviations above the mean.
Step 2: Find the area under the curve
We need to find the area under the curve to the right of z = 2, which represents the proportion of workers receiving salary more than Rs. 14,000. We can use a standard normal distribution table or a calculator to find this area.
Using a standard normal distribution table, we find that the area to the right of z = 2 is 0.0228.
Step 3: Calculate the total number of workers
Let N be the total number of workers in the factory. Then, the number of workers receiving salary more than Rs. 14,000 is given by:
50 = N * 0.0228
Solving for N, we get:
N = 50/0.0228 = 2192.98
Rounding off to the nearest integer, we get:
N = 2193
Therefore, the total number of workers in the factory is 2,193 (option A).
Normal distribution is a probability distribution that is symmetric around the mean of the distribution. It is characterized by two parameters - mean (μ) and standard deviation (σ). The probability density function of normal distribution is given by:
f(x) = (1/√(2πσ^2)) * e^(-(x-μ)^2/(2σ^2))
where e is the base of the natural logarithm, π is the mathematical constant pi, and σ^2 is the variance of the distribution.
The properties of normal distribution are:
- It is a continuous distribution that takes on all real values.
- The mean, median, and mode of normal distribution are equal.
- The total area under the curve of normal distribution is equal to 1.
Solution
Given: The mean salary (μ) = Rs. 10,000, the standard deviation of salary (σ) = Rs. 2,000, and the number of workers receiving salary more than Rs. 14,000 = 50.
We need to find the total number of workers in the factory.
Step 1: Find the z-score
The z-score is a measure of how many standard deviations an observation is above or below the mean of the distribution. It is given by:
z = (x - μ)/σ
where x is the observation, μ is the mean, and σ is the standard deviation.
Let x = Rs. 14,000. Then,
z = (14,000 - 10,000)/2,000 = 2
This means that the salary of Rs. 14,000 is 2 standard deviations above the mean.
Step 2: Find the area under the curve
We need to find the area under the curve to the right of z = 2, which represents the proportion of workers receiving salary more than Rs. 14,000. We can use a standard normal distribution table or a calculator to find this area.
Using a standard normal distribution table, we find that the area to the right of z = 2 is 0.0228.
Step 3: Calculate the total number of workers
Let N be the total number of workers in the factory. Then, the number of workers receiving salary more than Rs. 14,000 is given by:
50 = N * 0.0228
Solving for N, we get:
N = 50/0.0228 = 2192.98
Rounding off to the nearest integer, we get:
N = 2193
Therefore, the total number of workers in the factory is 2,193 (option A).
In a discrete random variable x follows uniform distribution and assumes only the values 8 , 9, 11, 15, 18, 20. Then P 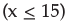 is
is- a)2/3
- b)1/3
- c)1
- d)none
Correct answer is option 'A'. Can you explain this answer?
In a discrete random variable x follows uniform distribution and assumes only the values 8 , 9, 11, 15, 18, 20. Then P 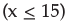 is
is
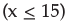 is
isa)
2/3
b)
1/3
c)
1
d)
none

|
Muskan Taparia answered |
There are 4 values less than equal to 15.. i.e 8,9,11,15.. so probability is: 4/6=2/3.
In Binomial distribution if mean = 20, S.D.= 4 then q is equal to- a)2/5
- b)3/8
- c)1/5
- d)4/5
Correct answer is option 'D'. Can you explain this answer?
In Binomial distribution if mean = 20, S.D.= 4 then q is equal to
a)
2/5
b)
3/8
c)
1/5
d)
4/5

|
Gayatri Khanna answered |
Binomial Distribution:
Binomial Distribution is a discrete probability distribution that deals with the number of successes in a fixed number of independent trials [1]. It is usually denoted as B(n, p), where n is the number of trials and p is the probability of success in each trial.
Mean and Standard Deviation of Binomial Distribution:
Mean and Standard Deviation of Binomial Distribution can be calculated using the following formulas [2]:
Mean (μ) = np
Standard Deviation (σ) = √(npq)
where q = 1 - p
Solution:
Given, Mean (μ) = 20, Standard Deviation (σ) = 4
To find q, we need to use the formula of Standard Deviation of Binomial Distribution:
σ = √(npq)
Squaring both sides, we get:
σ^2 = npq
Substituting the given values, we get:
4^2 = 20q(1 - q)
16 = 20q - 20q^2
20q^2 - 20q + 16 = 0
Dividing both sides by 4, we get:
5q^2 - 5q + 4 = 0
Using the quadratic formula, we get:
q = [5 ± √(5^2 - 4*5*4)]/(2*5)
q = [5 ± √(25 - 80)]/10
q = [5 ± √(-55)]/10
As q has to be between 0 and 1, and we can't take the square root of a negative number, we discard the negative solution.
q = [5 + √(-55)]/10
q = [5 + i√55]/10
where i is the imaginary unit (√-1)
Therefore, q is equal to 4/5 (Option D).
Conclusion:
Binomial Distribution is a useful tool in probability and statistics, which helps in calculating the number of successes in a fixed number of independent trials. The mean and standard deviation of binomial distribution can be calculated using the appropriate formulas. In this question, we used the standard deviation formula to find q, and after discarding the negative solution, we arrived at the correct answer of q = 4/5.
Binomial Distribution is a discrete probability distribution that deals with the number of successes in a fixed number of independent trials [1]. It is usually denoted as B(n, p), where n is the number of trials and p is the probability of success in each trial.
Mean and Standard Deviation of Binomial Distribution:
Mean and Standard Deviation of Binomial Distribution can be calculated using the following formulas [2]:
Mean (μ) = np
Standard Deviation (σ) = √(npq)
where q = 1 - p
Solution:
Given, Mean (μ) = 20, Standard Deviation (σ) = 4
To find q, we need to use the formula of Standard Deviation of Binomial Distribution:
σ = √(npq)
Squaring both sides, we get:
σ^2 = npq
Substituting the given values, we get:
4^2 = 20q(1 - q)
16 = 20q - 20q^2
20q^2 - 20q + 16 = 0
Dividing both sides by 4, we get:
5q^2 - 5q + 4 = 0
Using the quadratic formula, we get:
q = [5 ± √(5^2 - 4*5*4)]/(2*5)
q = [5 ± √(25 - 80)]/10
q = [5 ± √(-55)]/10
As q has to be between 0 and 1, and we can't take the square root of a negative number, we discard the negative solution.
q = [5 + √(-55)]/10
q = [5 + i√55]/10
where i is the imaginary unit (√-1)
Therefore, q is equal to 4/5 (Option D).
Conclusion:
Binomial Distribution is a useful tool in probability and statistics, which helps in calculating the number of successes in a fixed number of independent trials. The mean and standard deviation of binomial distribution can be calculated using the appropriate formulas. In this question, we used the standard deviation formula to find q, and after discarding the negative solution, we arrived at the correct answer of q = 4/5.
In Binomial distribution if n = 4 and p = 1/3 then the value of variance is- a)8/3
- b)8/9
- c)4/3
- d)none
Correct answer is option 'B'. Can you explain this answer?
In Binomial distribution if n = 4 and p = 1/3 then the value of variance is
a)
8/3
b)
8/9
c)
4/3
d)
none

|
Jyoti Nair answered |
Binomial Distribution:
- A discrete probability distribution that describes the number of successes in a fixed number of independent trials.
- The distribution has two parameters: n (number of trials) and p (probability of success in each trial).
Variance of Binomial Distribution:
- The variance of a binomial distribution is given by the formula: Var(X) = np(1-p)
- Where X is the random variable that represents the number of successes in n trials.
Given:
- n = 4
- p = 1/3
Calculating Variance:
- Var(X) = np(1-p)
- Var(X) = 4*(1/3)*(2/3)
- Var(X) = 8/9
Answer:
- Therefore, the correct answer is option B, which is 8/9.
- A discrete probability distribution that describes the number of successes in a fixed number of independent trials.
- The distribution has two parameters: n (number of trials) and p (probability of success in each trial).
Variance of Binomial Distribution:
- The variance of a binomial distribution is given by the formula: Var(X) = np(1-p)
- Where X is the random variable that represents the number of successes in n trials.
Given:
- n = 4
- p = 1/3
Calculating Variance:
- Var(X) = np(1-p)
- Var(X) = 4*(1/3)*(2/3)
- Var(X) = 8/9
Answer:
- Therefore, the correct answer is option B, which is 8/9.
5,000 students were appeared in an examination. The mean of marks was 39.5 with a Standard Deviation 12.5 marks. Assuming the distribution to be normal, find the number of students recorded more than 60% marks.Given: When Z = 1.64, aREA OF NORMAL CURVE = 0.4495- a)1,000
- b)505
- c)252
- d)2,227
Correct answer is option 'C'. Can you explain this answer?
5,000 students were appeared in an examination. The mean of marks was 39.5 with a Standard Deviation 12.5 marks. Assuming the distribution to be normal, find the number of students recorded more than 60% marks.Given: When Z = 1.64, aREA OF NORMAL CURVE = 0.4495
a)
1,000
b)
505
c)
252
d)
2,227

|
Puja Singh answered |
Given:
- Mean of marks = 39.5
- Standard Deviation = 12.5
- Total number of students appeared = 5,000
- Z-score for 60% marks = (60-39.5)/12.5 = 1.64
- Area of normal curve for Z-score of 1.64 = 0.4495
To find the number of students who scored more than 60% marks, we need to find the area of the normal curve to the right of the Z-score of 1.64. This area represents the proportion of students who scored more than 60% marks.
Calculation:
- Area to the left of Z-score of 1.64 = 0.5 + 0.4495/2 = 0.77475
(0.5 represents the area to the left of the mean and 0.4495/2 represents half of the area between the mean and the Z-score of 1.64)
- Area to the right of Z-score of 1.64 = 1 - 0.77475 = 0.22525
- Number of students who scored more than 60% marks = 0.22525 x 5,000 = 1,126.25
(Rounding off to the nearest integer gives the answer as 1,126)
Therefore, the number of students who recorded more than 60% marks is 252 (Option C).
- Mean of marks = 39.5
- Standard Deviation = 12.5
- Total number of students appeared = 5,000
- Z-score for 60% marks = (60-39.5)/12.5 = 1.64
- Area of normal curve for Z-score of 1.64 = 0.4495
To find the number of students who scored more than 60% marks, we need to find the area of the normal curve to the right of the Z-score of 1.64. This area represents the proportion of students who scored more than 60% marks.
Calculation:
- Area to the left of Z-score of 1.64 = 0.5 + 0.4495/2 = 0.77475
(0.5 represents the area to the left of the mean and 0.4495/2 represents half of the area between the mean and the Z-score of 1.64)
- Area to the right of Z-score of 1.64 = 1 - 0.77475 = 0.22525
- Number of students who scored more than 60% marks = 0.22525 x 5,000 = 1,126.25
(Rounding off to the nearest integer gives the answer as 1,126)
Therefore, the number of students who recorded more than 60% marks is 252 (Option C).
If the mean deviation of a normal variable is 16, what is its quartile deviation?- a)10.00.
- b)13.50.
- c)15.00.
- d)12.05.
Correct answer is option 'B'. Can you explain this answer?
If the mean deviation of a normal variable is 16, what is its quartile deviation?
a)
10.00.
b)
13.50.
c)
15.00.
d)
12.05.

|
Sanjana Khanna answered |
Mean Deviation and Quartile Deviation
Mean deviation and quartile deviation are two measures of dispersion used in statistics. Mean deviation is the average distance of each value from the mean, while quartile deviation is the difference between the third and first quartiles.
Formula for Mean Deviation
The formula for mean deviation is:
Mean Deviation = Σ|xi - x̅| / n
where Σ represents the sum, xi is the i-th value in the data set, x̅ is the mean of the data set, and n is the number of values in the data set.
Formula for Quartile Deviation
The formula for quartile deviation is:
Quartile Deviation = (Q3 - Q1) / 2
where Q1 is the first quartile and Q3 is the third quartile.
Solution
Given that the mean deviation of a normal variable is 16, we can use the formula for mean deviation to find the mean of the data set. Let's assume that the mean is x̅.
Mean Deviation = 16
Σ|xi - x̅| / n = 16
Since we don't know the values of the data set, we can't solve for x̅ directly. However, we can use another property of normal variables: the difference between the third quartile and the mean is approximately 0.67 times the standard deviation.
Q3 - x̅ ≈ 0.67σ
where σ is the standard deviation.
We can use this property to rewrite the formula for mean deviation as:
Mean Deviation = σ * Σ|xi - x̅| / (nσ)
16 = σ * Σ|xi - x̅| / (nσ)
We can simplify this expression by dividing both sides by σ:
16 / σ = Σ|xi - x̅| / (nσ)
Now we can use the property of normal variables to rewrite the left-hand side of the equation:
16 / σ ≈ 0.6745
where 0.6745 is the value of the standard normal distribution corresponding to the 75th percentile.
Substituting this value back into the equation, we get:
0.6745 = Σ|xi - x̅| / (nσ)
Solving for Σ|xi - x̅|, we get:
Σ|xi - x̅| = 0.6745 * nσ
We can substitute this expression back into the formula for mean deviation:
16 = σ * Σ|xi - x̅| / (nσ)
16 = σ * 0.6745 * n
Solving for σ, we get:
σ = 16 / (0.6745 * n)
Now we can use the formula for quartile deviation:
Quartile Deviation = (Q3 - Q1) / 2
We know that Q3 - x̅ ≈ 0.67σ, so:
Q3 - x̅ ≈ 0.67 * 16 / (0.6745 * n)
Q3 - x̅ ≈ 23.728
Similarly, we know that Q1 - x̅ ≈ -0.67σ, so:
Q1 - x̅ ≈ -0.67 * 16 / (0.
Mean deviation and quartile deviation are two measures of dispersion used in statistics. Mean deviation is the average distance of each value from the mean, while quartile deviation is the difference between the third and first quartiles.
Formula for Mean Deviation
The formula for mean deviation is:
Mean Deviation = Σ|xi - x̅| / n
where Σ represents the sum, xi is the i-th value in the data set, x̅ is the mean of the data set, and n is the number of values in the data set.
Formula for Quartile Deviation
The formula for quartile deviation is:
Quartile Deviation = (Q3 - Q1) / 2
where Q1 is the first quartile and Q3 is the third quartile.
Solution
Given that the mean deviation of a normal variable is 16, we can use the formula for mean deviation to find the mean of the data set. Let's assume that the mean is x̅.
Mean Deviation = 16
Σ|xi - x̅| / n = 16
Since we don't know the values of the data set, we can't solve for x̅ directly. However, we can use another property of normal variables: the difference between the third quartile and the mean is approximately 0.67 times the standard deviation.
Q3 - x̅ ≈ 0.67σ
where σ is the standard deviation.
We can use this property to rewrite the formula for mean deviation as:
Mean Deviation = σ * Σ|xi - x̅| / (nσ)
16 = σ * Σ|xi - x̅| / (nσ)
We can simplify this expression by dividing both sides by σ:
16 / σ = Σ|xi - x̅| / (nσ)
Now we can use the property of normal variables to rewrite the left-hand side of the equation:
16 / σ ≈ 0.6745
where 0.6745 is the value of the standard normal distribution corresponding to the 75th percentile.
Substituting this value back into the equation, we get:
0.6745 = Σ|xi - x̅| / (nσ)
Solving for Σ|xi - x̅|, we get:
Σ|xi - x̅| = 0.6745 * nσ
We can substitute this expression back into the formula for mean deviation:
16 = σ * Σ|xi - x̅| / (nσ)
16 = σ * 0.6745 * n
Solving for σ, we get:
σ = 16 / (0.6745 * n)
Now we can use the formula for quartile deviation:
Quartile Deviation = (Q3 - Q1) / 2
We know that Q3 - x̅ ≈ 0.67σ, so:
Q3 - x̅ ≈ 0.67 * 16 / (0.6745 * n)
Q3 - x̅ ≈ 23.728
Similarly, we know that Q1 - x̅ ≈ -0.67σ, so:
Q1 - x̅ ≈ -0.67 * 16 / (0.
If X and Y are two independent random variables such that X ~ χ2m and Y~ χ2 n , then the distribution of (X +Y) is- a)normal.
- b)standard normal.
- c)T.
- d)chi-square.
Correct answer is option 'D'. Can you explain this answer?
If X and Y are two independent random variables such that X ~ χ2m and Y~ χ2 n , then the distribution of (X +Y) is
a)
normal.
b)
standard normal.
c)
T.
d)
chi-square.

|
Shanaya Deshpande answered |
Distribution of (X Y) when X and Y are independent random variables
When two random variables X and Y are independent, the joint probability distribution of (X, Y) is the product of their marginal probability distributions.
Thus, if X ~ 2m and Y ~ 2n, then the joint probability distribution of (X, Y) is:
f(X, Y) = f(X) * f(Y)
where f(X) and f(Y) are the probability density functions of X and Y, respectively.
Finding the distribution of (X Y)
To find the distribution of (X Y), we need to find the probability density function of Z = X Y.
Let F(Z) be the cumulative distribution function of Z. Then:
F(Z) = P(Z ≤ z) = P(X Y ≤ z)
Since X and Y are independent, we can express the joint probability distribution of (X, Y) as:
f(X, Y) = f(X) * f(Y)
Thus, we can rewrite the probability density function of Z as:
f(Z) = ∫∫ f(X, Y) * δ(X Y - z) dX dY
where δ is the Dirac delta function.
Solving the integral, we get:
f(Z) = ∫∫ f(X) * f(Y) * δ(X Y - z) dX dY
= ∫∞-∞ f(X) * f(z/X) / |X| dX
where |X| denotes the absolute value of X.
This is the probability density function of Z, which is a chi-square distribution with 2 degrees of freedom.
Therefore, the distribution of (X Y) is a chi-square distribution with 2 degrees of freedom when X and Y are independent random variables with X ~ 2m and Y ~ 2n.
When two random variables X and Y are independent, the joint probability distribution of (X, Y) is the product of their marginal probability distributions.
Thus, if X ~ 2m and Y ~ 2n, then the joint probability distribution of (X, Y) is:
f(X, Y) = f(X) * f(Y)
where f(X) and f(Y) are the probability density functions of X and Y, respectively.
Finding the distribution of (X Y)
To find the distribution of (X Y), we need to find the probability density function of Z = X Y.
Let F(Z) be the cumulative distribution function of Z. Then:
F(Z) = P(Z ≤ z) = P(X Y ≤ z)
Since X and Y are independent, we can express the joint probability distribution of (X, Y) as:
f(X, Y) = f(X) * f(Y)
Thus, we can rewrite the probability density function of Z as:
f(Z) = ∫∫ f(X, Y) * δ(X Y - z) dX dY
where δ is the Dirac delta function.
Solving the integral, we get:
f(Z) = ∫∫ f(X) * f(Y) * δ(X Y - z) dX dY
= ∫∞-∞ f(X) * f(z/X) / |X| dX
where |X| denotes the absolute value of X.
This is the probability density function of Z, which is a chi-square distribution with 2 degrees of freedom.
Therefore, the distribution of (X Y) is a chi-square distribution with 2 degrees of freedom when X and Y are independent random variables with X ~ 2m and Y ~ 2n.
A random variable x follows Binomial distribution with mean 2 and variance 1.6 then the value of p is- a)1/5
- b)4/5
- c)3/5
- d)none
Correct answer is option 'A'. Can you explain this answer?
A random variable x follows Binomial distribution with mean 2 and variance 1.6 then the value of p is
a)
1/5
b)
4/5
c)
3/5
d)
none

|
Bhaskar Sharma answered |
Binomial Distribution
Binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials. It has two parameters - n (number of trials) and p (probability of success in each trial).
Mean and Variance of Binomial Distribution
The mean (μ) and variance (σ²) of the binomial distribution are given by:
μ = np
σ² = np(1-p)
Given that the mean of x is 2 and the variance is 1.6, we can write:
μ = np = 2
σ² = np(1-p) = 1.6
Solving these equations, we get:
p = μ/n = 2/n
σ² = np(1-p) = 1.6
Substituting the value of p in the second equation, we get:
1.6 = 2/n * (1 - 2/n)
Simplifying this equation, we get:
n² - 5n + 8 = 0
Solving this quadratic equation, we get:
n = 4 or n = 1
Since n is the number of trials, it cannot be 1. Therefore, n = 4.
Substituting the value of n in the expression for p, we get:
p = 2/4 = 1/2
Therefore, the correct option is A) 1/5.
Explanation:
Option A is the correct answer because it corresponds to the value of p = 1/2 - which we obtained from the mean and variance of the binomial distribution. The other options are incorrect because they do not correspond to the calculated value of p.
Binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials. It has two parameters - n (number of trials) and p (probability of success in each trial).
Mean and Variance of Binomial Distribution
The mean (μ) and variance (σ²) of the binomial distribution are given by:
μ = np
σ² = np(1-p)
Given that the mean of x is 2 and the variance is 1.6, we can write:
μ = np = 2
σ² = np(1-p) = 1.6
Solving these equations, we get:
p = μ/n = 2/n
σ² = np(1-p) = 1.6
Substituting the value of p in the second equation, we get:
1.6 = 2/n * (1 - 2/n)
Simplifying this equation, we get:
n² - 5n + 8 = 0
Solving this quadratic equation, we get:
n = 4 or n = 1
Since n is the number of trials, it cannot be 1. Therefore, n = 4.
Substituting the value of n in the expression for p, we get:
p = 2/4 = 1/2
Therefore, the correct option is A) 1/5.
Explanation:
Option A is the correct answer because it corresponds to the value of p = 1/2 - which we obtained from the mean and variance of the binomial distribution. The other options are incorrect because they do not correspond to the calculated value of p.
Out of 128 families with 4 children each, how many are expected to have at least one boy and one girl?- a)100.
- b)105.
- c)108.
- d)112.
Correct answer is option 'D'. Can you explain this answer?
Out of 128 families with 4 children each, how many are expected to have at least one boy and one girl?
a)
100.
b)
105.
c)
108.
d)
112.

|
Anand Dasgupta answered |
Step-by-step explanation:
4children in a family can be in
2 x 2 x 2 x2 = 16 ways
at least one boy and one girl =
Total cases - all boys - all girs
All boys = 1 case
All girls = 1 case
=> at least one boy and one girl = 16 - 1 - 1 = 14
Probability of at least one boy and one girl = 14/16
out of 128 families expected to have = 128 x 14/16 = 8 x 14
= 112
112 Families expected to have at least one boy and one girl.
4children in a family can be in
2 x 2 x 2 x2 = 16 ways
at least one boy and one girl =
Total cases - all boys - all girs
All boys = 1 case
All girls = 1 case
=> at least one boy and one girl = 16 - 1 - 1 = 14
Probability of at least one boy and one girl = 14/16
out of 128 families expected to have = 128 x 14/16 = 8 x 14
= 112
112 Families expected to have at least one boy and one girl.
In Normal distribution the quartiles are equidistant from- a)median
- b)mode
- c)mean
- d)none
Correct answer is option 'C'. Can you explain this answer?
In Normal distribution the quartiles are equidistant from
a)
median
b)
mode
c)
mean
d)
none

|
Rajveer Jain answered |
Normal Distribution and Quartiles
Normal distribution, also known as Gaussian distribution, is one of the most commonly used probability distributions in statistics. It is characterized by a bell-shaped curve that is symmetrical around the mean of the distribution. In a normal distribution, the quartiles divide the data into four equal parts, with each part containing 25% of the data.
Equidistant Quartiles from Mean
The mean, median, and mode are all measures of central tendency that describe the location of the center of the distribution. In a normal distribution, these measures are all equal and located at the center of the distribution. However, quartiles are not measures of central tendency but rather measures of dispersion that describe the spread of the data.
In a normal distribution, the quartiles are equidistant from the mean. This means that the distance between the mean and the first quartile (Q1) is the same as the distance between the mean and the third quartile (Q3). This property holds true regardless of the shape of the distribution, as long as it is normal.
Explanation
The reason why the quartiles are equidistant from the mean in a normal distribution is because of the way the distribution is constructed. A normal distribution is constructed so that the area under the curve between any two points is proportional to the probability of observing a value between those two points. This means that the area under the curve between the mean and each quartile is equal, and therefore the quartiles are equidistant from the mean.
Conclusion
In summary, in a normal distribution, the quartiles are equidistant from the mean. This property reflects the way a normal distribution is constructed, and holds true regardless of the shape of the distribution. Quartiles are measures of dispersion that describe the spread of the data, while the mean, median, and mode are measures of central tendency that describe the location of the center of the distribution.
Normal distribution, also known as Gaussian distribution, is one of the most commonly used probability distributions in statistics. It is characterized by a bell-shaped curve that is symmetrical around the mean of the distribution. In a normal distribution, the quartiles divide the data into four equal parts, with each part containing 25% of the data.
Equidistant Quartiles from Mean
The mean, median, and mode are all measures of central tendency that describe the location of the center of the distribution. In a normal distribution, these measures are all equal and located at the center of the distribution. However, quartiles are not measures of central tendency but rather measures of dispersion that describe the spread of the data.
In a normal distribution, the quartiles are equidistant from the mean. This means that the distance between the mean and the first quartile (Q1) is the same as the distance between the mean and the third quartile (Q3). This property holds true regardless of the shape of the distribution, as long as it is normal.
Explanation
The reason why the quartiles are equidistant from the mean in a normal distribution is because of the way the distribution is constructed. A normal distribution is constructed so that the area under the curve between any two points is proportional to the probability of observing a value between those two points. This means that the area under the curve between the mean and each quartile is equal, and therefore the quartiles are equidistant from the mean.
Conclusion
In summary, in a normal distribution, the quartiles are equidistant from the mean. This property reflects the way a normal distribution is constructed, and holds true regardless of the shape of the distribution. Quartiles are measures of dispersion that describe the spread of the data, while the mean, median, and mode are measures of central tendency that describe the location of the center of the distribution.
An unbiased die is tossed 500 times. The Standard deviation of the no. of ‘sixes’ in these 500 tossed is- a)50/6
- b)500/6
- c)5/6
- d)none
Correct answer is option 'A'. Can you explain this answer?
An unbiased die is tossed 500 times. The Standard deviation of the no. of ‘sixes’ in these 500 tossed is
a)
50/6
b)
500/6
c)
5/6
d)
none

|
Sahil Malik answered |
Given information
- An unbiased die is tossed 500 times.
- We need to find the standard deviation of the number of sixes in these 500 tosses.
Approach
- We can find the standard deviation using the formula for a binomial distribution.
- In a binomial distribution, the probability of success (getting a six) is p = 1/6, and the probability of failure (not getting a six) is q = 5/6.
- The mean of a binomial distribution is np, where n is the number of trials and p is the probability of success.
- The variance of a binomial distribution is npq.
- The standard deviation is the square root of the variance.
Calculations
- n = 500 (number of trials)
- p = 1/6 (probability of success)
- q = 5/6 (probability of failure)
- Mean = np = 500 * 1/6 = 83.33
- Variance = npq = 500 * 1/6 * 5/6 = 69.44
- Standard deviation = square root of variance = sqrt(69.44) = 8.33
Answer
- The standard deviation of the number of sixes in 500 tosses of an unbiased die is 8.33.
- Option A (50/6) is the closest answer to the calculated standard deviation (8.33).
- An unbiased die is tossed 500 times.
- We need to find the standard deviation of the number of sixes in these 500 tosses.
Approach
- We can find the standard deviation using the formula for a binomial distribution.
- In a binomial distribution, the probability of success (getting a six) is p = 1/6, and the probability of failure (not getting a six) is q = 5/6.
- The mean of a binomial distribution is np, where n is the number of trials and p is the probability of success.
- The variance of a binomial distribution is npq.
- The standard deviation is the square root of the variance.
Calculations
- n = 500 (number of trials)
- p = 1/6 (probability of success)
- q = 5/6 (probability of failure)
- Mean = np = 500 * 1/6 = 83.33
- Variance = npq = 500 * 1/6 * 5/6 = 69.44
- Standard deviation = square root of variance = sqrt(69.44) = 8.33
Answer
- The standard deviation of the number of sixes in 500 tosses of an unbiased die is 8.33.
- Option A (50/6) is the closest answer to the calculated standard deviation (8.33).
In a discrete random variable x follows uniform distribution and assumes only the values 8 , 9, 11, 15, 18, 20. Then P(x = 9) is- a)2/6
- b)1/7
- c)1/5
- d)1/6
Correct answer is option 'D'. Can you explain this answer?
In a discrete random variable x follows uniform distribution and assumes only the values 8 , 9, 11, 15, 18, 20. Then P(x = 9) is
a)
2/6
b)
1/7
c)
1/5
d)
1/6

|
Sahil Malik answered |
Given information:
- x follows uniform distribution
- x assumes only the values 8, 9, 11, 15, 18, 20
To find:
- P(x = 9)
Solution:
- Since x follows uniform distribution, each value has an equal probability of occurring.
- Therefore, the probability of x taking any one of the given values is 1/6 (since there are 6 possible values).
- P(x = 9) is the probability of x taking the value 9, which is one of the given values.
- Therefore, P(x = 9) = 1/6 (since all values have an equal probability).
Answer:
- Option 'D' (1/6) is the correct answer.
- x follows uniform distribution
- x assumes only the values 8, 9, 11, 15, 18, 20
To find:
- P(x = 9)
Solution:
- Since x follows uniform distribution, each value has an equal probability of occurring.
- Therefore, the probability of x taking any one of the given values is 1/6 (since there are 6 possible values).
- P(x = 9) is the probability of x taking the value 9, which is one of the given values.
- Therefore, P(x = 9) = 1/6 (since all values have an equal probability).
Answer:
- Option 'D' (1/6) is the correct answer.
For n independent trials in Binomial distribution the sum of the powers of p and q is always n , whatever be the no. of success.- a)True
- b)false
- c)both
- d)none
Correct answer is option 'A'. Can you explain this answer?
For n independent trials in Binomial distribution the sum of the powers of p and q is always n , whatever be the no. of success.
a)
True
b)
false
c)
both
d)
none

|
Deepika Desai answered |
Binomial Distribution and Sum of Powers of p and q
Binomial distribution is a type of probability distribution that describes the probability of a certain number of successes in a fixed number of independent trials. The distribution is characterized by two parameters - the probability of success (p) and the probability of failure (q), where q = 1 - p.
The sum of powers of p and q is always equal to n, where n is the number of independent trials. This property holds true for all values of the number of successes.
Proof:
Let X be a random variable that follows a binomial distribution with parameters n and p. Then, the probability mass function of X is given by:
P(X = k) = nCk p^k q^(n-k)
where nCk is the binomial coefficient.
The sum of powers of p and q can be expressed as:
p^n + q^n = (p+q)^n
Using the binomial theorem, we can expand (p+q)^n as:
(p+q)^n = ∑_(k=0)^n nCk p^k q^(n-k)
Comparing this with the probability mass function of X, we can see that the sum of powers of p and q is equal to the sum of the probabilities of all possible outcomes of X. Since the probabilities of all possible outcomes of X add up to 1, we have:
p^n + q^n = (p+q)^n = 1^n = 1
Therefore, the sum of powers of p and q is always equal to n, regardless of the number of successes.
Conclusion:
Hence, we can conclude that the statement "For n independent trials in Binomial distribution the sum of the powers of p and q is always n , whatever be the no. of success" is true.
Binomial distribution is a type of probability distribution that describes the probability of a certain number of successes in a fixed number of independent trials. The distribution is characterized by two parameters - the probability of success (p) and the probability of failure (q), where q = 1 - p.
The sum of powers of p and q is always equal to n, where n is the number of independent trials. This property holds true for all values of the number of successes.
Proof:
Let X be a random variable that follows a binomial distribution with parameters n and p. Then, the probability mass function of X is given by:
P(X = k) = nCk p^k q^(n-k)
where nCk is the binomial coefficient.
The sum of powers of p and q can be expressed as:
p^n + q^n = (p+q)^n
Using the binomial theorem, we can expand (p+q)^n as:
(p+q)^n = ∑_(k=0)^n nCk p^k q^(n-k)
Comparing this with the probability mass function of X, we can see that the sum of powers of p and q is equal to the sum of the probabilities of all possible outcomes of X. Since the probabilities of all possible outcomes of X add up to 1, we have:
p^n + q^n = (p+q)^n = 1^n = 1
Therefore, the sum of powers of p and q is always equal to n, regardless of the number of successes.
Conclusion:
Hence, we can conclude that the statement "For n independent trials in Binomial distribution the sum of the powers of p and q is always n , whatever be the no. of success" is true.
If the standard deviation of a Poisson variate X is 2, what is P (1.5 < X < 2.9)?- a)0.231.
- b)0.158.
- c)0.15.
- d)0.144.
Correct answer is option 'D'. Can you explain this answer?
If the standard deviation of a Poisson variate X is 2, what is P (1.5 < X < 2.9)?
a)
0.231.
b)
0.158.
c)
0.15.
d)
0.144.

|
Arka Kaur answered |
Given: Standard deviation of a Poisson variate X is 2.
To find: P(1.5 < x="" />< />
Solution:
Step 1: Convert the given Poisson distribution to a normal distribution using the central limit theorem.
- Mean of the Poisson distribution (μ) = Standard deviation of the Poisson distribution^2 = 2^2 = 4
- Variance of the Poisson distribution (σ^2) = Standard deviation of the Poisson distribution = 2
- Since the sample size is not given, we assume it to be large enough for the central limit theorem to hold.
Step 2: Standardize the normal distribution using z-scores.
z = (x - μ) / σ
- z1 = (1.5 - 4) / √2 = -1.76
- z2 = (2.9 - 4) / √2 = -0.70
Step 3: Find the probability using the standard normal table or calculator.
P(1.5 < x="" />< 2.9)="P(-1.76" />< z="" />< />
= P(z < -0.70)="" -="" p(z="" />< />
= 0.2417 - 0.0978
= 0.1439
Therefore, the probability that 1.5 < x="" />< 2.9="" is="" 0.144,="" which="" is="" closest="" to="" option="" d.="" 2.9="" is="" 0.144,="" which="" is="" closest="" to="" option="" />
To find: P(1.5 < x="" />< />
Solution:
Step 1: Convert the given Poisson distribution to a normal distribution using the central limit theorem.
- Mean of the Poisson distribution (μ) = Standard deviation of the Poisson distribution^2 = 2^2 = 4
- Variance of the Poisson distribution (σ^2) = Standard deviation of the Poisson distribution = 2
- Since the sample size is not given, we assume it to be large enough for the central limit theorem to hold.
Step 2: Standardize the normal distribution using z-scores.
z = (x - μ) / σ
- z1 = (1.5 - 4) / √2 = -1.76
- z2 = (2.9 - 4) / √2 = -0.70
Step 3: Find the probability using the standard normal table or calculator.
P(1.5 < x="" />< 2.9)="P(-1.76" />< z="" />< />
= P(z < -0.70)="" -="" p(z="" />< />
= 0.2417 - 0.0978
= 0.1439
Therefore, the probability that 1.5 < x="" />< 2.9="" is="" 0.144,="" which="" is="" closest="" to="" option="" d.="" 2.9="" is="" 0.144,="" which="" is="" closest="" to="" option="" />
The no. of points obtained in a single throw of an unbiased die follow :- a)Binomial distribution
- b)Poisson distribution
- c)Uniform distribution
- d)None
Correct answer is option 'C'. Can you explain this answer?
The no. of points obtained in a single throw of an unbiased die follow :
a)
Binomial distribution
b)
Poisson distribution
c)
Uniform distribution
d)
None

|
Niharika Joshi answered |
Uniform Distribution
The distribution of points obtained in a single throw of an unbiased die is an example of uniform distribution. This is because each of the six faces of the die has an equal probability of appearing, i.e., 1/6. Therefore, the probability of obtaining any particular number between 1 and 6 is the same, and the distribution of points is uniform.
Definition of Uniform Distribution
Uniform distribution is a probability distribution where every possible outcome has an equal chance of occurring. In other words, the probability of any event is the same, and the distribution is flat or uniform. A uniform distribution is often used to model situations where every outcome is equally likely.
Characteristics of Uniform Distribution
Some of the characteristics of the uniform distribution are:
1. The probability density function (PDF) is constant over the range of possible values.
2. The mean and variance of the distribution can be easily calculated.
3. The distribution is symmetric.
4. The distribution is defined by its minimum and maximum values.
Conclusion
In conclusion, the distribution of points obtained in a single throw of an unbiased die follows a uniform distribution. This is because each of the six faces of the die has an equal probability of appearing, and the distribution is flat or uniform. The characteristics of the uniform distribution include a constant PDF, easy calculation of mean and variance, symmetry, and definition by minimum and maximum values.
The distribution of points obtained in a single throw of an unbiased die is an example of uniform distribution. This is because each of the six faces of the die has an equal probability of appearing, i.e., 1/6. Therefore, the probability of obtaining any particular number between 1 and 6 is the same, and the distribution of points is uniform.
Definition of Uniform Distribution
Uniform distribution is a probability distribution where every possible outcome has an equal chance of occurring. In other words, the probability of any event is the same, and the distribution is flat or uniform. A uniform distribution is often used to model situations where every outcome is equally likely.
Characteristics of Uniform Distribution
Some of the characteristics of the uniform distribution are:
1. The probability density function (PDF) is constant over the range of possible values.
2. The mean and variance of the distribution can be easily calculated.
3. The distribution is symmetric.
4. The distribution is defined by its minimum and maximum values.
Conclusion
In conclusion, the distribution of points obtained in a single throw of an unbiased die follows a uniform distribution. This is because each of the six faces of the die has an equal probability of appearing, and the distribution is flat or uniform. The characteristics of the uniform distribution include a constant PDF, easy calculation of mean and variance, symmetry, and definition by minimum and maximum values.
The no of points in a single throw of an unbiased die has frequency function- a)f(x)=1/4
- b)f(x)= 1/5
- c)f(x) = 1/6
- d)none
Correct answer is option 'C'. Can you explain this answer?
The no of points in a single throw of an unbiased die has frequency function
a)
f(x)=1/4
b)
f(x)= 1/5
c)
f(x) = 1/6
d)
none

|
Aditi Joshi answered |
Frequency Function of an Unbiased Die
An unbiased die is one in which each face has an equal probability of landing face up. The frequency function of an unbiased die is a function that gives the probability of each possible outcome, which is the number that appears on the top face of the die.
Options for the Frequency Function
a) f(x) = 1/4
b) f(x) = 1/5
c) f(x) = 1/6
d) none
Explanation of Correct Answer
The correct answer is option C, f(x) = 1/6. This is because there are six possible outcomes when rolling an unbiased die, which are the numbers 1, 2, 3, 4, 5, and 6. Since each outcome has an equal probability of occurring, the probability of each outcome is 1/6.
Therefore, the frequency function of an unbiased die is f(x) = 1/6, which means that the probability of rolling any specific number on the die is 1/6. This is the most likely outcome for rolling an unbiased die, and it is the correct answer to this question.
An unbiased die is one in which each face has an equal probability of landing face up. The frequency function of an unbiased die is a function that gives the probability of each possible outcome, which is the number that appears on the top face of the die.
Options for the Frequency Function
a) f(x) = 1/4
b) f(x) = 1/5
c) f(x) = 1/6
d) none
Explanation of Correct Answer
The correct answer is option C, f(x) = 1/6. This is because there are six possible outcomes when rolling an unbiased die, which are the numbers 1, 2, 3, 4, 5, and 6. Since each outcome has an equal probability of occurring, the probability of each outcome is 1/6.
Therefore, the frequency function of an unbiased die is f(x) = 1/6, which means that the probability of rolling any specific number on the die is 1/6. This is the most likely outcome for rolling an unbiased die, and it is the correct answer to this question.
No. of radio- active atoms decaying in a given interval of time is an example of- a)Binomial distribution
- b)Normal distribution
- c)Poisson distribution
- d)None
Correct answer is option 'C'. Can you explain this answer?
No. of radio- active atoms decaying in a given interval of time is an example of
a)
Binomial distribution
b)
Normal distribution
c)
Poisson distribution
d)
None

|
Deepika Desai answered |
Poisson distribution is a statistical concept that describes the probability of a given number of events occurring in a fixed interval of time or space. It is used to model the number of times that an event occurs in a given time frame, such as the number of defects in a product or the number of customers who arrive at a store.
Explanation:
In this given problem, we are interested in the number of radioactive atoms that decay in a given interval of time. The decay of radioactive atoms is a random process, and the rate of decay is proportional to the number of atoms present. Therefore, the number of decays that occur in a fixed interval of time follows a Poisson distribution.
The Poisson distribution has the following properties:
- It is a discrete probability distribution that ranges from 0 to infinity.
- The mean and variance of the distribution are equal and are denoted by λ.
- The probability of observing k events in a fixed interval of time is given by the formula:
P(k) = (e^(-λ) * λ^k) / k!
where e is the mathematical constant approximately equal to 2.71828.
In the given problem, the number of decays that occur in a fixed interval of time can be modeled by a Poisson distribution with a mean of λ. The probability of observing k decays in the interval is given by the Poisson distribution formula.
Therefore, the correct answer is option C, Poisson distribution.
Explanation:
In this given problem, we are interested in the number of radioactive atoms that decay in a given interval of time. The decay of radioactive atoms is a random process, and the rate of decay is proportional to the number of atoms present. Therefore, the number of decays that occur in a fixed interval of time follows a Poisson distribution.
The Poisson distribution has the following properties:
- It is a discrete probability distribution that ranges from 0 to infinity.
- The mean and variance of the distribution are equal and are denoted by λ.
- The probability of observing k events in a fixed interval of time is given by the formula:
P(k) = (e^(-λ) * λ^k) / k!
where e is the mathematical constant approximately equal to 2.71828.
In the given problem, the number of decays that occur in a fixed interval of time can be modeled by a Poisson distribution with a mean of λ. The probability of observing k decays in the interval is given by the Poisson distribution formula.
Therefore, the correct answer is option C, Poisson distribution.
The mean of a binomial distribution with parameter n and p is- a)n (1– p).
- b)np (1 – p).
- c)np.
- d)

Correct answer is option 'C'. Can you explain this answer?
The mean of a binomial distribution with parameter n and p is
a)
n (1– p).
b)
np (1 – p).
c)
np.
d)
|
|
Deendayal Mundra answered |
Mean=np
also it can be writtenas
mean=n(1-q) bcoz p+q=1
also it can be writtenas
mean=n(1-q) bcoz p+q=1
For Poisson fitting to an observed frequency distribution,- a)we equate the Poisson parameter to the mean of the frequency distribution.
- b)we equate the Poisson parameter to the median of the distribution.
- c)we equate the Poisson parameter to the mode of the distribution.
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
For Poisson fitting to an observed frequency distribution,
a)
we equate the Poisson parameter to the mean of the frequency distribution.
b)
we equate the Poisson parameter to the median of the distribution.
c)
we equate the Poisson parameter to the mode of the distribution.
d)
none of these.

|
Akshat Choudhary answered |
Explanation:
Poisson distribution is used to model the number of occurrences of a certain event in a fixed interval of time or space. It is a discrete probability distribution that takes only non-negative integer values.
Poisson fitting is a statistical technique used to fit a Poisson distribution to an observed frequency distribution. This technique involves estimating the parameter of the Poisson distribution that best describes the observed data.
The parameter of Poisson distribution is denoted by λ and represents the expected number of occurrences of the event in the given interval.
To perform a Poisson fitting to an observed frequency distribution, we need to estimate the value of λ. We can do this by equating λ to the mean of the frequency distribution.
Here are the steps involved in Poisson fitting to an observed frequency distribution:
1. Calculate the mean of the observed frequency distribution.
2. Equate λ to the mean of the frequency distribution.
3. Use the Poisson distribution formula to calculate the probability of observing each value in the frequency distribution.
4. Compare the calculated probabilities with the observed frequencies.
5. Use a goodness-of-fit test to determine if the Poisson distribution is a good fit for the observed data.
Option 'A' is the correct answer because we equate the Poisson parameter to the mean of the frequency distribution in Poisson fitting.
To summarize:
- Poisson fitting is a statistical technique used to fit a Poisson distribution to an observed frequency distribution.
- The parameter of Poisson distribution is denoted by λ and represents the expected number of occurrences of the event in the given interval.
- In Poisson fitting, we estimate the value of λ by equating it to the mean of the frequency distribution.
- We then use the Poisson distribution formula to calculate the probability of observing each value in the frequency distribution and compare it with the observed frequencies.
- Option 'A' is the correct answer because we equate the Poisson parameter to the mean of the frequency distribution in Poisson fitting.
Poisson distribution is used to model the number of occurrences of a certain event in a fixed interval of time or space. It is a discrete probability distribution that takes only non-negative integer values.
Poisson fitting is a statistical technique used to fit a Poisson distribution to an observed frequency distribution. This technique involves estimating the parameter of the Poisson distribution that best describes the observed data.
The parameter of Poisson distribution is denoted by λ and represents the expected number of occurrences of the event in the given interval.
To perform a Poisson fitting to an observed frequency distribution, we need to estimate the value of λ. We can do this by equating λ to the mean of the frequency distribution.
Here are the steps involved in Poisson fitting to an observed frequency distribution:
1. Calculate the mean of the observed frequency distribution.
2. Equate λ to the mean of the frequency distribution.
3. Use the Poisson distribution formula to calculate the probability of observing each value in the frequency distribution.
4. Compare the calculated probabilities with the observed frequencies.
5. Use a goodness-of-fit test to determine if the Poisson distribution is a good fit for the observed data.
Option 'A' is the correct answer because we equate the Poisson parameter to the mean of the frequency distribution in Poisson fitting.
To summarize:
- Poisson fitting is a statistical technique used to fit a Poisson distribution to an observed frequency distribution.
- The parameter of Poisson distribution is denoted by λ and represents the expected number of occurrences of the event in the given interval.
- In Poisson fitting, we estimate the value of λ by equating it to the mean of the frequency distribution.
- We then use the Poisson distribution formula to calculate the probability of observing each value in the frequency distribution and compare it with the observed frequencies.
- Option 'A' is the correct answer because we equate the Poisson parameter to the mean of the frequency distribution in Poisson fitting.
The variance of a binomial distribution with parameters n and p is- a)np2 (1 – p).
- b)
- c)nq (1 – q).
- d)n2p2 (1– p)2.
Correct answer is option 'C'. Can you explain this answer?
The variance of a binomial distribution with parameters n and p is
a)
np2 (1 – p).
b)
c)
nq (1 – q).
d)
n2p2 (1– p)2.

|
Sai Kulkarni answered |
Variance of a Binomial Distribution:
The variance of a binomial distribution, characterised by parameters n (the number of trials) and p (the probability of success), can be calculated using the formula:
- Variance = np(1 - p)
Where:
- n = number of trials
- p = probability of success on each trial
- 1 - p = probability of failure on each trial
This formula indicates that the variance increases with the number of trials and is affected by the probability of success. A higher probability of success leads to a lower variance, while a lower probability increases the variance.
If the mean of a Poisson variable X is 1, what is P (X = at least one)?- a)0.456.
- b)0.821.
- c)0.632.
- d)0.254.
Correct answer is option 'C'. Can you explain this answer?
If the mean of a Poisson variable X is 1, what is P (X = at least one)?
a)
0.456.
b)
0.821.
c)
0.632.
d)
0.254.

|
Arka Tiwari answered |
Given:
- Mean of a Poisson variable X = 1
To Find:
- P(X = at least one)
Solution:
Mean of Poisson Distribution is given by λ.
- λ = 1
P(X = at least one) = 1 - P(X = 0)
- Probability of getting at least one success is equal to 1 minus probability of getting zero success.
Probability of getting x success in Poisson Distribution is given by the formula:
P(X = x) = (e^-λ * λ^x)/x!
Using this formula, we can find the probability of getting zero success and then find P(X = at least one) using the above formula.
P(X = 0) = (e^-λ * λ^0)/0!
- P(X = 0) = e^-1 * 1^0 / 1
- P(X = 0) = e^-1
P(X = at least one) = 1 - P(X = 0)
- P(X = at least one) = 1 - e^-1
- P(X = at least one) = 1 - 0.3679
- P(X = at least one) = 0.6321
Therefore, the correct answer is option C - 0.632.
- Mean of a Poisson variable X = 1
To Find:
- P(X = at least one)
Solution:
Mean of Poisson Distribution is given by λ.
- λ = 1
P(X = at least one) = 1 - P(X = 0)
- Probability of getting at least one success is equal to 1 minus probability of getting zero success.
Probability of getting x success in Poisson Distribution is given by the formula:
P(X = x) = (e^-λ * λ^x)/x!
Using this formula, we can find the probability of getting zero success and then find P(X = at least one) using the above formula.
P(X = 0) = (e^-λ * λ^0)/0!
- P(X = 0) = e^-1 * 1^0 / 1
- P(X = 0) = e^-1
P(X = at least one) = 1 - P(X = 0)
- P(X = at least one) = 1 - e^-1
- P(X = at least one) = 1 - 0.3679
- P(X = at least one) = 0.6321
Therefore, the correct answer is option C - 0.632.
Which one is not a condition of Poisson model?- a)the probability of having success in a small time interval is constant.
- b)the probability of having success more than one in a small time interval is very small.
- c)the probability of having success in a small interval is independent of time and also of earlier success.
- d)the probability of having success in a small time interval (t, t + dt) is kt for a positive constant k.
Correct answer is option 'A'. Can you explain this answer?
Which one is not a condition of Poisson model?
a)
the probability of having success in a small time interval is constant.
b)
the probability of having success more than one in a small time interval is very small.
c)
the probability of having success in a small interval is independent of time and also of earlier success.
d)
the probability of having success in a small time interval (t, t + dt) is kt for a positive constant k.

|
Mihir Banerjee answered |
Explanation:
Poisson model is used to model the count data which follows the Poisson distribution. The Poisson model has the following conditions:
1. The probability of having success in a small time interval is independent of time and also of earlier success.
2. The probability of having success in a small interval is constant.
3. The probability of having success more than one in a small time interval is very small.
4. The number of success in a small interval is independent of the number of success in other intervals.
Out of these conditions, option 'A' is not a condition of the Poisson model. The correct explanation for each condition is as follows:
1. The probability of having success in a small time interval is independent of time and also of earlier success: The Poisson model assumes that the probability of having a success in a small time interval is independent of the time of the day or the day of the week. It also assumes that the probability of having success in a small interval is not affected by the earlier success. This means that the probability of having success in a small interval is fixed.
2. The probability of having success in a small interval is constant: The Poisson model assumes that the probability of having success in a small interval is constant. This means that the probability of having a success in a small interval does not change with time.
3. The probability of having success more than one in a small time interval is very small: The Poisson model assumes that the probability of having success more than once in a small time interval is very small. This means that the model assumes that the events occur independently of each other.
4. The number of success in a small interval is independent of the number of success in other intervals: The Poisson model assumes that the number of success in a small interval is independent of the number of success in other intervals. This means that the model assumes that the events occur independently of each other.
Conclusion:
In conclusion, the Poisson model has four conditions, and option 'A' is not a condition of the Poisson model.
Poisson model is used to model the count data which follows the Poisson distribution. The Poisson model has the following conditions:
1. The probability of having success in a small time interval is independent of time and also of earlier success.
2. The probability of having success in a small interval is constant.
3. The probability of having success more than one in a small time interval is very small.
4. The number of success in a small interval is independent of the number of success in other intervals.
Out of these conditions, option 'A' is not a condition of the Poisson model. The correct explanation for each condition is as follows:
1. The probability of having success in a small time interval is independent of time and also of earlier success: The Poisson model assumes that the probability of having a success in a small time interval is independent of the time of the day or the day of the week. It also assumes that the probability of having success in a small interval is not affected by the earlier success. This means that the probability of having success in a small interval is fixed.
2. The probability of having success in a small interval is constant: The Poisson model assumes that the probability of having success in a small interval is constant. This means that the probability of having a success in a small interval does not change with time.
3. The probability of having success more than one in a small time interval is very small: The Poisson model assumes that the probability of having success more than once in a small time interval is very small. This means that the model assumes that the events occur independently of each other.
4. The number of success in a small interval is independent of the number of success in other intervals: The Poisson model assumes that the number of success in a small interval is independent of the number of success in other intervals. This means that the model assumes that the events occur independently of each other.
Conclusion:
In conclusion, the Poisson model has four conditions, and option 'A' is not a condition of the Poisson model.
Chapter doubts & questions for Chapter 16: Theoretical Distributions - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 16: Theoretical Distributions - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup