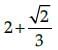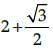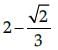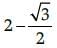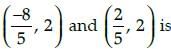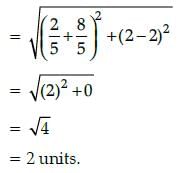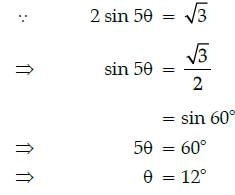All Exams >
Class 10 >
CBSE Sample Papers For Class 10 >
All Questions
All questions of CBSE Sample Question Papers for 2021-22 for Class 10 Exam
Aarti had bought a circular pot wherein area of cross-section is mentioned as 38.5 cm2. She wantedto calculate the radius of the circle and observed its value.- a)3.5 cm
- b)7 cm
- c)4 cm
- d)7.5 cm
Correct answer is option 'A'. Can you explain this answer?
Aarti had bought a circular pot wherein area of cross-section is mentioned as 38.5 cm2. She wantedto calculate the radius of the circle and observed its value.
a)
3.5 cm
b)
7 cm
c)
4 cm
d)
7.5 cm

|
Let's Tute answered |
Area of a circle = 38.5 cm
2
πr2 = 38.5


Rational number 7/125 will terminate after ........ decimal places.- a)2
- b)1
- c)4
- d)3
Correct answer is option 'D'. Can you explain this answer?
Rational number 7/125 will terminate after ........ decimal places.
a)
2
b)
1
c)
4
d)
3
|
|
Krishna Iyer answered |
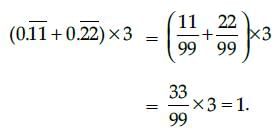
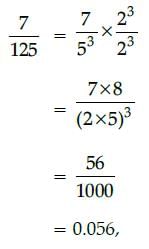
which terminates after 3 places.
If two positive integers p and q are written as p = a3b4 and q = a4b4, where a and b are prime numbers,then LCM (p, q) × HCF (p, q) is :- a)a7b6
- b)a6b7
- c)a8b7
- d)a7b8
Correct answer is option 'D'. Can you explain this answer?
If two positive integers p and q are written as p = a3b4 and q = a4b4, where a and b are prime numbers,then LCM (p, q) × HCF (p, q) is :
a)
a7b6
b)
a6b7
c)
a8b7
d)
a7b8
|
|
Arun Sharma answered |
p = a3b4
and q = a4b4
Then LCM (p, q) = a4 b4
and HCF (p, q) = a3 b4
∴ LCM (p, q) x HCF (p, q)
= a4 b4 x a3 b4
= a7 b8
and q = a4b4
Then LCM (p, q) = a4 b4
and HCF (p, q) = a3 b4
∴ LCM (p, q) x HCF (p, q)
= a4 b4 x a3 b4
= a7 b8
In evening, during family time, Radha observed the dimensions of room. If the length, breadth andheight of a room are 24 m, 18 m and 9 m respectively, then the length of the longest rod that canmeasure the dimensions of the room exactly is :- a)2
- b)3
- c)4
- d)5
Correct answer is option 'B'. Can you explain this answer?
In evening, during family time, Radha observed the dimensions of room. If the length, breadth andheight of a room are 24 m, 18 m and 9 m respectively, then the length of the longest rod that canmeasure the dimensions of the room exactly is :
a)
2
b)
3
c)
4
d)
5
|
|
Rohit Sharma answered |
Length = 24 m, breadth = 18 m and height = 9 m
Since, the length of the longest rod is equal to HCF (24, 18, 9), i.e., 24 = 23 × 3
18 = 2 × 32
and 9 = 32
Then, HCF (24, 18 and 9) = 3
Thus, the longest rod that can measure the dimensions of the room exactly = 3 m.
Since, the length of the longest rod is equal to HCF (24, 18, 9), i.e., 24 = 23 × 3
18 = 2 × 32
and 9 = 32
Then, HCF (24, 18 and 9) = 3
Thus, the longest rod that can measure the dimensions of the room exactly = 3 m.
A box contains 80 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime number less than 30, is:- a)1/8
- b)9/80
- c)11/80
- d)3/20
Correct answer is option 'A'. Can you explain this answer?
A box contains 80 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime number less than 30, is:
a)
1/8
b)
9/80
c)
11/80
d)
3/20
|
|
Ananya Das answered |
Total number outcomes = 80
i.e., n(S) = 80
Prime number less than 30 = 2, 3, 5, 7, 11,
13, 17, 19, 23, 29
i.e., n(E) = 10
∴ Required probability,
i.e., n(S) = 80
Prime number less than 30 = 2, 3, 5, 7, 11,
13, 17, 19, 23, 29
i.e., n(E) = 10
∴ Required probability,
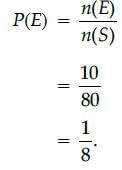
The distance of the point P(– 4, 3) from the origin is:- a)1 unit
- b)7 units
- c)5 units
- d)6 units
Correct answer is option 'C'. Can you explain this answer?
The distance of the point P(– 4, 3) from the origin is:
a)
1 unit
b)
7 units
c)
5 units
d)
6 units
|
|
Mira Sharma answered |
Here, two points (–4, 3) and
(0, 0) are given, then
x1 = – 4, y1 = 3 and x2 = 0, y2 = 0
∴ Distance between them
(0, 0) are given, then
x1 = – 4, y1 = 3 and x2 = 0, y2 = 0
∴ Distance between them
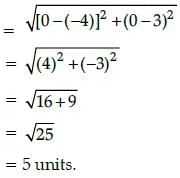
If a piece of wire 30 cm long is bent into the form of an arc of a circle, subtending an angle of 60° at its centre, then radius of the circle is :a)90 /π cmb)45 /π cmc)60 /π cmd)30 /π cmCorrect answer is option 'A'. Can you explain this answer?
|
|
Alisha kapoor answered |
Given :
A piece of wire is bent in the form of an arc of a circle, of length: 30 cm
A piece of wire is bent in the form of an arc of a circle, of length: 30 cm
Angle subtended : 60 degree
Solution :
Here,
Here,
A wire of 30 cm subtends an angle of 60 degree or π/3 at the center.
Now, if we have another wire long enough to form an entire circle, that circle will subtend an angle of 360 degree or 2π at the center.
So in the second case , the length of arc will be ,
30 cm = π/3
x cm = 2π
Therefore, x = 180 cm
This is now the circumference of the circle,
Therefore , 2πr = 180
or r = 90 / π
r = 28.6 cm (approx)
Final answer :
Hence, the radius of the circle is 90 / π or 28.6 cm.
You can go through the course for Class 10 Sample Papers of all subjects:
If a number when divided by 71 gives 37 as quotient and 42 as remainder, then the number is:- a)2668
- b)2669
- c)2670
- d)2667
Correct answer is option 'B'. Can you explain this answer?
If a number when divided by 71 gives 37 as quotient and 42 as remainder, then the number is:
a)
2668
b)
2669
c)
2670
d)
2667
|
|
Meera Rana answered |
Here, divisor = 71, quotient = 37 and remainder = 42.
∴ Dividend = Divisor × Quotient + Remainder
= (71 × 37) + 42
= 2669.
∴ Dividend = Divisor × Quotient + Remainder
= (71 × 37) + 42
= 2669.
If the sum of ages of father and son is 40 years and its difference is 20 years then age of father will be:- a)30 years
- b)25 years
- c)20 years
- d)35 years
Correct answer is option 'A'. Can you explain this answer?
If the sum of ages of father and son is 40 years and its difference is 20 years then age of father will be:
a)
30 years
b)
25 years
c)
20 years
d)
35 years
|
|
Rohit Sharma answered |
Let father's age be x years and son's age be y, then
x + y = 40 ...(i)
and x – y = 20
On adding eq. (i) and (ii), we get
2x = 60
⇒ x = 30.
x + y = 40 ...(i)
and x – y = 20
On adding eq. (i) and (ii), we get
2x = 60
⇒ x = 30.
In the given figure, if PQ = 8 cm and PR = 6 cm, then the radius of the circle is ..... cm, where O is thecentre of circle.
- a)5
- b)6
- c)7
- d)4
Correct answer is option 'A'. Can you explain this answer?
In the given figure, if PQ = 8 cm and PR = 6 cm, then the radius of the circle is ..... cm, where O is thecentre of circle.

a)
5
b)
6
c)
7
d)
4

|
Ashwani Mishra answered |
Since ∠P in a semicircle, so
∠P = 90°
∴ In DRPQ, RQ2 = PR2 + PQ2
(Using Pythagoras theorem)
= (6)2 + (8)2
= 100
∴ RQ = 10 cm
∴ Radius = 1/2RQ
= 5 cm
∠P = 90°
∴ In DRPQ, RQ2 = PR2 + PQ2
(Using Pythagoras theorem)
= (6)2 + (8)2
= 100
∴ RQ = 10 cm
∴ Radius = 1/2RQ
= 5 cm
If the radius of a circle with centre O is 3.5 cm and two radii OA and OB are drawn at right angles toeach other, then the area of minor segment is :- a)2.5 cm2
- b)4.5 cm2
- c)5.5 cm2
- d)3.5 cm2
Correct answer is option 'D'. Can you explain this answer?
If the radius of a circle with centre O is 3.5 cm and two radii OA and OB are drawn at right angles toeach other, then the area of minor segment is :
a)
2.5 cm2
b)
4.5 cm2
c)
5.5 cm2
d)
3.5 cm2
|
|
Vikram Kapoor answered |
Here,
r = 3.5 cm, θ = 90°
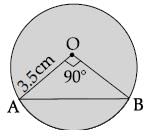
r = 3.5 cm, θ = 90°

∴ Area of minor segment
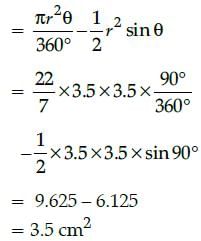
If the sum of the zeroes of the quadratic polynomial 5x2 – px + 8 is 4, then the value of k is:- a)10
- b)20
- c)30
- d)40
Correct answer is option 'B'. Can you explain this answer?
If the sum of the zeroes of the quadratic polynomial 5x2 – px + 8 is 4, then the value of k is:
a)
10
b)
20
c)
30
d)
40
|
|
Radha Iyer answered |
Let the zeroes of the given polynomial be a and b, then sum of the zeroes = 4
i.e p/5 = 4
⇒ p = 20
i.e p/5 = 4
⇒ p = 20
If the polynomial is p(x) = x3 - 3x2 + x + 1, then the value of p(- 3) is:- a)56
- b)– 56
- c)58
- d)57
Correct answer is option 'B'. Can you explain this answer?
If the polynomial is p(x) = x3 - 3x2 + x + 1, then the value of p(- 3) is:
a)
56
b)
– 56
c)
58
d)
57
|
|
Aditya Shah answered |
We have,
p(x) = x3 – 3x2 + x + 1
Then, p(– 3) = (-3)3 – 3(– 3)2 + (– 3)
+ 1
= – 27 – 27 – 3 + 1
= – 56.
p(x) = x3 – 3x2 + x + 1
Then, p(– 3) = (-3)3 – 3(– 3)2 + (– 3)
+ 1
= – 27 – 27 – 3 + 1
= – 56.
The difference of (3 + 2 √3) and (3 − 2 √3) is :- a)2 √3
- b)3 √3
- c)4 √3
- d)5 √3
Correct answer is option 'C'. Can you explain this answer?
The difference of (3 + 2 √3) and (3 − 2 √3) is :
a)
2 √3
b)
3 √3
c)
4 √3
d)
5 √3

|
Anirudh Maheshwari answered |
(3 2/3) - (3 - 2/3) = 3 2/3 - 3 2/3= 3 - 3 2/3 2/3 = 4/3 Thus, option (c) is the correct option Note :- I have used '/' as the symbol for root.
The difference of LCM and HCF of 28 and 42 is:- a)50
- b)60
- c)80
- d)70
Correct answer is option 'D'. Can you explain this answer?
The difference of LCM and HCF of 28 and 42 is:
a)
50
b)
60
c)
80
d)
70

|
Vp Classes answered |
28 = 22 × 7
and 42 = 2 x 3 x 7
∴ HCF (28, 42) = 2 x 7 = 14
and LCM (28, 42) = 22 x 3 x 7 = 84
Now, difference = 84 – 14 = 70.
and 42 = 2 x 3 x 7
∴ HCF (28, 42) = 2 x 7 = 14
and LCM (28, 42) = 22 x 3 x 7 = 84
Now, difference = 84 – 14 = 70.
The system of equations 2x + ay = 1 and 5x – 7y = 9 are given.
If the system has a unique solution, then all real values except :- a)- 14/5
- b)-13/5
- c)-12/5
- d)-11/5
Correct answer is option 'A'. Can you explain this answer?
The system of equations 2x + ay = 1 and 5x – 7y = 9 are given.
If the system has a unique solution, then all real values except :
If the system has a unique solution, then all real values except :
a)
- 14/5
b)
-13/5
c)
-12/5
d)
-11/5

|
Gunjan Lakhani answered |
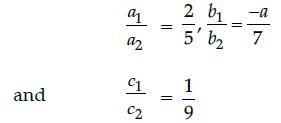
∵ The system of equations has unique
solution
solution
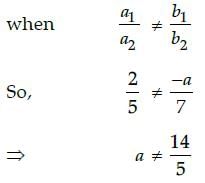
i.e., all real values except - 14/5
The zeroes of the quadratic polynomial 3x2 + 2x – 1 = 0 are :- a)-1 and 1/3
- b)-1 and 2/3
- c)1 and 1/3
- d)1 and 2/3
Correct answer is option 'A'. Can you explain this answer?
The zeroes of the quadratic polynomial 3x2 + 2x – 1 = 0 are :
a)
-1 and 1/3
b)
-1 and 2/3
c)
1 and 1/3
d)
1 and 2/3
|
|
Avinash Patel answered |
Given, 3x2 + 2x – 1 = 0
⇒ 3x2 + 3x – x – 1 = 0
⇒ 3x(x + 1) – 1 (x + 1) = 0
⇒ (x + 1) (3x – 1) = 0
⇒ x = – 1 and 1/3
⇒ 3x2 + 3x – x – 1 = 0
⇒ 3x(x + 1) – 1 (x + 1) = 0
⇒ (x + 1) (3x – 1) = 0
⇒ x = – 1 and 1/3
Case StudyThe diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using, - Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape
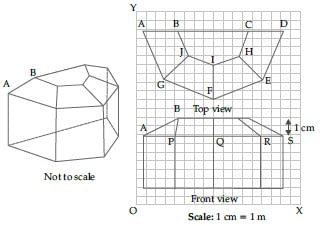 Refer to front view, the distance between the points A and S is
Refer to front view, the distance between the points A and S is- a)4
- b)8
- c)14
- d)20
Correct answer is option 'C'. Can you explain this answer?
Case Study
The diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using,
the sun room are square clear glass panels. The roof is made using,
- Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape

Refer to front view, the distance between the points A and S is
a)
4
b)
8
c)
14
d)
20
|
|
Ishan Choudhury answered |
A's coordinates = (1, 8)
S's coordinates = (15, 8)
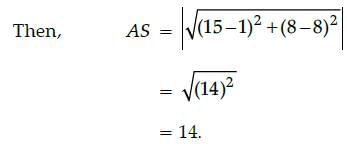
S's coordinates = (15, 8)
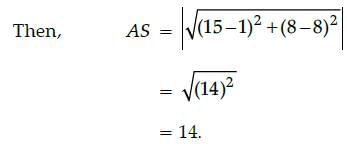
What number must be added to numerator and denominator of 2/7 to make fraction equal to 2/3 ?- a)8
- b)5
- c)3
- d)1
Correct answer is option 'A'. Can you explain this answer?
What number must be added to numerator and denominator of 2/7 to make fraction equal to 2/3 ?
a)
8
b)
5
c)
3
d)
1
|
|
Aditya Shah answered |
Let x be added to numerator and denominator of 2/7, so
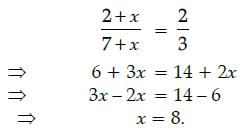
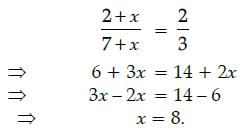
If the area of a sector of the circle of radius 18 cm is 72π cm2, then the angle q is :- a)80°
- b)70°
- c)90°
- d)60°
Correct answer is option 'A'. Can you explain this answer?
If the area of a sector of the circle of radius 18 cm is 72π cm2, then the angle q is :
a)
80°
b)
70°
c)
90°
d)
60°
|
|
Amit Kumar answered |
Here, r = 18 cm and area of sector = 72 π
cm2
cm2
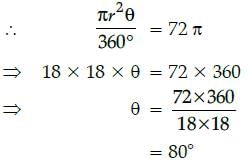
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour. Assuming that the speed of first car and second car be u km/h and v km/h respectively.What is the relative speed of both cars while they are travelling in the same direction ?
Assuming that the speed of first car and second car be u km/h and v km/h respectively.What is the relative speed of both cars while they are travelling in the same direction ?- a)85
- b)15 km/hr
- c)10/7 km/hr
- d)1750 km/hr
Correct answer is option 'B'. Can you explain this answer?
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.

Assuming that the speed of first car and second car be u km/h and v km/h respectively.
What is the relative speed of both cars while they are travelling in the same direction ?
a)
85
b)
15 km/hr
c)
10/7 km/hr
d)
1750 km/hr
|
|
Vikram Kapoor answered |
Relative speed of both cars while they are travelling in same direction
= (50 – 35) km/hr = 15 km/h.
= (50 – 35) km/hr = 15 km/h.
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour. The given problem is based on which mathematical concept
The given problem is based on which mathematical concept- a)Pair of linear equations
- b)Quadratic equations
- c)Polynomials
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.

The given problem is based on which mathematical concept
a)
Pair of linear equations
b)
Quadratic equations
c)
Polynomials
d)
None of the above
|
|
Meera Rana answered |
The given problem is based
on pair of linear equations.
on pair of linear equations.
If sin A = 1/√2, then the value of tan A + cot A is:- a)0
- b)1
- c)2
- d)1/2
Correct answer is option 'C'. Can you explain this answer?
If sin A = 1/√2, then the value of tan A + cot A is:
a)
0
b)
1
c)
2
d)
1/2
|
|
Anita Menon answered |
∵ sin A = 1/√2,
∴ sin A = sin 45°
⇒ A = 45°
Now, tan A + cot A = tan 45° + cot 45°
= 1 + 1
= 2.
∴ sin A = sin 45°
⇒ A = 45°
Now, tan A + cot A = tan 45° + cot 45°
= 1 + 1
= 2.
Case StudyThe diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using, - Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape
 Refer to Top View, find the mid-point of the segment joining the points J(6, 17) and I(9, 16).
Refer to Top View, find the mid-point of the segment joining the points J(6, 17) and I(9, 16).- a)33/2, 15/2
- b)3/2, 1/2
- c)15/2,33/2
- d)1/2, 3/2
Correct answer is option 'C'. Can you explain this answer?
Case Study
The diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using,
the sun room are square clear glass panels. The roof is made using,
- Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape

Refer to Top View, find the mid-point of the segment joining the points J(6, 17) and I(9, 16).
a)
33/2, 15/2
b)
3/2, 1/2
c)
15/2,33/2
d)
1/2, 3/2
|
|
Kiran Mehta answered |
Mid-point of J(6, 17) and I (9, 16) is
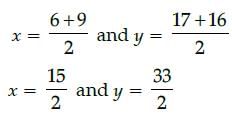
The point 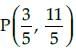 divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:
divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:- a)2 : 3
- b)5 : 2
- c)2 : 5
- d)3 : 2
Correct answer is option 'A'. Can you explain this answer?
The point 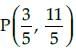 divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:
divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:
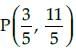 divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:
divide the line segment joining the points A(3, 5) and (– 3, – 2) is the ratio:a)
2 : 3
b)
5 : 2
c)
2 : 5
d)
3 : 2
|
|
Vivek Rana answered |
Let the required ratio be k : 1, then the coordinates of P are

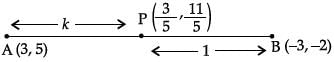


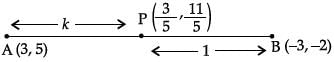

⇒ –15k + 15 = 3k + 3 and –10k + 25 = 11k + 11
⇒ –18k = –12 and –21k = –14
⇒ k = 2/3 and k = 2/3
Hence the point P divides AB in the ratio
2 : 3.
⇒ –18k = –12 and –21k = –14
⇒ k = 2/3 and k = 2/3
Hence the point P divides AB in the ratio
2 : 3.
Which of the following can not be the probability of an event ?- a)1/5
- b)0.4
- c)4 %
- d)9/8
Correct answer is option 'D'. Can you explain this answer?
Which of the following can not be the probability of an event ?
a)
1/5
b)
0.4
c)
4 %
d)
9/8
|
|
Ishan Choudhury answered |
Probability of an event can not be more than one or negative 9/8 > 1.
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour. What is the actual speed of other car?
What is the actual speed of other car?- a)60 km/hr
- b)30 km/hr
- c)100 km/hr
- d)20 km/hr
Correct answer is option 'B'. Can you explain this answer?
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.

What is the actual speed of other car?
a)
60 km/hr
b)
30 km/hr
c)
100 km/hr
d)
20 km/hr
|
|
Aditya Shah answered |
Let the speeds of first car
and second car be u km/hr and v km/hr
respectively.
According to the given information.
4 (u – v) = 80
i.e,. u – v = 20 ...(i)
and u + v = 80 ...(ii)
Solving eqs. (i) and (ii), we get u = 50
km/hr and v = 30 km/hr.
and second car be u km/hr and v km/hr
respectively.
According to the given information.
4 (u – v) = 80
i.e,. u – v = 20 ...(i)
and u + v = 80 ...(ii)
Solving eqs. (i) and (ii), we get u = 50
km/hr and v = 30 km/hr.
Case StudyThe diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using, - Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape
 Refer to front View, the distance of the point P from the y-axis is:
Refer to front View, the distance of the point P from the y-axis is:- a)4
- b)15
- c)19
- d)25
Correct answer is option 'A'. Can you explain this answer?
Case Study
The diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using,
the sun room are square clear glass panels. The roof is made using,
- Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape

Refer to front View, the distance of the point P from the y-axis is:
a)
4
b)
15
c)
19
d)
25
|
|
Anita Menon answered |
The distance of the point P from the Y-axis = 4.
If cot (A + B – C) = √3 and cos (B + C – A) = 1/2, then the value of B is :- a)45°
- b)30°
- c)60°
- d)90°
Correct answer is option 'A'. Can you explain this answer?
If cot (A + B – C) = √3 and cos (B + C – A) = 1/2, then the value of B is :
a)
45°
b)
30°
c)
60°
d)
90°
|
|
Rohit Sharma answered |
cot (A + B + C) = √3 = cot 30°
⇒ A + B – C = 30° ...(i)
and cos (B + C – A) = 1/2
⇒ cos (B + C – A)= cos 60°
⇒ B + C – A = 60° ...(ii)
Adding eq. (i) and (ii), we get
2B = 90°
⇒ B = 45°
⇒ A + B – C = 30° ...(i)
and cos (B + C – A) = 1/2
⇒ cos (B + C – A)= cos 60°
⇒ B + C – A = 60° ...(ii)
Adding eq. (i) and (ii), we get
2B = 90°
⇒ B = 45°
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour. What is the actual speed of one car?
What is the actual speed of one car?- a)50 km/hr
- b)40 km/hr
- c)100 km/hr
- d)20 km/hr
Correct answer is option 'A'. Can you explain this answer?
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.

What is the actual speed of one car?
a)
50 km/hr
b)
40 km/hr
c)
100 km/hr
d)
20 km/hr
|
|
Raghav Bansal answered |
Let the speeds of first car and second car be u km/hr and v km/hr respectively.
According to the given information.
4 (u – v) = 80
i.e,. u – v = 20 ...(i)
and u + v = 80 ...(ii)
Solving eqs. (i) and (ii), we get u = 50 km/hr.
According to the given information.
4 (u – v) = 80
i.e,. u – v = 20 ...(i)
and u + v = 80 ...(ii)
Solving eqs. (i) and (ii), we get u = 50 km/hr.
The circumference of a circle of radius 4 cm is: (Use π = 3.14)- a)24.12 cm
- b)25.12 cm
- c)26.12 cm
- d)23.12 cm
Correct answer is option 'B'. Can you explain this answer?
The circumference of a circle of radius 4 cm is: (Use π = 3.14)
a)
24.12 cm
b)
25.12 cm
c)
26.12 cm
d)
23.12 cm
|
|
Vikram Kapoor answered |
Given, radius (r) = 4 cm
∴ Circumference, (C) = 2πr
= 2 × 3.14 × 4 cm
= 25. 12 cm.
∴ Circumference, (C) = 2πr
= 2 × 3.14 × 4 cm
= 25. 12 cm.
Case StudyThe diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using, - Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape
 Refer to front view, if a point (x, y) is equidistant from the Q(9, 8) and S(17, 8), then
Refer to front view, if a point (x, y) is equidistant from the Q(9, 8) and S(17, 8), then- a)x + y = 13
- b)x – 13 = 0
- c)y – 13 = 0
- d)x – y = 13
Correct answer is option 'B'. Can you explain this answer?
Case Study
The diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using,
the sun room are square clear glass panels. The roof is made using,
- Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape

Refer to front view, if a point (x, y) is equidistant from the Q(9, 8) and S(17, 8), then
a)
x + y = 13
b)
x – 13 = 0
c)
y – 13 = 0
d)
x – y = 13
|
|
Ananya Das answered |
Let point be P(x, y)
PQ2 = PS2
or, (x – 9)2 + (y – 8)2 = (x – 17)2 + (y – 8)2
or, x – 13 = 0
PQ2 = PS2
or, (x – 9)2 + (y – 8)2 = (x – 17)2 + (y – 8)2
or, x – 13 = 0
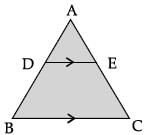 In the given figure, If DE || BC, AD = 2 cm, BD = 2.5 cm, AE = 3.2 cm and DE = 4 cm, then BC = 9 cmFind AC.
In the given figure, If DE || BC, AD = 2 cm, BD = 2.5 cm, AE = 3.2 cm and DE = 4 cm, then BC = 9 cmFind AC.- a)7.2 cm
- b)6.2 cm
- c)8.2 cm
- d)5.2 cm
Correct answer is option 'A'. Can you explain this answer?

In the given figure, If DE || BC, AD = 2 cm, BD = 2.5 cm, AE = 3.2 cm and DE = 4 cm, then BC = 9 cmFind AC.
a)
7.2 cm
b)
6.2 cm
c)
8.2 cm
d)
5.2 cm
|
|
Ishan Choudhury answered |
∵ DE || BC (given)
∴ ∠ADE = ∠ABC (corresponding angles)
and ∠AED = ∠ACB (corresponding angles)
∴ DADE ~ DABC (By AA similarity)
∴ ∠ADE = ∠ABC (corresponding angles)
and ∠AED = ∠ACB (corresponding angles)
∴ DADE ~ DABC (By AA similarity)
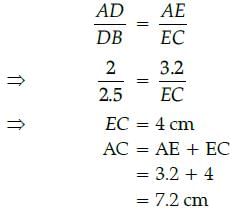
If x = 0, then the value of 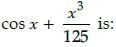
- a)126/125
- b)124/125
- c)1/125
- d)1
Correct answer is option 'D'. Can you explain this answer?
If x = 0, then the value of 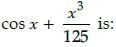
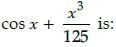
a)
126/125
b)
124/125
c)
1/125
d)
1
|
|
Amit Sharma answered |
We have,
x = 0
or cos x = cos 0
or cos x = 1
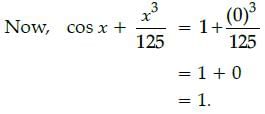
x = 0
or cos x = cos 0
or cos x = 1
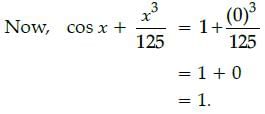
The number 0.121212 ...... is the form of p/q will be equal:- a)4/11
- b)2/11
- c)4/33
- d)2/33
Correct answer is option 'C'. Can you explain this answer?
The number 0.121212 ...... is the form of p/q will be equal:
a)
4/11
b)
2/11
c)
4/33
d)
2/33
|
|
Rohit Sharma answered |
Let x =0.121212.... ...(i)
100x =12.1212.... ...(ii)
On subtracting eqn. (i) from (ii)
100x =12.1212.... ...(ii)
On subtracting eqn. (i) from (ii)
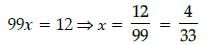
In a given ABC, DE || BC and AB/DB = 3/5. If AC = 5.6 cm, then AE = .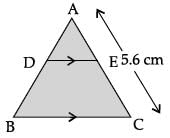
- a)2.5 cm
- b)2.8 cm
- c)2.1 cm
- d)2.6 cm
Correct answer is option 'C'. Can you explain this answer?
In a given ABC, DE || BC and AB/DB = 3/5. If AC = 5.6 cm, then AE = .

a)
2.5 cm
b)
2.8 cm
c)
2.1 cm
d)
2.6 cm
|
|
Aditya Shah answered |
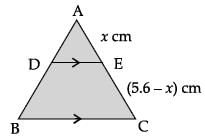
Let AE = x cm,
then EC = (5.6 – x) cm
and DE || BC (given)
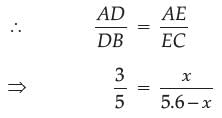
⇒ 3(5.6 – x) = 5x
⇒ 16.8 – 3x = 5x
⇒ 8x = 16.8
⇒ x = 2.1
then EC = (5.6 – x) cm
and DE || BC (given)
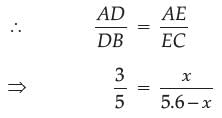
⇒ 3(5.6 – x) = 5x
⇒ 16.8 – 3x = 5x
⇒ 8x = 16.8
⇒ x = 2.1
Case StudyThe diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using, - Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape
 Refer to front view, find the co-ordinates of the point which divides the line segment joining the points
Refer to front view, find the co-ordinates of the point which divides the line segment joining the points
A and B in the ratio 1 : 3 internally.- a)(8.5, 2.0)
- b)(2.0, 9.5)
- c)(3.0, 7.5)
- d)(2.0, 8.5)
Correct answer is option 'D'. Can you explain this answer?
Case Study
The diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of
the sun room are square clear glass panels. The roof is made using,
the sun room are square clear glass panels. The roof is made using,
- Four clear glass panels, trapezium in shape, all of the same size
- One tinted glass panel, half a regular octagon in shape

Refer to front view, find the co-ordinates of the point which divides the line segment joining the points
A and B in the ratio 1 : 3 internally.
A and B in the ratio 1 : 3 internally.
a)
(8.5, 2.0)
b)
(2.0, 9.5)
c)
(3.0, 7.5)
d)
(2.0, 8.5)
|
|
Aditya Shah answered |
The coordinates of A = (1, 8)
The coordinates of B = (4, 10)
Also, m = 1 and n = 3
Then,
The coordinates of B = (4, 10)
Also, m = 1 and n = 3
Then,
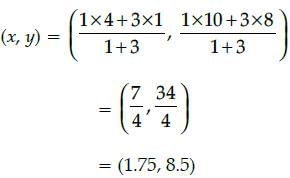
If 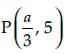 is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:
is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:- a)– 10
- b)– 15
- c)10
- d)15
Correct answer is option 'B'. Can you explain this answer?
If 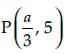 is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:
is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:
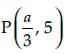 is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:
is the mid point of the line segment joining the points A(–7, 3) and B(– 3, 7), then the value of a is:a)
– 10
b)
– 15
c)
10
d)
15
|
|
Amit Sharma answered |
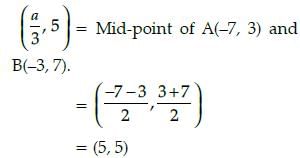
Then, comparing on both sides, we get
a/3 = – 5
⇒ a = – 15.
a/3 = – 5
⇒ a = – 15.
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour. What is the relative speed of both cars while they are travelling towards each other ?
What is the relative speed of both cars while they are travelling towards each other ?- a)85 km/hr
- b)15 km/hr
- c)10/7km/hr
- d)1750 km/hr
Correct answer is option 'A'. Can you explain this answer?
Case Study
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.
Places A and B are 80 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If they travel towards each other, they meet in 1 hour.

What is the relative speed of both cars while they are travelling towards each other ?
a)
85 km/hr
b)
15 km/hr
c)
10/7km/hr
d)
1750 km/hr
|
|
Ishan Choudhury answered |
Relative speed of both cars while they are travelling in opposite directions i.e., travelling towards each other
= (50 + 35) km/hr = 85 km/h.
= (50 + 35) km/hr = 85 km/h.
Chapter doubts & questions for CBSE Sample Question Papers for 2021-22 - CBSE Sample Papers For Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of CBSE Sample Question Papers for 2021-22 - CBSE Sample Papers For Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup




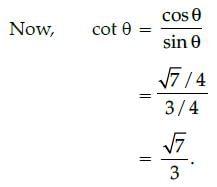
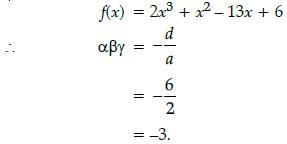
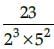 will terminate after:
will terminate after: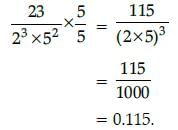
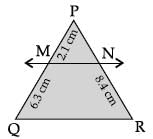
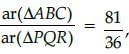 and AC = 18 cm then the value of QR is :
and AC = 18 cm then the value of QR is :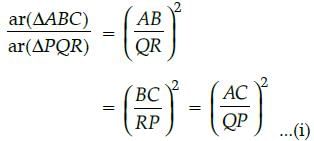
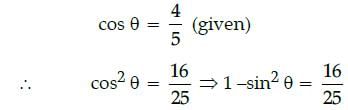
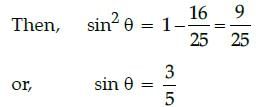
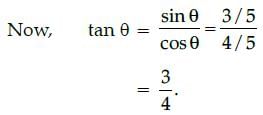

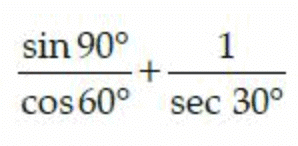 is:
is: