All questions of Signals & Systems for Electronics and Communication Engineering (ECE) Exam
The transform function H(s) of a causal system is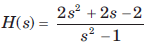 The impulse response is
The impulse response is- a)
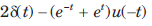
- b)
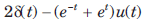
- c)
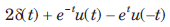
- d)
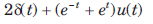
Correct answer is option 'D'. Can you explain this answer?
The transform function H(s) of a causal system is
The impulse response is
a)
b)
c)
d)
|
|
Rhea Reddy answered |
For a causal system h(t) = 0 for t < 0
The transfer function of a system is given as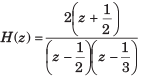 Consider the two statementsStatement(i) : System is causal and stable.
Consider the two statementsStatement(i) : System is causal and stable.
Statement(ii) : Inverse system is causal and stable.The correct option is- a)(i) is true
- b)(ii) is true
- c)Both (i) and (ii) are true
- d)Both are false
Correct answer is option 'C'. Can you explain this answer?
The transfer function of a system is given as
Consider the two statements
Statement(i) : System is causal and stable.
Statement(ii) : Inverse system is causal and stable.
Statement(ii) : Inverse system is causal and stable.
The correct option is
a)
(i) is true
b)
(ii) is true
c)
Both (i) and (ii) are true
d)
Both are false

|
Moumita Kulkarni answered |
For this system and inverse system all poles are inside |z| = 1. So both system are both causal and stable.
Let P be linearity, Q be time invariance, R be causality and S be stability. In question discrete time input x[n] and output y[n] relationship has been given. In the option properties of system has been given. Choose the option which match the properties for system.y[n] = nx[n]- a)P, Q, R, S
- b)Q, R, S
- c)P, R
- d)Q, S
Correct answer is option 'C'. Can you explain this answer?
Let P be linearity, Q be time invariance, R be causality and S be stability. In question discrete time input x[n] and output y[n] relationship has been given. In the option properties of system has been given. Choose the option which match the properties for system.
y[n] = nx[n]
a)
P, Q, R, S
b)
Q, R, S
c)
P, R
d)
Q, S

|
Anshu Kumar answered |
Since the system is homogeneous and additive, it is also linear.
At any discrete time, n = no the response depends only on the excitation at that same time. (Causal)
If the excitation is a constant, the response is unbounded as n approaches infinity. (Unstable)
x[n] as shown in fig.
- a)P, Q, R, S
- b)Q, R, S
- c)P, Q
- d)R, S
Correct answer is option 'B'. Can you explain this answer?
x[n] as shown in fig.
a)
P, Q, R, S
b)
Q, R, S
c)
P, Q
d)
R, S
|
|
Devansh Dasgupta answered |
An delay system is a system whose output is same as the input, but after a delay.
Unilateral Laplace Transform is applicable for the determination of linear constant coefficient differential equations with ________- a)Zero initial condition
- b)Non-zero initial condition
- c)Zero final condition
- d)Non-zero final condition
Correct answer is option 'B'. Can you explain this answer?
Unilateral Laplace Transform is applicable for the determination of linear constant coefficient differential equations with ________
a)
Zero initial condition
b)
Non-zero initial condition
c)
Zero final condition
d)
Non-zero final condition

|
Asha Nambiar answered |
Unilateral Laplace Transform for Constant Coefficient Differential Equations with Non-zero Initial Condition
Unilateral Laplace Transform is a mathematical tool used to solve linear constant coefficient differential equations. It is particularly useful in solving differential equations with non-zero initial conditions. Let us discuss in detail the application of Unilateral Laplace Transform for constant coefficient differential equations with a non-zero initial condition.
Constant Coefficient Differential Equations
A constant coefficient differential equation is a differential equation in which the coefficients are constant. These types of differential equations are commonly found in physics and engineering. Examples of constant coefficient differential equations include the following:
- d^2y/dt^2 + 3dy/dt + 2y = 0
- d^2y/dt^2 + 2dy/dt + 2y = f(t)
Unilateral Laplace Transform
Unilateral Laplace Transform is a mathematical tool used to solve linear constant coefficient differential equations. It is defined as follows:
L{f(t)} = F(s) = ∫0∞ e^-st f(t) dt
where L denotes the Laplace transform, f(t) is the function to be transformed, s is the complex variable, and F(s) is the Laplace transform of f(t). The Laplace transform is a powerful tool that can be used to solve differential equations.
Application of Unilateral Laplace Transform for Constant Coefficient Differential Equations with Non-zero Initial Condition
The Unilateral Laplace Transform can be used to solve constant coefficient differential equations with non-zero initial conditions. The general process involves the following steps:
- Take the Laplace transform of both sides of the differential equation.
- Solve for the Laplace transform of the dependent variable.
- Take the inverse Laplace transform to find the solution to the original differential equation.
For example, consider the following differential equation:
d^2y/dt^2 + 2dy/dt + 2y = 0, y(0) = 1, dy/dt(0) = 0
Taking the Laplace transform of both sides of the differential equation, we get:
s^2Y(s) - s + 2sY(s) + 2Y(s) = Y(0) + sdy/dt(0) + 2y(0)
Simplifying this equation, we get:
Y(s) = (s+1)/(s^2 + 2s + 2)
Taking the inverse Laplace transform, we get:
y(t) = e^-t(cos(t) - sin(t))
Thus, we have solved the differential equation with non-zero initial conditions using the Unilateral Laplace Transform.
Conclusion
In conclusion, the Unilateral Laplace Transform is a powerful tool that can be used to solve constant coefficient differential equations with non-zero initial conditions. By taking the Laplace transform of the differential equation, solving for the Laplace transform of the dependent variable, and taking the inverse Laplace transform, we can find the solution to the original differential equation.
Unilateral Laplace Transform is a mathematical tool used to solve linear constant coefficient differential equations. It is particularly useful in solving differential equations with non-zero initial conditions. Let us discuss in detail the application of Unilateral Laplace Transform for constant coefficient differential equations with a non-zero initial condition.
Constant Coefficient Differential Equations
A constant coefficient differential equation is a differential equation in which the coefficients are constant. These types of differential equations are commonly found in physics and engineering. Examples of constant coefficient differential equations include the following:
- d^2y/dt^2 + 3dy/dt + 2y = 0
- d^2y/dt^2 + 2dy/dt + 2y = f(t)
Unilateral Laplace Transform
Unilateral Laplace Transform is a mathematical tool used to solve linear constant coefficient differential equations. It is defined as follows:
L{f(t)} = F(s) = ∫0∞ e^-st f(t) dt
where L denotes the Laplace transform, f(t) is the function to be transformed, s is the complex variable, and F(s) is the Laplace transform of f(t). The Laplace transform is a powerful tool that can be used to solve differential equations.
Application of Unilateral Laplace Transform for Constant Coefficient Differential Equations with Non-zero Initial Condition
The Unilateral Laplace Transform can be used to solve constant coefficient differential equations with non-zero initial conditions. The general process involves the following steps:
- Take the Laplace transform of both sides of the differential equation.
- Solve for the Laplace transform of the dependent variable.
- Take the inverse Laplace transform to find the solution to the original differential equation.
For example, consider the following differential equation:
d^2y/dt^2 + 2dy/dt + 2y = 0, y(0) = 1, dy/dt(0) = 0
Taking the Laplace transform of both sides of the differential equation, we get:
s^2Y(s) - s + 2sY(s) + 2Y(s) = Y(0) + sdy/dt(0) + 2y(0)
Simplifying this equation, we get:
Y(s) = (s+1)/(s^2 + 2s + 2)
Taking the inverse Laplace transform, we get:
y(t) = e^-t(cos(t) - sin(t))
Thus, we have solved the differential equation with non-zero initial conditions using the Unilateral Laplace Transform.
Conclusion
In conclusion, the Unilateral Laplace Transform is a powerful tool that can be used to solve constant coefficient differential equations with non-zero initial conditions. By taking the Laplace transform of the differential equation, solving for the Laplace transform of the dependent variable, and taking the inverse Laplace transform, we can find the solution to the original differential equation.
Where is the ROC defined or specified for the signals containing causal as well as anti-causal terms?- a)Greater than the largest pole
- b)Less than the smallest pole
- c)Between two poles
- d)Cannot be defined
Correct answer is option 'C'. Can you explain this answer?
Where is the ROC defined or specified for the signals containing causal as well as anti-causal terms?
a)
Greater than the largest pole
b)
Less than the smallest pole
c)
Between two poles
d)
Cannot be defined
|
|
Pallavi Reddy answered |
The ROC defined or specified for the signals containing causal as well as anti-causal terms b
etween two poles.Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.Que: y[n] = x[n] - x[n + N/2 ] , (assume that N is even)- a)(1-(-1)k+1)X[2k]
- b)(1-(-1)k)X[k]
- c)(1-(-1)k+1)X[k]
- d)(1-(-1)k)X[2k]
Correct answer is option 'B'. Can you explain this answer?
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
Que: y[n] = x[n] - x[n + N/2 ] , (assume that N is even)
a)
(1-(-1)k+1)X[2k]
b)
(1-(-1)k)X[k]
c)
(1-(-1)k+1)X[k]
d)
(1-(-1)k)X[2k]
|
|
Vara Bhandari answered |
Understanding the Problem
The given periodic signal is defined as y[n] = x[n] - x[n + N/2], where x[n] is a periodic signal with period N. Here, N is even, indicating that the signal repeats every N samples.
Fourier Series Coefficients
The Fourier Series (FS) coefficients X[k] represent the frequency components of the periodic signal x[n]. To find the FS coefficients Y[k] of the modified signal y[n], we need to analyze the impact of the subtraction operation in y[n]:
- The term x[n + N/2] represents the signal shifted by half its period.
- Since N is even, x[n + N/2] will have a specific relationship with x[n].
Calculating the Coefficients
Using the properties of Fourier series:
- The FS coefficients of x[n + N/2] can be derived from X[k], specifically:
- X[k + N/2] if k is shifted by N/2.
Thus, for y[n]:
Y[k] = X[k] - X[k + N/2]
Now, we evaluate how this affects the coefficients:
- Since X[k + N/2] is the FS representation of x[n + N/2], and because x[n] is periodic, we can deduce that this will produce a specific pattern in the coefficients.
Identifying the Correct Option
After analysis, we can conclude:
- When analyzing the subtraction, we see that:
- The coefficients will cancel out in certain frequencies depending on the periodic nature.
- The correct expression that represents this relationship in the question is:
Y[k] = (1 - (-1)^k)X[k]
This indicates that Y[k] takes into account the effect of the periodic nature of x[n] and its shifted version. Each term contributes to Y[k] based on the evenness of the index k.
Final Conclusion
Thus, the correct answer is option 'B':
Y[k] = (1 - (-1)^k)X[k].
This option accurately reflects the properties of the periodic signal and its Fourier Series representation.
The given periodic signal is defined as y[n] = x[n] - x[n + N/2], where x[n] is a periodic signal with period N. Here, N is even, indicating that the signal repeats every N samples.
Fourier Series Coefficients
The Fourier Series (FS) coefficients X[k] represent the frequency components of the periodic signal x[n]. To find the FS coefficients Y[k] of the modified signal y[n], we need to analyze the impact of the subtraction operation in y[n]:
- The term x[n + N/2] represents the signal shifted by half its period.
- Since N is even, x[n + N/2] will have a specific relationship with x[n].
Calculating the Coefficients
Using the properties of Fourier series:
- The FS coefficients of x[n + N/2] can be derived from X[k], specifically:
- X[k + N/2] if k is shifted by N/2.
Thus, for y[n]:
Y[k] = X[k] - X[k + N/2]
Now, we evaluate how this affects the coefficients:
- Since X[k + N/2] is the FS representation of x[n + N/2], and because x[n] is periodic, we can deduce that this will produce a specific pattern in the coefficients.
Identifying the Correct Option
After analysis, we can conclude:
- When analyzing the subtraction, we see that:
- The coefficients will cancel out in certain frequencies depending on the periodic nature.
- The correct expression that represents this relationship in the question is:
Y[k] = (1 - (-1)^k)X[k]
This indicates that Y[k] takes into account the effect of the periodic nature of x[n] and its shifted version. Each term contributes to Y[k] based on the evenness of the index k.
Final Conclusion
Thus, the correct answer is option 'B':
Y[k] = (1 - (-1)^k)X[k].
This option accurately reflects the properties of the periodic signal and its Fourier Series representation.
Let P be linearity, Q be time invariance, R be causality and S be stability. In question discrete time input x[n] and output y[n] relationship has been given. In the option properties of system has been given. Choose the option which match the properties for system.Que: y[n] = rect (x[n])- a)P, Q, R
- b)Q, R, S
- c)R, S, P
- d)S , P, Q
Correct answer is option 'B'. Can you explain this answer?
Let P be linearity, Q be time invariance, R be causality and S be stability. In question discrete time input x[n] and output y[n] relationship has been given. In the option properties of system has been given. Choose the option which match the properties for system.
Que: y[n] = rect (x[n])
a)
P, Q, R
b)
Q, R, S
c)
R, S, P
d)
S , P, Q

|
Ishaan Kulkarni answered |
At any discrete time n = no , the response depends only on the excitation at that discrete time. (Causal)
No matter what values the excitation may have the response can only have the values zero or one.
x[n] as shown in fig
- a)P, Q, R, S
- b)P, Q, R
- c)P, Q
- d)Q, R, S
Correct answer is option 'B'. Can you explain this answer?
x[n] as shown in fig
a)
P, Q, R, S
b)
P, Q, R
c)
P, Q
d)
Q, R, S
|
|
Swati Kaur answered |
At any discrete time n no the response depends only on the excitation at that discrete time and previous discrete time. (Causal)
If the excitation is constant, the response increase without bound. (Unstable)
X(z) has poles at z =1/2 and z =-1.If x [1] = 1 x [-1] = 1, and the ROC includes the point z = 34. The time signal x[n] is- a)
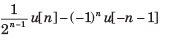
- b)
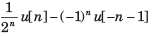
- c)
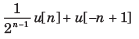
- d)
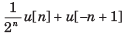
Correct answer is option 'A'. Can you explain this answer?
X(z) has poles at z =1/2 and z =-1.If x [1] = 1 x [-1] = 1, and the ROC includes the point z = 34. The time signal x[n] is
a)
b)
c)
d)

|
Mahesh Yadav answered |
Since the ROC includes the z = 3/4, ROC is
Given the z-transforms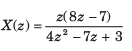 The limit of x[ ∞] is
The limit of x[ ∞] is- a)1
- b)2
- c)∞
- d)0
Correct answer is option 'A'. Can you explain this answer?
Given the z-transforms
The limit of x[ ∞] is
a)
1
b)
2
c)
∞
d)
0

|
Bhaskar Unni answered |
The function has poles at z = 1,3/4. Thus final value theorem applies.
X(z) of a system is specified by a pole zero pattern in fig.
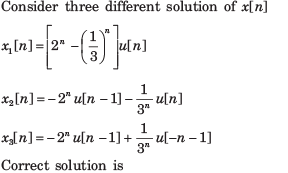
- a)x1[n]
- b)x2[n]
- c)x3[n]
- d)All three
Correct answer is option 'D'. Can you explain this answer?
X(z) of a system is specified by a pole zero pattern in fig.
a)
x1[n]
b)
x2[n]
c)
x3[n]
d)
All three

|
Aditya Patel answered |
All gives the same z transform with different ROC. So all are the solution.
Consider a continuous time periodic signal x(t) with fundamental period T and Fourier series coefficients X[k]. Determine the Fourier series coefficient of the signal y(t) given in question and choose correct option.Que: y(t) = Ev{x(t)}- a)
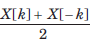
- b)
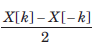
- c)
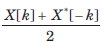
- d)
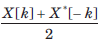
Correct answer is option 'A'. Can you explain this answer?
Consider a continuous time periodic signal x(t) with fundamental period T and Fourier series coefficients X[k]. Determine the Fourier series coefficient of the signal y(t) given in question and choose correct option.
Que: y(t) = Ev{x(t)}
a)
b)
c)
d)

|
Neha Basak answered |
The FS coefficients of x(t) are
Therefore, the FS coefficients of Ev{ x(t)} are
Consider three different signal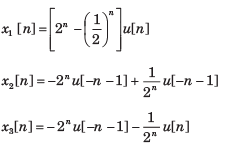 fig.shows the three different region. Choose the correct option for the ROC of signal
fig.shows the three different region. Choose the correct option for the ROC of signal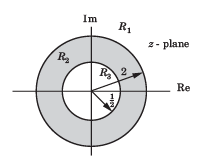 R1 , R2 , R3
R1 , R2 , R3- a)x1[n], x2[n], x3[n]
- b)x2[n], x3[n], x1[n]
- c)x1[n], x3[n], x2[n]
- d)x3[n], x2[n], x1[n]
Correct answer is option 'C'. Can you explain this answer?
Consider three different signal
fig.shows the three different region. Choose the correct option for the ROC of signal
R1 , R2 , R3
a)
x1[n], x2[n], x3[n]
b)
x2[n], x3[n], x1[n]
c)
x1[n], x3[n], x2[n]
d)
x3[n], x2[n], x1[n]
|
|
Avantika Chauhan answered |
x1[n] is right-sided signal
Chapter doubts & questions for Signals & Systems - RRB JE for Electronics & Communication Engineering 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Signals & Systems - RRB JE for Electronics & Communication Engineering in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
RRB JE for Electronics & Communication Engineering
3 videos|68 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup




























