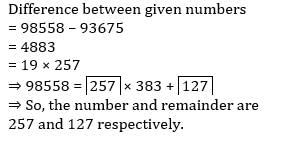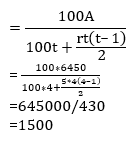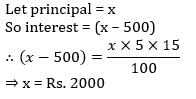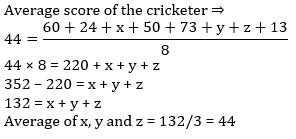All Exams >
CTET & State TET >
CTET (Central Teacher Eligibility Test) Mock Test Series 2025 >
All Questions
All questions of CTET Practice Test (Mathematics Paper 2) for CTET & State TET Exam
Six-elevenths of a number is equal to 22% of second number. Second number is equal to the one-fourth of third number. The value of the third number is 2400. What is the 45% of the first number? - a)108.9
- b)111.7
- c)117.6
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Six-elevenths of a number is equal to 22% of second number. Second number is equal to the one-fourth of third number. The value of the third number is 2400. What is the 45% of the first number?
a)
108.9
b)
111.7
c)
117.6
d)
None of these
|
|
Swati Chopra answered |
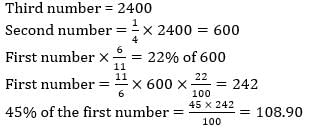
An Insurance employer reduces the number of his employees in the ratio 9: 8 and increases their wages in the ratio 14: 15. If the original wage bill was Rs. 18,900, find the ratio of decreased wage and original wage. - a)20: 21
- b)21: 29
- c)20: 19
- d)19: 21
Correct answer is option 'A'. Can you explain this answer?
An Insurance employer reduces the number of his employees in the ratio 9: 8 and increases their wages in the ratio 14: 15. If the original wage bill was Rs. 18,900, find the ratio of decreased wage and original wage.
a)
20: 21
b)
21: 29
c)
20: 19
d)
19: 21
|
|
Saikat Sengupta answered |
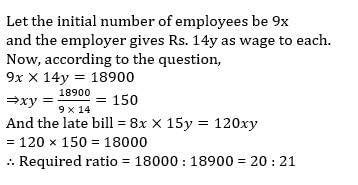
Suresh solved 60% of the question in an examination correctly. If out of 71 Questions solved by Suresh, 37 questions are correct and out of remaining every 7 questions, 5 questions have been solved by Suresh correctly. Then find the total number of questions asked in the examination? - a)49
- b)120
- c)81
- d)111
Correct answer is option 'B'. Can you explain this answer?
Suresh solved 60% of the question in an examination correctly. If out of 71 Questions solved by Suresh, 37 questions are correct and out of remaining every 7 questions, 5 questions have been solved by Suresh correctly. Then find the total number of questions asked in the examination?
a)
49
b)
120
c)
81
d)
111
|
|
Atharva Shah answered |
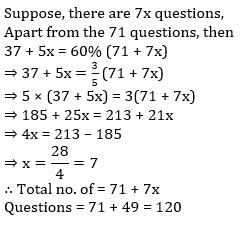
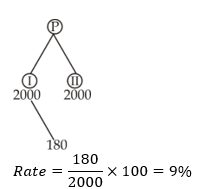
Anubhav lends Rs. 2500 to Bose and a certain sum to Chandra at the same time at 7% annual simple interest. If after 4 years Anubhav received interest of Rs. 1120 from Bose and Chandra, the sum lent to Chandra is - a)Rs. 700
- b)Rs. 6500
- c)Rs. 40000
- d)Rs. 1500
Correct answer is option 'D'. Can you explain this answer?
Anubhav lends Rs. 2500 to Bose and a certain sum to Chandra at the same time at 7% annual simple interest. If after 4 years Anubhav received interest of Rs. 1120 from Bose and Chandra, the sum lent to Chandra is
a)
Rs. 700
b)
Rs. 6500
c)
Rs. 40000
d)
Rs. 1500
|
|
Aarav Majumdar answered |
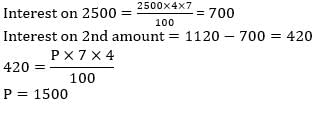
Walking from home at 2/3rd of his usual speed, a man reaches his office 30 minutes late. Had the person walked at 5/4th of his usual speed, find the time taken by the man to reach his office. - a)45 minutes
- b)50 minutes
- c)48 minutes
- d)60 minutes
Correct answer is option 'C'. Can you explain this answer?
Walking from home at 2/3rd of his usual speed, a man reaches his office 30 minutes late. Had the person walked at 5/4th of his usual speed, find the time taken by the man to reach his office.
a)
45 minutes
b)
50 minutes
c)
48 minutes
d)
60 minutes
|
|
Rashi Ahuja answered |
If distance is constant then time taken in inversely proportional to the speed. When speed becomes two-third of the normal speed, time taken will be 3/2 times of his normal time. If the normal time to reach the office is T, then the man is taking T/2 time extra to reach the office.
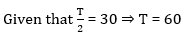
If the man walk at 5/4 th of the normal speed, time taken will be 4/5 th of the normal time
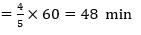
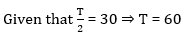
If the man walk at 5/4 th of the normal speed, time taken will be 4/5 th of the normal time
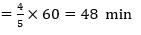
A train traveling 60% faster than a car. Both start from point A at the same time and reach point B, 160 km away at the same time. On the way, the train takes 20 minutes for stopping at the stations. What is the speed (in km/hr) of the train? - a)144
- b)168
- c)198
- d)288
Correct answer is option 'D'. Can you explain this answer?
A train traveling 60% faster than a car. Both start from point A at the same time and reach point B, 160 km away at the same time. On the way, the train takes 20 minutes for stopping at the stations. What is the speed (in km/hr) of the train?
a)
144
b)
168
c)
198
d)
288
|
|
Mehul Menon answered |
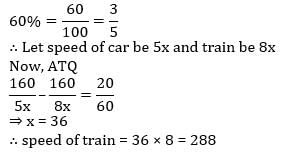
The measure of the four successive angles of a quadrilateral are in the ratio 7 : 11 : 7 : 11. The quadrilateral is a ______. - a)trapezium
- b)rectangle
- c)parallelogram
- d)square
Correct answer is option 'C'. Can you explain this answer?
The measure of the four successive angles of a quadrilateral are in the ratio 7 : 11 : 7 : 11. The quadrilateral is a ______.
a)
trapezium
b)
rectangle
c)
parallelogram
d)
square
|
|
Shounak Iyer answered |
Explanation:
Ratio of angles:
- The given ratio of the four successive angles of the quadrilateral is 7 : 11 : 7 : 11.
Sum of angles in a quadrilateral:
- In any quadrilateral, the sum of all four angles is always 360 degrees.
Calculating angle measurements:
- Let the angles be 7x, 11x, 7x, and 11x (in order) based on the given ratio.
- According to the ratio, the sum of the angles can be expressed as 7x + 11x + 7x + 11x = 360.
- Solving the equation, we get x = 15.
- Therefore, the angles are 105°, 165°, 105°, and 165°.
Identifying the quadrilateral:
- A quadrilateral with opposite angles being equal and the sum of all angles being 360 degrees is a parallelogram.
Conclusion:
- Hence, based on the ratio of the angles and the properties of a quadrilateral, the given quadrilateral is a parallelogram.
Ratio of angles:
- The given ratio of the four successive angles of the quadrilateral is 7 : 11 : 7 : 11.
Sum of angles in a quadrilateral:
- In any quadrilateral, the sum of all four angles is always 360 degrees.
Calculating angle measurements:
- Let the angles be 7x, 11x, 7x, and 11x (in order) based on the given ratio.
- According to the ratio, the sum of the angles can be expressed as 7x + 11x + 7x + 11x = 360.
- Solving the equation, we get x = 15.
- Therefore, the angles are 105°, 165°, 105°, and 165°.
Identifying the quadrilateral:
- A quadrilateral with opposite angles being equal and the sum of all angles being 360 degrees is a parallelogram.
Conclusion:
- Hence, based on the ratio of the angles and the properties of a quadrilateral, the given quadrilateral is a parallelogram.
A water filling pipe P is 5 times faster than second pipe Q. If Q fills a cistern in 30 minutes. How long will it take to fill the tank, when both the pipes are kept in operation simultaneous ? - a)7 min.
- b)6 min.
- c)8 min.
- d)5 min.
Correct answer is option 'D'. Can you explain this answer?
A water filling pipe P is 5 times faster than second pipe Q. If Q fills a cistern in 30 minutes. How long will it take to fill the tank, when both the pipes are kept in operation simultaneous ?
a)
7 min.
b)
6 min.
c)
8 min.
d)
5 min.
|
|
Madhavan Singh answered |
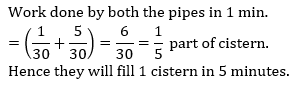
In a business, Abhiram and Chiru invested amounts in the ratio 2: 1, whereas the ratio between amounts invested by Abhiram and Bikash was 3: 2. If Rs. 1,57,300 was their profit, how much amount did Bikash receive? - a)Rs. 72600
- b)Rs. 48400
- c)Rs. 36300
- d)Rs. 24200
Correct answer is option 'B'. Can you explain this answer?
In a business, Abhiram and Chiru invested amounts in the ratio 2: 1, whereas the ratio between amounts invested by Abhiram and Bikash was 3: 2. If Rs. 1,57,300 was their profit, how much amount did Bikash receive?
a)
Rs. 72600
b)
Rs. 48400
c)
Rs. 36300
d)
Rs. 24200
|
|
Ashutosh Banerjee answered |

A, B and C can complete a work in 10, 12 and 15 days respectively. All three of them start together but after 3 days A leaves the job and B left the job 2 days before the work was completed. C completed the remaining work alone. In how many days was the total work completed? - a)25/9 days
- b)52/9 days
- c)26/9 days
- d)53/9 days
Correct answer is option 'B'. Can you explain this answer?
A, B and C can complete a work in 10, 12 and 15 days respectively. All three of them start together but after 3 days A leaves the job and B left the job 2 days before the work was completed. C completed the remaining work alone. In how many days was the total work completed?
a)
25/9 days
b)
52/9 days
c)
26/9 days
d)
53/9 days
|
|
Yash Malik answered |
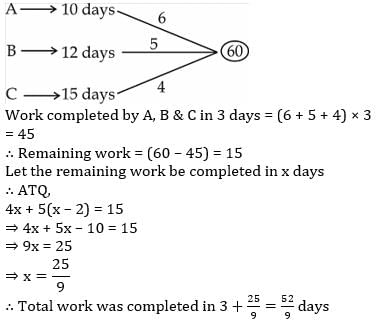
In an entrance examination Rockie scored 56% marks, perry scored 92% marks and Srifi scored 634 marks. The maximum marks of the examination are 875, what are the average mark scored by all the three girls together: - a)929
- b)815
- c)690
- d)643
Correct answer is option 'D'. Can you explain this answer?
In an entrance examination Rockie scored 56% marks, perry scored 92% marks and Srifi scored 634 marks. The maximum marks of the examination are 875, what are the average mark scored by all the three girls together:
a)
929
b)
815
c)
690
d)
643
|
|
Madhavan Singh answered |
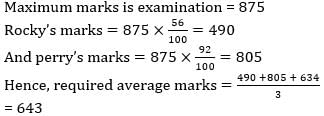
The number obtained by interchanging the digits of a two-digit number is less than the original number by 63. If the sum of the digits of the number is 11, what is the original number? - a)29
- b)92
- c)74
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
The number obtained by interchanging the digits of a two-digit number is less than the original number by 63. If the sum of the digits of the number is 11, what is the original number?
a)
29
b)
92
c)
74
d)
Cannot be determined
|
|
Sparsh Das answered |
Explanation:
Given conditions:
1. The number obtained by interchanging the digits of a two-digit number is less than the original number by 63.
2. The sum of the digits of the number is 11.
Let's assume the original two-digit number is represented as AB, where A and B are the digits.
Interchanging the digits:
- The number obtained by interchanging the digits is BA.
- So, the difference between the original number and the number obtained by interchanging the digits is given by:
- (10A + B) - (10B + A) = 63
- 9A - 9B = 63
- A - B = 7
Sum of the digits:
- Given that the sum of the digits of the number is 11.
- A + B = 11
- From the above equation A - B = 7 and A + B = 11, we can solve for A and B.
- Solving, we get A = 9 and B = 2.
Hence, the original two-digit number is 92 (Option B).
Given conditions:
1. The number obtained by interchanging the digits of a two-digit number is less than the original number by 63.
2. The sum of the digits of the number is 11.
Let's assume the original two-digit number is represented as AB, where A and B are the digits.
Interchanging the digits:
- The number obtained by interchanging the digits is BA.
- So, the difference between the original number and the number obtained by interchanging the digits is given by:
- (10A + B) - (10B + A) = 63
- 9A - 9B = 63
- A - B = 7
Sum of the digits:
- Given that the sum of the digits of the number is 11.
- A + B = 11
- From the above equation A - B = 7 and A + B = 11, we can solve for A and B.
- Solving, we get A = 9 and B = 2.
Hence, the original two-digit number is 92 (Option B).
A and B run a kilometer and A wins by 25 sec. A and C run a kilometer and A wins by 275 m. When B and C run the same distance, B wins by 30 sec. The time taken by A to run a kilometer is - a)2 min 25 sec
- b)2 min 50 sec
- c)2 min 20 sec
- d)3 min 30 sec
Correct answer is option 'A'. Can you explain this answer?
A and B run a kilometer and A wins by 25 sec. A and C run a kilometer and A wins by 275 m. When B and C run the same distance, B wins by 30 sec. The time taken by A to run a kilometer is
a)
2 min 25 sec
b)
2 min 50 sec
c)
2 min 20 sec
d)
3 min 30 sec
|
|
Atharva Sengupta answered |

In class 3/7 of the students are girls and rest are boys. If 2/9 of the girls and 1/11 of the boys are absent. What part of the total number of students are present? - a)197/231
- b)177/231
- c)197/242
- d)177/242
Correct answer is option 'A'. Can you explain this answer?
In class 3/7 of the students are girls and rest are boys. If 2/9 of the girls and 1/11 of the boys are absent. What part of the total number of students are present?
a)
197/231
b)
177/231
c)
197/242
d)
177/242
|
|
Tanishq Deshpande answered |
Understanding the Problem
To solve the problem, we need to determine the fraction of students present in class after accounting for absentees among both girls and boys.
Step 1: Identify Total Students
- Let the total number of students be represented as 'x'.
- According to the problem, 3/7 of the students are girls, meaning:
- Number of girls = (3/7)x
- Number of boys = x - (3/7)x = (4/7)x
Step 2: Calculate Absent Students
- Absent girls: 2/9 of the girls
- Absent girls = (2/9) * (3/7)x = (6/63)x = (2/21)x
- Absent boys: 1/11 of the boys
- Absent boys = (1/11) * (4/7)x = (4/77)x
Step 3: Calculate Present Students
- Present girls = Total girls - Absent girls
- Present girls = (3/7)x - (2/21)x
- To subtract, convert (3/7) to a common denominator:
- (3/7) = (9/21)
- Present girls = (9/21)x - (2/21)x = (7/21)x = (1/3)x
- Present boys = Total boys - Absent boys
- Present boys = (4/7)x - (4/77)x
- Convert (4/7) to a common denominator:
- (4/7) = (44/77)
- Present boys = (44/77)x - (4/77)x = (40/77)x
Step 4: Total Present Students
- Total present students = Present girls + Present boys
- Total present = (1/3)x + (40/77)x
- Convert to a common denominator (231):
- (1/3) = (77/231) and (40/77) = (120/231)
- Total present = (77/231)x + (120/231)x = (197/231)x
Step 5: Calculate the Fraction of Present Students
- Fraction of total students present = Total present / Total students
- = (197/231)x / x = 197/231
Thus, the final answer is 197/231, confirming that option (a) is correct.
To solve the problem, we need to determine the fraction of students present in class after accounting for absentees among both girls and boys.
Step 1: Identify Total Students
- Let the total number of students be represented as 'x'.
- According to the problem, 3/7 of the students are girls, meaning:
- Number of girls = (3/7)x
- Number of boys = x - (3/7)x = (4/7)x
Step 2: Calculate Absent Students
- Absent girls: 2/9 of the girls
- Absent girls = (2/9) * (3/7)x = (6/63)x = (2/21)x
- Absent boys: 1/11 of the boys
- Absent boys = (1/11) * (4/7)x = (4/77)x
Step 3: Calculate Present Students
- Present girls = Total girls - Absent girls
- Present girls = (3/7)x - (2/21)x
- To subtract, convert (3/7) to a common denominator:
- (3/7) = (9/21)
- Present girls = (9/21)x - (2/21)x = (7/21)x = (1/3)x
- Present boys = Total boys - Absent boys
- Present boys = (4/7)x - (4/77)x
- Convert (4/7) to a common denominator:
- (4/7) = (44/77)
- Present boys = (44/77)x - (4/77)x = (40/77)x
Step 4: Total Present Students
- Total present students = Present girls + Present boys
- Total present = (1/3)x + (40/77)x
- Convert to a common denominator (231):
- (1/3) = (77/231) and (40/77) = (120/231)
- Total present = (77/231)x + (120/231)x = (197/231)x
Step 5: Calculate the Fraction of Present Students
- Fraction of total students present = Total present / Total students
- = (197/231)x / x = 197/231
Thus, the final answer is 197/231, confirming that option (a) is correct.
Four Iron metal rods of lengths 78 cm, 104 cm, 117 cm, and 169 cm are to be cut into parts of equal length. Each part must be as long as possible. What is the maximum number of pieces that can be cut? - a)27
- b)36
- c)43
- d)400
Correct answer is option 'B'. Can you explain this answer?
Four Iron metal rods of lengths 78 cm, 104 cm, 117 cm, and 169 cm are to be cut into parts of equal length. Each part must be as long as possible. What is the maximum number of pieces that can be cut?
a)
27
b)
36
c)
43
d)
400
|
|
Saikat Sengupta answered |
Since each Iron rod must be cut into parts of equal length and
each part must be as long as possible, so HCF should be
taken.
HCF of 78, 104, 117 and 169 = 13.
No. of parts from 78cm. rod = 78 /13=6
No. of parts from 104 cm. rod =104/13=8
No. of parts from 117 cm. rod =117/ 13=9
No. of parts from 169 cm. rod =169 /13=13
Maximum no. of pieces = 6 + 8 + 9 + 13 = 36
each part must be as long as possible, so HCF should be
taken.
HCF of 78, 104, 117 and 169 = 13.
No. of parts from 78cm. rod = 78 /13=6
No. of parts from 104 cm. rod =104/13=8
No. of parts from 117 cm. rod =117/ 13=9
No. of parts from 169 cm. rod =169 /13=13
Maximum no. of pieces = 6 + 8 + 9 + 13 = 36
In a class, the number of girls is 20% more than that of the boys. The strength of the class is 66. If 4 more girls are admitted to the class, the ratio of the number of boys to that of the girls is. - a)1: 2
- b)3 : 4
- c)1: 4
- d)3: 5
Correct answer is option 'B'. Can you explain this answer?
In a class, the number of girls is 20% more than that of the boys. The strength of the class is 66. If 4 more girls are admitted to the class, the ratio of the number of boys to that of the girls is.
a)
1: 2
b)
3 : 4
c)
1: 4
d)
3: 5
|
|
Prateek Ghosh answered |

There were 35 students in a hostel. If the number of students increases by 7, the expenses of mess increase by Rs. 42 per day while the average expenditure per head diminishes by 1. Find the original expenditure of the mess. - a)Rs. 320
- b)Rs. 420
- c)Rs. 160
- d)Rs. 158
Correct answer is option 'B'. Can you explain this answer?
There were 35 students in a hostel. If the number of students increases by 7, the expenses of mess increase by Rs. 42 per day while the average expenditure per head diminishes by 1. Find the original expenditure of the mess.
a)
Rs. 320
b)
Rs. 420
c)
Rs. 160
d)
Rs. 158
|
|
Jaya Choudhary answered |
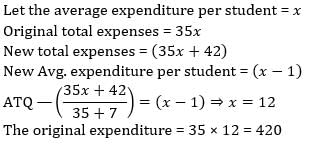
A is 1.5 times efficient than B therefore takes 8 days less than B to complete a work. If A and B work on alternate days and A works on first day, then in how many days the work will be completed? - a)17
- b)19
- c)19.5
- d)21
Correct answer is option 'B'. Can you explain this answer?
A is 1.5 times efficient than B therefore takes 8 days less than B to complete a work. If A and B work on alternate days and A works on first day, then in how many days the work will be completed?
a)
17
b)
19
c)
19.5
d)
21
|
|
Aaditya Joshi answered |
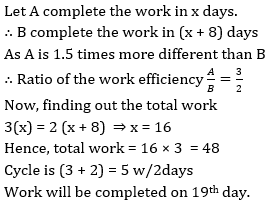
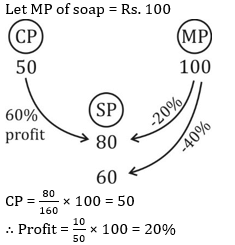
A Raymond’s Trader marked the selling price of an article at 10% above the cost price. At the same time of selling he allowed certain discount and suffers a loss of 1%. He allowed a discount of: - a)11%
- b)10%
- c)9%
- d)10.5%
Correct answer is option 'B'. Can you explain this answer?
A Raymond’s Trader marked the selling price of an article at 10% above the cost price. At the same time of selling he allowed certain discount and suffers a loss of 1%. He allowed a discount of:
a)
11%
b)
10%
c)
9%
d)
10.5%
|
|
Shounak Iyer answered |

A diligent man was engaged on a job for 40 days on the condition that he will get a wage of Rs. 180 for the day he works, but he will have to pay a fine of Rs. 20 for each day of his absence. If he gets Rs. 5200 at the end of the 40 days, then, he was absent for how many days? - a)12 days
- b)10 days
- c)6 days
- d)8 days
Correct answer is option 'B'. Can you explain this answer?
A diligent man was engaged on a job for 40 days on the condition that he will get a wage of Rs. 180 for the day he works, but he will have to pay a fine of Rs. 20 for each day of his absence. If he gets Rs. 5200 at the end of the 40 days, then, he was absent for how many days?
a)
12 days
b)
10 days
c)
6 days
d)
8 days
|
|
Atharva Shah answered |
Given:
- The man was engaged on a job for 40 days.
- He will receive Rs. 180 for each day he works.
- He will have to pay a fine of Rs. 20 for each day of his absence.
- He received a total of Rs. 5200 at the end of the 40 days.
To find:
The number of days the man was absent.
Solution:
Let's assume the number of days the man was absent is 'x'.
The total amount he received for working for 40 days is:
40 * Rs. 180 = Rs. 7200
The total amount he paid as a fine for x days of absence is:
x * Rs. 20 = Rs. 20x
Therefore, the total amount he received after deducting the fine is:
7200 - 20x
According to the given information, he received Rs. 5200, so we can write the equation:
7200 - 20x = 5200
Simplifying the equation:
-20x = 5200 - 7200
-20x = -2000
Dividing both sides of the equation by -20:
x = -2000 / -20
x = 100
Therefore, the man was absent for 100/20 = 5 days.
Answer:
The man was absent for 5 days, which is option C.
- The man was engaged on a job for 40 days.
- He will receive Rs. 180 for each day he works.
- He will have to pay a fine of Rs. 20 for each day of his absence.
- He received a total of Rs. 5200 at the end of the 40 days.
To find:
The number of days the man was absent.
Solution:
Let's assume the number of days the man was absent is 'x'.
The total amount he received for working for 40 days is:
40 * Rs. 180 = Rs. 7200
The total amount he paid as a fine for x days of absence is:
x * Rs. 20 = Rs. 20x
Therefore, the total amount he received after deducting the fine is:
7200 - 20x
According to the given information, he received Rs. 5200, so we can write the equation:
7200 - 20x = 5200
Simplifying the equation:
-20x = 5200 - 7200
-20x = -2000
Dividing both sides of the equation by -20:
x = -2000 / -20
x = 100
Therefore, the man was absent for 100/20 = 5 days.
Answer:
The man was absent for 5 days, which is option C.
In a classroom there are certain number of benches. If 6 students are made to sit on a bench, then to accommodate all of them, one more bench is needed. However, if 7 students are made to sit on a bench, then, after accommodating all of them, space for 5 students is left. What is the total number of students in the class? - a)30
- b)42
- c)72
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In a classroom there are certain number of benches. If 6 students are made to sit on a bench, then to accommodate all of them, one more bench is needed. However, if 7 students are made to sit on a bench, then, after accommodating all of them, space for 5 students is left. What is the total number of students in the class?
a)
30
b)
42
c)
72
d)
None of these
|
|
Sparsh Das answered |
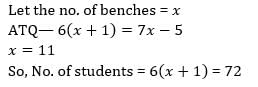
The cost of manufacturing of an article depends upon four components P, Q, R, S. Cost ratio of P, Q, R, S is 4:5:6:7 respectively. If there is a respective change of 30%, -20%, -8.33% and +20% in the cost of four components then by how much percent it would affect the manufacturing cost of the article. - a)10%
- b)20%
- c)5%
- d)15%
Correct answer is option 'C'. Can you explain this answer?
The cost of manufacturing of an article depends upon four components P, Q, R, S. Cost ratio of P, Q, R, S is 4:5:6:7 respectively. If there is a respective change of 30%, -20%, -8.33% and +20% in the cost of four components then by how much percent it would affect the manufacturing cost of the article.
a)
10%
b)
20%
c)
5%
d)
15%
|
|
Varun Majumdar answered |
A bus travels 2/5 of a total journey at its usual speed. The remaining distance was covered by bus at 6/7 of its usual speed. Due to slow speed it reaches its destination 50 minutes late. If the total distance is 200 kms, then what is the usual speed (in km/hr) of bus? - a)20.57
- b)24
- c)28
- d)26.52
Correct answer is option 'B'. Can you explain this answer?
A bus travels 2/5 of a total journey at its usual speed. The remaining distance was covered by bus at 6/7 of its usual speed. Due to slow speed it reaches its destination 50 minutes late. If the total distance is 200 kms, then what is the usual speed (in km/hr) of bus?
a)
20.57
b)
24
c)
28
d)
26.52
|
|
Pooja Khanna answered |

Chapter doubts & questions for CTET Practice Test (Mathematics Paper 2) - CTET (Central Teacher Eligibility Test) Mock Test Series 2025 2025 is part of CTET & State TET exam preparation. The chapters have been prepared according to the CTET & State TET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CTET & State TET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of CTET Practice Test (Mathematics Paper 2) - CTET (Central Teacher Eligibility Test) Mock Test Series 2025 in English & Hindi are available as part of CTET & State TET exam.
Download more important topics, notes, lectures and mock test series for CTET & State TET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup


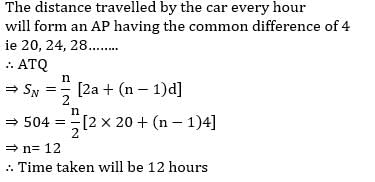


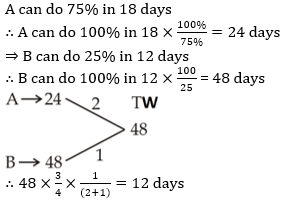

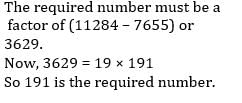
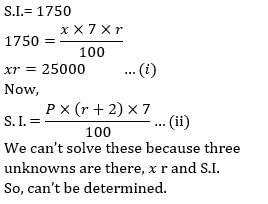
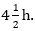 If the speed is increased by 5 km/hr, it would take
If the speed is increased by 5 km/hr, it would take 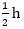 less to cover the same distance. Find the slower speed of the car.
less to cover the same distance. Find the slower speed of the car.