All Exams >
SSC CGL >
Quantitative Aptitude for SSC CGL >
All Questions
All questions of Triangles for SSC CGL Exam
Directions: Study the following question carefully and choose the right answer:If AD is the internal angular bisector of angle A of ΔABC with AB = 3 cm and AC= 1 cm, then what is BD : BC equal to?- a)1 : 3
- b)1 : 4
- c)2 : 3
- d)3 : 4
Correct answer is option 'D'. Can you explain this answer?
Directions: Study the following question carefully and choose the right answer:
If AD is the internal angular bisector of angle A of ΔABC with AB = 3 cm and AC= 1 cm, then what is BD : BC equal to?
a)
1 : 3
b)
1 : 4
c)
2 : 3
d)
3 : 4
|
|
Ishaan Roy answered |
Understanding the Problem
In triangle ABC, we have the angle bisector AD, with given lengths AB = 3 cm and AC = 1 cm. We need to find the ratio BD : BC.
Angle Bisector Theorem
The Angle Bisector Theorem states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the other two sides of the triangle. In this case:
- Let BD = x
- Let DC = y
According to the theorem:
x / y = AB / AC
Applying the Theorem
Substituting the known values:
- AB = 3 cm
- AC = 1 cm
This gives us:
x / y = 3 / 1
Expressing BD and BC
Now, since BD + DC = BC, we can express:
BC = x + y
To find the ratio BD : BC, we can substitute y in terms of x:
y = (1/3)x
Then, substituting this back into the expression for BC gives:
BC = x + (1/3)x = (4/3)x
Finding the Ratio
Now we find the ratio:
BD : BC = x : (4/3)x
This simplifies to:
BD : BC = 1 : (4/3)
To express it in a more conventional format:
BD : BC = 3 : 4
Conclusion
Thus, the final ratio of BD to BC is:
Correct answer: option 'D' (3 : 4).
In triangle ABC, we have the angle bisector AD, with given lengths AB = 3 cm and AC = 1 cm. We need to find the ratio BD : BC.
Angle Bisector Theorem
The Angle Bisector Theorem states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the other two sides of the triangle. In this case:
- Let BD = x
- Let DC = y
According to the theorem:
x / y = AB / AC
Applying the Theorem
Substituting the known values:
- AB = 3 cm
- AC = 1 cm
This gives us:
x / y = 3 / 1
Expressing BD and BC
Now, since BD + DC = BC, we can express:
BC = x + y
To find the ratio BD : BC, we can substitute y in terms of x:
y = (1/3)x
Then, substituting this back into the expression for BC gives:
BC = x + (1/3)x = (4/3)x
Finding the Ratio
Now we find the ratio:
BD : BC = x : (4/3)x
This simplifies to:
BD : BC = 1 : (4/3)
To express it in a more conventional format:
BD : BC = 3 : 4
Conclusion
Thus, the final ratio of BD to BC is:
Correct answer: option 'D' (3 : 4).
Directions: Study the following question carefully and choose the right answer:Consider the following statements
I. If G is the centroid of ΔABC, then GA = GB = GC.
II. If H is the orthocentre of ΔABC, then HA = HB = HC.
Which of the statements given above is/are correct?- a)Only I
- b)Only II
- c)Both I and II
- d)Neither I nor II
Correct answer is option 'D'. Can you explain this answer?
Directions: Study the following question carefully and choose the right answer:
Consider the following statements
I. If G is the centroid of ΔABC, then GA = GB = GC.
II. If H is the orthocentre of ΔABC, then HA = HB = HC.
Which of the statements given above is/are correct?
I. If G is the centroid of ΔABC, then GA = GB = GC.
II. If H is the orthocentre of ΔABC, then HA = HB = HC.
Which of the statements given above is/are correct?
a)
Only I
b)
Only II
c)
Both I and II
d)
Neither I nor II

|
Target Study Academy answered |
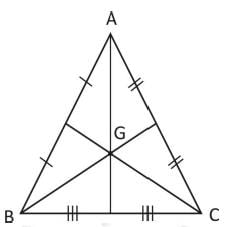
GA = GB = GC is true only and only for equilateral triangle and here it is not given that ABC is an equilateral triangle. So, only for equilateral triangle.
Hence, it is also not correct.
Hence, option D is correct
Hence, it is also not correct.
Hence, option D is correct
Directions: Kindly study the following Question carefully and choose the right answer:In a ΔABC, AD is perpendicular to BC and BE is perpendicular to AC. Which of the following is correct?- a)CE × CB = CA × CD
- b)CE × CA = CD × CB
- c) AD × BD = AE × BE
- d)AB × AC = AD × BE
Correct answer is option 'C'. Can you explain this answer?
Directions: Kindly study the following Question carefully and choose the right answer:
In a ΔABC, AD is perpendicular to BC and BE is perpendicular to AC. Which of the following is correct?
a)
CE × CB = CA × CD
b)
CE × CA = CD × CB
c)
AD × BD = AE × BE
d)
AB × AC = AD × BE

|
Bayshore Academy answered |
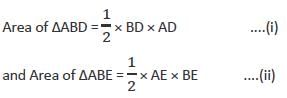

From Eqs. (i) and (ii),
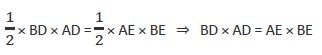
Hence, option C is correct.
Directions: Kindly study the following Question carefully and choose the right answer:The length of side AB and side BC of a scalene triangle ABC are 12 cm and 8 cm respectively. The value of angle C is 59°. Find the length of side AC.- a)12
- b)10
- c)14
- d)16
Correct answer is option 'C'. Can you explain this answer?
Directions: Kindly study the following Question carefully and choose the right answer:
The length of side AB and side BC of a scalene triangle ABC are 12 cm and 8 cm respectively. The value of angle C is 59°. Find the length of side AC.
a)
12
b)
10
c)
14
d)
16
|
|
Arnav Saini answered |
Given Data:
- Length of side AB = 12 cm
- Length of side BC = 8 cm
- Angle C = 59°
Calculating Side AC using Law of Cosines:
- Using Law of Cosines, we have the formula: c² = a² + b² - 2ab * cos(C)
- Substituting the given values, we get: AC² = 12² + 8² - 2 * 12 * 8 * cos(59°)
- Calculating the cosine value of 59°, we get: cos(59°) ≈ 0.5299
- Plugging in the values, we get: AC² = 144 + 64 - 192 * 0.5299
- Simplifying further, we get: AC² = 144 + 64 - 101.8368
- Therefore, AC² ≈ 106.1632
- Taking the square root of both sides, we get: AC ≈ √106.1632 ≈ 10.305
Final Answer:
Therefore, the length of side AC is approximately 10.3 cm. Hence, option 'C' (14) is the correct answer.
- Length of side AB = 12 cm
- Length of side BC = 8 cm
- Angle C = 59°
Calculating Side AC using Law of Cosines:
- Using Law of Cosines, we have the formula: c² = a² + b² - 2ab * cos(C)
- Substituting the given values, we get: AC² = 12² + 8² - 2 * 12 * 8 * cos(59°)
- Calculating the cosine value of 59°, we get: cos(59°) ≈ 0.5299
- Plugging in the values, we get: AC² = 144 + 64 - 192 * 0.5299
- Simplifying further, we get: AC² = 144 + 64 - 101.8368
- Therefore, AC² ≈ 106.1632
- Taking the square root of both sides, we get: AC ≈ √106.1632 ≈ 10.305
Final Answer:
Therefore, the length of side AC is approximately 10.3 cm. Hence, option 'C' (14) is the correct answer.
Directions: Study the following question carefully and choose the right answer:In the adjoining figure, if BC = a, AC = b, AB = c and ∠CAB = 120° , then the correct relation is :

- a)a2 = b2 + c2 + 2 bc
- b)a2 = b2 + c2 – 2 bc
- c)a2 = b2 + c2 + bc
- d)a2 = b2 + c2 – bc
Correct answer is option 'C'. Can you explain this answer?
Directions: Study the following question carefully and choose the right answer:
In the adjoining figure, if BC = a, AC = b, AB = c and ∠CAB = 120° , then the correct relation is :


a)
a2 = b2 + c2 + 2 bc
b)
a2 = b2 + c2 – 2 bc
c)
a2 = b2 + c2 + bc
d)
a2 = b2 + c2 – bc

|
Ssc Cgl answered |
Since ∠A is an obtuse angle in Δ ABC, so
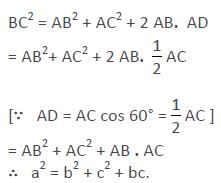
Hence, option C is correct.
Directions: Study the following question carefully and choose the right answer:AB is a straight line, C and D are points the same side of AB such that AC is perpendicular to AB and DB is perpendicular to AB. Let AD and BC meet at E.
what is 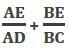 equal to?
equal to?- a)2
- b)1.5
- c)1
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Directions: Study the following question carefully and choose the right answer:
AB is a straight line, C and D are points the same side of AB such that AC is perpendicular to AB and DB is perpendicular to AB. Let AD and BC meet at E.
what is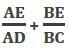 equal to?
equal to?
what is
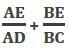 equal to?
equal to?a)
2
b)
1.5
c)
1
d)
None of these

|
Iq Funda answered |
Since, AB is a straight line and C and D are points such that AC ⊥ AB and BD ⊥ AB.
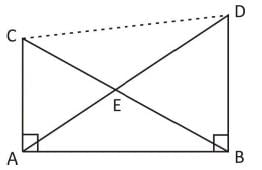
∴ AC || BD
So, ABCD forms trapezium.
Now, by property of trapezium diagonals intersect each other in the ratio of lengths of parallel sides.

∴ AC || BD
So, ABCD forms trapezium.
Now, by property of trapezium diagonals intersect each other in the ratio of lengths of parallel sides.
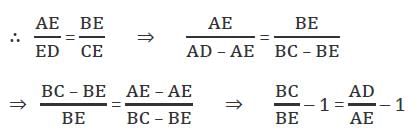
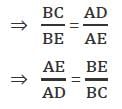
But the value of 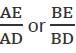 Can't be determined.
Can't be determined.
So, we can't find the value of
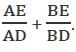
Hence, option D is correct.
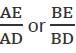 Can't be determined.
Can't be determined.So, we can't find the value of
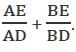
Hence, option D is correct.
Chapter doubts & questions for Triangles - Quantitative Aptitude for SSC CGL 2025 is part of SSC CGL exam preparation. The chapters have been prepared according to the SSC CGL exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Triangles - Quantitative Aptitude for SSC CGL in English & Hindi are available as part of SSC CGL exam.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
Quantitative Aptitude for SSC CGL
342 videos|301 docs|185 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









