All Exams >
Class 6 >
Maths Olympiad Class 6 >
All Questions
All questions of Playing with Numbers for Class 6 Exam
Which of the following is a composite number?- a)23
- b)29
- c)32
- d)41
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a composite number?
a)
23
b)
29
c)
32
d)
41
|
|
Ananya Das answered |
∴ 32 has 1, 2, 4, 8, 16, 32, as its factors.
∴ 32 is a composite number.
∴ 32 is a composite number.
Which of the following is not a twin prime?
- a)(11, 13)
- b)(17, 19)
- c)(23, 31)
- d)(41, 43)
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a twin prime?
a)
(11, 13)
b)
(17, 19)
c)
(23, 31)
d)
(41, 43)
|
|
Anita Menon answered |
(23, 31) is not a twin prime.
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair (17, 19) or (41, 43).
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair (17, 19) or (41, 43).
Which greatest number of 4 digits is exactly divisible by 12, 16, 28 & 36?- a)6072
- b)8072
- c)8972
- d)9072
Correct answer is option 'D'. Can you explain this answer?
Which greatest number of 4 digits is exactly divisible by 12, 16, 28 & 36?
a)
6072
b)
8072
c)
8972
d)
9072

|
Shreya Sarkar answered |
Here is the answer.
LCM of 12, 16, 24, 28 and 36
12= 3x2x2
16=2x2x2x2
24=2x2x2x3
28=2x2x7
36=2x2x3x3
so, LCM is 2x2x2x2x3x3x7= 1008
And the greatest 4-digit no. is 9999
so, dividing 9999 by 1008 we get, 9 as quotient and 927 as reminder .
So, the largest 4-digit no. divisible by all these nos. is 9999-927= 9072.
The HCF of two numbers is 21 and their LCM is 3003. If one of the numbers is 231. Then what is the other number?- a)273
- b)263
- c)283
- d)293
Correct answer is option 'A'. Can you explain this answer?
The HCF of two numbers is 21 and their LCM is 3003. If one of the numbers is 231. Then what is the other number?
a)
273
b)
263
c)
283
d)
293

|
Shalini Chakraborty answered |
Let the other number be x
We know,
HCF x LCM = PRODUCT OF THE NUMBERS
=> 21 x 3003 = 231 x x
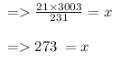
The HCF of two numbers is 16 and their product is 3072. What is the LCM?- a)182
- b)162
- c)192
- d)196
Correct answer is option 'C'. Can you explain this answer?
The HCF of two numbers is 16 and their product is 3072. What is the LCM?
a)
182
b)
162
c)
192
d)
196

|
Rajat Menon answered |
HCF x LCM = ab
16 x LCM = 3072
LCM = 3072 / 16
= 192
So, the LCM of the two number is 192
Which of the following is a prime number?- a)117
- b)171
- c)179
- d)169
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a prime number?
a)
117
b)
171
c)
179
d)
169
|
|
Ananya Das answered |
117, 171 are divisible by 3.
169 is divisible by 13.
179 is a prime number.
169 is divisible by 13.
179 is a prime number.
Which of the following number is not divisible by 9?- a)387459
- b)904806
- c)758934
- d)879134
Correct answer is option 'D'. Can you explain this answer?
Which of the following number is not divisible by 9?
a)
387459
b)
904806
c)
758934
d)
879134
|
|
Prachi chauhan answered |
3 + 8 + 7 + 4 + 5 + 9 = 36
9 + 0 + 4 + 8 + 0 + 6 = 27
7 + 5 + 8 + 9 +3 + 4 = 36
8 + 7 + 9 + 1 + 3 + 4 = 32
∴ 32 is not divisible by 9.
∴ 879134 is not divisible 9.
9 + 0 + 4 + 8 + 0 + 6 = 27
7 + 5 + 8 + 9 +3 + 4 = 36
8 + 7 + 9 + 1 + 3 + 4 = 32
∴ 32 is not divisible by 9.
∴ 879134 is not divisible 9.
Find the smallest number which when divided by 16, 36 & 40 leaves a remainder 7 in each case.- a)627
- b)727
- c)827
- d)927
Correct answer is option 'B'. Can you explain this answer?
Find the smallest number which when divided by 16, 36 & 40 leaves a remainder 7 in each case.
a)
627
b)
727
c)
827
d)
927
|
|
Amit Sharma answered |
LCM of 16, 36 and 40 is
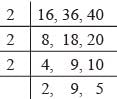
∴ LCM = 2 × 2 × 2 × 2 × 9 × 5
= 16 × 45 = 720
∴ required number = (720+7) = 727

∴ LCM = 2 × 2 × 2 × 2 × 9 × 5
= 16 × 45 = 720
∴ required number = (720+7) = 727
Four bells ring at intervals of 6, 8, 12 & 20 minutes. They ring simultaneously at 7 a.m. At what time will they ring together?- a)8 a.m.
- b)9 a.m.
- c)10 a.m.
- d)9:30 a.m.
Correct answer is option 'B'. Can you explain this answer?
Four bells ring at intervals of 6, 8, 12 & 20 minutes. They ring simultaneously at 7 a.m. At what time will they ring together?
a)
8 a.m.
b)
9 a.m.
c)
10 a.m.
d)
9:30 a.m.
|
|
Varun Kapoor answered |
Required time = LCM of 6, 8, 12 and 20
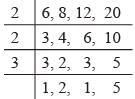
∴ Required time = 2 × 2 × 3 × 2 × 5
= 120 minutes = 2 hr.
∴ bell will again ring together at (7 + 2)
= 9 a.m.

∴ Required time = 2 × 2 × 3 × 2 × 5
= 120 minutes = 2 hr.
∴ bell will again ring together at (7 + 2)
= 9 a.m.
Which of the following number is divisible by 8?- a)162537
- b)764918
- c)825908
- d)694728
Correct answer is option 'D'. Can you explain this answer?
Which of the following number is divisible by 8?
a)
162537
b)
764918
c)
825908
d)
694728

|
Rohini Seth answered |
694728 is divisible by 2 as well as 4.
∴ 694728 is divisible by 8.
∴ 694728 is divisible by 8.
Find the greatest number which divides 126, 150 and 210 leaving remainder 6 in each case.- a)12
- b)14
- c)16
- d)22
Correct answer is option 'A'. Can you explain this answer?
Find the greatest number which divides 126, 150 and 210 leaving remainder 6 in each case.
a)
12
b)
14
c)
16
d)
22
|
|
Alpana singhania answered |
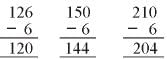
HCF of 120 and 144 = 12
HCF of 120 and 204 = 12
Required number = HCF of 120, 144, 204 = 12
The smallest number which when diminished by 3 is divisible by 21, 28, 36 and 45 is
- a)1163
- b)1263
- c)1283
- d)1293
Correct answer is option 'B'. Can you explain this answer?
The smallest number which when diminished by 3 is divisible by 21, 28, 36 and 45 is
a)
1163
b)
1263
c)
1283
d)
1293
|
|
Rohini khanna answered |
LCM of 21, 28, 36 and 45 is
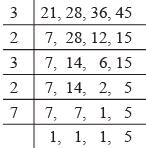
∴ LCM of 21, 28, 36 and 45
= 3 × 2 × 3 × 2 × 7 × 5
= 36 × 35
= 1260
∴ Required number = 1260 + 3 = 1263

∴ LCM of 21, 28, 36 and 45
= 3 × 2 × 3 × 2 × 7 × 5
= 36 × 35
= 1260
∴ Required number = 1260 + 3 = 1263
What is sum of first five multiples of 23?- a)341
- b)342
- c)343
- d)345
Correct answer is option 'D'. Can you explain this answer?
What is sum of first five multiples of 23?
a)
341
b)
342
c)
343
d)
345
|
|
Ishan Choudhury answered |
Sum of first five multiples of 23 = 23 + 23 × 2 + 23 × 3 + 23 × 4 + 23 × 5
= 23 (1 + 2 + 3 + 4 + 5)
= 23 × 15
= 345
= 23 (1 + 2 + 3 + 4 + 5)
= 23 × 15
= 345
Which longest tape can be used to measure exactly the length 7m, 3m 85cm and 12m 95 cm?- a)45 cm
- b)35 cm
- c)105 cm
- d)70 cm
Correct answer is option 'B'. Can you explain this answer?
Which longest tape can be used to measure exactly the length 7m, 3m 85cm and 12m 95 cm?
a)
45 cm
b)
35 cm
c)
105 cm
d)
70 cm
|
|
Anita Menon answered |
Required length = HCF of 700, 385 and 1295 = 35cm
What is the maximum even multiple of 25 between 500 & 700?- a)660
- b)600
- c)675
- d)650
Correct answer is option 'D'. Can you explain this answer?
What is the maximum even multiple of 25 between 500 & 700?
a)
660
b)
600
c)
675
d)
650
|
|
Sanjana Mukherjee answered |
The maximum even multiple of 25 between 500 and 1000 is 975.
Which of the following numbers is divisible by 3?- a)24357806
- b)33336433
- c)35769812
- d)83479560
Correct answer is option 'D'. Can you explain this answer?
Which of the following numbers is divisible by 3?
a)
24357806
b)
33336433
c)
35769812
d)
83479560
|
|
Dhruv Malik answered |
2 + 4 + 3 + 5 + 7 + 8 + 0 + 6 = 35
3 + 3 + 3 + 3 + 6 + 4 + 3 + 3 = 28
3 + 5 + 7 + 6 + 9 + 8 + 1 + 2 = 41
8 + 3 + 4 + 7 + 9 + 5 + 6 + 0 = 42
Since 42 is divisible by 3 then (d) is divisible by 3.
3 + 3 + 3 + 3 + 6 + 4 + 3 + 3 = 28
3 + 5 + 7 + 6 + 9 + 8 + 1 + 2 = 41
8 + 3 + 4 + 7 + 9 + 5 + 6 + 0 = 42
Since 42 is divisible by 3 then (d) is divisible by 3.
Four bells toll at intervals 4, 7, 12 & 84 seconds. The bells toll together at 7 o’clock. How many times will they again toll together in 28 minutes?- a)15
- b)20
- c)25
- d)30
Correct answer is option 'B'. Can you explain this answer?
Four bells toll at intervals 4, 7, 12 & 84 seconds. The bells toll together at 7 o’clock. How many times will they again toll together in 28 minutes?
a)
15
b)
20
c)
25
d)
30

|
Siddharth Chavan answered |
They will toll together for a 'common multiple' of (4,7,12,84), which is the l.c.m of these numbers.
4= 2^2
7 = 7
12 = 2^2 * 3
84 = 12 * 7 = 2^2 * 3 * 7
l.c.m(4,7,12,84) = 2^2 * 3 * 7 = 84 s
84 s = 1 min 24 sec
Hence they will toll together 84 seconds after 5 o'clock or 5:01:24 hrs ( 1 min 24 sec past 5 o'clock)
28 mins = 28*60 = 1680 sec
84 sec== toll 1 time
1680 sec== X times
X = 20 times
Hence,
They toll together at 5:01:24 hrs
In 28 mins they toll (together) 20 times.
The HCF of two numbers is 145 and their LCM is 2175. If one of the numbers is 725. What is the other number?- a)5
- b)290
- c)115
- d)435
Correct answer is option 'D'. Can you explain this answer?
The HCF of two numbers is 145 and their LCM is 2175. If one of the numbers is 725. What is the other number?
a)
5
b)
290
c)
115
d)
435

|
Lovely Yadav answered |
LCM = hcf ÷ a ×b
2175 =145÷725×b is farmula se anwer aa ye ga
2175 =145÷725×b is farmula se anwer aa ye ga
What is the least 5-digit number which is exactly divisible by 20, 25, 30?- a)10200
- b)10300
- c)10400
- d)10100
Correct answer is option 'A'. Can you explain this answer?
What is the least 5-digit number which is exactly divisible by 20, 25, 30?
a)
10200
b)
10300
c)
10400
d)
10100
|
|
Sonakshi dasgupta answered |
LCM of 20, 25, 30 is

∴ LCM of 20, 25, 30 = 2 × 5 × 2 × 5 × 3
= 300
∴ Ieast 5-digit number which is exactly divisible by 20, 25, 30 = 10200.

∴ LCM of 20, 25, 30 = 2 × 5 × 2 × 5 × 3
= 300
∴ Ieast 5-digit number which is exactly divisible by 20, 25, 30 = 10200.
Find the largest number that will divide 76, 113 and 186 leaving remainder 4, 5, 6 respectively.- a)24
- b)12
- c)36
- d)54
Correct answer is option 'C'. Can you explain this answer?
Find the largest number that will divide 76, 113 and 186 leaving remainder 4, 5, 6 respectively.
a)
24
b)
12
c)
36
d)
54
|
|
Debanshi Roy answered |
Solution:
The largest number that will divide 76, 113 and 186 leaving remainder 4, 5, 6 respectively is also known as the highest common factor (HCF) of (76-4), (113-5) and (186-6).
Step-by-step solution:
• Subtract the remainder from each number to get the actual number.
• So, the actual numbers are 72, 108, and 180.
• Now, find the common factors of these numbers.
• The common factors of 72, 108, and 180 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
• Out of these common factors, select the highest one which leaves the same remainder when divided by 4, 5, and 6 respectively.
• The highest common factor (HCF) of (76-4), (113-5) and (186-6) is 36.
• Hence, the correct option is (c) 36.
Therefore, the largest number that will divide 76, 113 and 186 leaving remainder 4, 5, 6 respectively is 36.
The largest number that will divide 76, 113 and 186 leaving remainder 4, 5, 6 respectively is also known as the highest common factor (HCF) of (76-4), (113-5) and (186-6).
Step-by-step solution:
• Subtract the remainder from each number to get the actual number.
• So, the actual numbers are 72, 108, and 180.
• Now, find the common factors of these numbers.
• The common factors of 72, 108, and 180 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
• Out of these common factors, select the highest one which leaves the same remainder when divided by 4, 5, and 6 respectively.
• The highest common factor (HCF) of (76-4), (113-5) and (186-6) is 36.
• Hence, the correct option is (c) 36.
Therefore, the largest number that will divide 76, 113 and 186 leaving remainder 4, 5, 6 respectively is 36.
1870 is divisible by 22. Which two numbers nearest to 1870 are each divisible by 22?- a)1848, 1892
- b)1893, 1914
- c)1826, 1914
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
1870 is divisible by 22. Which two numbers nearest to 1870 are each divisible by 22?
a)
1848, 1892
b)
1893, 1914
c)
1826, 1914
d)
None of these
|
|
Preethi Dasgupta answered |
To determine the two numbers nearest to 1870 that are each divisible by 22, we can use the concept of divisibility and apply it to the given options.
Divisibility Rule of 22: A number is divisible by 22 if it is divisible by both 2 and 11.
Let's analyze the given options one by one to see if they satisfy the divisibility rule of 22.
a) 1848, 1892:
- 1848: This number is divisible by 2 because the last digit is even (8). However, to determine if it is divisible by 11, we can use the divisibility rule of 11, which states that the difference between the sum of the digits in the odd place and the sum of the digits in the even place should be either 0 or a multiple of 11.
- In this case, 1 - 8 + 4 - 8 = -11, which is a multiple of 11. Therefore, 1848 is divisible by 11 and consequently divisible by 22.
- 1892: This number is divisible by 2 because the last digit is even (2). However, to determine if it is divisible by 11, we can use the divisibility rule of 11.
- In this case, 1 - 8 + 9 - 2 = 0, which is a multiple of 11. Therefore, 1892 is divisible by 11 and consequently divisible by 22.
Since both 1848 and 1892 satisfy the divisibility rule of 22, option A is correct.
b) 1893, 1914:
- 1893: This number is not divisible by 2 because the last digit is odd (3). Therefore, it is not divisible by 22.
- 1914: This number is divisible by 2 because the last digit is even (4). However, it is not divisible by 11 since 1 - 9 + 1 - 4 = -11, which is not a multiple of 11. Therefore, it is not divisible by 22.
Option B is incorrect.
c) 1826, 1914:
- 1826: This number is divisible by 2 because the last digit is even (6). However, it is not divisible by 11 since 1 - 8 + 2 - 6 = -11, which is not a multiple of 11. Therefore, it is not divisible by 22.
- 1914: This number is divisible by 2 because the last digit is even (4). However, it is not divisible by 11 since 1 - 9 + 1 - 4 = -11, which is not a multiple of 11. Therefore, it is not divisible by 22.
Option C is incorrect.
d) None of these:
Since we have found that option A is correct, option D is incorrect.
Therefore, the two numbers nearest to 1870 that are each divisible by 22 are 1848 and 1892, as stated in option A.
Divisibility Rule of 22: A number is divisible by 22 if it is divisible by both 2 and 11.
Let's analyze the given options one by one to see if they satisfy the divisibility rule of 22.
a) 1848, 1892:
- 1848: This number is divisible by 2 because the last digit is even (8). However, to determine if it is divisible by 11, we can use the divisibility rule of 11, which states that the difference between the sum of the digits in the odd place and the sum of the digits in the even place should be either 0 or a multiple of 11.
- In this case, 1 - 8 + 4 - 8 = -11, which is a multiple of 11. Therefore, 1848 is divisible by 11 and consequently divisible by 22.
- 1892: This number is divisible by 2 because the last digit is even (2). However, to determine if it is divisible by 11, we can use the divisibility rule of 11.
- In this case, 1 - 8 + 9 - 2 = 0, which is a multiple of 11. Therefore, 1892 is divisible by 11 and consequently divisible by 22.
Since both 1848 and 1892 satisfy the divisibility rule of 22, option A is correct.
b) 1893, 1914:
- 1893: This number is not divisible by 2 because the last digit is odd (3). Therefore, it is not divisible by 22.
- 1914: This number is divisible by 2 because the last digit is even (4). However, it is not divisible by 11 since 1 - 9 + 1 - 4 = -11, which is not a multiple of 11. Therefore, it is not divisible by 22.
Option B is incorrect.
c) 1826, 1914:
- 1826: This number is divisible by 2 because the last digit is even (6). However, it is not divisible by 11 since 1 - 8 + 2 - 6 = -11, which is not a multiple of 11. Therefore, it is not divisible by 22.
- 1914: This number is divisible by 2 because the last digit is even (4). However, it is not divisible by 11 since 1 - 9 + 1 - 4 = -11, which is not a multiple of 11. Therefore, it is not divisible by 22.
Option C is incorrect.
d) None of these:
Since we have found that option A is correct, option D is incorrect.
Therefore, the two numbers nearest to 1870 that are each divisible by 22 are 1848 and 1892, as stated in option A.
Which of the following is divisible by 11?- a)65483
- b)72493
- c)84527
- d)92056
Correct answer is option 'A'. Can you explain this answer?
Which of the following is divisible by 11?
a)
65483
b)
72493
c)
84527
d)
92056
|
|
Varsha nair answered |
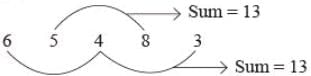
Difference = 13 – 13 = 0
∴ 65483 is divisible by 11.
In 467 * 381 replace * by which smallest digit to make it divisible by 3?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
In 467 * 381 replace * by which smallest digit to make it divisible by 3?
a)
1
b)
2
c)
3
d)
4
|
|
Veena Menon answered |
467 * 381
The sum of digits of the above number
= 4 + 6 + 7 + * + 3 + 8 + 1
= 10 + 7 + * + 3 + 8 + 1
= 29 + *
If, ∗ = 1, then, the sum of digits will become 30.
∴ required number = 1
The sum of digits of the above number
= 4 + 6 + 7 + * + 3 + 8 + 1
= 10 + 7 + * + 3 + 8 + 1
= 29 + *
If, ∗ = 1, then, the sum of digits will become 30.
∴ required number = 1
Find the smallest possible number which on adding 19 becomes exactly divisible by 28, 36 and 45.- a)1239
- b)1241
- c)1243
- d)1245
Correct answer is option 'B'. Can you explain this answer?
Find the smallest possible number which on adding 19 becomes exactly divisible by 28, 36 and 45.
a)
1239
b)
1241
c)
1243
d)
1245
|
|
Nishanth Iyer answered |
To find the smallest possible number that is divisible by 28, 36, and 45, we need to find the least common multiple (LCM) of these three numbers.
Step 1: Find the prime factors of each number.
- Prime factors of 28: 2, 2, 7 (2 x 2 x 7)
- Prime factors of 36: 2, 2, 3, 3 (2 x 2 x 3 x 3)
- Prime factors of 45: 3, 3, 5 (3 x 3 x 5)
Step 2: Identify the largest exponent for each prime factor.
- Largest exponent of 2: 2 (from 2 x 2)
- Largest exponent of 3: 3 (from 3 x 3)
- Largest exponent of 7: 1 (from 7)
- Largest exponent of 5: 1 (from 5)
Step 3: Multiply the prime factors with their largest exponents.
2^2 x 3^3 x 7^1 x 5^1 = 4 x 27 x 7 x 5 = 3780
Step 4: Add 19 to the result.
3780 + 19 = 3799
Hence, the smallest possible number that on adding 19 becomes exactly divisible by 28, 36, and 45 is 3799.
Therefore, option B (1241) is incorrect.
Step 1: Find the prime factors of each number.
- Prime factors of 28: 2, 2, 7 (2 x 2 x 7)
- Prime factors of 36: 2, 2, 3, 3 (2 x 2 x 3 x 3)
- Prime factors of 45: 3, 3, 5 (3 x 3 x 5)
Step 2: Identify the largest exponent for each prime factor.
- Largest exponent of 2: 2 (from 2 x 2)
- Largest exponent of 3: 3 (from 3 x 3)
- Largest exponent of 7: 1 (from 7)
- Largest exponent of 5: 1 (from 5)
Step 3: Multiply the prime factors with their largest exponents.
2^2 x 3^3 x 7^1 x 5^1 = 4 x 27 x 7 x 5 = 3780
Step 4: Add 19 to the result.
3780 + 19 = 3799
Hence, the smallest possible number that on adding 19 becomes exactly divisible by 28, 36, and 45 is 3799.
Therefore, option B (1241) is incorrect.
The greatest number that will divide 445, 572 & 699 leaving remainder 4, 5, 6 respectively.- a)84
- b)42
- c)49
- d)63
Correct answer is option 'D'. Can you explain this answer?
The greatest number that will divide 445, 572 & 699 leaving remainder 4, 5, 6 respectively.
a)
84
b)
42
c)
49
d)
63

|
Shruti Mishra answered |
Solution-> 445 - 4 = 441
572 - 5 = 567
699 - 6 = 693
Now find the greatest common factor of those 3 numbers:
441 = 3 x 3 x 7 x 7
572 = 3 x 3 x 3 x 3 x 7
693 = 3 x 3 x 7 x 11
The common factors are 3 x 3 x 7 = 63
HCF Of (441,567,693) = 63
445 / 63 = 7 remainder 4
572 / 63 = 9 remainder 5
699 / 63 = 11 remainder 6
63 is the largest divisor that will give the desired remainders.
The HCF of two numbers is 23 and their LCM is 1449. If one of the numbers is 161 what is the other?- a)107
- b)117
- c)167
- d)207
Correct answer is option 'D'. Can you explain this answer?
The HCF of two numbers is 23 and their LCM is 1449. If one of the numbers is 161 what is the other?
a)
107
b)
117
c)
167
d)
207

|
Amrita Roy answered |
HCF = 23
LCM = 1449
Let the two numbers be a and b. Let a = 161. We have to find b.
We know that
HCF(a,b) * LCM(a,b) = a*b
∴23 * 1449 = 161 * b
∴23*1449/161 = b
∴b = 23*9
∴b = 207
Thus, the other number is 207.
Find the greatest 3-digit number which is divisible by 8, 10 and 12.- a)840
- b)480
- c)960
- d)980
Correct answer is option 'C'. Can you explain this answer?
Find the greatest 3-digit number which is divisible by 8, 10 and 12.
a)
840
b)
480
c)
960
d)
980

|
Gayatri Roy answered |
L.C.M of 8, 10, 12 = 2 x 2 x 2 x 3 x 5 = 120
We have to find the greatest 3 digit multiple of 120
It can be seen that 120 x 8 =960 and 120 x 9 =1080.
Hence, the greatest 3- digit number exactly divisible by 8 , 10 and 12 is 960
Which of the following statement is true?- a)1509344 is divisible by 8.
- b)72493 is divisible by 11.
- c)8569 is not divisible by 11.
- d)115 is a multiple of 19.
Correct answer is option 'A'. Can you explain this answer?
Which of the following statement is true?
a)
1509344 is divisible by 8.
b)
72493 is divisible by 11.
c)
8569 is not divisible by 11.
d)
115 is a multiple of 19.
|
|
Surbhi Patel answered |
Explanation:
Divisibility by 8:
- To determine if a number is divisible by 8, we need to check if the last three digits of the number are divisible by 8.
- In the number 1509344, the last three digits are 344, which is divisible by 8 because 344 ÷ 8 = 43.
- Therefore, 1509344 is divisible by 8.
Divisibility by 11:
- To determine if a number is divisible by 11, we can use the rule that states that the difference between the sum of the digits at odd places and the sum of the digits at even places should be a multiple of 11.
- For the number 72493, the sum of the digits at odd places (7 + 4 + 3 = 14) is 14, and the sum of the digits at even places (2 + 9 = 11) is 11.
- The difference between 14 and 11 is 3, which is not a multiple of 11.
- Therefore, 72493 is not divisible by 11.
Conclusion:
- Based on the explanations above, the statement "1509344 is divisible by 8" is true.
Divisibility by 8:
- To determine if a number is divisible by 8, we need to check if the last three digits of the number are divisible by 8.
- In the number 1509344, the last three digits are 344, which is divisible by 8 because 344 ÷ 8 = 43.
- Therefore, 1509344 is divisible by 8.
Divisibility by 11:
- To determine if a number is divisible by 11, we can use the rule that states that the difference between the sum of the digits at odd places and the sum of the digits at even places should be a multiple of 11.
- For the number 72493, the sum of the digits at odd places (7 + 4 + 3 = 14) is 14, and the sum of the digits at even places (2 + 9 = 11) is 11.
- The difference between 14 and 11 is 3, which is not a multiple of 11.
- Therefore, 72493 is not divisible by 11.
Conclusion:
- Based on the explanations above, the statement "1509344 is divisible by 8" is true.
Chapter doubts & questions for Playing with Numbers - Maths Olympiad Class 6 2025 is part of Class 6 exam preparation. The chapters have been prepared according to the Class 6 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Playing with Numbers - Maths Olympiad Class 6 in English & Hindi are available as part of Class 6 exam.
Download more important topics, notes, lectures and mock test series for Class 6 Exam by signing up for free.
Maths Olympiad Class 6
6 videos|117 docs|60 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily














