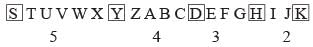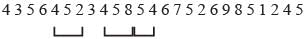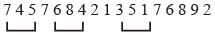All Exams >
Class 6 >
National Cyber Olympiad Class 6 >
All Questions
All questions of Alpha-Numeric Sequence Puzzle for Class 6 Exam
Arrange the given words in the alphabetical order and choose the one that comes last.- a)Transist
- b)Transport
- c)Transmit
- d)Translate
Correct answer is option 'B'. Can you explain this answer?
Arrange the given words in the alphabetical order and choose the one that comes last.
a)
Transist
b)
Transport
c)
Transmit
d)
Translate
|
|
Amit Sharma answered |
Transist, translate, transmit and transport. The correct option should be B.
Arrange the given words in the alphabetical order and choose the one that comes last.- a)Fault
- b)Finger
- c)Floor
- d)Forget
Correct answer is option 'D'. Can you explain this answer?
Arrange the given words in the alphabetical order and choose the one that comes last.
a)
Fault
b)
Finger
c)
Floor
d)
Forget
|
|
Sanjana Mukherjee answered |
Understanding Alphabetical Order
When arranging words in alphabetical order, we look at the first letter of each word. If the first letters are the same, we then compare the second letter, and so on, until we find a difference.
Words to Arrange
- Fault
- Finger
- Floor
- Forget
Step-by-Step Arrangement
1. First Letters Comparison:
- F (Fault)
- F (Finger)
- F (Floor)
- F (Forget)
All words start with the letter "F".
2. Second Letters Comparison:
- a (Fault)
- i (Finger)
- l (Floor)
- o (Forget)
Here, "a" comes first, followed by "i", then "l", and finally "o".
3. Arranging Based on Second Letters:
- Fault (a)
- Finger (i)
- Floor (l)
- Forget (o)
This indicates the order so far:
- Fault
- Finger
- Floor
- Forget
4. Final Arrangement:
- Fault
- Finger
- Floor
- Forget
Identifying the Last Word
In our final arrangement, "Forget" comes last because it has the highest alphabetical value based on the second letters.
Conclusion
Thus, the correct answer is option D: Forget, as it is the last word when all are arranged in alphabetical order.
When arranging words in alphabetical order, we look at the first letter of each word. If the first letters are the same, we then compare the second letter, and so on, until we find a difference.
Words to Arrange
- Fault
- Finger
- Floor
- Forget
Step-by-Step Arrangement
1. First Letters Comparison:
- F (Fault)
- F (Finger)
- F (Floor)
- F (Forget)
All words start with the letter "F".
2. Second Letters Comparison:
- a (Fault)
- i (Finger)
- l (Floor)
- o (Forget)
Here, "a" comes first, followed by "i", then "l", and finally "o".
3. Arranging Based on Second Letters:
- Fault (a)
- Finger (i)
- Floor (l)
- Forget (o)
This indicates the order so far:
- Fault
- Finger
- Floor
- Forget
4. Final Arrangement:
- Fault
- Finger
- Floor
- Forget
Identifying the Last Word
In our final arrangement, "Forget" comes last because it has the highest alphabetical value based on the second letters.
Conclusion
Thus, the correct answer is option D: Forget, as it is the last word when all are arranged in alphabetical order.
Shankar ranked 7th from the top and 34th from the bottom in a class. How many students are there in a class?- a)38
- b)39
- c)40
- d)41
Correct answer is option 'C'. Can you explain this answer?
Shankar ranked 7th from the top and 34th from the bottom in a class. How many students are there in a class?
a)
38
b)
39
c)
40
d)
41
|
|
Muskaan Joshi answered |
Given Information:
Shankar is ranked 7th from the top and 34th from the bottom in a class.
To find:
How many students are there in the class?
Approach to Solution:
Let's assume there are 'x' students in the class.
From the top:
- Shankar is ranked 7th from the top.
- Therefore, there are (7-1) = 6 students above Shankar.
From the bottom:
- Shankar is ranked 34th from the bottom.
- Therefore, there are (34-1) = 33 students below Shankar.
Total number of students:
- Total number of students = 6 (above Shankar) + 1 (Shankar) + 33 (below Shankar)
- Total number of students = 40
Therefore, there are 40 students in the class. Hence, the correct answer is option C) 40.
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. Which letter is sixteenth to the right of the letter which is fourth to the left of I?- a)U
- b)V
- c)T
- d)S
Correct answer is option 'A'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. Which letter is sixteenth to the right of the letter which is fourth to the left of I?
a)
U
b)
V
c)
T
d)
S

|
Keerthana Gupta answered |
The fourth letter to the left of I is E. the sixteenth letter to the right of E is U.
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?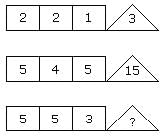
- a)11
- b)19
- c)15
- d)22
Correct answer is option 'D'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
11
b)
19
c)
15
d)
22

|
Ajmal Ram answered |
11
In a queue, Ravi is 13th from the back Amar is 12th from the front. Hari is standing between the two. What should be the minimum number of boys standing in queue?- a)14
- b)15
- c)16
- d)17
Correct answer is option 'A'. Can you explain this answer?
In a queue, Ravi is 13th from the back Amar is 12th from the front. Hari is standing between the two. What should be the minimum number of boys standing in queue?
a)
14
b)
15
c)
16
d)
17

|
Raj Mukherjee answered |
1 2 3 4 5 6 7 8 9 10 11 12 13

Minimum no. of boys = 13 + 1 = 14

Minimum no. of boys = 13 + 1 = 14
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. Which letter is seventh to the right of the thirteenth letter from the left end?- a)S
- b)U
- c)T
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. Which letter is seventh to the right of the thirteenth letter from the left end?
a)
S
b)
U
c)
T
d)
None of these
|
|
Aaditya Chawla answered |
Please provide the alphabet so that I can answer the questions.
Directions: In each of the following questions find out which of the letter series follows the given rule.Q. Number of letters skipped in between adjacent letters in the series doubles every time.- a)BDGLU
- b)EGJOF
- c)GJNSY
- d)ADIPY
Correct answer is option 'A'. Can you explain this answer?
Directions: In each of the following questions find out which of the letter series follows the given rule.
Q. Number of letters skipped in between adjacent letters in the series doubles every time.
a)
BDGLU
b)
EGJOF
c)
GJNSY
d)
ADIPY

|
Rahul Mehra answered |
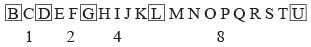
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. If only the first half of the given alphabet is reversed, how many letters will be there between K and R?- a)14
- b)16
- c)10
- d)6
Correct answer is option 'A'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. If only the first half of the given alphabet is reversed, how many letters will be there between K and R?
a)
14
b)
16
c)
10
d)
6

|
Sounak Chatterjee answered |
Reversing only the first 13 letters, we obtain the following letter series:
M L K J I H G F E D C B A N O P Q R S T U V W X Y Z.
Clearly, there are 14 letters between K and R in the above series.
M L K J I H G F E D C B A N O P Q R S T U V W X Y Z.
Clearly, there are 14 letters between K and R in the above series.
Directions: In each of the following questions find out which of the letter series follows the given rule.Q. Number of letters skipped in between adjacent letters of the series starting from behind increases by one.- a)ONLKJ
- b)OMKIG
- c)OIGDC
- d)OMJFA
Correct answer is option 'D'. Can you explain this answer?
Directions: In each of the following questions find out which of the letter series follows the given rule.
Q. Number of letters skipped in between adjacent letters of the series starting from behind increases by one.
a)
ONLKJ
b)
OMKIG
c)
OIGDC
d)
OMJFA

|
Malavika Kulkarni answered |
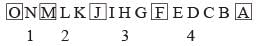
In the series given below, how many 8’s are there each of which is exactly divisible by its immediate preceding as well as succeeding numbers?
2 8 4 3 8 5 4 8 2 6 7 8 4 6 2 8 4 1 7 ? - a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
In the series given below, how many 8’s are there each of which is exactly divisible by its immediate preceding as well as succeeding numbers?
2 8 4 3 8 5 4 8 2 6 7 8 4 6 2 8 4 1 7 ?
2 8 4 3 8 5 4 8 2 6 7 8 4 6 2 8 4 1 7 ?
a)
1
b)
2
c)
3
d)
4
|
|
Rajat Chatterjee answered |
Understanding the Problem
In the given series, we need to identify the occurrences of the number 8 that are exactly divisible by both the numbers immediately before and after them.
Series Breakdown
The series is:
2, 8, 4, 3, 8, 5, 4, 8, 2, 6, 7, 8, 4, 6, 2, 8, 4, 1, 7
Identifying Relevant 8's
We will analyze each occurrence of the number 8:
- First 8 (2, 8, 4)
- Preceding number: 2
- Succeeding number: 4
- 8 is divisible by 2 (8 ÷ 2 = 4) and by 4 (8 ÷ 4 = 2).
- Valid 8
- Second 8 (3, 8, 5)
- Preceding number: 3
- Succeeding number: 5
- 8 is not divisible by 3 (8 ÷ 3 = 2.67) and not divisible by 5 (8 ÷ 5 = 1.6).
- Invalid 8
- Third 8 (4, 8, 2)
- Preceding number: 4
- Succeeding number: 2
- 8 is divisible by 4 (8 ÷ 4 = 2) and by 2 (8 ÷ 2 = 4).
- Valid 8
- Fourth 8 (6, 8, 4)
- Preceding number: 6
- Succeeding number: 4
- 8 is not divisible by 6 (8 ÷ 6 = 1.33) and by 4 (8 ÷ 4 = 2).
- Invalid 8
- Fifth 8 (2, 8, 4)
- Preceding number: 2
- Succeeding number: 4
- 8 is divisible by 2 and by 4.
- Valid 8
- Sixth 8 (4, 8, 1)
- Preceding number: 4
- Succeeding number: 1
- 8 is divisible by 4 and by 1.
- Valid 8
Conclusion
In total, we have three valid occurrences of 8 that meet the criteria. Therefore, the answer is 3.
In the given series, we need to identify the occurrences of the number 8 that are exactly divisible by both the numbers immediately before and after them.
Series Breakdown
The series is:
2, 8, 4, 3, 8, 5, 4, 8, 2, 6, 7, 8, 4, 6, 2, 8, 4, 1, 7
Identifying Relevant 8's
We will analyze each occurrence of the number 8:
- First 8 (2, 8, 4)
- Preceding number: 2
- Succeeding number: 4
- 8 is divisible by 2 (8 ÷ 2 = 4) and by 4 (8 ÷ 4 = 2).
- Valid 8
- Second 8 (3, 8, 5)
- Preceding number: 3
- Succeeding number: 5
- 8 is not divisible by 3 (8 ÷ 3 = 2.67) and not divisible by 5 (8 ÷ 5 = 1.6).
- Invalid 8
- Third 8 (4, 8, 2)
- Preceding number: 4
- Succeeding number: 2
- 8 is divisible by 4 (8 ÷ 4 = 2) and by 2 (8 ÷ 2 = 4).
- Valid 8
- Fourth 8 (6, 8, 4)
- Preceding number: 6
- Succeeding number: 4
- 8 is not divisible by 6 (8 ÷ 6 = 1.33) and by 4 (8 ÷ 4 = 2).
- Invalid 8
- Fifth 8 (2, 8, 4)
- Preceding number: 2
- Succeeding number: 4
- 8 is divisible by 2 and by 4.
- Valid 8
- Sixth 8 (4, 8, 1)
- Preceding number: 4
- Succeeding number: 1
- 8 is divisible by 4 and by 1.
- Valid 8
Conclusion
In total, we have three valid occurrences of 8 that meet the criteria. Therefore, the answer is 3.
Directions: In each of the following questions find out which of the letter series follows the given rule.Q. Number of letters skipped in between adjacent letters in the series decreases by one each time.- a)BHNSV
- b)TZEIL
- c)MSYBG
- d)IMTXB
Correct answer is option 'B'. Can you explain this answer?
Directions: In each of the following questions find out which of the letter series follows the given rule.
Q. Number of letters skipped in between adjacent letters in the series decreases by one each time.
a)
BHNSV
b)
TZEIL
c)
MSYBG
d)
IMTXB

|
Sounak Chatterjee answered |
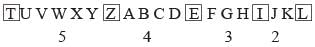
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. Which letter in the alphabet is as far from G as T is from M?- a)P
- b)O
- c)M
- d)N
Correct answer is option 'D'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. Which letter in the alphabet is as far from G as T is from M?
a)
P
b)
O
c)
M
d)
N
|
|
Muskaan Choudhury answered |
Distance Calculation:
The distance between two letters in the alphabet can be calculated by counting the number of letters between them.
Distance between T and M:
T is 5 letters away from M in the alphabet. (M, N, O, P, Q, T)
Distance between G and the letter:
To find a letter that is as far from G as T is from M, we need to find a letter that is also 5 letters away from G.
Finding the letter:
Starting from G, we count 5 letters ahead which gives us the letter N. (G, H, I, J, K, N)
Therefore, the letter that is as far from G as T is from M is N.
The distance between two letters in the alphabet can be calculated by counting the number of letters between them.
Distance between T and M:
T is 5 letters away from M in the alphabet. (M, N, O, P, Q, T)
Distance between G and the letter:
To find a letter that is as far from G as T is from M, we need to find a letter that is also 5 letters away from G.
Finding the letter:
Starting from G, we count 5 letters ahead which gives us the letter N. (G, H, I, J, K, N)
Therefore, the letter that is as far from G as T is from M is N.
Ashok is 8th from the left and Sanjay is 14th from the right end in a row of boys. If there are 12 boys between Ashok and Sanjay, how many boys are there in the row?- a)32
- b)33
- c)34
- d)35
Correct answer is option 'C'. Can you explain this answer?
Ashok is 8th from the left and Sanjay is 14th from the right end in a row of boys. If there are 12 boys between Ashok and Sanjay, how many boys are there in the row?
a)
32
b)
33
c)
34
d)
35
|
|
Saikat Rane answered |
To solve this problem, we need to analyze the given information step by step.
1. Ashok is 8th from the left end:
This means that there are 7 boys to the left of Ashok.
2. Sanjay is 14th from the right end:
This means that there are 13 boys to the right of Sanjay.
3. There are 12 boys between Ashok and Sanjay:
This means that there are 12 boys between Ashok and Sanjay, including Ashok and Sanjay themselves.
Now, let's calculate the total number of boys in the row.
Total number of boys to the left of Ashok = 7
Total number of boys to the right of Sanjay = 13
Number of boys between Ashok and Sanjay (excluding Ashok and Sanjay) = 12
To find the total number of boys in the row, we need to add these three values together:
Total number of boys = Total number of boys to the left of Ashok + Number of boys between Ashok and Sanjay + Total number of boys to the right of Sanjay
Total number of boys = 7 + 12 + 13
Total number of boys = 32
Therefore, the total number of boys in the row is 32.
Hence, the correct answer is option C) 34.
1. Ashok is 8th from the left end:
This means that there are 7 boys to the left of Ashok.
2. Sanjay is 14th from the right end:
This means that there are 13 boys to the right of Sanjay.
3. There are 12 boys between Ashok and Sanjay:
This means that there are 12 boys between Ashok and Sanjay, including Ashok and Sanjay themselves.
Now, let's calculate the total number of boys in the row.
Total number of boys to the left of Ashok = 7
Total number of boys to the right of Sanjay = 13
Number of boys between Ashok and Sanjay (excluding Ashok and Sanjay) = 12
To find the total number of boys in the row, we need to add these three values together:
Total number of boys = Total number of boys to the left of Ashok + Number of boys between Ashok and Sanjay + Total number of boys to the right of Sanjay
Total number of boys = 7 + 12 + 13
Total number of boys = 32
Therefore, the total number of boys in the row is 32.
Hence, the correct answer is option C) 34.
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. If the last ten letters of the alphabet are written in the reverse order, which of the following will be the sixth to the right of the thirteenth letter from the left end?- a)Y
- b)X
- c)W
- d)V
Correct answer is option 'B'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. If the last ten letters of the alphabet are written in the reverse order, which of the following will be the sixth to the right of the thirteenth letter from the left end?
a)
Y
b)
X
c)
W
d)
V

|
Upasana Basak answered |
The new alphabet series is:
A B C D E F G H I J K L M N O P Z Y X W V U T S R Q
The thirteenth letter from the left is M. The sixth letter to the right of M is X.
A B C D E F G H I J K L M N O P Z Y X W V U T S R Q
The thirteenth letter from the left is M. The sixth letter to the right of M is X.
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. In the following alphabets, which letter is eighth to the right of the fourteenth letter from the right end?
Z A B C D E F G H I J K L M N O P Q R S T U V W X Y - a)H
- b)R
- c)S
- d)T
Correct answer is option 'D'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. In the following alphabets, which letter is eighth to the right of the fourteenth letter from the right end?
Z A B C D E F G H I J K L M N O P Q R S T U V W X Y
Z A B C D E F G H I J K L M N O P Q R S T U V W X Y
a)
H
b)
R
c)
S
d)
T

|
Keerthana Gupta answered |
The fourteenth letter from the right is L. the eighth letter to the right of L is T.
Directions: In each of the following questions find out which of the letter series follows the given rule.Q. Number of letters skipped in between adjacent letters in the series decreases by three.- a)HVDKP
- b)HUELP
- c)HUELD
- d)DMSXA
Correct answer is option 'B'. Can you explain this answer?
Directions: In each of the following questions find out which of the letter series follows the given rule.
Q. Number of letters skipped in between adjacent letters in the series decreases by three.
a)
HVDKP
b)
HUELP
c)
HUELD
d)
DMSXA
|
|
Muskaan Choudhury answered |
Explanation:
Given Series:
- H V D K P
Counting the number of letters skipped between adjacent letters:
- H to V: 1 letter skipped (I)
- V to D: 4 letters skipped (W, X, Y, Z)
- D to K: 3 letters skipped (E, F, G)
- K to P: 2 letters skipped (L, M)
Following the rule "Number of letters skipped in between adjacent letters in the series decreases by three":
- We can see that the number of letters skipped between adjacent letters decreases by 3 each time.
Applying the rule to the given options:
a) H V D K P
b) H U E L P
c) H U E L D
d) D M S X A
Correct Answer: Option B - H U E L P
Explanation of the Correct Answer:
- H to U: 1 letter skipped (I)
- U to E: 4 letters skipped (V, W, X, Y)
- E to L: 3 letters skipped (F, G, H)
- L to P: 2 letters skipped (M, N)
Therefore, option B (HUELP) is the series that follows the given rule where the number of letters skipped in between adjacent letters decreases by three.
Given Series:
- H V D K P
Counting the number of letters skipped between adjacent letters:
- H to V: 1 letter skipped (I)
- V to D: 4 letters skipped (W, X, Y, Z)
- D to K: 3 letters skipped (E, F, G)
- K to P: 2 letters skipped (L, M)
Following the rule "Number of letters skipped in between adjacent letters in the series decreases by three":
- We can see that the number of letters skipped between adjacent letters decreases by 3 each time.
Applying the rule to the given options:
a) H V D K P
b) H U E L P
c) H U E L D
d) D M S X A
Correct Answer: Option B - H U E L P
Explanation of the Correct Answer:
- H to U: 1 letter skipped (I)
- U to E: 4 letters skipped (V, W, X, Y)
- E to L: 3 letters skipped (F, G, H)
- L to P: 2 letters skipped (M, N)
Therefore, option B (HUELP) is the series that follows the given rule where the number of letters skipped in between adjacent letters decreases by three.
Directions: In each of the following questions find out which of the letter series follows the given rule.Q. Number of letters skipped in between adjacent letters in the series is in the order of 2, 5, 7, 10. - a)QTZHS
- b)SYBEP
- c)FNKOT
- d)CEGLT
Correct answer is option 'A'. Can you explain this answer?
Directions: In each of the following questions find out which of the letter series follows the given rule.
Q. Number of letters skipped in between adjacent letters in the series is in the order of 2, 5, 7, 10.
a)
QTZHS
b)
SYBEP
c)
FNKOT
d)
CEGLT

|
Rishika Tiwari answered |
Q R S T U V W X Y Z A B C D E F G
2 5 7
H I J K L M N O P Q R S
10
2 5 7
H I J K L M N O P Q R S
10
Directions: In each of the following questions find out which of the letter series follows the given rule.
Q. Number of letters skipped in between adjacent letters in the series is odd.
- a)MPRUX
- b)FIMRX
- c)EIMQV
- d)BDHLR
Correct answer is option 'D'. Can you explain this answer?
Directions: In each of the following questions find out which of the letter series follows the given rule.
Q. Number of letters skipped in between adjacent letters in the series is odd.
a)
MPRUX
b)
FIMRX
c)
EIMQV
d)
BDHLR

|
Rishika Tiwari answered |
Let's analyze each option to determine which letter series has an odd number of letters skipped between adjacent letters.
Option 1: MPRUX
- M to P: 2 letters skipped (N, O) — Even
- P to R: 1 letter skipped (Q) — Odd
- R to U: 2 letters skipped (S, T) — Even
- U to X: 2 letters skipped (V, W) — Even
- This series does not have all odd skips. So, not correct.
Option 2: FIMRX
- F to I: 2 letters skipped (G, H) — Even
- I to M: 3 letters skipped (J, K, L) — Odd
- M to R: 4 letters skipped (N, O, P, Q) — Even
- R to X: 5 letters skipped (S, T, U, V, W) — Odd
- This series has a mix of odd and even skips. So, not correct.
Option 3: EIMQV
- E to I: 3 letters skipped (F, G, H) — Odd
- I to M: 3 letters skipped (J, K, L) — Odd
- M to Q: 3 letters skipped (N, O, P) — Odd
- Q to V: 4 letters skipped (R, S, T, U) — Even
- This series also has a mix of odd and even skips. So, not correct.
Option 4: BDHLR
- B to D: 1 letter skipped (C) — Odd
- D to H: 3 letters skipped (E, F, G) — Odd
- H to L: 3 letters skipped (I, J, K) — Odd
- L to R: 5 letters skipped (M, N, O, P, Q) — Odd
- All skips between letters in this series are odd.
Conclusion:
The correct answer is Option 4: BDHLR, as it is the only series where the number of letters skipped between adjacent letters is consistently odd.

How many 4's are there in the following number series, each of which is immediately preceded and followed by an even digit?
6 4 3 2 4 8 3 1 5 4 2 3 2 4 6 4 8 1 3 2 4 2 6 4 5
- a)Four
- b)Two
- c)Three
- d)One
Correct answer is option 'A'. Can you explain this answer?
How many 4's are there in the following number series, each of which is immediately preceded and followed by an even digit?
6 4 3 2 4 8 3 1 5 4 2 3 2 4 6 4 8 1 3 2 4 2 6 4 5
6 4 3 2 4 8 3 1 5 4 2 3 2 4 6 4 8 1 3 2 4 2 6 4 5
a)
Four
b)
Two
c)
Three
d)
One

|
Torcia Education answered |
There is only one occurrence of 4 in the sequence that is immediately preceded and followed by an even digit: 2 4 8.
Saket is 7 ranks ahead of Manoj in a class of 50. If Manoj’s rank is 17th from the last, what is Saket’s rank from the start?- a)25
- b)26
- c)27
- d)28
Correct answer is option 'C'. Can you explain this answer?
Saket is 7 ranks ahead of Manoj in a class of 50. If Manoj’s rank is 17th from the last, what is Saket’s rank from the start?
a)
25
b)
26
c)
27
d)
28

|
Rahul Mehra answered |
Manoj’s rank is 17th from the last.
Saket’s rank = 17 + 7 = 24th from the last.
No. of students ahead of Saket = 50 – 24 = 26
Saket’s rank from start = 26 + 1 = 27th
Saket’s rank = 17 + 7 = 24th from the last.
No. of students ahead of Saket = 50 – 24 = 26
Saket’s rank from start = 26 + 1 = 27th
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?
- a)14
- b)22
- c)32
- d)320
Correct answer is option 'C'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
14
b)
22
c)
32
d)
320

|
Raksha Roy answered |
From figure I (5 × 6 × 4)/10 = 12 and from figure II (6 × 7 × 5)/10 = 21 Therefore, from figure III ? = (4 × 8 × 10)/10 = 32
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?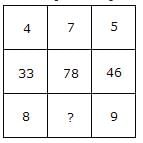
- a)12
- b)13
- c)11
- d)10
Correct answer is option 'C'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
12
b)
13
c)
11
d)
10

|
Athira Desai answered |
From column I (4 × 8) + 1 = 33
From column II (5 × 9) + 1 = 46
Similarly, from column III (7 × ?) + 1 = 78
From column II (5 × 9) + 1 = 46
Similarly, from column III (7 × ?) + 1 = 78
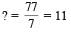
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q.Which one will replace the question mark?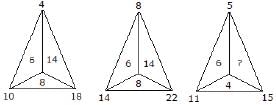
- a)8
- b)14
- c)10
- d)6
Correct answer is option 'C'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q.Which one will replace the question mark?

a)
8
b)
14
c)
10
d)
6

|
Moumita Desai answered |
For first triangle, 10 – 4 = 6
18 – 10 = 8
18 – 4 = 14
For second triangle, 14 – 8 = 6
22 – 14 = 8
22 – 8 = 14
For third triangle, 11 – 5 = 6
15 – 11 = 4
∴ ? = 15 – 5 = 10
18 – 10 = 8
18 – 4 = 14
For second triangle, 14 – 8 = 6
22 – 14 = 8
22 – 8 = 14
For third triangle, 11 – 5 = 6
15 – 11 = 4
∴ ? = 15 – 5 = 10
Ranjan ranks 18th in a class of 49 students. What is his rank from last?- a)28
- b)29
- c)31
- d)32
Correct answer is option 'D'. Can you explain this answer?
Ranjan ranks 18th in a class of 49 students. What is his rank from last?
a)
28
b)
29
c)
31
d)
32

|
Rahul Mehra answered |
Here, 49 – 18 = 31
So, Ranjan’s rank = 31 + 1 = 32nd form the last.
So, Ranjan’s rank = 31 + 1 = 32nd form the last.
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?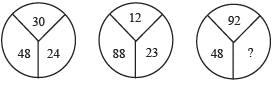
- a)60
- b)46
- c)86
- d)75
Correct answer is option 'C'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
60
b)
46
c)
86
d)
75

|
Moumita Desai answered |
(30 – 24) × 8 = 48
and (23 – 12) × 8 = 88
Therefore, (92 – ?) × 8 = 48
⇒ 92 – ? = 6
⇒ ? = 92 –6 = 86
and (23 – 12) × 8 = 88
Therefore, (92 – ?) × 8 = 48
⇒ 92 – ? = 6
⇒ ? = 92 –6 = 86
In a row of boys Raja is 10th from the left and Pramod, who is 9th from the right interchange their positions, Raja becomes 15th from the left. How many boys are there in the row?- a)23
- b)24
- c)25
- d)26
Correct answer is option 'A'. Can you explain this answer?
In a row of boys Raja is 10th from the left and Pramod, who is 9th from the right interchange their positions, Raja becomes 15th from the left. How many boys are there in the row?
a)
23
b)
24
c)
25
d)
26

|
Nitin Iyer answered |
Raja’s new position is 15th from the left and this is the same as 9th position from the right for Pramod.
No. of boys = 15 + 9 – 1 = 23
No. of boys = 15 + 9 – 1 = 23
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?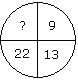
- a)40
- b)38
- c)44
- d)39
Correct answer is option 'B'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
40
b)
38
c)
44
d)
39

|
Moumita Desai answered |
Here,
9 + (2)2 = 13
and 13 + (3)2 = 22
and ? = 22 + (4)2 = 38
9 + (2)2 = 13
and 13 + (3)2 = 22
and ? = 22 + (4)2 = 38
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?
- a)660
- b)670
- c)610
- d)690
Correct answer is option 'D'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
660
b)
670
c)
610
d)
690

|
Athira Desai answered |
From figure I (1)2 + (5)2 + (4)2 + (3)2
=51 × 10 = 510
and from figure II (3)2 + (4)2 + (6)2 + (2)2
= 65 × 10 = 650
Similarly, from figure III (0)2 + (1)2 + (2)2 + (8)2 = 69 × 10 = 690
=51 × 10 = 510
and from figure II (3)2 + (4)2 + (6)2 + (2)2
= 65 × 10 = 650
Similarly, from figure III (0)2 + (1)2 + (2)2 + (8)2 = 69 × 10 = 690
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?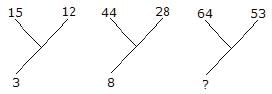
- a)30
- b)13
- c)70
- d)118
Correct answer is option 'B'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
30
b)
13
c)
70
d)
118

|
Siddharth Nambiar answered |
(15 + 12)/9 = 3
and (44 + 28)/9 = 8 Therefore, ? = (64 + 53)/9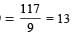
and (44 + 28)/9 = 8 Therefore, ? = (64 + 53)/9
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?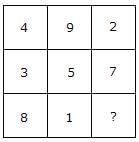
- a)9
- b)6
- c)15
- d)14
Correct answer is option 'B'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
9
b)
6
c)
15
d)
14

|
Pragati Das answered |
Here,
(4 + 9 + 2) = (3 + 5 + 7) = (8 + 1 + ?)
⇒ ? = 15 – 9 = 6
Total in each case = 15
(4 + 9 + 2) = (3 + 5 + 7) = (8 + 1 + ?)
⇒ ? = 15 – 9 = 6
Total in each case = 15
Arrange the given words in the alphabetical order and choose the one that comes last.- a)Temperature
- b)Transition
- c)Temple
- d)Transmit
Correct answer is option 'D'. Can you explain this answer?
Arrange the given words in the alphabetical order and choose the one that comes last.
a)
Temperature
b)
Transition
c)
Temple
d)
Transmit
|
|
Palak Nair answered |
Temperature, Temple, Transition and Transmit.
How many times the difference between two consecutive terms is 5?1 3 4 6 9 8 4 2 7 6 4 9 6 3 8 2 6 4 1 6 7 4 - a)3
- b)4
- c)5
- d)6
Correct answer is option 'B'. Can you explain this answer?
How many times the difference between two consecutive terms is 5?
1 3 4 6 9 8 4 2 7 6 4 9 6 3 8 2 6 4 1 6 7 4
a)
3
b)
4
c)
5
d)
6
|
|
Jaideep Banerjee answered |
Identifying the Consecutive Terms
To find the consecutive terms where the difference is 5, we need to analyze the sequence provided.
Calculating the Differences
1 3 (difference: 2)
3 4 (difference: 1)
4 6 (difference: 2)
6 9 (difference: 3)
9 8 (difference: 1)
8 4 (difference: 4)
4 2 (difference: 2)
2 7 (difference: 5)
7 6 (difference: 1)
6 4 (difference: 2)
4 9 (difference: 5)
9 6 (difference: 3)
6 3 (difference: 3)
3 8 (difference: 5)
8 2 (difference: 6)
2 6 (difference: 4)
6 4 (difference: 2)
4 1 (difference: 3)
1 6 (difference: 5)
6 7 (difference: 1)
7 4 (difference: 3)
Identifying Consecutive Terms with Difference of 5
From the calculations, we can see that there are 4 instances where the difference between two consecutive terms is 5:
- 2 and 7
- 4 and 9
- 3 and 8
- 1 and 6
Therefore, the correct answer is option 'B' - 4 times.
To find the consecutive terms where the difference is 5, we need to analyze the sequence provided.
Calculating the Differences
1 3 (difference: 2)
3 4 (difference: 1)
4 6 (difference: 2)
6 9 (difference: 3)
9 8 (difference: 1)
8 4 (difference: 4)
4 2 (difference: 2)
2 7 (difference: 5)
7 6 (difference: 1)
6 4 (difference: 2)
4 9 (difference: 5)
9 6 (difference: 3)
6 3 (difference: 3)
3 8 (difference: 5)
8 2 (difference: 6)
2 6 (difference: 4)
6 4 (difference: 2)
4 1 (difference: 3)
1 6 (difference: 5)
6 7 (difference: 1)
7 4 (difference: 3)
Identifying Consecutive Terms with Difference of 5
From the calculations, we can see that there are 4 instances where the difference between two consecutive terms is 5:
- 2 and 7
- 4 and 9
- 3 and 8
- 1 and 6
Therefore, the correct answer is option 'B' - 4 times.
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?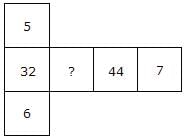
- a)33
- b)38
- c)32
- d)37
Correct answer is option 'D'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
33
b)
38
c)
32
d)
37

|
Gayatri Roy answered |
Here, (5 × 6) + 2 = 32
(7 × 6) + 2 = 44
∴ ? = (7 × 5) + 2 = 37
(7 × 6) + 2 = 44
∴ ? = (7 × 5) + 2 = 37
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. If the order of the English alphabet is reversed, then which letter would be exactly in the middle?- a)M
- b)N
- c)L
- d)None of these?
Correct answer is option 'D'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. If the order of the English alphabet is reversed, then which letter would be exactly in the middle?
a)
M
b)
N
c)
L
d)
None of these?

|
Shreya Sarkar answered |
The new letter series obtained on reversing the order of the English alphabet is
Z Y X W V U T S R Q P O N M L K J I H G F E D C B A.
Since the series has an even number of letters there is no such letter which lies exactly in the middle.
Z Y X W V U T S R Q P O N M L K J I H G F E D C B A.
Since the series has an even number of letters there is no such letter which lies exactly in the middle.
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y ZQ. Which letter is exactly midway between G and Q in the given alphabet?- a)K
- b)L
- c)N
- d)M
Correct answer is option 'B'. Can you explain this answer?
Directions: Each of the following questions is based on the following alphabet – series:
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V
W X Y Z
Q. Which letter is exactly midway between G and Q in the given alphabet?
a)
K
b)
L
c)
N
d)
M

|
Anirudh Kumar answered |
There are nine letters between G and Q – H, I, J, K, L, M, N, O, P. Clearly, the middle letter is L.
If in a single line, Mohan is 23rd from both the ends. How many boys are there in the class?- a)44
- b)45
- c)46
- d)47
Correct answer is option 'B'. Can you explain this answer?
If in a single line, Mohan is 23rd from both the ends. How many boys are there in the class?
a)
44
b)
45
c)
46
d)
47

|
Raj Mukherjee answered |
Required no. of boys = 22 + 1 + 22 = 45
If the numbers from 1 to 100, which are exactly divisible by 5 are arranged in descending order, which would come at the 11th position from the bottom?- a)50
- b)55
- c)60
- d)65
Correct answer is option 'B'. Can you explain this answer?
If the numbers from 1 to 100, which are exactly divisible by 5 are arranged in descending order, which would come at the 11th position from the bottom?
a)
50
b)
55
c)
60
d)
65

|
Raj Mukherjee answered |
95, 90, 85, 80, 75, 70, 65, 60, 55, 50, 45, 40,
35, 30, 25, 20, 15, 10, 5
35, 30, 25, 20, 15, 10, 5
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?
- a)25
- b)625
- c)125
- d)50
Correct answer is option 'C'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
25
b)
625
c)
125
d)
50

|
Moumita Desai answered |
All numbers are cubes,
(7)3 = 343
(1)3 = 1
(3)3 = 27
Similarly, ? = (5)3 = 125
(7)3 = 343
(1)3 = 1
(3)3 = 27
Similarly, ? = (5)3 = 125
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.Q. Which one will replace the question mark?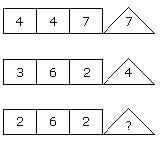
- a)2
- b)4
- c)6
- d)8
Correct answer is option 'C'. Can you explain this answer?
Directions: In this type of questions, a figure or a matrix is given in which some numbers are filled according to a rule. A place is left blank. You have to find out a character (a number or a letter) from the given possible answers which may be filled in the blank space.
Q. Which one will replace the question mark?

a)
2
b)
4
c)
6
d)
8

|
Harshad Shah answered |
(4 × 7) ÷ 4 = 7
and (6 × 2) ÷ 3 = 4
Therefore, (6 × 2) ÷ 2 = 6
and (6 × 2) ÷ 3 = 4
Therefore, (6 × 2) ÷ 2 = 6
If Aman finds that he is 12th from the right in a line of boys and 4th from the left. How many boys should be added to the line such that there are 35 students in the line?- a)18
- b)19
- c)20
- d)21
Correct answer is option 'C'. Can you explain this answer?
If Aman finds that he is 12th from the right in a line of boys and 4th from the left. How many boys should be added to the line such that there are 35 students in the line?
a)
18
b)
19
c)
20
d)
21

|
Upasana Basak answered |
No. of boys in the line = 12 + 4 – 1 = 15.
No. of boys to be added = 35 – 15 = 20
No. of boys to be added = 35 – 15 = 20
Chapter doubts & questions for Alpha-Numeric Sequence Puzzle - National Cyber Olympiad Class 6 2025 is part of Class 6 exam preparation. The chapters have been prepared according to the Class 6 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Alpha-Numeric Sequence Puzzle - National Cyber Olympiad Class 6 in English & Hindi are available as part of Class 6 exam.
Download more important topics, notes, lectures and mock test series for Class 6 Exam by signing up for free.
National Cyber Olympiad Class 6
1 docs|37 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup