All Exams >
JEE >
Mathematics (Maths) for JEE Main & Advanced >
All Questions
All questions of Binomial Theorem & its Simple Applications for JEE Exam
In the expansion of the binomial expansion (a + b)n, which of the following is incorrect ?
- a)The exponent of a decreases from n to 0.
- b)The number of terms is n+1.
- c)The exponent of b increases from 0 to n.
- d)The binomial coefficients in (a+b)n, which are equidistant from beginning and end are not equal.
Correct answer is option 'D'. Can you explain this answer?
In the expansion of the binomial expansion (a + b)n, which of the following is incorrect ?
a)
The exponent of a decreases from n to 0.
b)
The number of terms is n+1.
c)
The exponent of b increases from 0 to n.
d)
The binomial coefficients in (a+b)n, which are equidistant from beginning and end are not equal.
|
|
Krishna Iyer answered |
Correct Answer: d
Explanation:- The coefficient of terms (x+a)n equidistant from the beginning and the end are equal. These coefficients are known as the binomial coefficients.
nCr = nCn – r, r = 0,1,2,…,n.
The middle term in the expansion of (x + y)10 is the- a)6th term
- b)5th term
- c)average of 5th and 6th terms
- d)7th term
Correct answer is option 'A'. Can you explain this answer?
The middle term in the expansion of (x + y)10 is the
a)
6th term
b)
5th term
c)
average of 5th and 6th terms
d)
7th term
|
|
Vikas Kapoor answered |
Number of terms(n) = 10
Middle term = (n/2) + 1
Middle term = (n/2) + 1
= (10/2) + 1
= 5 + 1
= 6th term
= 5 + 1
= 6th term
The number of terms in the expansion of (x – y + 2z)7 are:- a)35
- b)38
- c)36
- d)37
Correct answer is option 'C'. Can you explain this answer?
The number of terms in the expansion of (x – y + 2z)7 are:
a)
35
b)
38
c)
36
d)
37
|
|
Tejas Verma answered |
Here the number of terms can be calculated by:
= ((n+ 1) * (n+2)) /2
where, n =7
= ((n+ 1) * (n+2)) /2
where, n =7
∴ Number of terms = 36
The number of terms in the expansion of (2x - 3y)8 is- a)6
- b)9
- c)8
- d)5
Correct answer is option 'B'. Can you explain this answer?
The number of terms in the expansion of (2x - 3y)8 is
a)
6
b)
9
c)
8
d)
5
|
|
Aryan Khanna answered |
Since this binomial is to the power 8, there will be nine terms in the expansion.
In the expansion of (a+b)n, nN the number of terms is:- a)n + 1
- b)n
- c)n – 1
- d)an
Correct answer is option 'A'. Can you explain this answer?
In the expansion of (a+b)n, nN the number of terms is:
a)
n + 1
b)
n
c)
n – 1
d)
an
|
|
Tanishq Saini answered |
Explanation:
Binomial Expansion:
In the expansion of (a+b)^n, where n is a positive integer, the number of terms in the expansion is (n+1).
Proof:
When we expand (a+b)^n using binomial theorem, the general term of the expansion is given by:
T(r+1) = nCr * a^(n-r) * b^r
where r is the index of the term and nCr represents the binomial coefficient.
Number of Terms:
To find the number of terms in the expansion, we need to find the values of r that satisfy 0 ≤ r ≤ n.
Counting the Terms:
- When r = 0, we get the first term: nC0 * a^n * b^0 = a^n
- When r = 1, we get the second term: nC1 * a^(n-1) * b^1
- ...
- When r = n, we get the (n+1)th term: nCn * a^0 * b^n = b^n
Total Number of Terms:
Since we have considered all values of r from 0 to n, there are (n+1) terms in the expansion of (a+b)^n.
Therefore, the correct answer is option A) n + 1.
Binomial Expansion:
In the expansion of (a+b)^n, where n is a positive integer, the number of terms in the expansion is (n+1).
Proof:
When we expand (a+b)^n using binomial theorem, the general term of the expansion is given by:
T(r+1) = nCr * a^(n-r) * b^r
where r is the index of the term and nCr represents the binomial coefficient.
Number of Terms:
To find the number of terms in the expansion, we need to find the values of r that satisfy 0 ≤ r ≤ n.
Counting the Terms:
- When r = 0, we get the first term: nC0 * a^n * b^0 = a^n
- When r = 1, we get the second term: nC1 * a^(n-1) * b^1
- ...
- When r = n, we get the (n+1)th term: nCn * a^0 * b^n = b^n
Total Number of Terms:
Since we have considered all values of r from 0 to n, there are (n+1) terms in the expansion of (a+b)^n.
Therefore, the correct answer is option A) n + 1.
The expansion of 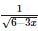 , in powers of x, is valid if
, in powers of x, is valid if- a)|x| > 2
- b)x < 2
- c)x > 2
- d)|x| < 2
Correct answer is option 'D'. Can you explain this answer?
The expansion of 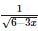 , in powers of x, is valid if
, in powers of x, is valid if
a)
|x| > 2
b)
x < 2
c)
x > 2
d)
|x| < 2

|
Knowledge Hub answered |
In case of negative or fractional power, expansion (1+x)^n is valid only when |x| < 1
(6 - 3x)-1/2
= (6-1/2 (1 - x/2)-1/2)
So, this equation exists only when |x/2| < 1
|x| < 2
(6 - 3x)-1/2
= (6-1/2 (1 - x/2)-1/2)
So, this equation exists only when |x/2| < 1
|x| < 2
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are- a)additive inverse of each other
- b)multiplicative inverse of each other
- c)equal
- d)nothing can be said
Correct answer is option 'C'. Can you explain this answer?
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are
a)
additive inverse of each other
b)
multiplicative inverse of each other
c)
equal
d)
nothing can be said
|
|
Hansa Sharma answered |
(x+a)n = nC0 xn + nC1 x(n-1) a1 + nC2 x(n-2) a2 + ..........+ nC(n-1) xa(n-1) + nCn an
Now, nC0 = nCn, nC1 = nCn-1, nC2 = nCn-2,........
therefore, nCr = nCn-r
The binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are equal.
Now, nC0 = nCn, nC1 = nCn-1, nC2 = nCn-2,........
therefore, nCr = nCn-r
The binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are equal.
The coefficient of y in the expansion of (y² + c/y)5 is - a)10c
- b)10c²
- c)10c³
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The coefficient of y in the expansion of (y² + c/y)5 is
a)
10c
b)
10c²
c)
10c³
d)
None of these
|
|
Varun Kapoor answered |
Given, binomial expression is (y² + c / y)5
Now, Tr+1 = 5Cr × (y²)5-r × (c / y)r
= 5Cr × y10-3r × Cr
Now, 10 – 3r = 1
⇒ 3r = 9
⇒ r = 3
So, the coefficient of y = 5C3 × c³ = 10c³
Now, Tr+1 = 5Cr × (y²)5-r × (c / y)r
= 5Cr × y10-3r × Cr
Now, 10 – 3r = 1
⇒ 3r = 9
⇒ r = 3
So, the coefficient of y = 5C3 × c³ = 10c³
What is the coefficient of x5 in the expansion of (1-x)-6 ?- a)252
- b)250
- c)-252
- d)251
Correct answer is option 'A'. Can you explain this answer?
What is the coefficient of x5 in the expansion of (1-x)-6 ?
a)
252
b)
250
c)
-252
d)
251
|
|
Preeti Iyer answered |
(1-x)-6
=> (1-x)(-6/1)
It is in the form of (1-x)(-p/q), p =6, q=1
=> (1-x)(-6/1)
It is in the form of (1-x)(-p/q), p =6, q=1
(1-x)(-p/q) = 1+p/1!(x/q)1 + p(p+q)/2!(x/q)2 + p(p+q)(p+2q)/3!(x/q)3 + p(p+q)(p+2q)(p+3q)/4!(x/q)4........
= 1+6/1!(x/1)1 + 6(7)/2!(x/1)2 + 6(7)(8)/3!(x/1)3 + 6(7)(8)(9)/4!(x/1)4 +.......................
So, coefficient of x5 is (6*7*8*9*10)/120
= 252
= 252
If in the expansion of (1+x)20, the coefficients of rth and (r+4)th terms are equal, then the value of r is equal to:- a)9
- b)7
- c)10
- d)8
Correct answer is option 'A'. Can you explain this answer?
If in the expansion of (1+x)20, the coefficients of rth and (r+4)th terms are equal, then the value of r is equal to:
a)
9
b)
7
c)
10
d)
8
|
|
Raghav Bansal answered |
Coefficients of the rth and (r+4)th terms in the given expansion are Cr−120 and 20Cr+3.
Here,Cr−120 = 20Cr+3
⇒ r−1+r+3 = 20
[∵ if nCx = nCy ⇒ x = y or x+y = n]
Here,Cr−120 = 20Cr+3
⇒ r−1+r+3 = 20
[∵ if nCx = nCy ⇒ x = y or x+y = n]
⇒ r = 2 or 2r = 18
⇒ r = 9
⇒ r = 9
The general term in the expansion of (a - b)n is- a)Tr+1 = (-1)r nCr an-r br
- b)Tr+1 = nCr an-r br
- c)Tr+1 = nCr ar br
- d)Tr+1 = (-1)r nCr ar br
Correct answer is option 'A'. Can you explain this answer?
The general term in the expansion of (a - b)n is
a)
Tr+1 = (-1)r nCr an-r br
b)
Tr+1 = nCr an-r br
c)
Tr+1 = nCr ar br
d)
Tr+1 = (-1)r nCr ar br
|
|
Poonam Reddy answered |
If a and b are real numbers and n is a positive integer, then:
(a - b)n = nC0 an + nC1 a(n – 1) b1 + nC2 a(n – 2) b2+ ...... + nCr a(n – r) br+ ... + nCnbn,
(a - b)n = nC0 an + nC1 a(n – 1) b1 + nC2 a(n – 2) b2+ ...... + nCr a(n – r) br+ ... + nCnbn,
The general term or (r + 1)th term in the expansion is given by:
Tr + 1 = (-1)Cr a(n–r) br
Tr + 1 = (-1)Cr a(n–r) br
If 2nd, 3rd and 4th terms in the expansion of (x+a)n are 240, 720 and 1080 respectively, then the value of n is- a)15
- b)20
- c)5
- d)10
Correct answer is option 'C'. Can you explain this answer?
If 2nd, 3rd and 4th terms in the expansion of (x+a)n are 240, 720 and 1080 respectively, then the value of n is
a)
15
b)
20
c)
5
d)
10

|
Shiksha Academy answered |
General term Tr+1 of (x+y)n is given by
Tr+1 = nCr xn-r yr
T2 = nC2 xn-2 y = 240
T3 = nC3 xn-3 y2 = 720
T4 = nC4 xn-4 y3 = 1080
T3/T2 = [(n-1)/2] * [y/x] = 3......(1)
T4/T2 = {[(n-1)(n-2)]/(3*2)} * x2/y2 = 9/2
T4/T3 = [(n-2)/3] * [y/x] = 3/2...(2)
Dividing 1 by 2
[(n-1)/2] * [3/(n-2)] = 2
⇒ 3n−3 = 4n−8
⇒ 5 = n
Tr+1 = nCr xn-r yr
T2 = nC2 xn-2 y = 240
T3 = nC3 xn-3 y2 = 720
T4 = nC4 xn-4 y3 = 1080
T3/T2 = [(n-1)/2] * [y/x] = 3......(1)
T4/T2 = {[(n-1)(n-2)]/(3*2)} * x2/y2 = 9/2
T4/T3 = [(n-2)/3] * [y/x] = 3/2...(2)
Dividing 1 by 2
[(n-1)/2] * [3/(n-2)] = 2
⇒ 3n−3 = 4n−8
⇒ 5 = n
The coefficient of x3 in the binomial expansion of 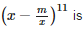
- a)792m5
- b)942m7
- c)330m4
- d)792m6
Correct answer is option 'C'. Can you explain this answer?
The coefficient of x3 in the binomial expansion of 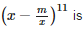
a)
792m5
b)
942m7
c)
330m4
d)
792m6
|
|
Geetika Shah answered |
T(r+1) = 11Cr x(11-2r) (m/r)r (-1)r
= 11Cr x(11-2r) mr (-1)r
Coefficient of x3 = 11 - 2r = 3
8 = 2r
r = 4
T5 = 11C4 x3 m4 (-1)
Coefficient of x3 = 11C4 m4
= 330 m4
= 11Cr x(11-2r) mr (-1)r
Coefficient of x3 = 11 - 2r = 3
8 = 2r
r = 4
T5 = 11C4 x3 m4 (-1)
Coefficient of x3 = 11C4 m4
= 330 m4
The coefficient of x17 in the expansion of (x- 1) (x- 2) …..(x – 18) is- a)- 171
- b)342
- c)171/2
- d)684
Correct answer is option 'A'. Can you explain this answer?
The coefficient of x17 in the expansion of (x- 1) (x- 2) …..(x – 18) is
a)
- 171
b)
342
c)
171/2
d)
684

|
Infinity Academy answered |
The coefficient of x17 is given by
−1 + (−2) + (−3) + ….. (−18)
= −1 − 2 − 3….. − 18
= − (18(18+1))/2
= − 9(19)
= − 171
−1 + (−2) + (−3) + ….. (−18)
= −1 − 2 − 3….. − 18
= − (18(18+1))/2
= − 9(19)
= − 171
In the expansion of (1+x)60, the sum of coefficients of odd powers of x is- a)261
- b)260
- c)259
- d)none of these.
Correct answer is option 'C'. Can you explain this answer?
In the expansion of (1+x)60, the sum of coefficients of odd powers of x is
a)
261
b)
260
c)
2
59
d)
none of these.
|
|
Mohit Mittal answered |
C is correct as
sum of ( 1+ x )^60 gives 2^60 which includes both even and odd powers of x
so for only one type of power ( odd power) of x we divide 2^ 60 by 2 so we get 2^ 59
sum of ( 1+ x )^60 gives 2^60 which includes both even and odd powers of x
so for only one type of power ( odd power) of x we divide 2^ 60 by 2 so we get 2^ 59
If the second, third, and fourth terms in the expansion of (x + y)n are 135, 30, and 10/3, respectively, then 6 (n3 + x2 + y) is equal to ________.Correct answer is '806'. Can you explain this answer?
If the second, third, and fourth terms in the expansion of (x + y)n are 135, 30, and 10/3, respectively, then 6 (n3 + x2 + y) is equal to ________.

|
Nipuns Institute answered |
T2 = nC1 y1 x(n-1) = 135
T3 = nC2 y2 x(n-2) = 30
T4 = nC3 y3 x(n-3) = 10/3
⇒ 135/30 = (x/y) * n * 2 / n(n-1) = (2 / n-1) * (x/y) ... (i)
30 / (10/3) = n(n-1) / 2 / n(n-1)(n-2) * 3! * (x/y)
9 = (3 / n-2) * (x/y)
3(n - 2) = 135 / 60 (n - 1) ⇒ n = 5
⇒ x = 9y ... (i)
y * x4 = 27 ⇒ x / 9 * x4 = 33
⇒ x5 = 35 ⇒ x = 3y = 1/3
⇒ 6 (53 + 32 + 1/3) = 6 (125 + 9 + 1/3)
= 6(134) + 2 = 806
T3 = nC2 y2 x(n-2) = 30
T4 = nC3 y3 x(n-3) = 10/3
⇒ 135/30 = (x/y) * n * 2 / n(n-1) = (2 / n-1) * (x/y) ... (i)
30 / (10/3) = n(n-1) / 2 / n(n-1)(n-2) * 3! * (x/y)
9 = (3 / n-2) * (x/y)
3(n - 2) = 135 / 60 (n - 1) ⇒ n = 5
⇒ x = 9y ... (i)
y * x4 = 27 ⇒ x / 9 * x4 = 33
⇒ x5 = 35 ⇒ x = 3y = 1/3
⇒ 6 (53 + 32 + 1/3) = 6 (125 + 9 + 1/3)
= 6(134) + 2 = 806
Number of integral terms in the expansion of (71/2 + 111/6)824 is equal to ________.Correct answer is '138'. Can you explain this answer?
Number of integral terms in the expansion of (71/2 + 111/6)824 is equal to ________.

|
Sai Kulkarni answered |
General term in expansion of (71/2 + 111/6)824 is T(r+1) = 824Cr * 7((824-r)/2) * 11(r/6)
For integral term, r must be a multiple of 6.
Hence r = 0, 6, 12, ..., 822
For integral term, r must be a multiple of 6.
Hence r = 0, 6, 12, ..., 822
If the expansion of 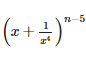 in powers of x contains the term x2r, then n−2r is
in powers of x contains the term x2r, then n−2r is- a)even
- b)odd
- c)a positive integral multiple of 5
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the expansion of 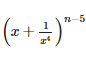 in powers of x contains the term x2r, then n−2r is
in powers of x contains the term x2r, then n−2r is
a)
even
b)
odd
c)
a positive integral multiple of 5
d)
none of these
|
|
Geetika Shah answered |
T(r+1) = nCr xn-r ar
T(r+1) = n-5Cr xn-5-r (1/x4)r
= n-5Cr xn-5-r (1/x4r)
= n-5Cr xn-5-5r
=> n - 5 - 5r = 2r
=> n - 2r = 5(r + 1)
T(r+1) = n-5Cr xn-5-r (1/x4)r
= n-5Cr xn-5-r (1/x4r)
= n-5Cr xn-5-5r
=> n - 5 - 5r = 2r
=> n - 2r = 5(r + 1)
n-1Cr = (k² - 8) nCr+1 if and only if:- a)2√2 < k < 2√3
- b)2√2 ≤ k ≤ 3
- c)2√3 < k < 3√3
- d)2√3 ≤ k ≤ 3√2
Correct answer is option 'B'. Can you explain this answer?
n-1Cr = (k² - 8) nCr+1 if and only if:
a)
2√2 < k < 2√3
b)
2√2 ≤ k ≤ 3
c)
2√3 < k < 3√3
d)
2√3 ≤ k ≤ 3√2

|
KP Classes answered |
n-1Cr = (k² - 8) nCr+1
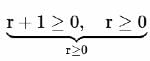
(n-1Cr) / (nCr+1) = k² - 8
(r + 1) / n = k² - 8
⇒ k² - 8 > 0
(k - 2√2)(k + 2√2) > 0
k ∈ (-∞, -2√2) ∪ (2√2, ∞) .... (I)
∴ n ≥ r + 1, (r + 1) / n ≤ 1
⇒ k² - 8 ≤ 1
k² - 9 ≤ 0
-3 ≤ k ≤ 3 .... (II)
From equation (I) and (II) we get
k ∈ [-3, -2√2) ∪ (2√2, 3]
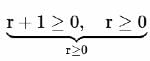
(n-1Cr) / (nCr+1) = k² - 8
(r + 1) / n = k² - 8
⇒ k² - 8 > 0
(k - 2√2)(k + 2√2) > 0
k ∈ (-∞, -2√2) ∪ (2√2, ∞) .... (I)
∴ n ≥ r + 1, (r + 1) / n ≤ 1
⇒ k² - 8 ≤ 1
k² - 9 ≤ 0
-3 ≤ k ≤ 3 .... (II)
From equation (I) and (II) we get
k ∈ [-3, -2√2) ∪ (2√2, 3]
Find the value of r, if the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x)18 are equal.- a)6
- b)5
- c)4
- d)3
Correct answer is option 'A'. Can you explain this answer?
Find the value of r, if the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x)18 are equal.
a)
6
b)
5
c)
4
d)
3
|
|
Pallavi Ahuja answered |
Understanding the Problem
We need to find the value of r such that the coefficients of the (2r + 4)th term and the (r - 2)th term in the expansion of (1 + x)^18 are equal.
Expansion of Binomial Expression
The general term (T_k) in the expansion of (1 + x)^n is given by:
- T_k = C(n, k-1) * x^(k-1)
Where C(n, k-1) is the binomial coefficient.
Identifying the Terms
For our case, with n = 18:
- Coefficient of (2r + 4)th term: C(18, 2r + 4 - 1) = C(18, 2r + 3)
- Coefficient of (r - 2)th term: C(18, r - 2 - 1) = C(18, r - 3)
Setting the Coefficients Equal
We set these coefficients equal to each other:
- C(18, 2r + 3) = C(18, r - 3)
Using the property of binomial coefficients, we know that:
- C(n, k) = C(n, n-k)
This gives us:
- 2r + 3 = 18 - (r - 3)
Simplifying the Equation
Now, we simplify the equation:
1. 2r + 3 = 18 - r + 3
2. 2r + r = 18 + 3 - 3
3. 3r = 18
4. r = 6
Conclusion
Thus, the value of r that satisfies the condition is:
- r = 6
Therefore, the correct answer is option 'A'.
We need to find the value of r such that the coefficients of the (2r + 4)th term and the (r - 2)th term in the expansion of (1 + x)^18 are equal.
Expansion of Binomial Expression
The general term (T_k) in the expansion of (1 + x)^n is given by:
- T_k = C(n, k-1) * x^(k-1)
Where C(n, k-1) is the binomial coefficient.
Identifying the Terms
For our case, with n = 18:
- Coefficient of (2r + 4)th term: C(18, 2r + 4 - 1) = C(18, 2r + 3)
- Coefficient of (r - 2)th term: C(18, r - 2 - 1) = C(18, r - 3)
Setting the Coefficients Equal
We set these coefficients equal to each other:
- C(18, 2r + 3) = C(18, r - 3)
Using the property of binomial coefficients, we know that:
- C(n, k) = C(n, n-k)
This gives us:
- 2r + 3 = 18 - (r - 3)
Simplifying the Equation
Now, we simplify the equation:
1. 2r + 3 = 18 - r + 3
2. 2r + r = 18 + 3 - 3
3. 3r = 18
4. r = 6
Conclusion
Thus, the value of r that satisfies the condition is:
- r = 6
Therefore, the correct answer is option 'A'.
The greatest coefficient in the expansion of (1+x)12 is- a)C (12, 4)
- b)C (12, 6)
- c)C (12, 5)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The greatest coefficient in the expansion of (1+x)12 is
a)
C (12, 4)
b)
C (12, 6)
c)
C (12, 5)
d)
none of these
|
|
Naina Bansal answered |
The binomial expansion formula states that:
(a + b)^n = a^n + n*a^(n-1)*b + C(n,2)*a^(n-2)*b^2 + ... + b^n
where C(n,k) is the binomial coefficient, given by:
C(n,k) = n! / (k! * (n-k)!)
In the expansion of (1+x)^12, the greatest coefficient will be the one with the largest value of k. Since we are given that n = 12, the greatest coefficient will be the one with the largest value of k such that k <= n. The largest value of k that satisfies this condition is 6, which corresponds to the coefficient C(12,6).
Therefore, the greatest coefficient in the expansion of (1+x)^12 is C(12,6). The correct answer is therefore (b) C (12, 6).
If x = 9950+1005 and y = (101)50, then- a)x < y
- b)x = y
- c)x > y
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If x = 9950+1005 and y = (101)50, then
a)
x < y
b)
x = y
c)
x > y
d)
none of these
|
|
Nitya Yadav answered |
The given equations are:
Ifx = 9950
1005andy = (101)50
To solve for x, we divide both sides of the first equation by 100:
Ifx/100 = 9950/100
x = 99.5
To solve for y, we divide both sides of the second equation by 1005:
andy = (101)50/1005
andy = 50
Therefore, the values of x and y are:
x = 99.5
y = 50
Ifx = 9950
1005andy = (101)50
To solve for x, we divide both sides of the first equation by 100:
Ifx/100 = 9950/100
x = 99.5
To solve for y, we divide both sides of the second equation by 1005:
andy = (101)50/1005
andy = 50
Therefore, the values of x and y are:
x = 99.5
y = 50
The coefficient of xn in expansion of (1+x)(1−x)n is- a)(−1)n(n+1)
- b)(−1)n(1−n)
- c)(−1)n
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The coefficient of xn in expansion of (1+x)(1−x)n is
a)
(−1)n(n+1)
b)
(−1)n(1−n)
c)
(−1)n
d)
none of these
|
|
Lavanya Menon answered |
We can expand (1+x)(1−x)n as
= (1+x)(nC0− nC1.x + nC2.x2 + ........ +(−1)n nCnxn)
= (1+x)(nC0− nC1.x + nC2.x2 + ........ +(−1)n nCnxn)
Coefficient of xn is
(−1)n nCn + (−1)n−1 nCn−1
=(−1)n(1−n)
If in the expansion of(1+x)43, the coefficients of (2r+1)th and (r+2)th terms are equal, then r is equal to- a)7 or 1
- b)21 or 1
- c)1 or 14
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If in the expansion of(1+x)43, the coefficients of (2r+1)th and (r+2)th terms are equal, then r is equal to
a)
7 or 1
b)
21 or 1
c)
1 or 14
d)
none of these
|
|
Pallabi Nambiar answered |
Understanding the Problem
In the expansion of (1 + x)^43, we need to find the values of r for which the coefficients of the (2r + 1)th term and the (r + 2)th term are equal.
Finding the Coefficients
The general term T_k in the expansion of (1 + x)^n can be expressed as:
- T_k = C(n, k) * x^k
Where C(n, k) is the binomial coefficient.
For our case, n = 43:
- Coefficient of the (2r + 1)th term: C(43, 2r)
- Coefficient of the (r + 2)th term: C(43, r)
We set these coefficients equal:
- C(43, 2r) = C(43, r)
Using Binomial Coefficient Properties
Using the property of binomial coefficients, we know that:
- C(n, k) = C(n, n - k)
Thus, we can rewrite:
- C(43, 2r) = C(43, 43 - 2r)
- C(43, r) = C(43, 43 - r)
This leads to two scenarios:
1. 2r = r → r = 0 (not valid since we want a positive r)
2. 2r + r = 43 → 3r = 43 → r = 14.33 (not an integer)
Now we consider:
Finding Integer Values for r
Considering the nature of binomial coefficients, we check for values of r:
- r can be integers such that 2r ≤ 43 and r ≤ 43.
- Possible values of r include 1, 7, 14, and others.
By checking:
- If r = 1: C(43, 2) = C(43, 1)
- If r = 14: C(43, 28) = C(43, 14)
Both conditions satisfy the equality.
Conclusion
Thus, the values of r are 1 and 14. Therefore, the correct option is:
- Option C: 1 or 14.
In the expansion of (1 + x)^43, we need to find the values of r for which the coefficients of the (2r + 1)th term and the (r + 2)th term are equal.
Finding the Coefficients
The general term T_k in the expansion of (1 + x)^n can be expressed as:
- T_k = C(n, k) * x^k
Where C(n, k) is the binomial coefficient.
For our case, n = 43:
- Coefficient of the (2r + 1)th term: C(43, 2r)
- Coefficient of the (r + 2)th term: C(43, r)
We set these coefficients equal:
- C(43, 2r) = C(43, r)
Using Binomial Coefficient Properties
Using the property of binomial coefficients, we know that:
- C(n, k) = C(n, n - k)
Thus, we can rewrite:
- C(43, 2r) = C(43, 43 - 2r)
- C(43, r) = C(43, 43 - r)
This leads to two scenarios:
1. 2r = r → r = 0 (not valid since we want a positive r)
2. 2r + r = 43 → 3r = 43 → r = 14.33 (not an integer)
Now we consider:
Finding Integer Values for r
Considering the nature of binomial coefficients, we check for values of r:
- r can be integers such that 2r ≤ 43 and r ≤ 43.
- Possible values of r include 1, 7, 14, and others.
By checking:
- If r = 1: C(43, 2) = C(43, 1)
- If r = 14: C(43, 28) = C(43, 14)
Both conditions satisfy the equality.
Conclusion
Thus, the values of r are 1 and 14. Therefore, the correct option is:
- Option C: 1 or 14.
If rth ,(r+1)th and (r+2)th terms in the expansion of (1+x)n are in A.P. then- a)(n+2r)3 = n−2
- b)(n−2r)2 = n+2
- c)(n+2r)2 = n+2
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If rth ,(r+1)th and (r+2)th terms in the expansion of (1+x)n are in A.P. then
a)
(n+2r)3 = n−2
b)
(n−2r)2 = n+2
c)
(n+2r)2 = n+2
d)
none of these
|
|
Mayank Dasgupta answered |
To determine the relationship between the terms (rth, (r+1)th, and (r+2)th) in the expansion of (1+x)^n, we can use the binomial theorem.
The general term of the expansion of (1+x)^n is given by:
C(n, r)*x^r*(1)^n-r
The rth term is given by:
C(n, r)*x^r*(1)^(n-r)
The (r+1)th term is given by:
C(n, r+1)*x^(r+1)*(1)^(n-r-1)
The (r+2)th term is given by:
C(n, r+2)*x^(r+2)*(1)^(n-r-2)
To determine if these terms are in an arithmetic progression (A.P.), we need to find the common difference between the terms. We can subtract consecutive terms to find the common difference:
(r+1)th term - rth term:
[C(n, r+1)*x^(r+1)*(1)^(n-r-1)] - [C(n, r)*x^r*(1)^(n-r)]
Simplifying this expression, we get:
C(n, r+1)*x^(r+1)*(1)^(n-r-1) - C(n, r)*x^r*(1)^(n-r)
= [C(n, r+1)*x^(r+1)*(1)^(n-r-1) - C(n, r)*x^r*(1)^(n-r)] / [x^r*(1)^(n-r)]
Similarly, the (r+2)th term - (r+1)th term can be found as:
[C(n, r+2)*x^(r+2)*(1)^(n-r-2)] - [C(n, r+1)*x^(r+1)*(1)^(n-r-1)]
Simplifying this expression, we get:
C(n, r+2)*x^(r+2)*(1)^(n-r-2) - C(n, r+1)*x^(r+1)*(1)^(n-r-1)
= [C(n, r+2)*x^(r+2)*(1)^(n-r-2) - C(n, r+1)*x^(r+1)*(1)^(n-r-1)] / [x^(r+1)*(1)^(n-r-1)]
Since we want the terms to be in an arithmetic progression, the common difference between these terms should be the same. Therefore, we can equate the expressions for the common difference and solve for x:
[C(n, r+1)*x^(r+1)*(1)^(n-r-1) - C(n, r)*x^r*(1)^(n-r)] / [x^r*(1)^(n-r)]
= [C(n, r+2)*x^(r+2)*(1)^(n-r-2) - C(n, r+1)*x^(r+1)*(1)^(n-r-1)] / [x^(r+1)*(1)^(n-r-1)]
Simplifying this expression and canceling out the common factors, we get:
[C(n, r+1)*x -
The general term of the expansion of (1+x)^n is given by:
C(n, r)*x^r*(1)^n-r
The rth term is given by:
C(n, r)*x^r*(1)^(n-r)
The (r+1)th term is given by:
C(n, r+1)*x^(r+1)*(1)^(n-r-1)
The (r+2)th term is given by:
C(n, r+2)*x^(r+2)*(1)^(n-r-2)
To determine if these terms are in an arithmetic progression (A.P.), we need to find the common difference between the terms. We can subtract consecutive terms to find the common difference:
(r+1)th term - rth term:
[C(n, r+1)*x^(r+1)*(1)^(n-r-1)] - [C(n, r)*x^r*(1)^(n-r)]
Simplifying this expression, we get:
C(n, r+1)*x^(r+1)*(1)^(n-r-1) - C(n, r)*x^r*(1)^(n-r)
= [C(n, r+1)*x^(r+1)*(1)^(n-r-1) - C(n, r)*x^r*(1)^(n-r)] / [x^r*(1)^(n-r)]
Similarly, the (r+2)th term - (r+1)th term can be found as:
[C(n, r+2)*x^(r+2)*(1)^(n-r-2)] - [C(n, r+1)*x^(r+1)*(1)^(n-r-1)]
Simplifying this expression, we get:
C(n, r+2)*x^(r+2)*(1)^(n-r-2) - C(n, r+1)*x^(r+1)*(1)^(n-r-1)
= [C(n, r+2)*x^(r+2)*(1)^(n-r-2) - C(n, r+1)*x^(r+1)*(1)^(n-r-1)] / [x^(r+1)*(1)^(n-r-1)]
Since we want the terms to be in an arithmetic progression, the common difference between these terms should be the same. Therefore, we can equate the expressions for the common difference and solve for x:
[C(n, r+1)*x^(r+1)*(1)^(n-r-1) - C(n, r)*x^r*(1)^(n-r)] / [x^r*(1)^(n-r)]
= [C(n, r+2)*x^(r+2)*(1)^(n-r-2) - C(n, r+1)*x^(r+1)*(1)^(n-r-1)] / [x^(r+1)*(1)^(n-r-1)]
Simplifying this expression and canceling out the common factors, we get:
[C(n, r+1)*x -
The sum of coefficients in the expansion of (x+2y+z)n is (n being a positive integer)- a)3n
- b)2n
- c)1
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The sum of coefficients in the expansion of (x+2y+z)n is (n being a positive integer)
a)
3n
b)
2n
c)
1
d)
none of these
|
|
Maitri Kumar answered |
Explanation:
To find the sum of coefficients in the expansion of (x + 2y + z)^n, we can use the Binomial Theorem.
The Binomial Theorem states that for any positive integer n, the expansion of (x + y)^n can be written as:
(x + y)^n = C(n, 0)x^n y^0 + C(n, 1)x^(n-1) y^1 + C(n, 2)x^(n-2) y^2 + ... + C(n, n-1)x^1 y^(n-1) + C(n, n)x^0 y^n
Where C(n, k) is the binomial coefficient, given by:
C(n, k) = n! / (k!(n-k)!)
In the case of (x + 2y + z)^n, the coefficients will be found by replacing x with 1, y with 2, and z with 1. Therefore, the expansion becomes:
(1 + 2(2y) + 1)^n = (1 + 4y + 1)^n
Now we can apply the Binomial Theorem to find the coefficients. The sum of the coefficients will be the sum of the terms in the expansion.
Applying the Binomial Theorem:
Using the Binomial Theorem, the expansion of (1 + 4y + 1)^n can be written as:
(1 + 4y + 1)^n = C(n, 0)(1)^n (4y)^0 + C(n, 1)(1)^(n-1) (4y)^1 + C(n, 2)(1)^(n-2) (4y)^2 + ... + C(n, n-1)(1)^1 (4y)^(n-1) + C(n, n)(1)^0 (4y)^n
Simplifying this expression, we get:
(1 + 4y + 1)^n = C(n, 0) + 4C(n, 1)y + 6C(n, 2)(4y)^2 + ... + nC(n, n-1)(4y)^(n-1) + C(n, n)(4y)^n
The sum of the coefficients will be the sum of the terms in this expansion.
Calculating the Sum of the Coefficients:
To calculate the sum of the coefficients, we need to sum up all the terms in the expansion.
The sum of the coefficients can be written as:
C(n, 0) + 4C(n, 1) + 6C(n, 2) + ... + nC(n, n-1) + C(n, n)
Each term in this sum is a binomial coefficient multiplied by a constant factor.
Conclusion:
In general, the sum of the coefficients in the expansion of (x + 2y + z)^n is not equal to any of the given options (a, b, c). Therefore, the correct answer is option D, "none of these".
To find the sum of coefficients in the expansion of (x + 2y + z)^n, we can use the Binomial Theorem.
The Binomial Theorem states that for any positive integer n, the expansion of (x + y)^n can be written as:
(x + y)^n = C(n, 0)x^n y^0 + C(n, 1)x^(n-1) y^1 + C(n, 2)x^(n-2) y^2 + ... + C(n, n-1)x^1 y^(n-1) + C(n, n)x^0 y^n
Where C(n, k) is the binomial coefficient, given by:
C(n, k) = n! / (k!(n-k)!)
In the case of (x + 2y + z)^n, the coefficients will be found by replacing x with 1, y with 2, and z with 1. Therefore, the expansion becomes:
(1 + 2(2y) + 1)^n = (1 + 4y + 1)^n
Now we can apply the Binomial Theorem to find the coefficients. The sum of the coefficients will be the sum of the terms in the expansion.
Applying the Binomial Theorem:
Using the Binomial Theorem, the expansion of (1 + 4y + 1)^n can be written as:
(1 + 4y + 1)^n = C(n, 0)(1)^n (4y)^0 + C(n, 1)(1)^(n-1) (4y)^1 + C(n, 2)(1)^(n-2) (4y)^2 + ... + C(n, n-1)(1)^1 (4y)^(n-1) + C(n, n)(1)^0 (4y)^n
Simplifying this expression, we get:
(1 + 4y + 1)^n = C(n, 0) + 4C(n, 1)y + 6C(n, 2)(4y)^2 + ... + nC(n, n-1)(4y)^(n-1) + C(n, n)(4y)^n
The sum of the coefficients will be the sum of the terms in this expansion.
Calculating the Sum of the Coefficients:
To calculate the sum of the coefficients, we need to sum up all the terms in the expansion.
The sum of the coefficients can be written as:
C(n, 0) + 4C(n, 1) + 6C(n, 2) + ... + nC(n, n-1) + C(n, n)
Each term in this sum is a binomial coefficient multiplied by a constant factor.
Conclusion:
In general, the sum of the coefficients in the expansion of (x + 2y + z)^n is not equal to any of the given options (a, b, c). Therefore, the correct answer is option D, "none of these".
5th term from the end in the expansion of 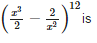
- a)7920x4
- b)−7920x4
- c)7920x−4
- d)−7920x−4
Correct answer is option 'C'. Can you explain this answer?
5th term from the end in the expansion of 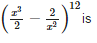
a)
7920x4
b)
−7920x4
c)
7920x−4
d)
−7920x−4
|
|
Akanksha Reddy answered |
5th term in the expansion of (x2/2 − 2/x2)12 is
Tr+ 1= nCr xr* y(n−r)
T5 = 12C4[(x2/2)4 (-2/x2)8]
= (12! * x8 * 28)/ (4! * 8! *24 * x16)
= 7920x−4
Tr+ 1= nCr xr* y(n−r)
T5 = 12C4[(x2/2)4 (-2/x2)8]
= (12! * x8 * 28)/ (4! * 8! *24 * x16)
= 7920x−4
The coefficient of x99 in (x+1)(x+3)(x+5)………..(x+199) is- a)1.3.5…………..199
- b)1+3+5+……….+199
- c)1+2+3+………+99
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The coefficient of x99 in (x+1)(x+3)(x+5)………..(x+199) is
a)
1.3.5…………..199
b)
1+3+5+……….+199
c)
1+2+3+………+99
d)
none of these

|
Avantika Joshi answered |
Method to Solve:
Max power of x is 100
So x^99 is nothing but sum of the roots of that equation
So which will be equal to -(1+3+5…+199)
The coefficients of xn in the expansion of (1+2x + 3x2 + ........)1/2 is - a)1
- b)n
- c)n+1
- d)-1
Correct answer is option 'A'. Can you explain this answer?
The coefficients of xn in the expansion of (1+2x + 3x2 + ........)1/2 is
a)
1
b)
n
c)
n+1
d)
-1
|
|
Aarya Rane answered |
To find the coefficients of xn in the expansion of (1 + 2x + 3x^2 + ...)^1/2, we can use the binomial theorem. The binomial theorem states that for any real number a and b and any positive integer n, the expansion of (a + b)^n can be written as:
(a + b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + C(n, 2) * a^(n-2) * b^2 + ... + C(n, n-1) * a^1 * b^(n-1) + C(n, n) * a^0 * b^n
where C(n, r) is the binomial coefficient, also called "n choose r", and is given by the formula:
C(n, r) = n! / (r! * (n-r)!)
In the given expression (1 + 2x + 3x^2 + ...)^1/2, we have a = 1 and b = 2x + 3x^2 + ... Therefore, applying the binomial theorem, the expansion becomes:
(1 + 2x + 3x^2 + ...)^1/2 = C(1/2, 0) * 1^(1/2) * (2x + 3x^2 + ...)^0 + C(1/2, 1) * 1^(1/2 - 1) * (2x + 3x^2 + ...)^1/2 + ...
Simplifying this expression, we find that the coefficient of xn is given by:
C(1/2, n) * 1^(1/2 - n) * (2x + 3x^2 + ...)^n/2
Since C(1/2, n) = 1 for all values of n, and 1^(1/2 - n) = 1, the coefficient of xn simplifies to:
(2x + 3x^2 + ...)^n/2
From this, we can see that the coefficient of xn is simply the expression (2x + 3x^2 + ...)^n/2. Since this expression does not depend on n, the coefficient of xn is constant and equal to 1.
Therefore, the correct answer is option A) 1.
(a + b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + C(n, 2) * a^(n-2) * b^2 + ... + C(n, n-1) * a^1 * b^(n-1) + C(n, n) * a^0 * b^n
where C(n, r) is the binomial coefficient, also called "n choose r", and is given by the formula:
C(n, r) = n! / (r! * (n-r)!)
In the given expression (1 + 2x + 3x^2 + ...)^1/2, we have a = 1 and b = 2x + 3x^2 + ... Therefore, applying the binomial theorem, the expansion becomes:
(1 + 2x + 3x^2 + ...)^1/2 = C(1/2, 0) * 1^(1/2) * (2x + 3x^2 + ...)^0 + C(1/2, 1) * 1^(1/2 - 1) * (2x + 3x^2 + ...)^1/2 + ...
Simplifying this expression, we find that the coefficient of xn is given by:
C(1/2, n) * 1^(1/2 - n) * (2x + 3x^2 + ...)^n/2
Since C(1/2, n) = 1 for all values of n, and 1^(1/2 - n) = 1, the coefficient of xn simplifies to:
(2x + 3x^2 + ...)^n/2
From this, we can see that the coefficient of xn is simply the expression (2x + 3x^2 + ...)^n/2. Since this expression does not depend on n, the coefficient of xn is constant and equal to 1.
Therefore, the correct answer is option A) 1.
In a binomial expansion with power 13- a)one of the middle term is the 7th term
- b)the middle term is the average of the 6th and the 7th terms.
- c)the middle term is obtained by subtracting the 6th term from the 7th term.
- d)there are two middle terms, 6th and 7th
Correct answer is option 'A'. Can you explain this answer?
In a binomial expansion with power 13
a)
one of the middle term is the 7th term
b)
the middle term is the average of the 6th and the 7th terms.
c)
the middle term is obtained by subtracting the 6th term from the 7th term.
d)
there are two middle terms, 6th and 7th
|
|
Lavanya Menon answered |

Chapter doubts & questions for Binomial Theorem & its Simple Applications - Mathematics (Maths) for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Binomial Theorem & its Simple Applications - Mathematics (Maths) for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

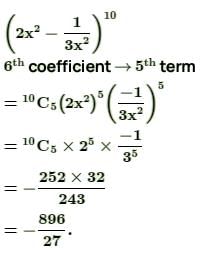


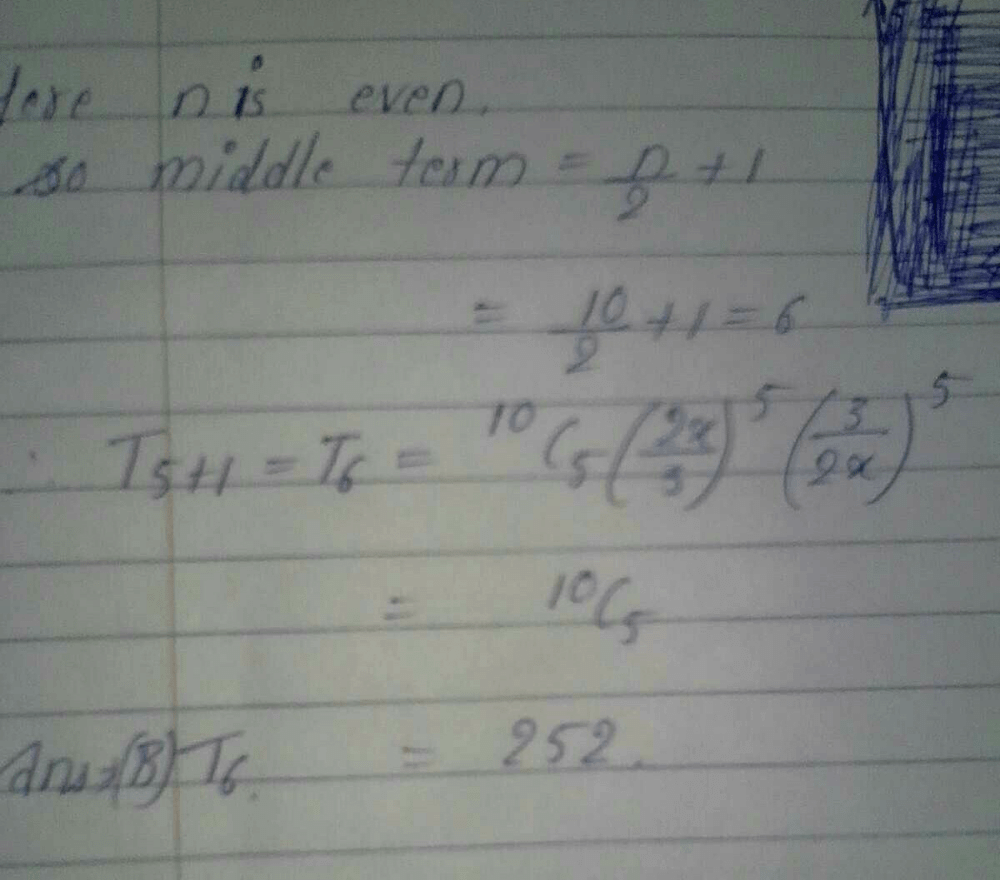



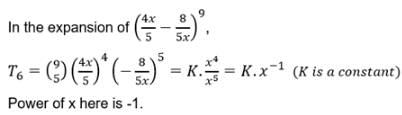



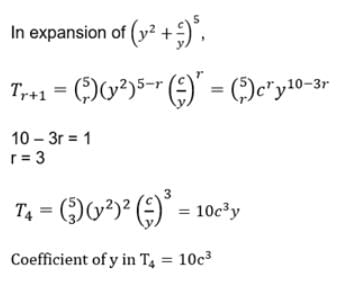


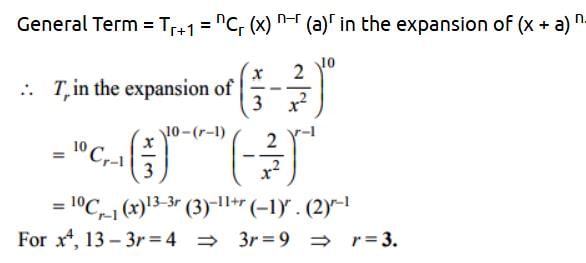
 + ........, then z2 + 2z is equal to
+ ........, then z2 + 2z is equal to







