All Exams >
Computer Science Engineering (CSE) >
Programming and Data Structures >
All Questions
All questions of Graphs for Computer Science Engineering (CSE) Exam
If we want to search any name in the phone directory , which is the most efficient data structure?- a)Binary search Tree
- b)Balanced BST
- c)Trie
- d)Linked list
Correct answer is option 'C'. Can you explain this answer?
If we want to search any name in the phone directory , which is the most efficient data structure?
a)
Binary search Tree
b)
Balanced BST
c)
Trie
d)
Linked list
|
Ravi Singh answered |
In BST and balanced BST searching takes time in order of mlogn , where m is the maximum string length and n is the number of strings in tree . But searching in Trie will take O(m) time.
Hence , option C is the correct answer.
Hence , option C is the correct answer.
You are given a graph containing n vertices and m edges and given that the graph doesn’t contain cycle of odd length. Time Complexity of the best known algorithm to find out whether the graph is bipartite or not is ?- a)O(m+n)
- b)O(1)
- c)O(mn)
- d)O(n2)
Correct answer is option 'B'. Can you explain this answer?
You are given a graph containing n vertices and m edges and given that the graph doesn’t contain cycle of odd length. Time Complexity of the best known algorithm to find out whether the graph is bipartite or not is ?
a)
O(m+n)
b)
O(1)
c)
O(mn)
d)
O(n2)
|
Neha Mishra answered |
Is connected. You are also given a starting vertex s. Implement a function to perform a depth-first search (DFS) on the graph starting from the given vertex.
Here's the Python code to perform DFS on a given graph:
```python
def dfs(graph, start):
visited = set() # Set to keep track of visited vertices
stack = [start] # Stack to store the vertices to be visited
while stack:
vertex = stack.pop() # Pop the top vertex from the stack
if vertex not in visited:
visited.add(vertex) # Mark the vertex as visited
for neighbor in graph[vertex]:
stack.append(neighbor) # Add the neighbors of the current vertex to the stack
return visited
```
In this code, the `graph` is represented as a dictionary where the keys are the vertices and the values are lists of neighbors. The `start` parameter specifies the starting vertex for the DFS.
The algorithm starts by initializing an empty set `visited` to keep track of the visited vertices and a stack `stack` to store the vertices to be visited. The starting vertex is added to the stack.
The algorithm then enters a loop that continues until the stack is empty. In each iteration, it pops the top vertex from the stack. If the vertex has not been visited before, it is added to the `visited` set. Then, for each neighbor of the current vertex, it is added to the stack.
Finally, the algorithm returns the set of visited vertices.
To use this function, you can call it with your graph and the starting vertex as arguments:
```python
graph = {
'A': ['B', 'C'],
'B': ['A', 'D'],
'C': ['A', 'D', 'E'],
'D': ['B', 'C', 'E'],
'E': ['C', 'D']
}
start_vertex = 'A'
result = dfs(graph, start_vertex)
print(result)
```
This will output the set of visited vertices during the DFS traversal.
Here's the Python code to perform DFS on a given graph:
```python
def dfs(graph, start):
visited = set() # Set to keep track of visited vertices
stack = [start] # Stack to store the vertices to be visited
while stack:
vertex = stack.pop() # Pop the top vertex from the stack
if vertex not in visited:
visited.add(vertex) # Mark the vertex as visited
for neighbor in graph[vertex]:
stack.append(neighbor) # Add the neighbors of the current vertex to the stack
return visited
```
In this code, the `graph` is represented as a dictionary where the keys are the vertices and the values are lists of neighbors. The `start` parameter specifies the starting vertex for the DFS.
The algorithm starts by initializing an empty set `visited` to keep track of the visited vertices and a stack `stack` to store the vertices to be visited. The starting vertex is added to the stack.
The algorithm then enters a loop that continues until the stack is empty. In each iteration, it pops the top vertex from the stack. If the vertex has not been visited before, it is added to the `visited` set. Then, for each neighbor of the current vertex, it is added to the stack.
Finally, the algorithm returns the set of visited vertices.
To use this function, you can call it with your graph and the starting vertex as arguments:
```python
graph = {
'A': ['B', 'C'],
'B': ['A', 'D'],
'C': ['A', 'D', 'E'],
'D': ['B', 'C', 'E'],
'E': ['C', 'D']
}
start_vertex = 'A'
result = dfs(graph, start_vertex)
print(result)
```
This will output the set of visited vertices during the DFS traversal.
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is- a)k
- b)k + 1
- c)n – k – 1
- d)n – k
Correct answer is option 'D'. Can you explain this answer?
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is
a)
k
b)
k + 1
c)
n – k – 1
d)
n – k
|
|
Ravi Singh answered |
Tree edges are the edges that are part of DFS tree. If there are x tree edges in a tree, then x+1 vertices in the tree.
The output of DFS is a forest if the graph is disconnected. Let us see below simple example where graph is disconnected.
The output of DFS is a forest if the graph is disconnected. Let us see below simple example where graph is disconnected.
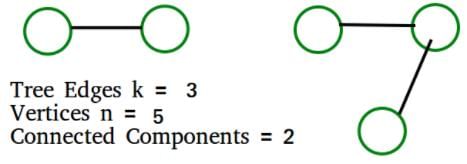
The above example matches with D option
More Examples:
1) All vertices of Graph are connected. k must be n-1. We get number of connected components = n- k = n – (n-1) = 1
2) No vertex is connected. k must be 0. We get number of connected components = n- k = n – 0 = n
1) All vertices of Graph are connected. k must be n-1. We get number of connected components = n- k = n – (n-1) = 1
2) No vertex is connected. k must be 0. We get number of connected components = n- k = n – 0 = n
An advantage of chained hash table (external hashing) over the open addressing scheme is- a)Worst case complexity of search operations is less
- b)Space used is less
- c)Deletion is easier
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
An advantage of chained hash table (external hashing) over the open addressing scheme is
a)
Worst case complexity of search operations is less
b)
Space used is less
c)
Deletion is easier
d)
None of the above
|
Pritam Chatterjee answered |
Deletion is easier, because chained hash table uses linked list
Consider a hash function that distributes keys uniformly. The hash table size is 20. After hashing of how many keys will the probability that any new key hashed collides with an existing one exceed 0.5.- a)5
- b)6
- c)7
- d)10
Correct answer is option 'B'. Can you explain this answer?
Consider a hash function that distributes keys uniformly. The hash table size is 20. After hashing of how many keys will the probability that any new key hashed collides with an existing one exceed 0.5.
a)
5
b)
6
c)
7
d)
10
|
Swara Basak answered |
Probability of hashed 1st key = 20/20 = 1
Probability of hashed 2nd key with no collision = 19/20
Probability of hashed 3rd key with no collision = 18/20
Similarly, probability of hashed rth key with no collision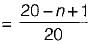
According to question: Probability of hashed (n + 1)th key with collision > 0.5 Probability of hashed (n + 1)th key with collision
P(C) = 1 - P (Till (nth) no collision)
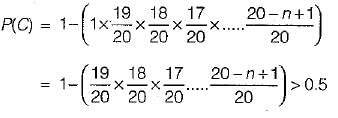
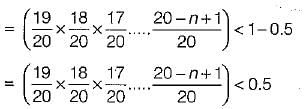
19 x 18 x 17 .... x 20 - n + 1 < 0.5 x (20)n-1
By put n = 5, we get 0.581, for n = 6, we get 0.436, which satisfies the equation.
Probability of hashed 2nd key with no collision = 19/20
Probability of hashed 3rd key with no collision = 18/20
Similarly, probability of hashed rth key with no collision
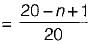
According to question: Probability of hashed (n + 1)th key with collision > 0.5 Probability of hashed (n + 1)th key with collision
P(C) = 1 - P (Till (nth) no collision)
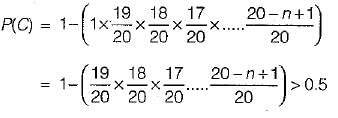
19 x 18 x 17 .... x 20 - n + 1 < 0.5 x (20)n-1
By put n = 5, we get 0.581, for n = 6, we get 0.436, which satisfies the equation.
How many real links are required to store a sparse matrix of 10 rows, 10 columns, and 15 non-zero entries, (Pick up the closest answer)- a)15
- b)20
- c)50
- d)100
Correct answer is option 'A'. Can you explain this answer?
How many real links are required to store a sparse matrix of 10 rows, 10 columns, and 15 non-zero entries, (Pick up the closest answer)
a)
15
b)
20
c)
50
d)
100
|
Ipsita Dasgupta answered |
Matrix of 10 rows and 10 columns can have m axim um 1 0 x 1 0 = 100 entries. S ince only 15 non-zero entries are present, so number of real link will be 15 only.
Assuming undirected graph.
Assuming undirected graph.
How many undirected graphs (not necessarily connected) can be constructed out of a given set V= {V 1, V 2,…V n} of n vertices ?- a)n(n-l)/2
- b)2n
- c)n!
- d)2(n(n-1)/2)
Correct answer is option 'D'. Can you explain this answer?
How many undirected graphs (not necessarily connected) can be constructed out of a given set V= {V 1, V 2,…V n} of n vertices ?
a)
n(n-l)/2
b)
2n
c)
n!
d)
2(n(n-1)/2)
|
|
Gitanjali Singh answered |
V n } of n vertices?
The total number of undirected graphs that can be constructed out of a given set V of n vertices is 2^(n*(n-1)/2). This is because each edge can either be present or absent, and there are (n choose 2) = n*(n-1)/2 possible edges in a graph with n vertices. Therefore, the total number of possible graphs is 2^(n*(n-1)/2).
The total number of undirected graphs that can be constructed out of a given set V of n vertices is 2^(n*(n-1)/2). This is because each edge can either be present or absent, and there are (n choose 2) = n*(n-1)/2 possible edges in a graph with n vertices. Therefore, the total number of possible graphs is 2^(n*(n-1)/2).
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.- a)O(n)
- b)O(m+n)
- c)O(n2)
- d)O(mn)
Correct answer is option 'C'. Can you explain this answer?
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
a)
O(n)
b)
O(m+n)
c)
O(n2)
d)
O(mn)
|
Sanya Agarwal answered |
Depth First Search of a graph takes O(m+n) time when the graph is represented using adjacency list.
In adjacency matrix representation, graph is represented as an “n x n” matrix. To do DFS, for every vertex, we traverse the row corresponding to that vertex to find all adjacent vertices (In adjacency list representation we traverse only the adjacent vertices of the vertex). Therefore time complexity becomes O(n2)
In an adjacency list representation of an undirected simple graph G = (V, E), each edge (u, v) has two adjacency list entries: [v] in the adjacency list of u, and [u] in the adjacency list of v. These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If |E| = m and |V | = n, and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?- a)Θ(n2)
- b)Θ(m+n)
- c)Θ(m2)
- d)Θ(n4)
Correct answer is option 'B'. Can you explain this answer?
In an adjacency list representation of an undirected simple graph G = (V, E), each edge (u, v) has two adjacency list entries: [v] in the adjacency list of u, and [u] in the adjacency list of v. These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If |E| = m and |V | = n, and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?
a)
Θ(n2)
b)
Θ(m+n)
c)
Θ(m2)
d)
Θ(n4)
|
|
Ravi Singh answered |
First you need to find twins of each node. You can do this using level order traversal (i.e., BFS) once. Time complexity of BFS is Θ(m +n).
And you have to use linked list for representation which is extra space (but memory size is not a constraint here).
Final, time complexity is Θ(m + n) to set twin pointer.
And you have to use linked list for representation which is extra space (but memory size is not a constraint here).
Final, time complexity is Θ(m + n) to set twin pointer.
Which of the following data structure is useful in traversing a given graph by breadth first search?- a)Stack
- b)List
- c)Queue
- d)None of the above.
Correct answer is option 'C'. Can you explain this answer?
Which of the following data structure is useful in traversing a given graph by breadth first search?
a)
Stack
b)
List
c)
Queue
d)
None of the above.
|
Harsh Sen answered |
Breadth First Search (BFS) Algorithm
The Breadth First Search (BFS) algorithm is used to traverse a graph, starting from a source vertex, in a breadth-first manner. It visits all the vertices at the same level before moving to the next level.
Data Structures Used in BFS
BFS algorithm uses a queue data structure to keep track of the vertices that have been visited but not yet explored. The queue is used to maintain the order in which the vertices are visited so that the algorithm can visit them in a breadth-first manner.
Why Queue is used in BFS?
A queue is used in BFS because it follows the First In First Out (FIFO) principle, which makes it easy to maintain the order of visited vertices. The algorithm visits the vertices in the order in which they were added to the queue. This helps to ensure that the algorithm visits all the vertices at the same level before moving to the next level.
Conclusion
In conclusion, the correct answer to the given question is option 'C'. A queue data structure is useful in traversing a given graph by breadth-first search because it maintains the order in which the vertices are visited, making it easy to visit all the vertices at the same level before moving to the next level. It is important to understand the data structures used in BFS to effectively implement the algorithm.
The Breadth First Search (BFS) algorithm is used to traverse a graph, starting from a source vertex, in a breadth-first manner. It visits all the vertices at the same level before moving to the next level.
Data Structures Used in BFS
BFS algorithm uses a queue data structure to keep track of the vertices that have been visited but not yet explored. The queue is used to maintain the order in which the vertices are visited so that the algorithm can visit them in a breadth-first manner.
Why Queue is used in BFS?
A queue is used in BFS because it follows the First In First Out (FIFO) principle, which makes it easy to maintain the order of visited vertices. The algorithm visits the vertices in the order in which they were added to the queue. This helps to ensure that the algorithm visits all the vertices at the same level before moving to the next level.
Conclusion
In conclusion, the correct answer to the given question is option 'C'. A queue data structure is useful in traversing a given graph by breadth-first search because it maintains the order in which the vertices are visited, making it easy to visit all the vertices at the same level before moving to the next level. It is important to understand the data structures used in BFS to effectively implement the algorithm.
The number of edges in a regular graph of degree d and n vertices is- a)Maximum of n, d
- b)n + d
- c)nd
- d)nd/2
Correct answer is option 'D'. Can you explain this answer?
The number of edges in a regular graph of degree d and n vertices is
a)
Maximum of n, d
b)
n + d
c)
nd
d)
nd/2
|
Soumya Pillai answered |
In a regular graph, all the vertices will be of the same degree. Total degrees of all the vertices is nd. Each edge will be increasing the total degree by 2. So, totally nd/2 edges.
Which of the following statement(s) is TRUE?
I. A hash function takes a message of arbitrary length and generates a fixed length code.
II. A hash function takes a message of fixed length and generates a code of variable length.
III. A hash function may give the same hash value for distinct messages.- a)! only
- b)II and III only
- c)I and llI only
- d)II only
Correct answer is option 'C'. Can you explain this answer?
Which of the following statement(s) is TRUE?
I. A hash function takes a message of arbitrary length and generates a fixed length code.
II. A hash function takes a message of fixed length and generates a code of variable length.
III. A hash function may give the same hash value for distinct messages.
I. A hash function takes a message of arbitrary length and generates a fixed length code.
II. A hash function takes a message of fixed length and generates a code of variable length.
III. A hash function may give the same hash value for distinct messages.
a)
! only
b)
II and III only
c)
I and llI only
d)
II only
|
Prerna Joshi answered |
A hash function takes a message of arbitrary length and generates a fixed length code, by taking mod (some value).
A hash function may give the same hash value for distinct messages.
A hash function may give the same hash value for distinct messages.
Consider the hash table of size seven, with starting index zero, and a hash function (3x + 4) mod 7. Assuming the has table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using dosed hashing?
Note that - denotes an empty location in the table- a)8, 10
- b)1, 8, 10, -, -, 3
- c)1 , 3
- d)1,10, 8, 3
Correct answer is option 'B'. Can you explain this answer?
Consider the hash table of size seven, with starting index zero, and a hash function (3x + 4) mod 7. Assuming the has table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using dosed hashing?
Note that - denotes an empty location in the table
Note that - denotes an empty location in the table
a)
8, 10
b)
1, 8, 10, -, -, 3
c)
1 , 3
d)
1,10, 8, 3
|
|
Tejas Ghoshal answered |
Size of hash table = 7
h(x) = (3x + 4) mod 7
h(1) =. (3.1 + 4) mod 7 = 7 mod 7
= 0; insert at 0th location.
h(3) = (3.3 + 4) mod 7 = 13 mod 7
= 6; insert at 6th location
h(8) = (3.8 + 4) mod 7 = 28 mod 7
= 0; 0th position is already filled by element 3 so insert 8 at next free location which is 1st position
h(10) = (3.10 + 4) mod 7 = 34 mod 7 = 6
but 6th position is already filled with the element 3 so insert 10 at next free location which is 2nd position
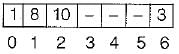
h(x) = (3x + 4) mod 7
h(1) =. (3.1 + 4) mod 7 = 7 mod 7
= 0; insert at 0th location.
h(3) = (3.3 + 4) mod 7 = 13 mod 7
= 6; insert at 6th location
h(8) = (3.8 + 4) mod 7 = 28 mod 7
= 0; 0th position is already filled by element 3 so insert 8 at next free location which is 1st position
h(10) = (3.10 + 4) mod 7 = 34 mod 7 = 6
but 6th position is already filled with the element 3 so insert 10 at next free location which is 2nd position
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively, in G. lf u is visited before v during the breadth-first traversal, which of the following statements is correct?- a)d(r, u) < d (r, v)
- b)d(r, u) > d(r, v)
- c)d(r, u) <= d (r, v)
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively, in G. lf u is visited before v during the breadth-first traversal, which of the following statements is correct?
a)
d(r, u) < d (r, v)
b)
d(r, u) > d(r, v)
c)
d(r, u) <= d (r, v)
d)
None of the above
|
Rounak Chavan answered |
B) d(r, u) < d(r,="" v)="" d(r,="" />
Consider a hash table with 9 slots. The hash function is h(k) = k mod 9. The collisions are resolved by chaining. The following 9 keys are inserted in the order:
5, 28, 19, 15, 20, 33, 12, 17, 10
The maximum, minimum, and average chain lengths in the hash table, respectively, are- a)3, 0, and 1
- b)3, 3, and 3
- c)4, 0, and 1
- d)3, 0, and 2
Correct answer is option 'A'. Can you explain this answer?
Consider a hash table with 9 slots. The hash function is h(k) = k mod 9. The collisions are resolved by chaining. The following 9 keys are inserted in the order:
5, 28, 19, 15, 20, 33, 12, 17, 10
The maximum, minimum, and average chain lengths in the hash table, respectively, are
5, 28, 19, 15, 20, 33, 12, 17, 10
The maximum, minimum, and average chain lengths in the hash table, respectively, are
a)
3, 0, and 1
b)
3, 3, and 3
c)
4, 0, and 1
d)
3, 0, and 2
|
|
Advait Shah answered |
Which of the following according to you is incorrect?- a)Trie is also known as prefix tree
- b)Trie requires less storage space than hashing
- c)Trie allows listing of all the words with same prefix
- d)Tries are collision free
Correct answer is option 'B'. Can you explain this answer?
Which of the following according to you is incorrect?
a)
Trie is also known as prefix tree
b)
Trie requires less storage space than hashing
c)
Trie allows listing of all the words with same prefix
d)
Tries are collision free
|
|
Sanya Agarwal answered |
Both the hashing and the trie provides searching in the linear time. But trie requires extra space for storage and it is collision free. And trie allows finding all the strings with same prefix, so it is also called prefix tree.
Hence, option B is the correct option.
Hence, option B is the correct option.
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity.- a)θ(n)
- b)θ(m)
- c)θ(m + n)
- d)θ(mn)
Correct answer is option 'C'. Can you explain this answer?
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity.
a)
θ(n)
b)
θ(m)
c)
θ(m + n)
d)
θ(mn)
|
|
Sanya Agarwal answered |
Connected components can be found in O(m + n) using Tarjan’s algorithm. Once we have connected components, we can count them.
A hash table contains 10 buckets and uses linear probing to resolve collisions. The key values are integers and the hash function used is key % 10. If the values 43,165,62,123,142 are inserted in the table, in what location would the key value 142 be inserted?- a)2
- b)3
- c)4
- d)6
Correct answer is option 'D'. Can you explain this answer?
A hash table contains 10 buckets and uses linear probing to resolve collisions. The key values are integers and the hash function used is key % 10. If the values 43,165,62,123,142 are inserted in the table, in what location would the key value 142 be inserted?
a)
2
b)
3
c)
4
d)
6
|
Alok Desai answered |
43,165,62,123 and 142 are inserted in the table. 43 mapped to location 3,165 mapped to location 5, 62 mapped to location 2, 123 mapped to location 3 (occupied), so it goes to location 4, 142 mapped to location 2 (occupied), 3, 4, and 5 are also probes, so it goes to location 6.
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?- a)1
- b)2
- c)3
- d)n
Correct answer is option 'C'. Can you explain this answer?
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?
a)
1
b)
2
c)
3
d)
n
|
|
Kiran Chakraborty answered |
If a graph contain n vertices and n edges and it is simple connected graph then it forms a cycle. Atleast 3 vertices should participate hence the number of spanning trees will be atleast 3.
The number of binary trees with 3 nodes which when traversed in post-order gives the sequence A, B, C is- a)3
- b)9
- c)7
- d)5
Correct answer is option 'D'. Can you explain this answer?
The number of binary trees with 3 nodes which when traversed in post-order gives the sequence A, B, C is
a)
3
b)
9
c)
7
d)
5
|
|
Snehal Desai answered |
The number of binary trees with 3 nodes is 5. The 5 possible binary trees with 3 nodes can be constructed by connecting the 3 nodes (A, B, and C) in different ways.
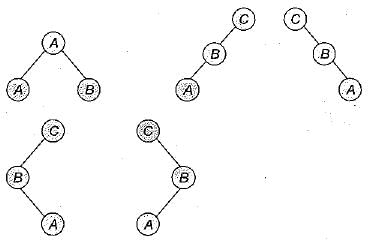
The post-order traversal of a binary tree visits the left subtree, right subtree and then the root node. The possible post-order traversals of these 5 binary trees are:
● ABC (A is the root, B and C are the left and right subtrees respectively)
● ACB (A is the root, C is the left subtree and B is the right subtree)
● BAC (B is the root, A is the left subtree and C is the right subtree)
● BCA (B is the root, C is the left subtree and A is the right subtree)
● CAB (C is the root, A is the left subtree and B is the right subtree)
It's important to note that these are not unique trees, just the order of traversal is different
Number of binary tree with 3 nodes with post order A, B, C
So there are 5 binary tree possible.
So there are 5 binary tree possible.
The minimum number of colors needed to color a graph having n (> 3) vertices and 2 edges is- a)4
- b)3
- c)2
- d)1
Correct answer is option 'C'. Can you explain this answer?
The minimum number of colors needed to color a graph having n (> 3) vertices and 2 edges is
a)
4
b)
3
c)
2
d)
1
|
Harshitha Sarkar answered |
As we observe that the graph is disconnected
n > 3 (number of vertices)
e = 2 (number of edges)
For example : n = 4
for this only 2 colors are sufficient.
n > 3 (number of vertices)
e = 2 (number of edges)
For example : n = 4
for this only 2 colors are sufficient.
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?- a)1/8
- b)1
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?
a)
1/8
b)
1
c)
7
d)
8
|
|
Sanya Agarwal answered |
A cycle of length 3 can be formed with 3 vertices. There can be total 8C3 ways to pick 3 vertices from 8. The probability that there is an edge between two vertices is 1/2. So expected number of unordered cycles of length 3 = (8C3)*(1/2)3 = 7
The cyclomatic complexity of the flow graph of a program provides - a)an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
- b)a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
- c)an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
- d)a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
Correct answer is option 'C'. Can you explain this answer?
The cyclomatic complexity of the flow graph of a program provides
a)
an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
b)
a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
c)
an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
d)
a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
|
|
Parth Sen answered |
Explanation:
Introduction:
Cyclomatic complexity is a software metric used to measure the complexity of a program. It is calculated based on the number of linearly independent paths through a program's source code.
Upper Bound for the Number of Tests:
- The cyclomatic complexity of the flow graph of a program provides an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once.
- This means that the cyclomatic complexity gives us an idea of the maximum number of tests needed to cover all possible paths through the program.
Ensuring All Statements are Executed at Least Once:
- A higher cyclomatic complexity indicates a program with more complex control flow, which means there are more possible paths through the program.
- To ensure that all statements have been executed at least once, we need to test each path through the program.
- Therefore, the cyclomatic complexity gives us an upper bound on the number of tests needed to achieve this coverage.
Conclusion:
- In conclusion, the cyclomatic complexity of a program provides an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once. This metric helps in understanding the testing effort required to achieve full coverage of the program's control flow.
Introduction:
Cyclomatic complexity is a software metric used to measure the complexity of a program. It is calculated based on the number of linearly independent paths through a program's source code.
Upper Bound for the Number of Tests:
- The cyclomatic complexity of the flow graph of a program provides an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once.
- This means that the cyclomatic complexity gives us an idea of the maximum number of tests needed to cover all possible paths through the program.
Ensuring All Statements are Executed at Least Once:
- A higher cyclomatic complexity indicates a program with more complex control flow, which means there are more possible paths through the program.
- To ensure that all statements have been executed at least once, we need to test each path through the program.
- Therefore, the cyclomatic complexity gives us an upper bound on the number of tests needed to achieve this coverage.
Conclusion:
- In conclusion, the cyclomatic complexity of a program provides an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once. This metric helps in understanding the testing effort required to achieve full coverage of the program's control flow.
Let G be a simple graph with 20 vertices and 8 components. If we delete a vertex in G, then number of components in G should lie between ____.- a)8 and 20
- b)8 and 19
- c)7 and 19
- d)7 and 20
Correct answer is option 'C'. Can you explain this answer?
Let G be a simple graph with 20 vertices and 8 components. If we delete a vertex in G, then number of components in G should lie between ____.
a)
8 and 20
b)
8 and 19
c)
7 and 19
d)
7 and 20
|
Gitanjali Datta answered |
To understand why the number of components in G should lie between 7 and 19 when a vertex is deleted, let's break down the problem step by step.
1. Understanding the Terminology:
- A graph is a collection of vertices (or nodes) and edges that connect these vertices.
- A simple graph is an undirected graph with no self-loops or multiple edges between the same pair of vertices.
- Components in a graph refer to the subgraphs that are disconnected from each other. In other words, they are the separate clusters or groups of vertices within the graph that are not connected to any other group.
2. Given Information:
- G is a simple graph with 20 vertices.
- G has 8 components.
3. Initial Scenario:
- Since G has 8 components, it means that there are 8 separate clusters of vertices that are disconnected from each other.
- Let's assume these components as C1, C2, C3, ..., C8.
4. Deleting a Vertex:
- Now, if we delete a vertex from G, we need to consider the possible scenarios that can arise.
- Deleting a vertex from a component can either:
a) Disconnect the component into smaller components, or
b) Leave the component as it is if the deleted vertex is not a part of that component.
5. Worst-case Scenario:
- To find the minimum and maximum number of components that can arise after deleting a vertex, we consider the worst-case scenario.
- The worst-case scenario occurs when the deleted vertex is a part of every component.
- In this case, deleting the vertex will disconnect all the components and create 8 new components.
- So, the minimum number of components after deleting a vertex is 8.
6. Best-case Scenario:
- To find the maximum number of components that can arise after deleting a vertex, we consider the best-case scenario.
- The best-case scenario occurs when the deleted vertex is not a part of any component.
- In this case, deleting the vertex will not affect the existing components, and the number of components will remain the same.
- So, the maximum number of components after deleting a vertex is 8.
7. Conclusion:
- Therefore, after deleting a vertex in G, the number of components in G should lie between 8 (minimum) and 8 (maximum).
- In other words, the number of components in G should be exactly 8, regardless of which vertex is deleted.
Hence, the correct answer is option 'C': 7 and 19.
1. Understanding the Terminology:
- A graph is a collection of vertices (or nodes) and edges that connect these vertices.
- A simple graph is an undirected graph with no self-loops or multiple edges between the same pair of vertices.
- Components in a graph refer to the subgraphs that are disconnected from each other. In other words, they are the separate clusters or groups of vertices within the graph that are not connected to any other group.
2. Given Information:
- G is a simple graph with 20 vertices.
- G has 8 components.
3. Initial Scenario:
- Since G has 8 components, it means that there are 8 separate clusters of vertices that are disconnected from each other.
- Let's assume these components as C1, C2, C3, ..., C8.
4. Deleting a Vertex:
- Now, if we delete a vertex from G, we need to consider the possible scenarios that can arise.
- Deleting a vertex from a component can either:
a) Disconnect the component into smaller components, or
b) Leave the component as it is if the deleted vertex is not a part of that component.
5. Worst-case Scenario:
- To find the minimum and maximum number of components that can arise after deleting a vertex, we consider the worst-case scenario.
- The worst-case scenario occurs when the deleted vertex is a part of every component.
- In this case, deleting the vertex will disconnect all the components and create 8 new components.
- So, the minimum number of components after deleting a vertex is 8.
6. Best-case Scenario:
- To find the maximum number of components that can arise after deleting a vertex, we consider the best-case scenario.
- The best-case scenario occurs when the deleted vertex is not a part of any component.
- In this case, deleting the vertex will not affect the existing components, and the number of components will remain the same.
- So, the maximum number of components after deleting a vertex is 8.
7. Conclusion:
- Therefore, after deleting a vertex in G, the number of components in G should lie between 8 (minimum) and 8 (maximum).
- In other words, the number of components in G should be exactly 8, regardless of which vertex is deleted.
Hence, the correct answer is option 'C': 7 and 19.
Trie is also known as _____.- a)Treap
- b)Binomial Tree
- c)2-3 Tree
- d)Digital Tree
Correct answer is option 'D'. Can you explain this answer?
Trie is also known as _____.
a)
Treap
b)
Binomial Tree
c)
2-3 Tree
d)
Digital Tree
|
|
Mohit Unni answered |
Trie Data Structure:
Trie is a tree-based data structure used to store and retrieve strings efficiently. It is also known as a digital tree, radix tree, or prefix tree. A trie is a type of search tree where each node represents a single character of a string. It is widely used in text processing and pattern matching applications.
Features of Trie:
- A trie is a tree-like data structure that stores strings.
- Each node in the trie represents a single character of a string.
- The root node represents an empty string.
- The children of a node represent the next character in the string.
- The leaf nodes represent the complete strings.
Applications of Trie:
- Spell checking
- Auto-completion
- IP routing
- Text processing
- Pattern matching
Advantages of Trie:
- Efficient searching and retrieval of strings.
- It has a predictable time complexity of O(k), where k is the length of the string.
- It can handle a large number of strings efficiently.
Disadvantages of Trie:
- It uses a lot of memory due to the large number of nodes.
- It can be slow for very long strings.
- It is not suitable for storing large amounts of data that does not have a common prefix.
Conclusion:
Trie is a powerful data structure that is widely used in text processing and pattern matching applications. It provides efficient searching and retrieval of strings and has a predictable time complexity. However, it uses a lot of memory and is not suitable for storing large amounts of data that does not have a common prefix.
Trie is a tree-based data structure used to store and retrieve strings efficiently. It is also known as a digital tree, radix tree, or prefix tree. A trie is a type of search tree where each node represents a single character of a string. It is widely used in text processing and pattern matching applications.
Features of Trie:
- A trie is a tree-like data structure that stores strings.
- Each node in the trie represents a single character of a string.
- The root node represents an empty string.
- The children of a node represent the next character in the string.
- The leaf nodes represent the complete strings.
Applications of Trie:
- Spell checking
- Auto-completion
- IP routing
- Text processing
- Pattern matching
Advantages of Trie:
- Efficient searching and retrieval of strings.
- It has a predictable time complexity of O(k), where k is the length of the string.
- It can handle a large number of strings efficiently.
Disadvantages of Trie:
- It uses a lot of memory due to the large number of nodes.
- It can be slow for very long strings.
- It is not suitable for storing large amounts of data that does not have a common prefix.
Conclusion:
Trie is a powerful data structure that is widely used in text processing and pattern matching applications. It provides efficient searching and retrieval of strings and has a predictable time complexity. However, it uses a lot of memory and is not suitable for storing large amounts of data that does not have a common prefix.
Let G be a directed graph whose vertex set is the set of numbers from 1 to 100. There is an edge from a vertex i to a vertex j iff either j = i + 1 or j = 3i. The minimum number of edges in a path in G from vertex 1 to vertex 100 is .- a)4
- b)7
- c)23
- d)99
Correct answer is option 'B'. Can you explain this answer?
Let G be a directed graph whose vertex set is the set of numbers from 1 to 100. There is an edge from a vertex i to a vertex j iff either j = i + 1 or j = 3i. The minimum number of edges in a path in G from vertex 1 to vertex 100 is .
a)
4
b)
7
c)
23
d)
99
|
|
Abhijeet Mehta answered |
In graph G there is a directed edge between i to j when j is either i + 1 or 3i.
Since minimum value is finding, so we need to make edge which maximum difference in i and j here (99 - 33) = 66 is maximum. So 7 edges are needed.
Since minimum value is finding, so we need to make edge which maximum difference in i and j here (99 - 33) = 66 is maximum. So 7 edges are needed.
Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is- a)Θ(∣E∣ + ∣V∣)
- b)Θ(∣E∣.∣V∣)
- c)Θ(E∣ log ∣V∣)
- d)Θ(∣V∣)
Correct answer is option 'D'. Can you explain this answer?
Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is
a)
Θ(∣E∣ + ∣V∣)
b)
Θ(∣E∣.∣V∣)
c)
Θ(E∣ log ∣V∣)
d)
Θ(∣V∣)
|
|
Ipsita Patel answered |
Is added to G with weight w. In order to update the MST T, we can follow the following steps:
1. Add the edge (u, v) to G with weight w.
2. If the weight of (u, v) is greater than the weight of the maximum weight edge in T, then the MST T remains unchanged.
3. Otherwise, find the cycle C in T that is formed by adding the edge (u, v).
4. Find the maximum weight edge e in cycle C. Remove edge e from T.
5. Add the edge (u, v) to T.
6. Repeat steps 3-5 until there are no cycles formed by adding edges.
By following these steps, we can update the MST T in O(log^2(V)) time complexity, where V is the number of vertices in the graph. This is because finding the cycle and the maximum weight edge in the cycle can be done in O(log(V)) time using a union-find data structure.
Note: If the graph is not connected, we need to consider each connected component separately and update the MST for each component.
1. Add the edge (u, v) to G with weight w.
2. If the weight of (u, v) is greater than the weight of the maximum weight edge in T, then the MST T remains unchanged.
3. Otherwise, find the cycle C in T that is formed by adding the edge (u, v).
4. Find the maximum weight edge e in cycle C. Remove edge e from T.
5. Add the edge (u, v) to T.
6. Repeat steps 3-5 until there are no cycles formed by adding edges.
By following these steps, we can update the MST T in O(log^2(V)) time complexity, where V is the number of vertices in the graph. This is because finding the cycle and the maximum weight edge in the cycle can be done in O(log(V)) time using a union-find data structure.
Note: If the graph is not connected, we need to consider each connected component separately and update the MST for each component.
Let G be the graph with 100 vertices numbered 1 to 100. Two vertices i and j are adjacent iff |i−j|=8 or |i−j|=12. The number of connected components in G is- a)8
- b)4
- c)12
- d)25
Correct answer is option 'B'. Can you explain this answer?
Let G be the graph with 100 vertices numbered 1 to 100. Two vertices i and j are adjacent iff |i−j|=8 or |i−j|=12. The number of connected components in G is
a)
8
b)
4
c)
12
d)
25
|
Moumita Yadav answered |
The graph G is a complete graph on 100 vertices. In a complete graph, every pair of distinct vertices is adjacent, which means there is an edge between them.
Since there are 100 vertices in G, each vertex is adjacent to all other vertices. Therefore, for any pair of distinct vertices i and j, the statement |i-j| < 4="" is="" always="" true.="" 4="" is="" always="" />
Since there are 100 vertices in G, each vertex is adjacent to all other vertices. Therefore, for any pair of distinct vertices i and j, the statement |i-j| < 4="" is="" always="" true.="" 4="" is="" always="" />
Given the following input (4322,1334,1471,9679, 1989, 6171,6173, 4199) and the hash function x mod 10, which of the following statements are true?
1. 9679,1989,4199 hash to the same value
2. 1471,6171 hash to the same value
3. All elements hash to the same value
4. Each element hashes to a different value- a)1 only
- b)2 only
- c)1 and 2 only
- d)3 and 4 only
Correct answer is option 'C'. Can you explain this answer?
Given the following input (4322,1334,1471,9679, 1989, 6171,6173, 4199) and the hash function x mod 10, which of the following statements are true?
1. 9679,1989,4199 hash to the same value
2. 1471,6171 hash to the same value
3. All elements hash to the same value
4. Each element hashes to a different value
1. 9679,1989,4199 hash to the same value
2. 1471,6171 hash to the same value
3. All elements hash to the same value
4. Each element hashes to a different value
a)
1 only
b)
2 only
c)
1 and 2 only
d)
3 and 4 only
|
|
Aarav Malik answered |
Input (4322,1334,1471,9679,1989,6171,6173, 4199)
Given Hash function,
h(a) = x mod 10
h(a) = h(1)
= {1471,6171} hash to the same value
h(a) = h(2) = {4322}
h(a) = h(3) = {6173}
h(a) = h(9)
= {9679,1989,4199}has to the same value.
h(0), h(5), h{6), h(7), h(8) are empty for given input.
So the statement (i) and (ii) are correct.
Given Hash function,
h(a) = x mod 10
h(a) = h(1)
= {1471,6171} hash to the same value
h(a) = h(2) = {4322}
h(a) = h(3) = {6173}
h(a) = h(9)
= {9679,1989,4199}has to the same value.
h(0), h(5), h{6), h(7), h(8) are empty for given input.
So the statement (i) and (ii) are correct.
Consider a complete binary tree with 7 nodes. Let A denote the set of first 3 elements obtained by performing Breadth-First Search (BFS) starting from the root. Let B denote the set of first 3 elements obtained by performing Depth-First Search (DFS) starting from the root.
The value of ∣A−B∣ is _______.- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
Consider a complete binary tree with 7 nodes. Let A denote the set of first 3 elements obtained by performing Breadth-First Search (BFS) starting from the root. Let B denote the set of first 3 elements obtained by performing Depth-First Search (DFS) starting from the root.
The value of ∣A−B∣ is _______.
The value of ∣A−B∣ is _______.
a)
1
b)
2
c)
3
d)
4
|
|
Amrutha Sengupta answered |
The value of A, the set of first 3 elements obtained by performing Breadth-First Search (BFS) starting from the root, would depend on the specific arrangement of the nodes in the complete binary tree.
Breadth-First Search (BFS) visits all the nodes at the same depth level before moving on to the next depth level. In a complete binary tree with 7 nodes, the root will be at level 0, its children will be at level 1, and their children will be at level 2.
To perform BFS, we start at the root and visit its children first, from left to right. Then, we move on to the next depth level and visit the children of the nodes at that level, again from left to right.
So, the value of A will depend on the specific arrangement of the nodes in the tree. Without knowing the arrangement of the nodes, it's not possible to determine the exact elements in set A.
Similarly, the value of B, the set of first 3 elements obtained by performing Depth-First Search (DFS) starting from the root, would also depend on the specific arrangement of the nodes in the complete binary tree.
Depth-First Search (DFS) explores as far as possible along each branch before backtracking. In a complete binary tree with 7 nodes, DFS can start from the root and explore the left branch first, then backtrack and explore the right branch.
Again, without knowing the arrangement of the nodes, it's not possible to determine the exact elements in set B.
In summary, the values of sets A and B would depend on the arrangement of the nodes in the complete binary tree and cannot be determined without that information.
Breadth-First Search (BFS) visits all the nodes at the same depth level before moving on to the next depth level. In a complete binary tree with 7 nodes, the root will be at level 0, its children will be at level 1, and their children will be at level 2.
To perform BFS, we start at the root and visit its children first, from left to right. Then, we move on to the next depth level and visit the children of the nodes at that level, again from left to right.
So, the value of A will depend on the specific arrangement of the nodes in the tree. Without knowing the arrangement of the nodes, it's not possible to determine the exact elements in set A.
Similarly, the value of B, the set of first 3 elements obtained by performing Depth-First Search (DFS) starting from the root, would also depend on the specific arrangement of the nodes in the complete binary tree.
Depth-First Search (DFS) explores as far as possible along each branch before backtracking. In a complete binary tree with 7 nodes, DFS can start from the root and explore the left branch first, then backtrack and explore the right branch.
Again, without knowing the arrangement of the nodes, it's not possible to determine the exact elements in set B.
In summary, the values of sets A and B would depend on the arrangement of the nodes in the complete binary tree and cannot be determined without that information.
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is- a)k
- b)k + 1
- c)n - k - 1
- d)n - k
Correct answer is option 'D'. Can you explain this answer?
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is
a)
k
b)
k + 1
c)
n - k - 1
d)
n - k
|
|
Puja Deshpande answered |
Depth-First Traversal and Tree Edges
In a depth-first traversal of a graph G with n vertices, we start at a given vertex and explore as far as possible along each branch before backtracking. This traversal results in a tree-like structure called a depth-first search tree. The edges in this tree are called tree edges.
The number of tree edges marked during the depth-first traversal is denoted as k.
Connected Components in a Graph
A connected component in a graph is a subgraph in which every pair of vertices is connected by a path. In other words, it is a maximal connected subgraph.
Explanation of the Answer
The number of connected components in a graph can be determined by analyzing the number of tree edges marked during a depth-first traversal.
- The given graph G has n vertices.
- In a depth-first traversal, k edges are marked as tree edges.
To understand why the correct answer is option 'D' (n - k), let's consider the following:
- In a connected component, every vertex is reachable from any other vertex.
- In the depth-first traversal, each tree edge connects two vertices.
- Since k edges are marked as tree edges, they connect k + 1 vertices (including the starting vertex).
- The remaining n - (k + 1) vertices are not connected to the tree edges.
Therefore, the number of connected components in G is equal to the number of remaining vertices that are not connected to the tree edges, which is n - (k + 1). Simplifying this expression gives us the answer n - k.
Hence, option 'D' (n - k) is the correct answer.
In a depth-first traversal of a graph G with n vertices, we start at a given vertex and explore as far as possible along each branch before backtracking. This traversal results in a tree-like structure called a depth-first search tree. The edges in this tree are called tree edges.
The number of tree edges marked during the depth-first traversal is denoted as k.
Connected Components in a Graph
A connected component in a graph is a subgraph in which every pair of vertices is connected by a path. In other words, it is a maximal connected subgraph.
Explanation of the Answer
The number of connected components in a graph can be determined by analyzing the number of tree edges marked during a depth-first traversal.
- The given graph G has n vertices.
- In a depth-first traversal, k edges are marked as tree edges.
To understand why the correct answer is option 'D' (n - k), let's consider the following:
- In a connected component, every vertex is reachable from any other vertex.
- In the depth-first traversal, each tree edge connects two vertices.
- Since k edges are marked as tree edges, they connect k + 1 vertices (including the starting vertex).
- The remaining n - (k + 1) vertices are not connected to the tree edges.
Therefore, the number of connected components in G is equal to the number of remaining vertices that are not connected to the tree edges, which is n - (k + 1). Simplifying this expression gives us the answer n - k.
Hence, option 'D' (n - k) is the correct answer.
What is the worst case efficiency for a path compression algorithm?- a)O(M log N)
- b)O(N log N)
- c)O(log N)
- d)O(N)
Correct answer is option 'A'. Can you explain this answer?
What is the worst case efficiency for a path compression algorithm?
a)
O(M log N)
b)
O(N log N)
c)
O(log N)
d)
O(N)
|
|
Rishabh Pillai answered |
Explanation:
Path Compression Algorithm:
- Path compression is a technique used in Union-Find data structures to optimize the efficiency of finding the root node of a given element in a disjoint set.
- In a path compression algorithm, each node on the path from the current node to the root node is linked directly to the root node, reducing the time complexity of future find operations.
Worst Case Efficiency:
- The worst-case efficiency of a path compression algorithm is determined by the number of operations required to perform path compression on a disjoint set of elements.
- In the worst-case scenario, if the path compression algorithm is not optimized properly, it may lead to a time complexity of O(M log N), where M is the number of union operations and N is the number of elements in the disjoint set.
- This worst-case scenario occurs when there are multiple paths of unoptimized trees that need to be compressed during a sequence of union operations.
Conclusion:
- In conclusion, the worst-case efficiency of a path compression algorithm is O(M log N), where M is the number of union operations and N is the number of elements in the disjoint set.
- It is important to implement path compression algorithms efficiently to ensure optimal performance in Union-Find data structures.
Consider a hash table of size 11 that uses open addressing with linear probing. Let h(k) = kmod 11 be the hash function used. A sequence of records with keys 43 36 92 87 11 4 71 13 14 is inserted into an initially empty hash table, the bins of which are indexed from zero to ten. What is the index of the bin into which the last record is inserted?- a)3
- b)4
- c)6
- d)7
Correct answer is option 'D'. Can you explain this answer?
Consider a hash table of size 11 that uses open addressing with linear probing. Let h(k) = kmod 11 be the hash function used. A sequence of records with keys 43 36 92 87 11 4 71 13 14 is inserted into an initially empty hash table, the bins of which are indexed from zero to ten. What is the index of the bin into which the last record is inserted?
a)
3
b)
4
c)
6
d)
7
|
|
Bijoy Iyer answered |
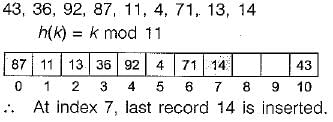
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim’s algorithm to construct a Minimum Spanning Tree?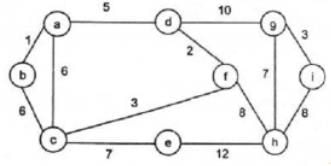
- a)(a, b), (d, f), (f, c), (g, i), (d, a), (g, h), (c, e), (f, h)
- b)(c, e), (c, f), (f, d), (d, a), (a, b), (g, h), (h, f), (g, i)
- c)(d, f), (f, c), (d, a), (a, b), (c, e), (f, h), (g, h), (g, i)
- d)(h, g), (g, i), (h, f), (f, c), (f, d), (d, a), (a, b), (c, e)
Correct answer is option 'C'. Can you explain this answer?
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim’s algorithm to construct a Minimum Spanning Tree?
a)
(a, b), (d, f), (f, c), (g, i), (d, a), (g, h), (c, e), (f, h)
b)
(c, e), (c, f), (f, d), (d, a), (a, b), (g, h), (h, f), (g, i)
c)
(d, f), (f, c), (d, a), (a, b), (c, e), (f, h), (g, h), (g, i)
d)
(h, g), (g, i), (h, f), (f, c), (f, d), (d, a), (a, b), (c, e)
|
|
Ravi Singh answered |
In prims algorithm we start with any node and keep on exploring minimum cost neighbors of nodes already covered.
The number of binary relations on a set with n elements is- a)n2
- b)2n
- c)2n2
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The number of binary relations on a set with n elements is
a)
n2
b)
2n
c)
2n2
d)
None of these
|
Kiran Reddy answered |
Number of elements in set = n
Number of possible binary relations = n2
Number of possible binary relations of the set = 2n2.
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is- a)E
- b)2E
- c)V
- d)2V
Correct answer is option 'B'. Can you explain this answer?
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is
a)
E
b)
2E
c)
V
d)
2V
|
|
Ravi Singh answered |
Since the given graph is undirected, every edge contributes as 2 to sum of degrees.
So the sum of degrees is 2E.
So the sum of degrees is 2E.
Which of the following statements is/are TRUE for an undirected graph?
P: Number of odd degree vertices is even
Q: Sum of degrees of all vertices is even- a)P Only
- b)Q Only
- c)Both P and Q
- d)Neither P nor Q
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is/are TRUE for an undirected graph?
P: Number of odd degree vertices is even
Q: Sum of degrees of all vertices is even
P: Number of odd degree vertices is even
Q: Sum of degrees of all vertices is even
a)
P Only
b)
Q Only
c)
Both P and Q
d)
Neither P nor Q
|
|
Ravi Singh answered |
P is true for undirected graph as adding an edge always increases degree of two vertices by 1.
Q is true: If we consider sum of degrees and subtract all even degrees, we get an even number because every edge increases the sum of degrees by 2. So total number of odd degree vertices must be even.
Consider the following graph,
Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?- a)I, II and IV only
- b)I and IV only
- c)II, III and IV only
- d)I, III and IV only
Correct answer is option 'D'. Can you explain this answer?
Consider the following graph,
Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?
Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?
a)
I, II and IV only
b)
I and IV only
c)
II, III and IV only
d)
I, III and IV only
|
|
Sanya Agarwal answered |
We can check all DFSs for following properties.
In DFS, if a vertex 'v' is visited
after 'u', then one of the following is true.
1) (u, v) is an edge.
u
/ \
v w
/ / \
x y z
after 'u', then one of the following is true.
1) (u, v) is an edge.
u
/ \
v w
/ / \
x y z
2) 'u' is a leaf node.
w
/ \
x v
/ / \
u y z
In DFS, after visiting a node, we first recur for all unvisited children. If there are no unvisited children (u is leaf), then control goes back to parent and parent then visits next unvisited children.
w
/ \
x v
/ / \
u y z
In DFS, after visiting a node, we first recur for all unvisited children. If there are no unvisited children (u is leaf), then control goes back to parent and parent then visits next unvisited children.
Consider the following directed graph.
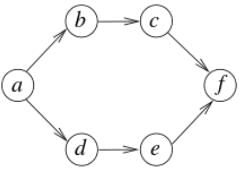
The number of different topological orderings of the vertices of the graph is- a)1
- b)2
- c)4
- d)6
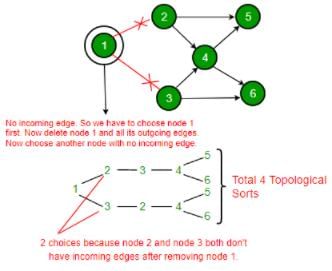
Correct answer is option 'D'. Can you explain this answer?
Consider the following directed graph.
The number of different topological orderings of the vertices of the graph is
The number of different topological orderings of the vertices of the graph is
a)
1
b)
2
c)
4
d)
6
|
|
Ravi Singh answered |
Following are different 6 Topological Sortings
a-b-c-d-e-f
a-d-e-b-c-f
a-b-d-c-e-f
a-d-b-c-e-f
a-b-d-e-c-f
a-d-b-e-c-f
a-b-c-d-e-f
a-d-e-b-c-f
a-b-d-c-e-f
a-d-b-c-e-f
a-b-d-e-c-f
a-d-b-e-c-f
Consider the graph in figure:
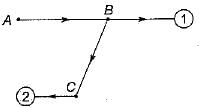
What should be the labels of nodes marked 1 and 2 if the breadth first traversal yields the list a b c d e?- a)D and E
- b)E and D
- c)Unpredictable
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Consider the graph in figure:
What should be the labels of nodes marked 1 and 2 if the breadth first traversal yields the list a b c d e?
What should be the labels of nodes marked 1 and 2 if the breadth first traversal yields the list a b c d e?
a)
D and E
b)
E and D
c)
Unpredictable
d)
None of these
|
Nandini Khanna answered |
In Breadth first traversal the nodes are searched level by level. Starting with vertex A, the only next choice is B. Then C, then 1 and lastly 2. Comparing with ABCDE.
In a directed acyclic graph with a source vertex s, the quality-score of a directed path is defined to be the product of the weights of the edges on the path. Further, for a vertex v other than s, the quality-score of v is defined to be the maximum among the quality-scores of all the paths from s to v. The quality-score of s is assumed to be 1.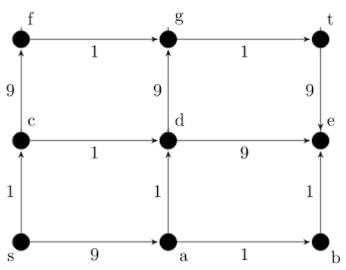
The sum of the quality-scores of all vertices on the graph shown above is _______ .- a)929
- b)81
- c)729
- d)1023
Correct answer is option 'A'. Can you explain this answer?
In a directed acyclic graph with a source vertex s, the quality-score of a directed path is defined to be the product of the weights of the edges on the path. Further, for a vertex v other than s, the quality-score of v is defined to be the maximum among the quality-scores of all the paths from s to v. The quality-score of s is assumed to be 1.
The sum of the quality-scores of all vertices on the graph shown above is _______ .
a)
929
b)
81
c)
729
d)
1023
|
|
Sanya Agarwal answered |
Let Q(V) denote the quality-score of vertex V.
Q(S) = 1 (Given)
Q(C) = 1 (S → C)
Q(F) = 1 * 9 (S → C → F)
Q(A) = 9 (S → A)
Q(D) = 9*1 (S → A → D)
Q(G) = 9 * 1 * 9 (S → A → D → G)
Q(B) = 9 * 1 (S → A → B)
Q(E) = 9 * 1 * 9 (S → A → D → E)
Q(T) = 9*1*9*9 (S → A → D → E → T)
Sum of quality-score of all vertices,
Q(C) = 1 (S → C)
Q(F) = 1 * 9 (S → C → F)
Q(A) = 9 (S → A)
Q(D) = 9*1 (S → A → D)
Q(G) = 9 * 1 * 9 (S → A → D → G)
Q(B) = 9 * 1 (S → A → B)
Q(E) = 9 * 1 * 9 (S → A → D → E)
Q(T) = 9*1*9*9 (S → A → D → E → T)
Sum of quality-score of all vertices,
= 1 + 1 + 9 + 9 + 9 + 81 + 9 + 81 + 729
= 929
= 929
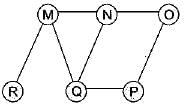
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
- a)MNOPQR
- b)NQMPOR
- c)QMNPRO
- d)GMNPOR
Correct answer is option 'C'. Can you explain this answer?
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
a)
MNOPQR
b)
NQMPOR
c)
QMNPRO
d)
GMNPOR
|
|
Puja Bajaj answered |
The BFS using Queue data structure is QMNPRO.
What is the maximum number of edges in an acyclic undirected graph with n vertices?- a)n-1
- b)n
- c)n + 1
- d)2n-1
Correct answer is option 'A'. Can you explain this answer?
What is the maximum number of edges in an acyclic undirected graph with n vertices?
a)
n-1
b)
n
c)
n + 1
d)
2n-1
|
|
Sanya Agarwal answered |
n * (n – 1) / 2 when cyclic. But acyclic graph with the maximum number of edges is actually a spanning tree and therefore, correct answer is n-1 edges.
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?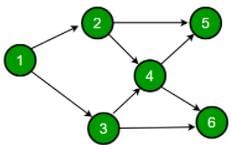
- a)1 2 3 4 5 6
- b)1 3 2 4 5 6
- c)1 3 2 4 6 5
- d)3 2 4 1 6 5
Correct answer is option 'D'. Can you explain this answer?
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
a)
1 2 3 4 5 6
b)
1 3 2 4 5 6
c)
1 3 2 4 6 5
d)
3 2 4 1 6 5
|
|
Sanya Agarwal answered |
In option D, 1 appears after 2 and 3 which is not possible in Topological Sorting.
In the given DAG it is directly visible that there is an outgoing edge from vertex 1 to vertex 2 and 3 hence 2 and 3 cannot come before vertex 1 so clearly option D is incorrect topological sort.
But for questions in which it is not directly visible we should know how to find topological sort of a DAG.
In the given DAG it is directly visible that there is an outgoing edge from vertex 1 to vertex 2 and 3 hence 2 and 3 cannot come before vertex 1 so clearly option D is incorrect topological sort.
But for questions in which it is not directly visible we should know how to find topological sort of a DAG.
Consider the graph in:
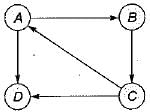
Which of the following is a valid strong component? - a)a, c, d
- b)a, b, d
- c)b, c, d
- d)a, b, c
Correct answer is option 'D'. Can you explain this answer?
Consider the graph in:
Which of the following is a valid strong component?
Which of the following is a valid strong component?
a)
a, c, d
b)
a, b, d
c)
b, c, d
d)
a, b, c
|
|
Keerthana Sarkar answered |
Strong component of a given graph is the maximal set of vertices such that for any two vertices i, j in the set, there is a path connecting i to j.
Obviously vertex ‘d' can’t be in the maximal set (as no vertex can be reached starting from vertex d).
Obviously vertex ‘d' can’t be in the maximal set (as no vertex can be reached starting from vertex d).
Consider the following graph:
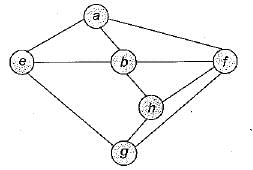Among the following sequences
1. a b e g h f
2. a b f e h g
3. a b f h g e
4. a f g h b eWhich are depth first traversals of the above graph?- a)1, 2 and 4 only
- b)1 and 4 only
- c)2, 3 and 4 only
- d)1, 3 and 4 only
Correct answer is option 'D'. Can you explain this answer?
Consider the following graph:
Among the following sequences
1. a b e g h f
2. a b f e h g
3. a b f h g e
4. a f g h b e
1. a b e g h f
2. a b f e h g
3. a b f h g e
4. a f g h b e
Which are depth first traversals of the above graph?
a)
1, 2 and 4 only
b)
1 and 4 only
c)
2, 3 and 4 only
d)
1, 3 and 4 only
|
|
Sarthak Desai answered |
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?- a)There exists a cutset in G having all edges of maximum weight.
- b)There exists a cycle in G having all edges of maximum weight
- c)Edge e cannot be contained in a cycle.
- d)All edges in G have the same weight
Correct answer is option 'A'. Can you explain this answer?
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
a)
There exists a cutset in G having all edges of maximum weight.
b)
There exists a cycle in G having all edges of maximum weight
c)
Edge e cannot be contained in a cycle.
d)
All edges in G have the same weight
|
|
Sanya Agarwal answered |
Background : Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together.
- A spanning tree has exactly V – 1 edges.
- A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.
- There can be more that one possible spanning trees of a graph. For example, the graph in this question has 6 possible spanning trees.
- MST has lightest edge of every cutset. Remember Prim’s algorithm which basically picks the lightest edge from every cutset.
Choices of this question :
a) There exists a cutset in G having all edges of maximum weight : This is correct. If there is a heaviest edge in MST, then there exist a cut with all edges with weight equal to heavies edge. See point 4 discussed in above background.
a) There exists a cutset in G having all edges of maximum weight : This is correct. If there is a heaviest edge in MST, then there exist a cut with all edges with weight equal to heavies edge. See point 4 discussed in above background.
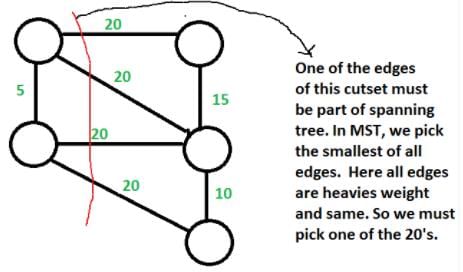
b) There exists a cycle in G having all edges of maximum weight : Not always TRUE. The cutset of heaviest edge may contain only one edge. In fact there may be overall one edge of heavies weight which is part of MST (Consider a graph with two components which are connected by only one edge and this edge is the heavies)
c) Edge e cannot be contained in a cycle. Not Always True. The curset may form cycle with other edges.
d) All edges in G have the same weight Not always True. As discussed in option b, there can be only one edge of heaviest weight.
Which kind of traversal order trie gives the lexicographical sorting of the set of the strings?- a)Preorder
- b)Postorder
- c)Level order
- d)Inorder
Correct answer is option 'A'. Can you explain this answer?
Which kind of traversal order trie gives the lexicographical sorting of the set of the strings?
a)
Preorder
b)
Postorder
c)
Level order
d)
Inorder
|
|
Sanya Agarwal answered |
To print the string in alphabetical order we have to first insert in the trie and then perform preorder traversal to print in alphabetical order.
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?- a)There must exist a vertex w adjacent to both u and n in G
- b)There must exist a vertex w whose removal disconnects u and n in G
- c)There must exist a cycle in G containing u and n
- d)There must exist a cycle in G containing u and all its neighbours in G.
Correct answer is option 'D'. Can you explain this answer?
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?
a)
There must exist a vertex w adjacent to both u and n in G
b)
There must exist a vertex w whose removal disconnects u and n in G
c)
There must exist a cycle in G containing u and n
d)
There must exist a cycle in G containing u and all its neighbours in G.
|
Lalit Yadav answered |
Below example shows that A and B are FALSE:
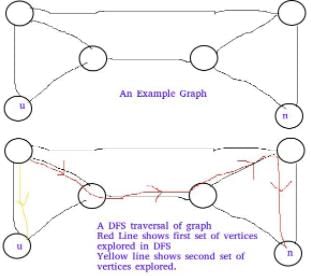
Below example shows C is false:
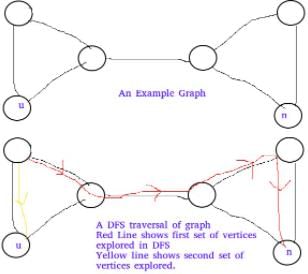
Below example shows C is false:
Consider a directed graph with n vertices and m edges such that all edges have same edge weights. Find the complexity of the best known algorithm to compute the minimum spanning tree of the graph?- a)O(m+n)
- b)O(m logn)
- c)O(mn)
- d)O(n logm)
Correct answer is option 'A'. Can you explain this answer?
Consider a directed graph with n vertices and m edges such that all edges have same edge weights. Find the complexity of the best known algorithm to compute the minimum spanning tree of the graph?
a)
O(m+n)
b)
O(m logn)
c)
O(mn)
d)
O(n logm)
|
|
Sanya Agarwal answered |
It’s a special case in which all edge weights are equal, so dfs would work and resultant depth first tree would be the spanning tree. So the answer would be O(m+n).
Chapter doubts & questions for Graphs - Programming and Data Structures 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Graphs - Programming and Data Structures in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Programming and Data Structures
124 docs|30 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup