All Exams >
Class 5 >
Mathematics for Class 5 >
All Questions
All questions of Circles for Class 5 Exam
Find the diameter of the circle below: r = 8
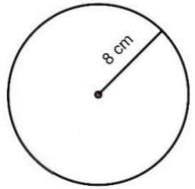
- a)8
- b)24
- c)16
- d)32
Correct answer is option 'C'. Can you explain this answer?
Find the diameter of the circle below: r = 8
a)
8
b)
24
c)
16
d)
32
|
|
Shreyanvi Dash answered |
Let us analyse this question -
So , the radius of the circle - 8r
The diameter - twice the radius.
So, if radius - 8 , diameter of the circle - 8+8 =16.
Therefore, diameter - 16
So , the radius of the circle - 8r
The diameter - twice the radius.
So, if radius - 8 , diameter of the circle - 8+8 =16.
Therefore, diameter - 16
Which of the following are the radii of two concentric circles?- a)4 cm, 8 cm
- b)6 cm, 6 cm
- c)3 cm, 3 cm
- d) Both (b) and (c)
Correct answer is option 'A'. Can you explain this answer?
Which of the following are the radii of two concentric circles?
a)
4 cm, 8 cm
b)
6 cm, 6 cm
c)
3 cm, 3 cm
d)
Both (b) and (c)
|
Aditi Sharma answered |
If two or more circles that have the same center, but different radii they are termed as concentric circles.
Which segment is a radius?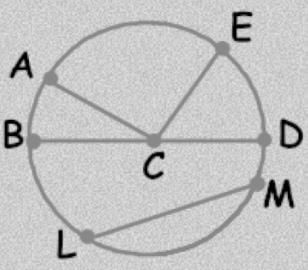
- a)LM
- b)BD
- c)AC
- d)DC
Correct answer is option 'D'. Can you explain this answer?
Which segment is a radius?
a)
LM
b)
BD
c)
AC
d)
DC
|
Shreya Shah answered |
From mine I think option D and C both options are correct . As in this it is written that the radius is half of the diameter and in a circle all the radii are of same length and DC is a radius but at the same time AC is also one radius.
What is the radius of a circle whose diameter is 15 cm?- a)30
- b)15
- c)7.5
- d)10
Correct answer is option 'C'. Can you explain this answer?
What is the radius of a circle whose diameter is 15 cm?
a)
30
b)
15
c)
7.5
d)
10
|
|
Prabhat mehra answered |
Given:
- Diameter of the circle = 15 cm
To find:
- Radius of the circle
Solution:
- The diameter of a circle is the distance across the circle passing through the center. It is twice the length of the radius.
- Therefore, the formula to find the radius of a circle is:
Radius = Diameter / 2
Calculation:
- Given diameter = 15 cm
- Using the formula, we can find the radius:
Radius = 15 cm / 2 = 7.5 cm
Conclusion:
- The radius of the circle with a diameter of 15 cm is 7.5 cm.
- Hence, option 'C' is the correct answer.
- Diameter of the circle = 15 cm
To find:
- Radius of the circle
Solution:
- The diameter of a circle is the distance across the circle passing through the center. It is twice the length of the radius.
- Therefore, the formula to find the radius of a circle is:
Radius = Diameter / 2
Calculation:
- Given diameter = 15 cm
- Using the formula, we can find the radius:
Radius = 15 cm / 2 = 7.5 cm
Conclusion:
- The radius of the circle with a diameter of 15 cm is 7.5 cm.
- Hence, option 'C' is the correct answer.
Which of the following is correct?- a)Only a limited number of radii can be drawn in a circle.
- b)An infinite number of diameters can be drawn in a circle.
- c)Some of the diameters do not pass through the centre of the circle.
- d)A circle may have infinite number of centres.
Correct answer is option 'B'. Can you explain this answer?
Which of the following is correct?
a)
Only a limited number of radii can be drawn in a circle.
b)
An infinite number of diameters can be drawn in a circle.
c)
Some of the diameters do not pass through the centre of the circle.
d)
A circle may have infinite number of centres.
|
|
Aditi Sharma answered |
We can draw infinite lines that pass through the center of the circle with endpoints on the circumference of the circle. Hence, a circle can have countless number of diameters.
Which of the following is a false statement?- a)Infinitely many chords can be drawn in a circle.
- b)A semicircle is an arc of the circle.
- c)The diameter of a circle passes through its centre.
- d)The line joining any two points on a circle is called its diameter.
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a false statement?
a)
Infinitely many chords can be drawn in a circle.
b)
A semicircle is an arc of the circle.
c)
The diameter of a circle passes through its centre.
d)
The line joining any two points on a circle is called its diameter.
|
|
Avinash Patel answered |
A diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle.
A bicycle tire has a diameter of 27 inches. What is the radius?- a)27
- b)81
- c)13.5
- d)54
Correct answer is option 'C'. Can you explain this answer?
A bicycle tire has a diameter of 27 inches. What is the radius?
a)
27
b)
81
c)
13.5
d)
54
|
Sravya Kaur answered |
To find the radius of a bicycle tire, we need to understand the relationship between the diameter and the radius of a circle.
The Relationship between Diameter and Radius:
- The diameter of a circle is the distance across the circle passing through its center.
- The radius of a circle is the distance from the center of the circle to any point on its edge.
- The radius is always half the length of the diameter.
Formula to Find the Radius:
- Radius = Diameter / 2
Now let's solve the problem:
Step 1: Given information
- The diameter of the bicycle tire = 27 inches
Step 2: Applying the formula
- Radius = Diameter / 2
- Radius = 27 inches / 2
- Radius = 13.5 inches
Therefore, the radius of the bicycle tire is 13.5 inches.
Explanation:
The diameter is the distance across the circle, and the radius is the distance from the center to the edge. Since the radius is always half the length of the diameter, we can divide the diameter by 2 to find the radius. In this case, the diameter of the bicycle tire is 27 inches, so we divide it by 2 to find the radius. The result is 13.5 inches, which means the radius of the bicycle tire is 13.5 inches.
Thus, the correct answer is option C) 13.5.
The Relationship between Diameter and Radius:
- The diameter of a circle is the distance across the circle passing through its center.
- The radius of a circle is the distance from the center of the circle to any point on its edge.
- The radius is always half the length of the diameter.
Formula to Find the Radius:
- Radius = Diameter / 2
Now let's solve the problem:
Step 1: Given information
- The diameter of the bicycle tire = 27 inches
Step 2: Applying the formula
- Radius = Diameter / 2
- Radius = 27 inches / 2
- Radius = 13.5 inches
Therefore, the radius of the bicycle tire is 13.5 inches.
Explanation:
The diameter is the distance across the circle, and the radius is the distance from the center to the edge. Since the radius is always half the length of the diameter, we can divide the diameter by 2 to find the radius. In this case, the diameter of the bicycle tire is 27 inches, so we divide it by 2 to find the radius. The result is 13.5 inches, which means the radius of the bicycle tire is 13.5 inches.
Thus, the correct answer is option C) 13.5.
The _____________ of a circle is two times the radius. - a)circumfrence
- b)chord
- c)diameter
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
The _____________ of a circle is two times the radius.
a)
circumfrence
b)
chord
c)
diameter
d)
None of the above
|
|
Aditi Sharma answered |
A circle's diameter is equal to twice its radius, or 2r.
Which segment is the diameter?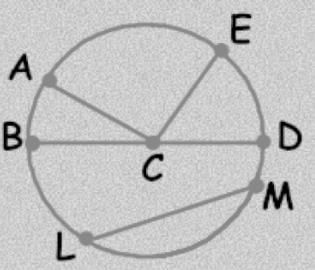
- a)BD
- b)CE
- c)LM
- d)AC
Correct answer is option 'A'. Can you explain this answer?
Which segment is the diameter?
a)
BD
b)
CE
c)
LM
d)
AC
|
Learning Enablers answered |
A diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle.
Hence, BD is the diameter in the image shown.
Find the radius of the circle below:d = 36ft.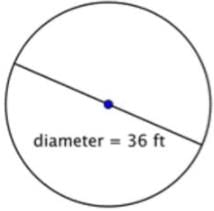
- a)72
- b)18
- c)24
- d)48
Correct answer is option 'B'. Can you explain this answer?
Find the radius of the circle below:d = 36ft.
a)
72
b)
18
c)
24
d)
48
|
Edgy Education answered |
Using the formula:
d = 2 r
Solving for r:
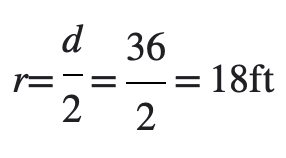
What is the circumference of the given circle?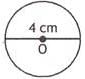
- a)π/4 cm
- b)4π cm
- c)π/2 cm
- d)2π cm
Correct answer is option 'B'. Can you explain this answer?
What is the circumference of the given circle?
a)
π/4 cm
b)
4π cm
c)
π/2 cm
d)
2π cm
|
Priyanka Sharma answered |
Circumference of a circle whose radius is r is given by 2 π r
Here d= 4 cm
Hence, r is 2 cm
Circumference of the circle = 2 π (2)
Circumference of the circle = 4 π cm
What is the radius if the diameter is 12 m ?- a)4 m
- b)6 m
- c)48 m
- d)24 m
Correct answer is option 'B'. Can you explain this answer?
What is the radius if the diameter is 12 m ?
a)
4 m
b)
6 m
c)
48 m
d)
24 m
|
Ashutosh Chaudhary answered |
Question Analysis:
The question asks for the radius of a circle when the diameter is given. To solve this problem, we need to understand the relationship between the diameter and the radius of a circle.
Concept Explanation:
- The diameter of a circle is a straight line that passes through the center of the circle and connects two points on the circumference.
- The radius of a circle is the distance from the center of the circle to any point on the circumference.
- The diameter is always twice the length of the radius.
- We can find the radius by dividing the diameter by 2.
Solution:
Given: Diameter = 12 m
We can find the radius by dividing the diameter by 2.
- Divide the diameter by 2: 12 m ÷ 2 = 6 m
Therefore, the radius of the circle is 6 m.
Verification:
To verify the answer, we can use the relationship between the diameter and the radius.
- Multiply the radius by 2: 6 m × 2 = 12 m
We can see that the calculated diameter is equal to the given diameter of 12 m. This confirms that the answer is correct.
Summary:
The radius of a circle with a diameter of 12 m is 6 m.
The question asks for the radius of a circle when the diameter is given. To solve this problem, we need to understand the relationship between the diameter and the radius of a circle.
Concept Explanation:
- The diameter of a circle is a straight line that passes through the center of the circle and connects two points on the circumference.
- The radius of a circle is the distance from the center of the circle to any point on the circumference.
- The diameter is always twice the length of the radius.
- We can find the radius by dividing the diameter by 2.
Solution:
Given: Diameter = 12 m
We can find the radius by dividing the diameter by 2.
- Divide the diameter by 2: 12 m ÷ 2 = 6 m
Therefore, the radius of the circle is 6 m.
Verification:
To verify the answer, we can use the relationship between the diameter and the radius.
- Multiply the radius by 2: 6 m × 2 = 12 m
We can see that the calculated diameter is equal to the given diameter of 12 m. This confirms that the answer is correct.
Summary:
The radius of a circle with a diameter of 12 m is 6 m.
Which of the following are collinear points?- a)The end points of a chord and the centre of the circle.
- b)The point of intersection of the diameters of a circle.
- c)The end points of a diameter and the centre of the circle.
- d)Any two points on the circumference of the circle.
Correct answer is option 'C'. Can you explain this answer?
Which of the following are collinear points?
a)
The end points of a chord and the centre of the circle.
b)
The point of intersection of the diameters of a circle.
c)
The end points of a diameter and the centre of the circle.
d)
Any two points on the circumference of the circle.
|
|
Aditi Sharma answered |
- Collinear points mean the points which lie on the same line or in the same direction.
- Since, the end points of a diameter and the centre of the circle lie on the same line, they are collinear points.
What is the radius if the diameter is 40 m ?- a)40
- b)20
- c)10
- d)80
Correct answer is option 'B'. Can you explain this answer?
What is the radius if the diameter is 40 m ?
a)
40
b)
20
c)
10
d)
80
|
|
Avinash Patel answered |
Using the formula:
d = 2 r
Solving for r:
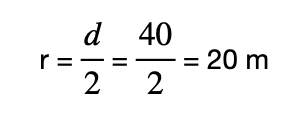
Which is the correct definition of a circle?- a)set of points on a flat surface with every point equidistant from a given point called the center
- b)a line segment connecting any two points on a circle
- c)a line segment that extends between the center and the circle
- d)a special chord that goes through the center of a circle
Correct answer is option 'A'. Can you explain this answer?
Which is the correct definition of a circle?
a)
set of points on a flat surface with every point equidistant from a given point called the center
b)
a line segment connecting any two points on a circle
c)
a line segment that extends between the center and the circle
d)
a special chord that goes through the center of a circle
|
|
Avinash Patel answered |
A circle is the set of all points in a plane that are equidistant from a given point called the center of the circle.
_____________ is a special chord that goes through the center of a circle.- a)diameter
- b)radius
- c)circumference
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
_____________ is a special chord that goes through the center of a circle.
a)
diameter
b)
radius
c)
circumference
d)
none of the above
|
Ruchi Basu answered |
The Answer:
The correct answer is option 'A', diameter.
Explanation:
A circle is a closed curve that is formed by a set of points that are equidistant from a fixed point called the center.
Diameter:
- The diameter of a circle is a special chord that passes through the center of the circle.
- It is defined as a line segment that connects any two points on the circle and passes through the center.
- The diameter is the longest chord in a circle, and it divides the circle into two equal halves called semicircles.
- The diameter is twice the length of the radius of the circle.
Radius:
- The radius of a circle is a line segment that connects the center of the circle to any point on the circle.
- The radius is always half the length of the diameter.
- It is the distance from the center of the circle to any point on the circumference (outer edge) of the circle.
Circumference:
- The circumference of a circle is the distance around the outer edge of the circle.
- It is the perimeter or the boundary of the circle.
- The circumference is calculated using the formula C = 2πr, where "C" represents the circumference and "r" represents the radius of the circle.
Conclusion:
In this question, the special chord that passes through the center of a circle is called the diameter. The diameter is different from the radius and the circumference of a circle.
The correct answer is option 'A', diameter.
Explanation:
A circle is a closed curve that is formed by a set of points that are equidistant from a fixed point called the center.
Diameter:
- The diameter of a circle is a special chord that passes through the center of the circle.
- It is defined as a line segment that connects any two points on the circle and passes through the center.
- The diameter is the longest chord in a circle, and it divides the circle into two equal halves called semicircles.
- The diameter is twice the length of the radius of the circle.
Radius:
- The radius of a circle is a line segment that connects the center of the circle to any point on the circle.
- The radius is always half the length of the diameter.
- It is the distance from the center of the circle to any point on the circumference (outer edge) of the circle.
Circumference:
- The circumference of a circle is the distance around the outer edge of the circle.
- It is the perimeter or the boundary of the circle.
- The circumference is calculated using the formula C = 2πr, where "C" represents the circumference and "r" represents the radius of the circle.
Conclusion:
In this question, the special chord that passes through the center of a circle is called the diameter. The diameter is different from the radius and the circumference of a circle.
Find the circumfrence of the circle whose radius, r = 7 cm- a)44
- b)48
- c)50
- d)52
Correct answer is option 'A'. Can you explain this answer?
Find the circumfrence of the circle whose radius, r = 7 cm
a)
44
b)
48
c)
50
d)
52
|
|
Aditi Sharma answered |
Circumference of a circle whose radius is r is given by 2 π r
Here r=7 cm
Hence,
Circumference of the circle = 2 π (7)
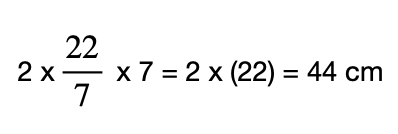
Is the black line a radius or diameter of the circle?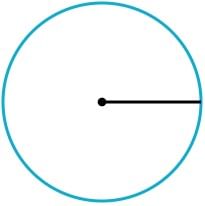
- a)Radius
- b)Diameter
Correct answer is option 'A'. Can you explain this answer?
Is the black line a radius or diameter of the circle?
a)
Radius
b)
Diameter
|
|
Priyanka Sharma answered |
The radius is half the length of the diameter and is joined to the centre at one end. Hence, it is the radius of the circle.
If the diameter of a circle is 14 cm, find its radius.- a)
- 3.5 cm
- b)
- 14 cm
- c)
- 28 cm
- d)
- 7 cm
Correct answer is option 'D'. Can you explain this answer?
If the diameter of a circle is 14 cm, find its radius.
a)
b)
c)
d)
|
Tutorpedia Coaching answered |
The radius of a circle is half its diameter. Here, radius = 14 divided by 2 = 7 cm.
Chapter doubts & questions for Circles - Mathematics for Class 5 2025 is part of Class 5 exam preparation. The chapters have been prepared according to the Class 5 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 5 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circles - Mathematics for Class 5 in English & Hindi are available as part of Class 5 exam.
Download more important topics, notes, lectures and mock test series for Class 5 Exam by signing up for free.
Mathematics for Class 5
95 videos|462 docs|47 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup