All Exams >
Mathematics >
Mathematics for Competitive Exams >
All Questions
All questions of System of Linear Equations, Eigen Values & Eigen Vectors for Mathematics Exam
For what value of k, the system linear equation has no solution(3k + 1)x + 3y - 2 = 0(k2 + 1)x + (k - 2)y - 5 = 0- a)1
- b)-1
- c)2
- d)6
Correct answer is option 'B'. Can you explain this answer?
For what value of k, the system linear equation has no solution
(3k + 1)x + 3y - 2 = 0
(k2 + 1)x + (k - 2)y - 5 = 0
a)
1
b)
-1
c)
2
d)
6
|
Orion Classes answered |
Given:
a1 = 3k + 1
b1 = 3
c1 = -2
a2 = k2 + 1
b2 = k - 2
c2 = -5
Formula Used:
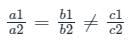
Calculation:
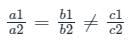
Calculation:
By cross multiplication
⇒ (3k + 1)(k - 2) = 3(k2 + 1)
⇒ 3k2 - 6k + k - 2 = 3k2 + 3
⇒ -5k - 2 = 3
⇒ -5k = 5
∴ k = -1
The correct option is 2 i.e. -1
Consider a matrix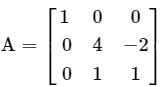 
The matrix A satisfies the equation 6A-1 = A2 + cA + dI, where c and d are scalars and I is the identity matrix. Then (c + d) is equal to- a)5
- b)17
- c)-6
- d)11
Correct answer is option 'A'. Can you explain this answer?
Consider a matrix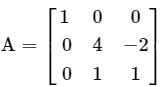
The matrix A satisfies the equation 6A-1 = A2 + cA + dI, where c and d are scalars and I is the identity matrix. Then (c + d) is equal to
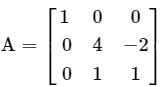
The matrix A satisfies the equation 6A-1 = A2 + cA + dI, where c and d are scalars and I is the identity matrix. Then (c + d) is equal to
a)
5
b)
17
c)
-6
d)
11
|
|
Orion Classes answered |
Concept:
for the given square matrix, the characteristic equation will be
|B - AI| = 0
B = Given matrix
I = Unit matrix
A = Characteristic roots
Calculation:
|B - AI| = 0
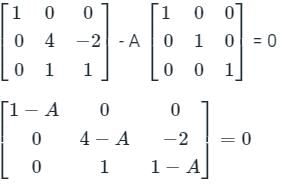
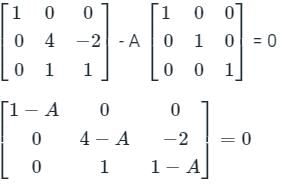
Take the determinant of matrix, then
(1 - A) [(4 - A) (1 - A) + 2] = 0
(1 - A) [4 - 4A - A + A2 + 2] = 0
(1 - A) [4 - 5A + A2 + 2] = 0
(1 - A) [A2 - 5A + 6] = 0
A2 - 5A + 6 - A3 + 5A2 - 6A = 0
-A3 + 6A2 - 11A + 6 = 0
A3 - 6A2 + 11A = 6
A2 - 6A + 11 = 6A-1 ........(1)
Given 6A-1 = A2 + cA + dI .........(2)
Compare 1 and 2
c = -6, d = +11
c + d = +5
For what value of λ, do the simultaneous equation 2x + 3y = 1, 4x + 6y = λ have infinite solutions?- a)λ = 0
- b)λ = 1
- c)λ ≠ 2
- d)λ = 2
Correct answer is option 'D'. Can you explain this answer?
For what value of λ, do the simultaneous equation 2x + 3y = 1, 4x + 6y = λ have infinite solutions?
a)
λ = 0
b)
λ = 1
c)
λ ≠ 2
d)
λ = 2
|
Ayesha Joshi answered |
Concept:
Non-homogeneous equation of type AX = B has infinite solutions;
if ρ(A | B) = ρ(A) < Number of unknowns
Calculation:
Given:
2x + 3y = 1
4x + 6y = λ
The augmented matrix is given by:
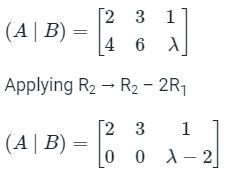
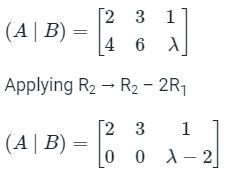
For the system to have infinite solutions, the last row must be a fully zero row.
So if λ = 2 then the system of equations has infinitely many solutions.
Key Points:
Remember the system of equations
AX = B have
1. Unique solution, if ρ(A : B) = ρ(A) = Number of unknowns.
2. Infinite many solutions, if ρ(A : B) = ρ(A) < Number of solutions
3. No solution, if ρ(A : B) ≠ ρ(A).
The system of linear equations -y + z = 0(4d - 1) x + y + Z = 0(4d - 1) z = 0 has a non-trivial solution, if d equals - a)1/2
- b)1/4
- c)3/4
- d)1
Correct answer is option 'B'. Can you explain this answer?
The system of linear equations
-y + z = 0
(4d - 1) x + y + Z = 0
(4d - 1) z = 0
has a non-trivial solution, if d equals
a)
1/2
b)
1/4
c)
3/4
d)
1
|
|
Orion Classes answered |
Concept
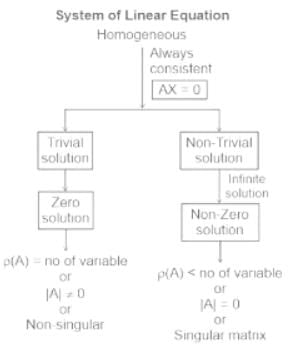
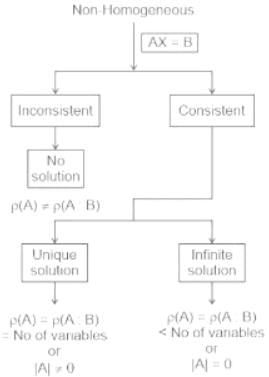
For a homogeneous system of linear equations:
Having non-trivial solution:
The rank of the matrix should be less than the number of variables.
Or determinant of the matrix should be equal to zero.
Calculation:
Given:
-y + z = 0
(4d - 1) x + y + Z = 0
(4d - 1) z = 0
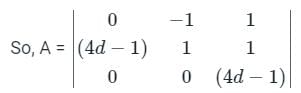
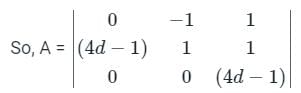
For non-trivial solution:
det. A = 0
⇒ |A| = 0
⇒ 0 × [(4d - 1) - 0] + 1 × [(4d - 1)2 - 0] + 1(0 - 0) = 0
⇒ (4d - 1)2 = 0
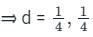
∴ The system of linear equations has a non-trivial solution if d equals to 1/4
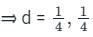
∴ The system of linear equations has a non-trivial solution if d equals to 1/4
The value of k for which the system of equations x + ky + 3z = 0, 4x + 3y + kz = 0, 2x + y + 2z = 0 has non-trivial solution is- a)k = 0 or 9/2
- b)k = 10
- c)k < 9
- d)k > 0
Correct answer is option 'A'. Can you explain this answer?
The value of k for which the system of equations x + ky + 3z = 0, 4x + 3y + kz = 0, 2x + y + 2z = 0 has non-trivial solution is
a)
k = 0 or 9/2
b)
k = 10
c)
k < 9
d)
k > 0
|
|
Orion Classes answered |
Concept:
Consider the system of m linear equations
a11 x1 + a12 x2 + … + a1n xn = 0
a21 x1 + a22 x2 + … + a2n xn = 0
am1 x1 + am2 x2 + … + amn xn = 0
- The above equations containing the n unknowns x1, x2, …, xn. To determine whether the above system of equations is consistent or not, we need to find the rank of the following matrix.
- A is the coefficient matrix of the given system of equations.
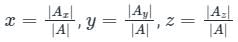
- Where, Ax, Ay, Az is the coefficient matrix of the given system of equations after replacing the first, second, and third columns from the constant term column which will be having all the entries as 0.
- In the case of homogeneous equations, the determinants of, Ax, Ay, Az will be 0 definitely.
- So, for the system of homogeneous equations having the the-trivial solution, the determinant of A should be zero.
- The system of homogeneous equations has a unique solution (trivial solution) if and only if the determinant of A is non-zero.
Calculation:
For non - trivial solution, the |A| = 0
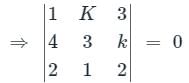
For non - trivial solution, the |A| = 0
⇒ 1(6 - K) - K(8 - 2K) + 3(4 - 6) = 0
⇒ 9K - 2K2 = 0
⇒ k = 0 or 9/2
If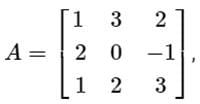 
then which one of the following is correct?- a)A3 - 3A2 - 4A + 11I = 0
- b)A3 - 4A2 - 3A + 11I = 0
- c)A3 + 4A2 - 3A + 11I = 0
- d)A3 - 3A2 + 4A + 11I = 0
Correct answer is option 'B'. Can you explain this answer?
If 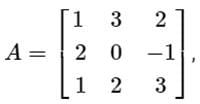then which one of the following is correct?
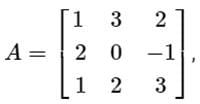then which one of the following is correct?a)
A3 - 3A2 - 4A + 11I = 0
b)
A3 - 4A2 - 3A + 11I = 0
c)
A3 + 4A2 - 3A + 11I = 0
d)
A3 - 3A2 + 4A + 11I = 0
|
|
Orion Classes answered |
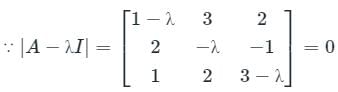
(1 - λ) (-3λ + λ2 + 2) - 3(6 - 2λ + 1) + 2(4 + λ) = 0
(1 - λ) (λ2 - 3λ + 2) - 3(7 - 2λ) + 2(4 + λ) = 0
λ3 - 4λ2 - 3λ + 11 = 0
By C-H theorem replace λ by A
A3 - 4A2 - 3A + 11I = 0
The value of k, for which the following system of linear equations has a non-trivial solution.x + 2y - 3z = 02x + y + z = 0x - y + kz = 0- a)4
- b)2
- c)3
- d)-4
Correct answer is option 'A'. Can you explain this answer?
The value of k, for which the following system of linear equations has a non-trivial solution.
x + 2y - 3z = 0
2x + y + z = 0
x - y + kz = 0
a)
4
b)
2
c)
3
d)
-4
|
Elijah Hines answered |
To find the value of k for which the given system of linear equations has a non-trivial solution, we need to analyze the coefficients of the variables in each equation and determine the conditions for a non-trivial solution.
The given system of equations is:
1) x + 2y - 3z = 0
2) 2x + y + z = 0
3) x - y + kz = 0
In order for the system to have a non-trivial solution, there must be dependence between the equations, meaning that one equation can be obtained as a linear combination of the other two.
Let's analyze the coefficients of the variables in the system:
1) The coefficient of x in equation 1 is 1.
2) The coefficient of x in equation 2 is 2.
3) The coefficient of x in equation 3 is 1.
Since the coefficients of x in the three equations are different, there is no linear combination that can eliminate the variable x. Therefore, the value of k does not affect the existence of a non-trivial solution.
Next, let's analyze the coefficients of y in the system:
1) The coefficient of y in equation 1 is 2.
2) The coefficient of y in equation 2 is 1.
3) The coefficient of y in equation 3 is -1.
The coefficients of y in equations 1 and 2 are different, but we can eliminate the variable y by adding equation 1 and equation 3. This gives us:
(x + 2y - 3z) + (x - y + kz) = 0
2x + (y - y) + (k - 3)z = 0
2x + (k - 3)z = 0
Now, let's analyze the coefficients of z in the system:
1) The coefficient of z in equation 1 is -3.
2) The coefficient of z in equation 2 is 1.
3) The coefficient of z in equation 3 is k.
If we want to eliminate the variable z, we need the coefficients in equations 1 and 2 to be equal. Therefore, we have the condition:
-3 = 1
This condition is not satisfied, so we cannot eliminate the variable z.
Therefore, the value of k does not affect the existence of a non-trivial solution. Hence, the correct answer is option A) 4.
The given system of equations is:
1) x + 2y - 3z = 0
2) 2x + y + z = 0
3) x - y + kz = 0
In order for the system to have a non-trivial solution, there must be dependence between the equations, meaning that one equation can be obtained as a linear combination of the other two.
Let's analyze the coefficients of the variables in the system:
1) The coefficient of x in equation 1 is 1.
2) The coefficient of x in equation 2 is 2.
3) The coefficient of x in equation 3 is 1.
Since the coefficients of x in the three equations are different, there is no linear combination that can eliminate the variable x. Therefore, the value of k does not affect the existence of a non-trivial solution.
Next, let's analyze the coefficients of y in the system:
1) The coefficient of y in equation 1 is 2.
2) The coefficient of y in equation 2 is 1.
3) The coefficient of y in equation 3 is -1.
The coefficients of y in equations 1 and 2 are different, but we can eliminate the variable y by adding equation 1 and equation 3. This gives us:
(x + 2y - 3z) + (x - y + kz) = 0
2x + (y - y) + (k - 3)z = 0
2x + (k - 3)z = 0
Now, let's analyze the coefficients of z in the system:
1) The coefficient of z in equation 1 is -3.
2) The coefficient of z in equation 2 is 1.
3) The coefficient of z in equation 3 is k.
If we want to eliminate the variable z, we need the coefficients in equations 1 and 2 to be equal. Therefore, we have the condition:
-3 = 1
This condition is not satisfied, so we cannot eliminate the variable z.
Therefore, the value of k does not affect the existence of a non-trivial solution. Hence, the correct answer is option A) 4.
Consider matrix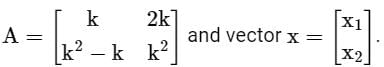 
The number of distinct real values of k for which the equation Ax = 0 has infinitely many solution is________
Correct answer is '2'. Can you explain this answer?
Consider matrix 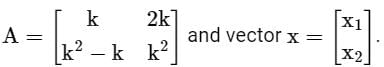The number of distinct real values of k for which the equation Ax = 0 has infinitely many solution is________
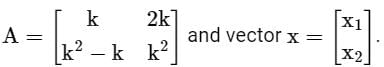The number of distinct real values of k for which the equation Ax = 0 has infinitely many solution is________|
|
Ayesha Joshi answered |
Concept:
We can find the consistency of the given system of equations as follows:
(i) If the rank of matrix A is equal to the rank of an augmented matrix and it is equal to the number of unknowns, then the system is consistent and there is a unique solution.
The rank of A = Rank of augmented matrix = n
(ii) If the rank of matrix A is equal to the rank of an augmented matrix and it is less than the number of unknowns, then the system is consistent and there are an infinite number of solutions.
The rank of A = Rank of augmented matrix < n
Then |A| = 0
(iii) If the rank of matrix A is not equal to the rank of the augmented matrix, then the system is inconsistent, and it has no solution.
The rank of A ≠ Rank of an augmented matrix
Application:
A system to have infinitely many solutions must satisfy:
|A| = 0
K2 (K – 2(K – 1) = 0
K2 (K – 2K + 2) = 0
K2 (-K + 2) = 0
K = 0, 0, 2
Hence, there are 3 eigen values, and two distinct eigen value and 1 repeated eigen value.
Consider the system of equations 
The value of x3 (round off to the nearest integer), is ______.
Correct answer is '3'. Can you explain this answer?
Consider the system of equations The value of x3 (round off to the nearest integer), is ______.
The value of x3 (round off to the nearest integer), is ______.|
|
Ayesha Joshi answered |
The given system has 4 equations and 3 unknowns.
Hence it is a over-determined system of equations.
The equations are;
x1 + 3x2 + 2x3 = 1 --(1)
2x1 + 2x2 - 3x3 = 1 ---(2)
4x1 + 4x2 - 6x3 = 2 ---(3)
2x1 + 5x2 + 2x3 = 1 ---(4)
Note that equation (2) and (3) are linearly dependent on each other and equation 3 is twice that of equation (2).
Hence considering equation 1, 2 and 4 -
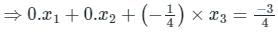
⇒ x3 = 3
Important Points:
- Under-determined system: Number of equations < Number of unknowns
- Over-Determined system: Number of equation > Number of unknowns
- Equally Determined system: Number of equation = Number of unknowns
The set of equationsx + y + z = 1ax – ay + 3z = 55x – 3y + az = 6has infinite solutions, if a =- a)-3
- b)3
- c)4
- d)-4
Correct answer is option 'C'. Can you explain this answer?
The set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
has infinite solutions, if a =
a)
-3
b)
3
c)
4
d)
-4
|
|
Ayesha Joshi answered |
Concept:
Non-homogeneous equation of type AX = B has infinite solutions if ρ(A : B) = ρ(A) < Number of unknowns
Calculation:
Given set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
a2 – a – 12 = 0
a2 – 4a + 3a – 12 = 0
a(a - 4) + 3(a - 4) = 0
(a - 4)(a + 3) = 0
A = 4, -3
When a = 4, then ρ(A : B) = ρ(A) = 2 < 3
Hence, given system of equations have infinite solutions when a = 4.
Note: here a = -3 we cannot consider because for a = -3 ρ(A : B) ≠ ρ(A)
Key Points:
Remember the system of equations
AX = B have
1. Unique solution, if ρ(A : B) = ρ(A) = Number of unknowns.
2. Infinite many solutions, if ρ(A : B) = ρ(A) < Number of unknowns
3. No solution, if ρ(A : B) ≠ ρ(A).
The approximate solution of the system of simultaneous equations2x - 5y + 3z = 7x + 4y - 2z = 32x + 3y + z = 2by applying Gauss-Seidel method one time (using initial approximation as x - 0, y - 0, z - 0) will be:- a)x = 2.32, y = 1.245, z = -3.157
- b)x = 1.25, y = -2.573, z = -3.135
- c)x = 2.45, y = -1.725, z = -3.565
- d)x = 3.5, y = -0.125, z = -4.625
Correct answer is option 'D'. Can you explain this answer?
The approximate solution of the system of simultaneous equations
2x - 5y + 3z = 7
x + 4y - 2z = 3
2x + 3y + z = 2
by applying Gauss-Seidel method one time (using initial approximation as x - 0, y - 0, z - 0) will be:
a)
x = 2.32, y = 1.245, z = -3.157
b)
x = 1.25, y = -2.573, z = -3.135
c)
x = 2.45, y = -1.725, z = -3.565
d)
x = 3.5, y = -0.125, z = -4.625
|
|
Ayesha Joshi answered |
Gauss Seidel Method:
In Gauss Seidel method, the value of x calculated is used in next calculation putting other variable as 0.
2x - 5y + 3z = 7
Putting y = 0, z = 0 ⇒ x = 3.5
x + 4y - 2z = 3
Putting x = 3.5, z = 0 ⇒ y = - 0.125
2x + 3y + z = 2
Putting x = 3.5, y = - 0.125 ⇒ z = 2 – 3(-0.125) – 2(3.5)
z = - 4.625
If the system2x – y + 3z = 2x + y + 2z = 25x – y + az = bHas infinitely many solutions, then the values of a and b, respectively, are- a)– 8 and 6
- b)8 and 6
- c)– 8 and –6
- d)8 and –6
Correct answer is option 'B'. Can you explain this answer?
If the system
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Has infinitely many solutions, then the values of a and b, respectively, are
a)
– 8 and 6
b)
8 and 6
c)
– 8 and –6
d)
8 and –6
|
Wyatt Turner answered |
It seems like you might have only provided a partial sentence or question. Could you please provide more information or clarify your question?
A set of linear equations is given in the form Ax = b, where A is a 2 × 4 matrix with real number entries and b ≠ 0. Will it be possible to solve for x and obtain a unique solution by multiplying both left and right sides of the equation by AT (the super script T denotes the transpose) and inverting the matrix AT A?- a)Yes, it is always possible to get a unique solution for any 2 × 4 matrix A.
- b)No, it is not possible to get a unique solution for any 2 × 4 matrix A.
- c)Yes, can obtain a unique solution provided the matrix AT A is well conditioned
- d)Yes, can obtain a unique solution provided the matrix A is well conditioned.
Correct answer is option 'B'. Can you explain this answer?
A set of linear equations is given in the form Ax = b, where A is a 2 × 4 matrix with real number entries and b ≠ 0. Will it be possible to solve for x and obtain a unique solution by multiplying both left and right sides of the equation by AT (the super script T denotes the transpose) and inverting the matrix AT A?
a)
Yes, it is always possible to get a unique solution for any 2 × 4 matrix A.
b)
No, it is not possible to get a unique solution for any 2 × 4 matrix A.
c)
Yes, can obtain a unique solution provided the matrix AT A is well conditioned
d)
Yes, can obtain a unique solution provided the matrix A is well conditioned.
|
|
Ayesha Joshi answered |
Concept:
From the properties of a matrix,
The rank of m × n matrix is always ≤ min {m, n}
If the rank of matrix A is ρ(A) and rank of matrix B is ρ(B), then the rank of matrix AB is given by
ρ(AB) ≤ min {ρ(A), ρ(B)}
If n × n matrix is singular, the rank will be less than ≤ n
Calculation:
Given:
AX = B
Where A is 2 × 4 matrices and b ≠ 0
The order of AT is 4 × 2
The order of ATA is 4 × 4
Rank of (A) ≤ min (2, 4) = 2
Rank of (AT) ≤ min (2, 4) = 2
Rank (ATA) ≤ min (2, 2) = 2
As the matrix ATA is of order 4 × 4, to have a unique solution the rank of ATA should be 4.
Therefore, the unique solution of this equation is not possible.
The nine numbers x1, x2, x3 ... x9, are in ascending order. Their average m is strictly greater than all the first eight numbers. Which of the following is true?- a)Average (x1, x2, ... x9, m) > m and Average (x2, x3 ... x9) > m
- b)Average (x1, x2 ... x9, m) < m and Average (x2, x3 ... x9) < m
- c)Average (x1, x2 ... x9, m) = m and Average (x2, x3 ... x9) > m
- d)Average (x1, x2 ... x9, m) < m and Average (x2, x3 ... x9) = m
Correct answer is option 'C'. Can you explain this answer?
The nine numbers x1, x2, x3 ... x9, are in ascending order. Their average m is strictly greater than all the first eight numbers. Which of the following is true?
a)
Average (x1, x2, ... x9, m) > m and Average (x2, x3 ... x9) > m
b)
Average (x1, x2 ... x9, m) < m and Average (x2, x3 ... x9) < m
c)
Average (x1, x2 ... x9, m) = m and Average (x2, x3 ... x9) > m
d)
Average (x1, x2 ... x9, m) < m and Average (x2, x3 ... x9) = m
|
Top Rankers answered |
Let's take the example of it
The nine numbers x1, x2, x3 ... x9, are in ascending order
Let the nine number is 1,1,1,1,1,1,1,1,10
Their Avg will be = 18/9 = 2
Also, this satisfies that their average m is strictly greater than all the first eight numbers.
now varifing
Average (x1, x2 ... x9, m) = m
Avg[1,1,1,1,1,1,1,1,10,2] will be 20/10 = 2
Which satisfies the given statement
Now checking Average (x2, x3 ... x9) > m
Average (1,1,1,1,1,1,1,10) will 17/8 = 2.12
Which is greater then 2
So it is also satisfied Average (x2, x3 ... x9) > m
So, Average (x1, x2 ... x9, m) = m and Average (x2, x3 ... x9) > m is the true statement.
The nine numbers x1, x2, x3 ... x9, are in ascending order
Let the nine number is 1,1,1,1,1,1,1,1,10
Their Avg will be = 18/9 = 2
Also, this satisfies that their average m is strictly greater than all the first eight numbers.
now varifing
Average (x1, x2 ... x9, m) = m
Avg[1,1,1,1,1,1,1,1,10,2] will be 20/10 = 2
Which satisfies the given statement
Now checking Average (x2, x3 ... x9) > m
Average (1,1,1,1,1,1,1,10) will 17/8 = 2.12
Which is greater then 2
So it is also satisfied Average (x2, x3 ... x9) > m
So, Average (x1, x2 ... x9, m) = m and Average (x2, x3 ... x9) > m is the true statement.
Gauss-Seidel method is used to solve the following equations (as per the given order):x1 + 2x2 + 3x3 = 52x1 + 3x2 + x3 = 13x1 + 2x2 + x3 = 3Assuming initial guess as x1 = x2 = x3 = 0, the value of x3 after the first iteration is ________
Correct answer is '-6'. Can you explain this answer?
Gauss-Seidel method is used to solve the following equations (as per the given order):
x1 + 2x2 + 3x3 = 5
2x1 + 3x2 + x3 = 1
3x1 + 2x2 + x3 = 3
Assuming initial guess as x1 = x2 = x3 = 0, the value of x3 after the first iteration is ________
|
|
Ayesha Joshi answered |
Gauss Seidel Method:
In Gauss Seidel method, the value of x calculated is used in next calculation putting other variable as 0.
x1 + 2x2 + 3x3 = 5
Putting x2 = 0, x3 = 0 ⇒ x1 = 5
2x1 + 3x2 + x3 = 1
Putting x1 = 5, x3 = 0 ⇒ x2 = -3
3x1 + 2x2 + x3 = 3
Putting x1 = 5, x2 = -3 ⇒ x3 = 3 – 3(5) – 2 (-3)
x3 = 3 – 15 + 6
x3 = -6
Mistake Point: Don’t arrange them diagonally because It is given in question solve as per given order.
For what value of k, the system linear equation has no solution
(3k + 1)x + 3y - 2 = 0
(k2 + 1)x + (k - 2)y - 5 = 0- a)1
- b)-1
- c)2
- d)6
Correct answer is option 'B'. Can you explain this answer?
For what value of k, the system linear equation has no solution
(3k + 1)x + 3y - 2 = 0
(k2 + 1)x + (k - 2)y - 5 = 0
(3k + 1)x + 3y - 2 = 0
(k2 + 1)x + (k - 2)y - 5 = 0
a)
1
b)
-1
c)
2
d)
6
|
Chirag Gupta answered |
Explanation:
1. Determining no solution
To find the value of k for which the system of linear equations has no solution, we need to check the determinant of the coefficient matrix.
2. Writing the coefficient matrix
The coefficient matrix of the system is:
\[ \begin{pmatrix} 3k + 1 & 3 \\ k^2 + 1 & k - 2 \end{pmatrix} \]
3. Calculating the determinant
The determinant of the coefficient matrix is given by:
\[ \text{det} = (3k + 1)(k - 2) - 3(k^2 + 1) \]
\[ \text{det} = 3k^2 - 6k + k - 2 - 3k^2 - 3 \]
\[ \text{det} = -8 \]
4. Determining no solution condition
For a system of linear equations to have no solution, the determinant of the coefficient matrix should be non-zero.
5. Solving for k
Setting the determinant to zero:
\[ -8 = 0 \]
This implies that the system has no solution for any value of k.
6. Choosing the correct option
The correct option for the value of k for which the system has no solution is when the determinant is non-zero, which corresponds to option -1 (b).
1. Determining no solution
To find the value of k for which the system of linear equations has no solution, we need to check the determinant of the coefficient matrix.
2. Writing the coefficient matrix
The coefficient matrix of the system is:
\[ \begin{pmatrix} 3k + 1 & 3 \\ k^2 + 1 & k - 2 \end{pmatrix} \]
3. Calculating the determinant
The determinant of the coefficient matrix is given by:
\[ \text{det} = (3k + 1)(k - 2) - 3(k^2 + 1) \]
\[ \text{det} = 3k^2 - 6k + k - 2 - 3k^2 - 3 \]
\[ \text{det} = -8 \]
4. Determining no solution condition
For a system of linear equations to have no solution, the determinant of the coefficient matrix should be non-zero.
5. Solving for k
Setting the determinant to zero:
\[ -8 = 0 \]
This implies that the system has no solution for any value of k.
6. Choosing the correct option
The correct option for the value of k for which the system has no solution is when the determinant is non-zero, which corresponds to option -1 (b).
The set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
has infinite solutions, if a =- a)-3
- b)3
- c)4
- d)-4
Correct answer is option 'C'. Can you explain this answer?
The set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
has infinite solutions, if a =
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
has infinite solutions, if a =
a)
-3
b)
3
c)
4
d)
-4
|
Infinity Academy answered |
Non-homogeneous equation of type AX = B has infinite solutions if ρ(A : B) = ρ(A) < Number of unknowns
Given set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
R2 → R2 – aR1 and R3 → R3 – 5R1
a2 – a – 12 = 0
a2 – 4a + 3a – 12 = 0
a(a - 4) + 3(a - 4) = 0
(a - 4)(a + 3) = 0
a = 4, -3
When a = 4, then ρ(A : B) = ρ(A) = 2 < 3
Hence, given system of equations have infinite solutions when a = 4.
Note: here a = -3 we cannot consider because for a = -3 ρ(A : B) ≠ ρ(A)
Remember the system of equations
AX = B have
(1) Unique solution, if ρ(A : B) = ρ(A) = Number of unknowns.
(2) Infinite many solutions, if ρ(A : B) = ρ(A) < Number of unknowns
(3) No solution, if ρ(A : B) ≠ ρ(A).
Given set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
R2 → R2 – aR1 and R3 → R3 – 5R1
a2 – a – 12 = 0
a2 – 4a + 3a – 12 = 0
a(a - 4) + 3(a - 4) = 0
(a - 4)(a + 3) = 0
a = 4, -3
When a = 4, then ρ(A : B) = ρ(A) = 2 < 3
Hence, given system of equations have infinite solutions when a = 4.
Note: here a = -3 we cannot consider because for a = -3 ρ(A : B) ≠ ρ(A)
Remember the system of equations
AX = B have
(1) Unique solution, if ρ(A : B) = ρ(A) = Number of unknowns.
(2) Infinite many solutions, if ρ(A : B) = ρ(A) < Number of unknowns
(3) No solution, if ρ(A : B) ≠ ρ(A).
The value of k for which the system of equations.
kx - y = 2
6x - 2y = 3
has a unique solution is- a)= 3
- b)≠ 3
- c)≠ 0
- d)= 0
Correct answer is option 'B'. Can you explain this answer?
The value of k for which the system of equations.
kx - y = 2
6x - 2y = 3
has a unique solution is
kx - y = 2
6x - 2y = 3
has a unique solution is
a)
= 3
b)
≠ 3
c)
≠ 0
d)
= 0
|
EduRev JEE answered |
Let consider a standard pair of linear equation such that,
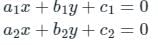
For the pair of linear equations, the condition for the unique solution is,
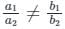
Given a pair of linear equation is,
kx - y = 2
6x - 2y = 3
These equations can be written as,
⇒ kx - y - 2 = 0
⇒ 6x - 2y - 3 = 0
On comparing it with standard pair of linear equation, we get,
⇒ a1 = k, b1 = -1, c1 = -2
⇒ a2 = 6, b2 = -2, c2 = -3
Using the condition for unique solution,
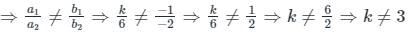
So, the value of k for which the system of equations has unique solution,
k ≠ 3
Hence, the correct option is 2.
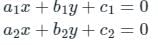
For the pair of linear equations, the condition for the unique solution is,
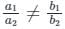
Given a pair of linear equation is,
kx - y = 2
6x - 2y = 3
These equations can be written as,
⇒ kx - y - 2 = 0
⇒ 6x - 2y - 3 = 0
On comparing it with standard pair of linear equation, we get,
⇒ a1 = k, b1 = -1, c1 = -2
⇒ a2 = 6, b2 = -2, c2 = -3
Using the condition for unique solution,
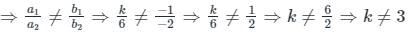
So, the value of k for which the system of equations has unique solution,
k ≠ 3
Hence, the correct option is 2.
A set of linear equations is given in the form Ax = b, where A is a 2 × 4 matrix with real number entries and b ≠ 0. Will it be possible to solve for x and obtain a unique solution by multiplying both left and right sides of the equation by AT (the super script T denotes the transpose) and inverting the matrix AT A? Answer is - a)Yes, it is always possible to get a unique solution for any 2 × 4 matrix A.
- b)No, it is not possible to get a unique solution for any 2 × 4 matrix A.
- c)Yes, can obtain a unique solution provided the matrix AT A is well conditioned
- d)Yes, can obtain a unique solution provided the matrix A is well conditioned.
Correct answer is option 'B'. Can you explain this answer?
A set of linear equations is given in the form Ax = b, where A is a 2 × 4 matrix with real number entries and b ≠ 0. Will it be possible to solve for x and obtain a unique solution by multiplying both left and right sides of the equation by AT (the super script T denotes the transpose) and inverting the matrix AT A? Answer is
a)
Yes, it is always possible to get a unique solution for any 2 × 4 matrix A.
b)
No, it is not possible to get a unique solution for any 2 × 4 matrix A.
c)
Yes, can obtain a unique solution provided the matrix AT A is well conditioned
d)
Yes, can obtain a unique solution provided the matrix A is well conditioned.
|
Learners Habitat answered |
From the properties of a matrix,
The rank of m × n matrix is always ≤ min {m, n}
If the rank of matrix A is ρ(A) and rank of matrix B is ρ(B), then the rank of matrix AB is given by
ρ(AB) ≤ min {ρ(A), ρ(B)}
If n × n matrix is singular, the rank will be less than ≤ n
Given:
AX = B
Where A is 2 × 4 matrices and b ≠ 0
The order of AT is 4 × 2
The order of ATA is 4 × 4
Rank of (A) ≤ min (2, 4) = 2
Rank of (AT) ≤ min (2, 4) = 2
Rank (ATA) ≤ min (2, 2) = 2
As the matrix ATA is of order 4 × 4, to have a unique solution the rank of ATA should be 4.
Therefore, the unique solution of this equation is not possible.
The rank of m × n matrix is always ≤ min {m, n}
If the rank of matrix A is ρ(A) and rank of matrix B is ρ(B), then the rank of matrix AB is given by
ρ(AB) ≤ min {ρ(A), ρ(B)}
If n × n matrix is singular, the rank will be less than ≤ n
Given:
AX = B
Where A is 2 × 4 matrices and b ≠ 0
The order of AT is 4 × 2
The order of ATA is 4 × 4
Rank of (A) ≤ min (2, 4) = 2
Rank of (AT) ≤ min (2, 4) = 2
Rank (ATA) ≤ min (2, 2) = 2
As the matrix ATA is of order 4 × 4, to have a unique solution the rank of ATA should be 4.
Therefore, the unique solution of this equation is not possible.
The value of k, for which the following system of linear equations has a non-trivial solution.
x + 2y - 3z = 0
2x + y + z = 0
x - y + kz = 0- a)4
- b)2
- c)3
- d)-4
Correct answer is option 'A'. Can you explain this answer?
The value of k, for which the following system of linear equations has a non-trivial solution.
x + 2y - 3z = 0
2x + y + z = 0
x - y + kz = 0
x + 2y - 3z = 0
2x + y + z = 0
x - y + kz = 0
a)
4
b)
2
c)
3
d)
-4
|
|
Infinity Academy answered |
Consider the system of m linear equations
a11 x1 + a12 x2 + … + a1n xn = 0
a21 x1 + a22 x2 + … + a2n xn = 0
…
am1 x1 + am2 x2 + … + amn xn = 0
The above equations containing the n unknowns x1, x2, …, xn. To determine whether the above system of equations is consistent or not, we need to find the rank of the following matrix.
A is the coefficient matrix of the given system of equations.
a11 x1 + a12 x2 + … + a1n xn = 0
a21 x1 + a22 x2 + … + a2n xn = 0
…
am1 x1 + am2 x2 + … + amn xn = 0
The above equations containing the n unknowns x1, x2, …, xn. To determine whether the above system of equations is consistent or not, we need to find the rank of the following matrix.
A is the coefficient matrix of the given system of equations.
- The system of homogeneous equations has a unique solution (trivial solution) if and only if the determinant of A is non-zero.
- The system of homogeneous equations has a Non - trivial solution if and only if the determinant of A is zero.
Given:
x + 2y – 3z = 0
2x + y + z = 0
x – y + kz = 0
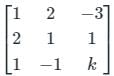
For non-trivial, solution the determinant should be zero
∴ 1(k + 1) – 2(2k - 1) – 3(-2 - 1) = 0
∴ k + 1 – 4k + 2 + 9 = 0
∴ 12 = 3k
∴ k = 4
x + 2y – 3z = 0
2x + y + z = 0
x – y + kz = 0
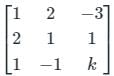
For non-trivial, solution the determinant should be zero
∴ 1(k + 1) – 2(2k - 1) – 3(-2 - 1) = 0
∴ k + 1 – 4k + 2 + 9 = 0
∴ 12 = 3k
∴ k = 4
A 3 × 3 matrix is such that, P3 = P. Then the eigenvalues of P are
- a)1, 2, −1
- b)
- c)
- d)0, 1, −1
Correct answer is option 'D'. Can you explain this answer?
A 3 × 3 matrix is such that, P3 = P. Then the eigenvalues of P are
a)
1, 2, −1
b)
c)
d)
0, 1, −1
|
Bs Academy answered |
CAYLEY-HAMILTON THEOREM:
Statement: Every square matrix satisfies its own characteristic equation.
The Cayley–Hamilton theorem states that substituting the matrix A for x in polynomial, p(x) = det(xIn – A), results in the zero matrices, such as:
p(A) = 0
It states that a ‘n x n’ matrix A is demolished by its characteristic polynomial det(tI – A), which is monic polynomial of degree n.
Uses of Cayley-Hamilton theorem:
(1) To calculate the positive integral powers of A
(2) To calculate the inverse of a square matrix A
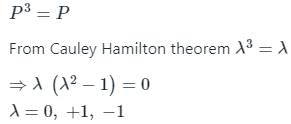
Statement: Every square matrix satisfies its own characteristic equation.
The Cayley–Hamilton theorem states that substituting the matrix A for x in polynomial, p(x) = det(xIn – A), results in the zero matrices, such as:
p(A) = 0
It states that a ‘n x n’ matrix A is demolished by its characteristic polynomial det(tI – A), which is monic polynomial of degree n.
Uses of Cayley-Hamilton theorem:
(1) To calculate the positive integral powers of A
(2) To calculate the inverse of a square matrix A
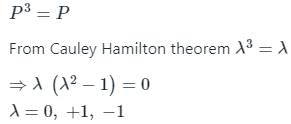
Let v1, . . . , v9 be the column vectors of a non-zero 9 × 9 real matrix A. Let a1, . . . , a9 ∈ ℝ, not all zero, be such that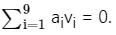 
Then the system Ax = 
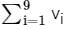has- a)no solution
- b)a unique solution
- c)more than one but only finitely many solutions
- d)infinitely many solutions
Correct answer is option 'D'. Can you explain this answer?
Let v1, . . . , v9 be the column vectors of a non-zero 9 × 9 real matrix A. Let a1, . . . , a9 ∈ ℝ, not all zero, be such that 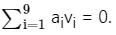Then the system Ax = 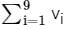has
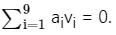Then the system Ax = 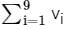hasa)
no solution
b)
a unique solution
c)
more than one but only finitely many solutions
d)
infinitely many solutions
|
|
EduRev JEE answered |
v1, . . . , vn be the column vectors of a non-zero n × n real matrix A. Let a1, . . . , an ∈ ℝ, not all zero, be such that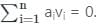 
that means v1, . . . , vn are Linearly independent.
In the system of equations when the system is L.I. then rank (A) = number of unknowns then it has a unique solution.
if at least one ���� not equal to zero vector(s) are Linearly dependent.
In the system of equations when rank of A < n then it has infinitely many solution(s)
Here, given that ,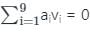
where all ���� are not zero Hence vectors are linearly dependent
When vectors are Linearly independent then in system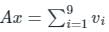
rank of A is less than 9 (number of column vectors )
Hence, it has infinitely many solutions.
Therefore, the Correct Option is Option (4).
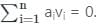
that means v1, . . . , vn are Linearly independent.
In the system of equations when the system is L.I. then rank (A) = number of unknowns then it has a unique solution.
if at least one ���� not equal to zero vector(s) are Linearly dependent.
In the system of equations when rank of A < n then it has infinitely many solution(s)
Here, given that ,
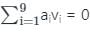where all ���� are not zero Hence vectors are linearly dependent When vectors are Linearly independent then in system
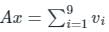rank of A is less than 9 (number of column vectors )Hence, it has infinitely many solutions.
Therefore, the Correct Option is Option (4).
If the system
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Has infinitely many solutions, then the values of a and b, respectively, are- a)– 8 and 6
- b)8 and 6
- c)– 8 and –6
- d)8 and –6
Correct answer is option 'B'. Can you explain this answer?
If the system
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Has infinitely many solutions, then the values of a and b, respectively, are
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Has infinitely many solutions, then the values of a and b, respectively, are
a)
– 8 and 6
b)
8 and 6
c)
– 8 and –6
d)
8 and –6
|
|
Bs Academy answered |
Consider the system of m linear equations
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
…
am1 x1 + am2 x2 + … + amn xn = bm
The above equations containing the n unknowns x1, x2, …, xn. To determine whether the above system of equations is consistent or not, we need to find the rank of following matrices.
A is the coefficient matrix and [A|B] is called as augmented matrix of the given system of equations.
We can find the consistency of the given system of equations as follows:
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
…
am1 x1 + am2 x2 + … + amn xn = bm
The above equations containing the n unknowns x1, x2, …, xn. To determine whether the above system of equations is consistent or not, we need to find the rank of following matrices.
A is the coefficient matrix and [A|B] is called as augmented matrix of the given system of equations.
We can find the consistency of the given system of equations as follows:
- If the rank of matrix A is equal to the rank of augmented matrix and it is equal to the number of unknowns, then the system is consistent and there is a unique solution, i.e.
Rank of A = Rank of augmented matrix = n - If the rank of matrix A is equal to the rank of augmented matrix and it is less than the number of unknowns, then the system is consistent and there are an infinite number of solutions.
Rank of A = Rank of augmented matrix < n - If the rank of matrix A is not equal to the rank of the augmented matrix, then the system is inconsistent, and it has no solution.
Rank of A ≠ Rank of augmented matrix
Calculation:
Given linear system is
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Then augmented matrix form is written below;
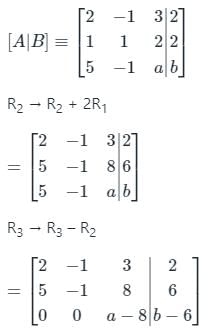
For rank (A) < n = 3
‘a’ must be = 8
For rank [A|B] < 3, b = 6
Therefore a = 8 & b = 6
Given linear system is
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Then augmented matrix form is written below;
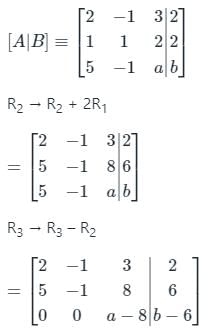
For rank (A) < n = 3
‘a’ must be = 8
For rank [A|B] < 3, b = 6
Therefore a = 8 & b = 6
If a system of simultaneous equations has infinite solutions, then that system of equations is called:- a)Opposite
- b)Unopposite
- c)Dependent
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If a system of simultaneous equations has infinite solutions, then that system of equations is called:
a)
Opposite
b)
Unopposite
c)
Dependent
d)
None of these
|
|
Top Rankers answered |
When a system of simultaneous equations has infinite solutions, it's called a "dependent" system of equations.
In such a scenario, the equations are representing the same line or are multiples of each other, leading to an infinite number of solutions where the equations overlap entirely.
Therefore, the correct term for a system with infinite solutions is "dependent."
In such a scenario, the equations are representing the same line or are multiples of each other, leading to an infinite number of solutions where the equations overlap entirely.
Therefore, the correct term for a system with infinite solutions is "dependent."
Chapter doubts & questions for System of Linear Equations, Eigen Values & Eigen Vectors - Mathematics for Competitive Exams 2025 is part of Mathematics exam preparation. The chapters have been prepared according to the Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of System of Linear Equations, Eigen Values & Eigen Vectors - Mathematics for Competitive Exams in English & Hindi are available as part of Mathematics exam.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Mathematics for Competitive Exams
98 videos|37 docs|32 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup