All questions of Algebra for Mechanical Engineering Exam
If f(x) = -2x + 8 & f(p) = 16, find the value of p?- a)-12
- b)-8
- c)-4
- d)4
- e)12
Correct answer is option 'C'. Can you explain this answer?
If f(x) = -2x + 8 & f(p) = 16, find the value of p?
a)
-12
b)
-8
c)
-4
d)
4
e)
12
|
Palak Saha answered |
Given, f(x) = -2x + 8 and f(p) = 16
To find: The value of p
Solution:
Substitute f(p) = 16 in the equation f(x) = -2x + 8
f(p) = -2p + 8 = 16
-2p = 16 - 8
-2p = 8
Divide both sides by -2
p = 8/-2
p = -4
Therefore, the value of p is -4.
Hence, the correct option is (c) -4.
To find: The value of p
Solution:
Substitute f(p) = 16 in the equation f(x) = -2x + 8
f(p) = -2p + 8 = 16
-2p = 16 - 8
-2p = 8
Divide both sides by -2
p = 8/-2
p = -4
Therefore, the value of p is -4.
Hence, the correct option is (c) -4.
If g(x) = -2x2 + 8 and g (-q) = -24, which of the following could be the value of q?- a)-4
- b)-2
- c)-1
- d)1
- e)2
Correct answer is option 'A'. Can you explain this answer?
If g(x) = -2x2 + 8 and g (-q) = -24, which of the following could be the value of q?
a)
-4
b)
-2
c)
-1
d)
1
e)
2
|
|
Parth Singh answered |
Given:
- g(x) = -2x^2 + 8
- g(-q) = -24
To find:
- Possible values of q
Solution:
Substitute -q in place of x in g(x) to get g(-q)
g(-q) = -2(-q)^2 + 8
g(-q) = -2q^2 + 8
Given that g(-q) = -24, we can set up the equation:
-2q^2 + 8 = -24
Simplifying, we get:
-2q^2 = -32
Dividing by -2, we get:
q^2 = 16
Taking the square root of both sides, we get:
q = ±4
Therefore, the possible values of q are -4 and 4.
Option A (-4) is the correct answer.
- g(x) = -2x^2 + 8
- g(-q) = -24
To find:
- Possible values of q
Solution:
Substitute -q in place of x in g(x) to get g(-q)
g(-q) = -2(-q)^2 + 8
g(-q) = -2q^2 + 8
Given that g(-q) = -24, we can set up the equation:
-2q^2 + 8 = -24
Simplifying, we get:
-2q^2 = -32
Dividing by -2, we get:
q^2 = 16
Taking the square root of both sides, we get:
q = ±4
Therefore, the possible values of q are -4 and 4.
Option A (-4) is the correct answer.
A polynomial function P(x) is defined as,
P(x) = 4x3 – 2x2
If P (z -2) =0 & z ≠ 2, find the value of z?
- a)-3/2
- b)+1/2
- c)1
- d)+5/2
- e)+7/2
Correct answer is option 'D'. Can you explain this answer?
A polynomial function P(x) is defined as,
P(x) = 4x3 – 2x2
If P (z -2) =0 & z ≠ 2, find the value of z?
a)
-3/2
b)
+1/2
c)
1
d)
+5/2
e)
+7/2
|
Siddharth Pillai answered |
Solution:
Given, P(x) = 4x3 - 2x2
Let z-2 = k
P(z-2) = P(k) = 4k3 - 2k2
We know that P(k) = 0
Therefore, 4k3 - 2k2 = 0
2k2(2k - 1) = 0
k = 0 or k = 1/2
Now, z-2 = k
So, z = k+2
For k = 0, z = 2
For k = 1/2, z = 5/2
Therefore, the possible values of z are 2 and 5/2, but since z ≤ 2, the only possible value of z is 5/2.
Hence, the correct answer is option (D) 5/2.
Given, P(x) = 4x3 - 2x2
Let z-2 = k
P(z-2) = P(k) = 4k3 - 2k2
We know that P(k) = 0
Therefore, 4k3 - 2k2 = 0
2k2(2k - 1) = 0
k = 0 or k = 1/2
Now, z-2 = k
So, z = k+2
For k = 0, z = 2
For k = 1/2, z = 5/2
Therefore, the possible values of z are 2 and 5/2, but since z ≤ 2, the only possible value of z is 5/2.
Hence, the correct answer is option (D) 5/2.
$x = 6x +4 and £x = 8x – 2Find the value of x for which $x = £x?- a)-3
- b)-2
- c)1
- d)2
- e)3
Correct answer is option 'E'. Can you explain this answer?
$x = 6x +4 and £x = 8x – 2
Find the value of x for which $x = £x?
a)
-3
b)
-2
c)
1
d)
2
e)
3
|
|
Bhavana Kulkarni answered |
Solution:
Given, $x = 6x + 4$ and $x = 8x - 2$
Simplifying the above equations, we get
$5x = -4$ and $7x = 2$
Solving for x, we get
$x = -\frac{4}{5}$ and $x = \frac{2}{7}$
Since both values of x are not equal, we cannot find the value of x for which $x = x$ from the given equations.
Therefore, the answer is none of the given options.
Given, $x = 6x + 4$ and $x = 8x - 2$
Simplifying the above equations, we get
$5x = -4$ and $7x = 2$
Solving for x, we get
$x = -\frac{4}{5}$ and $x = \frac{2}{7}$
Since both values of x are not equal, we cannot find the value of x for which $x = x$ from the given equations.
Therefore, the answer is none of the given options.
If the sum of the first five terms of an Arithmetic sequence is equal to 120 and the sum of the next five terms of the same Arithmetic Sequence is equal to 245, what is the 4th term of this Sequence?- a)29
- b)34
- c)81
- d)86
- e)91
Correct answer is option 'A'. Can you explain this answer?
If the sum of the first five terms of an Arithmetic sequence is equal to 120 and the sum of the next five terms of the same Arithmetic Sequence is equal to 245, what is the 4th term of this Sequence?
a)
29
b)
34
c)
81
d)
86
e)
91
|
Lavanya Menon answered |
Given:
- Sum of the first 5 terms of an arithmetic sequence = 120
- Sum of the next 5 terms of the same arithmetic sequence = 245
- Let the first term of this arithmetic sequence be x1 and let the common difference be d.
To Find:
- 4th term of the arithmetic sequence.
- So the 4th term of the sequence will become x1+3d
- So we need to find the value of x1 and d or the value of x1+3d to find the 4th term of the sequence.
Approach:
- We know that the sum of first n terms of the Arithmetic Sequence is given as
where n is the number of terms in the arithmetic sequence.- Using the formula above for the sum of first 5 terms of the sequence, we will get an equation in terms of and common difference d, as we are given the sum of first 5 terms of the sequence.
- We are also given the sum of next 5 terms of the sequence. So, we will be able to calculate the sum of first 10 terms of the sequence.
→ Sum of first 10 terms of sequence = Sum of first 5 terms + sum of next 5 terms. - Using the formula above for the sum of first 10 terms of sequence, we will get another equation in terms of x1 and common difference d.
- Using these two equations in x1 and d, we will be able to calculate the value of x1 and d.
- Knowing the values of x1 and d, we will be able to calculate the fourth term of the sequence, which is equal to x1+3d
Working out:
- Sum of first 5 terms of the arithmetic sequence = 120
- Putting this in formula of sum of first n terms, where n=5 and z=120, we get
- Sum of the next 5 terms of the sequence = 245
- Sum of the first 10 terms of the sequence = Sum of the first five terms + Sum of the next five terms.
- Sum of the first 10 terms of the sequence = 120+245 = 365
- Sum of the first 10 terms of the sequence = 120+245 = 365
- Now, using the formula of the sum of first n terms of an arithmetic sequence, we get
- Solving Equations 1 and 2.
- Multiplying ‘equation 1’ by 2, we have 10x1+20d =240 ...(Equation 3)
Now that we have values of x1 and d. The value of 4th term of the sequence will be
⇒ x1+3(d)=14+3(5)=29
Answer:
- The value of 4th term of the sequence is 29.
- Hence the correct answer is option A
Alternate method
- Let the first term be 'a' and common dfference between any two cosecutive terms be 'd'
Therefore,
- 1st term = a
- 5th term = a + 4d
- 6th term = a + 5d
- 10th term = a + 9d
- Average of first five terms of an arithemetic sequence = (First term + Last term)/2 = (a + a +4d) / 2 = a + 2d
- Sum of first five terms = Average of first five terms * 5 = (a + 2d) * 5 = 120
- a + 2d = 120/5 = 24 ---------------- Eq(1)
- Average of next five terms of the arithemetic sequence = (First term + Last term)/2 = (a+ 5d + a +9d) / 2 = a + 7d
- Sum of five terms = Average of five terms * 5 = (a + 7d) * 5 = 245
- a + 7d = 245/5 = 49---------------- Eq(2)
Solving Eq(1) and (2) we get
- d = 5
- 4th term =
- a + 3d = (a+2d)+ d = 24 + 5 = 29
Correct Answer: Option A
If f(x) = 3x + 6, then what is the value of f (2) + f(7)? - a)f(8)
- b)f(9)
- c)f(10)
- d)f(11)
- e)f(12)
Correct answer is option 'D'. Can you explain this answer?
If f(x) = 3x + 6, then what is the value of f (2) + f(7)?
a)
f(8)
b)
f(9)
c)
f(10)
d)
f(11)
e)
f(12)
|
|
Arjun Iyer answered |
Solution:
Given: f(x) = 3x - 6
We need to find f(2) + f(7)
Substituting x = 2 and x = 7 in the given equation, we get:
f(2) = 3(2) - 6 = 0
f(7) = 3(7) - 6 = 15
Therefore, f(2) + f(7) = 0 + 15 = 15
Hence, the correct answer is option D.
Given: f(x) = 3x - 6
We need to find f(2) + f(7)
Substituting x = 2 and x = 7 in the given equation, we get:
f(2) = 3(2) - 6 = 0
f(7) = 3(7) - 6 = 15
Therefore, f(2) + f(7) = 0 + 15 = 15
Hence, the correct answer is option D.
If one of the roots of the quadratic equation x2 + bx + 98 = 0 is the average (arithmetic mean) of the roots of the equation x2 + 28x – 588 = 0, what is the other root of the equation x2 + bx + 98 = 0?- a)-7
- b)−5/2
- c)5/2
- d)7
- e)21
Correct answer is option 'A'. Can you explain this answer?
If one of the roots of the quadratic equation x2 + bx + 98 = 0 is the average (arithmetic mean) of the roots of the equation x2 + 28x – 588 = 0, what is the other root of the equation x2 + bx + 98 = 0?
a)
-7
b)
−5/2
c)
5/2
d)
7
e)
21
|
|
Pranab Dasgupta answered |
Given
To Find: value of n?
Approach
- We know that the product of roots m and n is equal to c/a
- So, we can write m*n = 98, i.e. n = 98/m
- So, for finding n, we need to find m
- We are given that m = (p+q)/2
- We know that sum of roots of the quadratic equation is −b/a
- We will use this relation to find the value of p + q and hence the value of m
Hence, the other root of the equation x2 + bx + 98 = 0 is -7
Answer: A
For any integers x and y, min(x, y) and max(x, y) denote the minimum and the maximum of x and y, respectively. For example, min(2, 1) = 1 and max(2,1) = 2. If a, b, c and d are distinct positive integers, is max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))) ?(1) b, c and d are factors of a(2) a – 2d = b + c- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
For any integers x and y, min(x, y) and max(x, y) denote the minimum and the maximum of x and y, respectively. For example, min(2, 1) = 1 and max(2,1) = 2. If a, b, c and d are distinct positive integers, is max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))) ?
(1) b, c and d are factors of a
(2) a – 2d = b + c
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Sounak Iyer answered |
Problem Analysis:
We are given the expressions max(a, max(b, min(c, d))) and max(d, max(a, min(b, c))). We need to determine if these two expressions are equal.
Statement 1: b, c, and d are factors of a.
If b, c, and d are factors of a, it means that a is divisible by b, c, and d. In other words, a should be the multiple of b, c, and d.
Statement 2: a - 2d = b and ca
From this statement, we can deduce that b = a - 2d and c = a - 2d. This implies that b and c are both positive integers.
Combined Analysis:
From Statement 1, we know that a is divisible by b, c, and d. Therefore, a is a multiple of b, c, and d.
From Statement 2, we know that b = a - 2d and c = a - 2d. Substituting these values in the expression max(a, max(b, min(c, d))) gives us:
max(a, max(a - 2d, min(a - 2d, d)))
We can simplify this expression as follows:
1. If a > a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
2. If a < a="" -="" 2d,="" then="" max(a="" -="" 2d,="" min(a="" -="" 2d,="" d))="max(a" -="" 2d,="" a="" -="" 2d)="a" -="" />
3. If a = a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
Therefore, in all cases, max(a, max(b, min(c, d))) = a - 2d.
Similarly, substituting the values in the expression max(d, max(a, min(b, c))) gives us:
max(d, max(a, min(a - 2d, d)))
We can simplify this expression as follows:
1. If d > a, then max(a, min(a - 2d, d)) = max(a, d) = d
2. If d < a,="" then="" max(a,="" min(a="" -="" 2d,="" d))="max(a," a="" -="" 2d)="" />
3. If d = a, then max(a, min(a - 2d, d)) = max(a, d) = a
Therefore, in all cases, max(d, max(a, min(b, c))) = a - 2d.
Since both expressions simplify to a - 2d, we can conclude that max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))).
Therefore, both statements together are sufficient to answer the question.
Answer: (C) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
We are given the expressions max(a, max(b, min(c, d))) and max(d, max(a, min(b, c))). We need to determine if these two expressions are equal.
Statement 1: b, c, and d are factors of a.
If b, c, and d are factors of a, it means that a is divisible by b, c, and d. In other words, a should be the multiple of b, c, and d.
Statement 2: a - 2d = b and ca
From this statement, we can deduce that b = a - 2d and c = a - 2d. This implies that b and c are both positive integers.
Combined Analysis:
From Statement 1, we know that a is divisible by b, c, and d. Therefore, a is a multiple of b, c, and d.
From Statement 2, we know that b = a - 2d and c = a - 2d. Substituting these values in the expression max(a, max(b, min(c, d))) gives us:
max(a, max(a - 2d, min(a - 2d, d)))
We can simplify this expression as follows:
1. If a > a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
2. If a < a="" -="" 2d,="" then="" max(a="" -="" 2d,="" min(a="" -="" 2d,="" d))="max(a" -="" 2d,="" a="" -="" 2d)="a" -="" />
3. If a = a - 2d, then max(a - 2d, min(a - 2d, d)) = max(a - 2d, d) = a - 2d
Therefore, in all cases, max(a, max(b, min(c, d))) = a - 2d.
Similarly, substituting the values in the expression max(d, max(a, min(b, c))) gives us:
max(d, max(a, min(a - 2d, d)))
We can simplify this expression as follows:
1. If d > a, then max(a, min(a - 2d, d)) = max(a, d) = d
2. If d < a,="" then="" max(a,="" min(a="" -="" 2d,="" d))="max(a," a="" -="" 2d)="" />
3. If d = a, then max(a, min(a - 2d, d)) = max(a, d) = a
Therefore, in all cases, max(d, max(a, min(b, c))) = a - 2d.
Since both expressions simplify to a - 2d, we can conclude that max(a, max(b, min(c, d))) = max(d, max(a, min(b, c))).
Therefore, both statements together are sufficient to answer the question.
Answer: (C) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
In the equation ax2 + bx + c = 0, where a, b and c are constants and a ≠ 0, what is the value of b?(1) 3 and 4 are roots of the equation.(2) The product of the roots of the equation is 12.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
In the equation ax2 + bx + c = 0, where a, b and c are constants and a ≠ 0, what is the value of b?
(1) 3 and 4 are roots of the equation.
(2) The product of the roots of the equation is 12.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Pranav Das answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given equation is
ax2+bx+c=0
It is also given that a, b and c are constants and that a≠0.
We need to find the value of b.
Step 3: Analyze Statement 1
It is given that 3 and 4 are the roots of the equation.
We know that for a quadratic equation
ax2+bx+c=0
ax2+bx+c=0
Sum of roots = −b/a
Product of roots = c/a
Therefore, we have:
−ba = 3 + 4 = 7………..(I)
c/ a = 3 * 4 = 12 …………(II)
Note that these are two linear equations in three variables. So we cannot solve exclusively for b.
Statement 1 alone is not sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
It is given that the product of roots is 12.
Therefore, we have:
c/a = 12 …….(III)
Notice that (III) is a single linear equation in two variables. Moreover, it doesn’t provide any information about b.
So statement 2 alone is not sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
Now let us look at both the statements together.
Statement 1 gives us (I) and (II)
Statement 2 gives us (III).
However, notice that (III) is essentially same as (II).
In other words, we are simply left with (I) and (II) (essentially the same situation as in statement 1).
Therefore statement 1 and statement 2 combined together are not sufficient to arrive at a unique answer.
Answer: Option (E)
The sequence a1, a2,…an is such that an = an-1 +n*d for all n > 1, where d is a positive integer. If a3 = 20 and a5 = 47, what is the value of a7?- a)53
- b)65
- c)75
- d)80
- e)86
Correct answer is option 'E'. Can you explain this answer?
The sequence a1, a2,…an is such that an = an-1 +n*d for all n > 1, where d is a positive integer. If a3 = 20 and a5 = 47, what is the value of a7?
a)
53
b)
65
c)
75
d)
80
e)
86
|
|
Kavya Chakraborty answered |
Given
- A sequence a1, a2,…an
- an = an-1 +n*d for all n > 1, where d is an integer > 0
- a3 = 20
- a5 = 47
To Find: a7?
Approach
- As an = an-1 +n*d, we can express a7 in terms of a1 and d
- So, we need to find the value of a1 and d.
- As we are given the values of a3 and a5, we will express them in terms of a1 and d to get 2 equations in a1 and d.
- We will then solve these two equations to find out the value of a1 and d.
Working Out
Solving (1) and (2), we have a1 = 5 and d = 3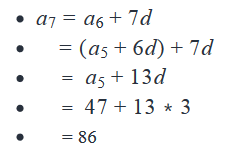 
Answer: E
If f(x) = 3x2 – 5x + 9 and g(x) = 4x – 5, then find the value of g( f(x)) at x = 3. - a)7
- b)51
- c)56
- d)79
- e)121
Correct answer is option 'D'. Can you explain this answer?
If f(x) = 3x2 – 5x + 9 and g(x) = 4x – 5, then find the value of g( f(x)) at x = 3.
a)
7
b)
51
c)
56
d)
79
e)
121
|
|
Kiran Nambiar answered |
The information provided in the question is:
f(x) = 3x2 – 5x + 9
g(x) = 4x – 5
We have to find out the value of g( f(x)) at x = 3.
f(x) = 3x2 – 5x + 9
f(3) = 3*(3)2 – 5*3 + 9
= 27 – 15 + 9
= 21
g(x) = 4x – 5
g(f(x)) = 4f(x) -5
g( f(3)) = 4f(3) – 5
= 4*21 – 5
= 84 – 5
= 79
Answer: Option (D)
If the sum of the first 30 positive odd integers is k, what is the sum of first 30 non-negative even integers?- a)k-29
- b)k-30
- c)k
- d)k+29
- e)k+30
Correct answer is option 'B'. Can you explain this answer?
If the sum of the first 30 positive odd integers is k, what is the sum of first 30 non-negative even integers?
a)
k-29
b)
k-30
c)
k
d)
k+29
e)
k+30
|
|
Moumita Sen answered |
Given
- 1 + 3 + 5………..30*2 -1 = k.
- Let’s call this sequence O
To Find: 0 + 2+ 4………30 *2 -2 = ?
- Let’s call this sequence E
Approach
- To express the sum of sequence E in terms of k, we need to express the terms of sequence E in terms of sequence O
- Now, we see that we can write 0 = 1 – 1
- Similarly, we can write 2 = 3 -1
- Continuing the same pattern, we can write 58 = 59 -1
- Observe that 1, 3…..59 are terms of sequence O. So, using the above process we have captured all the terms of sequence O in sequence E
- We will use the above logic to represent the sum of sequence E in terms of k
Working Out
- 0 + 2+ 4……58 = (1-1) + (3-1) +…….(59- 1) = 1+ 3+ 5…….59 – (1 + 1 + 1……….30 times)
- 0 + 2 + 4 …….+ 58 = k – 30
Answer: B
The nth term of an increasing sequence S is given by Sn = Sn-1 + Sn-2 for n > 2 and the nth term of a sequence S’ is given by S’n = S’n-1 - S’n-2 for n > 2. If S5 = S’5, what is the average (arithmetic mean) of S2 and S’2?(1) The difference between the fourth term and the second term of sequence S is 14.(2) The sum of the fourth term and the second term of sequence S’ is 14.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
The nth term of an increasing sequence S is given by Sn = Sn-1 + Sn-2 for n > 2 and the nth term of a sequence S’ is given by S’n = S’n-1 - S’n-2 for n > 2. If S5 = S’5, what is the average (arithmetic mean) of S2 and S’2?
(1) The difference between the fourth term and the second term of sequence S is 14.
(2) The sum of the fourth term and the second term of sequence S’ is 14.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
Aarav Sharma answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Increasing sequence S whose nth term is represented as Sn = Sn-1 + Sn-2 for n > 2
- For a sequence S’, the nth term of which is represented as S’n = S’n-1 - S’n-2 for n > 2
- S5 = S’5
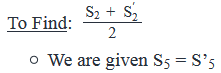
Thus we need to find the value of S3 to find the average of S2 andS′2
Step 3: Analyze Statement 1 independently
(1) The difference between the fourth term and the second term of sequence S is 14
- S4−S2=14
- Substituting the expression of S4=S3+S2
- (S3+S2)−S2=14,i.e.S3=14
As we know the value of S3, the statement is sufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The sum of the fourth term and the second term of sequence S’ is 14.
- S′2+S′4=14
- Substituting the expression of S′4=S′3−S′2
- S′2+(S′3−S′2)=14
- S′3=14
Does not tell us anything about the value of S3, the statement is insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step -3, this step is not required.
Answer: A
For which of the following functions is f(ab) = f(a) * f(b)? - f(x) = x2
- f (x) = √x
- f (x) = 2x
- a)I only
- b)I, II and III
- c)III only
- d)I and II
Correct answer is 'D'. Can you explain this answer?
For which of the following functions is f(ab) = f(a) * f(b)?
- f(x) = x2
- f (x) = √x
- f (x) = 2x
a)
I only
b)
I, II and III
c)
III only
d)
I and II
|
|
Srestha Basu answered |
Ex
The function f(x) = ex satisfies the property f(ab) = f(a) * f(b) because:
f(ab) = eab = ea * eb = f(a) * f(b)
Using the laws of exponents, we can see that eab = ea * eb, which means that f(ab) = f(a) * f(b) for this function.
The function f(x) = ex satisfies the property f(ab) = f(a) * f(b) because:
f(ab) = eab = ea * eb = f(a) * f(b)
Using the laws of exponents, we can see that eab = ea * eb, which means that f(ab) = f(a) * f(b) for this function.
If f(x) = x + x2, is f(a+1) – f(a) divisible by 4, where a is an integer > 0(1) f(a) is divisible by 4(2) (-1)a < (-1)a+1- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
If f(x) = x + x2, is f(a+1) – f(a) divisible by 4, where a is an integer > 0
(1) f(a) is divisible by 4
(2) (-1)a < (-1)a+1
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Disha Mehta answered |
Steps 1 & 2: Understand Question and Draw Inferences
The question wants us to know whether f(a+1) – f(a) is divisible by 4. Let’s simplify the expression given to us.
f(a+1) – f(a) = (a+1) + (a+1)2 – (a + a2)
Simplifying we get f(a+1) – f(a) = (a + 1 –a) + ((a+1)2 -a2))
- 1 + (a + 1 –a)(a+1+a) = 2 + 2a = 2(1+a) … (using a2 – b2 = (a-b)(a+b))
- From the statement above we can conclude that the given expression is always divisible by 2.
Hence, for f(a+1) – f(a) to be divisible by 4, (1+a) must be divisible by 2, which means that a must be odd.
Step 3: Analyze Statement 1
Statement 1 says that f(a) is divisible by 4.
f(a) = a(1+a)
a(1+a) is the product of two consecutive integers. Therefore, one term out of a and 1+a will be even and the other will be odd. The product of these two terms will be even and will always be divisible by 2.
But, we are given that a(1+a) is divisible by 4 also.
This can happen only if
a) a is divisible by 4 or
b) 1+a is divisible by 4 or
c) Both a and 1+a are divisible by 2
Case c) is ruled out since a and 1+a are consecutive terms. Therefore, they cannot be both even.
If a is divisible by 4, then a is even.
If 1+a is divisible by 4, then a is odd.
Thus, we cannot determine with confidence whether a is odd or not.
Since Statement 1 does not give us a unique answer, it is not sufficient.
Step 4: Analyze Statement 2
Statement 2 says that (-1)a < (-1)a+1
This is only possible if a is odd, implying that a+1 is even.
Thus, a is indeed odd.
Since statement 2 gives us a unique answer, it is sufficient to arrive at the conclusion.
Step 5: Analyze Both Statements Together (if needed)
Since statement 2 gave us a unique answer, this step is not needed.
Correct Answer: B
The function {x} is defined as the lowest odd integer greater than x. What is the value of {x}?(1) -3.1 < x < -2.5(2) x2 < 9- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
The function {x} is defined as the lowest odd integer greater than x. What is the value of {x}?
(1) -3.1 < x < -2.5
(2) x2 < 9
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Sreemoyee Nambiar answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let’s understand the meaning of {x}. If x = 2, then the odd integers greater than 2 are 3, 5, etc. The lowest among them is 3. Therefore {2} = 3.
Step 3: Analyze Statement 1
If x is between -3.1 and -3, then {x} = -3. If x is between -3 and -2.5, then {x} = -1.
INSUFFICIENT.
Step 4: Analyze Statement 2
x2 < 9 only for values of x between -3 and 3.
If x = is between -3 and – 1, {x} = -1, if x is between -1 and 1, {x} = 1 and if x is between 1 and 3, {x} = 3.
Therefore, {x} can be -1, 1 or 3.
INSUFFICIENT.
Step 5: Analyze Both Statements Together (if needed)
When we combine statements (1) and (2),
We know that
-3.1 < x < -2.5
AND
-3 < x < 3
The common solution is: -3 < x < -2.5
For this set of values, {x} = -1.
SUFFICIENT.
Answer: Option (C)
If x ≠ 0, for which of following functions is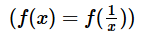 
, for all values of x?- a)
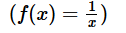
- b)
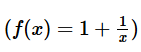
- c)
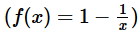
- d)
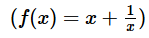
- e)
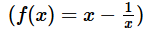
Correct answer is 'D'. Can you explain this answer?
If x ≠ 0, for which of following functions is 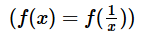, for all values of x?
, for all values of x?a)
b)
c)
d)
e)
|
KS Coaching Center answered |
Step 1: Question statement and Inferences
We have to pick the only option for which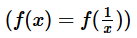 
, Since the option will have to be true for all the values of x, substituting numbers is not the best approach. We shall try to replace x with 1/x in each option.
, Since the option will have to be true for all the values of x, substituting numbers is not the best approach. We shall try to replace x with 1/x in each option.Step 2 & 3: Finding required values and finding the final answer
Let’s check each option one by one.
A.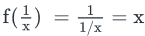 
.
.Not equal to f(x)
B. 
Not equal to f(x)
C.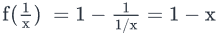 
. Not equal to f(x)
. Not equal to f(x)D.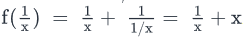 
Not equal to f(x)
Not equal to f(x)In the exam, you need not evaluate option (E) – since we already know that Option D is the answer- but here for practice, let’s evaluate it.
Not equal to f(x).
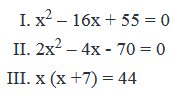Given the three quadratic equations above, which pair of equations has at least one common root?- a)I and II
- b)II and III
- c)I and III
- d)I, II and III
- e)None of the above
Correct answer is option 'E'. Can you explain this answer?
Given the three quadratic equations above, which pair of equations has at least one common root?
a)
I and II
b)
II and III
c)
I and III
d)
I, II and III
e)
None of the above
|
|
Nandita Chauhan answered |
Given
- Three quadratic equations:
- x2 – 16x + 55 = 0
- 2x2 – 4x - 70 = 0
- x (x +7) = 44
To Find: Which pair of equations has at least one common root?
Approach
- As we need to find the common roots among the equation, we will solve each quadratic equation to find their roots and then find the pair of equations that have at least one common root.
Working Out
So, the roots of Equations I, II and III are (5, 11), (-5, 7) and (-11, 4) respectively.
Hence, none of the equations have even one root in common.
Answer: E
For the positive integers k, m and n, k(m)n means that the remainder when m is divided by n is k. If k(13766)9 and p(137)k, where p is a positive integer, then p is equal to.- a)1
- b)2
- c)5
- d)7
- e)8
Correct answer is option 'B'. Can you explain this answer?
For the positive integers k, m and n, k(m)n means that the remainder when m is divided by n is k. If k(13766)9 and p(137)k, where p is a positive integer, then p is equal to.
a)
1
b)
2
c)
5
d)
7
e)
8
|
|
Mrinalini Dasgupta answered |
To solve this problem, we need to understand the properties of the operation k(m)n and use them to find the value of p in p(137)k.
Understanding the operation k(m)n:
- In the operation k(m)n, the remainder when m is divided by n is k.
- This means that k is the difference between m and the largest multiple of n that is less than or equal to m.
Solving k(13766)9:
- We are given that k(13766)9.
- This means that the remainder when 13766 is divided by 9 is k.
- To find k, we need to find the largest multiple of 9 that is less than or equal to 13766.
- The largest multiple of 9 less than or equal to 13766 is 13761 (9 * 1529).
- Therefore, k = 13766 - 13761 = 5.
Finding the value of p in p(137)k:
- We are given that p(137)k.
- This means that the remainder when 137 is divided by k is p.
- To find p, we need to find the largest multiple of k that is less than or equal to 137.
- Since k = 5, we need to find the largest multiple of 5 that is less than or equal to 137.
- The largest multiple of 5 less than or equal to 137 is 135 (5 * 27).
- Therefore, p = 137 - 135 = 2.
Conclusion:
- The value of p in p(137)k is 2.
- Therefore, the correct answer is option B.
Understanding the operation k(m)n:
- In the operation k(m)n, the remainder when m is divided by n is k.
- This means that k is the difference between m and the largest multiple of n that is less than or equal to m.
Solving k(13766)9:
- We are given that k(13766)9.
- This means that the remainder when 13766 is divided by 9 is k.
- To find k, we need to find the largest multiple of 9 that is less than or equal to 13766.
- The largest multiple of 9 less than or equal to 13766 is 13761 (9 * 1529).
- Therefore, k = 13766 - 13761 = 5.
Finding the value of p in p(137)k:
- We are given that p(137)k.
- This means that the remainder when 137 is divided by k is p.
- To find p, we need to find the largest multiple of k that is less than or equal to 137.
- Since k = 5, we need to find the largest multiple of 5 that is less than or equal to 137.
- The largest multiple of 5 less than or equal to 137 is 135 (5 * 27).
- Therefore, p = 137 - 135 = 2.
Conclusion:
- The value of p in p(137)k is 2.
- Therefore, the correct answer is option B.
What is the number of integral solutions of the equation 2x2 – 3x – 2 = 0?- a)0
- b)1
- c)2
- d)3
- e)4
Correct answer is option 'B'. Can you explain this answer?
What is the number of integral solutions of the equation 2x2 – 3x – 2 = 0?
a)
0
b)
1
c)
2
d)
3
e)
4
|
EduRev GATE answered |
- Using the quadratic formula:
- (3 ± √25) /4
- The two roots are:
- 8 /4 = 2
- -2 /4 = -1⁄2
- Since only x = 2 is an integer, the number of integral solutions is: 1
Edward invested five-ninths of his money at an annual rate of 2r% compounded semi-annually, and the remaining money at an annual rate of r% compounded annually. If after one year, Edward’s money had grown by one-thirds, the value of r is equal to which of the following?- a)10%
- b)15%
- c)20%
- d)25%
- e)33%
Correct answer is option 'C'. Can you explain this answer?
Edward invested five-ninths of his money at an annual rate of 2r% compounded semi-annually, and the remaining money at an annual rate of r% compounded annually. If after one year, Edward’s money had grown by one-thirds, the value of r is equal to which of the following?
a)
10%
b)
15%
c)
20%
d)
25%
e)
33%
|
|
Tanishq Choudhury answered |
Given: Let the total money be y
- First Investment:
-
-
- Rate of interest = 2r% p.a. compounded every 6 months = r% per 6-months
- Time = 1 year
-
- Second Investment:
-
-
- Rate of interest = r% p.a.
- Time = 1 year
-
- Total Interest earned in 1 year
To find: The value of r
Approach
1. Total interest earned in 1 year = (Interest earned from 1st investment) + (Interest earned from 2nd investment)
i. In the given time frame of 1 year, the 1st investment will pay interest twice (since this investment pays interest every 6 months). So, the formula for compound interest will be applicable for the 1st investment
ii. The 2nd investment pays interest after 1 year. Since the given time frame is also 1 year, this investment will yield simple interest
2. The only unknown in the above equation will be r. So, using this equation, we can find the value of r
Working Out
- Amount of the first investment after 1 year
- Compound Interest earned from 1st investment
- Calculating the interest earned from the 2nd investment:
- Simple interest earned from 2nd investment =
- So, Total interest earned in 1 year =
- Multiplying both sides of the above equation with 9/y :
- Simple interest earned from 2nd investment =
- Rejecting the negative value since the money is given to have grown.
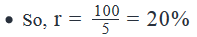
Looking at the answer choices, we see that Option C is correct
(Note: You could also have solved this question by framing the first equation in terms of the amount that each investment grows to, as under:
(Total Amount after 1 year) = (Amount that the 1st investment grows to) + (Amount that the 2nd investment grows to)
This equation leads to a similar calculation and the same result as in the solution above /End of Note)
If x2+4x+p=13 , where p is a constant, what is the product of the roots of this quadratic equation?(1) -2 is one of the roots of the quadratic equation(2) x2+4x+p=13 has equal roots- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If x2+4x+p=13 , where p is a constant, what is the product of the roots of this quadratic equation?
(1) -2 is one of the roots of the quadratic equation
(2) x2+4x+p=13 has equal roots
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Saumya Sharma answered |
Step 1 & Step 2: Understanding the Question statement and Drawing Inferences
Given Info:
- x2+4x+p=13
- Rewriting the above quadratic equation in standard form ax2+bx+c=0
- Subtracting 13 from both sides, we have
⇒ x2+4x+p−13=13−13
⇒ x2+4x+p−13=0
To find:
- We need to find the product of the quadratic equation → x2+4x+p−13=0
- To find the product of the roots:
- We need to know the roots or
- Products of roots of the quadratic equation ax2+bx+c=0 , is given by c/a
- So product of roots of the above quadratic equation will be (p−13)/1 , as →c=p-13 and a=1
- Now since we do not know the value of p-13, we will not be able to determine the product of roots of the quadratic equation.
- Thus we need to analyse the given statements further to determine the value of p, to be able to calculate the product of roots of the quadratic equation.
Step 3: Analyze statement 1 independently
Statement 1:
- -2 is one of the roots of the quadratic equation
- So, -2 will satisfy the given quadratic equation → x2+4x+p−13=0
⇒ (-2)2 + 4(-2) + p - 13 = 0
⇒ 4 - 8 + p - 13 = 0
⇒ p = 17
- Now since we know the value of p, we will be able to find the value of p-13 and thus will be able to calculate the value of product of quadratic equation.
- Hence statement 1 is sufficient to answer the question.
Step 4: Analyze statement 2 independently
Statement 2:
- Quadratic equation has equal roots
- For equal roots, we will use the relation of sum of roots of the quadratic equation to determine the value of the equal root.
- Sum of roots of the quadratic equation ax2+bx+c=0 , is −b/a
- So sum of roots of the quadratic equation → x2+4x+p−13=0 will be −4/1 , where b=4 and a=1
- Now since both roots are equal and the sum of the roots is coming as -4, both roots will thus be equal to – 2 each.
- Now, the equal root → -2, will satisfy the given quadratic equation x2+4x+p−13=0
⇒(-2)2 + 4(-2) + p - 13 = 0
⇒ p=17
- Now since we know the value of p, we will be able to find the value of p-13 and thus will be able to calculate the value of product of quadratic equation.
- Hence statement 2 is sufficient to answer the question
Step 5: Analyze the two statements together
- Since from statement 1 and statement 2, we are able to arrive at a unique answer, combining and analysing statements together is not required.
Hence the correct answer is option D
If [z] denotes the least integer greater than or equal to z and [z2] = 2, which of the following could be the value of [z]?I. 2II. 1III. -2- a)I only
- b)II only
- c)III only
- d)I and II only
- e)II and III only
Correct answer is option 'A'. Can you explain this answer?
If [z] denotes the least integer greater than or equal to z and [z2] = 2, which of the following could be the value of [z]?
I. 2
II. 1
III. -2
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
II and III only
|
|
Arjun Iyer answered |
Given:
- The function [z]
- [z2] = 2
To find: Can [z] be {2, 1, -2}?
Approach:
- To find which values of [z] are possible and which are not, we need to first know the range of possible values of z. Once we know what z can be, we’ll be able to find what [z] can be.
- We’ll get an idea of the possible values of z from the fact that [z2] = 2
Working Out:
- [z2] = 2
- This means, the least integer that is greater than or equal to z2 is 2.
- So, the value of z2 must be equal to 2 or must lie between 1 and 2 (because if z2 is less than 1 then [z2] would be 1 or less and not 2)
- We can write: 1 < z2 ≤ 2
- The above inequality contains 2 inequalities: z2 > 1 AND z2 ≤ 2
- So now, we’ll solve these inequalities one by one, and then find the values of z that satisfy both these inequalities
- Solving z2 > 1
- This means, z < - 1 or z > 1 . . . (1)
- The gray zones in the above figure represent the overlap zones, that is, those values of z that satisfy both the inequalities
- So, either -√2 ≤ z < -1 or 1 < z ≤ √2
Thus, we see that [z] is either equal to -1 or equal to 2. Out of the 3 given values, only value I (which is 2) is therefore possible.
Looking at the answer choices, we see that the correct answer is Option A
List A consists of 10 distinct integers arranged in ascending order. Is the difference between the sixth term and the fifth term of list A greater than 5?(1) The difference between any two integers in list A is a multiple of 5.(2) The median of the list is an integer.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
List A consists of 10 distinct integers arranged in ascending order. Is the difference between the sixth term and the fifth term of list A greater than 5?
(1) The difference between any two integers in list A is a multiple of 5.
(2) The median of the list is an integer.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Rhea Gupta answered |
Given:
- List A = {a1, a2, a3, a4, a5, a6, a7, a8, a9, a10}
- consists of all integers,
- where a10 > a9> a8…> a2> a1
To Find: Is a6 – a5 > 5?
Step 4: Analyse Statement 2 independently
The median of the list is an integer.
- Median =?
- List contains 10 elements
- a5 & a6 are integers at the centre of the list (in ascending order)
- Median of the list = a5+a62
-
- = m, where m is an integer
- Rearranging, we get a5+ a6 = 2m = even
- If sum of a6 & a5 is even, then
- Difference of a6 & a5 is also even
- No information about values of the terms , so cannot tell if (a6 – a5) > 5
- Hence, statement 2 is insufficient to answer the question.
Step 5: Analyse Both Statements Together (if needed)
- From statement 1, a6 – a5 = {5, 10, 15}
- From statement 2, a6 – a5 = even
- Combining the two,
- a6 – a5 = even multiples of 5 = {10, 20, 30…}
- a6 – a5 > 5
- So, we can answer the question.
- Hence statement 1 and statement 2 together are sufficient to arrive at a definite answer.
Answer: C
Step 3: Analyse Statement 1 independently
The difference between any two integers in list A is a multiple of 5.
- Difference between any two terms of A can be = {5,10,15…}
- a6 – a5 = {5, 10, 15…}
- Since the difference can also = 5, we cannot be certain that a6 – a5 > 5.
- Hence, Statement 1 is insufficient to answer the question.
Ted and Robin start from the same point at 7 AM and drive in opposite directions. Ted doubles his speed after every 90 minutes whereas Robin reduces her speed by half after every 120 minutes. If Ted starts driving at a speed of 10 kilometers/hour and Robin starts driving at a speed of 120 kilometers/hour, how far in kilometers will they be from one another at 1 PM?- a)195
- b)485
- c)525
- d)645
- e)675
Correct answer is option 'D'. Can you explain this answer?
Ted and Robin start from the same point at 7 AM and drive in opposite directions. Ted doubles his speed after every 90 minutes whereas Robin reduces her speed by half after every 120 minutes. If Ted starts driving at a speed of 10 kilometers/hour and Robin starts driving at a speed of 120 kilometers/hour, how far in kilometers will they be from one another at 1 PM?
a)
195
b)
485
c)
525
d)
645
e)
675
|
|
Srestha Basu answered |
Given
- Ted starts at 7 AM
- Ted’s initial speed = 10 kilometers/hour
- Ted doubles his speed after every 1.5 hours
- Robin starts at 7 AM from the same point as Ted and travels in opposite directions
- Robin’s initial speed = 120 kilometers/hour
- Robin reduces her speed by half after every 2 hours
To Find: Distance between Ted and Robin at 1 PM
- Find the distance travelled by Ted in 6 hours
- Find the distance travelled by Robin in 6 hours
Approach
Distance = Speed * Time
1. We need to find the distance travelled by Ted in 6 hours As Ted doubles his speed after every 1.5 hours, he will travel at 6/1.5=4
- different speeds during the period
- We know his initial speed and we know that he doubles his speed after every interval of 1.5 hours. So, we can calculate his speed for each interval
2. We need to find the distance travelled by Robin in 6 hours
- As Robin reduces her speed after every 2 hours, she will travel at 6/2=3
- different speeds during the period
- We know her initial speed and we know that she reduces her speed by half after every interval of 2 hours. So, we can calculate her speed for each interval.
Working Out
1. Ted
2. Robin
Distance between Ted and Robin at 1 PM = 225 + 420 = 645 kilometers
Answer: D
A quadratic equation ax2 + bx + c = 0 has two integral roots x1 and x2. If the square of the sum of the roots is 6 greater than the sum of the squares of the roots, which of the following could be the value of the ordered set (a, b, c)?I. (-1, 4, -3)II. (1, 4, 3)III. (3, -10√3, 9) - a)I Only
- b)II Only
- c)III Only
- d)I and II Only
- e)I, II and III Only
Correct answer is option 'D'. Can you explain this answer?
A quadratic equation ax2 + bx + c = 0 has two integral roots x1 and x2. If the square of the sum of the roots is 6 greater than the sum of the squares of the roots, which of the following could be the value of the ordered set (a, b, c)?
I. (-1, 4, -3)
II. (1, 4, 3)
III. (3, -10√3, 9)
a)
I Only
b)
II Only
c)
III Only
d)
I and II Only
e)
I, II and III Only
|
|
Nitya Kumar answered |
Given
To Find: Values of (a, b, c)
Approach
- For finding the values of (a, b, c), we would first need to find the value of x1 , x2
- We will use the relation
-
- to find out the values of x1 , x2
- Also, we will keep in mind the constraint that x1 , x2 are integers
- Now, we know that
- We will use the relation
- We will use the above relation to find out the possible values of (a, b, c)
As x1 , x2 are integers, the possible cases for (x1 , x2) is either (3,1) or (-3,-1)
- Using (1), (2) and (3), the values of (a, b, c) can be of the form ( a, 4a, 3a) or (a, -4a, 3a)
- Among the options,
- Option-I (-1, 4, -3) is of the form (a, -4a, 3a) and
- Option- II (1, 4, 3) is of the form (a, 4a, 3a)
Hence, options I and II can be the value of ordered set (a, b, c).
Answer: D
If the equation
(1 + t²) x² + 2 t c x + (c² – a²) = 0
has equal roots then which of the following is true?- a)t² = c² (1 + a²)
- b)a² = c² (1 + t²)
- c)c² = a² (1 + t²)
- d) ↵More than one of the above
Correct answer is option 'B'. Can you explain this answer?
If the equation
(1 + t²) x² + 2 t c x + (c² – a²) = 0
has equal roots then which of the following is true?
(1 + t²) x² + 2 t c x + (c² – a²) = 0
has equal roots then which of the following is true?
a)
t² = c² (1 + a²)
b)
a² = c² (1 + t²)
c)
c² = a² (1 + t²)
d)
↵
More than one of the above
|
|
Chirag Roy answered |
Understanding the Problem
To determine the conditions for the quadratic equation
(1 + t²)x² + 2tcx + (c² - a²) = 0
to have equal roots, we need to analyze its discriminant.
Discriminant Condition
For a quadratic equation Ax² + Bx + C = 0, the condition for equal roots is:
B² - 4AC = 0.
In our case:
- A = 1 + t²
- B = 2tc
- C = c² - a²
We substitute these values into the discriminant condition:
(2tc)² - 4(1 + t²)(c² - a²) = 0.
This simplifies to:
4t²c² - 4(1 + t²)(c² - a²) = 0.
Rearranging the Equation
Dividing through by 4, we get:
t²c² = (1 + t²)(c² - a²).
Expanding the right-hand side results in:
t²c² = c² + t²c² - a² - t²a².
Simplifying this gives:
0 = c² - a² - t²a².
Isolating a²
Rearranging the equation provides:
a² = c²(1 + t²).
This confirms that option B is correct: a² = c²(1 + t²).
Conclusion
Thus, for the quadratic equation to have equal roots, the condition that must hold true is option B.
To determine the conditions for the quadratic equation
(1 + t²)x² + 2tcx + (c² - a²) = 0
to have equal roots, we need to analyze its discriminant.
Discriminant Condition
For a quadratic equation Ax² + Bx + C = 0, the condition for equal roots is:
B² - 4AC = 0.
In our case:
- A = 1 + t²
- B = 2tc
- C = c² - a²
We substitute these values into the discriminant condition:
(2tc)² - 4(1 + t²)(c² - a²) = 0.
This simplifies to:
4t²c² - 4(1 + t²)(c² - a²) = 0.
Rearranging the Equation
Dividing through by 4, we get:
t²c² = (1 + t²)(c² - a²).
Expanding the right-hand side results in:
t²c² = c² + t²c² - a² - t²a².
Simplifying this gives:
0 = c² - a² - t²a².
Isolating a²
Rearranging the equation provides:
a² = c²(1 + t²).
This confirms that option B is correct: a² = c²(1 + t²).
Conclusion
Thus, for the quadratic equation to have equal roots, the condition that must hold true is option B.
r and s are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0 & s >0, such that r is 50 percent greater than s. If the product of the roots of the equation is 150, what is the sum of the roots of the equation?- a)-25
- b)-15
- c)15
- d)25
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
r and s are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0 & s >0, such that r is 50 percent greater than s. If the product of the roots of the equation is 150, what is the sum of the roots of the equation?
a)
-25
b)
-15
c)
15
d)
25
e)
Cannot be determined
|
|
Hridoy Gupta answered |
To solve this problem, let's start by assigning variables to the roots of the quadratic equation. Let's say that r is one root and s is the other root.
Given that r is 50% greater than s, we can express this relationship as:
r = 1.5s
We are also given that the product of the roots is 150. This means that:
rs = 150
Now, let's express the quadratic equation in terms of the roots:
ax^2 + bx + c = 0
Since r and s are the roots, we can write the equation as:
a(x - r)(x - s) = 0
Expanding this equation, we get:
ax^2 - (ar + as)x + rs = 0
Now, let's substitute the values of r and s into the equation:
ax^2 - (1.5as + as)x + 150 = 0
Simplifying further, we get:
ax^2 - 2.5asx + 150 = 0
Since the quadratic equation is in the form ax^2 + bx + c = 0, we can equate the coefficients to find the sum of the roots:
b/a = -2.5as/a
b = -2.5as
Since the sum of the roots is equal to -b/a, we can substitute the value of b:
Sum of roots = -(-2.5as)/a
Sum of roots = 2.5s
Now, we can substitute the value of rs = 150 into the equation rs = 150:
s(1.5s) = 150
1.5s^2 = 150
Dividing both sides by 1.5, we get:
s^2 = 100
Taking the square root of both sides, we get:
s = 10
Now, substituting the value of s into the equation for the sum of the roots:
Sum of roots = 2.5s
Sum of roots = 2.5(10)
Sum of roots = 25
Therefore, the sum of the roots of the quadratic equation is 25. So, the correct answer is option D) 25.
Given that r is 50% greater than s, we can express this relationship as:
r = 1.5s
We are also given that the product of the roots is 150. This means that:
rs = 150
Now, let's express the quadratic equation in terms of the roots:
ax^2 + bx + c = 0
Since r and s are the roots, we can write the equation as:
a(x - r)(x - s) = 0
Expanding this equation, we get:
ax^2 - (ar + as)x + rs = 0
Now, let's substitute the values of r and s into the equation:
ax^2 - (1.5as + as)x + 150 = 0
Simplifying further, we get:
ax^2 - 2.5asx + 150 = 0
Since the quadratic equation is in the form ax^2 + bx + c = 0, we can equate the coefficients to find the sum of the roots:
b/a = -2.5as/a
b = -2.5as
Since the sum of the roots is equal to -b/a, we can substitute the value of b:
Sum of roots = -(-2.5as)/a
Sum of roots = 2.5s
Now, we can substitute the value of rs = 150 into the equation rs = 150:
s(1.5s) = 150
1.5s^2 = 150
Dividing both sides by 1.5, we get:
s^2 = 100
Taking the square root of both sides, we get:
s = 10
Now, substituting the value of s into the equation for the sum of the roots:
Sum of roots = 2.5s
Sum of roots = 2.5(10)
Sum of roots = 25
Therefore, the sum of the roots of the quadratic equation is 25. So, the correct answer is option D) 25.
Mike took 5 mock tests before appearing for the GMAT. In each mock test he scored 10 points more than the previous mock test. If he scored 760 on the GMAT and his average score for the mocks was 720, what is the difference between his last mock score and his GMAT score?- a)10
- b)20
- c)30
- d)40
- e)50
Correct answer is option 'B'. Can you explain this answer?
Mike took 5 mock tests before appearing for the GMAT. In each mock test he scored 10 points more than the previous mock test. If he scored 760 on the GMAT and his average score for the mocks was 720, what is the difference between his last mock score and his GMAT score?
a)
10
b)
20
c)
30
d)
40
e)
50
|
|
Rhea Gupta answered |
Given
Mike took 5 mock tests
- Let his score in the 1st mock be x.
- So, his scores in the other mocks = x+ 10, x+20, x+30, x + 40
- Mike’s score on GMAT = 760
- Average score of mocks = 720
To Find:
- 760 – (x +40)
Working Out
Average score of mocks = (x + x + 10 + … x + 40) /5 = (5x + 100)/5 = x + 20
(The other way to think about this is, as Mike’s scores in the mocks are in arithmetic sequence, average will be the middle term)
(The other way to think about this is, as Mike’s scores in the mocks are in arithmetic sequence, average will be the middle term)
- Mike’s average score in the mocks = x + 20 = 720
- x = 700
Therefore
- x + 40 = 740
- 760 – (x+40) = 760 – 740 = 20
Correct Answer: Option B
If v* = (1/v), find the value ofv* + (v*)* + ((v*)*)* if v = 1/2.- a)3
- b)7/2
- c)4
- d)9/2
- e)5
Correct answer is option 'D'. Can you explain this answer?
If v* = (1/v), find the value of
v* + (v*)* + ((v*)*)* if v = 1/2.
a)
3
b)
7/2
c)
4
d)
9/2
e)
5
|
|
Abhishek Choudhury answered |
Step 1: Question statement and Inferences
A function has been defined called v* such that v* = 1v
Step 2 & 3: Finding required values and calculating the final answer
v = 1/2
=> v*=1v=2
=> (v*)* = (2)* = 1/2
=> ((v*)*)* = (1/2)* = 2
=> v* + (v*)* + ((v*)*)* = 2 + 1/2 + 2 = 9/2.
Answer: Option (D)
What is the value of s+t if the equation 3x2 + tx + s has 2 and 3 as its roots?- a)1
- b)2
- c)3
- d)4
- e)5
Correct answer is option 'C'. Can you explain this answer?
What is the value of s+t if the equation 3x2 + tx + s has 2 and 3 as its roots?
a)
1
b)
2
c)
3
d)
4
e)
5
|
|
EduRev GATE answered |
- Given the equation 3x² + tx + s = 0 with roots 2 and 3:
- Sum of roots: 2 + 3 = 5 ⇒ -t /3 = 5 ⇒ t = -15
- Product of roots: 2 × 3 = 6 ⇒ s /3 = 6 ⇒ s = 18
- s + t = 18 + (-15) = 3
- Answer: 3
If p and q are the roots of the quadratic equation ax2 + bx + c = 0, where a*b*c ≠ 0, is the product of p and q greater than 0?(1) |p + q| = |p| + |q|(2) ac > 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If p and q are the roots of the quadratic equation ax2 + bx + c = 0, where a*b*c ≠ 0, is the product of p and q greater than 0?
(1) |p + q| = |p| + |q|
(2) ac > 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Pallavi Sharma answered |
Understanding the Problem
We need to determine if the product of the roots p and q of the quadratic equation ax² + bx + c = 0 is greater than 0, given that a, b, and c are non-zero.
Key Concept
The product of the roots of a quadratic equation is given by the formula p*q = c/a. To determine if p*q > 0, we need to analyze the signs of c and a.
Statement (1): |p + q| = |p| + |q|
This statement implies that both p and q have the same sign. When both roots share the same sign, their product p*q will be positive.
Thus, statement (1) alone is sufficient to conclude that the product of the roots is greater than 0.
Statement (2): ac > 0
This statement means that both a and c are either positive or negative.
- If both a and c are positive, then p*q = c/a > 0.
- If both a and c are negative, then p*q = c/a > 0.
In both cases, the product p*q is greater than 0, making statement (2) alone sufficient as well.
Conclusion
Since both statements independently confirm the product of the roots p and q is greater than 0, we can conclude:
- Statement (1) alone is sufficient.
- Statement (2) alone is sufficient.
Thus, the correct answer is option 'd': EACH statement ALONE is sufficient to answer the question asked.
We need to determine if the product of the roots p and q of the quadratic equation ax² + bx + c = 0 is greater than 0, given that a, b, and c are non-zero.
Key Concept
The product of the roots of a quadratic equation is given by the formula p*q = c/a. To determine if p*q > 0, we need to analyze the signs of c and a.
Statement (1): |p + q| = |p| + |q|
This statement implies that both p and q have the same sign. When both roots share the same sign, their product p*q will be positive.
Thus, statement (1) alone is sufficient to conclude that the product of the roots is greater than 0.
Statement (2): ac > 0
This statement means that both a and c are either positive or negative.
- If both a and c are positive, then p*q = c/a > 0.
- If both a and c are negative, then p*q = c/a > 0.
In both cases, the product p*q is greater than 0, making statement (2) alone sufficient as well.
Conclusion
Since both statements independently confirm the product of the roots p and q is greater than 0, we can conclude:
- Statement (1) alone is sufficient.
- Statement (2) alone is sufficient.
Thus, the correct answer is option 'd': EACH statement ALONE is sufficient to answer the question asked.
A function f(x) is defined as f(x)=3x2−20x+c, where c is a constant. Also given f(1) = -16. What is the value of f(c) + f(-c) ?- a)6
- b)8
- c)10
- d)12
- e)30
Correct answer is option 'B'. Can you explain this answer?
A function f(x) is defined as f(x)=3x2−20x+c, where c is a constant. Also given f(1) = -16. What is the value of f(c) + f(-c) ?
a)
6
b)
8
c)
10
d)
12
e)
30
|
|
Sankar Desai answered |
Given Information:
- Function f(x) = 3x^2 + 20x + c
- f(1) = -16
Calculating the value of c:
Given f(1) = -16
Substitute x = 1 into the function:
3(1)^2 + 20(1) + c = -16
3 + 20 + c = -16
23 + c = -16
c = -16 - 23
c = -39
Calculating f(c) and f(-c):
Substitute x = c into the function:
f(c) = 3c^2 + 20c + c
f(c) = 3(-39)^2 + 20(-39) - 39
f(c) = 3(1521) - 780 - 39
f(c) = 4563 - 780 - 39
f(c) = 3744 - 39
f(c) = 3705
Substitute x = -c into the function:
f(-c) = 3(-c)^2 + 20(-c) - 39
f(-c) = 3(39)^2 - 20(39) - 39
f(-c) = 3(1521) - 780 - 39
f(-c) = 4563 - 780 - 39
f(-c) = 3744 - 39
f(-c) = 3705
Calculating f(c) + f(-c):
f(c) + f(-c) = 3705 + 3705
f(c) + f(-c) = 7410
Therefore, the value of f(c) + f(-c) is 7410, which corresponds to option B.
- Function f(x) = 3x^2 + 20x + c
- f(1) = -16
Calculating the value of c:
Given f(1) = -16
Substitute x = 1 into the function:
3(1)^2 + 20(1) + c = -16
3 + 20 + c = -16
23 + c = -16
c = -16 - 23
c = -39
Calculating f(c) and f(-c):
Substitute x = c into the function:
f(c) = 3c^2 + 20c + c
f(c) = 3(-39)^2 + 20(-39) - 39
f(c) = 3(1521) - 780 - 39
f(c) = 4563 - 780 - 39
f(c) = 3744 - 39
f(c) = 3705
Substitute x = -c into the function:
f(-c) = 3(-c)^2 + 20(-c) - 39
f(-c) = 3(39)^2 - 20(39) - 39
f(-c) = 3(1521) - 780 - 39
f(-c) = 4563 - 780 - 39
f(-c) = 3744 - 39
f(-c) = 3705
Calculating f(c) + f(-c):
f(c) + f(-c) = 3705 + 3705
f(c) + f(-c) = 7410
Therefore, the value of f(c) + f(-c) is 7410, which corresponds to option B.
Given the equation x2 + bx + c = 0, where b and c are constants, what is the value of c?(1) The sum of the roots of the equation is zero.(2) The sum of the squares of the roots of the equation is equal to 18.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
Given the equation x2 + bx + c = 0, where b and c are constants, what is the value of c?
(1) The sum of the roots of the equation is zero.
(2) The sum of the squares of the roots of the equation is equal to 18.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Kiran Nambiar answered |
Solution:
Given equation is x2 bx c = 0, where b and c are constants
To find: value of c
Statement 1: The sum of the roots of the equation is zero.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
The sum of the roots is zero, so:
α + β = 0
−b = 0
b = 0
From the equation, we can conclude that c = αβ = 0. This statement alone is sufficient to answer the question.
Statement 2: The sum of the squares of the roots of the equation is equal to 18.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
We are given that:
α2 + β2 = 18
Squaring the equation α + β = −b, we get:
α2 + 2αβ + β2 = b2
Substituting the values of αβ and b2, we get:
α2 + 2c + β2 = b2
α2 + β2 = b2 − 2c
Substituting the given value of α2 + β2, we get:
18 = b2 − 2c
We can solve for c in terms of b:
c = (b2 − 18)/2
However, we do not know the value of b, so we cannot determine the value of c. This statement alone is not sufficient to answer the question.
Together, statements 1 and 2 give us:
b = 0
α2 + β2 = b2 − 2c = 0 − 2c = −2c
Substituting the given value of α2 + β2, we get:
18 = −2c
c = −9
Therefore, both statements together are sufficient to answer the question. The answer is (C).
Given equation is x2 bx c = 0, where b and c are constants
To find: value of c
Statement 1: The sum of the roots of the equation is zero.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
The sum of the roots is zero, so:
α + β = 0
−b = 0
b = 0
From the equation, we can conclude that c = αβ = 0. This statement alone is sufficient to answer the question.
Statement 2: The sum of the squares of the roots of the equation is equal to 18.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
We are given that:
α2 + β2 = 18
Squaring the equation α + β = −b, we get:
α2 + 2αβ + β2 = b2
Substituting the values of αβ and b2, we get:
α2 + 2c + β2 = b2
α2 + β2 = b2 − 2c
Substituting the given value of α2 + β2, we get:
18 = b2 − 2c
We can solve for c in terms of b:
c = (b2 − 18)/2
However, we do not know the value of b, so we cannot determine the value of c. This statement alone is not sufficient to answer the question.
Together, statements 1 and 2 give us:
b = 0
α2 + β2 = b2 − 2c = 0 − 2c = −2c
Substituting the given value of α2 + β2, we get:
18 = −2c
c = −9
Therefore, both statements together are sufficient to answer the question. The answer is (C).
If p and q are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0, what are the roots of the equation ayx2 + byx + cy = 0 where 0 < y ≤ 1?- a)p and q
- b)py and qy
- c)p/yand q/y
- d)y and -y
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
If p and q are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0, what are the roots of the equation ayx2 + byx + cy = 0 where 0 < y ≤ 1?
a)
p and q
b)
py and qy
c)
p/yand q/y
d)
y and -y
e)
Cannot be determined
|
|
Rajdeep Nair answered |
Given
- ax2+bx+c=0
- has two roots p and q a ≠ 0, 0 < y ≤ 1
To Find
- Roots of ayx2+byx+cy=0
Approach
- To find the roots of the equation ayx2+byx+cy=0 , we will do the following steps:
- Take y common and the get the equation in terms of ax2+bx+c=0
- As we know the roots of ax2+bx+c=0, we will use this knowledge to find the roots of the equation ayx2+byx+cy=0
- Working OutSolving the equation ayx2+byx+cy=0
- ayx2+byx+cy=0
- y(ax2+bx+c)=0
So we have either y = 0 or ax2+bx+c=0
Since we are given that y > 0, y ≠ 0.
Hence ax2+bx+c=0
.As the roots of the equation ax2+bx+c=0 are p and q, the roots of the equation ayx2+byx+cy=0 will also be p and q.
Answer: A
The function SCI is defined as SCI(x, y) = z, where z is the sum of y consecutive positive integers starting from positive integer x. If a and n are positive integers, is SCI(a,n) divisible by n?(1) 3n +2a is not divisible by 2(2) 3a +2n is divisible by 2- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
The function SCI is defined as SCI(x, y) = z, where z is the sum of y consecutive positive integers starting from positive integer x. If a and n are positive integers, is SCI(a,n) divisible by n?
(1) 3n +2a is not divisible by 2
(2) 3a +2n is divisible by 2
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Kiran Nambiar answered |
Steps 1 & 2: Understand Question and Draw Inferences
- SCI(x, y) = z, where z = x+ x+1 +x+2…….x+y-1 and x, y, z are integers > 0
- a, n are integers > 0
To Find: Is SCI(a, n) = nb, where quotient b is an integer?
- SCI(a, n) = a+ a+1….a+n -1
- The terms a, a + 1, a + 2…. a + n -1 are in arithmetic sequence with common difference = 1
- SCI(a, n) = Sum of an arithmetic sequence =
- For SCI
to be divisible by n, 
should be an integer. - That is
should be an integer - That is,
should be an integer, i.e. n -1 should be divisible by 2.
- That is
- For n -1 to be divisible by 2, n-1 = even, i.e. n = odd.
- Thus, if n is odd SCI(a, n) is divisible by n, else it is not. Hence, we need to find the even-odd nature of n.Step 3: Analyze Statement 1 independently(1) 3n +2a is not divisible by 2
- As 3n + 2a is not divisible by 2, 3n + 2a is odd
- 3n +2a = odd
- 3n + even = odd
- 3n = odd
- n = odd
- Since we know the even-odd nature of n, the statement is sufficient to answer.Step 4: Analyze Statement 2 independently(2) 3a +2n is divisible by 2
- As 3a + 2n is divisible by 2, 3a + 2n is even
- 3a + 2n = even
- 3a + even = even
- 3a = even
- Does not tell us anything about the even-odd nature of n.Insufficient to answer.Step 5: Analyze Both Statements Together (if needed)As we have a unique answer from step-3, this step is not required.Answer: A
If x is an integer and 
what is the value of x?- a)-3
- b)-1
- c)0
- d)2
- e)3
Correct answer is option 'E'. Can you explain this answer?
If x is an integer and 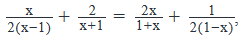what is the value of x?
what is the value of x?a)
-3
b)
-1
c)
0
d)
2
e)
3
|
|
Devika Yadav answered |
Given equation is
And, we need to find the value of x, given that x is an integer.
Step 2 & 3: Finding required values and calculating the final answer
Let us rewriting the last term of (I) to get x-1 in the denominator:
Let us now bring the terms with the same denominator together:
- (x + 1)2 = {2(x – 1)}2
- [(x+1)2-{2(x-1)}2 ]=0 ………….. (II)
- Observe that this is of the form a2 – b2 = (a+b)(a-b)So let us say:a = x + 1b = 2(x – 1) = 2x - 2Therefore:a + b = x + 1 + 2x – 2 = 3x -1a – b = x + 1 - 2x + 2 = -x + 3Therefore we can rewrite (II) as:(3x-1)(3-x)=0
- Putting each factor to zero:
Since it is given that x is an integer,
Thus, x = 3 is the required answer.
Answer: Option (E)
An increasing sequence consists of 4 negative integers and 6 positive integers. Is the sum of the sequence positive?(1) The difference between any two consecutive negative integers is 5 and the difference between any two consecutive positive integers is 2(2) The first term of the sequence is -16- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
An increasing sequence consists of 4 negative integers and 6 positive integers. Is the sum of the sequence positive?
(1) The difference between any two consecutive negative integers is 5 and the difference between any two consecutive positive integers is 2
(2) The first term of the sequence is -16
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Kirti Roy answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Let the sequence be
where 
To Find: Is 
Step 3: Analyze Statement 1 independently
(1) The difference between any two consecutive negative integers is 5 and the difference between any two consecutive positive integers is 2
Need to know the value of a1 and a5 to know if the sum of the sequence is greater than 0.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The first term of the sequence is -16
- a1=−16
- We do not know the difference between consecutive terms
Hence,
- Statement 2 alone is not sufficient
Step 5: Analyze Both Statements Together (if needed)
From Statement 1 we got
From Statement 2 we got
- a1 = -16
Combining both we get:
Now, if we notice carefully a5 is a positive integer,
- a5 ≥ 1
Therefore
- 6a5≥6
Hence
- 6a5−4 is always greater than zero.
Combining both statements was sufficient to answer the question
Correct Answer: C
if 2x2 = 24 -x4 and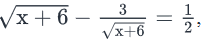 
which of the following can be the value of x?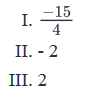
- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
if 2x2 = 24 -x4 and 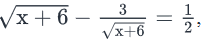which of the following can be the value of x?
which of the following can be the value of x?a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above
|
|
Sandeep Mehra answered |
Given:
Approach:
- To answer the question, we need to know the possible values of x.
- So, we’ll first solve Equation 1, then Equation 2 and then find the common roots of both these equations. These will be the possible values of x
- Then, we’ll evaluate the 3 options.
Working Out:
- Solving Equation I
- 2x2 = 24 -x4
- We can factorize this equation as it is, but if powers like x4 intimidate you, then it’s better to substitute x2 with a new variable, say z. That ways, the equation will look simpler: 2z = 24 – z2
- Rearranging the terms: z2 + 2z – 24 = 0
- z2 + 6z – 4z – 24 = 0
- z(z+6) – 4(z+6) = 0
- (z+6)(z-4) = 0
- This means, z = -6 or 4
- But z = x2. So, x2 = -6 or 4
- Perfect square x2 cannot be negative. Therefore, we can reject the negative root.
- So, x2 = 4
- Therefore, x = +2 or -2
- Thus, Equation I has 2 roots: 2 and -2
- Solving Equation II
- This equation looks difficult primarily because it involves a square root term,
. So, for the ease of our calculations, let’s substitute =y - So, the equation becomes:
- Multiplying both sides with 2y, we get: 2y2 – 6 = y
- Rearranging the terms: 2y2 – y – 6 = 0
-
- This means, y = -3/2 or y = 2
- Since y = we can write:
- However, since the square root of a number is always positive, the value of cannot be -3/2 .
- If you’ve any doubt about this, think: When you write z2 = 16 and then take the square root on both sides, you write: Either z = √16 or z = -√16. Note here that, in the ‘or’ case, you put the minus sign outside the value of √16. This minus sign makes z negative (we get z = -4 in the ‘or’ case) but √16 is always positive (equal to 4).
- Similarly, if we have z2 = x + 6, then on taking the square root on both sides, we will write: Either or
- z= - So, z may be positive or negative but will always be positive.
- So, =2
- Upon squaring both sides of this equation, we get: x + 6 = 4
- Therefore, x = -2
- Thus, we get a single value of x from Equation II
- Finding the possible values of x
- From Equation I: x = 2 or -2
- From Equation II: x = -2
- So, the value of x that satisfies both equations: x = -2
- Thus, only 1 value of x is possible: {-2}
- Evaluating the 3 options
- Out of the 3 given options, x can only be equal to -2
- Looking at the answer choices, we see that the correct answer is Option B
The area of a rectangle is 28 square centimeter. What is the perimeter of the rectangle?(1) If the length of the rectangle is increased by 10 centimeter and the breadth is decreased by 5 centimeter, the perimeter of the rectangle is eight times the original length of the rectangle.(2) If the length of the rectangle is increased by 350% and the breadth is increased to 350% of the original breadth, the perimeter of the rectangle is 63 centimeters more than the original perimeter of the rectangle.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
The area of a rectangle is 28 square centimeter. What is the perimeter of the rectangle?
(1) If the length of the rectangle is increased by 10 centimeter and the breadth is decreased by 5 centimeter, the perimeter of the rectangle is eight times the original length of the rectangle.
(2) If the length of the rectangle is increased by 350% and the breadth is increased to 350% of the original breadth, the perimeter of the rectangle is 63 centimeters more than the original perimeter of the rectangle.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Prashanth Chawla answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
Let the length and breadth of rectangle be L and B respectively
- LB = 28…..............................................(1)
To find: The value of 2(L+B)
- To find perimeter, we need to know the value of L and B.
Step 3: Analyze Statement 1 independently
(1) If the length of the rectangle is increased by 10 centimeter and the breadth is decreased by 5 centimeter, the perimeter of the rectangle is eight times the original length of the rectangle.
- New L = L +10
- New B = B - 5
So,
- New Perimeter = 2(L+10 + B-5)
- 2(L+10 + B-5) = 8L
- 2L + 2B + 10 = 8L
- 6L – 2B – 10 = 0
- 3L – B – 5 = 0
- B = 3L - 5 . . . . . . . . . . . . . . .. . . . .(2)
Substituting (2) in (1):
- 2 values of L (roots) will be obtained from this quadratic equation
Comparing this with the standard quadratic form : ax2 + bx + c = 0, we get : a = 1 ; b = -5/3 ; c = -28/3
- Product of these 2 values = (c/a) −283
-
- Since the product is negative, one root is positive and the other is negative
- The negative root will be rejected
- L, being the length of a rectangle, cannot be negative
- Thus, a unique value of L is obtained
- Using Equation (2), a unique value of B is also obtained
Hence, Statement 1 alone is sufficient.
Step 4: Analyze Statement 2 independently
- If the length of the rectangle is increased by 350% and the breadth is increased to 350% of the original breadth, the perimeter of the rectangle is 63 centimeters more than the original perimeter of the rectangle
- New L = 4.5L
- New B = 3.5B
So,
Substituting (3) in (1):
- 2 values of L (roots) will be obtained from this quadratic equation
Comparing this with the standard quadratic form : ax2 + bx + c = 0, we get :
a = 1 ; b = - 9 ; c = 20
- Product of these 2 values = (c/a) = 20
- Since the product is positive, the two roots are either both positive or both negative
- Sum of roots = (-b/a) = -(-9) = 9
- Since the sum is positive, it means both roots are positive
- Thus, St. 2 leads to 2 values of L
- From Equation (3), 2 values of B will be obtained
- So, 2 values of Perimeter will be obtained.
St. 2 is not sufficient to obtain a unique value of the perimeter.
Step 5: Analyze Both Statements Together (if needed)
Since we get a unique answer in Step 3, this step is not required
Answer: Option A
An arithmetic sequence is a sequence in which each term after the first is equal to the sum of the preceding term and a constant, which is also known as the common difference of that arithmetic sequence. An increasing arithmetic sequence N consists of a set of distinct negative integers and an increasing arithmetic sequence P consists of a set of distinct positive integers. The sequence C contains all the terms of arithmetic sequences N and P such that the number of terms in sequence C is equal to the number of terms in arithmetic sequences N and P. Is sequence C an arithmetic sequence?(1) The sum of the largest term of the sequence N and the smallest term of the sequence P is zero.(2) For every integer in sequence N, there exists an integer in sequence P with the same magnitude.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
An arithmetic sequence is a sequence in which each term after the first is equal to the sum of the preceding term and a constant, which is also known as the common difference of that arithmetic sequence. An increasing arithmetic sequence N consists of a set of distinct negative integers and an increasing arithmetic sequence P consists of a set of distinct positive integers. The sequence C contains all the terms of arithmetic sequences N and P such that the number of terms in sequence C is equal to the number of terms in arithmetic sequences N and P. Is sequence C an arithmetic sequence?
(1) The sum of the largest term of the sequence N and the smallest term of the sequence P is zero.
(2) For every integer in sequence N, there exists an integer in sequence P with the same magnitude.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Moumita Sen answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Increasing arithmetic sequence N consist of distinct negative integers with common difference n
- Increasing arithmetic sequence P consist of distinct positive integers with common difference m.
- Sequence C consist of terms of sequences N and P only.
To Find: Is sequence C an arithmetic sequence?
- As sequence C consists of terms of arithmetic sequences N and P only, for sequence C to be arithmetic, sequences N and P should have the same common difference.
- Also, sequences N and P will not have any common terms (as sequence N has all negative integers and sequence P has only positive integers), for sequence C to be arithmetic, the difference between the largest term of sequence N and the smallest term of sequence P should be equal to the common difference of the sequences.
- For ex: Consider N = { -10, -9, -8……-1) and P = { 2, 3, 4, 5, ….}. In this case, both the sequences N and P have the same common difference but combining their terms does not result in an arithmetic sequence because the difference between -1 and 2 is not equal to the common difference of the sequences.
- Consider N = { -14, -10, -6, -2} and P = {2, 6, 10}. In this case, as the difference between -2 and 2 is equal to the common differences of the sequences(i.e. 4), combining the terms of both the sequences results in an arithemetic sequence.
Step 3: Analyze Statement 1 independently
(1) The sum of the largest term of the sequence N and the smallest term of the sequence P is zero.
- Let the largest term of sequence N be x and the smallest term of the sequence P be y.
- So, x + y = 0
- x = -y
- So, difference between y and x = y – x = 2y
However we do not know the value of the common differences of the sequences as well as we do not know the value of y.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) For every integer in sequence N, there exists an integer in sequence P with the same magnitude.
- It tells us that integers in sequence P consist of negative of all the integers in sequence N. Following cases are possible:
- Number of terms of sequence N and P are the same. For ex: N= {-8, -6, -4} and P = {4, 6, 8}. In this case the common difference of both the sequences will be equal.
- Number of terms in sequence P is greater than the number of terms in sequence N. For ex: N = {-8, -6, -4} and P = {3, 4, 5, 6, 7, 8, 9} or { 4, 6, 8, 10, 12}. In this case the common difference may or may not be equal.
Also, as we do not know the difference between the largest term of sequence N and the smallest term of sequence P, the statement is insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
- Difference between the largest term of sequence N( i.e. x) and the smallest term of sequence P(i.e. y) is equal to 2y.
- For every integer in sequence N, there exists an integer in sequence P with the same magnitude
Combining both the statements tell us that the largest term of sequence N (i.e. x) and the smallest term of sequence P(i.e. y ) have the same magnitude.
However it does not tell us:
- the value of y and
- if the sequences have the same common difference
Hence, combining the statements is also insufficient to answer.
Answer: E
Steven and Stuart took a job in different companies at the same time. Steven’s salary increased by a fixed amount at the end of every year and Stuart’s salary increased by a fixed percentage at the end of every year. If the increase in the salary of Steven at the end of the third year was equal to the increase in the salary of Stuart at the end of the second year, what was the difference in the salaries of Steven and Stuart when they took the job?(1) Steven’s salary after 2 years was 20% more than the salary at which he took the job(2) The increase in the salary of Stuart at the end of the second year was 11% of the salary at which he took the job.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Steven and Stuart took a job in different companies at the same time. Steven’s salary increased by a fixed amount at the end of every year and Stuart’s salary increased by a fixed percentage at the end of every year. If the increase in the salary of Steven at the end of the third year was equal to the increase in the salary of Stuart at the end of the second year, what was the difference in the salaries of Steven and Stuart when they took the job?
(1) Steven’s salary after 2 years was 20% more than the salary at which he took the job
(2) The increase in the salary of Stuart at the end of the second year was 11% of the salary at which he took the job.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Kavya Chakraborty answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Let Steven’s initial salary be S1
and Stuart’s initial salary be S1
- Let Steven’s salary increase by x every year and Steven’s salary increase by y% every year.
- Steven’s salary increase in the 3rd year = x
- Stuart’s salary increase at the end of the 2nd year = y% of (Stuart’s salary in the 2nd year)
- Steven’s salary increase in the 3rd year = Stuart’s salary increase in the 2nd year
To Find: S1−S2
Step 3: Analyze Statement 1 independently
(1) Steven’s salary after 2 years was 20% more than the salary at which he took the job
- Steven’s salary after 2 years =S1+2x
However, we do not know anything about the values of S2, x and y.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The increase in the salary of Stuart at the end of the second year was 11% of the salary at which he took the job.
- Increase in Stuart’s salary at the end of the 2nd year =
Insufficient to answer as it does give us the value of S1,S2orx
Step 5: Analyze Both Statements Together (if needed)
Need to know the value of x to answer the question.
Insufficient to answer.
Answer: E
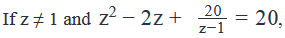then how many negative values can z take ? - a)None
- b)One
- c)Two
- d)Three
- e)A finite number greater than three
Correct answer is option 'B'. Can you explain this answer?
then how many negative values can z take ?a)
None
b)
One
c)
Two
d)
Three
e)
A finite number greater than three
|
|
Prateek Gupta answered |
To Find: Number of negative values of z
Approach:
- Solve the given equation
- Note that the denominator is z - 1.
- To remove the denominator, we will need to multiply each term of this equation with z - 1.
- This will be time consuming (because we will have to multiply each term with z as well as with -1. Example:
and is likely to result in a tedious calculation. - To simplify this process, we will substitute (z - 1) as x
- Find the value of z
- Count the number of negative values of z
Substitute z - 1 = x
Therefore z = x + 1 ; z - 2 = x -1
Hence
This is a cubic equation (involves x3) and you may feel that you do not know how to solve a cubic equation.
However, before giving up, think about how you solve a quadratic equation? By rewriting the given equation into its factors.
Let’s try if the cubic equation above can be similarly written into factors. We’ll find that the middle term, -21x, can be broken down as under:
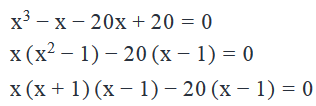
That is
- z - 1 = 1 or 4 or -5
- z = 2 or 5 or -4
- Thus, we get three values of z. However, the question asks specifically about the number of negative values of z.
- Among the 3 possible values of z, we see that only one value of z is negative.
Correct Answer: Option B
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is - a)13
- b)9
- c)21
- d)17
Correct answer is option 'C'. Can you explain this answer?
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is
a)
13
b)
9
c)
21
d)
17
|
|
EduRev GATE answered |
- Let 3 consecutive terms A.P is a –d, a , a + d. and the sum is 51
- so, (a –d) + a + (a + d) = 51
- ⇒ 3a –d + d = 51
- ⇒ 3a = 51
- ⇒ a = 17
- The product of first and third terms is 273
- So it stand for ( a –d) (a + d) = 273
- ⇒ a2 –d2 = 273
- ⇒ 172 –d 2 = 273
- ⇒ 289 –d 2 = 273
- ⇒ d 2 = 289 –273
- ⇒ d 2 = 16
- ⇒ d = 4
- Hence the 3rd terms ( a+d )= 17 + 4 = 21
If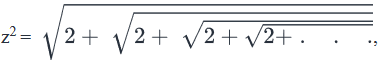 
where the given expression extends till infinity, which of the following statements must be true ?I. Two values are possible for zII. 4 - z2 = 2III. z8 = 16 - a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
If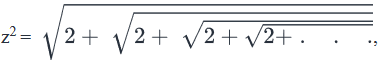
where the given expression extends till infinity, which of the following statements must be true ?
I. Two values are possible for z
II. 4 - z2 = 2
III. z8 = 16
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above
|
|
Kirti Roy answered |
Given:
.To find: Which of the given 3 statements must be true about z?
Approach:
- Looking at the 3 statements, we realize that in order to validate them, we’ll need to know the value of z
- We’re given an expression for z2. Using that expression, we’ll find the value of z
Working Out:
- Finding the value of z
-
- Notice that the series of within within
is never-ending. So, we can write:
-
To make our calculations easy, let’s replace z2 with another variable, say 'y'
- So, we get:
- Now, squaring both sides:
- y2 = 2 + y
- y2 – y – 2 = 0
- (y-2)(y+1) = 0
- So, y = 2 or y = -1
- Since y = z2 and perfect squares are never negative, y cannot be -1
- So, y = z2 = 2
- This means, either z√2 or z-√2
- Checking the validity of the 3 Statements
- Statement I: Two values are possible for z
-
- As we’ve found above, indeed only 2 values are possible for z
- Therefore, this statement is true
- Statement II: 4 - z2 = 2
- As we calculated above, z2 = 2
- So, 4 – z2 = 4 – 2 = 2
- So, this statement too is true
- Statement III: z8 = 16
- Since z2 = 2, (z2)4 = 24
- So, z8 = 16
- Therefore, this statement is true as well
- Looking at the answer choices, we see that the correct answer is Option D
A number x is multiplied with itself and then added to the product of 4 and x. If the result of these two operations is -4, what is the value of x?- a)-4
- b)-2
- c)2
- d)4
- e)Cannot be determined.
Correct answer is option 'B'. Can you explain this answer?
A number x is multiplied with itself and then added to the product of 4 and x. If the result of these two operations is -4, what is the value of x?
a)
-4
b)
-2
c)
2
d)
4
e)
Cannot be determined.
|
|
Rajdeep Nair answered |
Given
- x∗x+4∗x=−4
- x2 + 4x + 4 = 0
To Find: value of x?
Approach
- As we have a quadratic equation x2+4x+4=0
- , we will solve this equation to find out the value of x
Working Out
x2+4x+4=0
⇒(x+2)2=0
⇒x=−2
Answer: B
If x is a negative number, what is the value of x?(1) 16x2 – 16x – 5 = 0(2) ||4x+3| - 5| = 3- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
If x is a negative number, what is the value of x?
(1) 16x2 – 16x – 5 = 0
(2) ||4x+3| - 5| = 3
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Pranab Dasgupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: x < 0
To find: x = ?
Step 3: Analyze Statement 1 independently
(1) 16x2 – 16x – 5 = 0
x2–x−5/16=0
- 2 values of x (roots) will be obtained from this quadratic equation
- Product of these 2 values = −5/16
-
-
- Since the product is negative, one root is positive and the other is negative
-
- The positive root will be rejected (given: x < 0)
Thus, a unique value of x will be obtained from Statement 1
Statement 1 is sufficient to answer the question.
Step 4: Analyze Statement 2 independently
x= -5/4 We can reject this value as we know that x < 0
Thus, we get 3 possible negative values of x from Statement 2:
Not sufficient to find a unique value of x
Step 5: Analyze Both Statements Together (if needed)
Since we get a unique answer in Step 3, this step is not required
Answer: Option A
If x is equal to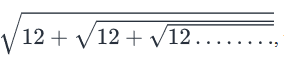 
, where the given expressions extend to an infinite number of roots, then what is the value of x?- a)-3
- b)-4
- c)3
- d)4
- e)12
Correct answer is option 'D'. Can you explain this answer?
If x is equal to 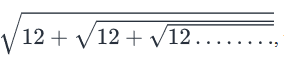, where the given expressions extend to an infinite number of roots, then what is the value of x?
, where the given expressions extend to an infinite number of roots, then what is the value of x?a)
-3
b)
-4
c)
3
d)
4
e)
12
|
|
Saumya Sharma answered |
Given
- to an infinite terms
- As the value of x is equal to the square root of something, x ≥ 0
To Find:
The value of x
Approach
x= 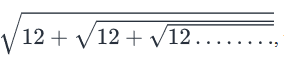to an infinite terms.
to an infinite terms.- Since the expression under the root extends infinitely, the expression under the root will be equal to x itself.
- So,
0………….(1) - By solving this equation and applying the constraint that x ≥0, we will find the value of x
Working Out
a.
b. Squaring both sides, we have
As we know that x≥ 0, x = 4
Answer: D
Alternate solution
- Once we have deduced that x will be positive the options -3 and -4 are eliminated
- We know √9 is 3. So the value of √(12+ ……) will be more than 3. Now we are left with 4 and 12 in the options
- Now √(12 + …..) cannot give us 12..
- So the answer has be 4.
Which one of the following is not a document related to fulfill the customs formalities- a)Letter of insurance
- b)Shipping bill
- c)Export licence
- d)Proforma invoice
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is not a document related to fulfill the customs formalities
a)
Letter of insurance
b)
Shipping bill
c)
Export licence
d)
Proforma invoice
|
Notes Wala answered |
Document Related to Fulfilling Customs Formalities:
There are several documents that are typically required to fulfill customs formalities. However, one of the following is not a document related to fulfilling customs formalities:
A: Letter of insurance
- The letter of insurance is not directly related to customs formalities but rather pertains to insurance coverage for the shipment.
B: Shipping bill
- The shipping bill is a document that contains details about the exported goods and is required by the customs authorities to process the shipment.
C: Export license
- An export license is a document issued by the appropriate government authority that grants permission to export specific goods. It is an essential document for customs clearance.
D: Proforma invoice
- The proforma invoice is a preliminary invoice that provides a detailed description of the goods to be exported, including their value and other relevant information. It is a crucial document for customs purposes.
Answer: D
- The proforma invoice is indeed a document related to fulfilling customs formalities. The correct answer is D, as stated in the question.
There are several documents that are typically required to fulfill customs formalities. However, one of the following is not a document related to fulfilling customs formalities:
A: Letter of insurance
- The letter of insurance is not directly related to customs formalities but rather pertains to insurance coverage for the shipment.
B: Shipping bill
- The shipping bill is a document that contains details about the exported goods and is required by the customs authorities to process the shipment.
C: Export license
- An export license is a document issued by the appropriate government authority that grants permission to export specific goods. It is an essential document for customs clearance.
D: Proforma invoice
- The proforma invoice is a preliminary invoice that provides a detailed description of the goods to be exported, including their value and other relevant information. It is a crucial document for customs purposes.
Answer: D
- The proforma invoice is indeed a document related to fulfilling customs formalities. The correct answer is D, as stated in the question.
For distinct positive integers x and y, where x < y, the function FP(x, y) returns the smallest prime number between x and y, exclusive, or the text string ‘NULL’ if no such number is found. If FP(a, b) +FP(c, d) = FP(e, f), where a, b, c, d, e and f are distinct positive integers, what is the value of ca ?(1) FP(g, h) = a, where g and h are distinct positive integers(2) c is less than the minimum possible value of the function FP(x,y).- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
For distinct positive integers x and y, where x < y, the function FP(x, y) returns the smallest prime number between x and y, exclusive, or the text string ‘NULL’ if no such number is found. If FP(a, b) +FP(c, d) = FP(e, f), where a, b, c, d, e and f are distinct positive integers, what is the value of ca ?
(1) FP(g, h) = a, where g and h are distinct positive integers
(2) c is less than the minimum possible value of the function FP(x,y).
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Pallavi Sharma answered |
Steps 1 & 2: Understand Question and Draw Inferences
- For positive integers x and y where x < y, FP(x, y) returns the smallest prime number between x and y, exclusive
- FP(a, b) +FP(c, d) = FP(e, f)
- FP(a, b), FP(c, d) and FP(e, f) each return a prime number
- So, the above equation conveys that the Sum of two prime numbers is equal to another prime number
- As all prime numbers except 2 are odd, FP(e, f) will be odd and either of FP(a, b) or FP(c, d) will be even i.e. 2
- For example, if both FP(a,b) and FP(c, d) are odd, then their sum i.e. FP(e, f) will be even, i.e. 2, which is not possible as there are no prime numbers less than 2
- So, the only case possible is that either of FP(a, b) or FP(c, d) is 2 and hence the sum of FP(a, b) and FP(c, d), which is FP (e, f) is odd
- If FP(a, b) = 2
- a = 1, ca = c
- If FP(c, d) = 2
- If c = 1, ca = 1
To Find: Value of c
Step 3: Analyze Statement 1 independently
(1) FP(g, h) = a, where g and h are distinct positive integers
- Since we know that FP(g, h) will return a prime number, we can infer that a is a prime number
- As a is a prime number, a > 1. So, FP(a, b) ≠ 2
- Hence FP(c, d) = 2
- For this to be possible, c = 1
If c = 1, ca = 1
Sufficient to answer
Step 4: Analyze Statement 2 independently
(2) c is less than the minimum possible value of the function FP(x,y).
- Minimum possible value of the function FP(x, y) = smallest prime number = 2
- So, c < 2,
- As c is given to be a positive integer and now we know that c < 2, the only possible value of c = 1
Hence ca = 1
Sufficient to answer
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from steps 3 and 4, this step is not required.
Answer: D
Chapter doubts & questions for Algebra - RRB JE Mock Test Series for Mechanical Engineering (ME) 2026 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Algebra - RRB JE Mock Test Series for Mechanical Engineering (ME) 2026 in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup