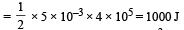All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Thermodynamics for NEET Exam
A mass of diatomic gas (γ= 1.4) at a pressure of 2 atmospheres is compressed adiabatically so that its temperature rises from 27°C to 927°C.The pressure of the gas in final state is [2011M]- a)28 atm
- b)68.7 atm
- c)256 atm
- d)8 atm
Correct answer is option 'C'. Can you explain this answer?
A mass of diatomic gas (γ= 1.4) at a pressure of 2 atmospheres is compressed adiabatically so that its temperature rises from 27°C to 927°C.The pressure of the gas in final state is [2011M]
a)
28 atm
b)
68.7 atm
c)
256 atm
d)
8 atm
|
|
Surendra Bishnoi answered |
Which of the following is not thermodynamical function ? [1993]- a)Enthalpy
- b)Work done
- c)Gibb's energy
- d)Internal energy
Correct answer is option 'B'. Can you explain this answer?
Which of the following is not thermodynamical function ? [1993]
a)
Enthalpy
b)
Work done
c)
Gibb's energy
d)
Internal energy

|
Anirudh Datta answered |
Work done is not a thermodynamical function.
One mole of an ideal gas goes from an initial state A to final state B via two processes : It first undergoes isothermal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The correct P-V diagram representing the two processes is : [2012]- a)

- b)

- c)

- d)

Correct answer is option 'D'. Can you explain this answer?
One mole of an ideal gas goes from an initial state A to final state B via two processes : It first undergoes isothermal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The correct P-V diagram representing the two processes is : [2012]
a)

b)

c)

d)


|
Shivani Tiwari answered |
1st process is isothermal expansion which is only correct shown in option (d) 2nd process is isobaric compression which is correctly shown in option (d)
During an isothermal expansion, a confined ideal gas does –150 J of work against its surroundings. This implies that [2011]- a)150 J heat has been removed from the gas
- b)300 J of heat has been added to the gas
- c)no heat is transferred because the process is isothermal
- d)150 J of heat has been added to the gas
Correct answer is option 'D'. Can you explain this answer?
During an isothermal expansion, a confined ideal gas does –150 J of work against its surroundings. This implies that [2011]
a)
150 J heat has been removed from the gas
b)
300 J of heat has been added to the gas
c)
no heat is transferred because the process is isothermal
d)
150 J of heat has been added to the gas

|
Vaibhav Basu answered |
From the first law of thermodynamics
ΔU = Q + W
For isothermal process, ΔU = 0
therefore, Q = - W
Given W = - 150
Therefore, Q = + 150
When Q is positive, the heat is added to the gas.
The internal energy change in a system that has absorbed 2 kcals of heat and done 500 J of work is: [2009]- a)6400 J
- b)5400 J
- c)7900 J
- d)8900 J
Correct answer is option 'C'. Can you explain this answer?
The internal energy change in a system that has absorbed 2 kcals of heat and done 500 J of work is: [2009]
a)
6400 J
b)
5400 J
c)
7900 J
d)
8900 J

|
Shivani Rane answered |
According to first law of thermodynamics Q = ΔU + W
ΔU = Q – W
= 2 × 4.2 × 1000 – 500 = 8400 –500
= 7900 J
ΔU = Q – W
= 2 × 4.2 × 1000 – 500 = 8400 –500
= 7900 J
An engine has an efficiency of 1/6. When the temperature of sink is reduced by 62°C, its efficiency is doubled. Temperature of the source is- a)37°C
- b)62°C [2007]
- c)99°C
- d)124°C
Correct answer is option 'C'. Can you explain this answer?
An engine has an efficiency of 1/6. When the temperature of sink is reduced by 62°C, its efficiency is doubled. Temperature of the source is
a)
37°C
b)
62°C [2007]
c)
99°C
d)
124°C
|
|
Jaya Singh answered |
°F, its efficiency becomes 1/4. Find the initial and final temperatures of the sink.
We can use the formula for the efficiency of a heat engine:
efficiency = 1 - (temperature of sink / temperature of source)
Let's call the initial temperature of the source Ts and the initial temperature of the sink T0. We can set up two equations based on the given information:
1/6 = 1 - (T0 / Ts)
1/4 = 1 - ((T0 - 62) / Ts)
We can solve this system of equations for Ts and T0. One way to do this is to solve for one variable in terms of the other, and then substitute into one of the equations to solve for the remaining variable. Here's one possible method:
1/6 = 1 - (T0 / Ts)
T0 / Ts = 5/6
T0 = (5/6)Ts
1/4 = 1 - ((T0 - 62) / Ts)
(T0 - 62) / Ts = 3/4
T0 - 62 = (3/4)Ts
Substituting T0 = (5/6)Ts into the second equation:
(5/6)Ts - 62 = (3/4)Ts
(1/12)Ts = 62
Ts = 744
Substituting Ts = 744 into T0 = (5/6)Ts:
T0 = (5/6)(744) = 620
Therefore, the initial temperature of the source was 744°F and the initial temperature of the sink was 620°F. When the temperature of the sink was reduced by 62°F, its final temperature was 558°F.
We can use the formula for the efficiency of a heat engine:
efficiency = 1 - (temperature of sink / temperature of source)
Let's call the initial temperature of the source Ts and the initial temperature of the sink T0. We can set up two equations based on the given information:
1/6 = 1 - (T0 / Ts)
1/4 = 1 - ((T0 - 62) / Ts)
We can solve this system of equations for Ts and T0. One way to do this is to solve for one variable in terms of the other, and then substitute into one of the equations to solve for the remaining variable. Here's one possible method:
1/6 = 1 - (T0 / Ts)
T0 / Ts = 5/6
T0 = (5/6)Ts
1/4 = 1 - ((T0 - 62) / Ts)
(T0 - 62) / Ts = 3/4
T0 - 62 = (3/4)Ts
Substituting T0 = (5/6)Ts into the second equation:
(5/6)Ts - 62 = (3/4)Ts
(1/12)Ts = 62
Ts = 744
Substituting Ts = 744 into T0 = (5/6)Ts:
T0 = (5/6)(744) = 620
Therefore, the initial temperature of the source was 744°F and the initial temperature of the sink was 620°F. When the temperature of the sink was reduced by 62°F, its final temperature was 558°F.
A sample of gas expands from volume V1 to V2.The amount of work done by the gas is greatest, when the expansion is [1997]- a)adiabatic
- b)isobaric
- c)isothermal
- d)equal in all cases
Correct answer is option 'B'. Can you explain this answer?
A sample of gas expands from volume V1 to V2.The amount of work done by the gas is greatest, when the expansion is [1997]
a)
adiabatic
b)
isobaric
c)
isothermal
d)
equal in all cases

|
Shanaya Rane answered |
In thermodynamics for same change in volume, the work done is maximum in isobaric process because in P – V graph, area enclosed by curve and volume axis is maximum in isobaric process.
So, the choice (b) is correct.
So, the choice (b) is correct.
The temperature of source and sink of a heat engine are 127ºC and 27ºC respectively. An inventor claims its efficiency to be 26%, then:- a)it is impossible [2001]
- b)it is possible with high probability
- c)it is possible with low probability
- d)data are insufficient.
Correct answer is option 'A'. Can you explain this answer?
The temperature of source and sink of a heat engine are 127ºC and 27ºC respectively. An inventor claims its efficiency to be 26%, then:
a)
it is impossible [2001]
b)
it is possible with high probability
c)
it is possible with low probability
d)
data are insufficient.

|
Arnab Iyer answered |
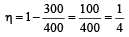
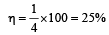
Hence, it is not possible to have efficiency more than 25%.
First law of thermodynamics is consequence of conservation of [1988]- a)work
- b)energy
- c)heat
- d)all of these
Correct answer is option 'B'. Can you explain this answer?
First law of thermodynamics is consequence of conservation of [1988]
a)
work
b)
energy
c)
heat
d)
all of these

|
Krish Patel answered |
The first law of thermodynamics is just a conservation of energy.
A Carnot engine whose sink is at 300 K has an efficiency of 40%. By how much should the temperature of source be increased so as to increase, its efficiency by 50% of original efficiency ? [2006]- a)325 K
- b)250 K
- c)380 K
- d)275 K
Correct answer is option 'B'. Can you explain this answer?
A Carnot engine whose sink is at 300 K has an efficiency of 40%. By how much should the temperature of source be increased so as to increase, its efficiency by 50% of original efficiency ? [2006]
a)
325 K
b)
250 K
c)
380 K
d)
275 K
|
|
Tejas Kumar answered |
We know that efficiency of Carnot Engine

where, T1 is temp. of source & T2 is temp. of sink
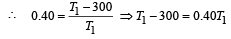
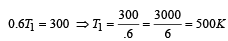
Now efficiency to be increased by 50%
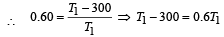
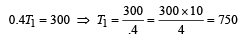
Increase in temp = 750 – 500 = 250 K
A reversible engine converts one-sixth of the heat input into work. When the temperature of the sink is reduced by 62ºC, the efficiency of the engine is doubled. The temperatures of the source and sink are [2000]- a)99ºC, 37ºC
- b)80ºC, 37ºC
- c)95ºC, 37ºC
- d)90ºC, 37ºC
Correct answer is option 'A'. Can you explain this answer?
A reversible engine converts one-sixth of the heat input into work. When the temperature of the sink is reduced by 62ºC, the efficiency of the engine is doubled. The temperatures of the source and sink are [2000]
a)
99ºC, 37ºC
b)
80ºC, 37ºC
c)
95ºC, 37ºC
d)
90ºC, 37ºC
|
|
Aarav Shah answered |
Initially the efficiency of the engine was 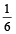 which increases to
which increases to 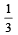 when the sinktemperature reduces by 62º C.
when the sinktemperature reduces by 62º C.
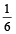 which increases to
which increases to 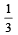 when the sinktemperature reduces by 62º C.
when the sinktemperature reduces by 62º C. when T2 = sink temperature T1 = source temperature
when T2 = sink temperature T1 = source temperature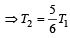
Secondly,
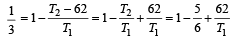
or, T1 = 62 × 6 = 372K =372– 273 = 99ºC
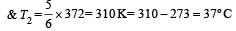
Two Carnot engines A and B are operated in series. The engine A receives heat from the source at temperature T1 and rejects the heat to the sink at temperature T. The second engine B receives the heat at temperature T and rejects to its sink at temperature T2. For what value of T the efficiencies of the two engines are equal? [NEET Kar. 2013]- a)
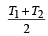
- b)

- c)T1T2
- d)
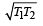
Correct answer is option 'D'. Can you explain this answer?
Two Carnot engines A and B are operated in series. The engine A receives heat from the source at temperature T1 and rejects the heat to the sink at temperature T. The second engine B receives the heat at temperature T and rejects to its sink at temperature T2. For what value of T the efficiencies of the two engines are equal? [NEET Kar. 2013]
a)
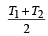
b)

c)
T1T2
d)
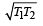

|
Abhijeet Goyal answered |
Efficiency of engine A, 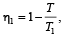
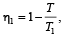
Efficiency of engine B, 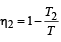
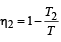
Here, η1 = η2
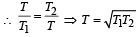
If for a gas, 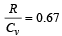 , the gas is made up of molecules which are [1992]
, the gas is made up of molecules which are [1992]- a)diatomic
- b)mixture of diatomic and polyatomic molecules
- c)monoatomic
- d)polyatomic
Correct answer is option 'C'. Can you explain this answer?
If for a gas, 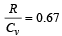 , the gas is made up of molecules which are [1992]
, the gas is made up of molecules which are [1992]
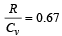 , the gas is made up of molecules which are [1992]
, the gas is made up of molecules which are [1992]a)
diatomic
b)
mixture of diatomic and polyatomic molecules
c)
monoatomic
d)
polyatomic
|
|
Yash Modi answered |
Given, Cv / R = 3/2. ( 0.67 = 2/3)
So, Cv = 3R/2 , hence the gas is monoatomic.
So, Cv = 3R/2 , hence the gas is monoatomic.
The molar specific heat at constant pressure of an ideal gas is (7/2) R. The ratio of specific heat at constant pressure to that at constant volume is- a)8/7
- b)5/7
- c)9/7
- d)7/5 [2006]
Correct answer is option 'D'. Can you explain this answer?
The molar specific heat at constant pressure of an ideal gas is (7/2) R. The ratio of specific heat at constant pressure to that at constant volume is
a)
8/7
b)
5/7
c)
9/7
d)
7/5 [2006]
|
|
Yash Modi answered |
Cp = 7R/2 so Cv = 5R/2 (Cp-Cv = R)
So Cp/Cv = 7/5
So Cp/Cv = 7/5
Which of the following relations does not give the equation of an adiabatic process, where terms have their usual meaning?- a)PγT1–γ = constant [NEET Kar. 2013]
- b)P1–γTγ = constant
- c)PVγ = constant
- d)TVγ–1 = constant
Correct answer is option 'A'. Can you explain this answer?
Which of the following relations does not give the equation of an adiabatic process, where terms have their usual meaning?
a)
PγT1–γ = constant [NEET Kar. 2013]
b)
P1–γTγ = constant
c)
PVγ = constant
d)
TVγ–1 = constant

|
Aniket Chawla answered |
Adiabatic equations of state are PVγ = constant
TVγ–1 = constant
P1–γTγ = constant.
TVγ–1 = constant
P1–γTγ = constant.
If Q, E and W denote respectively the heat added, change in internal energy and the work done in a closed cyclic process, then: [2008]- a)W = 0
- b)Q = W = 0
- c)E = 0
- d)Q = 0
Correct answer is option 'C'. Can you explain this answer?
If Q, E and W denote respectively the heat added, change in internal energy and the work done in a closed cyclic process, then: [2008]
a)
W = 0
b)
Q = W = 0
c)
E = 0
d)
Q = 0

|
Rhea Sarkar answered |
In a cyclic process, the initial state coincides with the final state. Hence, the change in internal energy is zero, as it depends only on the initial and final states. But Q & W are non-zero during a cycle process.
If Q1, Q2, Q3 indicate the heat a absorbed by the gas along the three processes and ΔU1, ΔU2, ΔU3 indicate the change in internal energy along the three processes respectively, then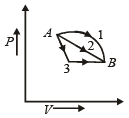
- a)Q1 > Q2 > Q3 and ΔU1 = ΔU2 = ΔU3
- b)Q3 > Q2 > Q1 and ΔU1= ΔU2 = ΔU3
- c)Q1 = Q2 = Q3 and ΔU1 > ΔU2 > ΔU3
- d)Q3 > Q2 > Q1 and ΔU1> ΔU2 > ΔU3
Correct answer is option 'A'. Can you explain this answer?
If Q1, Q2, Q3 indicate the heat a absorbed by the gas along the three processes and ΔU1, ΔU2, ΔU3 indicate the change in internal energy along the three processes respectively, then

a)
Q1 > Q2 > Q3 and ΔU1 = ΔU2 = ΔU3
b)
Q3 > Q2 > Q1 and ΔU1= ΔU2 = ΔU3
c)
Q1 = Q2 = Q3 and ΔU1 > ΔU2 > ΔU3
d)
Q3 > Q2 > Q1 and ΔU1> ΔU2 > ΔU3

|
Mahi Shah answered |
Initial and final condition is same for all process ΔU1 = ΔU2 = ΔU3
from first law of thermodynamics ΔQ = ΔU + ΔW
Work done ΔW1 > ΔW2 > ΔW3 (Area of P.V. graph)
So ΔQ1 > ΔQ2 > ΔQ3
from first law of thermodynamics ΔQ = ΔU + ΔW
Work done ΔW1 > ΔW2 > ΔW3 (Area of P.V. graph)
So ΔQ1 > ΔQ2 > ΔQ3
An ideal gas heat engine operates in a Carnot cycle between 227ºC and 127ºC. It absorbs 6 kcal at the higher temperature. The amount of heat (in kcal) converted into work is equal to- a)1.2
- b)4.8
- c)3.5
- d)1.6
Correct answer is option 'A'. Can you explain this answer?
An ideal gas heat engine operates in a Carnot cycle between 227ºC and 127ºC. It absorbs 6 kcal at the higher temperature. The amount of heat (in kcal) converted into work is equal to
a)
1.2
b)
4.8
c)
3.5
d)
1.6

|
Shanaya Rane answered |
Efficiency =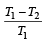
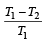
T1 = 227 + 273 = 500 K
T2 = 127 + 273 = 400 K
T2 = 127 + 273 = 400 K
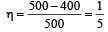
Hence, output work
= (η) Heat input = 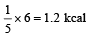
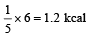
In thermodynamic processes which of the following statements is not true? [2009]- a)In an isochoric process pressure remains constant
- b)In an isothermal process the temperature remains constant
- c)In an adiabatic process PVγ = constant
- d)In an adiabatic process the system is insulated from the surroundings
Correct answer is option 'A'. Can you explain this answer?
In thermodynamic processes which of the following statements is not true? [2009]
a)
In an isochoric process pressure remains constant
b)
In an isothermal process the temperature remains constant
c)
In an adiabatic process PVγ = constant
d)
In an adiabatic process the system is insulated from the surroundings

|
Rajesh Datta answered |
In an isochoric process volume remains constant whereas pressure remains constant in isobaric process.
An ideal gas A and a real gas B have their volumes increased from V to 2V under isothermal conditions. The increase in internal energy [1993]- a)will be same in both A and B
- b)will be zero in both the gases
- c)of B will be more than that of A
- d)of A will be more than that of B
Correct answer is option 'B'. Can you explain this answer?
An ideal gas A and a real gas B have their volumes increased from V to 2V under isothermal conditions. The increase in internal energy [1993]
a)
will be same in both A and B
b)
will be zero in both the gases
c)
of B will be more than that of A
d)
of A will be more than that of B

|
Shalini Saha answered |
Under isothermal conditions, there is no change in internal energy.
For hydrogen gas, Cp – Cv = a and for oxygen gas, Cp – Cv = b, so the relation between a and b is given by [1991]- a)a = -16 b
- b)a = b
- c)a = 4 b
- d)a = 16b
Correct answer is option 'D'. Can you explain this answer?
For hydrogen gas, Cp – Cv = a and for oxygen gas, Cp – Cv = b, so the relation between a and b is given by [1991]
a)
a = -16 b
b)
a = b
c)
a = 4 b
d)
a = 16b
|
|
Charvi Nair answered |
There are different values of Cp for hydrogen gas depending on the temperature and pressure conditions. However, at standard temperature and pressure (STP), which is 0°C and 1 atm, the specific heat capacity at constant pressure (Cp) for hydrogen gas is approximately 14.31 J/(mol·K).
A Carnot engine whose efficiency is 50% has an exhaust temperature of 500 K. If the efficiency is to be 60% with the same intake temperature, the exhaust temperature must be (in K) [2002]- a)800
- b)200
- c)400
- d)600
Correct answer is option 'C'. Can you explain this answer?
A Carnot engine whose efficiency is 50% has an exhaust temperature of 500 K. If the efficiency is to be 60% with the same intake temperature, the exhaust temperature must be (in K) [2002]
a)
800
b)
200
c)
400
d)
600

|
Shivani Tiwari answered |
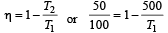
⇒ T1 = 1000K
An ideal gas undergoing adiabatic change has the following pressure-temperature relationship [1996]- a)Pγ -1Tγ = constant
- b)PγTγ -1 = constant
- c)PγT1 - γ = constant
- d)P1 - γTγ = constant
Correct answer is option 'D'. Can you explain this answer?
An ideal gas undergoing adiabatic change has the following pressure-temperature relationship [1996]
a)
Pγ -1Tγ = constant
b)
PγTγ -1 = constant
c)
PγT1 - γ = constant
d)
P1 - γTγ = constant

|
Shivani Rane answered |
We know that in adiabatic process, PVγ = constant ....(1)
From ideal gas equation, we know that PV = nRT
From ideal gas equation, we know that PV = nRT
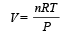 ....(2)
....(2)Puttingt the value from equation (2) in equation (1),
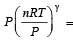 constant
constantP(1 – γ) Tγ = constant
A gas at 27ºC temperature and 30 atmospheric pressure is allowed to expand to the atmospheric pressure. If the volume becomes 10 times its initial volume, then the final temperature becomes- a)100ºC
- b)173ºC [2001]
- c)273ºC
- d)–173ºC
Correct answer is option 'D'. Can you explain this answer?
A gas at 27ºC temperature and 30 atmospheric pressure is allowed to expand to the atmospheric pressure. If the volume becomes 10 times its initial volume, then the final temperature becomes
a)
100ºC
b)
173ºC [2001]
c)
273ºC
d)
–173ºC
|
|
Shraddha Sengupta answered |
°C and 1 atm pressure has a volume of 22.4 L. This is known as the molar volume of a gas at standard temperature and pressure (STP).
At different temperatures and pressures, the volume of a gas will change according to the ideal gas law, PV = nRT, where P is the pressure, V is the volume, n is the number of moles of gas, R is the gas constant, and T is the temperature in Kelvin.
For example, if the temperature of the gas is increased to 100°C (373 K), and the pressure remains at 1 atm, the volume of the gas will increase to approximately 36.7 L, assuming the number of moles of gas and the gas constant remain constant.
Similarly, if the pressure of the gas is increased to 2 atm, and the temperature remains at 27°C, the volume of the gas will decrease to approximately 11.2 L.
These calculations demonstrate that the volume of a gas is directly proportional to the temperature and inversely proportional to the pressure, as predicted by the ideal gas law.
At different temperatures and pressures, the volume of a gas will change according to the ideal gas law, PV = nRT, where P is the pressure, V is the volume, n is the number of moles of gas, R is the gas constant, and T is the temperature in Kelvin.
For example, if the temperature of the gas is increased to 100°C (373 K), and the pressure remains at 1 atm, the volume of the gas will increase to approximately 36.7 L, assuming the number of moles of gas and the gas constant remain constant.
Similarly, if the pressure of the gas is increased to 2 atm, and the temperature remains at 27°C, the volume of the gas will decrease to approximately 11.2 L.
These calculations demonstrate that the volume of a gas is directly proportional to the temperature and inversely proportional to the pressure, as predicted by the ideal gas law.
If ΔU and ΔW repr esent the in crease in internal energy and work done by the system respectively in a thermodynamical process, which of the following is true? [2010]- a)ΔU = -ΔW , in an adiabatic process
- b)ΔU = ΔW , in an isothermal process
- c)ΔU = ΔW , in an adiabatic process
- d)ΔU = -ΔW , in an isothermal process
Correct answer is option 'A'. Can you explain this answer?
If ΔU and ΔW repr esent the in crease in internal energy and work done by the system respectively in a thermodynamical process, which of the following is true? [2010]
a)
ΔU = -ΔW , in an adiabatic process
b)
ΔU = ΔW , in an isothermal process
c)
ΔU = ΔW , in an adiabatic process
d)
ΔU = -ΔW , in an isothermal process

|
Mahi Shah answered |
By first law of thermodynamics, ΔQ = ΔU + ΔW
In adiabatic process, ΔQ = 0
∴ ΔU = -ΔW
In isothermal process, ΔU = 0
∴ ΔQ -ΔW
In adiabatic process, ΔQ = 0
∴ ΔU = -ΔW
In isothermal process, ΔU = 0
∴ ΔQ -ΔW
We consider a thermodynamic system. If ΔU represents the increase in its internal energy and W the work done by the system, which of the following statements is true? [1998]- a)ΔU = – W in an adiabatic process
- b)ΔU = W in an isothermal process
- c)ΔU = –W in an isothermal process
- d)ΔU = W in an adiabatic process
Correct answer is option 'A'. Can you explain this answer?
We consider a thermodynamic system. If ΔU represents the increase in its internal energy and W the work done by the system, which of the following statements is true? [1998]
a)
ΔU = – W in an adiabatic process
b)
ΔU = W in an isothermal process
c)
ΔU = –W in an isothermal process
d)
ΔU = W in an adiabatic process

|
Arnab Iyer answered |
ΔQ = ΔU + W
For adiabatic process, ΔQ = 0
ΔU = –W
For adiabatic process, ΔQ = 0
ΔU = –W
One mole of an ideal gas at an initial temperature of T K does 6R joules of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of gas will be [2004]- a)(T – 4) K
- b)(T + 2.4) K
- c)(T – 2.4) K
- d)(T + 4) K
Correct answer is option 'A'. Can you explain this answer?
One mole of an ideal gas at an initial temperature of T K does 6R joules of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of gas will be [2004]
a)
(T – 4) K
b)
(T + 2.4) K
c)
(T – 2.4) K
d)
(T + 4) K
|
|
Nayanika Menon answered |
We know that for an adiabatic process, $PV^\gamma$ is constant, where $\gamma$ is the ratio of specific heats. Let the initial pressure and volume be $P_i$ and $V_i$, and let the final pressure and volume be $P_f$ and $V_f$. Then we have:
$$P_i V_i^\gamma = P_f V_f^\gamma$$
We also know that the work done by the gas is given by:
$$W = \frac{\gamma}{\gamma - 1} P_i V_i \left(\left(\frac{V_f}{V_i}\right)^{\gamma - 1} - 1\right)$$
Since we are given that the gas does 6R joules of work, we can set $W = 6R$ and solve for $V_f/V_i$:
$$6R = \frac{\gamma}{\gamma - 1} P_i V_i \left(\left(\frac{V_f}{V_i}\right)^{\gamma - 1} - 1\right)$$
$$\frac{V_f}{V_i} = \left(1 + \frac{6R(\gamma - 1)}{\gamma P_i V_i}\right)^{1/(\gamma - 1)}$$
Finally, we can use the ideal gas law to relate the initial and final temperatures:
$$\frac{P_i V_i}{T_i} = \frac{P_f V_f}{T_f}$$
Substituting in our expressions for $P_i V_i$, $P_f V_f$, and $V_f/V_i$, we get:
$$\frac{T_f}{T_i} = \frac{P_i V_i}{P_f V_f} = \left(\frac{V_i}{V_f}\right)^{\gamma - 1} = \left(1 + \frac{6R(\gamma - 1)}{\gamma P_i V_i}\right)^{-(\gamma - 1)/\gamma}$$
Substituting in $\gamma = 5/3$ and simplifying, we get:
$$\frac{T_f}{T_i} = \left(1 - \frac{2}{5}\frac{R}{C_V T_i}\right)$$
where $C_V$ is the specific heat at constant volume. Since the gas is ideal and monoatomic, we have $C_V = \frac{3}{2}R$, so we can simplify further:
$$\frac{T_f}{T_i} = \left(1 - \frac{4}{15}\frac{1}{T_i}\right)$$
Thus, the final temperature is:
$$T_f = T_i\left(1 - \frac{4}{15}\frac{1}{T_i}\right) = \frac{11}{15}T_i$$
Therefore, the answer is (d) $\frac{11}{15}T$.
$$P_i V_i^\gamma = P_f V_f^\gamma$$
We also know that the work done by the gas is given by:
$$W = \frac{\gamma}{\gamma - 1} P_i V_i \left(\left(\frac{V_f}{V_i}\right)^{\gamma - 1} - 1\right)$$
Since we are given that the gas does 6R joules of work, we can set $W = 6R$ and solve for $V_f/V_i$:
$$6R = \frac{\gamma}{\gamma - 1} P_i V_i \left(\left(\frac{V_f}{V_i}\right)^{\gamma - 1} - 1\right)$$
$$\frac{V_f}{V_i} = \left(1 + \frac{6R(\gamma - 1)}{\gamma P_i V_i}\right)^{1/(\gamma - 1)}$$
Finally, we can use the ideal gas law to relate the initial and final temperatures:
$$\frac{P_i V_i}{T_i} = \frac{P_f V_f}{T_f}$$
Substituting in our expressions for $P_i V_i$, $P_f V_f$, and $V_f/V_i$, we get:
$$\frac{T_f}{T_i} = \frac{P_i V_i}{P_f V_f} = \left(\frac{V_i}{V_f}\right)^{\gamma - 1} = \left(1 + \frac{6R(\gamma - 1)}{\gamma P_i V_i}\right)^{-(\gamma - 1)/\gamma}$$
Substituting in $\gamma = 5/3$ and simplifying, we get:
$$\frac{T_f}{T_i} = \left(1 - \frac{2}{5}\frac{R}{C_V T_i}\right)$$
where $C_V$ is the specific heat at constant volume. Since the gas is ideal and monoatomic, we have $C_V = \frac{3}{2}R$, so we can simplify further:
$$\frac{T_f}{T_i} = \left(1 - \frac{4}{15}\frac{1}{T_i}\right)$$
Thus, the final temperature is:
$$T_f = T_i\left(1 - \frac{4}{15}\frac{1}{T_i}\right) = \frac{11}{15}T_i$$
Therefore, the answer is (d) $\frac{11}{15}T$.
A thermodynamic system is taken from state A to B along ACB and is brought back to A along BDA as shown in the PV diagram. The net work done during the complete cycle is given by the area[1992]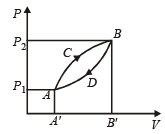
- a)P1ACBP2P1
- b)ACBB'A'A
- c)ACBDA
- d)ADBB'A'A
Correct answer is option 'C'. Can you explain this answer?
A thermodynamic system is taken from state A to B along ACB and is brought back to A along BDA as shown in the PV diagram. The net work done during the complete cycle is given by the area[1992]

a)
P1ACBP2P1
b)
ACBB'A'A
c)
ACBDA
d)
ADBB'A'A

|
Rhea Sarkar answered |
Work done = Area under curve ACBDA
A thermodynamic process is shown in the figure.
The pressures and volumes corresponding to some points in the figure are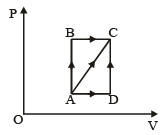 PA = 3 × 104 Pa
PA = 3 × 104 Pa
VA = 2 × 10-3 m3
PB = 8 × 104 Pa
VD = 5 × 10–3 m3.
In process AB, 600 J of heat is added to the system and in process BC, 200 J of heat is added to the system. The change in internal energy of the system in process AC would be [1991] - a)560 J
- b)800 J
- c)600 J
- d)640 J
Correct answer is option 'A'. Can you explain this answer?
A thermodynamic process is shown in the figure.
The pressures and volumes corresponding to some points in the figure are
The pressures and volumes corresponding to some points in the figure are

PA = 3 × 104 Pa
VA = 2 × 10-3 m3
PB = 8 × 104 Pa
VD = 5 × 10–3 m3.
In process AB, 600 J of heat is added to the system and in process BC, 200 J of heat is added to the system. The change in internal energy of the system in process AC would be [1991]
VA = 2 × 10-3 m3
PB = 8 × 104 Pa
VD = 5 × 10–3 m3.
In process AB, 600 J of heat is added to the system and in process BC, 200 J of heat is added to the system. The change in internal energy of the system in process AC would be [1991]
a)
560 J
b)
800 J
c)
600 J
d)
640 J

|
Nayanika Reddy answered |
Since AB is an isochoric process, so, no work is done. BC is isobaric process,
∴ W = PB × (VD – VA) = 240 J
ΔQ = 600 + 200 = 800 J
Using ΔQ = ΔU + ΔW
⇒ ΔU = ΔQ – ΔW = 800 – 240 = 560 J
∴ W = PB × (VD – VA) = 240 J
ΔQ = 600 + 200 = 800 J
Using ΔQ = ΔU + ΔW
⇒ ΔU = ΔQ – ΔW = 800 – 240 = 560 J
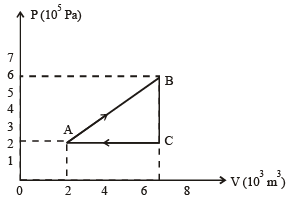
A thermodynamic system is taken through the cycle ABCD as shown in figure. Heat rejected by the gas during the cycle is : [2012]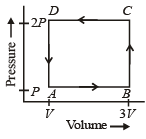
- a)2 PV
- b)4 PV
- c)

- d)P V
Correct answer is option 'A'. Can you explain this answer?
A thermodynamic system is taken through the cycle ABCD as shown in figure. Heat rejected by the gas during the cycle is : [2012]

a)
2 PV
b)
4 PV
c)

d)
P V

|
Nayanika Reddy answered |
∵ Internal energy is the state function.
∴ In cyclie process; ΔU = 0
According to 1st law of thermodynamics
∴ In cyclie process; ΔU = 0
According to 1st law of thermodynamics
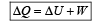
So heat absorbed ΔQ = W = Area under the curve
= – (2V) (P) = – 2PV
So heat rejected = 2PV
= – (2V) (P) = – 2PV
So heat rejected = 2PV
The efficiency of a Carn ot engine operating between the temperatures of 100ºC and –23ºC will be
[1997]- a)
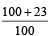
- b)
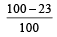
- c)
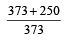
- d)
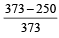
Correct answer is option 'D'. Can you explain this answer?
The efficiency of a Carn ot engine operating between the temperatures of 100ºC and –23ºC will be
[1997]
[1997]
a)
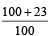
b)
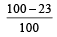
c)
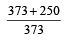
d)
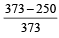

|
Aashna Mukherjee answered |
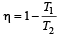
T1 = –23°C = 250 K, T2 = 100°C = 373K
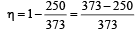
If the ratio of specific heat of a gas at constant pressure to that at constant volume is γ, the change in internal energy of a mass of gas, when the volume changes from V to 2V at constant pressure P, is [1998]- a)
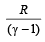
- b)PV
- c)
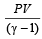
- d)
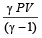
Correct answer is option 'C'. Can you explain this answer?
If the ratio of specific heat of a gas at constant pressure to that at constant volume is γ, the change in internal energy of a mass of gas, when the volume changes from V to 2V at constant pressure P, is [1998]
a)
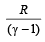
b)
PV
c)
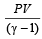
d)
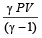

|
Smruti Sucharita answered |

If γ be the ratio of specific heats of a perfect gas, the number of degrees of freedom of a molecule of the gas is [2000]- a)
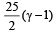
- b)
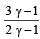
- c)
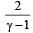
- d)
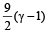
Correct answer is option 'C'. Can you explain this answer?
If γ be the ratio of specific heats of a perfect gas, the number of degrees of freedom of a molecule of the gas is [2000]
a)
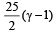
b)
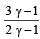
c)
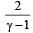
d)
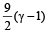

|
Anirudh Datta answered |
We know that ratio of specific heats,
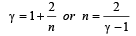
[where n = Degree of freedom]
An ideal gas heat engine oper ates in Car not cycle between 227°C and 127°C. It absorbs 6 × 104 cals of heat at higher temperature. Amount of heat converted to work is [2005]- a)4.8 × 104 cals
- b)6 × 104 cals
- c)2.4 × 104 cals
- d)1.2 × 104 cals
Correct answer is option 'D'. Can you explain this answer?
An ideal gas heat engine oper ates in Car not cycle between 227°C and 127°C. It absorbs 6 × 104 cals of heat at higher temperature. Amount of heat converted to work is [2005]
a)
4.8 × 104 cals
b)
6 × 104 cals
c)
2.4 × 104 cals
d)
1.2 × 104 cals

|
Shalini Saha answered |
We know that efficiency of carnot engine =
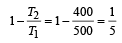
[∵ T1 = (273 + 227)K = 500 K
and T2 = (273 + 127)K = 400 K]
and T2 = (273 + 127)K = 400 K]
Efficiency of Heat engine = 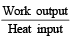
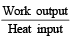
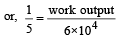
⇒ work output = 1.2 × 104 cal
A system is taken from state a to state c by two paths adc and abc as shown in the figure. The internal energy at a is Ua = 10 J. Along the path adc the amount of heat absorbed δQ1 = 50 J and the work done δW1 = 20 J whereas along the path abc the heat absorbed δQ2 = 36 J. The amount of work done along the path abc is [NEET Kar. 2013]
- a)6 J
- b)10 J
- c)12 J
- d)36 J
Correct answer is option 'A'. Can you explain this answer?
A system is taken from state a to state c by two paths adc and abc as shown in the figure. The internal energy at a is Ua = 10 J. Along the path adc the amount of heat absorbed δQ1 = 50 J and the work done δW1 = 20 J whereas along the path abc the heat absorbed δQ2 = 36 J. The amount of work done along the path abc is [NEET Kar. 2013]

a)
6 J
b)
10 J
c)
12 J
d)
36 J

|
Nayanika Reddy answered |
From first law of thermodynamics
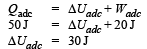
Again,
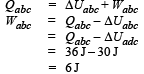
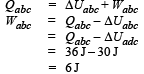
Which of the following processes is reversible?[2005]- a)Transfer of heat by conduction
- b)Transfer of heat by radiation
- c)Isothermal compression
- d)Electrical heating of a nich rome wire
Correct answer is option 'C'. Can you explain this answer?
Which of the following processes is reversible?[2005]
a)
Transfer of heat by conduction
b)
Transfer of heat by radiation
c)
Isothermal compression
d)
Electrical heating of a nich rome wire

|
Ruchi Chakraborty answered |
For a process to be reversible, it must be quasi-static. For quasi static process, all changes take place infinitely slowly.
Isothermal process occur very slowly so it is quasi-static and hence it is reversible.
Isothermal process occur very slowly so it is quasi-static and hence it is reversible.
Chapter doubts & questions for Thermodynamics - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Thermodynamics - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup




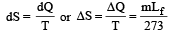

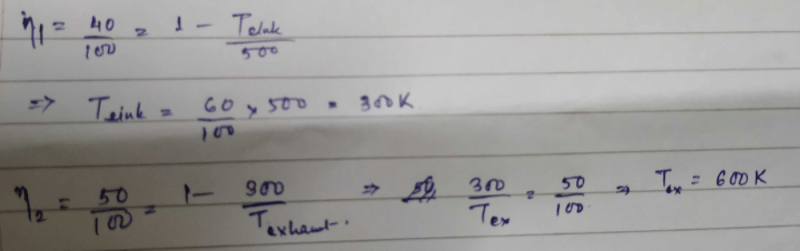
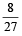 of its original volume. The rise in temperature is
of its original volume. The rise in temperature is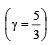 [1999]
[1999]
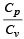 for the gas is [NEET 2013]
for the gas is [NEET 2013]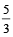
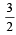
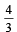
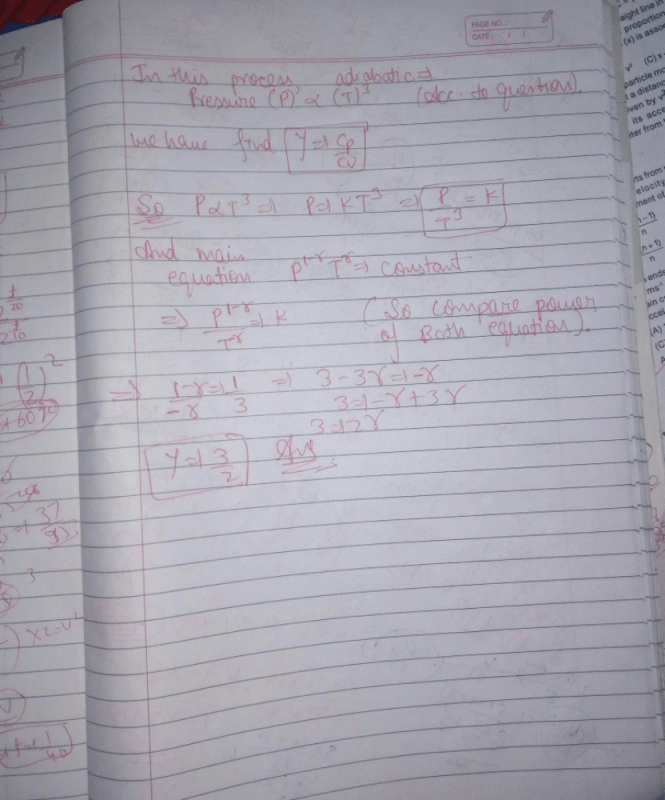

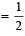 AC × BC
AC × BC