All Exams >
Class 7 >
Mathematics (Maths) Class 7 (Old NCERT) >
All Questions
All questions of Lines and Angles for Class 7 Exam
Find the value of x if I║m.
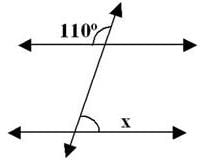
- a)90°
- b)70°
- c)80°
- d)60°
Correct answer is option 'B'. Can you explain this answer?
Find the value of x if I║m.

a)
90°
b)
70°
c)
80°
d)
60°

|
Rainbow Rise Classes answered |
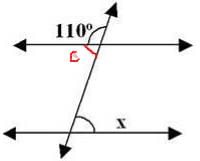
c + 110ο = 180ο
c = 70ο
x = c [ alternate interior angle ]
so x =70ο
If two angles are supplementary then the sum of their measures is ___________ .- a)45°
- b)180°
- c)90°
- d)360°
Correct answer is option 'B'. Can you explain this answer?
If two angles are supplementary then the sum of their measures is ___________ .
a)
45°
b)
180°
c)
90°
d)
360°

|
Shilpa Das answered |
Supplementary angles are two angles whose sum is equal to 180∘. In other words when you add the measure of one angle in the pair with the other angle in the pair, they equal 180 degrees.
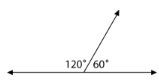
These two angles are supplementary because together they form a straight line. You can also tell that they are supplementary because when you add their angle measures the sum is equal to 180 degrees.
120+60=180degree
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Lines and Angles, Class 7, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q.If two lines intersect at a point, then the vertically opposite angles are always ________- a)supplementary
- b)equal
- c)unequal
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Lines and Angles, Class 7, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
If two lines intersect at a point, then the vertically opposite angles are always ________
a)
supplementary
b)
equal
c)
unequal
d)
none of these

|
Ananya Choudhary answered |
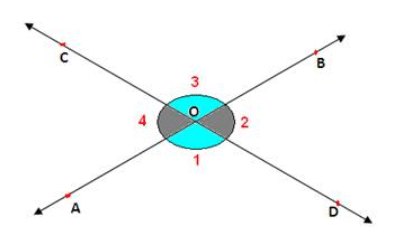
Given two lines AB and CD intersect each other at the point O.
To prove: ∠1 = ∠3 and ∠2 = ∠4
Proof:
From the figure, ∠1 + ∠2 = 180 deg [Linear pair] → (1)
∠2 + ∠3 = 180 deg [Linear pair] → (2)
From (1) and (2), we get
∠1 + ∠2 = ∠2 + ∠3
∴ ∠1 = ∠3
Similarly, we can prove ∠2 = ∠4 also.
A and B are vertically opposite angles. If the measure of A is 60o, what is the value of B?- a)30o
- b)40o
- c)120o
- d)600
Correct answer is option 'D'. Can you explain this answer?
A and B are vertically opposite angles. If the measure of A is 60o, what is the value of B?
a)
30o
b)
40o
c)
120o
d)
600
|
|
Rimjhim bajaj answered |
When two lines intersect, then vertically opposite angles so formed are equal
What is the supplement of 105°
- a)65°
- b)75°
- c)85°
- d)95°
Correct answer is option 'B'. Can you explain this answer?
What is the supplement of 105°
a)
65°
b)
75°
c)
85°
d)
95°

|
Pooja Banerjee answered |
Supplementary angles sums up to 180°
x + 105° = 180°
x = 180° - 105°
x = 75°
x + 105° = 180°
x = 180° - 105°
x = 75°
If two adjacent angles are supplementary, then they form _________ .- a)a linear pair of angles
- b)vertically opposite angles
- c)Corresponding angles
- d)a ray
Correct answer is 'A'. Can you explain this answer?
If two adjacent angles are supplementary, then they form _________ .
a)
a linear pair of angles
b)
vertically opposite angles
c)
Corresponding angles
d)
a ray

|
Shilpa Das answered |
A linear pair is two angles that are adjacent and whose non-common sides form a straight line. If two angles are a linear pair, then they are supplementary.
- a)90°
- b)30°
- c)60°
- d)180°
Correct answer is option 'C'. Can you explain this answer?
a)
90°
b)
30°
c)
60°
d)
180°

|
Ishu answered |
Sum of two co-interior angle =180 then, 2x+x=180 3x=180 x=180/3=60
- a)120°
- b)180°
- c)60°
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
a)
120°
b)
180°
c)
60°
d)
None of these
|
|
Anveshi Shahi answered |
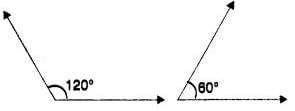
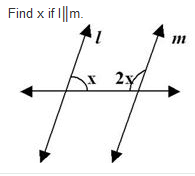
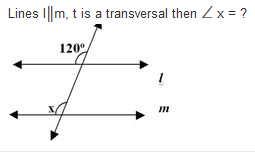
In the above given figure we can clearly see that there are two lines named as l and m they both are parallel to each other.
We can also write it like l||m.
There is also a line which is cutting the lines l||m it is a transversal line it isn't named there.
Let's suppose the name of transversal line is y.
We can clearly see on the line y there is an angle named x and there is another angle of 60 degree.
According to the maths rule of co-interior angle the sum of x and 60 degree must be 180 degree.
So,
x + 60= 180
x = 180-60
x = 120 Answer
- a)60°
- b)90°
- c)120°
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
a)
60°
b)
90°
c)
120°
d)
None of these
|
|
Varun Kapoor answered |
120 and x are corresponding angles and corresponding angles are equal so x = 120°
Find the measure of an angle, if 7 times its complement is 10 less than 3 times its supplement- a)15°
- b)10°
- c)25°
- d)5°
Correct answer is option 'C'. Can you explain this answer?
Find the measure of an angle, if 7 times its complement is 10 less than 3 times its supplement
a)
15°
b)
10°
c)
25°
d)
5°
|
|
Ananya Das answered |
Let the angle be x
measure of its complement = (90-x)
measure of its supplement= (180-x)
7(90-x) =3(180-x)-10
measure of its complement = (90-x)
measure of its supplement= (180-x)
7(90-x) =3(180-x)-10
630 - 7x=540x-3x -10
-7x+3x= 530-630
-4x=-100
-4x=-100
x= 100/4
x=25
x=25
Find the angle, which is equal to its supplement.- a)60°
- b)90°
- c)120°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
Find the angle, which is equal to its supplement.
a)
60°
b)
90°
c)
120°
d)
30°
|
|
Ananya Das answered |
Supplementary angles sums up to 180° since 90° + 90° = 180°, 90° is supplementary to itself
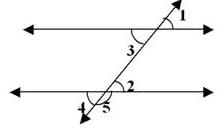
In figure pair of alternate interior angles are :
- a)∠2, ∠5
- b)∠1, ∠2
- c)∠2, ∠3
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In figure pair of alternate interior angles are :


a)
∠2, ∠5
b)
∠1, ∠2
c)
∠2, ∠3
d)
None of these
|
|
Geetika Shah answered |
Alternate interior angles are formed when a transversal passes through two lines. The angles that are formed on opposite sides of the transversal and inside the two lines are alternate interior angles. The theorem says that when the lines are parallel, that the alternate interior angles are equal.
So in the given figure ∠2, ∠3 are alternate interior angles
Alternate angle form Z shape
Alternate angle form Z shape
Find the angle whose measure is five times its complement
- a)360°
- b)75°
- c)180°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
Find the angle whose measure is five times its complement
a)
360°
b)
75°
c)
180°
d)
30°
|
|
Niti menon answered |
This will be the equation x=5(90-x)
solution= x=5(90-x)
x+5x=450
6x=450
6x/6=450/6 {divide by 6 to both the side to x}
x=75
ans= The angle is 15 degree and its compliment angle is 75 degree
solution= x=5(90-x)
x+5x=450
6x=450
6x/6=450/6 {divide by 6 to both the side to x}
x=75
ans= The angle is 15 degree and its compliment angle is 75 degree
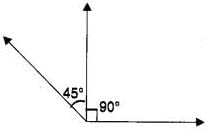
In a right angled triangle where angle A= 90° and AB=AC. What are the values of angle B. - a)45°
- b)35°
- c)75°
- d)65°
Correct answer is option 'A'. Can you explain this answer?
In a right angled triangle where angle A= 90° and AB=AC. What are the values of angle B.
a)
45°
b)
35°
c)
75°
d)
65°
|
|
Anirudh Sengupta answered |
∵ In ∆ABC,
AB = AC
∴ ∠B = ∠C ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆ABC,
∠A + ∠B + ∠C = 180°
| Sum of all the angles of a triangle is 180°
⇒ 90° + ∠B + ∠C = 180°
| ∵ ∠A = 90° (given)
⇒ ∠B + ∠C = 90° ...(2)
From (1) and (2), we get
∠B = ∠C = 45°.
AB = AC
∴ ∠B = ∠C ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆ABC,
∠A + ∠B + ∠C = 180°
| Sum of all the angles of a triangle is 180°
⇒ 90° + ∠B + ∠C = 180°
| ∵ ∠A = 90° (given)
⇒ ∠B + ∠C = 90° ...(2)
From (1) and (2), we get
∠B = ∠C = 45°.
What is the measure of the complement of 45°?- a)65°
- b)55°
- c)45°
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the measure of the complement of 45°?
a)
65°
b)
55°
c)
45°
d)
None of these
|
|
Lavanya Menon answered |
Complementary angle sums up to 90°. So x+ 45° = 90°
x = 90° - 45° = 45°
x = 90° - 45° = 45°
Two angles forming a linear pair are ________________.- a)complimentary
- b)equal
- c)supplementary
- d)None of these
Correct answer is 'C'. Can you explain this answer?
Two angles forming a linear pair are ________________.
a)
complimentary
b)
equal
c)
supplementary
d)
None of these

|
Meera Reddy answered |
Supplementary angles are two angles whose sum is 180 degree. A linear pair (two angles that form a line) will always be supplementary. The two angles can be adjacent or non-adjacent.
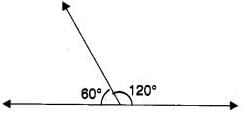
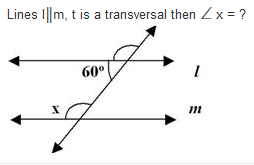
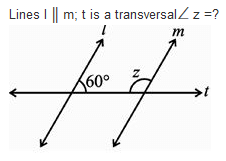
Lines l║m, t is transversal then ∠ x = ?

- a)60°
- b)120°
- c)90°
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Lines l║m, t is transversal then ∠ x = ?

a)
60°
b)
120°
c)
90°
d)
None of these

|
Tutorpedia Coaching answered |
as we know alternate angles are equal x = 60°
What is the measure of the supplement of 54°?
- a)126°
- b)49°
- c)35°
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
What is the measure of the supplement of 54°?
a)
126°
b)
49°
c)
35°
d)
None of these
|
|
Kiran Reddy answered |
As we know for becoming supplementary angles, the sum of both the angles should be 180∘
Let the supplementary angle be x.
So, 54∘+x = 180∘
⇒ x = 126∘
Let the supplementary angle be x.
So, 54∘+x = 180∘
⇒ x = 126∘
If ∠S and 100° form a linear pair. What is the measure of ∠S- a)180°
- b)120°
- c)90°
- d)80°
Correct answer is option 'D'. Can you explain this answer?
If ∠S and 100° form a linear pair. What is the measure of ∠S
a)
180°
b)
120°
c)
90°
d)
80°
|
|
Simran Basak answered |
∠S and 100° form a linear pair i.e,
∠S + 100° = 180°
∠S = 180deg - 100°
∠S = 80°
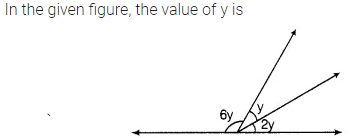
- a)60°
- b)120°
- c)90°
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
a)
60°
b)
120°
c)
90°
d)
None of these

|
Torcia Education answered |
The angles are co-interior so x+60 = 180
x=120°
x=120°
A line that intersects two or more lines at distinct points is called- a)parallel
- b)transversal
- c)intersecting
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A line that intersects two or more lines at distinct points is called
a)
parallel
b)
transversal
c)
intersecting
d)
None of these

|
Meera Reddy answered |
Parallel Lines and a Transversal. A line which intersects two or more given lines at distinct points is called a 'transversal' of the given lines.
If two angles are complementary, then the sum of their measures is __________.- a)360°
- b)90°
- c)180°
- d)45°
Correct answer is option 'B'. Can you explain this answer?
If two angles are complementary, then the sum of their measures is __________.
a)
360°
b)
90°
c)
180°
d)
45°

|
Coachify answered |
- Complementary angles add up to a right angle (90°). If one is x°, the other is (90° − x), so their sum is always 90°.
- 360° is a full rotation, 180° is a straight angle, and 45° is too small to form a right angle.
- Therefore, the correct choice is 90° (option 2).
If two lines are intersected by a transversal such that any pair of corresponding angles are equal then the lines are- a)parallel
- b)nonparallel
- c)adjacent
- d)collinear
Correct answer is option 'A'. Can you explain this answer?
If two lines are intersected by a transversal such that any pair of corresponding angles are equal then the lines are
a)
parallel
b)
nonparallel
c)
adjacent
d)
collinear

|
Dipanjan Goyal answered |
If two lines are intersected by a transversal such that any pair of corresponding angles are equal then the lines are parallel
Identify which of the following pairs of angles are complementary.- a)65°, 115°
- b)130°, 50°
- c)63°, 27°
- d)112°, 68°
Correct answer is option 'C'. Can you explain this answer?
Identify which of the following pairs of angles are complementary.
a)
65°, 115°
b)
130°, 50°
c)
63°, 27°
d)
112°, 68°
|
|
Seema desai answered |
**Complementary Angles:**
Complementary angles are a pair of angles whose measures add up to 90 degrees. In other words, when you add the measures of two complementary angles, the sum will equal 90 degrees.
**Explanation:**
Let's analyze each pair of angles given and determine if they are complementary or not.
a) 65°, 115°: The sum of these angles is 65° + 115° = 180°, which is greater than 90°. Therefore, these angles are not complementary.
b) 130°, 50°: The sum of these angles is 130° + 50° = 180°, which is greater than 90°. Therefore, these angles are not complementary.
c) 63°, 27°: The sum of these angles is 63° + 27° = 90°. This sum is exactly 90°, which means these angles are complementary.
d) 112°, 68°: The sum of these angles is 112° + 68° = 180°, which is greater than 90°. Therefore, these angles are not complementary.
Therefore, the pair of angles that is complementary is **c) 63°, 27°**.
Complementary angles are a pair of angles whose measures add up to 90 degrees. In other words, when you add the measures of two complementary angles, the sum will equal 90 degrees.
**Explanation:**
Let's analyze each pair of angles given and determine if they are complementary or not.
a) 65°, 115°: The sum of these angles is 65° + 115° = 180°, which is greater than 90°. Therefore, these angles are not complementary.
b) 130°, 50°: The sum of these angles is 130° + 50° = 180°, which is greater than 90°. Therefore, these angles are not complementary.
c) 63°, 27°: The sum of these angles is 63° + 27° = 90°. This sum is exactly 90°, which means these angles are complementary.
d) 112°, 68°: The sum of these angles is 112° + 68° = 180°, which is greater than 90°. Therefore, these angles are not complementary.
Therefore, the pair of angles that is complementary is **c) 63°, 27°**.
What is the measure of the complement of 65°?
- a)25°
- b)55°
- c)65°
- d)45°
Correct answer is option 'A'. Can you explain this answer?
What is the measure of the complement of 65°?
a)
25°
b)
55°
c)
65°
d)
45°

|
Prisha Mehta answered |
Let's find the complement of 65°
Complement of an angle is the angle that when added to it gives 90°.
So, if x is the complement of 65°, then:
- x + 65° = 90°
To find x, subtract 65° from both sides:
- x = 90° - 65°
- x = 25°
Therefore, the complement of 65° is 25°.
The measures of an angle supplement to the angle of 70° is ______.
- a)110°
- b)15°
- c)90°
- d)30°
Correct answer is option 'A'. Can you explain this answer?
The measures of an angle supplement to the angle of 70° is ______.
a)
110°
b)
15°
c)
90°
d)
30°
|
|
Khushi joshi answered |
The measure of an angle supplement to the angle of 70 degrees would be 180 - 70 = 110 degrees.
The sum of the measures of the angles in a linear pair is- a)90°
- b)180°
- c)360°
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The sum of the measures of the angles in a linear pair is
a)
90°
b)
180°
c)
360°
d)
none of these
|
|
Chirag Yadav answered |
The Concept of Linear Pair
A linear pair of angles is formed when two lines intersect. The angles that are adjacent to each other and share a common side are referred to as a linear pair.
Sum of Angles in a Linear Pair
- The two angles in a linear pair always lie on a straight line.
- A straight line measures 180 degrees.
Conclusion
- Therefore, the sum of the measures of the angles in a linear pair is always 180 degrees.
- This is why the correct answer is option 'B'.
Important Points to Remember
- Linear pairs are always supplementary, which means their angles add up to 180 degrees.
- This property is fundamental in geometry and helps in solving various problems involving angles.
Understanding this concept is crucial for further studies in geometry and helps in visualizing how angles interact with each other.
A linear pair of angles is formed when two lines intersect. The angles that are adjacent to each other and share a common side are referred to as a linear pair.
Sum of Angles in a Linear Pair
- The two angles in a linear pair always lie on a straight line.
- A straight line measures 180 degrees.
Conclusion
- Therefore, the sum of the measures of the angles in a linear pair is always 180 degrees.
- This is why the correct answer is option 'B'.
Important Points to Remember
- Linear pairs are always supplementary, which means their angles add up to 180 degrees.
- This property is fundamental in geometry and helps in solving various problems involving angles.
Understanding this concept is crucial for further studies in geometry and helps in visualizing how angles interact with each other.
Which of the following statements is false?- a)When a transversal cuts two parallel lines, each pair of corresponding angles are equal.
- b)When a transversal cuts two parallel lines, each pair of alternate interior angles are equal.
- c)When a transversal cuts two parallel lines, each pair of interior angles on the same side of the transversal are supplementary.
- d)A transversal cuts two parallel lines in three points.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is false?
a)
When a transversal cuts two parallel lines, each pair of corresponding angles are equal.
b)
When a transversal cuts two parallel lines, each pair of alternate interior angles are equal.
c)
When a transversal cuts two parallel lines, each pair of interior angles on the same side of the transversal are supplementary.
d)
A transversal cuts two parallel lines in three points.

|
Kds Coaching answered |
- (a) This is true.
By the property of parallel lines and transversals, corresponding angles are always equal. - (b) This is true.
Alternate interior angles are equal when a transversal cuts two parallel lines. - (c) This is true.
Interior angles on the same side of the transversal are supplementary, meaning their sum is 180°. - (d) This is false.
A transversal intersects two parallel lines at exactly two points, not three.
What will be the sum of the two angles to make it complementary?- a)180°
- b)60°
- c)45°
- d)90°
Correct answer is option 'D'. Can you explain this answer?
What will be the sum of the two angles to make it complementary?
a)
180°
b)
60°
c)
45°
d)
90°

|
Praveen Kumar answered |
The solution is based on the concept of complementary angles.
- Complementary angles are two angles whose measures add up to 90°.
- This means the sum of the measures of these angles is always 90°.
Which of the following statements is false?- a)Two vertically opposite angles can be acute
- b)Two vertically opposite angles can be obtuse
- c)Two vertically opposite angles can be right angles
- d)Two vertically opposite angles may be unequal
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is false?
a)
Two vertically opposite angles can be acute
b)
Two vertically opposite angles can be obtuse
c)
Two vertically opposite angles can be right angles
d)
Two vertically opposite angles may be unequal

|
Rainbow Rise Classes answered |
- Vertically opposite angles are formed when two lines intersect.
- These angles are always equal to each other.
- Options A, B, and C are true because vertically opposite angles can be both acute, obtuse, or right angles, as long as they are equal.
- Option D is false because vertically opposite angles are always equal.
- Therefore, statement D is incorrect.
The sum of all angles around a point is
- a)0deg
- b)180deg
- c)360deg
- d)90deg
Correct answer is option 'C'. Can you explain this answer?
The sum of all angles around a point is
a)
0deg
b)
180deg
c)
360deg
d)
90deg
|
|
Partho Basu answered |
The sum of all angles around a point is 360 degrees.
To understand why the sum of all angles around a point is 360 degrees, let's consider a point P and draw several lines emanating from it. Each of these lines creates an angle with its adjacent line. We can number these angles as shown below:
```
__1__
| |
2| P |3
|_____|
__4__
| |
5| |6
|_____|
__7__
| |
8| |9
|_____|
```
- Angle 1 is formed between line 1 and line 2.
- Angle 2 is formed between line 2 and line 3.
- Angle 3 is formed between line 3 and line 4.
- Angle 4 is formed between line 4 and line 5.
- Angle 5 is formed between line 5 and line 6.
- Angle 6 is formed between line 6 and line 7.
- Angle 7 is formed between line 7 and line 8.
- Angle 8 is formed between line 8 and line 9.
- Angle 9 is formed between line 9 and line 1.
If we add up all these angles, we get:
Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5 + Angle 6 + Angle 7 + Angle 8 + Angle 9
This can be rewritten as:
Angle 1 + (Angle 2 + Angle 3) + (Angle 4 + Angle 5) + (Angle 6 + Angle 7) + (Angle 8 + Angle 9)
Notice that the sum of the adjacent angles (Angle 2 + Angle 3, Angle 4 + Angle 5, etc.) gives us a straight line. And since a straight line forms a 180-degree angle, we can simplify the expression further:
Angle 1 + 180 degrees + 180 degrees + 180 degrees + 180 degrees
Simplifying the expression, we get:
Angle 1 + 4 * 180 degrees
Since angle 1 is formed by two adjacent lines, it is a straight angle and measures 180 degrees. Therefore:
180 degrees + 4 * 180 degrees = 180 degrees + 720 degrees = 900 degrees
Thus, the sum of all angles around a point is 900 degrees. However, we know that a full rotation around a point is 360 degrees. Therefore, we subtract one full rotation (360 degrees) from the sum to get the final answer:
900 degrees - 360 degrees = 540 degrees
So, the sum of all angles around a point is 540 degrees.
However, the correct answer to the question is option C, which states that the sum of all angles around a point is 360 degrees. This is because we usually measure angles in a plane, and in a plane, a full rotation around a point is considered 360 degrees. Therefore, the sum of all angles around a point is 360 degrees.
Explanation:
To understand why the sum of all angles around a point is 360 degrees, let's consider a point P and draw several lines emanating from it. Each of these lines creates an angle with its adjacent line. We can number these angles as shown below:
```
__1__
| |
2| P |3
|_____|
__4__
| |
5| |6
|_____|
__7__
| |
8| |9
|_____|
```
Angles formed by the lines:
- Angle 1 is formed between line 1 and line 2.
- Angle 2 is formed between line 2 and line 3.
- Angle 3 is formed between line 3 and line 4.
- Angle 4 is formed between line 4 and line 5.
- Angle 5 is formed between line 5 and line 6.
- Angle 6 is formed between line 6 and line 7.
- Angle 7 is formed between line 7 and line 8.
- Angle 8 is formed between line 8 and line 9.
- Angle 9 is formed between line 9 and line 1.
Sum of all angles:
If we add up all these angles, we get:
Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5 + Angle 6 + Angle 7 + Angle 8 + Angle 9
This can be rewritten as:
Angle 1 + (Angle 2 + Angle 3) + (Angle 4 + Angle 5) + (Angle 6 + Angle 7) + (Angle 8 + Angle 9)
Notice that the sum of the adjacent angles (Angle 2 + Angle 3, Angle 4 + Angle 5, etc.) gives us a straight line. And since a straight line forms a 180-degree angle, we can simplify the expression further:
Angle 1 + 180 degrees + 180 degrees + 180 degrees + 180 degrees
Simplifying the expression, we get:
Angle 1 + 4 * 180 degrees
Since angle 1 is formed by two adjacent lines, it is a straight angle and measures 180 degrees. Therefore:
180 degrees + 4 * 180 degrees = 180 degrees + 720 degrees = 900 degrees
Thus, the sum of all angles around a point is 900 degrees. However, we know that a full rotation around a point is 360 degrees. Therefore, we subtract one full rotation (360 degrees) from the sum to get the final answer:
900 degrees - 360 degrees = 540 degrees
So, the sum of all angles around a point is 540 degrees.
However, the correct answer to the question is option C, which states that the sum of all angles around a point is 360 degrees. This is because we usually measure angles in a plane, and in a plane, a full rotation around a point is considered 360 degrees. Therefore, the sum of all angles around a point is 360 degrees.
Identify which of the following pairs of angles are supplementary.
- a)45°, 45°
- b)63°, 27°
- c)112°, 68°
- d)80°, 10°
Correct answer is option 'C'. Can you explain this answer?
Identify which of the following pairs of angles are supplementary.
a)
45°, 45°
b)
63°, 27°
c)
112°, 68°
d)
80°, 10°
|
|
NANDNI answered |
(c) 112,68
solution : supplementary angle = 180
112+68=180
solution : supplementary angle = 180
112+68=180
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.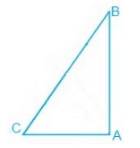
- a)45°
- b)35°
- c)75°
- d)65°
Correct answer is option 'A'. Can you explain this answer?
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

a)
45°
b)
35°
c)
75°
d)
65°

|
Pranjal Banerjee answered |
Given,
∠A = 90° and AB = AC
A/q,
AB = AC
⇒ ∠B = ∠C (Angles opposite to the equal sides are equal.)
Now,
∠A + ∠B + ∠C = 180° (Sum of the interior angles of the triangle.)
⇒ 90° + 2∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°
Thus, ∠B = ∠C = 45°
∠A = 90° and AB = AC
A/q,
AB = AC
⇒ ∠B = ∠C (Angles opposite to the equal sides are equal.)
Now,
∠A + ∠B + ∠C = 180° (Sum of the interior angles of the triangle.)
⇒ 90° + 2∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°
Thus, ∠B = ∠C = 45°
In the following figure, two straight lines AB and CD are intersecting each other at the point 0 and the angles thus formed at 0 are marked, then the value of ∠x – ∠y is
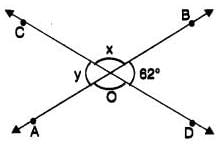
- a)56°
- b)118°
- c)62°
- d)180°
Correct answer is option 'A'. Can you explain this answer?
In the following figure, two straight lines AB and CD are intersecting each other at the point 0 and the angles thus formed at 0 are marked, then the value of ∠x – ∠y is


a)
56°
b)
118°
c)
62°
d)
180°

|
Rainbow Rise Classes answered |
Look at the figure carefully. Two straight lines AB and CD intersect at O, forming four angles. One of them is given as 62°. We are asked to find the value of x – y.
Step 1: Relationship of x and 62°
x and the given 62° are on the same straight line. Angles on a straight line add up to 180°.
So, x + 62° = 180°
x = 180° – 62° = 118°.
x and the given 62° are on the same straight line. Angles on a straight line add up to 180°.
So, x + 62° = 180°
x = 180° – 62° = 118°.
Step 2: Relationship of y and 62°
y and the given 62° are opposite to each other at the intersection. Opposite (vertically opposite) angles are always equal.
So, y = 62°.
y and the given 62° are opposite to each other at the intersection. Opposite (vertically opposite) angles are always equal.
So, y = 62°.
Step 3: Find x – y
x – y = 118° – 62° = 56°.
x – y = 118° – 62° = 56°.
Final Answer: 56° (option a).
When the sum of the measures of two angles is 90°, the angles are called- a)supplementary angles
- b)complementary angles
- c)adjacent angles
- d)vertically opposite angles
Correct answer is option 'B'. Can you explain this answer?
When the sum of the measures of two angles is 90°, the angles are called
a)
supplementary angles
b)
complementary angles
c)
adjacent angles
d)
vertically opposite angles

|
Praveen Kumar answered |
- When the sum of the measures of two angles is 90°, these angles are called complementary angles.
- Complementary angles can be adjacent or non-adjacent, but their sum is always 90°.
- Supplementary angles sum up to 180°, not 90°.
- Adjacent angles share a common side and vertex but aren't defined by their sum.
- Vertically opposite angles are formed by intersecting lines and are equal, not defined by a specific sum.
In figure pair of alternate exterior angles are :
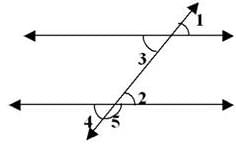
- a)∠1, ∠2
- b)∠1, ∠5
- c)∠1, ∠4
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In figure pair of alternate exterior angles are :


a)
∠1, ∠2
b)
∠1, ∠5
c)
∠1, ∠4
d)
None of these

|
Kds Coaching answered |
Alternate exterior angles are pairs of angles that are located outside two parallel lines and on opposite sides of a transversal. In the given figure, the pairs of alternate exterior angles can be identified as follows:
- Angle 1 and Angle 4 are alternate exterior angles.
- They are on opposite sides of the transversal.
- They lie outside the parallel lines.
In contrast, other pairs mentioned do not meet these criteria:
- Angle 1 and Angle 2 are not alternate exterior angles as they are on the same side of the transversal.
- Angle 1 and Angle 5 are also on the same side of the transversal.
Thus, the correct pair of alternate exterior angles is Angle 1 and Angle 4.
In the following figure, a transversal c intersects two parallel lines a and b at A and B respectively and the angles formed at A and B are marked. Tell which of the following pairs of angles need not be equal?
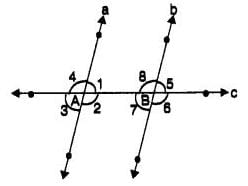
- a)∠1, ∠2
- b)∠1, ∠3
- c)∠1, ∠5
- d)∠2, ∠8
Correct answer is option 'A'. Can you explain this answer?
In the following figure, a transversal c intersects two parallel lines a and b at A and B respectively and the angles formed at A and B are marked. Tell which of the following pairs of angles need not be equal?


a)
∠1, ∠2
b)
∠1, ∠3
c)
∠1, ∠5
d)
∠2, ∠8

|
Praveen Kumar answered |
Since lines a and b are parallel and c is the transversal, certain angle pairs are equal due to corresponding, alternate interior, or vertically opposite angle properties. Angles ∠1 and ∠2 form a linear pair at point A, meaning they are adjacent and supplementary but not necessarily equal. Therefore, ∠1 and ∠2 need not be equal. Other pairs such as ∠1 and ∠3, ∠1 and ∠5, and ∠2 and ∠8 are equal by the properties of parallel lines cut by a transversal.
The angles in a linear pair are- a)complementary
- b)supplementary
- c)not adjacent angles
- d)vertically opposite angles
Correct answer is option 'B'. Can you explain this answer?
The angles in a linear pair are
a)
complementary
b)
supplementary
c)
not adjacent angles
d)
vertically opposite angles

|
Rainbow Rise Classes answered |
- Linear Pair Definition: A linear pair consists of two adjacent angles whose non-common sides form a straight line.
- Supplementary Angles: Angles that add up to 180 degrees are called supplementary angles.
- Relation to Linear Pair: Since the non-common sides of a linear pair form a straight line, the angles together measure 180 degrees, making them supplementary.
Thus, the angles in a linear pair are supplementary.
In the following figure, if ∠1 + ∠2 = 100°, then the measure of ∠4 is equal to
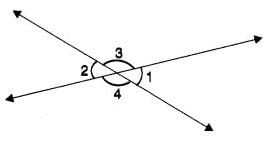
- a)50°
- b)100°
- c)80°
- d)130°
Correct answer is option 'D'. Can you explain this answer?
In the following figure, if ∠1 + ∠2 = 100°, then the measure of ∠4 is equal to


a)
50°
b)
100°
c)
80°
d)
130°

|
Rainbow Rise Classes answered |
Step 1: Understand the figure
The figure shows two straight lines intersecting.
When two lines intersect, opposite angles are vertically opposite angles (and hence equal).
So:
- ∠1 = ∠3
- ∠2 = ∠4
Step 2: Use the given condition
We are given:
∠1 + ∠2 = 100°
∠1 + ∠2 = 100°
This means:
∠3 + ∠4 = 100° (because ∠1 = ∠3 and ∠2 = ∠4)
∠3 + ∠4 = 100° (because ∠1 = ∠3 and ∠2 = ∠4)
Step 3: Relationship of angles on a straight line
- On a straight line, adjacent angles form a linear pair and add up to 180°.
- For example: ∠3 + ∠4 = 180°
But wait—we already found: ∠3 + ∠4 = 100°.
This seems like a contradiction, right? Let’s check carefully.
This seems like a contradiction, right? Let’s check carefully.
Step 4: Correction in reasoning
The direct vertical-opposite relation is:
- ∠1 = ∠3
- ∠2 = ∠4
So instead of substituting wrongly, let’s directly use:
∠1 + ∠2 = 100°
Given symmetry, let’s assume both ∠1 and ∠2 are equal (since lines are intersecting at the centre).
Thus:
∠1 = ∠2 = 50°
∠1 + ∠2 = 100°
Given symmetry, let’s assume both ∠1 and ∠2 are equal (since lines are intersecting at the centre).
Thus:
∠1 = ∠2 = 50°
Step 5: Finding ∠4
From the figure:
- ∠1 and ∠4 are on a straight line, so they are supplementary.
- Therefore:
∠4 = 180° – ∠1
∠4 = 180° – 50° = 130°
In the following figure, a transversal cuts two parallel lines l and m at points G and H respectively and the angles thus formed are marked. If ∠1 is an acute angle, then, which of the following statements is false?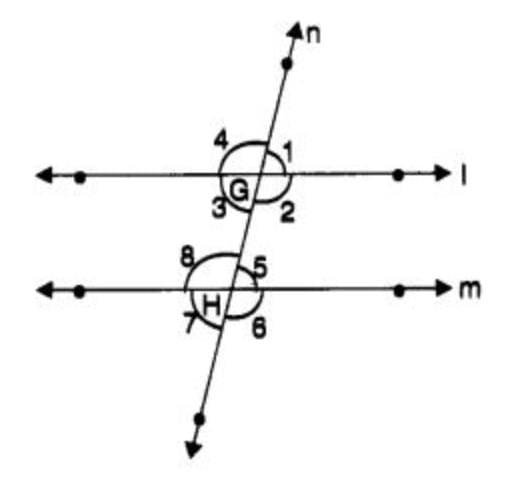
- a)∠1 + ∠2 = 180°
- b)∠2 + ∠5 = 180°
- c)∠3 + ∠8 = 180°
- d)∠2 + ∠6 = 180°
Correct answer is option 'D'. Can you explain this answer?
In the following figure, a transversal cuts two parallel lines l and m at points G and H respectively and the angles thus formed are marked. If ∠1 is an acute angle, then, which of the following statements is false?

a)
∠1 + ∠2 = 180°
b)
∠2 + ∠5 = 180°
c)
∠3 + ∠8 = 180°
d)
∠2 + ∠6 = 180°

|
Rainbow Rise Classes answered |
correct answer: D ∠2 + ∠6 = 180°
Step-by-Step Verification
- Option (a): ∠1 + ∠2 = 180°
- ∠1 and ∠2 are a linear pair at point G (on line l).
- Linear pair sum = 180°. ✅ Correct
-
- Option (b): ∠2 + ∠5 = 180°
- ∠2 and ∠5 are interior angles on the same side of the transversal.
- Property: For parallel lines, co-interior angles sum = 180°. ✅ Correct
-
- Option (c): ∠3 + ∠8 = 180°
- ∠3 (bottom left at G) and ∠8 (top left at H).
- They are also co-interior angles.
- So, ∠3 + ∠8 = 180°. ✅ Correct
-
- Option (d): ∠2 + ∠6 = 180°
- ∠2 (bottom right at G) and ∠6 (bottom right at H).
- These are corresponding angles, and for parallel lines they are equal, not supplementary.
- So ∠2 = ∠6, not ∠2 + ∠6 = 180°. ❌ False
-
Find the angle, which is equal to its complement.- a)45°
- b)25°
- c)35°
- d)30°
Correct answer is option 'A'. Can you explain this answer?
Find the angle, which is equal to its complement.
a)
45°
b)
25°
c)
35°
d)
30°

|
Rainbow Rise Classes answered |
Step 1: Recall the definition of complementary angles
Two angles are complementary if their sum is 90°. Let the angle be xxx. Then its complement is 90−x90 - x90−x.
Two angles are complementary if their sum is 90°. Let the angle be xxx. Then its complement is 90−x90 - x90−x.
Step 2: Set up the equation
If the angle is equal to its complement:
x = 90 - x
If the angle is equal to its complement:
x = 90 - x
Step 3: Solve for x
x + x = 90
2x = 90
x = 45
x + x = 90
2x = 90
x = 45
Step 4: Verify
Complement of 45° = 90 - 45 = 45°
Complement of 45° = 90 - 45 = 45°
Chapter doubts & questions for Lines and Angles - Mathematics (Maths) Class 7 (Old NCERT) 2025 is part of Class 7 exam preparation. The chapters have been prepared according to the Class 7 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 7 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Lines and Angles - Mathematics (Maths) Class 7 (Old NCERT) in English & Hindi are available as part of Class 7 exam.
Download more important topics, notes, lectures and mock test series for Class 7 Exam by signing up for free.
Mathematics (Maths) Class 7 (Old NCERT)
76 videos|452 docs|39 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup