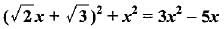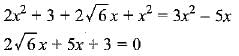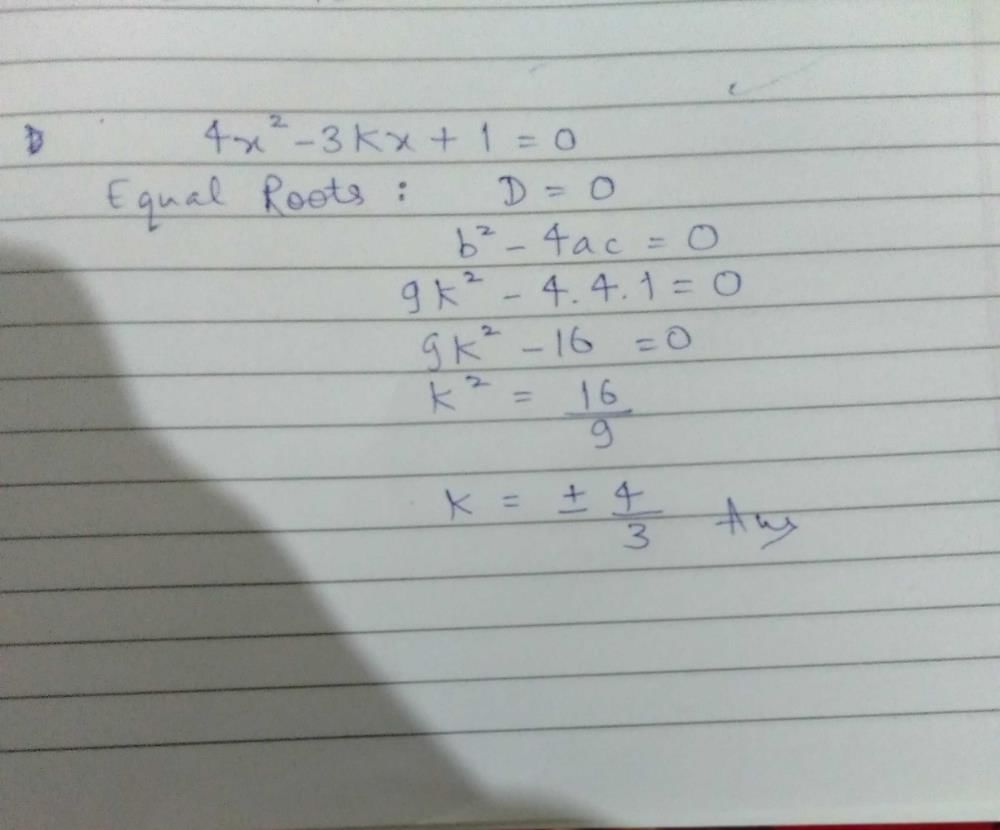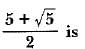All Exams >
Class 10 >
Online MCQ Tests for Class 10 >
All Questions
All questions of Quadratic Equations for Class 10 Exam
Solve 9x2 = 36- a)±2
- b)±6
- c)±4
- d)2
Correct answer is option 'A'. Can you explain this answer?
Solve 9x2 = 36
a)
±2
b)
±6
c)
±4
d)
2
|
|
Nilanjan Shah answered |
Solution:
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
5x2+8x+4 = 2x2+4x+6 is a- a)linear equation
- b)constant
- c)cubic equation
- d)quadratic equation
Correct answer is option 'D'. Can you explain this answer?
5x2+8x+4 = 2x2+4x+6 is a
a)
linear equation
b)
constant
c)
cubic equation
d)
quadratic equation

|
Palak Patel answered |
Given: 5x2+8x+4 = 2x2+4x+6
⇒ 5x2−2x2+8x−4x+4−6 = 0
⇒ 3x2+4x−2 = 0
Here, the degree is 2, therefore it is a quadratic equation.
⇒ 5x2−2x2+8x−4x+4−6 = 0
⇒ 3x2+4x−2 = 0
Here, the degree is 2, therefore it is a quadratic equation.
The two consecutive odd positive integers, sum of whose squares is 290 are- a)13, 15
- b)11, 13
- c)7, 9
- d)5, 7
Correct answer is option 'B'. Can you explain this answer?
The two consecutive odd positive integers, sum of whose squares is 290 are
a)
13, 15
b)
11, 13
c)
7, 9
d)
5, 7
|
|
Drishti Kumari answered |
Let first consecutive odd positive integer be x
Secon = x + 2
(x)^2 + ( x + 2 )^2 = 290
x^2 + x^2 + 4 + 4x = 290
2x^2 + 4x = 290 - 4
2x^2 + 4x = 286
2x^2 + 4x - 286 = 0
x^2 + 2x - 143 = 0
x^2 + 13x - 11x - 143 = 0
x ( x + 13 ) - 11 ( x + 13 ) = 0
( x -11) ( x + 13) = 0
x = 11 Or x = -13
Second = 11 + 2 = 13
Hence option (B) is correct .
(x2 + 1)2 - x2 = 0 has
- a)Four real roots
- b)Two real roots
- c)No real roots
- d)One real root
Correct answer is option 'C'. Can you explain this answer?
(x2 + 1)2 - x2 = 0 has
a)
Four real roots
b)
Two real roots
c)
No real roots
d)
One real root
|
|
Arun Sharma answered |
Given equation is (x2 + 1)2 - x2 = 0
⇒ x4 + 1 + 2x2 - x2 = 0 [∵ (a + b)2 = a2 + b2 + 2ab]
⇒ x4 + x2 + 1 = 0
Let x2 = y
∴ (x2)2 + x2 + 1 = 0
y2 + y + 1 = 0
On comparing with ay2 + by + c = 0, we get
a = 1, b = 1 and c = 1
Discriminant, D = b2 - 4ac
= (1)2 - 4(1)(1)
= 1 - 4 = -3
Since, D < 0
∴ y2 + y + 1 = 0 i.e., x4 + x2 + 1 = 0 or (x2 + 1)2 - x2 = 0 has no real roots.
⇒ x4 + 1 + 2x2 - x2 = 0 [∵ (a + b)2 = a2 + b2 + 2ab]
⇒ x4 + x2 + 1 = 0
Let x2 = y
∴ (x2)2 + x2 + 1 = 0
y2 + y + 1 = 0
On comparing with ay2 + by + c = 0, we get
a = 1, b = 1 and c = 1
Discriminant, D = b2 - 4ac
= (1)2 - 4(1)(1)
= 1 - 4 = -3
Since, D < 0
∴ y2 + y + 1 = 0 i.e., x4 + x2 + 1 = 0 or (x2 + 1)2 - x2 = 0 has no real roots.
Write the general form of a quadratic polynomia- a)ax2 + bx + c where a, b and c are real numbers
- b)ax2 + bx + c=0
- c)ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
- d)ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
Correct answer is option 'C'. Can you explain this answer?
Write the general form of a quadratic polynomia
a)
ax2 + bx + c where a, b and c are real numbers
b)
ax2 + bx + c=0
c)
ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
d)
ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
|
|
Krishna Iyer answered |
If the coefficient of x2 is zero , then the equation is not a quadratic equation , its a linear equation. So its necessary condition for the quadratic equation.
Which of the following in not a quadratic equation:- a)(x – 2)2 + 1 = 2x – 3
- b)(x + 2)2 = x3 – 4
- c)x(2x + 3) = x2 + 1
- d)x(x + 1) + 8 = (x + 2) (x – 2)
Correct answer is option 'D'. Can you explain this answer?
Which of the following in not a quadratic equation:
a)
(x – 2)2 + 1 = 2x – 3
b)
(x + 2)2 = x3 – 4
c)
x(2x + 3) = x2 + 1
d)
x(x + 1) + 8 = (x + 2) (x – 2)

|
Rahul Kumar answered |
Option (B) and (D) , both are the correct answers. We have x(x + 1) + 8 = (x + 2) (x – 2)
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
The equation 4x2 = 4x has following solution/solutions- a)1
- b)-1, 0
- c)1, -1
- d)0, 1
Correct answer is option 'D'. Can you explain this answer?
The equation 4x2 = 4x has following solution/solutions
a)
1
b)
-1, 0
c)
1, -1
d)
0, 1
|
|
Pooja Shah answered |
We have 4x2=4x
4x2 - 4x=0
4x(x-1)=0
Either 4x=0 = x=0
Or x-1=0 = x=1
4x2 - 4x=0
4x(x-1)=0
Either 4x=0 = x=0
Or x-1=0 = x=1
Can you explain the answer of this question below: If 4 is a root of the equation 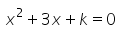 , then k is
, then k is
- A:
-28
- B:
-12
- C:
12
- D:
28
The answer is a.
If 4 is a root of the equation , then k is
-28
-12
12
28

|
Vp Classes answered |
4 is the solution , this means that if we put x=4 we get 0. So putting x=4 in the equation x2+3x+k=0 we get 42+3*4+k=0
16+12+k=0 ⇒ k=-28
16+12+k=0 ⇒ k=-28
Solve for x : 6x2 + 40 = 31x- a)

- b)

- c)0,8/3
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Solve for x : 6x2 + 40 = 31x
a)

b)

c)
0,8/3
d)
None of the above
|
|
Nirmal Kumar answered |
6x²-31x+40=0,
a=6,
b=-31,
c=40,
by quadratic formula-->
x=-b±√b²-4ac/2a,
by putting the values of a,b and c, we get,
x=-(-31)±√(-31)²-4(6)(40)/2(6),
=31±√961-960/12,
=31±√1/12,
=31±1/12,
x=30/12or ,32/12,
x=5/2 or, 8/3,
hence , option B is correct
a=6,
b=-31,
c=40,
by quadratic formula-->
x=-b±√b²-4ac/2a,
by putting the values of a,b and c, we get,
x=-(-31)±√(-31)²-4(6)(40)/2(6),
=31±√961-960/12,
=31±√1/12,
=31±1/12,
x=30/12or ,32/12,
x=5/2 or, 8/3,
hence , option B is correct
If x = 1 is a common root of the equation x2 + ax – 3 = 0 and bx2 – 7x + 2 = 0 then ab =
- a)10
- b)-3
- c)6
- d)7
Correct answer is option 'A'. Can you explain this answer?
If x = 1 is a common root of the equation x2 + ax – 3 = 0 and bx2 – 7x + 2 = 0 then ab =
a)
10
b)
-3
c)
6
d)
7
|
|
Zachary Foster answered |
Given:
- x = 1 is a common root of the equations:
- x² + ax - 3 = 0
- bx² - 7x + 2 = 0
To find:
- The value of ab.
Solution:
Since x = 1 is a root of both equations, we can substitute x = 1 in both equations.
Equation 1:
- 1² + a(1) - 3 = 0
- 1 + a - 3 = 0
- a = 2
Equation 2:
- b(1)² - 7(1) + 2 = 0
- b - 7 + 2 = 0
- b = 5
Therefore, ab = 2 * 5 = 10
So, the value of ab is 10.
The difference of a number and its reciprocal is 1.5. Then, the number is/are: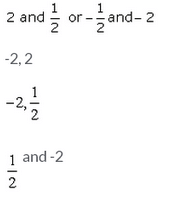
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'A'. Can you explain this answer?
The difference of a number and its reciprocal is 1.5. Then, the number is/are:
a)
A
b)
B
c)
C
d)
D
|
|
Mysterio Man answered |
Let the number=x,
reciprocal of the number=1/x,
given that:->x-1/x=1.5,
x²-1/x=15/10,
(x²-1)10=15x,
10x²-10-15x=0,
5(2x²-2-3x)=0,
2x²-3x-2=0,
by splitting the middle term,
2x²-4x+x-2=0,
2x(x-2)+1(x-2)=0,
(2x+1)=0,or, (x-2)=0,
x=-1/2,or,x=2,
if x=2 then 1/x=1/2 and if x=-1/2 then x=-2
reciprocal of the number=1/x,
given that:->x-1/x=1.5,
x²-1/x=15/10,
(x²-1)10=15x,
10x²-10-15x=0,
5(2x²-2-3x)=0,
2x²-3x-2=0,
by splitting the middle term,
2x²-4x+x-2=0,
2x(x-2)+1(x-2)=0,
(2x+1)=0,or, (x-2)=0,
x=-1/2,or,x=2,
if x=2 then 1/x=1/2 and if x=-1/2 then x=-2
Which of the following is not a quadratic equation?- a)2(x - 1)2 = 4x2 - 2x + 1
- b)2x - x2 = x2 + 5
- c)
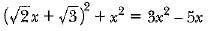
- d)(x2 + 2 x)2 = x4 + 3 + 4x3
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a quadratic equation?
a)
2(x - 1)2 = 4x2 - 2x + 1
b)
2x - x2 = x2 + 5
c)
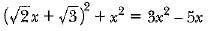
d)
(x2 + 2 x)2 = x4 + 3 + 4x3
|
|
Pooja Shah answered |
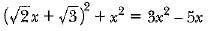
2x2 + 3 + 2√6x + x2 = 3x2 - 5x
3 + 2√6x + 5x= 0
Which is not a quadratic equation.
Which of the following equations has - 1 as a root?- a) x2 + 3x - 10 = 0
- b) x2 - x - 12 = 0
- c) 3x2 - 2x - 5 = 0
- d) 9x2 + 24x + 16 = 0
Correct answer is option 'C'. Can you explain this answer?
Which of the following equations has - 1 as a root?
a)
x2 + 3x - 10 = 0
b)
x2 - x - 12 = 0
c)
3x2 - 2x - 5 = 0
d)
9x2 + 24x + 16 = 0
|
|
Gaurav Kumar answered |
3x² - 2x - 5 = 0
3x² + 3x - 5x - 5 = 0
3x(x+1) - 5(x+1) = 0
(x+1)(3x-5) = 0
x = -1 and 5/3.
3x² + 3x - 5x - 5 = 0
3x(x+1) - 5(x+1) = 0
(x+1)(3x-5) = 0
x = -1 and 5/3.
Hence roots of given polynomial are -1 and 5/3.
The value/s of x when (x – 4) (3x + 2) = 0 ________- a)4, -2/3
- b)-4, – 2/ 3
- c)4, 2/3
- d)-4, 2/3
Correct answer is option 'A'. Can you explain this answer?
The value/s of x when (x – 4) (3x + 2) = 0 ________
a)
4, -2/3
b)
-4, – 2/ 3
c)
4, 2/3
d)
-4, 2/3
|
|
Drishti Kumari answered |
( x - 4 ) ( 3x + 2 ) = 0
x - 4 = 0
x = 4
3x + 2 = 0
3x = -2
x = -2 / 3
Therefore option (A) is correct.
x - 4 = 0
x = 4
3x + 2 = 0
3x = -2
x = -2 / 3
Therefore option (A) is correct.
The nature of the roots of the equation x2 – 5x + 7 = 0 is –- a)No real roots
- b)1 real root
- c)Can't be determined
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The nature of the roots of the equation x2 – 5x + 7 = 0 is –
a)
No real roots
b)
1 real root
c)
Can't be determined
d)
None of these
|
|
Krishna Iyer answered |
Given equation is x2-5x+7=0
We have discriminant as b2-4ac=(-5)2-4*1*7= -3
And x =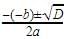 , Since we do not have any real number which is a root of a negative number, the roots are not real.
, Since we do not have any real number which is a root of a negative number, the roots are not real.
We have discriminant as b2-4ac=(-5)2-4*1*7= -3
And x =
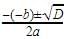 , Since we do not have any real number which is a root of a negative number, the roots are not real.
, Since we do not have any real number which is a root of a negative number, the roots are not real.Value(s) of k for which the quadratic equation 2x2 -kx + k = 0 has equal roots is
- a)0
- b)4
- c)8
- d)0 and 8
Correct answer is option 'D'. Can you explain this answer?
Value(s) of k for which the quadratic equation 2x2 -kx + k = 0 has equal roots is
a)
0
b)
4
c)
8
d)
0 and 8
|
|
Kuldeep Kuldeep answered |
Solution:-
Compare given Quadratic equation 2x²-kx+k=0 with ax²+bx+c=0, we get
a = 2,
b = -k ,
c = k,
Discriminant (D) = 0
[ Given roots are equal ]
=> b²-4ac = 0
=> (-k)²-4×2×k=0
=> k²-8k=0
=> k(k-8)=0
=> k = 0 or k=8.
So, option d is correct.
Compare given Quadratic equation 2x²-kx+k=0 with ax²+bx+c=0, we get
a = 2,
b = -k ,
c = k,
Discriminant (D) = 0
[ Given roots are equal ]
=> b²-4ac = 0
=> (-k)²-4×2×k=0
=> k²-8k=0
=> k(k-8)=0
=> k = 0 or k=8.
So, option d is correct.
The roots of quadratic equation are 2x2+3x-9 = 0 are:- a)1.5 and 3
- b)1.5 and -3
- c)-1.5 and -3
- d)-1.5 and 3
Correct answer is option 'B'. Can you explain this answer?
The roots of quadratic equation are 2x2+3x-9 = 0 are:
a)
1.5 and 3
b)
1.5 and -3
c)
-1.5 and -3
d)
-1.5 and 3
|
|
Alisha desai answered |
Explanation:
To find the roots of the quadratic equation 2x^2 + 3x - 9 = 0, we can use the quadratic formula:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
Step 1:
Identify the values of a, b, and c from the given quadratic equation.
a = 2, b = 3, c = -9
Step 2:
Substitute the values of a, b, and c in the quadratic formula.
x = (-3 ± sqrt(3^2 - 4(2)(-9))) / 2(2)
Simplifying the equation, we get:
x = (-3 ± sqrt(105)) / 4
Step 3:
Now we need to simplify the square root of 105.
105 = 3 x 5 x 7
We can simplify the square root of 105 as:
sqrt(105) = sqrt(3 x 5 x 7) = sqrt(3) x sqrt(5) x sqrt(7)
Step 4:
Substitute the simplified value of square root of 105 in the quadratic formula.
x = (-3 ± sqrt(3) x sqrt(5) x sqrt(7)) / 4
Now we can simplify further by dividing the numerator and denominator by 2.
x = (-3/2) ± (sqrt(3) x sqrt(35)) / 4
Step 5:
We can simplify the expression by separating it into two roots.
x = (-3/2) + (sqrt(3) x sqrt(35)) / 4 or x = (-3/2) - (sqrt(3) x sqrt(35)) / 4
Step 6:
We can further simplify the expression by dividing the numerator and denominator of each root by 2.
x = (-3/4) + (sqrt(3) x sqrt(35)) / 8 or x = (-3/4) - (sqrt(3) x sqrt(35)) / 8
Step 7:
Simplify the expression by finding the common denominator.
x = (-6 + sqrt(3 x 35)) / 8 or x = (-6 - sqrt(3 x 35)) / 8
Step 8:
Simplify further by multiplying and dividing the numerator of each root by 2.
x = (-6 + sqrt(105)) / 8 or x = (-6 - sqrt(105)) / 8
Step 9:
Now we can see that the roots are 1.5 and -3.
x = (1.5) or x = (-3)
Therefore, the correct answer is option B, which is 1.5 and -3.
To find the roots of the quadratic equation 2x^2 + 3x - 9 = 0, we can use the quadratic formula:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
Step 1:
Identify the values of a, b, and c from the given quadratic equation.
a = 2, b = 3, c = -9
Step 2:
Substitute the values of a, b, and c in the quadratic formula.
x = (-3 ± sqrt(3^2 - 4(2)(-9))) / 2(2)
Simplifying the equation, we get:
x = (-3 ± sqrt(105)) / 4
Step 3:
Now we need to simplify the square root of 105.
105 = 3 x 5 x 7
We can simplify the square root of 105 as:
sqrt(105) = sqrt(3 x 5 x 7) = sqrt(3) x sqrt(5) x sqrt(7)
Step 4:
Substitute the simplified value of square root of 105 in the quadratic formula.
x = (-3 ± sqrt(3) x sqrt(5) x sqrt(7)) / 4
Now we can simplify further by dividing the numerator and denominator by 2.
x = (-3/2) ± (sqrt(3) x sqrt(35)) / 4
Step 5:
We can simplify the expression by separating it into two roots.
x = (-3/2) + (sqrt(3) x sqrt(35)) / 4 or x = (-3/2) - (sqrt(3) x sqrt(35)) / 4
Step 6:
We can further simplify the expression by dividing the numerator and denominator of each root by 2.
x = (-3/4) + (sqrt(3) x sqrt(35)) / 8 or x = (-3/4) - (sqrt(3) x sqrt(35)) / 8
Step 7:
Simplify the expression by finding the common denominator.
x = (-6 + sqrt(3 x 35)) / 8 or x = (-6 - sqrt(3 x 35)) / 8
Step 8:
Simplify further by multiplying and dividing the numerator of each root by 2.
x = (-6 + sqrt(105)) / 8 or x = (-6 - sqrt(105)) / 8
Step 9:
Now we can see that the roots are 1.5 and -3.
x = (1.5) or x = (-3)
Therefore, the correct answer is option B, which is 1.5 and -3.
If b2 - 4ac = 0 then The roots of the Quadratic equation ax2 + bx + c = 0 are given by :- a)
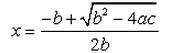
- b)
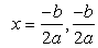
- c)
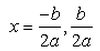
- d)
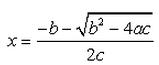
Correct answer is option 'B'. Can you explain this answer?
If b2 - 4ac = 0 then The roots of the Quadratic equation ax2 + bx + c = 0 are given by :
a)
b)
c)
d)

|
Udexy Coaching Center answered |
Formula for finding the roots of a quadratic equation is

So since
b2 - 4ac = 0, putting this value in the equation
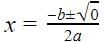
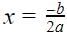 So there are repeated roots
So there are repeated roots
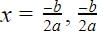

So since
b2 - 4ac = 0, putting this value in the equation
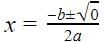
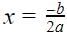 So there are repeated roots
So there are repeated roots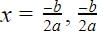
Which of the following is not a quadratic equation ?- a)5x + 3y2 = 0
- b)z2 - 2z = 0
- c)3x + 4 - 7x2 = 0
- d)5x2 - 125 = 0
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a quadratic equation ?
a)
5x + 3y2 = 0
b)
z2 - 2z = 0
c)
3x + 4 - 7x2 = 0
d)
5x2 - 125 = 0
|
|
Priyanshu Intelligent answered |
In equation first there are two variables.
That's why it is not a quadratic equation.
That's why it is not a quadratic equation.
The two positive numbers differ by 5 and square of their sum is 169 are
- a)2,4
- b)5,6
- c)4,9
- d)3,7
Correct answer is option 'C'. Can you explain this answer?
The two positive numbers differ by 5 and square of their sum is 169 are
a)
2,4
b)
5,6
c)
4,9
d)
3,7
|
|
Apoorv khanna answered |
Explanation:
Let the two numbers be x and y, where x is greater than y.
Given, x - y = 5
=> x = y + 5
Also, (x+y)^2 = 169
=> (y+5+y)^2 = 169 (Substituting x = y + 5)
=> (2y+5)^2 = 169
=> 4y^2 + 20y + 25 = 169 (Expanding the square)
=> 4y^2 + 20y - 144 = 0
=> y^2 + 5y - 36 = 0
=> (y + 9)(y - 4) = 0
=> y = -9 or y = 4
Since the numbers are positive, y = 4
Therefore, x = y + 5 = 9
Hence, the two numbers are 4 and 9.
Therefore, option C is the correct answer.
Let the two numbers be x and y, where x is greater than y.
Given, x - y = 5
=> x = y + 5
Also, (x+y)^2 = 169
=> (y+5+y)^2 = 169 (Substituting x = y + 5)
=> (2y+5)^2 = 169
=> 4y^2 + 20y + 25 = 169 (Expanding the square)
=> 4y^2 + 20y - 144 = 0
=> y^2 + 5y - 36 = 0
=> (y + 9)(y - 4) = 0
=> y = -9 or y = 4
Since the numbers are positive, y = 4
Therefore, x = y + 5 = 9
Hence, the two numbers are 4 and 9.
Therefore, option C is the correct answer.
Ruhi’s mother is 26 years older than her. The product of their ages (in years) 3 years from now will be 360. Form a Quadratic equation so as to find Ruhi’s age- a)x 2 + 32 x – 273 = 0
- b)x 2 -32 x – 273=0
- c)x 2 + 32 x + 273 = 0
- d)x 2 – 32 x +273 = 0
Correct answer is option 'A'. Can you explain this answer?
Ruhi’s mother is 26 years older than her. The product of their ages (in years) 3 years from now will be 360. Form a Quadratic equation so as to find Ruhi’s age
a)
x 2 + 32 x – 273 = 0
b)
x 2 -32 x – 273=0
c)
x 2 + 32 x + 273 = 0
d)
x 2 – 32 x +273 = 0
|
|
Amit Sharma answered |
Ruhi’s mother is 26 years older than her
So let Ruhi’s age is x
So mother’s age is x+26
The product of their ages 3 years from now will be 360
So After three years , Ruhi’s age will be x+3
Mother’s age will be x+26+3=x+29
Product of their ages =(x + 3)(x + 29)=360
x2+(3+29)x+87=360
x2+32x-273=0
So let Ruhi’s age is x
So mother’s age is x+26
The product of their ages 3 years from now will be 360
So After three years , Ruhi’s age will be x+3
Mother’s age will be x+26+3=x+29
Product of their ages =(x + 3)(x + 29)=360
x2+(3+29)x+87=360
x2+32x-273=0
The value of q if x = 2 is a solution of 8x2 + qx – 4 = 0 is _____- a)14
- b)-28
- c)-14
- d)28
Correct answer is option 'C'. Can you explain this answer?
The value of q if x = 2 is a solution of 8x2 + qx – 4 = 0 is _____
a)
14
b)
-28
c)
-14
d)
28
|
|
Kuldeep Raj answered |
Let us place 2 in the place of "x" for 8x² + qx - 4 = 0 (According to the question).
8(2)² + q(2) - 4 = 0.
8(4) + 2q - 4 = 0.
32 + 2q - 4 = 0.
Shift (32) to the right side.
2q - 4 = -32.
Shift (-4) to the right side. Then,
2q = -32 + 4.
2q = -28.
q = -28/2.
q = -14.
Therefore, the value of q if x = 2 is a solution of 8x² + qx - 4 = 0 is -14.
Hence, option (c) is correct friend...
8(2)² + q(2) - 4 = 0.
8(4) + 2q - 4 = 0.
32 + 2q - 4 = 0.
Shift (32) to the right side.
2q - 4 = -32.
Shift (-4) to the right side. Then,
2q = -32 + 4.
2q = -28.
q = -28/2.
q = -14.
Therefore, the value of q if x = 2 is a solution of 8x² + qx - 4 = 0 is -14.
Hence, option (c) is correct friend...
The solution of x2 + 4x + 4 = 0 is- a)2
- b)-2
- c)0
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The solution of x2 + 4x + 4 = 0 is
a)
2
b)
-2
c)
0
d)
None of these
|
|
Priyanshu Intelligent answered |
(-2)^2 + 4(-2) + 4
= 4 - 8 + 4
=8-8
=0.
Hence , option b) is the right answer.
= 4 - 8 + 4
=8-8
=0.
Hence , option b) is the right answer.
Read the following text and answer the following questions on the basis of the same:
Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.
 Q. Which of the following quadratic equations describe the speed of Nidhi’s car?
Q. Which of the following quadratic equations describe the speed of Nidhi’s car?
- a)x2 – 5x – 500 = 0
- b)x2 + 4x – 400 = 0
- c)x2 + 5x – 500 = 0
- d)x2 – 4x + 400 = 0
Correct answer is option 'C'. Can you explain this answer?
Read the following text and answer the following questions on the basis of the same:
Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.

Q. Which of the following quadratic equations describe the speed of Nidhi’s car?
a)
x2 – 5x – 500 = 0
b)
x2 + 4x – 400 = 0
c)
x2 + 5x – 500 = 0
d)
x2 – 4x + 400 = 0
|
|
Avinash Patel answered |
Let Speed of Nidhi = x km/h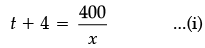
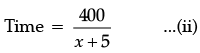

Time taken = t + 4 km/h
Time = D/s
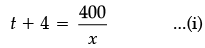
Speed of Ria = (x + 5) km/h
Time taken = t hour
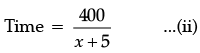
According to the question,

⇒ 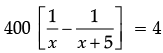
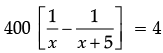
⇒ 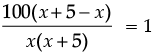
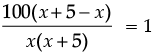
⇒ x2 + 5x – 500 = 0
If p,q and r are rational numbers and p ≠ q ≠ r, then roots of the equation (p2 - q2)x2 - (q2 - r2)x + (r2 - p2) = 0 are- a)
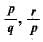
- b)
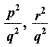
- c)
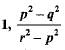
- d)
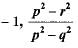
Correct answer is option ''. Can you explain this answer?
If p,q and r are rational numbers and p ≠ q ≠ r, then roots of the equation (p2 - q2)x2 - (q2 - r2)x + (r2 - p2) = 0 are
a)
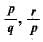
b)
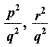
c)
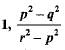
d)
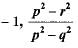

|
Let's Tute answered |
Putting x = - 1, we have
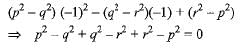 ∴ x = - 1 is one root.
∴ x = - 1 is one root.
Only option (d) has one root - 1.
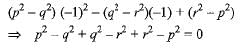 ∴ x = - 1 is one root.
∴ x = - 1 is one root.Only option (d) has one root - 1.
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Quadratic Equations" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths) Q. Which of the following quadratic expression can be expressed as a product of real linear factors?- a)x2 – 2x + 3
- b)3x2 – √2x – √3
- c)√2x2 – √5x + 3
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Quadratic Equations" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
Q. Which of the following quadratic expression can be expressed as a product of real linear factors?
a)
x2 – 2x + 3
b)
3x2 – √2x – √3
c)
√2x2 – √5x + 3
d)
None of these
|
|
Amit Kumar answered |
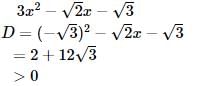
Thus, it can be expressed as product of linear factors.
If one root of a Quadratic equation is m + , then the other root is- a)m – √n
- b)m +√n
- c)Can not be determined
- d)√m + n
Correct answer is option 'A'. Can you explain this answer?
If one root of a Quadratic equation is m + , then the other root is
a)
m – √n
b)
m +√n
c)
Can not be determined
d)
√m + n
|
|
Arun Sharma answered |
In a quadratic equation with rational coefficients has an irrational root α + √β, then it has a conjugate root α - √β.
So if the root is m+ √n the other root will be m- √n
So if the root is m+ √n the other root will be m- √n
Which of the following equations has no real roots ?- a)
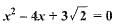
- b)
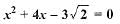
- c)
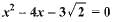
- d)
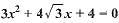
Correct answer is option 'A'. Can you explain this answer?
Which of the following equations has no real roots ?
a)
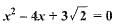
b)
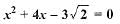
c)
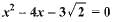
d)
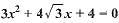
|
|
Amit Kumar answered |
(a) The given equation is x2 - 4x + 3√2 = 0.
On comparing with ax2 + bx + c = 0, we get
a = 1, b = -4 and c = 3√2
The discriminant of x2 - 4x + 3√2 = 0 is
D = b2 - 4ac
= (-4)2 - 4(1)(3√2) = 16 - 12√2 = 16 - 12 x (1.41)
= 16 - 16.92 = -0.92
⇒ b2 - 4ac < 0
(b) The given equation is x2 + 4x - 3√2 = 0
On comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = 4 and c = -3√2
Then, D = b2 - 4ac = (-4)2 - 4(1)(-3√2)
= 16 + 12√2 > 0
Hence, the equation has real roots.
(c) Given equation is x2 - 4x - 3√2 = 0
On comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -4 and c = -3√2
Then, D = b2 - 4ac = (-4)2 - 4(1) (-3√2)
= 16 + 12√2 > 0
Hence, the equation has real roots.
(d) Given equation is 3x2 + 4√3x + 4 = 0.
On comparing the equation with ax2 + bx + c = 0, we get
a = 3, b = 4√3 and c = 4
Then, D = b2 - 4ac = (4√3)2 - 4(3)(4) = 48 - 48 = 0
Hence, the equation has real roots.
Hence, x2 - 4x + 3√2 = 0 has no real roots.
On comparing with ax2 + bx + c = 0, we get
a = 1, b = -4 and c = 3√2
The discriminant of x2 - 4x + 3√2 = 0 is
D = b2 - 4ac
= (-4)2 - 4(1)(3√2) = 16 - 12√2 = 16 - 12 x (1.41)
= 16 - 16.92 = -0.92
⇒ b2 - 4ac < 0
(b) The given equation is x2 + 4x - 3√2 = 0
On comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = 4 and c = -3√2
Then, D = b2 - 4ac = (-4)2 - 4(1)(-3√2)
= 16 + 12√2 > 0
Hence, the equation has real roots.
(c) Given equation is x2 - 4x - 3√2 = 0
On comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -4 and c = -3√2
Then, D = b2 - 4ac = (-4)2 - 4(1) (-3√2)
= 16 + 12√2 > 0
Hence, the equation has real roots.
(d) Given equation is 3x2 + 4√3x + 4 = 0.
On comparing the equation with ax2 + bx + c = 0, we get
a = 3, b = 4√3 and c = 4
Then, D = b2 - 4ac = (4√3)2 - 4(3)(4) = 48 - 48 = 0
Hence, the equation has real roots.
Hence, x2 - 4x + 3√2 = 0 has no real roots.
The quadratic equation 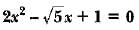 has
has- a)two distinct real roots
- b)two equal real roots
- c)no real root
- d)more than two real roots
Correct answer is option 'C'. Can you explain this answer?
The quadratic equation 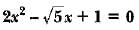 has
has
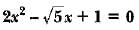 has
hasa)
two distinct real roots
b)
two equal real roots
c)
no real root
d)
more than two real roots
|
|
Amit Kumar answered |
We have a quadratic equation: 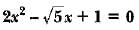
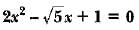
If we have standard equation ax2 + bx + c then D = b2 - 4ac
a= 2, b= -√5, c= 1
D = (-√5)2 - (4x2x1)
D= 5 - 8
D = -3
As the value of D<0 so there is no real root
Root of the equation x2 - 0.09 = 0 is- a)0.3
- b)0.03
- c)no root
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Root of the equation x2 - 0.09 = 0 is
a)
0.3
b)
0.03
c)
no root
d)
none of these
|
|
Vikram Kapoor answered |
x2 - 0.09 = 0
x2 = 0.09
x = √0.09
x = 0.3
x2 = 0.09
x = √0.09
x = 0.3
if 1/2 is a root of the equation  then the value of k is
then the value of k is- a)2
- b)-2
- c)1/4
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
if 1/2 is a root of the equation  then the value of k is
then the value of k is
 then the value of k is
then the value of k isa)
2
b)
-2
c)
1/4
d)
1/2
|
|
Ishan Choudhury answered |
As 1/2 is a root then it will satisfy the given equation.
Put x = 1/2
1/4 +(k×1/2) - 5/4 =0
k×1/2 =5/4 -1/4
k =2
k×1/2 =5/4 -1/4
k =2
(x2+1)2−x2 = 0 has- a)1 real root
- b)2 real roots
- c)4 real roots
- d)no real roots
Correct answer is 'A'. Can you explain this answer?
(x2+1)2−x2 = 0 has
a)
1 real root
b)
2 real roots
c)
4 real roots
d)
no real roots

|
Jhanvi Pillai answered |
Given: (x2+1)2 − x2 = 0
⇒ x2 + 1 + 2x − x2 = 0
⇒ 2x + 1 = 0
⇒ x = −1/2
Therefore, (x2+1)2 − x2 = 0 has no real roots.
⇒ x2 + 1 + 2x − x2 = 0
⇒ 2x + 1 = 0
⇒ x = −1/2
Therefore, (x2+1)2 − x2 = 0 has no real roots.
The roots of x2 – 8x + 12 = 0, are- a)x = 0
- b)no real roots
- c)real and unequal
- d)real and equal
Correct answer is option 'C'. Can you explain this answer?
The roots of x2 – 8x + 12 = 0, are
a)
x = 0
b)
no real roots
c)
real and unequal
d)
real and equal
|
|
Shweta singh answered |
The roots of the equation x^2 are x = 0.
If the area of a rectangle is 24 m2 and its perimeter is 20 m, the equation to find its length and breadth would be:
- a)x2 – 10x + 24 = 0
- b)x2 + 1 2x + 24 = 0
- c)x2 – 10x – 24 = 0
- d)x2 + 10x + 28 = 0
Correct answer is option 'A'. Can you explain this answer?
If the area of a rectangle is 24 m2 and its perimeter is 20 m, the equation to find its length and breadth would be:
a)
x2 – 10x + 24 = 0
b)
x2 + 1 2x + 24 = 0
c)
x2 – 10x – 24 = 0
d)
x2 + 10x + 28 = 0
|
|
Aashu Mehra answered |
Perimeter = 2(l+b)=20
l+b=10
lxb=24
so correct option is A
If a,b,c are real and b2-4ac >0 then roots of equation are- a)real roots
- b)real and equal
- c)real and unequal
- d)No real roots
Correct answer is option 'C'. Can you explain this answer?
If a,b,c are real and b2-4ac >0 then roots of equation are
a)
real roots
b)
real and equal
c)
real and unequal
d)
No real roots
|
|
Ram trivedi answered |
The expression b^2 - 4ac is the discriminant of a quadratic equation of the form ax^2 + bx + c = 0. It determines the nature of the solutions of the equation.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
The condition for equation ax2 + bx + c = 0 to be linear is- a)a > 0, b = 0
- b)a ≠ 0, b = 0
- c)a < 0, b = 0
- d)a = 0, b ≠ 0
Correct answer is option 'D'. Can you explain this answer?
The condition for equation ax2 + bx + c = 0 to be linear is
a)
a > 0, b = 0
b)
a ≠ 0, b = 0
c)
a < 0, b = 0
d)
a = 0, b ≠ 0
|
|
Tanisha answered |
Answer is d...bcoz to make ax^2 +bx+c=0,linear equation.
we need to eliminate ax^2.
So, we will put a=0 ,to make the degree of this equation 1 ...and b should not be equal to 0,bcoz if b will be 0 ,then it will be a constant equation,instead of a linear equation.
we need to eliminate ax^2.
So, we will put a=0 ,to make the degree of this equation 1 ...and b should not be equal to 0,bcoz if b will be 0 ,then it will be a constant equation,instead of a linear equation.
Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.- a)14 and 2
- b)11 and 5
- c)12 and 4
- d)10 and 6
Correct answer is option 'D'. Can you explain this answer?
Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.
a)
14 and 2
b)
11 and 5
c)
12 and 4
d)
10 and 6
|
|
Anjana Khatri answered |
Let x and (16 - x) are two parts of 16 where (16 - x) is longer and x is smaller .
A/C to question,
2 * square of longer = square of smaller + 164
⇒ 2 * (16 - x)^2 = x^2 + 164
⇒ 2 * (256 + x^2 - 32x ) = x^2 + 164
⇒ 512 + 2x^2 - 64x = x^2 + 164
⇒ x^2 - 64x + 512 - 164 = 0
⇒ x^2 - 64x + 348 = 0
⇒x^2 - 58x - 6x + 348 = 0
⇒ x(x - 58) - 6(x - 58) = 0
⇒(x - 6)(x - 58) = 0
⇒ x = 6 and 58
But x ≠ 58 because x < 16
so, x = 6 and 16 - x = 10
Hence, answer is 6 and 10
Which of following is not a quadratic equation:
- a)
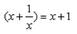
- b)(x + 3)2 = 3x(x - 2)
- c)x3 - 4x2 - x+1 = (x-1)3
- d)x2 + x+8 = 3x2 - 4
Correct answer is option 'A'. Can you explain this answer?
Which of following is not a quadratic equation:
a)
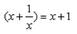
b)
(x + 3)2 = 3x(x - 2)
c)
x3 - 4x2 - x+1 = (x-1)3
d)
x2 + x+8 = 3x2 - 4

|
Adi2003bro answered |
Simplification of LHS x+1/x =. x^2+1/x .transposing deno.x to RHS will give. x(x+1). =. x^2+ x. now combining RHS&LHS . x^2+1=x^2+x . x=1 hence highest power 1 hence not a quad. equ.
Chapter doubts & questions for Quadratic Equations - Online MCQ Tests for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Quadratic Equations - Online MCQ Tests for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Related Class 10 Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup