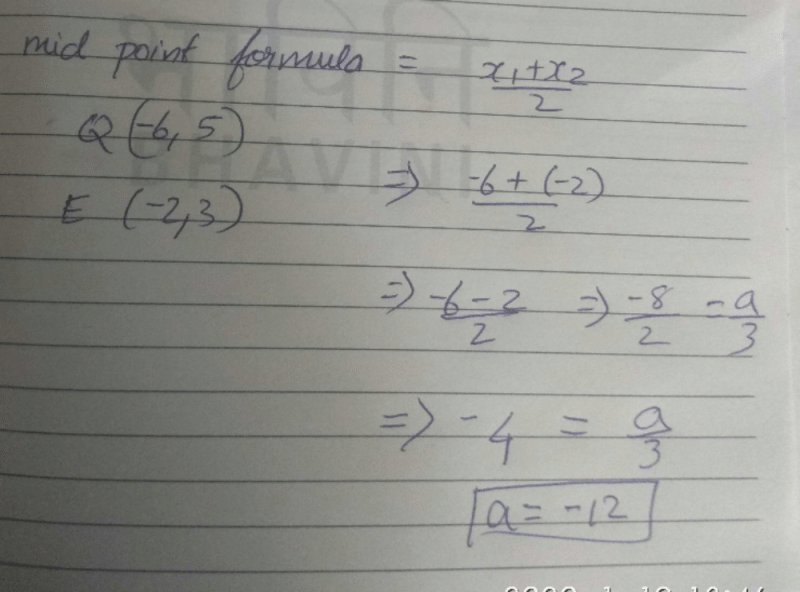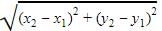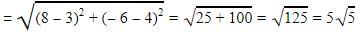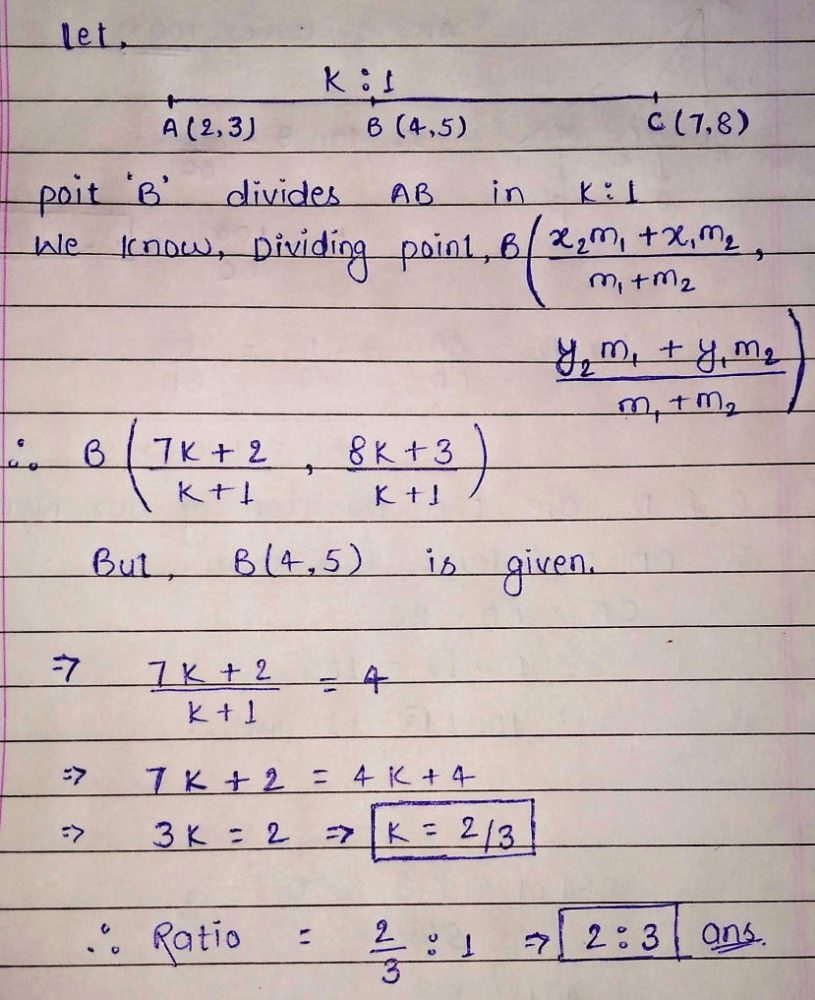All Exams >
Class 10 >
Online MCQ Tests for Class 10 >
All Questions
All questions of Coordinate Geometry for Class 10 Exam
The distance of the point P (2, 3) from the x-axis is
- a)2
- b)3
- c)1
- d)5
Correct answer is option 'B'. Can you explain this answer?
The distance of the point P (2, 3) from the x-axis is
a)
2
b)
3
c)
1
d)
5

|
Kamna Science Academy answered |
To find the distance of point P(2, 3) from the x-axis:
- The distance from a point (x, y) to the x-axis is the absolute value of the y-coordinate.
- For point P(2, 3), the y-coordinate is 3.
- Therefore, the distance of point P from the x-axis is 3.
- Hence, the correct answer is B: 3.
- The distance from a point (x, y) to the x-axis is the absolute value of the y-coordinate.
- For point P(2, 3), the y-coordinate is 3.
- Therefore, the distance of point P from the x-axis is 3.
- Hence, the correct answer is B: 3.
If the co – ordinates of a point are (3, – 7), then its ordinate is- a)– 3
- b)– 7
- c)3
- d)7
Correct answer is option 'B'. Can you explain this answer?
If the co – ordinates of a point are (3, – 7), then its ordinate is
a)
– 3
b)
– 7
c)
3
d)
7
|
|
Amit Sharma answered |
Since y−coordinate is called ordinate.
Therefore, ordinate is −7.
Therefore, ordinate is −7.
The distance of the point P (-6, 8) from the origin is- a)8
- b)2√7
- c)10
- d)6
Correct answer is option 'C'. Can you explain this answer?
The distance of the point P (-6, 8) from the origin is
a)
8
b)
2√7
c)
10
d)
6
|
|
Nirmal Kumar answered |
Let A(-6,8) and B(0,0),
by distance formula-->
distance between A and B=
√(x1-x2)²+(y1-y2)²,
=√(-6-0)²+(8-0)²,
=√(36)+(64),
=√100=10
by distance formula-->
distance between A and B=
√(x1-x2)²+(y1-y2)²,
=√(-6-0)²+(8-0)²,
=√(36)+(64),
=√100=10
Origin divides the join of points (1,1) and (2,2) externally in the ratio- a)1:2
- b)1:-2
- c)-1:-2
- d)-1:2
Correct answer is option 'A'. Can you explain this answer?
Origin divides the join of points (1,1) and (2,2) externally in the ratio
a)
1:2
b)
1:-2
c)
-1:-2
d)
-1:2
|
|
Kiran Mehta answered |
We have external section formula as
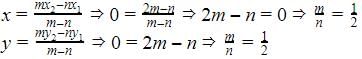
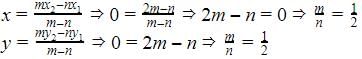
The points (k + 1, 1), (2k + 1, 3) and (2k + 2, 2k) are collinear if- a)k = - 1, 2
- b)

- c)k = 2, 1
- d)

Correct answer is option 'D'. Can you explain this answer?
The points (k + 1, 1), (2k + 1, 3) and (2k + 2, 2k) are collinear if
a)
k = - 1, 2
b)

c)
k = 2, 1
d)

|
|
Kiran Mehta answered |
∵ Points are collinear.
∴ (k + 1) (3 - 2k) + (2k, + 1) (2k - 1) + (2k + 2) (1 - 3) = 0
⇒ 3k+3 - 2k2 - 2k + 4k2 - 1 - 4k - 4 = 0 ⇒ 2k2 - 3k - 2 = 0
⇒ 2k2 - 4k + k - 2 = 0
⇒ 2k(k - 2) + 1(k - 2) = 0
⇒ (2k + 1) (k - 2) = 0
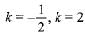
∴ (k + 1) (3 - 2k) + (2k, + 1) (2k - 1) + (2k + 2) (1 - 3) = 0
⇒ 3k+3 - 2k2 - 2k + 4k2 - 1 - 4k - 4 = 0 ⇒ 2k2 - 3k - 2 = 0
⇒ 2k2 - 4k + k - 2 = 0
⇒ 2k(k - 2) + 1(k - 2) = 0
⇒ (2k + 1) (k - 2) = 0
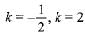
The distance between the points A (0, 6) and B (0, -2) is- a)6
- b)8
- c)4
- d)2
Correct answer is option 'B'. Can you explain this answer?
The distance between the points A (0, 6) and B (0, -2) is
a)
6
b)
8
c)
4
d)
2
|
|
Amit Kumar answered |
Since both these points lie on a straight line i.e x axis, distance will be the difference between the respective y coordinates
(0,-2) & (0,6) => 6-(-2)) = 6+2 = 8
(0,-2) & (0,6) => 6-(-2)) = 6+2 = 8
The graph of the equation x = 3 is:- a)a point
- b)straight line parallel to y axis
- c)straight line passing through the origin
- d)straight line parallel to x axis
Correct answer is option 'B'. Can you explain this answer?
The graph of the equation x = 3 is:
a)
a point
b)
straight line parallel to y axis
c)
straight line passing through the origin
d)
straight line parallel to x axis
|
|
Naina Sharma answered |
x=3 is fixed. This means the value of x is constant. So y can vary but x has only one value. For example (3,0),(3,2),(3,5) etc. So the line drawn will be parallel to y axis as y can vary.
The ratio in which the line 2x+y-4 = 0 divides the line segment joining A(2,-2) and B(3,7) is- a)4:3
- b)1:9
- c)8:9
- d)2:9
Correct answer is option 'D'. Can you explain this answer?
The ratio in which the line 2x+y-4 = 0 divides the line segment joining A(2,-2) and B(3,7) is
a)
4:3
b)
1:9
c)
8:9
d)
2:9

|
Shipra Rekha Acharya answered |
Let us assume the line divides AB in k : 1 ratio.
Coordinates of point of division can be given as follows:
x=2+3k/k+1
y=−2+7k/k+1
Substituting the values of x and y in following equation;
2x+y−4−0
Or,
2(2+3k/k+1)+ (−2+7k/k+1)−4=0
Or,
(4+6k/k+1)+ (−2+7k/k+1−4)=0
4+6k−2+7k−4(k+1)=0
4+6k−2+7k−4k−4=0
−2+9k=0
9k=0+2
k=2/9
Hence, the ratio is 2 : 9.
i hope it's helpful for us...
Coordinates of point of division can be given as follows:
x=2+3k/k+1
y=−2+7k/k+1
Substituting the values of x and y in following equation;
2x+y−4−0
Or,
2(2+3k/k+1)+ (−2+7k/k+1)−4=0
Or,
(4+6k/k+1)+ (−2+7k/k+1−4)=0
4+6k−2+7k−4(k+1)=0
4+6k−2+7k−4k−4=0
−2+9k=0
9k=0+2
k=2/9
Hence, the ratio is 2 : 9.
i hope it's helpful for us...
If the distance between the points (2, - 2) and (-1, x) is 5, one of the values of x is
- a)-2
- b)2
- c)-1
- d)1
Correct answer is option 'B'. Can you explain this answer?
If the distance between the points (2, - 2) and (-1, x) is 5, one of the values of x is
a)
-2
b)
2
c)
-1
d)
1
|
|
Naina Sharma answered |
Let us consider the points as
A = (2, -2)
B = (-1, x)
AB = 5 units
Using the distance formula
AB2 = (x₂ - x₁)2 + (y₂ - y₁)2
Substituting the values
52 = (-1 - 2)2 + (x + 2)2
25 = (-3)2 + (x + 2)2
Using the algebraic identity
(a + b)2 = a2 + b2 + 2ab
25 = 9 + x2 + 4 + 4x
By further calculation
25 = x2 + 4x + 13
x2 + 4x + 13 - 25 = 0
x2 + 4x - 12 = 0
By splitting the middle term
x2 + 6x - 2x - 12 = 0
Taking out the common terms
x(x + 6) - 2(x + 6) = 0
(x + 6)(x - 2) = 0
So we get
x + 6 = 0
x = -6
And
x - 2 = 0
x = 2
The distance of a point from the y – axis is called- a)abscissa
- b)origin
- c)ordinate
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The distance of a point from the y – axis is called
a)
abscissa
b)
origin
c)
ordinate
d)
none of these
|
|
Ananya Das answered |
The distance of a point from the y – axis is called abscissa.
The value of x, for which the points (x,-1), (2,1) and (4,5) lie on a line is- a)2
- b)1
- c)3
- d)0
Correct answer is option 'B'. Can you explain this answer?
The value of x, for which the points (x,-1), (2,1) and (4,5) lie on a line is
a)
2
b)
1
c)
3
d)
0

|
Dr Manju Sen answered |
Let A(x,−1),B(2,1) and C(4,5)
For the points to be collinear:
x1(y2−y3)+x2(y3−y1)+x3(y1−y2)=0
(i.e)x(1−5)+2(5+1)+4(−1−1)=0
⟹−4x+12−8=0
⟹x=1
For the points to be collinear:
x1(y2−y3)+x2(y3−y1)+x3(y1−y2)=0
(i.e)x(1−5)+2(5+1)+4(−1−1)=0
⟹−4x+12−8=0
⟹x=1
The end points of diameter of circle are (2, 4) and (-3, -1). The radius of the circle is
- a)

- b)5√2
- c)3√2
- d)
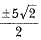
Correct answer is option 'A'. Can you explain this answer?
The end points of diameter of circle are (2, 4) and (-3, -1). The radius of the circle is
a)

b)
5√2
c)
3√2
d)
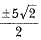

|
Nk Classes answered |
radius = Diameter/2
diameter = √((2-(-3))2 + (4-(-1))2)
= √52+52 = √50 = 5√2
If the distance between the points (p, – 5) and (2, 7) is 13 units, then the value of ‘p’ is- a)– 3, 7
- b)– 3, – 7
- c)3, – 7
- d)3, 7
Correct answer is option 'A'. Can you explain this answer?
If the distance between the points (p, – 5) and (2, 7) is 13 units, then the value of ‘p’ is
a)
– 3, 7
b)
– 3, – 7
c)
3, – 7
d)
3, 7

|
Rahul Kumar answered |
Let point A be (p,−5)(p,−5) and point B (2, 7) and distance between A and B = 13 units
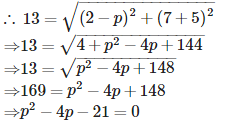

The distance between the points A (0, 7) and B (0, -3) is- a)4 units
- b)10 units
- c)7 units
- d)3 units
Correct answer is option 'B'. Can you explain this answer?
The distance between the points A (0, 7) and B (0, -3) is
a)
4 units
b)
10 units
c)
7 units
d)
3 units
|
|
Amit Sharma answered |
Since both these points lie on a straight line i.e x axis, distance will be the difference between the respective y coordinates
(0,-3) (0,7)
7-(-3) = 7+3 = 10
The line segment joining (2, – 3) and (5, 6) is divided by x-axis in the ratio:- a)2 : 1
- b)3 : 1
- c)1 : 2
- d)1 : 3.
Correct answer is option 'A'. Can you explain this answer?
The line segment joining (2, – 3) and (5, 6) is divided by x-axis in the ratio:
a)
2 : 1
b)
3 : 1
c)
1 : 2
d)
1 : 3.
|
|
Krishna Iyer answered |
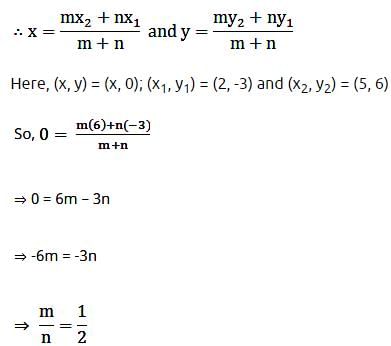
Hence, the ratio is 1:2 and the division is internal.
If the points (a,1), (1,-1) and (11,4) are collinear then the value of a is
- a)5
- b)-5
- c)6
- d)4
Correct answer is option 'A'. Can you explain this answer?
If the points (a,1), (1,-1) and (11,4) are collinear then the value of a is
a)
5
b)
-5
c)
6
d)
4
|
|
Ishan Choudhury answered |
Let A(a, 1), B(1, -1) and C(11, 4) be the given points
Area of ΔABC
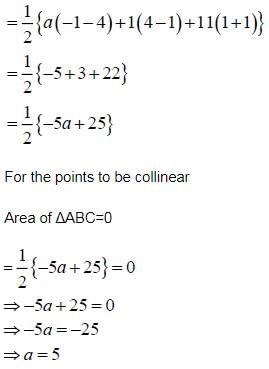
If P(1, 2), Q(4,6), R(5,7) and S(a, b) are the vertices of a parallelogram PQRS, then- a)a = 2, b = 4
- b)a = 3, b = 4
- c)a = 2, b = 3
- d)a = 3, b = 5
Correct answer is option 'C'. Can you explain this answer?
If P(1, 2), Q(4,6), R(5,7) and S(a, b) are the vertices of a parallelogram PQRS, then
a)
a = 2, b = 4
b)
a = 3, b = 4
c)
a = 2, b = 3
d)
a = 3, b = 5

|
Manasa Deshpande answered |
PQRS is a parallelogram if and only if the mid point of the diagonals PR is same as that of the mid point of Q, S. That is, if and only if

The point on x-axis which is equidistant from (5,9) and (-4,6) is- a)(3,0)
- b)(1,0)
- c)(2,0)
- d)(4,1)
Correct answer is option 'A'. Can you explain this answer?
The point on x-axis which is equidistant from (5,9) and (-4,6) is
a)
(3,0)
b)
(1,0)
c)
(2,0)
d)
(4,1)
|
|
Vikas Kumar answered |
for 2 points to be equidistant to 2 another the length of the line drawn to them should the first two should be equal to the next two.
let that point be (x,0) (y=0 as it leis on the x axis)
using distance formula-
root of ((x+4)2 +(0-6)2)=root of ((x-5)2 +(0-9)2)
squaring both sides and opening the brackets we get-
x2 + 8x + 16 + 36 = x2 - 10x + 25 +81
bring variables to one side and constants to another we get-
18x = 54
x = 54/18 = 3
therefore x = 3 and y =0 (since it leis in the x axis)
The points A (9, 0), B (9, 6), C (-9, 6) and D (-9, 0) are the vertices of a- a)square
- b)rectangle
- c)rhombus
- d)trapezium
Correct answer is option 'B'. Can you explain this answer?
The points A (9, 0), B (9, 6), C (-9, 6) and D (-9, 0) are the vertices of a
a)
square
b)
rectangle
c)
rhombus
d)
trapezium
|
|
Pratibha das answered |
Here is the solution to your question:
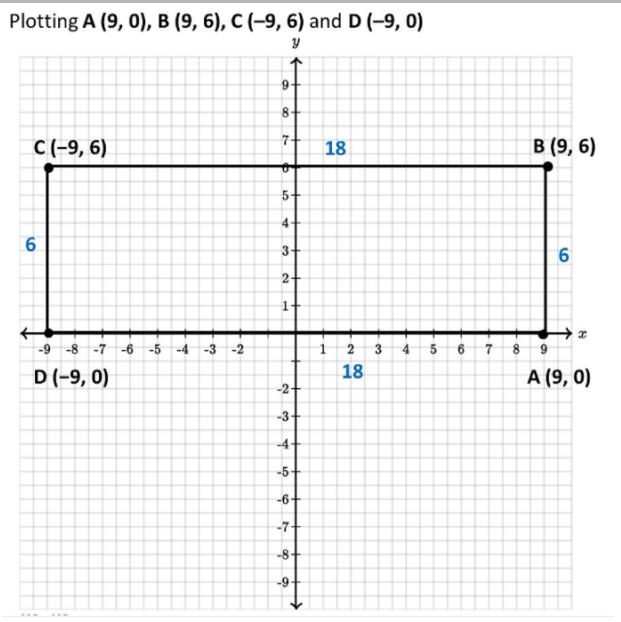
Since,
• Opposite sides are equal
• Sides are perpendicular to each other
Therefore, ABCD is a rectangle
So, the correct answer is B.
You can learn everything about Coordinate Geometry for Class 10 through the link:
Therefore, ABCD is a rectangle
So, the correct answer is B.
You can learn everything about Coordinate Geometry for Class 10 through the link:
The values of x and y, if the distance of the point (x,y) from (-3,0) as well as from (3,0) is 4 are- a)x = 1, y = 7
- b)x = 2, y = 7
- c)x = 0, y = – √7
- d)x = 0, y = ± √7
Correct answer is option 'D'. Can you explain this answer?
The values of x and y, if the distance of the point (x,y) from (-3,0) as well as from (3,0) is 4 are
a)
x = 1, y = 7
b)
x = 2, y = 7
c)
x = 0, y = – √7
d)
x = 0, y = ± √7
|
|
Nisha Choudhury answered |
Given, the distance of point P(x, y ) from A(– 3, 0) and B(3, 0) is 4 units.
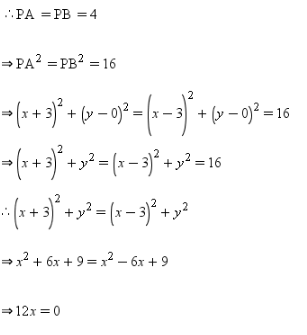
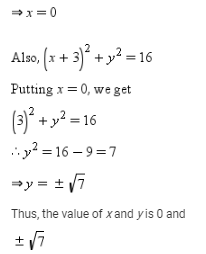
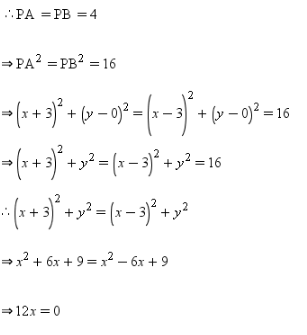
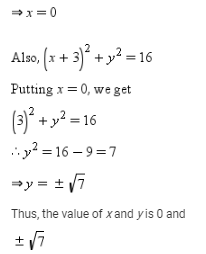
The ordinate of a point is twice its abscissa. If its distance from the point (4,3) is √10, then the coordinates of the point are- a)(1,2) or (3,6)
- b)(1,2) or (3,5)
- c)(2,1) or (3,6)
- d)(2,1) or (6,3)
Correct answer is option 'A'. Can you explain this answer?
The ordinate of a point is twice its abscissa. If its distance from the point (4,3) is √10, then the coordinates of the point are
a)
(1,2) or (3,6)
b)
(1,2) or (3,5)
c)
(2,1) or (3,6)
d)
(2,1) or (6,3)
|
|
Rahul Kapoor answered |
let the coordinate of that point be P(x,2x).
let the given point (4,3) be Q(4,3).
Then PQ=
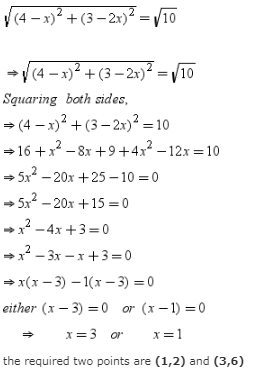
The point (-1,-5) lies in the Quadrant- a)3rd
- b)1st
- c)2nd
- d)4th
Correct answer is option 'A'. Can you explain this answer?
The point (-1,-5) lies in the Quadrant
a)
3rd
b)
1st
c)
2nd
d)
4th
|
|
Rising Star answered |
Quadrant 1 = +,+
Quadrant 2= -,+
Quadrant 3= -,-
Quadrant 4 = +,-
Thus,the point (-1,-5 ) will lie in Quadrant 3 !!!
Quadrant 2= -,+
Quadrant 3= -,-
Quadrant 4 = +,-
Thus,the point (-1,-5 ) will lie in Quadrant 3 !!!
The vertices of a quadrilateral are (1, 7), (4, 2), (– 1, – 1) and (– 4, 4). The quadrilateral is a- a)square
- b)rectangle
- c)parallelogram
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The vertices of a quadrilateral are (1, 7), (4, 2), (– 1, – 1) and (– 4, 4). The quadrilateral is a
a)
square
b)
rectangle
c)
parallelogram
d)
none of these
|
|
Vikram Kapoor answered |
Let A (1, 7), B (4, 2), C (-1, -1) and D(-4, 4) are the vertices of a quardinate
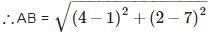
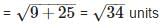
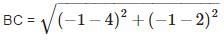
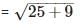
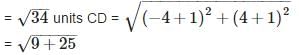

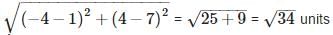
Since, all sides are equal and both diagonals are also equal.
Therefore, the given quadrilateral is a square.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If the distance between the point (4, p) and (1, 0) is 5, then the value of p is 4.Reason (R): The point which divides the line segment joining the points (7, – 6) and (3, 4) in ratio 1 : 2 internally lies in the fourth quadrant.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'D'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the distance between the point (4, p) and (1, 0) is 5, then the value of p is 4.
Reason (R): The point which divides the line segment joining the points (7, – 6) and (3, 4) in ratio 1 : 2 internally lies in the fourth quadrant.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Radha Iyer answered |
In case of assertion: Distance between two points (x1, y1) and (x2, y2) is given as,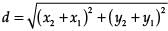

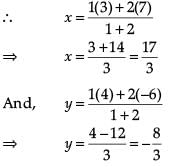
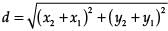
where, (x1, y1) = (4, p)
(x2, y2) = (1, 0)
And, d = 5
Put the values, we have
52 = (1 − 4)2 + (0 – p)2
25 = (–3)2 + (–p)2
25 – 9 = p2
16 = p2
+4, –4 = p
∴ Assertion is incorrect.
In case of reason:
Let (x, y) be the point

Here, x1 = 7, y1 = –6, x2 = 3, y2 = 4, m = 1 and n = 2
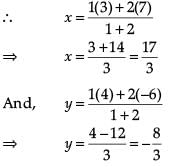
So, the required point  lies in IVth quadrant.
lies in IVth quadrant.
 lies in IVth quadrant.
lies in IVth quadrant.∴ Reason is correct.
Hence, assertion is incorrect but reason is correct.
Three consecutive vertices of a parallelogram ABCD are A(1, 2), B(1, 0) and C(4, 0). The co – ordinates of the fourth vertex D are- a)(– 4, – 2)
- b)(4, – 2)
- c)(– 4, 2)
- d)(4, 2)
Correct answer is option 'D'. Can you explain this answer?
Three consecutive vertices of a parallelogram ABCD are A(1, 2), B(1, 0) and C(4, 0). The co – ordinates of the fourth vertex D are
a)
(– 4, – 2)
b)
(4, – 2)
c)
(– 4, 2)
d)
(4, 2)
|
|
Radha Iyer answered |
Let coordinates of D be (x, y).
Since diagonals of a parallelogram bisect each other.
Since diagonals of a parallelogram bisect each other.
Therefore, coordinates of O will be 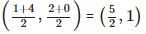
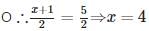
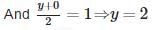
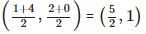
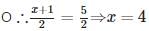
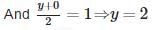
Therefore, the required coordinates are (4, 2).

The point where the medians of a triangle meet is called the ________ of the triangle- a)centroid
- b)circumcentre
- c)orthocentre
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The point where the medians of a triangle meet is called the ________ of the triangle
a)
centroid
b)
circumcentre
c)
orthocentre
d)
none of these
|
|
Ananya Das answered |
The point where the medians of a triangle meet is called thecentroidof the triangle.
For the triangle whose sides are along the lines y = 15, 3x – 4y = 0, 5x + 12y = 0, the incentre is :- a)(1, 8)
- b)(8, 1)
- c)(-1, 8)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
For the triangle whose sides are along the lines y = 15, 3x – 4y = 0, 5x + 12y = 0, the incentre is :
a)
(1, 8)
b)
(8, 1)
c)
(-1, 8)
d)
None of these
|
|
Raghav Bansal answered |
Given equations:
3x – 4y = 0 …(1)
5x+12y = 0 …(2)
Y-15 = 0 …(3)
From the given equations, (1), (2) and (3) represent the sides AB, BC and CA respectively.
Solving (1) and (2), we get
x= 0, and y= 0
Therefore, the side AB and BC intersect at the point B (0, 0)
Solving (1) and (3), we get
x= 20, y= 15
Hence, the side AB and CA intersect at the point A (20, 15)
Solving (2) and (3), we get
x= -36, y = 15
Thus, the side BC and CA intersect at the point C (-36, 15)
Now,
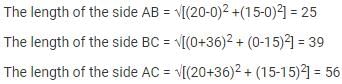
BC = a = 39
CA = b = 56
AB = c = 25
Similarly, (x1, y1) = A(20, 15)
CA = b = 56
AB = c = 25
Similarly, (x1, y1) = A(20, 15)
(x2, y2) = B(0, 0)
(x3, y3) = C(-36, 15)
(x3, y3) = C(-36, 15)
Therefore, incentre is
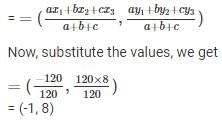
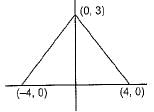
A triangle with vertices (4, 0), (- 1, - 1) and (3, 5) is a/an- a)equilateral triangle
- b)right-angled triangle
- c)isosceles right-angled triangle
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A triangle with vertices (4, 0), (- 1, - 1) and (3, 5) is a/an
a)
equilateral triangle
b)
right-angled triangle
c)
isosceles right-angled triangle
d)
none of these

|
Ananya Kumar answered |
A(4, 0), B(-1, -1), C(3, 5) are the vertices of a triangle. Then
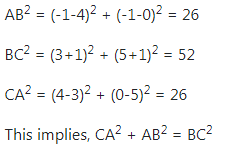
Thus, the triangle is isosceles and right angle triangle.
The area of triangle whose vertices are (2,3),(-1,0) and (2,-4), is- a)27 sq. units
- b)21 sq. units
- c)20.5 sq. units
- d)10.5 sq. units
Correct answer is option 'D'. Can you explain this answer?
The area of triangle whose vertices are (2,3),(-1,0) and (2,-4), is
a)
27 sq. units
b)
21 sq. units
c)
20.5 sq. units
d)
10.5 sq. units
|
|
Juhi malhotra answered |
Given, the vertices of the triangle are (2,3),(-1,0) and (2,-4).
Formula used:
The area of the triangle whose vertices are (x1,y1),(x2,y2) and (x3,y3) is given by the formula:
Area = [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]/2
Calculation:
Substituting the given values in the formula, we get:
Area = [2(0 + 4) + (-1)(3 + 4) + 2(3 - 0)]/2
Area = [8 - 7 + 6]/2
Area = 7/2
Area = 3.5 sq. units
Therefore, the correct option is (d) 10.5 sq. units.
Error in the question:
The correct answer should be 3.5 sq. units instead of 10.5 sq. units. The given options are incorrect.
Formula used:
The area of the triangle whose vertices are (x1,y1),(x2,y2) and (x3,y3) is given by the formula:
Area = [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]/2
Calculation:
Substituting the given values in the formula, we get:
Area = [2(0 + 4) + (-1)(3 + 4) + 2(3 - 0)]/2
Area = [8 - 7 + 6]/2
Area = 7/2
Area = 3.5 sq. units
Therefore, the correct option is (d) 10.5 sq. units.
Error in the question:
The correct answer should be 3.5 sq. units instead of 10.5 sq. units. The given options are incorrect.
The point where the perpendicular bisector of the line segment joining the points A(2, 5) and B(4, 7) cuts is:- a)(6, 3)
- b)(3, 6)
- c)(0, 0)
- d)(2, 5)
Correct answer is option 'B'. Can you explain this answer?
The point where the perpendicular bisector of the line segment joining the points A(2, 5) and B(4, 7) cuts is:
a)
(6, 3)
b)
(3, 6)
c)
(0, 0)
d)
(2, 5)
|
|
Krishna Iyer answered |
Since, the point, where the perpendicular bisector of a line segment cuts, is the mid-point of that line segment.
∴ Coordinates of Mid-point of line segment AB =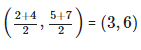
∴ Coordinates of Mid-point of line segment AB =
The perimeter of the triangle formed by the points A(0,0), B(1,0) and C(0,1) is- a)√2 + 1
- b)1 ± √2
- c)2 + √2
- d)3
Correct answer is option 'C'. Can you explain this answer?
The perimeter of the triangle formed by the points A(0,0), B(1,0) and C(0,1) is
a)
√2 + 1
b)
1 ± √2
c)
2 + √2
d)
3
|
|
Nisha Choudhury answered |
Consider A (0,0),B (1,0),C (0,1)
=>AB=root(X2-X1)^2+(Y2-Y1)^2
=>AB=root (1-0)^2+(1-0)^2
=>AB=1
similarly,
BC=root2
and
AC=1
Perimeter=AB+BC+AC
=1+root1+1
=2+root2
If A and B are the points (-6, 7) and (-1, -5) respectively, then the distance 2AB is equal to- a)26
- b)169
- c)13
- d)238
Correct answer is option 'A'. Can you explain this answer?
If A and B are the points (-6, 7) and (-1, -5) respectively, then the distance 2AB is equal to
a)
26
b)
169
c)
13
d)
238
|
|
Aditi bajaj answered |
To find the distance between two points, we can use the distance formula. The distance formula is derived from the Pythagorean theorem and allows us to calculate the distance between two points in a coordinate plane.
The distance formula is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points.
In this case, we are given the points A (-6, 7) and B (-1, -5). We need to find the distance 2AB, which means we need to find the distance between A and B and then multiply it by 2.
Let's calculate the distance between A and B first:
x1 = -6, y1 = 7 (coordinates of A)
x2 = -1, y2 = -5 (coordinates of B)
Using the distance formula:
dAB = sqrt((-1 - (-6))^2 + (-5 - 7)^2)
= sqrt(5^2 + (-12)^2)
= sqrt(25 + 144)
= sqrt(169)
= 13
Now, to find the distance 2AB, we multiply the distance between A and B by 2:
2AB = 2 * 13
= 26
So, the distance 2AB is equal to 26. Therefore, the correct answer is option A.
The distance formula is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points.
In this case, we are given the points A (-6, 7) and B (-1, -5). We need to find the distance 2AB, which means we need to find the distance between A and B and then multiply it by 2.
Let's calculate the distance between A and B first:
x1 = -6, y1 = 7 (coordinates of A)
x2 = -1, y2 = -5 (coordinates of B)
Using the distance formula:
dAB = sqrt((-1 - (-6))^2 + (-5 - 7)^2)
= sqrt(5^2 + (-12)^2)
= sqrt(25 + 144)
= sqrt(169)
= 13
Now, to find the distance 2AB, we multiply the distance between A and B by 2:
2AB = 2 * 13
= 26
So, the distance 2AB is equal to 26. Therefore, the correct answer is option A.
The distance of the point (– 3, 4) from the origin is- a)25 units
- b)1 unit
- c)7 units
- d)5 units
Correct answer is option 'D'. Can you explain this answer?
The distance of the point (– 3, 4) from the origin is
a)
25 units
b)
1 unit
c)
7 units
d)
5 units

|
Ayush Choudhary answered |
Let the given point be (x1, y1) = (-3, 4) and the orgin is (x2, y2) = (0, 0)
∴ Distance of the given point from the orgin =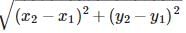
∴ Distance of the given point from the orgin =
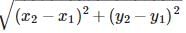
The ratio in which the x-axis divides the segment joining A(3,6) and B(12,-3) is- a)1:2
- b)-2:1
- c)2:1
- d)-1:-1
Correct answer is option 'C'. Can you explain this answer?
The ratio in which the x-axis divides the segment joining A(3,6) and B(12,-3) is
a)
1:2
b)
-2:1
c)
2:1
d)
-1:-1
|
|
Manisha choudhary answered |
Given: A(3,6), B(12,-3)
To find: The ratio in which the x-axis divides the segment joining A and B
Solution:
Step 1: Plot the given points A and B on the graph.
Step 2: Draw a line parallel to the y-axis passing through A and B.
Step 3: Let O be the point where the line intersects the x-axis.
Step 4: Find the distance OA and OB.
OA = 3 (since the point A lies on the x-axis)
OB = distance between points B and O
Using distance formula, OB = √[(12-0)² + (-3-0)²] = √(144+9) = √153
Step 5: Find the ratio in which point O divides the line segment AB.
Let the ratio be k:1
By section formula, we have:
x-coordinate of O = (k * x-coordinate of B + 1 * x-coordinate of A)/(k+1)
Since the point O lies on the x-axis, its y-coordinate is 0.
Therefore, we have:
(k * 12 + 3)/(k+1) = 0
k * 12 + 3 = 0
k = -3/12 = -1/4
The ratio in which the x-axis divides the segment joining A and B is 1: (-1/4) = 4: (-1)
Since the ratio is negative, we can write it as -4:1.
Therefore, the correct answer is option C) 2:1.
To find: The ratio in which the x-axis divides the segment joining A and B
Solution:
Step 1: Plot the given points A and B on the graph.
Step 2: Draw a line parallel to the y-axis passing through A and B.
Step 3: Let O be the point where the line intersects the x-axis.
Step 4: Find the distance OA and OB.
OA = 3 (since the point A lies on the x-axis)
OB = distance between points B and O
Using distance formula, OB = √[(12-0)² + (-3-0)²] = √(144+9) = √153
Step 5: Find the ratio in which point O divides the line segment AB.
Let the ratio be k:1
By section formula, we have:
x-coordinate of O = (k * x-coordinate of B + 1 * x-coordinate of A)/(k+1)
Since the point O lies on the x-axis, its y-coordinate is 0.
Therefore, we have:
(k * 12 + 3)/(k+1) = 0
k * 12 + 3 = 0
k = -3/12 = -1/4
The ratio in which the x-axis divides the segment joining A and B is 1: (-1/4) = 4: (-1)
Since the ratio is negative, we can write it as -4:1.
Therefore, the correct answer is option C) 2:1.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Centroid of a triangle formed by the points (a, b) (b, c), and (c, a) is at origin, Then a + b + c = 0 .Reason : Centroid of a △ABC with vertices A (x1, y1), B(x2, y2) and C (x3, y3) is given by
- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'A'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : Centroid of a triangle formed by the points (a, b) (b, c), and (c, a) is at origin, Then a + b + c = 0 .
Reason : Centroid of a △ABC with vertices A (x1, y1), B(x2, y2) and C (x3, y3) is given by

a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Avinash Patel answered |
Centroid of a triangle with vertices (a, b) (b, c), and (c, a) is



a + b + c = 0
Chapter doubts & questions for Coordinate Geometry - Online MCQ Tests for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Coordinate Geometry - Online MCQ Tests for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Related Class 10 Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

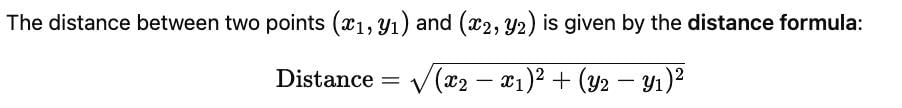








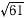 units from origin
units from origin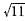 units from origin
units from origin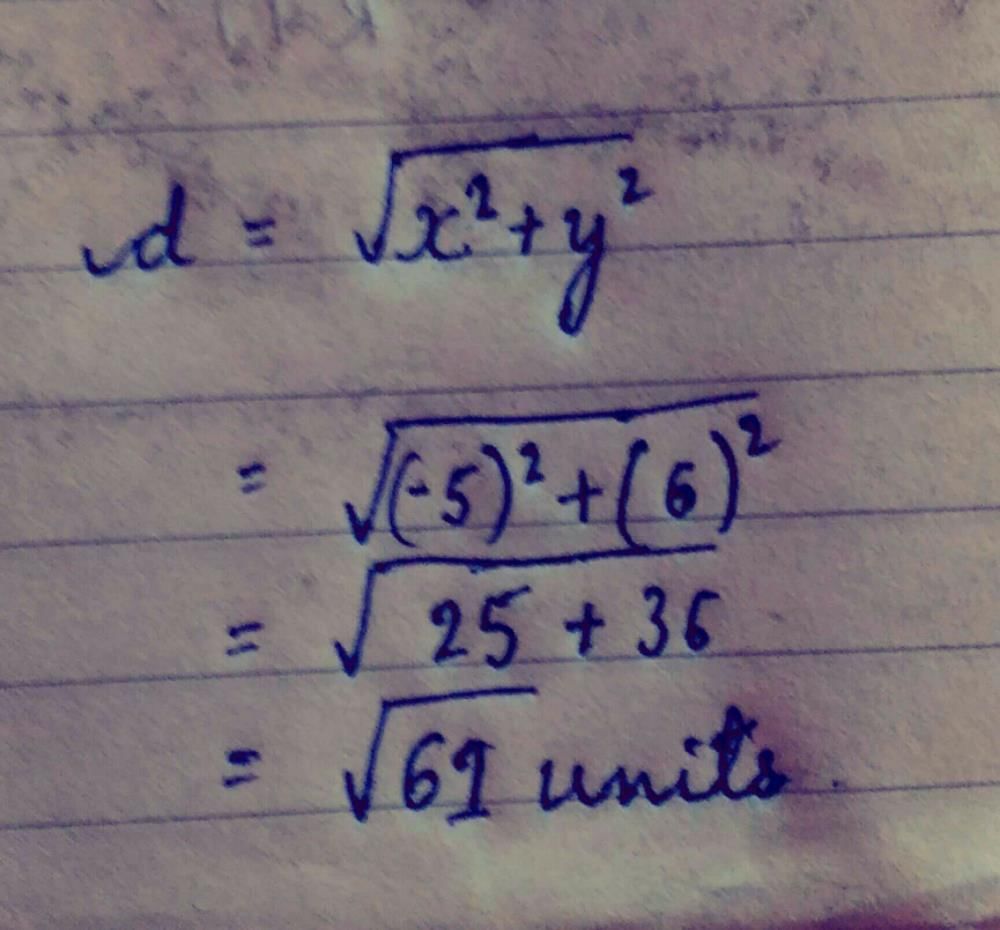



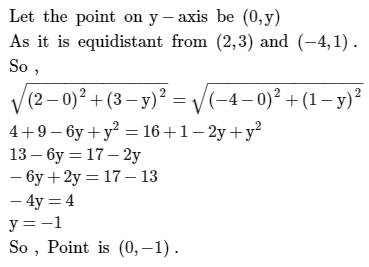
 is the mid-point of the line segment joining the points Q (-6, 5) and E (-2, 3), then the value of a is
is the mid-point of the line segment joining the points Q (-6, 5) and E (-2, 3), then the value of a is