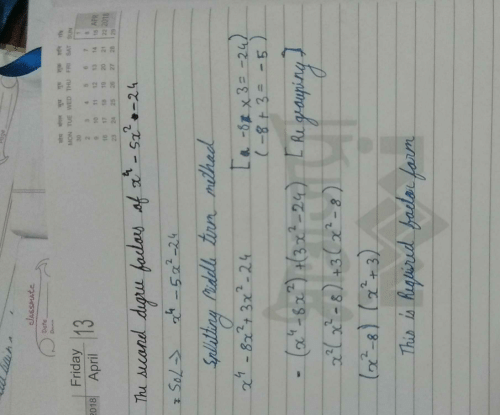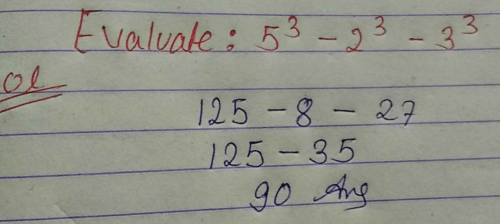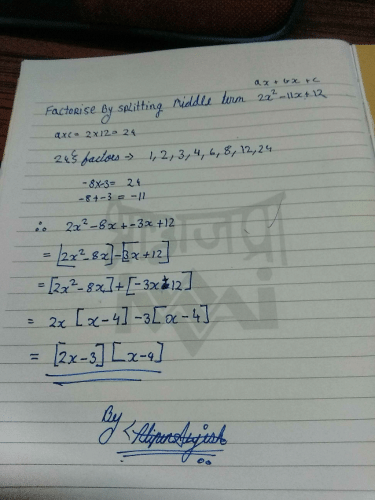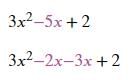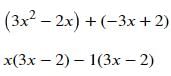All Exams >
Class 8 >
Advance Learner Course: Mathematics (Maths) Class 8 >
All Questions
All questions of Polynomials for Class 8 Exam
The number of zeros of x2 + 4x + 2 - a)1
- b)2
- c)3
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The number of zeros of x2 + 4x + 2
a)
1
b)
2
c)
3
d)
none of these
|
|
Harshit Agrawal answered |
The given equation has 2 zeros as it has degree of 2
Polynomials having only three terms are called ________- a)monomial
- b)binomial
- c)trinomials
- d)multinomial
Correct answer is option 'C'. Can you explain this answer?
Polynomials having only three terms are called ________
a)
monomial
b)
binomial
c)
trinomials
d)
multinomial
|
Mayank Jaiswal answered |
Polynomials having only three term are called Trinomial.
The degree of the polynomial x4 – 3x3 + 2x2 – 5x + 3 is:- a)2
- b)1
- c)4
- d)3
Correct answer is option 'C'. Can you explain this answer?
The degree of the polynomial x4 – 3x3 + 2x2 – 5x + 3 is:
a)
2
b)
1
c)
4
d)
3
|
Tarun Sengupta answered |
**Explanation:**
The degree of a polynomial is the highest power of the variable in that polynomial. In this case, the polynomial is:
x^4 + 3x^3 + 2x^2 + 5x - 3
To find the degree of this polynomial, we need to identify the term with the highest power of x. Let's break down each term in the polynomial:
- The term x^4 has a power of 4.
- The term 3x^3 has a power of 3.
- The term 2x^2 has a power of 2.
- The term 5x has a power of 1.
- The constant term -3 has a power of 0.
As we can see, the term with the highest power of x is x^4. Therefore, the degree of the polynomial is 4.
Therefore, option C is the correct answer.
The degree of a polynomial is the highest power of the variable in that polynomial. In this case, the polynomial is:
x^4 + 3x^3 + 2x^2 + 5x - 3
To find the degree of this polynomial, we need to identify the term with the highest power of x. Let's break down each term in the polynomial:
- The term x^4 has a power of 4.
- The term 3x^3 has a power of 3.
- The term 2x^2 has a power of 2.
- The term 5x has a power of 1.
- The constant term -3 has a power of 0.
As we can see, the term with the highest power of x is x^4. Therefore, the degree of the polynomial is 4.
Therefore, option C is the correct answer.
The remainder obtained when the polynomial p(x) is divided by (b – ax) is- a)
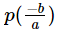
- b)
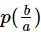
- c)
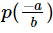
- d)
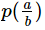
Correct answer is option 'B'. Can you explain this answer?
The remainder obtained when the polynomial p(x) is divided by (b – ax) is
a)
b)
c)
d)
|
|
Meera Rana answered |
ANSWER :- b
Solution :- b-ax=0
b=ax
b/a=x
i.e. remainder is p(b/a)
Evaluate (11)3
- a)1313
- b)1331
- c)3131
- d)3113
Correct answer is option 'B'. Can you explain this answer?
Evaluate (11)3
a)
1313
b)
1331
c)
3131
d)
3113
|
Ananya Das answered |
(a+b)3 = a3 + b3 + 3ab(a + b)
11³= (10+1)³=1000+1+30(11)=1001+330=1331
11³= (10+1)³=1000+1+30(11)=1001+330=1331
If (x-2) is the factor of x2 + 2x+ a, find the value of ‘a’.- a)a = -16
- b)a = -8
- c)a = 16
- d)a = 8
Correct answer is option 'B'. Can you explain this answer?
If (x-2) is the factor of x2 + 2x+ a, find the value of ‘a’.
a)
a = -16
b)
a = -8
c)
a = 16
d)
a = 8
|
|
Himaja Ammu answered |
If x-2 is a factor then 2 is the zero of the polynomial
by substituting 2 in the given polynomial,we get
2^2+2(2)+a=0
8+a=0
a=-8
by substituting 2 in the given polynomial,we get
2^2+2(2)+a=0
8+a=0
a=-8
What is the value of p if x-2 is a factor of x2 – 6x + p ?
- a)4
- b)-4
- c)8
- d)-8
Correct answer is option 'C'. Can you explain this answer?
What is the value of p if x-2 is a factor of x2 – 6x + p ?
a)
4
b)
-4
c)
8
d)
-8
|
Prachi Rathore answered |
X-2=0,=x=2,Now,x²-6x+p=2²-6×2+p=4-12+p=-8+p=p=8 the real ans is c
Which of the following are the factors of a2 + ab +bc + ca
- a)(a + b) (a + c)
- b)(a + b + c)
- c)(a + b) (b + c)
- d)(b + c) (c + a)
Correct answer is option 'A'. Can you explain this answer?
Which of the following are the factors of a2 + ab +bc + ca
a)
(a + b) (a + c)
b)
(a + b + c)
c)
(a + b) (b + c)
d)
(b + c) (c + a)
|
Nilotpal Unni answered |
Factors of a2 ab bc ca
To find the factors of a2 ab bc ca, we need to factor out the common terms from all the terms. In this case, the common term is 'a'. So, we can write:
a2 ab bc ca = a(a b c + b c a)
Now, we need to factor the expression inside the parentheses. We can see that it contains two terms, 'abc' and 'bca', which have a common factor of 'bc'. So, we can write:
a(a b c + b c a) = a(bc(a + c))
Finally, we can factor out the common factor of 'a' and 'bc', which gives us:
a(bc(a + c)) = ab(a + c) ac(a + c)
Therefore, the factors of a2 ab bc ca are (a b) (a c).
To find the factors of a2 ab bc ca, we need to factor out the common terms from all the terms. In this case, the common term is 'a'. So, we can write:
a2 ab bc ca = a(a b c + b c a)
Now, we need to factor the expression inside the parentheses. We can see that it contains two terms, 'abc' and 'bca', which have a common factor of 'bc'. So, we can write:
a(a b c + b c a) = a(bc(a + c))
Finally, we can factor out the common factor of 'a' and 'bc', which gives us:
a(bc(a + c)) = ab(a + c) ac(a + c)
Therefore, the factors of a2 ab bc ca are (a b) (a c).
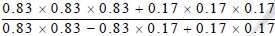is equal to :-
- a)1
- b)(0.83)3 + (0.17)3
- c)0
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
is equal to :-a)
1
b)
(0.83)3 + (0.17)3
c)
0
d)
None of these
|
Shalini Shahi answered |
Yes answer is 1. a=0.83 ,b=0.17 0.83×0.83×0.83 +0.17×0.17×0.17. / 0.83× 0.83+0.83× 0.17+0.17×0.17. = formula = a³+b³=( a+b)(a²-ab +b²) / a²-ab+ b² = cut the up and down a²-ab +b² = only a+b here ,add a+b =0.83+0.17= 1.00= 1, correct answer a) 1..
What is the product of (x+a) and (x+b)
a) x2 + (a+b)x + ab
b) x2 + (a+b)x - ab
c) x2 + (a+b)x - ab
d) x2+ (a-b)x + ab
Correct answer is option 'A'. Can you explain this answer?
|
Shail Kapoor answered |
Product of (x + a) and (x + b)
The given expression is of the form (x + a)(x + b). To find the product, we can use the distributive property of multiplication over addition.
Using the distributive property, we can multiply the terms inside the parentheses:
(x + a)(x + b) = x(x + b) + a(x + b)
Now, we can simplify each term separately:
x(x + b) = x * x + x * b = x^2 + bx
a(x + b) = a * x + a * b = ax + ab
Putting it all together, we get:
(x + a)(x + b) = x^2 + bx + ax + ab
Simplifying further, we can combine like terms:
x^2 + bx + ax + ab = x^2 + (a + b)x + ab
Therefore, the product of (x + a) and (x + b) is x^2 + (a + b)x + ab, which is option 'A'.
The given expression is of the form (x + a)(x + b). To find the product, we can use the distributive property of multiplication over addition.
Using the distributive property, we can multiply the terms inside the parentheses:
(x + a)(x + b) = x(x + b) + a(x + b)
Now, we can simplify each term separately:
x(x + b) = x * x + x * b = x^2 + bx
a(x + b) = a * x + a * b = ax + ab
Putting it all together, we get:
(x + a)(x + b) = x^2 + bx + ax + ab
Simplifying further, we can combine like terms:
x^2 + bx + ax + ab = x^2 + (a + b)x + ab
Therefore, the product of (x + a) and (x + b) is x^2 + (a + b)x + ab, which is option 'A'.
The value of the polynomial 5x−4x2+3, when x = −1 is
- a)- 6
- b)1
- c)9
- d)-1
Correct answer is option 'A'. Can you explain this answer?
The value of the polynomial 5x−4x2+3, when x = −1 is
a)
- 6
b)
1
c)
9
d)
-1
|
Zachary Foster answered |
It is given that
p(x) = 5x - 4x² + 3
We have to find the value when x = -1
p(-1) = 5(-1) - 4(-1)² + 3
By further calculation
p(-1) = -5 - 4 + 3
So we get
p(-1) = -9 + 3
p(-1) = -6
Therefore, the value is -6.
Find the value of the polynomial 6 – 4x + 3x2 at x = 3
- a)– 24
- b)21
- c)18
- d)-21
Correct answer is option 'B'. Can you explain this answer?
Find the value of the polynomial 6 – 4x + 3x2 at x = 3
a)
– 24
b)
21
c)
18
d)
-21
|
Bibek Ghoshal answered |
The value of the polynomial 6 is 6.
A linear polynomial will have how many zeroes.- a)2
- b)1
- c)0
- d)3
Correct answer is option 'B'. Can you explain this answer?
A linear polynomial will have how many zeroes.
a)
2
b)
1
c)
0
d)
3
|
Rahul Kumar answered |
A linear polynomial has 1 zero.
A quadratic polynomial has 2 zeroes.
A cubic polynomial has 3 zeroes.
In general, any polynomial has as many zeroes as its degree.
What are the two factors of quadratic polynomial x2-16x+64?- a)(x-16) and (x-64)
- b)(x+8) and (x-8)
- c)(x+16) and (x-4)
- d)(x-8) and (x-8)
Correct answer is option 'D'. Can you explain this answer?
What are the two factors of quadratic polynomial x2-16x+64?
a)
(x-16) and (x-64)
b)
(x+8) and (x-8)
c)
(x+16) and (x-4)
d)
(x-8) and (x-8)
|
Niharika Kapoor answered |
Solution:
To find the factors of the quadratic polynomial x2-16x+64, we can use the factorization formula for perfect square trinomials.
Formula: (a-b)2 = a2-2ab+b2
Comparing x2-16x+64 with the formula, we can see that a = x and b = 8.
Therefore, (x-8)2 = x2-16x+64
Taking the square root of both sides, we get:
x-8 = ±√(x2-16x+64)
x-8 = ±(x-8)
Now, we can solve for x in each case:
Case 1: x-8 = x-8
Simplifying, we get 0 = 0, which is always true. Therefore, this case gives us only one factor.
Factor 1: x-8
Case 2: x-8 = -(x-8)
Simplifying, we get 2x = 16, which gives us x = 8. Therefore, this case gives us another factor.
Factor 2: x-8
Thus, the two factors of the quadratic polynomial x2-16x+64 are (x-8) and (x-8), which can be written as (x-8)2.
Therefore, the correct answer is option D, (x-8) and (x-8).
To find the factors of the quadratic polynomial x2-16x+64, we can use the factorization formula for perfect square trinomials.
Formula: (a-b)2 = a2-2ab+b2
Comparing x2-16x+64 with the formula, we can see that a = x and b = 8.
Therefore, (x-8)2 = x2-16x+64
Taking the square root of both sides, we get:
x-8 = ±√(x2-16x+64)
x-8 = ±(x-8)
Now, we can solve for x in each case:
Case 1: x-8 = x-8
Simplifying, we get 0 = 0, which is always true. Therefore, this case gives us only one factor.
Factor 1: x-8
Case 2: x-8 = -(x-8)
Simplifying, we get 2x = 16, which gives us x = 8. Therefore, this case gives us another factor.
Factor 2: x-8
Thus, the two factors of the quadratic polynomial x2-16x+64 are (x-8) and (x-8), which can be written as (x-8)2.
Therefore, the correct answer is option D, (x-8) and (x-8).
If one of the factor of x2 + x – 20 is (x + 5). Find the other
- a)x – 4
- b)x + 2
- c)x + 4
- d)x – 5
Correct answer is option 'A'. Can you explain this answer?
If one of the factor of x2 + x – 20 is (x + 5). Find the other
a)
x – 4
b)
x + 2
c)
x + 4
d)
x – 5
|
Tara Singh answered |
We cannot complete the question as it is incomplete. Please provide the complete question.
If p(x) = 7 – 3x + 2x2 then value of p(-2) is:- a)22
- b)12
- c)21
- d)31
Correct answer is option 'C'. Can you explain this answer?
If p(x) = 7 – 3x + 2x2 then value of p(-2) is:
a)
22
b)
12
c)
21
d)
31
|
Indu Gupta answered |
p(-2) = 7 - 3(-2) + 2(-2)2
= 7+6+8 = 21
A polynomial containing three nonzero terms is called a ________.- a)monomial
- b)binomial
- c)trinomial
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A polynomial containing three nonzero terms is called a ________.
a)
monomial
b)
binomial
c)
trinomial
d)
none of these
|
|
Ananya Sharma answered |
A polynomial containing two nonzero terms is called a binomial .For example :- (3+6x) , (x-5y)
If p(x) = x + 3, then p(x) + p(-x) is equal to- a)0
- b)3
- c)6
- d)2x
Correct answer is option 'C'. Can you explain this answer?
If p(x) = x + 3, then p(x) + p(-x) is equal to
a)
0
b)
3
c)
6
d)
2x
|
Sanjana answered |
we have , p(x) = x+3.........(1) Replacing x by -x ,we get p(-x)= -x+3 ............(2) adding the corresponding sides of (1)and (2),we get p(x)+p(-x) = 6
The expansion of (2a – 3b + 5c)2.- a)
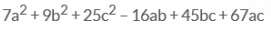
- b)
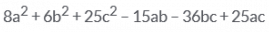
- c)
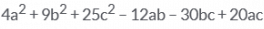
- d)
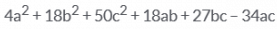
Correct answer is option 'C'. Can you explain this answer?
The expansion of (2a – 3b + 5c)2.
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
The expansion of (2a - 3b + 5c)² -: (2a)² + (- 3b)² + (5c)² + 2× 2a × (-3b) + 2× (-3b)× 5c + 2× 5c + 2a. = 4a² + 9b² + 25c² - 12ab - 30bc + 20ac
For two polynomials p(x) and q(x), x-a and x-b are their factors, respectively.Which of the following is true?- a)p(a)+q(b) = 0
- b)p(a) x q(b) = 2
- c)p(a) x q(b) = 1
- d)p(a) + q(b) = 1
Correct answer is option 'A'. Can you explain this answer?
For two polynomials p(x) and q(x), x-a and x-b are their factors, respectively.Which of the following is true?
a)
p(a)+q(b) = 0
b)
p(a) x q(b) = 2
c)
p(a) x q(b) = 1
d)
p(a) + q(b) = 1
|
Ritika Kumar answered |
Solution:
Given that x-a and x-b are factors of polynomials p(x) and q(x) respectively.
This implies that,
p(a) = 0 and q(b) = 0
We need to find the expression that is true from the given options.
Option A: p(a)q(b) = 0
Since p(a) and q(b) both are zero, the product of p(a) and q(b) is also zero. Hence, option A is correct.
Option B: p(a) x q(b) = 2
This is not true for any polynomial p(x) and q(x).
Option C: p(a) x q(b) = 1
This is not true for any polynomial p(x) and q(x).
Option D: p(a) q(b) = 1
This is not true for any polynomial p(x) and q(x).
Therefore, the correct option is A.
Given that x-a and x-b are factors of polynomials p(x) and q(x) respectively.
This implies that,
p(a) = 0 and q(b) = 0
We need to find the expression that is true from the given options.
Option A: p(a)q(b) = 0
Since p(a) and q(b) both are zero, the product of p(a) and q(b) is also zero. Hence, option A is correct.
Option B: p(a) x q(b) = 2
This is not true for any polynomial p(x) and q(x).
Option C: p(a) x q(b) = 1
This is not true for any polynomial p(x) and q(x).
Option D: p(a) q(b) = 1
This is not true for any polynomial p(x) and q(x).
Therefore, the correct option is A.
(101)2 is equal to
- a)10201
- b)10211
- c)10001
- d)10011
Correct answer is option 'A'. Can you explain this answer?
(101)2 is equal to
a)
10201
b)
10211
c)
10001
d)
10011
|
|
Prachi Rathore answered |
(101)²=101×101=10201 this is ur answer
If (2x + 5) is a factor of 2x2 – k, then the value of k is.- a)25/2
- b)2
- c)25
- d)-1
Correct answer is 'A'. Can you explain this answer?
If (2x + 5) is a factor of 2x2 – k, then the value of k is.
a)
25/2
b)
2
c)
25
d)
-1
|
|
Krishna Iyer answered |
Let p(x) = 2x2 − k
Since, (2x+5) is a factor of p(x), then by factor
theorem,
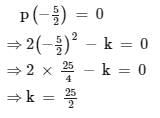
Since, (2x+5) is a factor of p(x), then by factor
theorem,
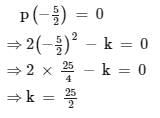
Factorise the quadratic polynomial by splitting the middle term:
x2 + 14x + 45- a)(x + 9) (x+5)
- b)(x - 9) (x+5)
- c)(x-9) ( x-5)
- d)(x+9) ( x-5)
Correct answer is option 'A'. Can you explain this answer?
Factorise the quadratic polynomial by splitting the middle term:
x2 + 14x + 45
x2 + 14x + 45
a)
(x + 9) (x+5)
b)
(x - 9) (x+5)
c)
(x-9) ( x-5)
d)
(x+9) ( x-5)
|
|
Shashwat Singh answered |
=x^2+14x+45
=x^2+9x+5x+45
=x(x+9)+5(x+9)
=(x+9)(x+5)
Which of the following polynomials has -3 as a zero?- a)x2 + 3
- b)(x – 3)
- c)x2 – 9
- d)x2 – 3x
Correct answer is option 'C'. Can you explain this answer?
Which of the following polynomials has -3 as a zero?
a)
x2 + 3
b)
(x – 3)
c)
x2 – 9
d)
x2 – 3x
|
Zayeda Pyare answered |
Put x=(-3) in option (c)..uu will get 0.. ..
If (x-1) is a factor of ax – a, then find the value of a- a)a = 1
- b)a = 2
- c)a = 3
- d)All values of a
Correct answer is option 'D'. Can you explain this answer?
If (x-1) is a factor of ax – a, then find the value of a
a)
a = 1
b)
a = 2
c)
a = 3
d)
All values of a
|
|
Gaurav Kumar answered |
ANSWER :- d
Solution :- f(x) = ax - a……………………..(1)
x - 1 = 0
x = 1
Putting in eq(1)
(1)x - 1 => x - 1
For eg :- if we put x = 100
Putting in eq(1)
(100)x - 100 => x - 100
So, all the values of a
The number of zeros of x2 + 4x + 2- a) 1
- b) 2
- c) 3
- d) none of these
Correct answer is option 'B'. Can you explain this answer?
The number of zeros of x2 + 4x + 2
a)
1
b)
2
c)
3
d)
none of these
|
Shreya Singh answered |
The answer will be option d non of these.
When the polynomial x3 + 3x2 + 3x + 1 is divided by x + 1, the remainder is :-- a)1
- b)8
- c)0
- d)- 6
Correct answer is option 'C'. Can you explain this answer?
When the polynomial x3 + 3x2 + 3x + 1 is divided by x + 1, the remainder is :-
a)
1
b)
8
c)
0
d)
- 6
|
Hansa Sharma answered |
The zero of x + 1 is –1
And by remainder theorem, when
p(x) = x3 + 3x2 + 3x + 1 is divided by x + 1, then remainder is p(–1).
∴ p(–1) = (–1)3 + 3 (–1)2 + 3(–1) + 1
= –1 + (3 × 1) + (–3) + 1
= –1 + 3 – 3 + 1
= 0
Thus, the required = 0
The value of 101 x 99 is- a)8998
- b)1111
- c)9889
- d)9999
Correct answer is option 'D'. Can you explain this answer?
The value of 101 x 99 is
a)
8998
b)
1111
c)
9889
d)
9999
|
|
Arun Sharma answered |
(100+1)×(100 - 1) it is the formula of a²-b² so, (100)² -(1)² = 10000-1 = 9999.
What is the value 83 – 33 (without solving the cubes)?
- a)485
- b)845
- c)458
- d)854
Correct answer is option 'A'. Can you explain this answer?
What is the value 83 – 33 (without solving the cubes)?
a)
485
b)
845
c)
458
d)
854
|
Pranab Datta answered |
The value 83 is a positive integer that represents a quantity or amount. It is a prime number and comes after 82 and before 84 in the number sequence.
If P(x) = 10x−4x2−3, then the value of p(0)+p(1) is
- a)1
- b)3
- c)-3
- d)0
Correct answer is option 'D'. Can you explain this answer?
If P(x) = 10x−4x2−3, then the value of p(0)+p(1) is
a)
1
b)
3
c)
-3
d)
0
|
|
Madhurima Ahuja answered |
I'm sorry, your question is incomplete. Please provide more details or context for me to understand and respond accurately.
- a)2p = r
- b)p = 2r
- c)p = r
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
a)
2p = r
b)
p = 2r
c)
p = r
d)
none of these
|
|
Amit Sharma answered |
Let f(x) = px2 + 5 x + r
If (x - 2) is a factor of f (x), then by factor theorem
f(2) = 0 | x - 2 = 0 ⇒ x = 2
⇒ p(2)2 + 5(2) + r = 0
⇒ 4p + r + 10 = 0 ...(1)
If (x - 2) is a factor of f (x), then by factor theorem
f(2) = 0 | x - 2 = 0 ⇒ x = 2
⇒ p(2)2 + 5(2) + r = 0
⇒ 4p + r + 10 = 0 ...(1)
If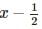 
is a factor of f (x), then by factor theorem,
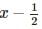is a factor of f (x), then by factor theorem,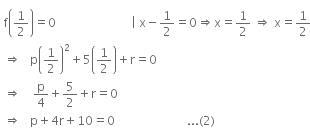
Subtracting (2) from (1), we get
3p - 3r = 0
⇒ p = r
3p - 3r = 0
⇒ p = r
The zero of the polynomial (x−2)2−(x+2)2 is- a)1
- b)-2
- c)2
- d)0
Correct answer is option 'D'. Can you explain this answer?
The zero of the polynomial (x−2)2−(x+2)2 is
a)
1
b)
-2
c)
2
d)
0
|
|
Sanjana answered |
{(x)² + (2)² - 2× x ×2} - {(x)² + (2)² + 2 × x×2} = (x² + 4 - 4x) - (x² + 4 + 4x) = x² + 4 - 4x - x²- 4 - 4x = 0.........ans
Can you explain the answer of this question below:Factorise : 8a3+ b3 + 12a2b + 6a b2
- A:
(2a + b) (2a + b) (2a + b)
- B:
(2a – b) (2a – b) (2a + b)
- C:
(2a-b)(2a-b)(2a-b)
- D:
(-2a + b) (-2a + b) (2a + b)
The answer is a.
Factorise : 8a3+ b3 + 12a2b + 6a b2
(2a + b) (2a + b) (2a + b)
(2a – b) (2a – b) (2a + b)
(2a-b)(2a-b)(2a-b)
(-2a + b) (-2a + b) (2a + b)
|
Ishan Nair answered |
8a3 + b3+ 12a2b + 6ab2
8a3 + b3+ 12a2b + 6ab2
= (2a)3 + (b)3 + 3(2a)(b) (2a + b)
= (2a + b)3 | Using Identity VI
= (2a + b)(2a + b)(2a + b)
8a3 + b3+ 12a2b + 6ab2
= (2a)3 + (b)3 + 3(2a)(b) (2a + b)
= (2a + b)3 | Using Identity VI
= (2a + b)(2a + b)(2a + b)
√2 is a polynomial of degree- a)1
- b)0
- c)2
- d)√2
Correct answer is option 'B'. Can you explain this answer?
√2 is a polynomial of degree
a)
1
b)
0
c)
2
d)
√2
|
Vivek Rana answered |
The highest power of the variable is known as the degree of the polynomial.
√2x^0 = √2
hence the degree of the polynomial is zero.
√2x^0 = √2
hence the degree of the polynomial is zero.
Find the zero of the polynomial of p (x) = ax + b ; a ≠ 0- a)b/a
- b)a/b
- c)-b/a
- d)-a/b
Correct answer is 'C'. Can you explain this answer?
Find the zero of the polynomial of p (x) = ax + b ; a ≠ 0
a)
b/a
b)
a/b
c)
-b/a
d)
-a/b
|
|
Saranya Nair answered |
Finding the Zero of a Polynomial
To find the zero of a polynomial, we need to solve for x when p(x) = 0. In other words, we need to find the value of x that makes the polynomial equal to zero.
Given p(x) = ax^b, where a ≠ 0 and b ≥ 1, we need to find the zero of the polynomial.
Solution
To find the zero of the polynomial, we need to solve for x when p(x) = 0. Substituting the given polynomial, we get:
ax^b = 0
Since a ≠ 0 and b ≥ 1, we know that the only value of x that satisfies the equation is x = 0. Therefore, the zero of the polynomial is x = 0.
Option (c) is the correct answer, as it corresponds to x = 0.
Explanation
The given polynomial p(x) = ax^b has only one term, which is ax^b. This term can only equal zero if x = 0, since any non-zero value of x raised to a positive power will be non-zero.
Therefore, the zero of the polynomial is x = 0, which corresponds to option (c).
To find the zero of a polynomial, we need to solve for x when p(x) = 0. In other words, we need to find the value of x that makes the polynomial equal to zero.
Given p(x) = ax^b, where a ≠ 0 and b ≥ 1, we need to find the zero of the polynomial.
Solution
To find the zero of the polynomial, we need to solve for x when p(x) = 0. Substituting the given polynomial, we get:
ax^b = 0
Since a ≠ 0 and b ≥ 1, we know that the only value of x that satisfies the equation is x = 0. Therefore, the zero of the polynomial is x = 0.
Option (c) is the correct answer, as it corresponds to x = 0.
Explanation
The given polynomial p(x) = ax^b has only one term, which is ax^b. This term can only equal zero if x = 0, since any non-zero value of x raised to a positive power will be non-zero.
Therefore, the zero of the polynomial is x = 0, which corresponds to option (c).
If the polynomial 2x3 – 3x2 + 2x – 4 is divided by x – 2, then the remainder is :-- a)- 4
- b)4
- c)-40
- d)2
Correct answer is option 'B'. Can you explain this answer?
If the polynomial 2x3 – 3x2 + 2x – 4 is divided by x – 2, then the remainder is :-
a)
- 4
b)
4
c)
-40
d)
2
|
|
Mahi Sharma answered |
3x2 - 5x + 7 is divided by x - 2, the remainder is:
To find the remainder, we can use the remainder theorem which states that if a polynomial f(x) is divided by x - a, the remainder is equal to f(a).
Therefore, if we substitute x = 2 in the given polynomial, we get:
2(2)3 - 3(2)2 - 5(2) + 7 = 16 - 12 - 10 + 7 = 1
Hence, the remainder when the polynomial 2x3 + 3x2 - 5x + 7 is divided by x - 2 is 1.
To find the remainder, we can use the remainder theorem which states that if a polynomial f(x) is divided by x - a, the remainder is equal to f(a).
Therefore, if we substitute x = 2 in the given polynomial, we get:
2(2)3 - 3(2)2 - 5(2) + 7 = 16 - 12 - 10 + 7 = 1
Hence, the remainder when the polynomial 2x3 + 3x2 - 5x + 7 is divided by x - 2 is 1.
(x + 1) is a factor of the polynomial- a)x4+3x3+3x2+x+1
- b)x3+x2−x+1
- c)x4+x3+x2+1
- d)x3+x2+x+1
Correct answer is option 'D'. Can you explain this answer?
(x + 1) is a factor of the polynomial
a)
x4+3x3+3x2+x+1
b)
x3+x2−x+1
c)
x4+x3+x2+1
d)
x3+x2+x+1
|
|
Krishna Singi answered |
Option d is the best answer in india reason is given in r d sharma and r s aggrawal or Google search
(a – b)3 + (b – c)3 + (c – a)3 is equal to :-- a)3abc
- b)3a3b3c3
- c)3(a – b) (b – c) (c – a)
- d)[a – (b + c)]3
Correct answer is option 'C'. Can you explain this answer?
(a – b)3 + (b – c)3 + (c – a)3 is equal to :-
a)
3abc
b)
3a3b3c3
c)
3(a – b) (b – c) (c – a)
d)
[a – (b + c)]3
|
|
Indu Gupta answered |
Let x = (a – b), y = (b – c) and z = (c – a)
Consider, x + y + z = (a – b) + (b – c) + (c – a) = 0
⇒ x3 + y3 + z3 = 3xyz
That is (a – b)3 + (b – c)3 + (c – a)3 = 3(a – b)(b – c)(c – a)
Consider, x + y + z = (a – b) + (b – c) + (c – a) = 0
⇒ x3 + y3 + z3 = 3xyz
That is (a – b)3 + (b – c)3 + (c – a)3 = 3(a – b)(b – c)(c – a)
If 3a – 7b = 26 and ab = 5, then the value of 9a2 + 49b2.- a)643
- b)886
- c)872
- d)516
Correct answer is 'B'. Can you explain this answer?
If 3a – 7b = 26 and ab = 5, then the value of 9a2 + 49b2.
a)
643
b)
886
c)
872
d)
516
|
|
Amit Sharma answered |
2ab = (a2 + b2) - (a - b)2
= 29 - 9 = 20
⇒ ab = 10.
= 29 - 9 = 20
⇒ ab = 10.
Factorize the quadratic polynomial by splitting the middle term: y2 – 4 y –21
- a)(y – 7) (y – 3)
- b)(y – 7) (y + 3)
- c)(y + 7) (y – 3)
- d)(y + 7) (y + 3)
Correct answer is option 'B'. Can you explain this answer?
Factorize the quadratic polynomial by splitting the middle term: y2 – 4 y –21
a)
(y – 7) (y – 3)
b)
(y – 7) (y + 3)
c)
(y + 7) (y – 3)
d)
(y + 7) (y + 3)
|
|
Ujwal Das answered |
+ 7y + 10
To factorize this quadratic polynomial, we need to find two numbers that multiply to give the constant term (10) and add to give the coefficient of the middle term (7).
The factors of 10 are:
1 x 10
2 x 5
Since we need the sum of the factors to be 7, we can see that 2 and 5 are the two numbers we are looking for.
So, we can rewrite the middle term as 2y + 5y:
y2 + 2y + 5y + 10
Now, we can group the first two terms and the last two terms together and factorize each group separately:
y(y + 2) + 5(y + 2)
Notice that both groups have a common factor of (y + 2), so we can factorize it out:
(y + 2)(y + 5)
Therefore, the factored form of the quadratic polynomial y2 + 7y + 10 is (y + 2)(y + 5).
To factorize this quadratic polynomial, we need to find two numbers that multiply to give the constant term (10) and add to give the coefficient of the middle term (7).
The factors of 10 are:
1 x 10
2 x 5
Since we need the sum of the factors to be 7, we can see that 2 and 5 are the two numbers we are looking for.
So, we can rewrite the middle term as 2y + 5y:
y2 + 2y + 5y + 10
Now, we can group the first two terms and the last two terms together and factorize each group separately:
y(y + 2) + 5(y + 2)
Notice that both groups have a common factor of (y + 2), so we can factorize it out:
(y + 2)(y + 5)
Therefore, the factored form of the quadratic polynomial y2 + 7y + 10 is (y + 2)(y + 5).
Can you explain the answer of this question below:What should be subtracted to x2+2x+2 to make it a perfect square?
- A:
1
- B:
3
- C:
2
- D:
4
The answer is a.
What should be subtracted to x2+2x+2 to make it a perfect square?
1
3
2
4
|
|
Janhavi Sen answered |
Solution:
To make x^2 + 2x + 2 a perfect square, we need to find a number 'a' that satisfies the following equation:
(x + a)^2 = x^2 + 2x + 2
Expanding the left-hand side of the equation, we get:
x^2 + 2ax + a^2 = x^2 + 2x + 2
Comparing the coefficients of x^2, x, and the constant term on both sides, we get:
a^2 = 2 (coefficient of x^2 on both sides is 1)
2a = 2 (coefficient of x on both sides is 2)
a = 1 (constant terms on both sides are equal)
Therefore, we need to subtract 1 from x^2 + 2x + 2 to make it a perfect square.
Hence, the answer is option 'A'.
To make x^2 + 2x + 2 a perfect square, we need to find a number 'a' that satisfies the following equation:
(x + a)^2 = x^2 + 2x + 2
Expanding the left-hand side of the equation, we get:
x^2 + 2ax + a^2 = x^2 + 2x + 2
Comparing the coefficients of x^2, x, and the constant term on both sides, we get:
a^2 = 2 (coefficient of x^2 on both sides is 1)
2a = 2 (coefficient of x on both sides is 2)
a = 1 (constant terms on both sides are equal)
Therefore, we need to subtract 1 from x^2 + 2x + 2 to make it a perfect square.
Hence, the answer is option 'A'.
Chapter doubts & questions for Polynomials - Advance Learner Course: Mathematics (Maths) Class 8 2025 is part of Class 8 exam preparation. The chapters have been prepared according to the Class 8 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polynomials - Advance Learner Course: Mathematics (Maths) Class 8 in English & Hindi are available as part of Class 8 exam.
Download more important topics, notes, lectures and mock test series for Class 8 Exam by signing up for free.
Advance Learner Course: Mathematics (Maths) Class 8
5 videos|57 docs|20 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup