All Exams >
Class 6 >
Online MCQ Tests for Class 6 >
All Questions
All questions of Practical Geometry for Class 6 Exam
Which geometrical instrument used to draw and measure angles?- a)Protractor
- b)Set squares
- c)Divider
- d)Compasses
Correct answer is 'D'. Can you explain this answer?
Which geometrical instrument used to draw and measure angles?
a)
Protractor
b)
Set squares
c)
Divider
d)
Compasses
|
|
Shilpa Shah answered |
Protractor
A protractor is a geometrical instrument that is used to draw and measure angles. It is a semi-circular tool made of plastic or metal and has a degree scale from 0 to 180 degrees. Protractors are commonly used in geometry, trigonometry, and other mathematical fields to measure angles and draw precise angles.
Uses of Protractor
Protractors have many uses, including:
- Measuring angles: A protractor can be used to determine the size of an angle, which is measured in degrees. It is placed on the angle so that one of its arms coincides with one side of the angle, and the other arm points to the other side of the angle. The degree scale on the protractor can then be read to determine the size of the angle.
- Drawing angles: A protractor can also be used to draw precise angles. The center of the protractor is placed on the vertex of the angle, and one of its arms is aligned with one side of the angle. The desired angle can then be drawn by tracing along the edge of the protractor.
Advantages of Protractor
The advantages of using a protractor include:
- Precision: A protractor allows precise measurement and drawing of angles, making it an essential tool in many fields.
- Easy to use: Protractors are easy to use and can be used by anyone, including students, teachers, and professionals.
- Versatile: Protractors can be used in various applications, including construction, engineering, and design.
Conclusion
In conclusion, a protractor is an essential geometrical instrument used to draw and measure angles accurately. It is a versatile tool that can be used in many fields, including mathematics, engineering, and design.
A protractor is a geometrical instrument that is used to draw and measure angles. It is a semi-circular tool made of plastic or metal and has a degree scale from 0 to 180 degrees. Protractors are commonly used in geometry, trigonometry, and other mathematical fields to measure angles and draw precise angles.
Uses of Protractor
Protractors have many uses, including:
- Measuring angles: A protractor can be used to determine the size of an angle, which is measured in degrees. It is placed on the angle so that one of its arms coincides with one side of the angle, and the other arm points to the other side of the angle. The degree scale on the protractor can then be read to determine the size of the angle.
- Drawing angles: A protractor can also be used to draw precise angles. The center of the protractor is placed on the vertex of the angle, and one of its arms is aligned with one side of the angle. The desired angle can then be drawn by tracing along the edge of the protractor.
Advantages of Protractor
The advantages of using a protractor include:
- Precision: A protractor allows precise measurement and drawing of angles, making it an essential tool in many fields.
- Easy to use: Protractors are easy to use and can be used by anyone, including students, teachers, and professionals.
- Versatile: Protractors can be used in various applications, including construction, engineering, and design.
Conclusion
In conclusion, a protractor is an essential geometrical instrument used to draw and measure angles accurately. It is a versatile tool that can be used in many fields, including mathematics, engineering, and design.
If the diameter of a circle is 12 cm, then the radius of the circle is ____.- a)1.5 cm
- b)3 cm
- c)6 cm
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If the diameter of a circle is 12 cm, then the radius of the circle is ____.
a)
1.5 cm
b)
3 cm
c)
6 cm
d)
None of these
|
|
Aayu and Pihu show 🥰🥰 answered |
Radius is the half of an object so that the answer is 6 and option c
Which geometrical instrument used to draw perpendicular and parallel lines?- a)Divider
- b)Compasses
- c)Ruler
- d)Set squares
Correct answer is option 'D'. Can you explain this answer?
Which geometrical instrument used to draw perpendicular and parallel lines?
a)
Divider
b)
Compasses
c)
Ruler
d)
Set squares
|
|
Bibek Verma answered |
Set squares are used to draw perpendicular and parallel lines
Set squares are the geometrical instruments that are used to draw perpendicular and parallel lines.
- Perpendicular lines: Set squares are used to draw perpendicular lines. They are made up of two straight edges, one of which is fixed at right angles to the other. When the fixed edge is placed on a line, the other edge can be used to draw a perpendicular line.
- Parallel lines: Set squares are also used to draw parallel lines. By placing the fixed edge of the set square parallel to the line to be copied, the other edge can be used to draw a line parallel to it.
Other geometrical instruments and their uses
Other geometrical instruments that are commonly used are:
- Divider: Dividers are used to measure and transfer distances between two points.
- Compasses: Compasses are used to draw circles and arcs.
- Ruler: A ruler is used to draw straight lines and measure lengths.
However, none of these instruments can be used to draw perpendicular or parallel lines as accurately as set squares. Therefore, when it comes to drawing perpendicular or parallel lines, set squares are the best option.
A line has ___________ length.- a)definite
- b)no
- c)indefinite
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A line has ___________ length.
a)
definite
b)
no
c)
indefinite
d)
None of these
|
|
Rutuja Roy answered |
**Explanation:**
A line is a one-dimensional geometric figure that extends infinitely in both directions. It is made up of an infinite number of points that are all equidistant from each other. Since a line extends infinitely, it does not have a definite or measurable length.
**Infinite Length:**
- A line has an infinite length because it has no endpoints and continues indefinitely in both directions.
- No matter how far you extend a line, you can always extend it further without reaching an endpoint.
- This infinite nature of a line makes it impossible to assign a definite or measurable length to it.
**Comparison to Line Segments:**
- It is important to note the difference between a line and a line segment.
- A line segment is a portion of a line that has two distinct endpoints.
- Unlike a line, a line segment has a definite and measurable length because it has endpoints that mark its boundaries.
**Mathematical Representation:**
- In mathematics, a line can be represented by a lowercase letter with an arrow on top (∞).
- This symbol indicates that the line extends infinitely in both directions.
**Conclusion:**
- In conclusion, a line does not have a definite length because it extends infinitely in both directions.
- It is an infinite geometric figure made up of an infinite number of points.
- The length of a line is considered indefinite, as it cannot be measured or assigned a specific value.
A line is a one-dimensional geometric figure that extends infinitely in both directions. It is made up of an infinite number of points that are all equidistant from each other. Since a line extends infinitely, it does not have a definite or measurable length.
**Infinite Length:**
- A line has an infinite length because it has no endpoints and continues indefinitely in both directions.
- No matter how far you extend a line, you can always extend it further without reaching an endpoint.
- This infinite nature of a line makes it impossible to assign a definite or measurable length to it.
**Comparison to Line Segments:**
- It is important to note the difference between a line and a line segment.
- A line segment is a portion of a line that has two distinct endpoints.
- Unlike a line, a line segment has a definite and measurable length because it has endpoints that mark its boundaries.
**Mathematical Representation:**
- In mathematics, a line can be represented by a lowercase letter with an arrow on top (∞).
- This symbol indicates that the line extends infinitely in both directions.
**Conclusion:**
- In conclusion, a line does not have a definite length because it extends infinitely in both directions.
- It is an infinite geometric figure made up of an infinite number of points.
- The length of a line is considered indefinite, as it cannot be measured or assigned a specific value.
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Practical Geometry, Class 6, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q.Name the geometrical instrument having a semi-circular device graduated into 180 degree-parts.- a)Divider
- b)Compasses
- c)Set squares
- d)Protractor
Correct answer is option 'D'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Practical Geometry, Class 6, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
Name the geometrical instrument having a semi-circular device graduated into 180 degree-parts.
a)
Divider
b)
Compasses
c)
Set squares
d)
Protractor
|
|
Sarika garg answered |
A semi-circular device grduated into 180 degree-parts. The measure starts from 0° on the right hand side and ends with 180° on the left hand side and vice-versa.
A maths teacher asked his students to draw a pair of parallel lines. Which instrument(s) are the students most likely to use?- a)A ruler and a compass
- b)Two edges of a ruler
- c)A ruler and a setsquare
- d)Both [b] and [c]
Correct answer is option 'D'. Can you explain this answer?
A maths teacher asked his students to draw a pair of parallel lines. Which instrument(s) are the students most likely to use?
a)
A ruler and a compass
b)
Two edges of a ruler
c)
A ruler and a setsquare
d)
Both [b] and [c]

|
Aarav Saha answered |
The lines drawn using the two edges of a ruler are parallel. Also a ruler and a setsquare can be used to draw a pair of parallel lines.
Into what type of parts is a figure divided by bisecting it?- a)Unequal
- b)Equal
- c)Triangular
- d)Perpendicular
Correct answer is option 'B'. Can you explain this answer?
Into what type of parts is a figure divided by bisecting it?
a)
Unequal
b)
Equal
c)
Triangular
d)
Perpendicular

|
Shabir Ahmad answered |
By bisecting it we divide it into two equal halves
Number of circles passing through a given point are ____.- a)1
- b)2
- c)3
- d)infinite
Correct answer is option 'D'. Can you explain this answer?
Number of circles passing through a given point are ____.
a)
1
b)
2
c)
3
d)
infinite
|
|
Nilanjan Unni answered |
Explanation:
A circle is defined as a set of all points in a plane that are at a given distance from a given point, called the center of the circle.
When a point is given, there are infinite circles that could pass through that point. This is because a circle is defined by its center and radius, and there are infinite points that could serve as the center of a circle passing through the given point.
For example, consider a point P in a plane. We can draw a circle with center P and any positive radius r, and that circle will pass through P. We can also draw a circle with center Q, where Q is any point on the perpendicular bisector of the line segment between P and any other point in the plane, and that circle will also pass through P.
Therefore, the correct answer is option D, infinite.
A circle is defined as a set of all points in a plane that are at a given distance from a given point, called the center of the circle.
When a point is given, there are infinite circles that could pass through that point. This is because a circle is defined by its center and radius, and there are infinite points that could serve as the center of a circle passing through the given point.
For example, consider a point P in a plane. We can draw a circle with center P and any positive radius r, and that circle will pass through P. We can also draw a circle with center Q, where Q is any point on the perpendicular bisector of the line segment between P and any other point in the plane, and that circle will also pass through P.
Therefore, the correct answer is option D, infinite.
A few lines in a plane have a point in common. What type of lines can they be?- a)Intersecting lines
- b)Parallel lines
- c)Concurrent lines
- d)Either [a] or [c]
Correct answer is option 'D'. Can you explain this answer?
A few lines in a plane have a point in common. What type of lines can they be?
a)
Intersecting lines
b)
Parallel lines
c)
Concurrent lines
d)
Either [a] or [c]

|
Aarya Joshi answered |
If the lines are only two, then they are intersecting lines. If there are more than two lines, then they are concurrent lines.
If two lines have only one point in common, what are they called?- a)Parallel lines
- b)Intersecting lines
- c)Perpendicular lines
- d)Transversal
Correct answer is option 'B'. Can you explain this answer?
If two lines have only one point in common, what are they called?
a)
Parallel lines
b)
Intersecting lines
c)
Perpendicular lines
d)
Transversal

|
Athira Sengupta answered |
Intersecting lines have only one point in common.
Which of the following is done to draw an angle of 150∘ using compasses and a ruler?- a)Bisecting 120∘ and 180∘ angles.
- b)Bisecting 60∘ and 120∘ angles.
- c)Bisecting 0∘ and 60∘ angles.
- d)Bisecting a 360∘ angle.
Correct answer is option 'A'. Can you explain this answer?
Which of the following is done to draw an angle of 150∘ using compasses and a ruler?
a)
Bisecting 120∘ and 180∘ angles.
b)
Bisecting 60∘ and 120∘ angles.
c)
Bisecting 0∘ and 60∘ angles.
d)
Bisecting a 360∘ angle.
|
|
Anisha Iyer answered |
To draw an angle of 150° using compasses and a ruler, we need to follow the process of bisecting a 120° and 180° angle.
Here is a step-by-step explanation of how to draw an angle of 150° using compasses and a ruler:
1. Draw a line segment AB using a ruler.
2. Place the compasses on point A and draw an arc that intersects AB.
3. Without changing the compasses' width, place the compasses on point B and draw another arc that intersects the first arc.
4. Label the point where the two arcs intersect as C.
5. Place the compasses on point C and draw an arc that intersects the first arc.
6. Without changing the compasses' width, place the compasses on point B and draw another arc that intersects the second arc.
7. Label the point where the two arcs intersect as D.
8. Draw a line segment CD using a ruler.
9. Label the point of intersection between AB and CD as E.
Now, we have created a 120° angle ACE.
10. Place the compasses on point E and draw an arc that intersects AB.
11. Without changing the compasses' width, place the compasses on point A and draw another arc that intersects the first arc.
12. Label the point where the two arcs intersect as F.
13. Draw a line segment EF using a ruler.
Now, we have bisected the 120° angle ACE into two equal angles, which are each 60°. The angle EAF is 60°.
14. Place the compasses on point E and draw an arc that intersects CD.
15. Without changing the compasses' width, place the compasses on point D and draw another arc that intersects the first arc.
16. Label the point where the two arcs intersect as G.
17. Draw a line segment EG using a ruler.
Now, we have bisected the 60° angle EAF into two equal angles, which are each 30°. The angle EAG is 30°.
18. Place the compasses on point E and draw an arc that intersects AB.
19. Without changing the compasses' width, place the compasses on point A and draw another arc that intersects the first arc.
20. Label the point where the two arcs intersect as H.
21. Draw a line segment EH using a ruler.
Now, we have bisected the 30° angle EAG into two equal angles, which are each 15°. The angle EAH is 15°.
22. Measure the angle EAH using a protractor, and it will measure 15°.
Therefore, by bisecting a 120° angle and then bisecting the resulting 60° angle, we can construct an angle of 150° using compasses and a ruler.
Here is a step-by-step explanation of how to draw an angle of 150° using compasses and a ruler:
1. Draw a line segment AB using a ruler.
2. Place the compasses on point A and draw an arc that intersects AB.
3. Without changing the compasses' width, place the compasses on point B and draw another arc that intersects the first arc.
4. Label the point where the two arcs intersect as C.
5. Place the compasses on point C and draw an arc that intersects the first arc.
6. Without changing the compasses' width, place the compasses on point B and draw another arc that intersects the second arc.
7. Label the point where the two arcs intersect as D.
8. Draw a line segment CD using a ruler.
9. Label the point of intersection between AB and CD as E.
Now, we have created a 120° angle ACE.
10. Place the compasses on point E and draw an arc that intersects AB.
11. Without changing the compasses' width, place the compasses on point A and draw another arc that intersects the first arc.
12. Label the point where the two arcs intersect as F.
13. Draw a line segment EF using a ruler.
Now, we have bisected the 120° angle ACE into two equal angles, which are each 60°. The angle EAF is 60°.
14. Place the compasses on point E and draw an arc that intersects CD.
15. Without changing the compasses' width, place the compasses on point D and draw another arc that intersects the first arc.
16. Label the point where the two arcs intersect as G.
17. Draw a line segment EG using a ruler.
Now, we have bisected the 60° angle EAF into two equal angles, which are each 30°. The angle EAG is 30°.
18. Place the compasses on point E and draw an arc that intersects AB.
19. Without changing the compasses' width, place the compasses on point A and draw another arc that intersects the first arc.
20. Label the point where the two arcs intersect as H.
21. Draw a line segment EH using a ruler.
Now, we have bisected the 30° angle EAG into two equal angles, which are each 15°. The angle EAH is 15°.
22. Measure the angle EAH using a protractor, and it will measure 15°.
Therefore, by bisecting a 120° angle and then bisecting the resulting 60° angle, we can construct an angle of 150° using compasses and a ruler.
Identify the pair of parallel lines.
- a)(i) and (ii) only
- b)(ii) only
- c)(ii) and (iii) only
- d)(i), (ii) and (iii)
Correct answer is option 'B'. Can you explain this answer?
Identify the pair of parallel lines.

a)
(i) and (ii) only
b)
(ii) only
c)
(ii) and (iii) only
d)
(i), (ii) and (iii)

|
Athira Sengupta answered |
Parallel lines do not have any point in common.
Lines a, b, p, q, m, n and x have a point P common to all of them. What is the name of P?- a)Point of concurrence
- b)Point of intersection
- c)Common point
- d)Distinct point
Correct answer is option 'A'. Can you explain this answer?
Lines a, b, p, q, m, n and x have a point P common to all of them. What is the name of P?
a)
Point of concurrence
b)
Point of intersection
c)
Common point
d)
Distinct point

|
Prasad Chawla answered |
A point common to multiple lines is called a point of concurrence as the lines are concurrent lines.
The line segment forming a polygon is called _________________.- a)angle
- b)side
- c)vertex
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The line segment forming a polygon is called _________________.
a)
angle
b)
side
c)
vertex
d)
None of these
|
|
Priya Pillai answered |
Explanation:
Definition of a Side:
The line segment that forms a polygon is called a side. A side is a straight line segment that connects two consecutive vertices of a polygon.
Characteristics of a Side:
- Sides are straight lines with a definite length.
- In a polygon, sides do not intersect with each other except at the vertices.
- The number of sides in a polygon depends on the number of vertices it has.
Importance of Sides in a Polygon:
Sides play a crucial role in defining the shape and structure of a polygon. The sides of a polygon determine its perimeter, which is the total length of all its sides. Additionally, the sides also help in classifying polygons based on the number of sides they possess.
Conclusion:
In conclusion, the line segment forming a polygon is referred to as a side. Sides are essential components of polygons that contribute to defining their shape, structure, and classification. Understanding the concept of sides is fundamental in the study of geometry and polygons.
The line segment joining any two points on the circle is called _____.- a)radius
- b)chord
- c)diameter
- d)centre
Correct answer is option 'B'. Can you explain this answer?
The line segment joining any two points on the circle is called _____.
a)
radius
b)
chord
c)
diameter
d)
centre

|
Tanvi answered |
Yes because any point is said . centre is not said
 is the bisector of ∠PQZ = ∠PQR. Which of the following is true?
is the bisector of ∠PQZ = ∠PQR. Which of the following is true?
- a)∠PQZ = ∠PQR
- b)∠PQZ = ∠ZQR
- c)∠PQZ = 1/2 ∠PQR
- d)Both [b] and [c]
Correct answer is option 'D'. Can you explain this answer?
 is the bisector of ∠PQZ = ∠PQR. Which of the following is true?
is the bisector of ∠PQZ = ∠PQR. Which of the following is true?a)
∠PQZ = ∠PQR
b)
∠PQZ = ∠ZQR
c)
∠PQZ = 1/2 ∠PQR
d)
Both [b] and [c]

|
Aashna Chopra answered |
The correct option is Option D.
QZ bisects ∠PQR (Given)
Thus. ∠PQZ = ∠ZQR = 1/2 ∠PQR
Two lines are said to be perpendicular to each other when they meet at ____angle.- a)180∘
- b)90∘
- c)60∘
- d)360∘
Correct answer is option 'B'. Can you explain this answer?
Two lines are said to be perpendicular to each other when they meet at ____angle.
a)
180∘
b)
90∘
c)
60∘
d)
360∘
|
|
Sanchita Kulkarni answered |
Perpendicular Lines
Perpendicular lines are an important concept in geometry. They are two lines that intersect each other at a right angle, which is 90 degrees. Perpendicular lines are often used in architecture and engineering, as they help create stable structures and accurate measurements.
Definition
Perpendicular lines are two lines that meet at a right angle. This means that the angle formed by the intersection of the two lines is exactly 90 degrees. When two lines are perpendicular, they are said to be orthogonal.
Properties
Perpendicular lines have several important properties:
- The slopes of the two lines are negative reciprocals of each other. This means that if one line has a slope of m, the other line will have a slope of -1/m.
- The product of the slopes of two perpendicular lines is -1.
- If two lines are perpendicular, they will form four right angles at their intersection.
Examples
Here are some examples of perpendicular lines:
- The x-axis and y-axis on a coordinate plane are perpendicular.
- The sides of a square are all perpendicular to each other.
- The legs of a right triangle are perpendicular to each other.
Conclusion
Perpendicular lines are an important concept in geometry that can be found in many different areas of math and science. They are two lines that intersect at a right angle, and they have several important properties that make them useful in a variety of applications.
Perpendicular lines are an important concept in geometry. They are two lines that intersect each other at a right angle, which is 90 degrees. Perpendicular lines are often used in architecture and engineering, as they help create stable structures and accurate measurements.
Definition
Perpendicular lines are two lines that meet at a right angle. This means that the angle formed by the intersection of the two lines is exactly 90 degrees. When two lines are perpendicular, they are said to be orthogonal.
Properties
Perpendicular lines have several important properties:
- The slopes of the two lines are negative reciprocals of each other. This means that if one line has a slope of m, the other line will have a slope of -1/m.
- The product of the slopes of two perpendicular lines is -1.
- If two lines are perpendicular, they will form four right angles at their intersection.
Examples
Here are some examples of perpendicular lines:
- The x-axis and y-axis on a coordinate plane are perpendicular.
- The sides of a square are all perpendicular to each other.
- The legs of a right triangle are perpendicular to each other.
Conclusion
Perpendicular lines are an important concept in geometry that can be found in many different areas of math and science. They are two lines that intersect at a right angle, and they have several important properties that make them useful in a variety of applications.
If the diameter of a circle is 22 cm, then the radius of the circle is ____.- a)5.5 cm
- b)11 cm
- c)4.5 cm
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If the diameter of a circle is 22 cm, then the radius of the circle is ____.
a)
5.5 cm
b)
11 cm
c)
4.5 cm
d)
None of these
|
|
Aman Choudhury answered |
To find the radius of a circle when given the diameter, we can use the formula:
Radius = Diameter / 2
Let's solve the problem step by step:
Step 1: Given information
The diameter of the circle is 22 cm.
Step 2: Applying the formula
Using the formula mentioned above, we can calculate the radius:
Radius = Diameter / 2
Radius = 22 cm / 2
Step 3: Simplifying
Dividing 22 cm by 2 gives us:
Radius = 11 cm
Therefore, the radius of the circle is 11 cm.
Explanation:
- The diameter of a circle is the distance across the circle passing through the center. It is twice the length of the radius.
- The formula to find the radius of a circle when given the diameter is Radius = Diameter / 2.
- In this case, we are given a diameter of 22 cm, so we divide it by 2 to find the radius.
- Simplifying the calculation, we find that the radius is 11 cm.
Radius = Diameter / 2
Let's solve the problem step by step:
Step 1: Given information
The diameter of the circle is 22 cm.
Step 2: Applying the formula
Using the formula mentioned above, we can calculate the radius:
Radius = Diameter / 2
Radius = 22 cm / 2
Step 3: Simplifying
Dividing 22 cm by 2 gives us:
Radius = 11 cm
Therefore, the radius of the circle is 11 cm.
Explanation:
- The diameter of a circle is the distance across the circle passing through the center. It is twice the length of the radius.
- The formula to find the radius of a circle when given the diameter is Radius = Diameter / 2.
- In this case, we are given a diameter of 22 cm, so we divide it by 2 to find the radius.
- Simplifying the calculation, we find that the radius is 11 cm.
Name the geometrical instrument having two triangular pieces.- a)Compasses
- b)Set squares
- c)Protractor
- d)Divider
Correct answer is 'B'. Can you explain this answer?
Name the geometrical instrument having two triangular pieces.
a)
Compasses
b)
Set squares
c)
Protractor
d)
Divider

|
Rishika Chopra answered |
Set squares.
Compasses.
Protractor.
Divider.
How do you draw a 90∘ angle?- a)By drawing a perpendicular to a line from a point lying on it.
- b)By bisecting a 120∘ angle.
- c)By bisecting a 60∘ angle.
- d)By drawing multiples of 45∘ angle.
Correct answer is option 'A'. Can you explain this answer?
How do you draw a 90∘ angle?
a)
By drawing a perpendicular to a line from a point lying on it.
b)
By bisecting a 120∘ angle.
c)
By bisecting a 60∘ angle.
d)
By drawing multiples of 45∘ angle.
|
|
Shreyshi answered |
Two lines that intersect each other and formed the angle of 90degree are called Perpendicular line.
In this question, we have to draw a angle of 90 degree so when we draw a perpendicular line the angle of 90 degree will formed.
So, Option A is the correct answer.
In this question, we have to draw a angle of 90 degree so when we draw a perpendicular line the angle of 90 degree will formed.
So, Option A is the correct answer.
Name the geometrical instrument having a pair – a pointer on one end and a pencil on the other.- a)Set squares
- b)Divider
- c)Protractor
- d)Compasses
Correct answer is option 'D'. Can you explain this answer?
Name the geometrical instrument having a pair – a pointer on one end and a pencil on the other.
a)
Set squares
b)
Divider
c)
Protractor
d)
Compasses

|
Gayatri Chavan answered |
A pair of compasses, also known as a compass, is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as tools to measure distances, in particular on maps. Compasses can be used for mathematics, drafting, navigation and other purposes.
If the radius of a circle is 7 cm, then the diameter of the circle is ____.- a)10 cm
- b)14 cm
- c)3.5 cm
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If the radius of a circle is 7 cm, then the diameter of the circle is ____.
a)
10 cm
b)
14 cm
c)
3.5 cm
d)
None of these

|
Mayank Rajmane answered |
Diameter is always double of radius so, 7×2=14
For which of the following are the rails of a railway line an example?- a)Parallel lines
- b)Intersecting lines
- c)Perpendicular lines
- d)Coplanar lines
Correct answer is option 'A'. Can you explain this answer?
For which of the following are the rails of a railway line an example?
a)
Parallel lines
b)
Intersecting lines
c)
Perpendicular lines
d)
Coplanar lines

|
Rajveer Choudhury answered |
The rails of a railway line are an example of parallel lines.
Which geometrical instrument used to draw line segments and to measure their lengths?- a)Divider
- b)Compasses
- c)Set squares
- d)Ruler
Correct answer is option 'D'. Can you explain this answer?
Which geometrical instrument used to draw line segments and to measure their lengths?
a)
Divider
b)
Compasses
c)
Set squares
d)
Ruler

|
Sounak Chatterjee answered |
A ruler is a geometric tool used to measure the le... morength of a line segment. A
Which geometrical instrument used to draw and measure angles?- a)Protractor
- b)Set squares
- c)Divider
- d)Compasses
Correct answer is option 'D'. Can you explain this answer?
Which geometrical instrument used to draw and measure angles?
a)
Protractor
b)
Set squares
c)
Divider
d)
Compasses

|
Gayatri Chavan answered |
A protractor is a measuring instrument, typically ... moremade of transparent plastic or glass, for measuring angles. Most protractors measure angles in degrees .
Circles which have same centre and different radii are called ____ circles.- a)concentric
- b)same
- c)congruent
- d)equal
Correct answer is option 'A'. Can you explain this answer?
Circles which have same centre and different radii are called ____ circles.
a)
concentric
b)
same
c)
congruent
d)
equal
|
|
Ashwini Goyal answered |
Definition of Concentric Circles
Circles that share the same center but have different radii are referred to as concentric circles.
Characteristics of Concentric Circles
- Same Center: All concentric circles have a common center point from which they are drawn.
- Different Radii: While the center remains constant, the distance from the center varies, leading to circles of different sizes.
Examples of Concentric Circles
- Target Designs: The rings of a dartboard or a target are classic examples of concentric circles, where each ring is a different radius but all share the same center.
- Hula Hoops: If multiple hula hoops of varying sizes are placed one inside the other, they form concentric circles.
Why Not Other Options?
- Same Circles: This term implies that the circles are identical in size and properties, which is not the case here.
- Congruent Circles: Congruent circles have the same size and shape, meaning they share both center and radius, which again does not apply to concentric circles.
- Equal Circles: Similar to congruent, this term suggests equality in size and radius, which is not true for concentric circles.
Conclusion
Thus, the correct term for circles that share a center but have different radii is "concentric circles." This concept is fundamental in geometry and helps in understanding the relationships between different shapes.
Circles that share the same center but have different radii are referred to as concentric circles.
Characteristics of Concentric Circles
- Same Center: All concentric circles have a common center point from which they are drawn.
- Different Radii: While the center remains constant, the distance from the center varies, leading to circles of different sizes.
Examples of Concentric Circles
- Target Designs: The rings of a dartboard or a target are classic examples of concentric circles, where each ring is a different radius but all share the same center.
- Hula Hoops: If multiple hula hoops of varying sizes are placed one inside the other, they form concentric circles.
Why Not Other Options?
- Same Circles: This term implies that the circles are identical in size and properties, which is not the case here.
- Congruent Circles: Congruent circles have the same size and shape, meaning they share both center and radius, which again does not apply to concentric circles.
- Equal Circles: Similar to congruent, this term suggests equality in size and radius, which is not true for concentric circles.
Conclusion
Thus, the correct term for circles that share a center but have different radii is "concentric circles." This concept is fundamental in geometry and helps in understanding the relationships between different shapes.
Identify the one with no definite length.- a)
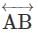
- b)

- c) -XYZ
- d)

Correct answer is option 'A'. Can you explain this answer?
Identify the one with no definite length.
a)
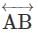
b)

c)
-XYZ
d)


|
Aarya Joshi answered |
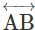 has no definite length.
has no definite length.Identify the instruments used to bisect a given line segment.- a)A scale and a protractor
- b)Scale and compasses
- c)Scale and setsquares
- d)A scale
Correct answer is option 'B'. Can you explain this answer?
Identify the instruments used to bisect a given line segment.
a)
A scale and a protractor
b)
Scale and compasses
c)
Scale and setsquares
d)
A scale
|
|
Ananya Das answered |
Using Scale and Compasses to Bisect a Line Segment:
Step 1:
Place the scale on the line segment that needs to be bisected.
Step 2:
Use the compasses to measure the length of the line segment.
Step 3:
Place the compasses at one end of the line segment and draw an arc that intersects the line.
Step 4:
Without changing the compass width, place the compasses at the other end of the line segment and draw another arc that intersects the first arc.
Step 5:
Draw a line connecting the intersection points of the two arcs. This line will bisect the original line segment.
Using a scale and compasses is the most accurate method for bisecting a line segment as it involves precise measurements and construction techniques. This combination allows for the creation of a perpendicular line that divides the line segment into two equal parts.
Step 1:
Place the scale on the line segment that needs to be bisected.
Step 2:
Use the compasses to measure the length of the line segment.
Step 3:
Place the compasses at one end of the line segment and draw an arc that intersects the line.
Step 4:
Without changing the compass width, place the compasses at the other end of the line segment and draw another arc that intersects the first arc.
Step 5:
Draw a line connecting the intersection points of the two arcs. This line will bisect the original line segment.
Using a scale and compasses is the most accurate method for bisecting a line segment as it involves precise measurements and construction techniques. This combination allows for the creation of a perpendicular line that divides the line segment into two equal parts.
Chapter doubts & questions for Practical Geometry - Online MCQ Tests for Class 6 2025 is part of Class 6 exam preparation. The chapters have been prepared according to the Class 6 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Practical Geometry - Online MCQ Tests for Class 6 in English & Hindi are available as part of Class 6 exam.
Download more important topics, notes, lectures and mock test series for Class 6 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily








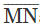 at N using a protractor and a point P is marked on it. Which of the following is true?
at N using a protractor and a point P is marked on it. Which of the following is true?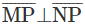
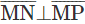
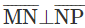

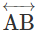 is such that
is such that 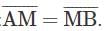 Which of the following is a false statement?
Which of the following is a false statement?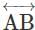
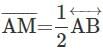
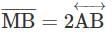

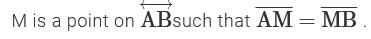
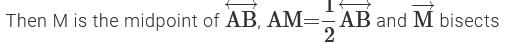


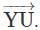 . Then what is the measure of∠UYZ?
. Then what is the measure of∠UYZ?







