All Exams >
Class 6 >
Online MCQ Tests for Class 6 >
All Questions
All questions of Perimeter and Area for Class 6 Exam
Akshi wants to put lace around a rectangular tablecloth that is 5 m long and 3 m wide. What is the length of the lace required?
- a)15 m
- b)8 m
- c)10 m
- d)16 m
Correct answer is option 'D'. Can you explain this answer?
Akshi wants to put lace around a rectangular tablecloth that is 5 m long and 3 m wide. What is the length of the lace required?
a)
15 m
b)
8 m
c)
10 m
d)
16 m
|
Rahul Kumar answered |
The perimeter of the rectangle is calculated by adding the lengths of all sides. Perimeter = 2 × (Length + Width) = 2 × (5 m + 3 m) = 2 × 8 m = 16 m. So, the lace required is 16 m.
A square park has a side length of 50 m. What is the distance covered by Usha if she takes two rounds of the park?- a)100 m
- b)200 m
- c)400 m
- d)600 m
Correct answer is option 'C'. Can you explain this answer?
a)
100 m
b)
200 m
c)
400 m
d)
600 m
|
Maitri Bajaj answered |
Understanding the Park's Dimensions
The park is a square, which means all four sides are equal. Given that the side length is 50 m, we can calculate the perimeter.
Calculating the Perimeter
The perimeter (P) of a square can be calculated using the formula:
P = 4 × side length
Substituting the given side length:
P = 4 × 50 m = 200 m
This means that one complete round around the park covers 200 meters.
Calculating the Total Distance for Two Rounds
To find the distance covered by Usha when she takes two rounds, we simply multiply the perimeter by 2:
Total Distance = 2 × Perimeter
Substituting the perimeter we calculated earlier:
Total Distance = 2 × 200 m = 400 m
Thus, Usha would cover a total distance of 400 meters after completing two rounds around the park.
Conclusion
The correct answer is option 'C', which states that the distance covered by Usha is 400 m.
The park is a square, which means all four sides are equal. Given that the side length is 50 m, we can calculate the perimeter.
Calculating the Perimeter
The perimeter (P) of a square can be calculated using the formula:
P = 4 × side length
Substituting the given side length:
P = 4 × 50 m = 200 m
This means that one complete round around the park covers 200 meters.
Calculating the Total Distance for Two Rounds
To find the distance covered by Usha when she takes two rounds, we simply multiply the perimeter by 2:
Total Distance = 2 × Perimeter
Substituting the perimeter we calculated earlier:
Total Distance = 2 × 200 m = 400 m
Thus, Usha would cover a total distance of 400 meters after completing two rounds around the park.
Conclusion
The correct answer is option 'C', which states that the distance covered by Usha is 400 m.
The area of a rectangle is 50 sq m, and its width is 5 m. What is its length?- a)5 m
- b)10 m
- c)15 m
- d)25 m
Correct answer is option 'B'. Can you explain this answer?
a)
5 m
b)
10 m
c)
15 m
d)
25 m
|
Torcia Education answered |
Area of a rectangle = Length × Width. So, Length = Area / Width = 50 sq m / 5 m = 10 m.
The area of a rectangular sheet of paper is 20 cm2. Its length is 5 cm. Find its width.- a)1 cm
- b)2 cm
- c)3 cm
- d)4 cm.
Correct answer is option 'D'. Can you explain this answer?
The area of a rectangular sheet of paper is 20 cm2. Its length is 5 cm. Find its width.
a)
1 cm
b)
2 cm
c)
3 cm
d)
4 cm.
|
Dr Manju Sen answered |
Step 1: Use the formula for the area of a rectangle.
The formula for the area A of a rectangle is:
A = Length × Width
Step 2: Rearrange the formula to solve for the width.
The width can be calculated by:
Width = A / Length
Step 3: Substitute the given values.
Substitute the given area and length:
Width = 20 / 5 = 4 cm
The width of the sheet of paper is 4 cm.
A square garden has a side length of 20 m. What will be the area of the garden?- a)40 sq m
- b)400 sq m
- c)100 sq m
- d)200 sq m
Correct answer is option 'B'. Can you explain this answer?
a)
40 sq m
b)
400 sq m
c)
100 sq m
d)
200 sq m
|
Saikat Rane answered |
Understanding the Area of a Square
To find the area of a square, you can use the formula:
- Area = Side Length × Side Length
In this case, the side length of the garden is given as 20 meters.
Calculating the Area
Let's apply the formula step by step:
- Step 1: Identify the side length:
The side length of the square garden is 20 m.
- Step 2: Use the formula for area:
Area = 20 m × 20 m
- Step 3: Perform the multiplication:
Area = 400 sq m
Conclusion
The area of the square garden is 400 square meters. Therefore, the correct answer is option 'B'.
Why the Other Options are Incorrect?
- Option A (40 sq m): This suggests a much smaller area than the actual measurement.
- Option C (100 sq m): This area corresponds to a side length of 10 m, not 20 m.
- Option D (200 sq m): This area would indicate a side length of approximately 14.14 m, which is also incorrect.
Final Note
Understanding how to calculate the area of a square is essential in various applications, from gardening to architectural design. Always remember to square the side length to find the area correctly!
To find the area of a square, you can use the formula:
- Area = Side Length × Side Length
In this case, the side length of the garden is given as 20 meters.
Calculating the Area
Let's apply the formula step by step:
- Step 1: Identify the side length:
The side length of the square garden is 20 m.
- Step 2: Use the formula for area:
Area = 20 m × 20 m
- Step 3: Perform the multiplication:
Area = 400 sq m
Conclusion
The area of the square garden is 400 square meters. Therefore, the correct answer is option 'B'.
Why the Other Options are Incorrect?
- Option A (40 sq m): This suggests a much smaller area than the actual measurement.
- Option C (100 sq m): This area corresponds to a side length of 10 m, not 20 m.
- Option D (200 sq m): This area would indicate a side length of approximately 14.14 m, which is also incorrect.
Final Note
Understanding how to calculate the area of a square is essential in various applications, from gardening to architectural design. Always remember to square the side length to find the area correctly!
Toshi and Akshi run around two different rectangular tracks. Akshi’s track has a perimeter of 220 m, and she completes 5 rounds. What is the total distance she runs?- a)1100 m
- b)220 m
- c)440 m
- d)660 m
Correct answer is option 'A'. Can you explain this answer?
a)
1100 m
b)
220 m
c)
440 m
d)
660 m
|
Vp Classes answered |
Total distance run by Akshi = Number of rounds × Perimeter = 5 × 220 m = 1100 m.
The area of a rectangle is 72 sq m and its length is 12 m. What is the width?- a)6 m
- b)8 m
- c)9 m
- d)12 m
Correct answer is option 'A'. Can you explain this answer?
a)
6 m
b)
8 m
c)
9 m
d)
12 m
|
Rutuja Roy answered |
Understanding the Problem
To find the width of a rectangle when the area and length are given, we can use the formula for the area of a rectangle:
- Area = Length × Width
In this case, we know:
- Area = 72 sq m
- Length = 12 m
Calculating the Width
To find the width, we rearrange the area formula:
- Width = Area / Length
Now, substituting the known values:
- Width = 72 sq m / 12 m
Performing the Calculation
Now we can perform the division:
- Width = 72 / 12
- Width = 6 m
Conclusion
Thus, the width of the rectangle is:
- 6 m, which corresponds to option 'A'.
Verification
To ensure our calculation is correct, we can verify by recalculating the area using the length and the width we found:
- Area = Length × Width
- Area = 12 m × 6 m
- Area = 72 sq m
Since this matches the given area, our answer is confirmed as correct.
In summary, the width of the rectangle is:
- 6 m (Option 'A').
To find the width of a rectangle when the area and length are given, we can use the formula for the area of a rectangle:
- Area = Length × Width
In this case, we know:
- Area = 72 sq m
- Length = 12 m
Calculating the Width
To find the width, we rearrange the area formula:
- Width = Area / Length
Now, substituting the known values:
- Width = 72 sq m / 12 m
Performing the Calculation
Now we can perform the division:
- Width = 72 / 12
- Width = 6 m
Conclusion
Thus, the width of the rectangle is:
- 6 m, which corresponds to option 'A'.
Verification
To ensure our calculation is correct, we can verify by recalculating the area using the length and the width we found:
- Area = Length × Width
- Area = 12 m × 6 m
- Area = 72 sq m
Since this matches the given area, our answer is confirmed as correct.
In summary, the width of the rectangle is:
- 6 m (Option 'A').
A rectangular garden has a perimeter of 60 m and a width of 10 m. What is the length of the garden?- a)10 m
- b)15 m
- c)20 m
- d)30 m
Correct answer is option 'C'. Can you explain this answer?
a)
10 m
b)
15 m
c)
20 m
d)
30 m
|
Coachify answered |
Perimeter of a rectangle = 2 × (Length + Width). Given 60 m = 2 × (Length + 10 m). Solving for Length, we get Length = (60 m / 2) - 10 m = 20 m.
A rectangle has a length of 15 m and a perimeter of 50 m. What is the breadth of the rectangle?
- a)10 m
- b)5 m
- c)20 m
- d)25 m
Correct answer is option 'A'. Can you explain this answer?
A rectangle has a length of 15 m and a perimeter of 50 m. What is the breadth of the rectangle?
a)
10 m
b)
5 m
c)
20 m
d)
25 m
|
Shiksha Academy answered |
Perimeter of a rectangle = 2 × (Length + Breadth). Given 50 m = 2 × (15 m + Breadth). Solving for Breadth, we get Breadth = 25 m / 2 = 5 m.
A field is shaped like a square and has a perimeter of 120 m. What is the area of the field?- a)900 sq m
- b)1200 sq m
- c)3600 sq m
- d)14400 sq m
Correct answer is option 'A'. Can you explain this answer?
a)
900 sq m
b)
1200 sq m
c)
3600 sq m
d)
14400 sq m
|
|
Priya Pillai answered |
Understanding the Problem
To find the area of a square field, we first need to understand the relationship between its perimeter and area.
Calculating the Side Length
- The formula for the perimeter (P) of a square is given by:
P = 4 × side length (s)
- Given that the perimeter of the field is 120 m:
4s = 120 m
- To find the side length, we divide both sides by 4:
s = 120 m / 4
s = 30 m
Calculating the Area
- The formula for the area (A) of a square is:
A = side length (s) × side length (s)
- Substituting the calculated side length:
A = 30 m × 30 m
A = 900 sq m
Conclusion
- Therefore, the area of the field is 900 sq m.
The correct answer is option 'A'.
To find the area of a square field, we first need to understand the relationship between its perimeter and area.
Calculating the Side Length
- The formula for the perimeter (P) of a square is given by:
P = 4 × side length (s)
- Given that the perimeter of the field is 120 m:
4s = 120 m
- To find the side length, we divide both sides by 4:
s = 120 m / 4
s = 30 m
Calculating the Area
- The formula for the area (A) of a square is:
A = side length (s) × side length (s)
- Substituting the calculated side length:
A = 30 m × 30 m
A = 900 sq m
Conclusion
- Therefore, the area of the field is 900 sq m.
The correct answer is option 'A'.
If the perimeter of a rectangle is 20 cm and its length is 6 cm, what is its breadth?- a)2 cm
- b)4 cm
- c)6 cm
- d)8 cm
Correct answer is option 'B'. Can you explain this answer?
a)
2 cm
b)
4 cm
c)
6 cm
d)
8 cm
|
|
Rahul Kumar answered |
Perimeter of a rectangle = 2 × (Length + Breadth). Given 20 cm = 2 × (6 cm + Breadth). Solving for Breadth, Breadth = (20 cm / 2) - 6 cm = 4 cm.
If the perimeter of a rectangle is 36 m and the length is 10 m, what is the width?
- a)4 m
- b)8 m
- c)6 m
- d)9 m
Correct answer is option 'B'. Can you explain this answer?
If the perimeter of a rectangle is 36 m and the length is 10 m, what is the width?
a)
4 m
b)
8 m
c)
6 m
d)
9 m
|
|
Shiksha Academy answered |
Perimeter of a rectangle = 2 × (Length + Width). Given 36 m = 2 × (10 m + Width). Solving for Width, we get Width = (36 m / 2) - 10 m = 6 m.
The perimeter of a square photo frame is 40 cm. What is the length of one side of the square?- a)5 cm
- b)10 cm
- c)20 cm
- d)40 cm
Correct answer is option 'B'. Can you explain this answer?
a)
5 cm
b)
10 cm
c)
20 cm
d)
40 cm
|
|
Dr Manju Sen answered |
The perimeter of a square is 4 × side length. Given perimeter = 40 cm. So, side length = 40 cm / 4 = 10 cm.
A farmer has a rectangular field of length 150 m and breadth 100 m. He needs to fence it with 2 rounds of wire. What is the total length of wire required?
- a)500 m
- b)1200 m
- c)600 m
- d)1000 m
Correct answer is option 'D'. Can you explain this answer?
A farmer has a rectangular field of length 150 m and breadth 100 m. He needs to fence it with 2 rounds of wire. What is the total length of wire required?
a)
500 m
b)
1200 m
c)
600 m
d)
1000 m
|
|
Coachify answered |
Perimeter of the rectangle = 2 × (Length + Breadth) = 2 × (150 m + 100 m) = 500 m. For 2 rounds, wire required = 2 × 500 m = 1000 m.
If the area of a square carpet is 81 sq m, what is the length of one side?- a)7 m
- b)8 m
- c)9 m
- d)10 m
Correct answer is option 'C'. Can you explain this answer?
a)
7 m
b)
8 m
c)
9 m
d)
10 m
|
Gunjan Lakhani answered |
The side length of the square = √Area = √81 sq m = 9 m.
A rectangle has a length of 7 m and a breadth of 5 m. What is the area of the rectangle?- a)12 sq m
- b)35 sq m
- c)24 sq m
- d)14 sq m
Correct answer is option 'B'. Can you explain this answer?
a)
12 sq m
b)
35 sq m
c)
24 sq m
d)
14 sq m
|
Saranya Chakraborty answered |
Calculation of Area of a Rectangle
Area of a rectangle is given by the formula:
Area = Length x Breadth
Given Data
- Length of the rectangle = 7 m
- Breadth of the rectangle = 5 m
Calculation
- Area = 7 m x 5 m
- Area = 35 sq m
Therefore, the area of the rectangle with a length of 7 m and a breadth of 5 m is 35 sq m.
Therefore, option 'B' (35 sq m) is the correct answer.
Area of a rectangle is given by the formula:
Area = Length x Breadth
Given Data
- Length of the rectangle = 7 m
- Breadth of the rectangle = 5 m
Calculation
- Area = 7 m x 5 m
- Area = 35 sq m
Therefore, the area of the rectangle with a length of 7 m and a breadth of 5 m is 35 sq m.
Therefore, option 'B' (35 sq m) is the correct answer.
The perimeter of the figure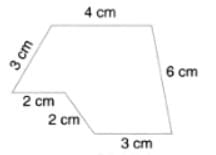
- a)20 cm
- b)10 cm
- c)24 cm
- d)15 cm
Correct answer is option 'A'. Can you explain this answer?
The perimeter of the figure
a)
20 cm
b)
10 cm
c)
24 cm
d)
15 cm
|
|
Shiksha Academy answered |
To find the perimeter of the given figure, we need to add the lengths of all the sides:
The sides are given as: 3 cm, 4 cm, 6 cm, 2 cm, 3 cm.
Now, add them together:
3 + 4 + 6 + 2 + 3 + 2 = 20 cm
The perimeter of the figure is 20 cm.
What is the perimeter of a square with a side length of 4 cm?- a)8 cm
- b)12 cm
- c)16 cm
- d)20 cm
Correct answer is option 'C'. Can you explain this answer?
a)
8 cm
b)
12 cm
c)
16 cm
d)
20 cm
|
|
Shiksha Academy answered |
The perimeter of a square is calculated by multiplying the length of one side by 4. So, Perimeter = 4 × 4 cm = 16 cm.
A triangle has sides of length 3 cm, 4 cm, and 5 cm. What is the perimeter of the triangle?- a)9 cm
- b)12 cm
- c)15 cm
- d)20 cm
Correct answer is option 'B'. Can you explain this answer?
a)
9 cm
b)
12 cm
c)
15 cm
d)
20 cm
|
EduRev Class 6 answered |
The perimeter of a triangle = sum of all its sides = 3 cm + 4 cm + 5 cm = 12 cm.
Chapter doubts & questions for Perimeter and Area - Online MCQ Tests for Class 6 2025 is part of Class 6 exam preparation. The chapters have been prepared according to the Class 6 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Perimeter and Area - Online MCQ Tests for Class 6 in English & Hindi are available as part of Class 6 exam.
Download more important topics, notes, lectures and mock test series for Class 6 Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily