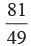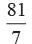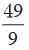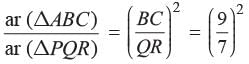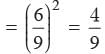All Exams >
Class 10 >
International Mathematics Olympiad (IMO) for Class 10 >
All Questions
All questions of Triangles for Class 10 Exam
The Perimeter of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm. Then what is the corresponding side of the second circle?- a)5.4 cm
- b)4.5 cm
- c)3.5 cm
- d)6.4 cm
Correct answer is option 'A'. Can you explain this answer?
The Perimeter of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm. Then what is the corresponding side of the second circle?
a)
5.4 cm
b)
4.5 cm
c)
3.5 cm
d)
6.4 cm
|
|
Priyanka Kapoor answered |
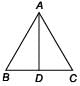
We know that if, ΔABC ~ ΔPQR, then
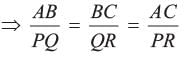
or, Applying componendo and dividendo, it can be clearly seen that,
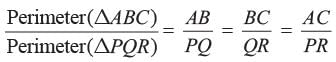
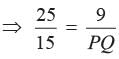
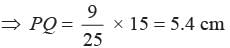
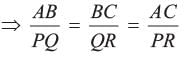
or, Applying componendo and dividendo, it can be clearly seen that,
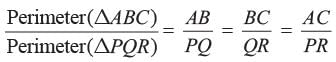
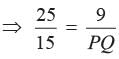
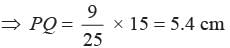
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1(1/2) hours?- a)300√67 km
- b)400√61 km
- c)200√61 km
- d)300√61 km
Correct answer is option 'D'. Can you explain this answer?
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1(1/2) hours?
a)
300√67 km
b)
400√61 km
c)
200√61 km
d)
300√61 km

|
Mehul Mehra answered |
Introduction
To determine the distance between the two planes after 1.5 hours, we will use the Pythagorean theorem, as they are flying at right angles to each other (one north and the other west).
Distance Calculations
- Plane 1 (North):
Speed = 1000 km/h
Time = 1.5 hours
Distance = Speed × Time = 1000 × 1.5 = 1500 km
- Plane 2 (West):
Speed = 1200 km/h
Time = 1.5 hours
Distance = Speed × Time = 1200 × 1.5 = 1800 km
Applying the Pythagorean Theorem
To find the distance between the two planes, we treat their paths as two sides of a right triangle:
- North Distance = 1500 km (Plane 1)
- West Distance = 1800 km (Plane 2)
The distance (D) between the two planes can be calculated as follows:
- D = √(North Distance² + West Distance²)
- D = √(1500² + 1800²)
Calculating the Squares
- 1500² = 2250000
- 1800² = 3240000
Now, add these values:
- Total = 2250000 + 3240000 = 5490000
Final Calculation
- D = √5490000
- D = √(1000² × 61) = 1000√61
Thus, the distance between the two planes after 1.5 hours is 300√61 km.
Conclusion
Therefore, the correct answer is option D) 300√61 km.
To determine the distance between the two planes after 1.5 hours, we will use the Pythagorean theorem, as they are flying at right angles to each other (one north and the other west).
Distance Calculations
- Plane 1 (North):
Speed = 1000 km/h
Time = 1.5 hours
Distance = Speed × Time = 1000 × 1.5 = 1500 km
- Plane 2 (West):
Speed = 1200 km/h
Time = 1.5 hours
Distance = Speed × Time = 1200 × 1.5 = 1800 km
Applying the Pythagorean Theorem
To find the distance between the two planes, we treat their paths as two sides of a right triangle:
- North Distance = 1500 km (Plane 1)
- West Distance = 1800 km (Plane 2)
The distance (D) between the two planes can be calculated as follows:
- D = √(North Distance² + West Distance²)
- D = √(1500² + 1800²)
Calculating the Squares
- 1500² = 2250000
- 1800² = 3240000
Now, add these values:
- Total = 2250000 + 3240000 = 5490000
Final Calculation
- D = √5490000
- D = √(1000² × 61) = 1000√61
Thus, the distance between the two planes after 1.5 hours is 300√61 km.
Conclusion
Therefore, the correct answer is option D) 300√61 km.
Two poles of heights 6 m, and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m. What is the distance between their tops?- a)13 m
- b)12 m
- c)15 m
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Two poles of heights 6 m, and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m. What is the distance between their tops?
a)
13 m
b)
12 m
c)
15 m
d)
None of these
|
|
Ritu Saxena answered |
CB = CD - BD = 11m - 6m = 5m
ED = AB = 12 m
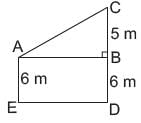
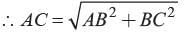
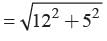
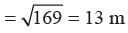
ED = AB = 12 m

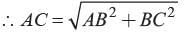
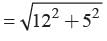
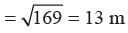
P and Q are points on sides AB and AC respectively of ΔABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, then BC =- a)PQ
- b)2PQ
- c)3PQ
- d)4PQ
Correct answer is option 'C'. Can you explain this answer?
P and Q are points on sides AB and AC respectively of ΔABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, then BC =
a)
PQ
b)
2PQ
c)
3PQ
d)
4PQ

|
Amar Roy answered |
Given Information:
- AP = 3 cm
- PB = 6 cm
- AQ = 5 cm
- QC = 10 cm
Calculation:
- Let's denote BC as x cm.
- By using the segment addition postulate in triangle ABC, we can find the lengths of BP and PC.
- AP + PB = AB
- 3 + 6 = 9 cm
- Since AB = BC, we can substitute BC with 9 cm.
- AQ + QC = AC
- 5 + 10 = 15 cm
- Since AC = AB + BC, we can substitute AB with 9 cm and BC with x cm.
- 9 + x = 15
- x = 6 cm
Conclusion:
- BC = 6 cm
- 3PQ = 3(5) = 15 cm
- Therefore, BC = 3PQ
- Hence, the correct answer is option 'C'.
- AP = 3 cm
- PB = 6 cm
- AQ = 5 cm
- QC = 10 cm
Calculation:
- Let's denote BC as x cm.
- By using the segment addition postulate in triangle ABC, we can find the lengths of BP and PC.
- AP + PB = AB
- 3 + 6 = 9 cm
- Since AB = BC, we can substitute BC with 9 cm.
- AQ + QC = AC
- 5 + 10 = 15 cm
- Since AC = AB + BC, we can substitute AB with 9 cm and BC with x cm.
- 9 + x = 15
- x = 6 cm
Conclusion:
- BC = 6 cm
- 3PQ = 3(5) = 15 cm
- Therefore, BC = 3PQ
- Hence, the correct answer is option 'C'.
A tree is broken of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. What is the original height of the tree?- a)20 m
- b)12 m
- c)16 m
- d)14 m
Correct answer is option 'C'. Can you explain this answer?
A tree is broken of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. What is the original height of the tree?
a)
20 m
b)
12 m
c)
16 m
d)
14 m
|
|
Priyanka Kapoor answered |
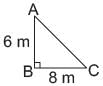
A is the point of cleavage C is the point where top of three touches the ground
In ΔABC
AB2 + BC2 = AC2 (Pythagoras’ Theorem)
62 + 82 = AC2
= AC = 10 m
∴ Total (original) height = 10 m + 6 m = 16 m
D and E are points on the sides AB and AC respectively of a DABC such that DE || BC find value of x if AD = (7x - 4) cm, AE = (5x - 2) cm, DB = (3x - 4) cm, EC = 3x cm- a)11
- b)5
- c)4
- d)2
Correct answer is option 'C'. Can you explain this answer?
D and E are points on the sides AB and AC respectively of a DABC such that DE || BC find value of x if AD = (7x - 4) cm, AE = (5x - 2) cm, DB = (3x - 4) cm, EC = 3x cm
a)
11
b)
5
c)
4
d)
2
|
|
Priyanka Kapoor answered |
∵ DE ║ BE
∴ DADE ~ DABC

⇒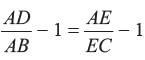
⇒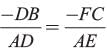 adjusting this expression, we have
adjusting this expression, we have
⇒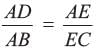
⇒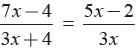
⇒ 21x2 -12x = 15x2 − 6x−8 + 20 x
⇒ 6x2 −26x+8 = 0
⇒ 6x2 −24x−2x +8=0
⇒ 6x(x −4)− 2(x −4)= 0
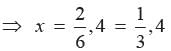
When,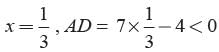
∴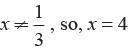
∴ DADE ~ DABC

⇒
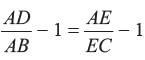
⇒
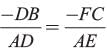 adjusting this expression, we have
adjusting this expression, we have⇒
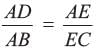
⇒
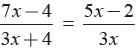
⇒ 21x2 -12x = 15x2 − 6x−8 + 20 x
⇒ 6x2 −26x+8 = 0
⇒ 6x2 −24x−2x +8=0
⇒ 6x(x −4)− 2(x −4)= 0
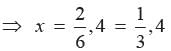
When,
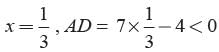
∴
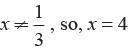
Two isosceles triangles with equal vertical angles have their areas in the ratio 225:289. What is the ratio between corresponding altitudes?- a)17:15
- b)15:17
- c)15:13
- d)13:15
Correct answer is option 'B'. Can you explain this answer?
Two isosceles triangles with equal vertical angles have their areas in the ratio 225:289. What is the ratio between corresponding altitudes?
a)
17:15
b)
15:17
c)
15:13
d)
13:15
|
|
Prabhat jha answered |
Given:
- Two isosceles triangles with equal vertical angles
- The areas of the triangles are in the ratio 225:289
To find:
- The ratio between corresponding altitudes of the triangles
Explanation:
Let's assume the two triangles are ABC and DEF, where angle BAC = angle EDF and angle ABC = angle DEF.
Step 1:
Let's assume the base of triangle ABC is BC and the base of triangle DEF is EF.
Since the triangles are isosceles, we can assume that BC = EF.
Step 2:
Let's assume the height of triangle ABC is h1 and the height of triangle DEF is h2.
We need to find the ratio h1/h2.
Step 3:
The area of a triangle can be calculated using the formula:
Area = (1/2) * base * height.
Given that the ratio of the areas of the triangles is 225:289, we can write:
(1/2) * BC * h1 / (1/2) * EF * h2 = 225/289
Simplifying the equation, we get:
BC * h1 / EF * h2 = 225/289
Step 4:
Since BC = EF, we can eliminate them from the equation:
h1/h2 = 225/289
Step 5:
To simplify the ratio, we can divide both sides of the equation by the greatest common divisor (GCD) of 225 and 289, which is 17.
(225/17)/(289/17) = 15/17
Therefore, the ratio between the corresponding altitudes of the two triangles is 15:17.
Answer:
The ratio between the corresponding altitudes of the two triangles is 15:17. (Option B)
- Two isosceles triangles with equal vertical angles
- The areas of the triangles are in the ratio 225:289
To find:
- The ratio between corresponding altitudes of the triangles
Explanation:
Let's assume the two triangles are ABC and DEF, where angle BAC = angle EDF and angle ABC = angle DEF.
Step 1:
Let's assume the base of triangle ABC is BC and the base of triangle DEF is EF.
Since the triangles are isosceles, we can assume that BC = EF.
Step 2:
Let's assume the height of triangle ABC is h1 and the height of triangle DEF is h2.
We need to find the ratio h1/h2.
Step 3:
The area of a triangle can be calculated using the formula:
Area = (1/2) * base * height.
Given that the ratio of the areas of the triangles is 225:289, we can write:
(1/2) * BC * h1 / (1/2) * EF * h2 = 225/289
Simplifying the equation, we get:
BC * h1 / EF * h2 = 225/289
Step 4:
Since BC = EF, we can eliminate them from the equation:
h1/h2 = 225/289
Step 5:
To simplify the ratio, we can divide both sides of the equation by the greatest common divisor (GCD) of 225 and 289, which is 17.
(225/17)/(289/17) = 15/17
Therefore, the ratio between the corresponding altitudes of the two triangles is 15:17.
Answer:
The ratio between the corresponding altitudes of the two triangles is 15:17. (Option B)
A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. What is the width of the street?- a)21 m
- b)20 m
- c)12 m
- d)15 m
Correct answer is option 'A'. Can you explain this answer?
A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. What is the width of the street?
a)
21 m
b)
20 m
c)
12 m
d)
15 m
|
|
Priyanka Kapoor answered |

In ΔABE,
AE2 + AB2 = BE2
⇒ 92 + AB2 = 152
⇒ AB2 = 225 - 81
= 144
⇒ AB = 12 m
Similarly,
In DBCD
⇒ BC2 = BD2 - DC2 = 152 - 122 = 92
BC = 9m
∴ width of street = (AB + BC) = 12 + 9 = 21 m
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, then the distance between their tops is- a)13 m
- b)12 m
- c)14 m
- d)15 m
Correct answer is option 'A'. Can you explain this answer?
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, then the distance between their tops is
a)
13 m
b)
12 m
c)
14 m
d)
15 m
|
|
Ritu Saxena answered |
Let AB and CD be the heights of given poles, BC be the distance between their feet and AD be the distance between their tops. Since, BCDE is a rectangle.
∴ EB = DC = 9 m and ED = BC = 12 m
AE = AB – EB = 14 m – 9 m = 5m
Now, ΔAED is a right angled triangle
∴ AD2 = AE2 + ED2 [By Pythagoras theorem]
⇒ AD2 = (5)2 + (12)2 = 169 ⇒ AD = 13 m
Hence, the distance between their tops is 13 m.
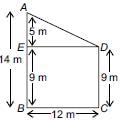
∴ EB = DC = 9 m and ED = BC = 12 m
AE = AB – EB = 14 m – 9 m = 5m
Now, ΔAED is a right angled triangle
∴ AD2 = AE2 + ED2 [By Pythagoras theorem]
⇒ AD2 = (5)2 + (12)2 = 169 ⇒ AD = 13 m
Hence, the distance between their tops is 13 m.

Which of the following statements is CORRECT?- a)The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
- b)If a line is drawn parallel to one side of the triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
- c)All similar figures are congruent.
- d)If in two triangles, two angles of one triangle is equal to the two angles of the other triangle then two triangles may or may not be congruent.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is CORRECT?
a)
The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
b)
If a line is drawn parallel to one side of the triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
c)
All similar figures are congruent.
d)
If in two triangles, two angles of one triangle is equal to the two angles of the other triangle then two triangles may or may not be congruent.
|
|
Sheena mehta answered |
Explanation:
Statement a: The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
- This statement is incorrect. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Statement b: If a line is drawn parallel to one side of the triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
- This statement is correct. This property is known as the Basic Proportionality Theorem (BPT) and is used to find unknown sides of similar triangles.
Statement c: All similar figures are congruent.
- This statement is incorrect. Similar figures have the same shape but not necessarily the same size, whereas congruent figures have the same shape and size.
Statement d: If in two triangles, two angles of one triangle is equal to the two angles of the other triangle then two triangles may or may not be congruent.
- This statement is correct. Two triangles with the same angle measures are not necessarily congruent, as the side lengths may differ.
Therefore, option B is the correct statement.
Statement a: The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
- This statement is incorrect. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Statement b: If a line is drawn parallel to one side of the triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
- This statement is correct. This property is known as the Basic Proportionality Theorem (BPT) and is used to find unknown sides of similar triangles.
Statement c: All similar figures are congruent.
- This statement is incorrect. Similar figures have the same shape but not necessarily the same size, whereas congruent figures have the same shape and size.
Statement d: If in two triangles, two angles of one triangle is equal to the two angles of the other triangle then two triangles may or may not be congruent.
- This statement is correct. Two triangles with the same angle measures are not necessarily congruent, as the side lengths may differ.
Therefore, option B is the correct statement.
If a tree casts a 18 feet shadow and at the same time, a child of height 3 feet casts a 2 feet shadow, then the height of the tree is- a)27 feet
- b)32 feet
- c)45 feet
- d)36 feet
Correct answer is option 'A'. Can you explain this answer?
If a tree casts a 18 feet shadow and at the same time, a child of height 3 feet casts a 2 feet shadow, then the height of the tree is
a)
27 feet
b)
32 feet
c)
45 feet
d)
36 feet
|
|
Naveen Gupta answered |
Given information:
- Height of the child = 3 feet
- Length of the shadow cast by the child = 2 feet
- Length of the shadow cast by the tree = 18 feet
To find: Height of the tree
The height of the tree can be determined by using the concept of similar triangles. The triangles formed by the child, its shadow, the tree, and its shadow are similar.
Similar triangles have proportional sides, meaning their corresponding sides are in the same ratio.
Using this concept, we can set up a proportion to find the height of the tree.
Let's denote:
- Height of the tree = x feet
Proportion:
(height of the tree) / (length of its shadow) = (height of the child) / (length of its shadow)
x / 18 = 3 / 2
Now, we can cross-multiply and solve for x:
2x = 18 * 3
2x = 54
x = 54 / 2
x = 27
Therefore, the height of the tree is 27 feet.
So, the correct answer is option A) 27 feet.
- Height of the child = 3 feet
- Length of the shadow cast by the child = 2 feet
- Length of the shadow cast by the tree = 18 feet
To find: Height of the tree
The height of the tree can be determined by using the concept of similar triangles. The triangles formed by the child, its shadow, the tree, and its shadow are similar.
Similar triangles have proportional sides, meaning their corresponding sides are in the same ratio.
Using this concept, we can set up a proportion to find the height of the tree.
Let's denote:
- Height of the tree = x feet
Proportion:
(height of the tree) / (length of its shadow) = (height of the child) / (length of its shadow)
x / 18 = 3 / 2
Now, we can cross-multiply and solve for x:
2x = 18 * 3
2x = 54
x = 54 / 2
x = 27
Therefore, the height of the tree is 27 feet.
So, the correct answer is option A) 27 feet.
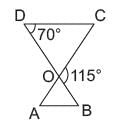
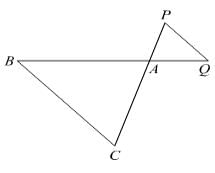
In the given figure, ΔODC ~ ΔOBA, ∠BOC = 115°, ∠CDO = 70°. What is the value of ∠OAB?
- a)45°
- b)65°
- c)35°
- d)55°
Correct answer is option 'A'. Can you explain this answer?
In the given figure, ΔODC ~ ΔOBA, ∠BOC = 115°, ∠CDO = 70°. What is the value of ∠OAB?


a)
45°
b)
65°
c)
35°
d)
55°
|
|
Priyanka Kapoor answered |
∠ CDO + ∠DCO = 115°
⇒ ∠DCO = 115° - 70° = 45°
∠OAB = 45° (∴ DODC ~ DOBA)
⇒ ∠DCO = 115° - 70° = 45°
∠OAB = 45° (∴ DODC ~ DOBA)
In the given figure BC is parallel to DE. Area of DABC is 25 cm2. Area of trapezium BCED is 24 cm2, if DE = 14 cm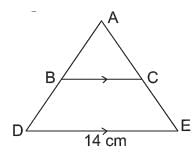 What is the length of BC?
What is the length of BC?- a)15 cm
- b)10 cm
- c)28 cm
- d)20 cm
Correct answer is option 'B'. Can you explain this answer?
In the given figure BC is parallel to DE. Area of DABC is 25 cm2. Area of trapezium BCED is 24 cm2, if DE = 14 cm

What is the length of BC?
a)
15 cm
b)
10 cm
c)
28 cm
d)
20 cm
|
|
Priyanka Kapoor answered |
∵ BC ║ DE
∴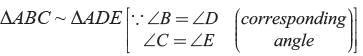
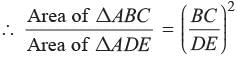
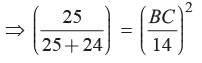
[Ar (DADE) = Ar(DABC) + Ar(¨BCED)
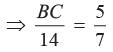
⇒ BC = 10 cm
∴
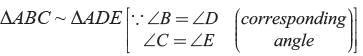
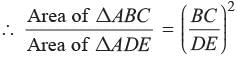
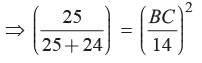
[Ar (DADE) = Ar(DABC) + Ar(¨BCED)
⇒ BC = 10 cm
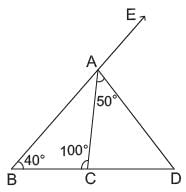
In the figure given below, what is the measures of angle ∠DAE?
- a)60°
- b)50°
- c)90°
- d)80°
Correct answer is option 'C'. Can you explain this answer?
In the figure given below, what is the measures of angle ∠DAE?


a)
60°
b)
50°
c)
90°
d)
80°
|
|
Ritu Saxena answered |
In ΔABC
∠BAC = 180° - (100° + 40°) = 40°
∠DAE = 180° - (50° + 40°) = 90° [linear pair]
∠BAC = 180° - (100° + 40°) = 40°
∠DAE = 180° - (50° + 40°) = 90° [linear pair]
In a triangle ABC, ∠B = 55°, ∠C = 35° then which of the following option is true?- a)BC2 = AB2 + AC2
- b)AC2 = AB2 + BC2
- c)AB2 = BC2 + AC2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In a triangle ABC, ∠B = 55°, ∠C = 35° then which of the following option is true?
a)
BC2 = AB2 + AC2
b)
AC2 = AB2 + BC2
c)
AB2 = BC2 + AC2
d)
None of these
|
|
Ritu Saxena answered |
∠A = 180° - (∠B + ∠C)
= 180° - (55° + 35°) = 90°
∴ ∠A is 90° or the triangle is right angled at A
∴ AB2 + AC2 = BC2 (pythagoras’ theorem)
= 180° - (55° + 35°) = 90°
∴ ∠A is 90° or the triangle is right angled at A
∴ AB2 + AC2 = BC2 (pythagoras’ theorem)
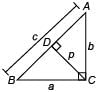
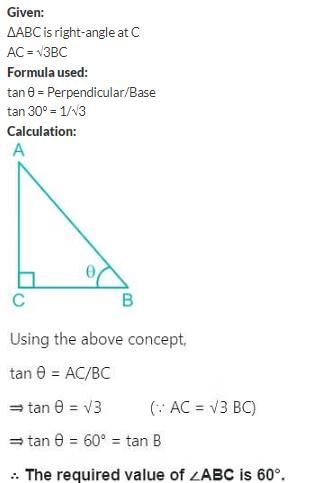
ABC is right triangle, right angled at C. If p is the length of the perpendicular from C to AB and a, b, c have the usual meaning, then 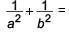
- a)1/p2
- b)2/p2
- c)p2
- d)2p2
Correct answer is option 'A'. Can you explain this answer?
ABC is right triangle, right angled at C. If p is the length of the perpendicular from C to AB and a, b, c have the usual meaning, then 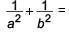

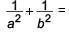

a)
1/p2
b)
2/p2
c)
p2
d)
2p2
|
|
Vivek Bansal answered |
Area of ΔABC = 1/2 × c × p = 1/2 × b × a
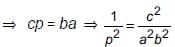
But, c2 = a2 + b2 [By Pythagoras theorem]
∴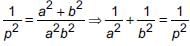
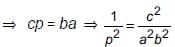
But, c2 = a2 + b2 [By Pythagoras theorem]
∴
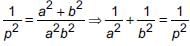
In the given figure, AD ⊥ BC, BE ⊥ AC, CF ⊥ AB, then AF2 + BD2 + CE2 =
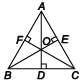
- a)OA2 + OB2 + OC2
- b)OD2 + OE2 + OF2
- c)AB2 + BC2 + AC2
- d)AE2 + BF2 + CD2
Correct answer is option 'D'. Can you explain this answer?
In the given figure, AD ⊥ BC, BE ⊥ AC, CF ⊥ AB, then AF2 + BD2 + CE2 =


a)
OA2 + OB2 + OC2
b)
OD2 + OE2 + OF2
c)
AB2 + BC2 + AC2
d)
AE2 + BF2 + CD2
|
|
Vivek Bansal answered |
In ΔODB and ΔODC, using pythagoras theorem,
OB2 = OD2 + BD2 and OC2 = OD2 + CD2
∴ OC2 = BD2 – CD2 ...(i)
Similarly, we have
OC2 – OA2 = CE2 – AE2 ...(ii)
And OA2 – OB2 = AF2 – BF2 ...(iii)
Adding (i), (ii) and (iii), we get
BD2 + CE2 + AF2 – CD2 – AE2 – BF2 = 0
⇒ BD2 + CE2 + AF2 = CD2 + AE2 + BF2
OB2 = OD2 + BD2 and OC2 = OD2 + CD2
∴ OC2 = BD2 – CD2 ...(i)
Similarly, we have
OC2 – OA2 = CE2 – AE2 ...(ii)
And OA2 – OB2 = AF2 – BF2 ...(iii)
Adding (i), (ii) and (iii), we get
BD2 + CE2 + AF2 – CD2 – AE2 – BF2 = 0
⇒ BD2 + CE2 + AF2 = CD2 + AE2 + BF2
In the given figure, ∠ ABC = 90° and BD ⊥ AC . If BD = 8 cm, AD = 4 cm, then CD =

- a)16 cm
- b)14 cm
- c)15 cm
- d)17 cm
Correct answer is option 'A'. Can you explain this answer?
In the given figure, ∠ ABC = 90° and BD ⊥ AC . If BD = 8 cm, AD = 4 cm, then CD =


a)
16 cm
b)
14 cm
c)
15 cm
d)
17 cm
|
|
Priyanka Kapoor answered |
In ΔDBA and ΔDCB, we have
∠BDA = ∠CDB [Each 90°]
and ∠DBA = ∠DCB [Each = 90° – ∠A]
∴ ΔDBA ~ ΔDCB [By AA similarity]
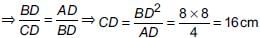
∠BDA = ∠CDB [Each 90°]
and ∠DBA = ∠DCB [Each = 90° – ∠A]
∴ ΔDBA ~ ΔDCB [By AA similarity]
In ΔABC, 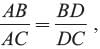 ∠B = 70°, ∠C = 50° then ∠BAD = ?
∠B = 70°, ∠C = 50° then ∠BAD = ?
- a)40°
- b)30°
- c)5°
- d)50°
Correct answer is option 'B'. Can you explain this answer?
In ΔABC, 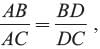 ∠B = 70°, ∠C = 50° then ∠BAD = ?
∠B = 70°, ∠C = 50° then ∠BAD = ?

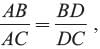 ∠B = 70°, ∠C = 50° then ∠BAD = ?
∠B = 70°, ∠C = 50° then ∠BAD = ?
a)
40°
b)
30°
c)
5°
d)
50°
|
|
Ritu Saxena answered |
In ΔABD and ΔACD
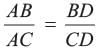
By Angle Bisector Theorem
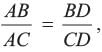 it is given,
it is given,
and ∠BAC = 180 - 70 - 50
= 180 - 120 = 60°
so, ∠BAD =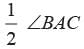

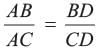
By Angle Bisector Theorem
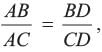 it is given,
it is given,and ∠BAC = 180 - 70 - 50
= 180 - 120 = 60°
so, ∠BAD =
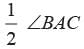

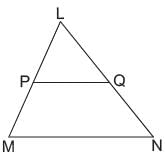
In ΔLMN, P and Q are the mid-points of LM and LN respectively. What is the ratio of the area of ΔLPQ, and ΔLMN?
- a)4:1
- b)1:4
- c)2:3
- d)3:2
Correct answer is option 'B'. Can you explain this answer?
In ΔLMN, P and Q are the mid-points of LM and LN respectively. What is the ratio of the area of ΔLPQ, and ΔLMN?


a)
4:1
b)
1:4
c)
2:3
d)
3:2
|
|
Ritu Saxena answered |
∵ P and Q are mid-points of ∠M and ∠N respectively
∠ PQ || MN (according to midpoint theorem) and, also,
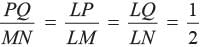
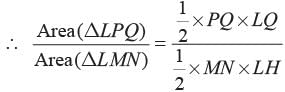
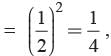 where G and H are feets of perpendicular dropped from L on PQ and MN respectively.
where G and H are feets of perpendicular dropped from L on PQ and MN respectively.
∠ PQ || MN (according to midpoint theorem) and, also,
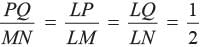
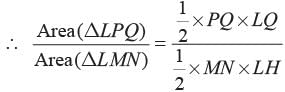
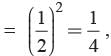 where G and H are feets of perpendicular dropped from L on PQ and MN respectively.
where G and H are feets of perpendicular dropped from L on PQ and MN respectively.In the given figure, DABC ~ DDCB, then AB × DB =
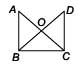
- a)OA × OD
- b)OB × OC
- c)AB × DC
- d)DC × AC
Correct answer is option 'D'. Can you explain this answer?
In the given figure, DABC ~ DDCB, then AB × DB =


a)
OA × OD
b)
OB × OC
c)
AB × DC
d)
DC × AC
|
|
Priyanka Kapoor answered |
Since Δ’s ABC and DCB are similar,
∴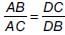 ⇒ AB × DB = DC × AC
⇒ AB × DB = DC × AC
∴
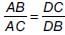 ⇒ AB × DB = DC × AC
⇒ AB × DB = DC × ACIn the given figure in DPQR, ST || QR, so that PS = (7x - 4) cm, PT = (5x - 2) cm, QS = (3x + 4) cm, RT = 3x cm. 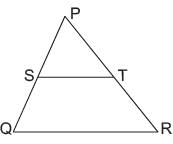 What is the value of x?
What is the value of x?- a)4
- b)3
- c)5
- d)2
Correct answer is option 'A'. Can you explain this answer?
In the given figure in DPQR, ST || QR, so that PS = (7x - 4) cm, PT = (5x - 2) cm, QS = (3x + 4) cm, RT = 3x cm.

What is the value of x?
a)
4
b)
3
c)
5
d)
2
|
|
Priyanka Kapoor answered |
In ΔPQR and ΔPST

⇒ According to Thales’ theorem
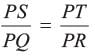
Subtracting unity from both sides, we have,
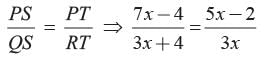
⇒ 21x2-12x = 15x2 - 6x + 20x - 8
⇒ 6x2 - 26x + 8 = 0
⇒ 3x2 - 13x + 4 = 0
⇒ 3x2 - 12x - x + 4 = 0
⇒ 3x(x - 4) - 1(x - 4) = 0
⇒ (x - 4) (3x - 1) = 0
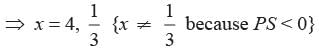 ∴x = 4
∴x = 4

⇒ According to Thales’ theorem
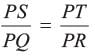
Subtracting unity from both sides, we have,
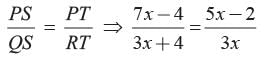
⇒ 21x2-12x = 15x2 - 6x + 20x - 8
⇒ 6x2 - 26x + 8 = 0
⇒ 3x2 - 13x + 4 = 0
⇒ 3x2 - 12x - x + 4 = 0
⇒ 3x(x - 4) - 1(x - 4) = 0
⇒ (x - 4) (3x - 1) = 0
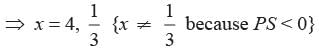 ∴x = 4
∴x = 4Match the following.

- a)(P)→(1), (Q)→(2), (R)→(3), (S)→(4)
- b)(P)→(2), (Q)→(1), (R)→(3), (S)→(4)
- c)(P)→(4), (Q)→(2), (R)→(1), (S)→(3)
- d)(P)→(3), (Q)→(1), (R)→(4), (S)→(2)
Correct answer is option 'B'. Can you explain this answer?
Match the following.


a)
(P)→(1), (Q)→(2), (R)→(3), (S)→(4)
b)
(P)→(2), (Q)→(1), (R)→(3), (S)→(4)
c)
(P)→(4), (Q)→(2), (R)→(1), (S)→(3)
d)
(P)→(3), (Q)→(1), (R)→(4), (S)→(2)
|
|
Ritu Saxena answered |
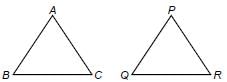
(P) Given :
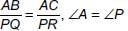
∴ ∠A is containing the sides AB and AC and ∠P is containing the sides PQ and PR.
∴ ΔABC ~ ΔPQR (By SAS criteria)
(Q) Given : ∠A = ∠P, ∠B = ∠Q
∴ ΔABC ~ ΔPQR (By AA criteria)
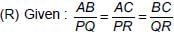
∵ Sides of the ΔABC and ΔPQR are in proportion
∴ ΔABC ~ ΔPQR (By SSS criteria)
(S) Given, DE || BC
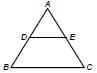
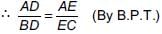
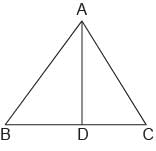
In an isosceles triangle AB = AC = 25 cm BC = 14 cm. What is the length of altitude from A on BC?- a)24 cm
- b)26 cm
- c)12 cm
- d)13 cm
Correct answer is option 'A'. Can you explain this answer?
In an isosceles triangle AB = AC = 25 cm BC = 14 cm. What is the length of altitude from A on BC?
a)
24 cm
b)
26 cm
c)
12 cm
d)
13 cm
|
|
Priyanka Kapoor answered |
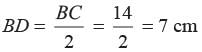
[fig. is in the previous ques]
∴AD2 = C2 - D2
= (25)2 - (7)2 = 576
⇒ AD = 24 cm
A 12 cm rod is held between a flashlight and a wall as shown. Find the length of the shadow on the wall if the rod is 45 cm from the wall and 15 cm from the light.
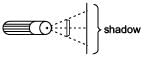
- a)75 cm
- b)96 cm
- c)48 cm
- d)60 cm
Correct answer is option 'C'. Can you explain this answer?
A 12 cm rod is held between a flashlight and a wall as shown. Find the length of the shadow on the wall if the rod is 45 cm from the wall and 15 cm from the light.


a)
75 cm
b)
96 cm
c)
48 cm
d)
60 cm
|
|
Ritu Saxena answered |
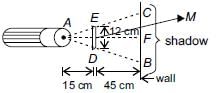
In ΔADM and ΔABF
∠DAM = ∠BAF (Common)
∠DMA = ∠BFM (Corresponding angles)
∴ ΔADM ~ ΔABF (By AA similarity)

∴ BC = BF + FC = 2BF = 48 cm (∵ CF = BF)
In the given figure, ∠BAC = ∠ADC, then CA/CB is
- a)CB × CD
- b)CA2
- c)DC/AC
- d)CD2
Correct answer is option 'C'. Can you explain this answer?
In the given figure, ∠BAC = ∠ADC, then CA/CB is


a)
CB × CD
b)
CA2
c)
DC/AC
d)
CD2
|
|
Ritu Saxena answered |
In Δ’s ABC and DAC,
∠BAC = ∠ADC (Given)
∠ACB = ∠ACD (Common angle)
∴ ΔABC ~ ΔDAC (By AA similarity)
∠BAC = ∠ADC (Given)
∠ACB = ∠ACD (Common angle)
∴ ΔABC ~ ΔDAC (By AA similarity)
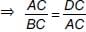

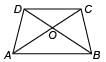
In the given trapezium ABCD, AB || CD and AB = 2CD. If area of ΔAOB = 84 cm2, then the area of ΔCOD is
- a)22 sq.cm
- b)25 sq.cm
- c)21 sq.cm
- d)24 sq.cm
Correct answer is option 'C'. Can you explain this answer?
In the given trapezium ABCD, AB || CD and AB = 2CD. If area of ΔAOB = 84 cm2, then the area of ΔCOD is


a)
22 sq.cm
b)
25 sq.cm
c)
21 sq.cm
d)
24 sq.cm
|
|
Priyanka Kapoor answered |
In ΔAOB and ΔCOD, we have
∠AOB = ∠COD
[Vertically opposite angles]
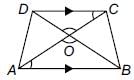
∠OAB = ∠OCD [Alternate interior angles]
∴ ΔAOB ~ ΔCOD [By AA similarity]
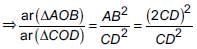 [∵ AB = 2CD]
[∵ AB = 2CD]
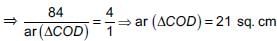
∠AOB = ∠COD
[Vertically opposite angles]

∠OAB = ∠OCD [Alternate interior angles]
∴ ΔAOB ~ ΔCOD [By AA similarity]
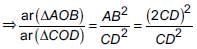 [∵ AB = 2CD]
[∵ AB = 2CD]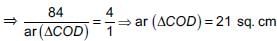
An exterior angle of a triangle measures 110° and its interior opposite angles are in the ratio 2:3. Which is the largest angle of the triangle?- a)66°
- b)70°
- c)44°
- d)64°
Correct answer is option 'B'. Can you explain this answer?
An exterior angle of a triangle measures 110° and its interior opposite angles are in the ratio 2:3. Which is the largest angle of the triangle?
a)
66°
b)
70°
c)
44°
d)
64°
|
|
Priyanka Kapoor answered |
Let the angles be 2x and 3x respectively
∴ 2x + 3x = 110°
⇒ 5x = 110°
⇒ x = 22°
∴ Angles are 44°, 66°, and 70°
∴ 2x + 3x = 110°
⇒ 5x = 110°
⇒ x = 22°
∴ Angles are 44°, 66°, and 70°
What is the perimeter of a rhombus the length of whose diagonal are 16 cm and 30 cm?- a)64 cm
- b)68 cm
- c)72 cm
- d)76 cm.
Correct answer is option 'B'. Can you explain this answer?
What is the perimeter of a rhombus the length of whose diagonal are 16 cm and 30 cm?
a)
64 cm
b)
68 cm
c)
72 cm
d)
76 cm.
|
|
Priyanka Kapoor answered |
Let the side of rhombus be x cm. Now, we know that the diagonals of rhombus bisect each other at right angles.
∴ By using Pythagoras’ Theorem
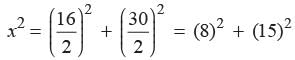
= 64 + 225= 289
⇒ x = 17 cm
∴ Perimeter = 4 × x = 4 × 17 = 68 cm
∴ By using Pythagoras’ Theorem
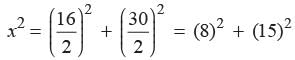
= 64 + 225= 289
⇒ x = 17 cm
∴ Perimeter = 4 × x = 4 × 17 = 68 cm
In rhombus ABCD, AB2 + BC2 + CD2 + DA2 =

- a)OA2 + OB2
- b)OB2 + OC2
- c)OC2 + OD2
- d)AC2 + BD2
Correct answer is option 'D'. Can you explain this answer?
In rhombus ABCD, AB2 + BC2 + CD2 + DA2 =


a)
OA2 + OB2
b)
OB2 + OC2
c)
OC2 + OD2
d)
AC2 + BD2
|
|
Ritu Saxena answered |
Let the length of sides of rhombus be x, length of OC be x1 and length of OD be y1. Then, AB2 + BC2 + CD2 + DA2 = 4x2
Since, AC and DB bisect each other at O.
∴ AC = 2x1 and BD = 2y1
In ΔAOD, ΔDOC, ΔAOB, ΔBOC
4[x21 + y21] = 4x2
⇒ AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Since, AC and DB bisect each other at O.
∴ AC = 2x1 and BD = 2y1
In ΔAOD, ΔDOC, ΔAOB, ΔBOC
4[x21 + y21] = 4x2
⇒ AC2 + BD2 = AB2 + BC2 + CD2 + AD2
P and Q are the mid-points of the sides CA and CB respectively of a DABC, right angled at C, then find :
(i) 4AC2 + BC2
(ii) 4BC2 + AC2
(iii) 4(AQ2 + BP2)

- a)A
- b)B
- c)C
- d)D
Correct answer is option 'A'. Can you explain this answer?
P and Q are the mid-points of the sides CA and CB respectively of a DABC, right angled at C, then find :
(i) 4AC2 + BC2
(ii) 4BC2 + AC2
(iii) 4(AQ2 + BP2)

(i) 4AC2 + BC2
(ii) 4BC2 + AC2
(iii) 4(AQ2 + BP2)

a)
A
b)
B
c)
C
d)
D
|
|
Ritu Saxena answered |
Construction : Join PQ, BP and AQ.
(i) 4AC2 + BC2 = 4AC2 + (2QC)2
[∵ Q is mid-point of BC]
= 4AC2 + 4QC2
= 4(AC2 + QC2)
= 4AQ2 [∵ AQC is right angled triangle]
(ii) 4BC2 + AC2 = 4BC2 + (2CP)2 [∵ P is mid-point of AC]
= 4BC2 + 4CP2 = 4(BC2 + CP2) = 4BP2 [∵ PBC is right angled triangle]
(iii) 4[AC2 + QC2] = 4(AQ)2 [from (i) part]
⇒ 4AC2 + BC2 = 4AQ2 ...(i)
4[BC2 + CP2] = 4(BP)2 [from (ii) part]
⇒ 4BC2 + AC2 = 4BP2 ...(ii)
Now, adding (i) and (ii), we get
4(AQ2 + BP2) = 5(AC2 + BC2) = 5AB2 [∵ ABC is right angled triangle]
(i) 4AC2 + BC2 = 4AC2 + (2QC)2
[∵ Q is mid-point of BC]
= 4AC2 + 4QC2
= 4(AC2 + QC2)
= 4AQ2 [∵ AQC is right angled triangle]
(ii) 4BC2 + AC2 = 4BC2 + (2CP)2 [∵ P is mid-point of AC]
= 4BC2 + 4CP2 = 4(BC2 + CP2) = 4BP2 [∵ PBC is right angled triangle]
(iii) 4[AC2 + QC2] = 4(AQ)2 [from (i) part]
⇒ 4AC2 + BC2 = 4AQ2 ...(i)
4[BC2 + CP2] = 4(BP)2 [from (ii) part]
⇒ 4BC2 + AC2 = 4BP2 ...(ii)
Now, adding (i) and (ii), we get
4(AQ2 + BP2) = 5(AC2 + BC2) = 5AB2 [∵ ABC is right angled triangle]
In the given figure,the line segment XY is parallel to side AC of ΔABC and it divides the triangle into two parts of equal area. Then, find
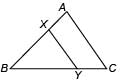
(i) AX : AB (ii) AC/XY
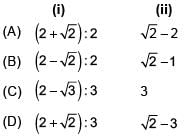
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'B'. Can you explain this answer?
In the given figure,the line segment XY is parallel to side AC of ΔABC and it divides the triangle into two parts of equal area. Then, find

(i) AX : AB (ii) AC/XY
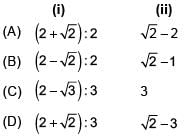

(i) AX : AB (ii) AC/XY
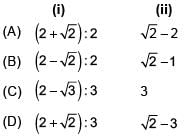
a)
A
b)
B
c)
C
d)
D
|
|
Priyanka Kapoor answered |
(i) Since, XY || AC, we have
∠A = ∠BXY and ∠C = ∠BYX [Corresponding angles]
∴ ΔABC ~ ΔXBY [By AA similarity]
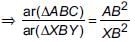 ...(i)
...(i)
But, ar(ΔABC) = 2 × ar(ΔXBY) [Given]
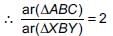 ...(ii)
...(ii)
From (i) and (ii), we get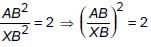

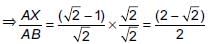
Hence, AX : AB = (2 − √2) : 2
(ii) Since, ΔABC ~ ΔXBY
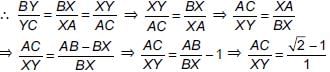
∠A = ∠BXY and ∠C = ∠BYX [Corresponding angles]
∴ ΔABC ~ ΔXBY [By AA similarity]
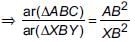 ...(i)
...(i)But, ar(ΔABC) = 2 × ar(ΔXBY) [Given]
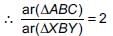 ...(ii)
...(ii)From (i) and (ii), we get
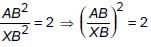

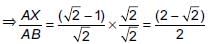
Hence, AX : AB = (2 − √2) : 2
(ii) Since, ΔABC ~ ΔXBY
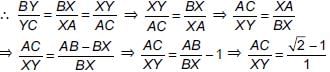
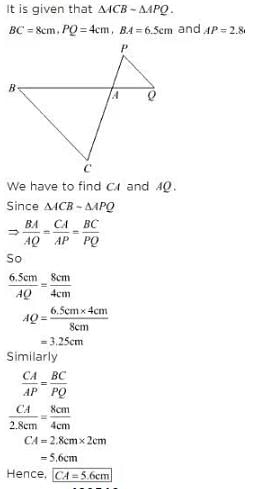
Mason Construction wants to connect two parks on opposite sides of town with a road. Surveyors have laid out a map as shown. The road can be built through the town or around town through point R. The roads intersect at a right angle at point R. The line joining Park A to Park B is parallel to the line joining C and D.
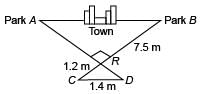
(i) What is the distance between the parks through town?
(ii) What is the distance from Park A to Park B through point R?- a)

- b)
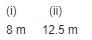
- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
Mason Construction wants to connect two parks on opposite sides of town with a road. Surveyors have laid out a map as shown. The road can be built through the town or around town through point R. The roads intersect at a right angle at point R. The line joining Park A to Park B is parallel to the line joining C and D.

(i) What is the distance between the parks through town?
(ii) What is the distance from Park A to Park B through point R?

(i) What is the distance between the parks through town?
(ii) What is the distance from Park A to Park B through point R?
a)

b)
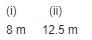
c)

d)

|
|
Ritu Saxena answered |
(i) Since, CD || AB [Given]
∴ In ΔRCD and ΔRBA, we have
∠BAR = ∠RDC [Alternate interior angles]
∠ABR = ∠RCD
∴ ΔRCD ~ ΔRBA [By AA similarity]
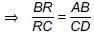 ... (i)
... (i)
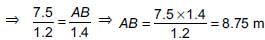
i.e., Distance between the parks through town is 8.75 m.
(ii) In right ΔCRD, we have
(CD)2 = (CR)2 + (RD)2
⇒ RD2 = (1.4)2 – (1.2)2 = 0.52 ⇒ RD = 0.72 m
Since ΔRCD ~ ΔRBA
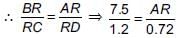
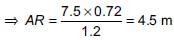
i.e., Distance from Park A to Park B through point R = AR + RB
= 4.5 m + 7.5 m = 12 m
∴ In ΔRCD and ΔRBA, we have
∠BAR = ∠RDC [Alternate interior angles]
∠ABR = ∠RCD
∴ ΔRCD ~ ΔRBA [By AA similarity]
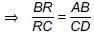 ... (i)
... (i)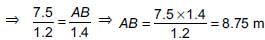
i.e., Distance between the parks through town is 8.75 m.
(ii) In right ΔCRD, we have
(CD)2 = (CR)2 + (RD)2
⇒ RD2 = (1.4)2 – (1.2)2 = 0.52 ⇒ RD = 0.72 m
Since ΔRCD ~ ΔRBA
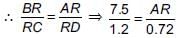
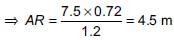
i.e., Distance from Park A to Park B through point R = AR + RB
= 4.5 m + 7.5 m = 12 m
In the given figure, ABC is a right triangle right-angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD = 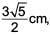 then the length of CE is
then the length of CE is
- a)4 cm
- b)2√5 cm
- c)3√5 cm
- d)5 cm
Correct answer is option 'B'. Can you explain this answer?
In the given figure, ABC is a right triangle right-angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD = 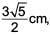 then the length of CE is
then the length of CE is

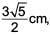 then the length of CE is
then the length of CE is
a)
4 cm
b)
2√5 cm
c)
3√5 cm
d)
5 cm
|
|
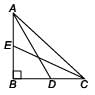
Ritu Saxena answered |
Since ΔABD is a right angled triangle
∴ AD2 = AB2 + BD2 [By using Pythagoras theorem]
⇒ AD2 = AB2 + (BC/2)2 [∵ AD is median on BC]
⇒ AD2 = AB2 + (1/4) BC2 ...(i)
Similarly in, ΔBCE
CE2 = BC2 + BE2 ⇒ CE2 = BC2 + (AB/2)2 [∵ EC is median on AB]
⇒ CE2 = BC2 + (1/4).AB2 ...(ii)
Adding (i) and (ii), we get
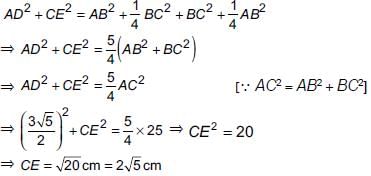
∴ AD2 = AB2 + BD2 [By using Pythagoras theorem]
⇒ AD2 = AB2 + (BC/2)2 [∵ AD is median on BC]
⇒ AD2 = AB2 + (1/4) BC2 ...(i)
Similarly in, ΔBCE
CE2 = BC2 + BE2 ⇒ CE2 = BC2 + (AB/2)2 [∵ EC is median on AB]
⇒ CE2 = BC2 + (1/4).AB2 ...(ii)
Adding (i) and (ii), we get
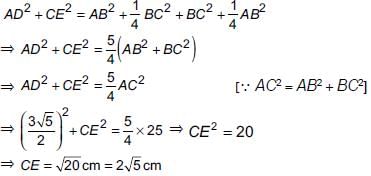
A vertical pole 12 m long casts a shadow of 8 m long on the ground. At the same time, a tower casts the shadow 40 m long on the ground. What is the height of the tower?- a)80 m
- b)20 m
- c)60 m
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A vertical pole 12 m long casts a shadow of 8 m long on the ground. At the same time, a tower casts the shadow 40 m long on the ground. What is the height of the tower?
a)
80 m
b)
20 m
c)
60 m
d)
None of these
|
|
Priyanka Kapoor answered |
Both Ds are right angled, and also the elevation of coming sunlight will be same.
∴ All the angles of the ΔABC and ΔPQR will be correspondingly identical.
∴ ΔABC ~ ΔPQR
⇒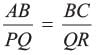
⇒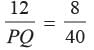
∴ All the angles of the ΔABC and ΔPQR will be correspondingly identical.
∴ ΔABC ~ ΔPQR
⇒
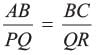
⇒
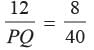
⇒ PQ = 12 × 5 = 60m
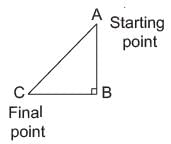
A man goes 10 m due south and then 24 m due west. How far is he from the starting point?- a)26 m
- b)25 cm
- c)27 cm
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A man goes 10 m due south and then 24 m due west. How far is he from the starting point?
a)
26 m
b)
25 cm
c)
27 cm
d)
None of these
|
|
Priyanka Kapoor answered |
In ΔABC
AC2 = AB2 + BC2 (Pythagoras’ theorem)
⇒ AC =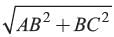
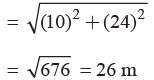
AC2 = AB2 + BC2 (Pythagoras’ theorem)

⇒ AC =
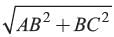
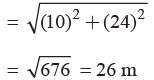
In an isosceles triangle ΔABC if AB = AC = 13 cm and altitude from A on BC is 5 cm. What is the length of BC?- a)12 cm
- b)24 cm
- c)6 cm
- d)None of these.
Correct answer is option 'B'. Can you explain this answer?
In an isosceles triangle ΔABC if AB = AC = 13 cm and altitude from A on BC is 5 cm. What is the length of BC?
a)
12 cm
b)
24 cm
c)
6 cm
d)
None of these.
|
|
Priyanka Kapoor answered |
In ΔABD

AB2 = BD2 + AD2
⇒ BD =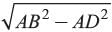
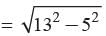
= 12 cm
∵ D bisects BC
∴ BC = 2 × BD
= 2 × 12 = 24 cm

AB2 = BD2 + AD2
⇒ BD =
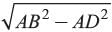
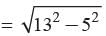
= 12 cm
∵ D bisects BC
∴ BC = 2 × BD
= 2 × 12 = 24 cm
ΔABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ΔDEF ~ ΔABC and EF = 4 cm, then perimeter of ΔDEF is- a)7.5 cm
- b)15 cm
- c)22.5 cm
- d)30 cm
Correct answer is option 'B'. Can you explain this answer?
ΔABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ΔDEF ~ ΔABC and EF = 4 cm, then perimeter of ΔDEF is
a)
7.5 cm
b)
15 cm
c)
22.5 cm
d)
30 cm
|
|
Priyanka Kapoor answered |
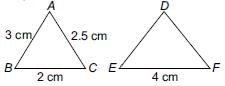
Since, ΔDEF ~ ΔABC [Given]
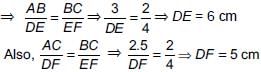
∴ Perimeter of ΔDEF = DE + EF + FD
= 6 cm + 4 cm + 5 cm = 15 cm
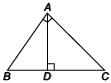
In the given ΔABC, AD⊥BC and ∠A is right angled. Then AD2 =
- a)AB × AC
- b)BD × CD
- c)BC × AC
- d)AB × BC
Correct answer is option 'B'. Can you explain this answer?
In the given ΔABC, AD⊥BC and ∠A is right angled. Then AD2 =


a)
AB × AC
b)
BD × CD
c)
BC × AC
d)
AB × BC
|
|
Priyanka Kapoor answered |
In Δ's CDA and BAD,
we have
∠BAD = 90° – ∠ABD
∠DAC = 90° – ∠BAD
= 90° – (90° – ∠ABD) = ∠ABD
⇒ ∠DAC = ∠ABD
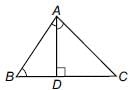
Now, in Δ's BDA and ADC, we have
∠ABD = ∠CAD
∠BDA = ∠ADC [Each 90°]
∴ ΔBDA ~ ΔADC [By AA similarity]
⇒
we have
∠BAD = 90° – ∠ABD
∠DAC = 90° – ∠BAD
= 90° – (90° – ∠ABD) = ∠ABD
⇒ ∠DAC = ∠ABD

Now, in Δ's BDA and ADC, we have
∠ABD = ∠CAD
∠BDA = ∠ADC [Each 90°]
∴ ΔBDA ~ ΔADC [By AA similarity]
⇒

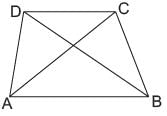
ABCD is a trapezium in which AB || DC and AB = 2CD. If the diagonals of the trapezium intersect each other at point O. What is the ratio of the area of ΔAOB and ΔCOD?
- a)1:4
- b)4:1
- c)1:9
- d)9:1
Correct answer is option 'B'. Can you explain this answer?
ABCD is a trapezium in which AB || DC and AB = 2CD. If the diagonals of the trapezium intersect each other at point O. What is the ratio of the area of ΔAOB and ΔCOD?


a)
1:4
b)
4:1
c)
1:9
d)
9:1
|
|
Ritu Saxena answered |
∠ CAB = ∠ACD
{ Alternate opposite int erior angles}
∠BDC = ∠DBA
∴ ΔAOB ~ ΔCOD (SS similarity)

{ Alternate opposite int erior angles}
∠BDC = ∠DBA
∴ ΔAOB ~ ΔCOD (SS similarity)

Chapter doubts & questions for Triangles - International Mathematics Olympiad (IMO) for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Triangles - International Mathematics Olympiad (IMO) for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
International Mathematics Olympiad (IMO) for Class 10
28 videos|149 docs|72 tests
|
Related Class 10 Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

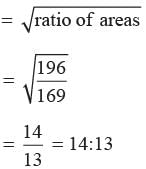
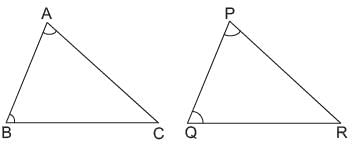
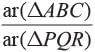 if BC : QR = 9:7?
if BC : QR = 9:7?