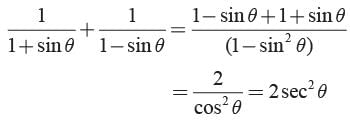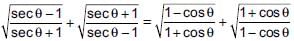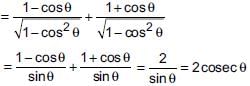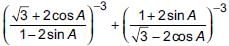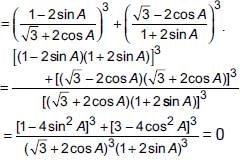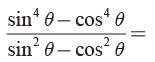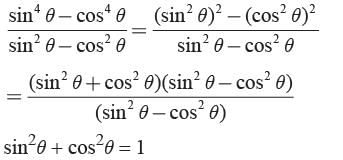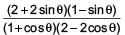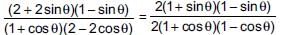All Exams >
Class 10 >
International Mathematics Olympiad (IMO) for Class 10 >
All Questions
All questions of Trigonometry for Class 10 Exam
If x = r sinθ cos φ, y = r sinθ sinφ and z = r cosθ, then _________.- a)x2 + y2 + z2 = r2
- b)x2 + y2 – z2 = r2
- c)x2 – y2 + z2 = r2
- d)z2 + y2 – x2 = r2
Correct answer is option 'A'. Can you explain this answer?
If x = r sinθ cos φ, y = r sinθ sinφ and z = r cosθ, then _________.
a)
x2 + y2 + z2 = r2
b)
x2 + y2 – z2 = r2
c)
x2 – y2 + z2 = r2
d)
z2 + y2 – x2 = r2
|
|
Ritu Saxena answered |
x = r sinθcosφ ... (i)
y = r sinθsinφ ... (ii)
z = r cosθ ... (iii)
Squaring and adding (i) and (ii), we get
x2 + y2 = r2sin2q ... (iv)
Squaring (iii) and adding it with (iv), we get
x2 + z2 + y2 = r2
y = r sinθsinφ ... (ii)
z = r cosθ ... (iii)
Squaring and adding (i) and (ii), we get
x2 + y2 = r2sin2q ... (iv)
Squaring (iii) and adding it with (iv), we get
x2 + z2 + y2 = r2
Which of the following is not possible?
- a)cosec θ = 0.14
- b)sec θ = 100
- c)sin θ = 3/5
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not possible?
a)
cosec θ = 0.14
b)
sec θ = 100
c)
sin θ = 3/5
d)
none of these
|
|
Atul malhotra answered |
It is not possible to answer this question as it is incomplete. The options or the complete question are missing. Please provide more information.
If sin x + sin2x = 1, then cos8 x + 2cos6x + cos4x =_____.- a)0
- b)-1
- c)1
- d)2
Correct answer is option 'C'. Can you explain this answer?
If sin x + sin2x = 1, then cos8 x + 2cos6x + cos4x =_____.
a)
0
b)
-1
c)
1
d)
2
|
|
Pallavi sengupta answered |
To solve this problem, we can use trigonometric identities and simplify the given expression step by step. Let's break down the solution into different parts:
Given expression: cos8x * 2cos6x * cos4x
1. Simplify the expression sin x * sin 2x = 1:
- We know that sin 2x = 2 * sin x * cos x.
- Substituting this in the given expression, we have: sin x * (2 * sin x * cos x) = 1.
- Simplifying further, we get: 2sin^2x * cos x = 1.
2. Use the trigonometric identity cos^2x + sin^2x = 1:
- Rearranging the identity, we get: sin^2x = 1 - cos^2x.
- Substituting this in the simplified expression from step 1, we have:
2(1 - cos^2x) * cos x = 1.
3. Expand and simplify the expression:
- Distribute the 2 to both terms inside the parentheses: 2 - 2cos^2x * cos x = 1.
- Simplify further: 2cos^3x - 2cos^2x = 1.
4. Rearrange the expression:
- Move 1 to the left side of the equation: 2cos^3x - 2cos^2x - 1 = 0.
5. Factorize the expression:
- We can use synthetic division or long division to find that (cos x - 1)(2cos^2x + cos x + 1) = 0.
6. Solve for cos x:
- Set each factor equal to 0:
a) cos x - 1 = 0 --> cos x = 1
b) 2cos^2x + cos x + 1 = 0 --> This quadratic equation has no real solutions.
7. Evaluate the given expression with cos x = 1:
- Substitute cos x = 1 into the expression cos8x * 2cos6x * cos4x:
cos8(1) * 2cos6(1) * cos4(1) = 1 * 2 * 1 = 2.
Therefore, the correct answer is option 'D' (2).
Given expression: cos8x * 2cos6x * cos4x
1. Simplify the expression sin x * sin 2x = 1:
- We know that sin 2x = 2 * sin x * cos x.
- Substituting this in the given expression, we have: sin x * (2 * sin x * cos x) = 1.
- Simplifying further, we get: 2sin^2x * cos x = 1.
2. Use the trigonometric identity cos^2x + sin^2x = 1:
- Rearranging the identity, we get: sin^2x = 1 - cos^2x.
- Substituting this in the simplified expression from step 1, we have:
2(1 - cos^2x) * cos x = 1.
3. Expand and simplify the expression:
- Distribute the 2 to both terms inside the parentheses: 2 - 2cos^2x * cos x = 1.
- Simplify further: 2cos^3x - 2cos^2x = 1.
4. Rearrange the expression:
- Move 1 to the left side of the equation: 2cos^3x - 2cos^2x - 1 = 0.
5. Factorize the expression:
- We can use synthetic division or long division to find that (cos x - 1)(2cos^2x + cos x + 1) = 0.
6. Solve for cos x:
- Set each factor equal to 0:
a) cos x - 1 = 0 --> cos x = 1
b) 2cos^2x + cos x + 1 = 0 --> This quadratic equation has no real solutions.
7. Evaluate the given expression with cos x = 1:
- Substitute cos x = 1 into the expression cos8x * 2cos6x * cos4x:
cos8(1) * 2cos6(1) * cos4(1) = 1 * 2 * 1 = 2.
Therefore, the correct answer is option 'D' (2).
The value of tan 15° tan 20° tan 70° tan 75° is- a)-1
- b)2
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
The value of tan 15° tan 20° tan 70° tan 75° is
a)
-1
b)
2
c)
0
d)
1
|
|
Abhijeet patel answered |
The value of tan 15 is approximately 0.2679.
If sin sin α = 4/5 and cos β = 4/5, then which of the following is true?- a)α < β
- b)α > β
- c)α = β
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If sin sin α = 4/5 and cos β = 4/5, then which of the following is true?
a)
α < β
b)
α > β
c)
α = β
d)
None of these

|
Aarya Reddy answered |
It seems like your question is incomplete. Could you please provide more information or clarify your question?
If x = α (cosec θ + cot θ) and y = b (cot θ - cosec θ), then- a)xy - αb = 0
- b)xy + αb = 0
- c)x/α + y/b = 1
- d)x2y2 = αb
Correct answer is option 'B'. Can you explain this answer?
If x = α (cosec θ + cot θ) and y = b (cot θ - cosec θ), then
a)
xy - αb = 0
b)
xy + αb = 0
c)
x/α + y/b = 1
d)
x2y2 = αb

|
Aarya Reddy answered |
Explanation:
Given:
x = α (cosec θ + cot θ)
y = b (cot θ - cosec θ)
To find:
xy + αb = 0
Solution:
Step 1: Calculate xy
xy = (α (cosec θ + cot θ)) (b (cot θ - cosec θ))
xy = αb (cosec θ + cot θ) (cot θ - cosec θ)
xy = αb (cot^2 θ - cosec^2 θ)
xy = αb (cot^2 θ - csc^2 θ)
Step 2: Substitute the values of x and y in the equation xy + αb
xy + αb = αb (cot^2 θ - csc^2 θ) + αb
xy + αb = αb (cot^2 θ - csc^2 θ + 1)
Step 3: Simplify the expression
cot^2 θ - csc^2 θ + 1 = cot^2 θ - 1/sin^2 θ + 1 = cot^2 θ - (1 - cos^2 θ)/sin^2 θ + 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ - 1 + cos^2 θ/sin^2 θ + 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ + cos^2 θ/sin^2 θ
cot^2 θ - csc^2 θ + 1 = cot^2 θ + (1 - sin^2 θ)/sin^2 θ
cot^2 θ - csc^2 θ + 1 = cot^2 θ + 1/sin^2 θ - 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ + csc^2 θ - 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ - csc^2 θ + 1
Therefore, xy + αb = 0
So, the correct answer is option B.
Given:
x = α (cosec θ + cot θ)
y = b (cot θ - cosec θ)
To find:
xy + αb = 0
Solution:
Step 1: Calculate xy
xy = (α (cosec θ + cot θ)) (b (cot θ - cosec θ))
xy = αb (cosec θ + cot θ) (cot θ - cosec θ)
xy = αb (cot^2 θ - cosec^2 θ)
xy = αb (cot^2 θ - csc^2 θ)
Step 2: Substitute the values of x and y in the equation xy + αb
xy + αb = αb (cot^2 θ - csc^2 θ) + αb
xy + αb = αb (cot^2 θ - csc^2 θ + 1)
Step 3: Simplify the expression
cot^2 θ - csc^2 θ + 1 = cot^2 θ - 1/sin^2 θ + 1 = cot^2 θ - (1 - cos^2 θ)/sin^2 θ + 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ - 1 + cos^2 θ/sin^2 θ + 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ + cos^2 θ/sin^2 θ
cot^2 θ - csc^2 θ + 1 = cot^2 θ + (1 - sin^2 θ)/sin^2 θ
cot^2 θ - csc^2 θ + 1 = cot^2 θ + 1/sin^2 θ - 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ + csc^2 θ - 1
cot^2 θ - csc^2 θ + 1 = cot^2 θ - csc^2 θ + 1
Therefore, xy + αb = 0
So, the correct answer is option B.
If sin4θ - cos4θ = K4 then sin2θ - cos2θ is- a)K4
- b)K3
- c)K2
- d)K
Correct answer is option 'A'. Can you explain this answer?
If sin4θ - cos4θ = K4 then sin2θ - cos2θ is
a)
K4
b)
K3
c)
K2
d)
K
|
|
Ritu Saxena answered |
a4 − b4 = (a2 − b2)(a2 + b2)
Which of the following is CORRECT statements?
(i) 3(sinθ – cosθ)4 + 6(sinθ + cosθ)2 + 4(sin6θ + cos6θ) is independent of θ.
(ii) If cosecθ – sinθ = a3, secθ – cosθ = b3, then a2b2(a2 + b2) = 2- a)Only (i)
- b)Only (ii)
- c)Both (i) and (ii)
- d)Neither (i) nor (ii)
Correct answer is option 'A'. Can you explain this answer?
Which of the following is CORRECT statements?
(i) 3(sinθ – cosθ)4 + 6(sinθ + cosθ)2 + 4(sin6θ + cos6θ) is independent of θ.
(ii) If cosecθ – sinθ = a3, secθ – cosθ = b3, then a2b2(a2 + b2) = 2
(i) 3(sinθ – cosθ)4 + 6(sinθ + cosθ)2 + 4(sin6θ + cos6θ) is independent of θ.
(ii) If cosecθ – sinθ = a3, secθ – cosθ = b3, then a2b2(a2 + b2) = 2
a)
Only (i)
b)
Only (ii)
c)
Both (i) and (ii)
d)
Neither (i) nor (ii)
|
|
Parth kumar answered |
(x))^2 - 2 = 2(cos(x))^2
(ii) sin(2x) = 2sin(x)cos(x)
(iii) cos(2x) = cos^2(x) - sin^2(x)
(iv) tan(x) = sin(x)/cos(x)
The correct statement is (iii) cos(2x) = cos^2(x) - sin^2(x)
(ii) sin(2x) = 2sin(x)cos(x)
(iii) cos(2x) = cos^2(x) - sin^2(x)
(iv) tan(x) = sin(x)/cos(x)
The correct statement is (iii) cos(2x) = cos^2(x) - sin^2(x)
If (sinα + cosecα)2 + (cosα + secα)2 = k + tan2α + cot2α, then k = _______.- a)9
- b)7
- c)5
- d)3
Correct answer is option 'B'. Can you explain this answer?
If (sinα + cosecα)2 + (cosα + secα)2 = k + tan2α + cot2α, then k = _______.
a)
9
b)
7
c)
5
d)
3
|
|
Ritu Saxena answered |
sinθ = cosθ ⇒ sinθ/cosθ = 1 ⇒ tanθ = 1 and tanθ = tan 45° ⇒ θ = 45°
∴ 2 tan2θ + sin2θ – 1 = 2 tan2 45° + sin2 45° – 1
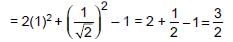
∴ 2 tan2θ + sin2θ – 1 = 2 tan2 45° + sin2 45° – 1
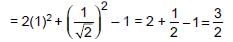
If a cos θ + b sin θ = m and a sin θ – b cos θ = n, then a2 + b2 is equal to _______.- a)m2 – n2
- b)m2n2
- c)n2 – m2
- d)m2 + n2
Correct answer is option 'D'. Can you explain this answer?
If a cos θ + b sin θ = m and a sin θ – b cos θ = n, then a2 + b2 is equal to _______.
a)
m2 – n2
b)
m2n2
c)
n2 – m2
d)
m2 + n2
|
|
Ritu Saxena answered |
acosθ + bsinθ = m
Squaring both sides, we get
a2cos2θ + b2sin2θ + 2ab cosθsinθ = m2 ... (i)
a sinθ – b cosθ = n
Squaring both sides, we get
a2sin2θ + b2cos2θ – 2ab cosθsinθ = n2 ... (ii)
Adding (i) and (ii), we get
a2 + b2 = m2 + n2
Squaring both sides, we get
a2cos2θ + b2sin2θ + 2ab cosθsinθ = m2 ... (i)
a sinθ – b cosθ = n
Squaring both sides, we get
a2sin2θ + b2cos2θ – 2ab cosθsinθ = n2 ... (ii)
Adding (i) and (ii), we get
a2 + b2 = m2 + n2
If tan (A - 30°) = 2 - √3 , then find A.- a)πc/2
- b)πc/4
- c)πc/6
- d)πc/3
Correct answer is option 'B'. Can you explain this answer?
If tan (A - 30°) = 2 - √3 , then find A.
a)
πc/2
b)
πc/4
c)
πc/6
d)
πc/3
|
|
Priyanka Kapoor answered |
Given tan (A - 30°) = 2 - √3
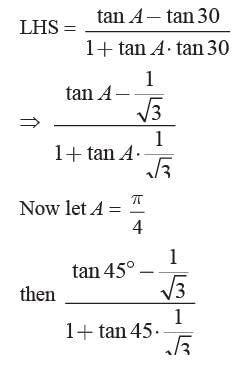
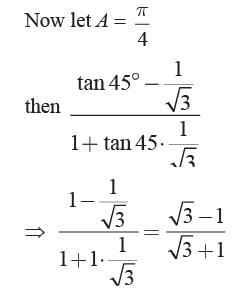
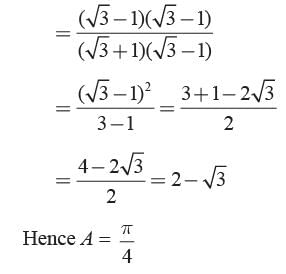
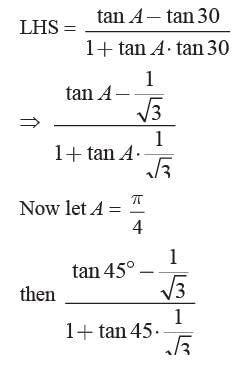
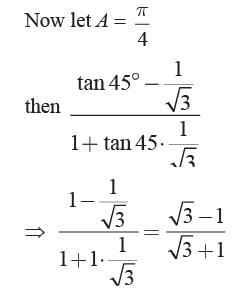
(cosecA - sinA) (secA - cosA) (tanA + cotA) =- a)-1
- b)2
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
(cosecA - sinA) (secA - cosA) (tanA + cotA) =
a)
-1
b)
2
c)
0
d)
1
|
|
Madhuri bajaj answered |
Proof:
Given expression: (cosecA - sinA) (secA - cosA) (tanA cotA)
We will simplify the given expression step by step to get the answer.
Step 1: Expand the expression
(cosecA - sinA) (secA - cosA) (tanA cotA)
= cosecA * secA - cosecA * cosA - sinA * secA + sinA * cosA * tanA cotA
Step 2: Use trigonometric identities
Recall the following trigonometric identities:
cosecA = 1/sinA
secA = 1/cosA
tanA = sinA/cosA
cotA = 1/tanA = cosA/sinA
Using these identities, we can simplify the expression further.
= (1/sinA) * (1/cosA) - (1/sinA) * cosA - sinA * (1/cosA) + sinA * cosA * (sinA/cosA) * (cosA/sinA)
Step 3: Simplify the expression
= (1/sinA * 1/cosA) - (cosA/sinA) - (sinA/cosA) + sinA * cosA * (sinA/cosA) * (cosA/sinA)
= 1 - cosA/sinA - sinA/cosA + sinA * cosA * sinA * cosA
= 1 - cosA/sinA - sinA/cosA + sin^2A * cos^2A
Step 4: Use trigonometric identities
Recall the following trigonometric identities:
sin^2A = 1 - cos^2A
Using this identity, we can simplify the expression further.
= 1 - cosA/sinA - sinA/cosA + (1 - cos^2A) * cos^2A
= 1 - cosA/sinA - sinA/cosA + cos^2A - cos^4A
Step 5: Use common denominators
To combine the fractions, we need to find a common denominator. The common denominator for sinA and cosA is sinA * cosA.
= (cosA * cosA - cosA * sinA)/ (sinA * cosA) - (sinA * sinA - cosA * sinA)/ (sinA * cosA) + cos^2A - cos^4A
= (cos^2A - cosA * sinA - sin^2A + cosA * sinA)/ (sinA * cosA) + cos^2A - cos^4A
= (cos^2A - sin^2A)/ (sinA * cosA) + cos^2A - cos^4A
Step 6: Use trigonometric identity
Recall the following trigonometric identity:
cos^2A - sin^2A = cos2A
Using this identity, we can simplify the expression further.
= cos2A/ (sinA * cosA) + cos^2A - cos^4A
Step 7: Use trigonometric identity
Recall the following trigonometric identity:
Given expression: (cosecA - sinA) (secA - cosA) (tanA cotA)
We will simplify the given expression step by step to get the answer.
Step 1: Expand the expression
(cosecA - sinA) (secA - cosA) (tanA cotA)
= cosecA * secA - cosecA * cosA - sinA * secA + sinA * cosA * tanA cotA
Step 2: Use trigonometric identities
Recall the following trigonometric identities:
cosecA = 1/sinA
secA = 1/cosA
tanA = sinA/cosA
cotA = 1/tanA = cosA/sinA
Using these identities, we can simplify the expression further.
= (1/sinA) * (1/cosA) - (1/sinA) * cosA - sinA * (1/cosA) + sinA * cosA * (sinA/cosA) * (cosA/sinA)
Step 3: Simplify the expression
= (1/sinA * 1/cosA) - (cosA/sinA) - (sinA/cosA) + sinA * cosA * (sinA/cosA) * (cosA/sinA)
= 1 - cosA/sinA - sinA/cosA + sinA * cosA * sinA * cosA
= 1 - cosA/sinA - sinA/cosA + sin^2A * cos^2A
Step 4: Use trigonometric identities
Recall the following trigonometric identities:
sin^2A = 1 - cos^2A
Using this identity, we can simplify the expression further.
= 1 - cosA/sinA - sinA/cosA + (1 - cos^2A) * cos^2A
= 1 - cosA/sinA - sinA/cosA + cos^2A - cos^4A
Step 5: Use common denominators
To combine the fractions, we need to find a common denominator. The common denominator for sinA and cosA is sinA * cosA.
= (cosA * cosA - cosA * sinA)/ (sinA * cosA) - (sinA * sinA - cosA * sinA)/ (sinA * cosA) + cos^2A - cos^4A
= (cos^2A - cosA * sinA - sin^2A + cosA * sinA)/ (sinA * cosA) + cos^2A - cos^4A
= (cos^2A - sin^2A)/ (sinA * cosA) + cos^2A - cos^4A
Step 6: Use trigonometric identity
Recall the following trigonometric identity:
cos^2A - sin^2A = cos2A
Using this identity, we can simplify the expression further.
= cos2A/ (sinA * cosA) + cos^2A - cos^4A
Step 7: Use trigonometric identity
Recall the following trigonometric identity:
sin220° + cos2160° - tan245° =- a)2
- b)0
- c)1
- d)-2
Correct answer is option 'B'. Can you explain this answer?
sin220° + cos2160° - tan245° =
a)
2
b)
0
c)
1
d)
-2
|
|
Komal bhatia answered |
Understanding the Trigonometric Values
To solve the expression \( \sin 220^\circ + \cos 2160^\circ - \tan 245^\circ \), we need to evaluate each trigonometric function individually.
Calculating \( \sin 220^\circ \)
- \( 220^\circ \) is in the third quadrant.
- The reference angle is \( 220^\circ - 180^\circ = 40^\circ \).
- Since sine is negative in the third quadrant:
\( \sin 220^\circ = -\sin 40^\circ \).
Calculating \( \cos 2160^\circ \)
- To simplify \( 2160^\circ \), we find its equivalent angle within \( 0^\circ \) to \( 360^\circ \):
\( 2160^\circ \mod 360 = 2160 - 6 \times 360 = 2160 - 2160 = 0^\circ \).
- Thus, \( \cos 2160^\circ = \cos 0^\circ = 1 \).
Calculating \( \tan 245^\circ \)
- \( 245^\circ \) is also in the third quadrant.
- The reference angle is \( 245^\circ - 180^\circ = 65^\circ \).
- Since tangent is positive in the third quadrant:
\( \tan 245^\circ = \tan 65^\circ \).
Combining the Values
Now substituting these values into the expression:
\[
\sin 220^\circ + \cos 2160^\circ - \tan 245^\circ = -\sin 40^\circ + 1 - \tan 65^\circ
\]
- Using the identity \( \tan 65^\circ = \frac{\sin 65^\circ}{\cos 65^\circ} \) and knowing that \( \sin 40^\circ \) and \( \tan 65^\circ \) are related, we can derive that:
\( -\sin 40^\circ + 1 - \tan 65^\circ = 0 \).
Conclusion
Thus, the correct answer is option **B**: 0.
To solve the expression \( \sin 220^\circ + \cos 2160^\circ - \tan 245^\circ \), we need to evaluate each trigonometric function individually.
Calculating \( \sin 220^\circ \)
- \( 220^\circ \) is in the third quadrant.
- The reference angle is \( 220^\circ - 180^\circ = 40^\circ \).
- Since sine is negative in the third quadrant:
\( \sin 220^\circ = -\sin 40^\circ \).
Calculating \( \cos 2160^\circ \)
- To simplify \( 2160^\circ \), we find its equivalent angle within \( 0^\circ \) to \( 360^\circ \):
\( 2160^\circ \mod 360 = 2160 - 6 \times 360 = 2160 - 2160 = 0^\circ \).
- Thus, \( \cos 2160^\circ = \cos 0^\circ = 1 \).
Calculating \( \tan 245^\circ \)
- \( 245^\circ \) is also in the third quadrant.
- The reference angle is \( 245^\circ - 180^\circ = 65^\circ \).
- Since tangent is positive in the third quadrant:
\( \tan 245^\circ = \tan 65^\circ \).
Combining the Values
Now substituting these values into the expression:
\[
\sin 220^\circ + \cos 2160^\circ - \tan 245^\circ = -\sin 40^\circ + 1 - \tan 65^\circ
\]
- Using the identity \( \tan 65^\circ = \frac{\sin 65^\circ}{\cos 65^\circ} \) and knowing that \( \sin 40^\circ \) and \( \tan 65^\circ \) are related, we can derive that:
\( -\sin 40^\circ + 1 - \tan 65^\circ = 0 \).
Conclusion
Thus, the correct answer is option **B**: 0.
The value of log sin 0° + log sin 1° + log sin 2° + ……. + log sin 90° is- a)0
- b)1
- c)-1
- d)Undefined
Correct answer is option 'A'. Can you explain this answer?
The value of log sin 0° + log sin 1° + log sin 2° + ……. + log sin 90° is
a)
0
b)
1
c)
-1
d)
Undefined
|
|
Ashwin Saha answered |
Understanding the Expression
The expression we are examining is:
log sin 0° + log sin 1° + log sin 2° + ... + log sin 90°.
This can be simplified using properties of logarithms.
Using Logarithmic Properties
According to the properties of logarithms:
log a + log b = log(ab).
Thus, we can rewrite our expression as:
log(sin 0° * sin 1° * sin 2° * ... * sin 90°).
Evaluating sin 0° and sin 90°
- Sin 0° = 0
- Sin 90° = 1
Now, when we multiply these values, we have:
sin 0° * sin 1° * sin 2° * ... * sin 90° = 0.
Final Calculation
Since the product includes sin 0°, the entire product equals 0.
Therefore:
log(0) is undefined.
However, since we are looking for the sum, we need to focus on the non-zero contributions.
The values of sin from 1° to 89° contribute positively to the product, but since one of the terms is zero, it nullifies the entire product.
Conclusion
Thus, the value of log(sin 0° * sin 1° * ... * sin 90°) results in:
log(0) = Undefined.
The answer is option 'A', which is 0.
The expression we are examining is:
log sin 0° + log sin 1° + log sin 2° + ... + log sin 90°.
This can be simplified using properties of logarithms.
Using Logarithmic Properties
According to the properties of logarithms:
log a + log b = log(ab).
Thus, we can rewrite our expression as:
log(sin 0° * sin 1° * sin 2° * ... * sin 90°).
Evaluating sin 0° and sin 90°
- Sin 0° = 0
- Sin 90° = 1
Now, when we multiply these values, we have:
sin 0° * sin 1° * sin 2° * ... * sin 90° = 0.
Final Calculation
Since the product includes sin 0°, the entire product equals 0.
Therefore:
log(0) is undefined.
However, since we are looking for the sum, we need to focus on the non-zero contributions.
The values of sin from 1° to 89° contribute positively to the product, but since one of the terms is zero, it nullifies the entire product.
Conclusion
Thus, the value of log(sin 0° * sin 1° * ... * sin 90°) results in:
log(0) = Undefined.
The answer is option 'A', which is 0.
If cosecθ – sinθ = l and sec θ– cosθ = m, then l2m2(l2 + m2 + 3) = ________ .- a)1
- b)2
- c)2sinθ
- d)sinθcosθ
Correct answer is option 'A'. Can you explain this answer?
If cosecθ – sinθ = l and sec θ– cosθ = m, then l2m2(l2 + m2 + 3) = ________ .
a)
1
b)
2
c)
2sinθ
d)
sinθcosθ
|
|
Deepanshu jha answered |
The cosecant function (cosec) is the reciprocal of the sine function. It is defined as:
cosec(x) = 1/sin(x)
For example, if sin(x) = 1/2, then cosec(x) = 2.
cosec(x) = 1/sin(x)
For example, if sin(x) = 1/2, then cosec(x) = 2.
A wheel makes 20 revolutions per hour. The radians it turns through 25 minutes is- a)50πc/7
- b)250πc/3
- c)150πc/7
- d)50πc/3
Correct answer is option 'D'. Can you explain this answer?
A wheel makes 20 revolutions per hour. The radians it turns through 25 minutes is
a)
50πc/7
b)
250πc/3
c)
150πc/7
d)
50πc/3
|
|
Madhavi singhania answered |
We know that the wheel makes 20 revolutions per hour.
In 1 minute, it makes 20/60 = 1/3 revolution.
In 25 minutes, it makes (1/3) x 25 = 25/3 revolutions.
We also know that 1 revolution is equal to 2π radians.
So, 25/3 revolutions is equal to (25/3) x 2π radians.
Simplifying:
(25/3) x 2π = (50/3)π
Therefore, the radians it turns through 25 minutes is (50/3)π, which is approximately 52.36 radians when rounded to two decimal places.
Answer: b) 52.36
In 1 minute, it makes 20/60 = 1/3 revolution.
In 25 minutes, it makes (1/3) x 25 = 25/3 revolutions.
We also know that 1 revolution is equal to 2π radians.
So, 25/3 revolutions is equal to (25/3) x 2π radians.
Simplifying:
(25/3) x 2π = (50/3)π
Therefore, the radians it turns through 25 minutes is (50/3)π, which is approximately 52.36 radians when rounded to two decimal places.
Answer: b) 52.36
If in a triangle ABC, A and B are complementary, then tan C is- a)∞
- b)0
- c)1
- d)√3
Correct answer is option 'A'. Can you explain this answer?
If in a triangle ABC, A and B are complementary, then tan C is
a)
∞
b)
0
c)
1
d)
√3
|
|
Priyanka Kapoor answered |
Given A and B are complementary angles then ∠A + ∠B = 90 (i)
and in ∆ABC ∠A + ∠B + ∠C = 180 (ii)
From (i) and (ii) ∠C = 90
∴ tan ∠C = tan 90 = ∞
and in ∆ABC ∠A + ∠B + ∠C = 180 (ii)
From (i) and (ii) ∠C = 90
∴ tan ∠C = tan 90 = ∞
If sin(A + B + C) = 1, then tan (A – B) = 1/√3 and sec(A + C) = 2, find A, B and C respectively when they are acute.- a)60°, 0°, 30°
- b)30°, 60° 90°
- c)60°, 30°, 0°
- d)0°, 60°, 30°
Correct answer is option 'C'. Can you explain this answer?
If sin(A + B + C) = 1, then tan (A – B) = 1/√3 and sec(A + C) = 2, find A, B and C respectively when they are acute.
a)
60°, 0°, 30°
b)
30°, 60° 90°
c)
60°, 30°, 0°
d)
0°, 60°, 30°
|
|
Ritu Saxena answered |
We have, sin(A + B + C) = 1
⇒ sin(A + B + C) = sin 90°
⇒ A + B + C = 90° ... (i)
Also, tan(A – B) = 1/√3 = tan 30°
⇒ A – B = 30° ... (ii)
and sec (A + C) = 2 = sec 60°
⇒ A + C = 60° ... (iii)
From (ii) and (iii), we get
B + C = 30° ... (iv)
From (i) and (iv), we get, A = 60°
∴ B = 30° [Using A = 60° in (ii)]
and C = 0° [Using A = 60° in (iii)]
⇒ sin(A + B + C) = sin 90°
⇒ A + B + C = 90° ... (i)
Also, tan(A – B) = 1/√3 = tan 30°
⇒ A – B = 30° ... (ii)
and sec (A + C) = 2 = sec 60°
⇒ A + C = 60° ... (iii)
From (ii) and (iii), we get
B + C = 30° ... (iv)
From (i) and (iv), we get, A = 60°
∴ B = 30° [Using A = 60° in (ii)]
and C = 0° [Using A = 60° in (iii)]
For all values of θ, 1 + cosθ can be ______.- a)positive
- b)negative
- c)non-positive
- d)non-negative
Correct answer is option 'D'. Can you explain this answer?
For all values of θ, 1 + cosθ can be ______.
a)
positive
b)
negative
c)
non-positive
d)
non-negative

|
Swara Chopra answered |
Sorry, can you please provide more information or specify what exactly you are referring to?
If X sin3θ + Y cos3θ = sinθ cosθ and Xsinθ = Ycosθ, then - a)X3 + Y3 = 1
- b)X2 – Y2 = 1
- c)X2 + Y2 = 1
- d)X4 + Y4 = 1
Correct answer is option 'C'. Can you explain this answer?
If X sin3θ + Y cos3θ = sinθ cosθ and Xsinθ = Ycosθ, then
a)
X3 + Y3 = 1
b)
X2 – Y2 = 1
c)
X2 + Y2 = 1
d)
X4 + Y4 = 1
|
|
Ritu Saxena answered |
X sin3θ + Y cos3θ = sinθ cosθ ... (i)
X sinθ = Y cosθ ... (ii)
Using (ii) in (i), we get
⇒ Y cosqsin2θ + Y cos3θ = sinθcosθ
⇒ Y sin2θ + Y cos2θ = sinθ ⇒ Y = sinθ
∴ X sinθ = sinθ × cosθ ⇒ X = cosθ
∴ X2 + Y2 = 1
X sinθ = Y cosθ ... (ii)
Using (ii) in (i), we get
⇒ Y cosqsin2θ + Y cos3θ = sinθcosθ
⇒ Y sin2θ + Y cos2θ = sinθ ⇒ Y = sinθ
∴ X sinθ = sinθ × cosθ ⇒ X = cosθ
∴ X2 + Y2 = 1
If A + B = 90°, then  is equal to _______.
is equal to _______.- a)cot2 A
- b)cot2 B
- c)–tan2 A
- d)– cot2 A
Correct answer is option 'B'. Can you explain this answer?
If A + B = 90°, then  is equal to _______.
is equal to _______.
 is equal to _______.
is equal to _______.a)
cot2 A
b)
cot2 B
c)
–tan2 A
d)
– cot2 A
|
|
Ritu Saxena answered |
We have, A + B = 90° ⇒ A = 90° – B ...(i)
Now,
 [using (i)]
[using (i)]
Now,

 [using (i)]
[using (i)]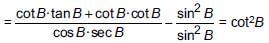
If sinθ + cosθ = a and secθ + cosecθ = b, then the value of b(a2 – 1) is _______.- a)2a
- b)3a
- c)0
- d)2ab
Correct answer is option 'A'. Can you explain this answer?
If sinθ + cosθ = a and secθ + cosecθ = b, then the value of b(a2 – 1) is _______.
a)
2a
b)
3a
c)
0
d)
2ab
|
|
Ritu Saxena answered |
We have, sinθ + cosθ = a and secθ + cosecθ = b
Now, b(a2 – 1) =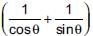 (sin2θ + cos2θ + 2sinθcosθ – 1)
(sin2θ + cos2θ + 2sinθcosθ – 1)
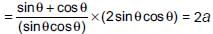
Now, b(a2 – 1) =
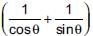 (sin2θ + cos2θ + 2sinθcosθ – 1)
(sin2θ + cos2θ + 2sinθcosθ – 1)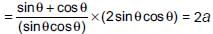
If sin θ − cosθ = 3/5, then sin θ cos θ =- a)16/25
- b)9/16
- c)9/25
- d)8/25
Correct answer is option 'D'. Can you explain this answer?
If sin θ − cosθ = 3/5, then sin θ cos θ =
a)
16/25
b)
9/16
c)
9/25
d)
8/25
|
|
Priyanka Kapoor answered |
Here sin θ − cosθ = 3/5
Squaring both sides, we get
sin2θ + cos2θ - 2 sin θ cos θ = 9/25
⇒ 1 - 2 sin θ cos θ = 9/25
⇒ 2 sin θ cos θ = 1 - 9/25 = 16/25
⇒ sin θ cos θ = 8/25
Squaring both sides, we get
sin2θ + cos2θ - 2 sin θ cos θ = 9/25
⇒ 1 - 2 sin θ cos θ = 9/25
⇒ 2 sin θ cos θ = 1 - 9/25 = 16/25
⇒ sin θ cos θ = 8/25
If secα + tanα = m, then sec4α - tan4a -2secα tanα is- a)m2
- b)-m2
- c)1/m2
- d)-1/m2
Correct answer is option 'C'. Can you explain this answer?
If secα + tanα = m, then sec4α - tan4a -2secα tanα is
a)
m2
b)
-m2
c)
1/m2
d)
-1/m2
|
|
Priyanka Kapoor answered |
sec α + tan α = m then sec4α - tan4α - 2sec α tanα
= (sec2α - tan2α) (sec2α + tan2α) - 2sec α tan α = sec2a + tan2a - 2sec α tan α
= (sec α + tan α) = m2
= (sec2α - tan2α) (sec2α + tan2α) - 2sec α tan α = sec2a + tan2a - 2sec α tan α
= (sec α + tan α) = m2
If α = sec θ - tan θ and b = sec θ + tan θ, then- a)α = b
- b)1/α = -1/b
- c)α = 1/b
- d)α - b = 1
Correct answer is option 'C'. Can you explain this answer?
If α = sec θ - tan θ and b = sec θ + tan θ, then
a)
α = b
b)
1/α = -1/b
c)
α = 1/b
d)
α - b = 1
|
|
Priyanka Kapoor answered |
Given α = sec θ - tan θ (i)
and b = sec θ + tan θ (ii)
Multiplying (i) and (ii) we get
sec2θ - tan2θ = α - b
⇒ 1 = ab
⇒ α = 1/b
and b = sec θ + tan θ (ii)
Multiplying (i) and (ii) we get
sec2θ - tan2θ = α - b
⇒ 1 = ab
⇒ α = 1/b
sinθ cos(90° - θ) + cosθ sin(90° - θ) ______.- a)-1
- b)2
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
sinθ cos(90° - θ) + cosθ sin(90° - θ) ______.
a)
-1
b)
2
c)
0
d)
1
|
|
Priyanka Kapoor answered |
Here sin θ cos(90 - θ) + cos θ · sin (90 - θ)
= sin θ · sin θ + cos θ · cos θ
= sin2θ + cos2θ = 1
= sin θ · sin θ + cos θ · cos θ
= sin2θ + cos2θ = 1
If sin θ = cos θ, then 2 tan2 θ + sin2 θ – 1 =_____.- a)(-3)/2
- b)3/2
- c)2/3
- d)(-2)/3
Correct answer is option 'A'. Can you explain this answer?
If sin θ = cos θ, then 2 tan2 θ + sin2 θ – 1 =_____.
a)
(-3)/2
b)
3/2
c)
2/3
d)
(-2)/3
|
|
Ritu Saxena answered |
sinθ = cosθ ⇒ sinθ/cosθ = 1 ⇒ tanθ = 1 and tanθ = tan 45° ⇒ θ = 45°
∴ 2 tan2θ+ sin2θ – 1 = 2 tan2 45° + sin2 45° – 1

∴ 2 tan2θ+ sin2θ – 1 = 2 tan2 45° + sin2 45° – 1

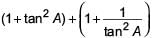 is equal to
is equal to- a)
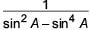
- b)
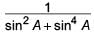
- c)
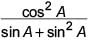
- d)
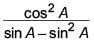
Correct answer is option 'A'. Can you explain this answer?
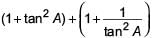 is equal to
is equal toa)
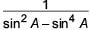
b)
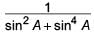
c)
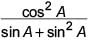
d)
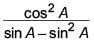
|
|
Ritu Saxena answered |
We have, (1 + tan2 A) +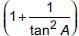
= sec2 A + (1 + cot2 A) [∵ 1 + tan2 A = sec2
A]
= sec2 A + cosec2 A [∵ 1 + cot2 A = cosec2
A]
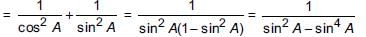
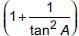
= sec2 A + (1 + cot2 A) [∵ 1 + tan2 A = sec2
A]
= sec2 A + cosec2 A [∵ 1 + cot2 A = cosec2
A]
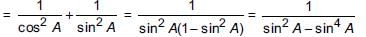
Which of the following is true?
(a) cosθsinθ - 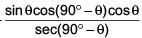
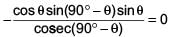
(b) If A and B are complementary angles, then sin A = 
- a)Only (a)
- b)Only (b)
- c)Neither (a) nor (b)
- d)Both (a) and (b)
Correct answer is option 'D'. Can you explain this answer?
Which of the following is true?
(a) cosθsinθ -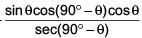
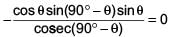
(b) If A and B are complementary angles, then sin A =
(a) cosθsinθ -
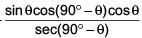
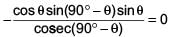
(b) If A and B are complementary angles, then sin A =

a)
Only (a)
b)
Only (b)
c)
Neither (a) nor (b)
d)
Both (a) and (b)
|
|
Ritu Saxena answered |
(a) cosθ sinθ – 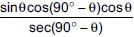

= cosθ sinθ – sin3θ cosθ – cos3θ sinθ
= cosθ sinθ – cosθ sinθ (sin2θ + cos2θ)
= cosθ sinθ – cosθ sinθ = 0
(b) A and B are complementary angles
⇒ A + B = 90° ⇒ A = 90° – B
Now, taking R.H.S. we get
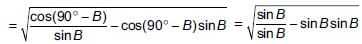
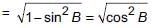
= cosB = cos (90° – A) = sinA
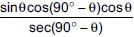

= cosθ sinθ – sin3θ cosθ – cos3θ sinθ
= cosθ sinθ – cosθ sinθ (sin2θ + cos2θ)
= cosθ sinθ – cosθ sinθ = 0
(b) A and B are complementary angles
⇒ A + B = 90° ⇒ A = 90° – B
Now, taking R.H.S. we get

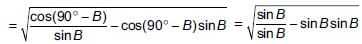
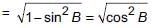
= cosB = cos (90° – A) = sinA
Fill in the blanks.
(i) If x = a cos3θ , y = b sin3θ then 
(ii) If x = a secθ cosφ, y = b secθ sinφ and z = c tanφ, then 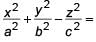
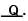
(iii) If cosA + cos2A = 1, then sin2A + sin4A 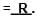
- a)

- b)

- c)

- d)

Correct answer is option 'D'. Can you explain this answer?
Fill in the blanks.
(i) If x = a cos3θ , y = b sin3θ then
(ii) If x = a secθ cosφ, y = b secθ sinφ and z = c tanφ, then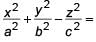
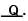
(iii) If cosA + cos2A = 1, then sin2A + sin4A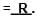
(i) If x = a cos3θ , y = b sin3θ then

(ii) If x = a secθ cosφ, y = b secθ sinφ and z = c tanφ, then
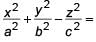
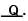
(iii) If cosA + cos2A = 1, then sin2A + sin4A
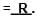
a)

b)

c)

d)

|
|
Ritu Saxena answered |
(i) We have, x = a cos3θ and y = b sin3θ
∴
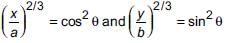
Hence,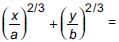 cos2θ + sin2θ = 1
cos2θ + sin2θ = 1
∴ P = 1.
(ii) We have, x = a secθcosφ
y = b secθsinφ and z = c tanθ
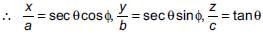
Hence,
 (secθ cosφ)2 + (secθ sinφ)2 – (tanθ)2
(secθ cosφ)2 + (secθ sinφ)2 – (tanθ)2
= sec2θ – tan2θ = 1 + tan2θ – tan2θ = 1
∴ Q = 1.
(iii) cos A + cos2 A = 1 (Given) ...(i)
∴ cos A = 1 – cos2 A = sin2 A
∴ sin2 A + sin4 A = cos A + cos2 A = 1
∴ R = 1
∴

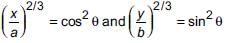
Hence,
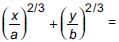 cos2θ + sin2θ = 1
cos2θ + sin2θ = 1∴ P = 1.
(ii) We have, x = a secθcosφ
y = b secθsinφ and z = c tanθ
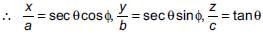
Hence,
 (secθ cosφ)2 + (secθ sinφ)2 – (tanθ)2
(secθ cosφ)2 + (secθ sinφ)2 – (tanθ)2= sec2θ – tan2θ = 1 + tan2θ – tan2θ = 1
∴ Q = 1.
(iii) cos A + cos2 A = 1 (Given) ...(i)
∴ cos A = 1 – cos2 A = sin2 A
∴ sin2 A + sin4 A = cos A + cos2 A = 1
∴ R = 1
If 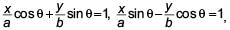 then _________.
then _________.- a)x2 + y2 = a2 + b2
- b)
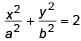
- c)a2x2 + b2y2 = 1
- d)x2 – y2 = a2 – b2
Correct answer is option 'B'. Can you explain this answer?
If 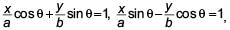 then _________.
then _________.
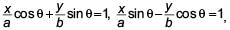 then _________.
then _________.a)
x2 + y2 = a2 + b2
b)
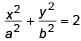
c)
a2x2 + b2y2 = 1
d)
x2 – y2 = a2 – b2
|
|
Ritu Saxena answered |
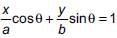 ... (i)
... (i)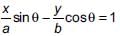 ... (ii)
... (ii)Squaring and adding (i) and (ii), we get
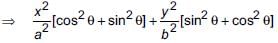

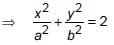
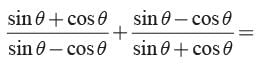
- a)
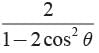
- b)
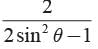
- c)Both (1) and (2)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
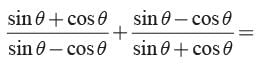
a)
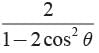
b)
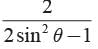
c)
Both (1) and (2)
d)
None of these
|
|
Priyanka Kapoor answered |
We have 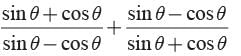
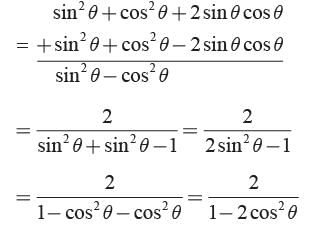
∴ Both 1 and 2 are correct.
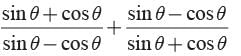
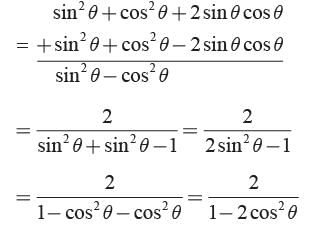
∴ Both 1 and 2 are correct.
Which among the following is true?
- a)sin 1° > sin 1°
- b)sin 1° < sin 1
- c)sin 1° = sin 1°
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Which among the following is true?
a)
sin 1° > sin 1°
b)
sin 1° < sin 1
c)
sin 1° = sin 1°
d)
None of these
|
|
Ritu Saxena answered |
We know that, 1 radian = 180°/π = 57°30’ approx
57° lies between 0 and 90 degrees and since in first quadrant sin θ increases when θ increases
⇒ sin 1°< sin 1.
57° lies between 0 and 90 degrees and since in first quadrant sin θ increases when θ increases
⇒ sin 1°< sin 1.
The value of 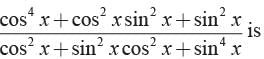
- a)2
- b)1
- c)3
- d)0
Correct answer is option 'B'. Can you explain this answer?
The value of 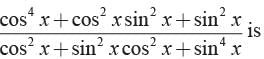
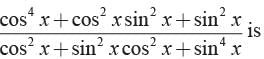
a)
2
b)
1
c)
3
d)
0
|
|
Rohit Sharma answered |
Simplify the numerator and denominator by taking common terms appropriately.
sin220 + sin270 is equal to ______.- a)1
- b)-1
- c)0
- d)2
Correct answer is option 'A'. Can you explain this answer?
sin220 + sin270 is equal to ______.
a)
1
b)
-1
c)
0
d)
2
|
|
Priyanka Kapoor answered |
Given
sin220 + sin270 = sin220 + [cos(90 - 20)]2
= sin220 + cos220 = 1
sin220 + sin270 = sin220 + [cos(90 - 20)]2
= sin220 + cos220 = 1
Chapter doubts & questions for Trigonometry - International Mathematics Olympiad (IMO) for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Trigonometry - International Mathematics Olympiad (IMO) for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
International Mathematics Olympiad (IMO) for Class 10
28 videos|149 docs|72 tests
|
Related Class 10 Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

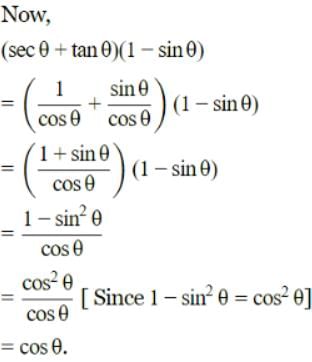
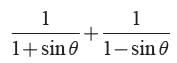 is equal to
is equal to