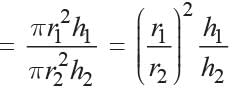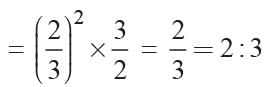All Exams >
Class 10 >
International Mathematics Olympiad (IMO) for Class 10 >
All Questions
All questions of Surface Area and Volume for Class 10 Exam
On increasing each of the radius of the base and the height of a cone by 20%. By what percent its volume will be increased?- a)72.8%
- b)60%
- c)40%
- d)30%
Correct answer is option 'A'. Can you explain this answer?
On increasing each of the radius of the base and the height of a cone by 20%. By what percent its volume will be increased?
a)
72.8%
b)
60%
c)
40%
d)
30%
|
|
Priyanka Kapoor answered |
Let the original radius be r and height be h.
Original volume = V = 1/3 πr2h
New radius = 120% of r = 120r/100 = 6r/5
New height = 120% of h = 120h/100 = 6h/5
New volume
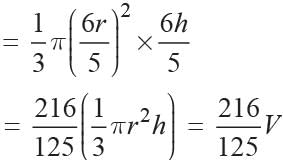
Increase in volume
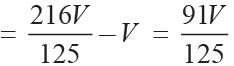
Increase %
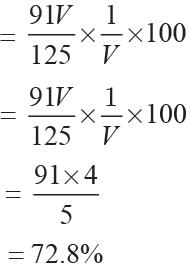
Original volume = V = 1/3 πr2h
New radius = 120% of r = 120r/100 = 6r/5
New height = 120% of h = 120h/100 = 6h/5
New volume
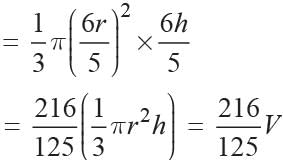
Increase in volume
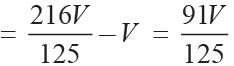
Increase %
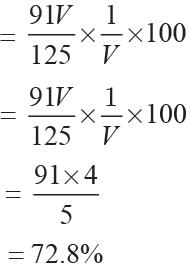
A tent is in the shape of a right circular cylinder up to a height of 3 m and then becomes a right circular cone with a maximum height of 13.5 m above the ground. Calculate the cost of painting the inner side of the tent at the rate of ₹ 2 per m2, if the radius of the base is 14 m.- a)₹ 2068
- b)₹ 2156
- c)₹ 2248
- d)₹ 1872
Correct answer is option 'A'. Can you explain this answer?
A tent is in the shape of a right circular cylinder up to a height of 3 m and then becomes a right circular cone with a maximum height of 13.5 m above the ground. Calculate the cost of painting the inner side of the tent at the rate of ₹ 2 per m2, if the radius of the base is 14 m.
a)
₹ 2068
b)
₹ 2156
c)
₹ 2248
d)
₹ 1872
|
|
Vivek Bansal answered |
Radius of cylinder = Radius of cone = 14 m.
Height of cylinder = 3 m
Height of cone = 10.5 m
Slant height of cone
= 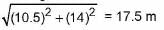
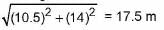
Total curved surface area of tent = Curved surface area of cylinder + Curved surface area of cone
= π(2x14x3 + 14x17.5)
= 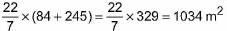
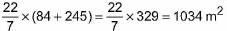
Cost of painting the inner surface at the rate of ₹ 2 per m2 = 2 x 1034 =₹ 2068
A sector of a circle of radius 12 cm has the angle 120°. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.- a)189.61 cm3
- b)169.51 cm3
- c)179.61 cm3
- d)125.51 cm3
Correct answer is option 'A'. Can you explain this answer?
A sector of a circle of radius 12 cm has the angle 120°. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
a)
189.61 cm3
b)
169.51 cm3
c)
179.61 cm3
d)
125.51 cm3

|
Bhavana Kaur answered |
To find the area of a sector, you can use the formula:
Area of sector = (θ/360) * π * r^2
where θ is the angle in degrees and r is the radius.
In this case, the radius is given as 12 cm and the angle is 120 degrees. Plugging these values into the formula, we get:
Area of sector = (120/360) * π * 12^2
= (1/3) * π * 144
= 48π cm^2
So, the area of the sector is 48π cm^2.
Area of sector = (θ/360) * π * r^2
where θ is the angle in degrees and r is the radius.
In this case, the radius is given as 12 cm and the angle is 120 degrees. Plugging these values into the formula, we get:
Area of sector = (120/360) * π * 12^2
= (1/3) * π * 144
= 48π cm^2
So, the area of the sector is 48π cm^2.
The ratio between the volume of two sphere is 8 : 27. What is the ratio between their surface areas?- a)4 : 9
- b)4 : 5
- c)5 : 6
- d)4 : 7
Correct answer is option 'A'. Can you explain this answer?
The ratio between the volume of two sphere is 8 : 27. What is the ratio between their surface areas?
a)
4 : 9
b)
4 : 5
c)
5 : 6
d)
4 : 7
|
|
Sheena mehta answered |
Given:
The ratio between the volume of two spheres is 8: 27.
To find:
The ratio between their surface areas.
Solution:
Let's consider two spheres with volumes V1 and V2, and surface areas S1 and S2 respectively.
Step 1:
We know that the volume of a sphere is given by the formula:
V = (4/3)πr³, where r is the radius of the sphere.
So, the given ratio between the volumes can be written as:
V1/V2 = 8/27
Step 2:
Let's assume the radii of the two spheres as r1 and r2 respectively.
Therefore, we can write the volumes as:
V1 = (4/3)πr1³
V2 = (4/3)πr2³
Step 3:
Now, let's simplify the given ratio using the expressions for volumes:
(4/3)πr1³ / (4/3)πr2³ = 8/27
The π and (4/3) terms cancel out on both sides, leaving us with:
(r1/r2)³ = 8/27
Step 4:
Taking the cube root of both sides, we get:
r1/r2 = 2/3
Step 5:
We know that the surface area of a sphere is given by the formula:
S = 4πr²
Substituting the radii r1 and r2, we can write the surface areas as:
S1 = 4πr1²
S2 = 4πr2²
Step 6:
Now, let's find the ratio between the surface areas:
S1/S2 = (4πr1²) / (4πr2²)
S1/S2 = (r1²/r2²)
Step 7:
Using the ratio r1/r2 = 2/3 from Step 4, we can substitute it into the above expression:
S1/S2 = (2/3)²
S1/S2 = 4/9
Conclusion:
Therefore, the ratio between the surface areas of the two spheres is 4:9.
Hence, the correct answer is option A) 4:9.
The ratio between the volume of two spheres is 8: 27.
To find:
The ratio between their surface areas.
Solution:
Let's consider two spheres with volumes V1 and V2, and surface areas S1 and S2 respectively.
Step 1:
We know that the volume of a sphere is given by the formula:
V = (4/3)πr³, where r is the radius of the sphere.
So, the given ratio between the volumes can be written as:
V1/V2 = 8/27
Step 2:
Let's assume the radii of the two spheres as r1 and r2 respectively.
Therefore, we can write the volumes as:
V1 = (4/3)πr1³
V2 = (4/3)πr2³
Step 3:
Now, let's simplify the given ratio using the expressions for volumes:
(4/3)πr1³ / (4/3)πr2³ = 8/27
The π and (4/3) terms cancel out on both sides, leaving us with:
(r1/r2)³ = 8/27
Step 4:
Taking the cube root of both sides, we get:
r1/r2 = 2/3
Step 5:
We know that the surface area of a sphere is given by the formula:
S = 4πr²
Substituting the radii r1 and r2, we can write the surface areas as:
S1 = 4πr1²
S2 = 4πr2²
Step 6:
Now, let's find the ratio between the surface areas:
S1/S2 = (4πr1²) / (4πr2²)
S1/S2 = (r1²/r2²)
Step 7:
Using the ratio r1/r2 = 2/3 from Step 4, we can substitute it into the above expression:
S1/S2 = (2/3)²
S1/S2 = 4/9
Conclusion:
Therefore, the ratio between the surface areas of the two spheres is 4:9.
Hence, the correct answer is option A) 4:9.
A box opened at the top has its outer dimensions 10 cm × 9 cm × 2.5 cm and its thickness is 0.5 cm, find the volume of the metal.- a)92.5 cm3
- b)72 cm3
- c)63.5 cm3
- d)81 cm3
Correct answer is option 'D'. Can you explain this answer?
A box opened at the top has its outer dimensions 10 cm × 9 cm × 2.5 cm and its thickness is 0.5 cm, find the volume of the metal.
a)
92.5 cm3
b)
72 cm3
c)
63.5 cm3
d)
81 cm3
|
|
Ritu Saxena answered |
Outer dimension s of the box are 10 cm, 9 cm and 2.5 cm.
Thickness of the box is 0.5 cm.
So, inner dimensions of the box is (10 - 2 x 0.5) cm,
(9 - 2 x 0.5) cm and (2.5 - 0.5) cm
i.e, 9 cm, 8 cm and 2 c
Volume of the metal = Volume of outer box - Volume of inner box
= 10 x 9 x 2.5 - 9 x 8 x 2 = 225 - 144 = 81 cm3
A hemispherical bowl is made of steel of 0.25 cm thickness. The inner radius of the bowl is 5 cm. The volume of steel used is _____. (Use π = 3.141)- a)42.15 cm3
- b)41.52 cm3
- c)41.25 cm3
- d)40 cm3
Correct answer is option 'C'. Can you explain this answer?
A hemispherical bowl is made of steel of 0.25 cm thickness. The inner radius of the bowl is 5 cm. The volume of steel used is _____. (Use π = 3.141)
a)
42.15 cm3
b)
41.52 cm3
c)
41.25 cm3
d)
40 cm3
|
|
Ritu Saxena answered |
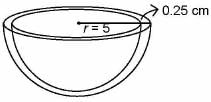
Let r a n d R be inner and outer radius of bowl respectively.
Then, r= 5 cm, R = 5 + 0.25 = 5.25 cm.
Volume of steel used = Outer volume - Inner volume
Volume of steel used = Outer volume - Inner volume
= 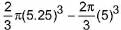
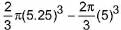
= 41.25 cm3
A solid sphere of copper of radius 10.5 cm is melted and right cones of radius 3.5 cm and height 3 cm are made from the material. What is the number of cones made?- a)136
- b)126
- c)156
- d)146
Correct answer is option 'B'. Can you explain this answer?
A solid sphere of copper of radius 10.5 cm is melted and right cones of radius 3.5 cm and height 3 cm are made from the material. What is the number of cones made?
a)
136
b)
126
c)
156
d)
146
|
|
Priyanka Kapoor answered |
Let the number of cones made be n. The volume of solid sphere = volume of resulting cones
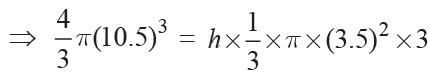
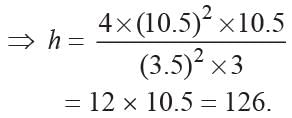
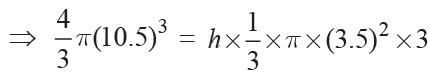
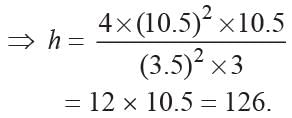
The weight of a metallic spherical shell is 11.176 kg. If the inner radius of the cell is 6 cm. 1 cm3 of the metal weights 21 g then what is the thickness of the shell?- a)1 cm
- b)2 cm
- c)3 cm
- d)4 cm
Correct answer is option 'A'. Can you explain this answer?
The weight of a metallic spherical shell is 11.176 kg. If the inner radius of the cell is 6 cm. 1 cm3 of the metal weights 21 g then what is the thickness of the shell?
a)
1 cm
b)
2 cm
c)
3 cm
d)
4 cm
|
|
Sanjula dubey answered |
To find the thickness of the metallic spherical shell, we need to use the concept of density and weight.
Given data:
- Weight of the metallic spherical shell = 11.176 kg
- Inner radius of the shell = 6 cm
- Density of the metal = 21 g/cm3
Let's solve the problem step by step:
1. Calculate the volume of the spherical shell:
The volume of a spherical shell can be calculated using the formula:
Volume = (4/3) * π * (R_outer^3 - R_inner^3)
Since the inner radius is given as 6 cm, we can assume the outer radius as R cm.
Volume = (4/3) * π * (R^3 - 6^3)
2. Calculate the weight of the metallic shell:
The weight of the metallic shell can be calculated using the formula:
Weight = Volume * Density
11.176 kg = Volume * 21 g/cm3
Now, let's convert the weight to grams:
11.176 kg = 11176 g
Therefore, Volume = 11176 g / 21 g/cm3
3. Substitute the value of Volume in the equation calculated in step 1 and solve for R:
11176 g / 21 g/cm3 = (4/3) * π * (R^3 - 6^3)
4. Simplify the equation:
(11176 g / 21 g/cm3) = (4/3) * π * (R^3 - 216)
5. Solve for R:
R^3 - 216 = (11176 g / 21 g/cm3) * (3/4π)
R^3 - 216 = 1596 g / 7 g/cm3
6. Simplify and solve for R:
R^3 = (1596 g / 7 g/cm3) + 216
R^3 = 228 g/cm3
Taking the cube root on both sides, we get:
R ≈ 6.2 cm
7. Calculate the thickness of the shell:
Thickness = R_outer - R_inner
Thickness = 6.2 cm - 6 cm
Thickness ≈ 0.2 cm
Therefore, the thickness of the metallic spherical shell is approximately 0.2 cm.
Given data:
- Weight of the metallic spherical shell = 11.176 kg
- Inner radius of the shell = 6 cm
- Density of the metal = 21 g/cm3
Let's solve the problem step by step:
1. Calculate the volume of the spherical shell:
The volume of a spherical shell can be calculated using the formula:
Volume = (4/3) * π * (R_outer^3 - R_inner^3)
Since the inner radius is given as 6 cm, we can assume the outer radius as R cm.
Volume = (4/3) * π * (R^3 - 6^3)
2. Calculate the weight of the metallic shell:
The weight of the metallic shell can be calculated using the formula:
Weight = Volume * Density
11.176 kg = Volume * 21 g/cm3
Now, let's convert the weight to grams:
11.176 kg = 11176 g
Therefore, Volume = 11176 g / 21 g/cm3
3. Substitute the value of Volume in the equation calculated in step 1 and solve for R:
11176 g / 21 g/cm3 = (4/3) * π * (R^3 - 6^3)
4. Simplify the equation:
(11176 g / 21 g/cm3) = (4/3) * π * (R^3 - 216)
5. Solve for R:
R^3 - 216 = (11176 g / 21 g/cm3) * (3/4π)
R^3 - 216 = 1596 g / 7 g/cm3
6. Simplify and solve for R:
R^3 = (1596 g / 7 g/cm3) + 216
R^3 = 228 g/cm3
Taking the cube root on both sides, we get:
R ≈ 6.2 cm
7. Calculate the thickness of the shell:
Thickness = R_outer - R_inner
Thickness = 6.2 cm - 6 cm
Thickness ≈ 0.2 cm
Therefore, the thickness of the metallic spherical shell is approximately 0.2 cm.
The volume of the cube is 1728 cm3. What is the total surface area of the cube?- a)824 cm2
- b)864 cm2
- c)924 cm2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The volume of the cube is 1728 cm3. What is the total surface area of the cube?
a)
824 cm2
b)
864 cm2
c)
924 cm2
d)
None of these
|
|
Ritu Saxena answered |
The volume of the cube = 1728
a3 = 1728 ⇒ A = 12 cm
Total surface area = 6a2 = 6 × (12)2
= 6 × 144 = 864 cm2.
a3 = 1728 ⇒ A = 12 cm
Total surface area = 6a2 = 6 × (12)2
= 6 × 144 = 864 cm2.
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be 1/27 of the volume of the given cone, at what height above the base is the section made?- a)20 cm
- b)25 cm
- c)10 cm
- d)15 cm
Correct answer is option 'A'. Can you explain this answer?
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be 1/27 of the volume of the given cone, at what height above the base is the section made?
a)
20 cm
b)
25 cm
c)
10 cm
d)
15 cm
|
|
Pragya joshi answered |
Understanding the Problem
The problem involves a cone with a height of 30 cm, from which a smaller cone is cut off. The volume of this smaller cone is 1/27 of the volume of the original cone.
Volume of a Cone
The volume (V) of a cone is given by the formula:
- V = (1/3) * π * r² * h
where r is the radius and h is the height of the cone.
Volume Ratio of the Cones
Given that the volume of the smaller cone is 1/27 of the larger cone, we can express this mathematically:
- V_small = (1/27) * V_large
Relationship Between Heights and Volumes
Since the smaller cone is similar to the larger cone (as the cutting plane is parallel to the base), the ratio of their volumes relates to the ratio of their heights:
- V_small / V_large = (h_small / h_large)³
Let h_small be the height of the smaller cone, and h_large = 30 cm (the height of the larger cone).
Setting up the ratio:
- 1/27 = (h_small / 30)³
Solve for h_small
To find h_small, we take the cube root of both sides:
- h_small / 30 = (1/3)
Thus, h_small = 30 / 3 = 10 cm.
Height Above the Base
To find the height above the base where the section is made, we subtract the height of the smaller cone from the height of the larger cone:
- Height above base = h_large - h_small = 30 cm - 10 cm = 20 cm.
Conclusion
The section is made at a height of 20 cm above the base of the original cone. Thus, the correct answer is option 'A'.
The problem involves a cone with a height of 30 cm, from which a smaller cone is cut off. The volume of this smaller cone is 1/27 of the volume of the original cone.
Volume of a Cone
The volume (V) of a cone is given by the formula:
- V = (1/3) * π * r² * h
where r is the radius and h is the height of the cone.
Volume Ratio of the Cones
Given that the volume of the smaller cone is 1/27 of the larger cone, we can express this mathematically:
- V_small = (1/27) * V_large
Relationship Between Heights and Volumes
Since the smaller cone is similar to the larger cone (as the cutting plane is parallel to the base), the ratio of their volumes relates to the ratio of their heights:
- V_small / V_large = (h_small / h_large)³
Let h_small be the height of the smaller cone, and h_large = 30 cm (the height of the larger cone).
Setting up the ratio:
- 1/27 = (h_small / 30)³
Solve for h_small
To find h_small, we take the cube root of both sides:
- h_small / 30 = (1/3)
Thus, h_small = 30 / 3 = 10 cm.
Height Above the Base
To find the height above the base where the section is made, we subtract the height of the smaller cone from the height of the larger cone:
- Height above base = h_large - h_small = 30 cm - 10 cm = 20 cm.
Conclusion
The section is made at a height of 20 cm above the base of the original cone. Thus, the correct answer is option 'A'.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. What is the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm?- a)120
- b)130
- c)150
- d)180
Correct answer is option 'C'. Can you explain this answer?
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. What is the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm?
a)
120
b)
130
c)
150
d)
180
|
|
Priyanka Kapoor answered |
Let the no. of marbles = x
Radius of marble = 1.4/2 = 0.7 cm
Radius of cylinder = 7/2 = 3.5 cm
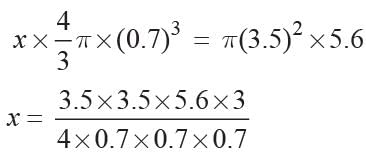
⇒ x = 150
Radius of marble = 1.4/2 = 0.7 cm
Radius of cylinder = 7/2 = 3.5 cm
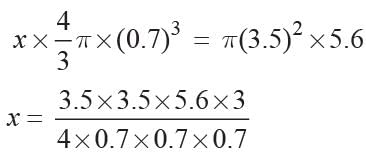
⇒ x = 150
The height of a right cylinder is 165 cm and the diameter of its base is 24 cm. Find the radius of the sphere whose volume is equal to the volume of the given cylinder.- a)12 cm
- b)6 cm
- c)16 cm
- d)24 cm
Correct answer is option 'A'. Can you explain this answer?
The height of a right cylinder is 165 cm and the diameter of its base is 24 cm. Find the radius of the sphere whose volume is equal to the volume of the given cylinder.
a)
12 cm
b)
6 cm
c)
16 cm
d)
24 cm
|
|
Ritu Saxena answered |
Volume of given cylinder = πr2h
= π(12)2 × 16
Now,
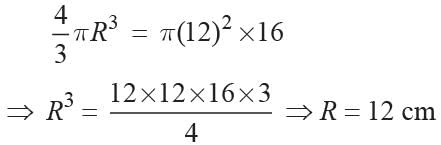
= π(12)2 × 16
Now,
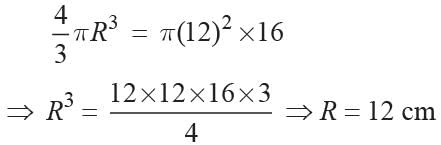
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere. Find the radius of the hemisphere, if height of the cone is 3 times the radius.- a)3 cm
- b)6 cm
- c)5 cm
- d)9 cm
Correct answer is option 'A'. Can you explain this answer?
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere. Find the radius of the hemisphere, if height of the cone is 3 times the radius.
a)
3 cm
b)
6 cm
c)
5 cm
d)
9 cm
|
|
Ritu Saxena answered |
Radius of cylinder = 12/2 = 6 cm
height = 15 cm
Volume of cylinder = πr2h
= 22/7 x 62 x 15
= 540π cm3
Volume of 12 toys = 540π cm3
Volume of 1 toy = 540π/12 = 45π cm3
Let the radius of the hemisphere be r cm.
Height of the cone = 3r cm
Volume of one toy = Volume of hemisphere + volume of cone

Now

height = 15 cm
Volume of cylinder = πr2h
= 22/7 x 62 x 15
= 540π cm3
Volume of 12 toys = 540π cm3
Volume of 1 toy = 540π/12 = 45π cm3
Let the radius of the hemisphere be r cm.
Height of the cone = 3r cm
Volume of one toy = Volume of hemisphere + volume of cone

Now

A right circular cone is 4.1 cm high and the radius of its base is 2.1 cm. Another right circular cone is 4.3 cm high and the radius of the base is 2.1 cm. Both the cones are melted and recast into a sphere. Find the diameter of the sphere.- a)6.4 cm
- b)4.2 cm
- c)2.1 cm
- d)5.6 cm
Correct answer is option 'B'. Can you explain this answer?
A right circular cone is 4.1 cm high and the radius of its base is 2.1 cm. Another right circular cone is 4.3 cm high and the radius of the base is 2.1 cm. Both the cones are melted and recast into a sphere. Find the diameter of the sphere.
a)
6.4 cm
b)
4.2 cm
c)
2.1 cm
d)
5.6 cm
|
|
Ritu Saxena answered |
Volume of cone of r = 2.1 cm &
h. = 4.1cm =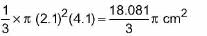
h. = 4.1cm =
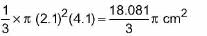
Volume of cone of r = 2.1 cm & h = 4.3 cm
= 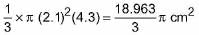
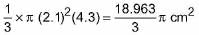
Let radius of the sphere be r cm.
Now, Volume of sphere = Sum of Volume of both cones.
Now, Volume of sphere = Sum of Volume of both cones.
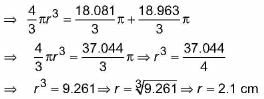
∴ Diameter of sphere = 4.2 cm.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. What is the ratio of their volumes?- a)20 : 27
- b)27 : 20
- c)9 : 4
- d)4 : 9
Correct answer is option 'A'. Can you explain this answer?
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. What is the ratio of their volumes?
a)
20 : 27
b)
27 : 20
c)
9 : 4
d)
4 : 9
|
|
Priyanka Kapoor answered |
Let the radii of two cylinders are 2r, 3r and heights be 5h and 3h.
Ratio of their volumes
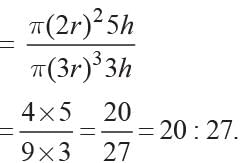
Ratio of their volumes
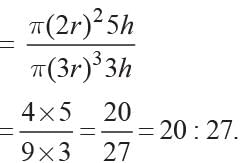
Five people will live in a tent. If each person requires 16 m2 of floor area and 100 m3 space for air then find the required height of the cone of the smallest size to accommodate those persons.- a)18.75 m
- b)20 m
- c)21.75 m
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Five people will live in a tent. If each person requires 16 m2 of floor area and 100 m3 space for air then find the required height of the cone of the smallest size to accommodate those persons.
a)
18.75 m
b)
20 m
c)
21.75 m
d)
None of these
|
|
Priyanka Kapoor answered |
Let the height of the required cone be h cm
∴ Required base area = (16) × 5
= 80 cm2 = πr2
Height = h cm volume = 1/3 (πr2)h
According to given condition
Total volume required = 5 × 100 cm3 = 500 cm3
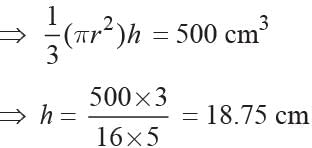
∴ Required base area = (16) × 5
= 80 cm2 = πr2
Height = h cm volume = 1/3 (πr2)h
According to given condition
Total volume required = 5 × 100 cm3 = 500 cm3
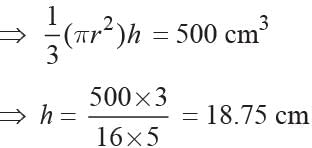
An inverted cone of vertical height 12 cm and the radius of base 9 cm contains water to a depth of 4 cm. Find the area of the interior surface of the cone not in contact with the water. [Use p = 22/7]- a)402.12 cm2
- b)298 cm2
- c)377.14 cm2
- d)315 cm2
Correct answer is option 'C'. Can you explain this answer?
An inverted cone of vertical height 12 cm and the radius of base 9 cm contains water to a depth of 4 cm. Find the area of the interior surface of the cone not in contact with the water. [Use p = 22/7]
a)
402.12 cm2
b)
298 cm2
c)
377.14 cm2
d)
315 cm2
|
|
Priyanka Kapoor answered |
Since, Δ OAB ~ Δ OCD
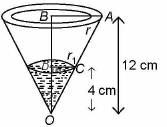
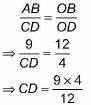
⇒ CD = 3 cm
Slant height of cone (/) = 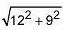
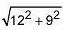
= 15 cm
A cylindrical vessel of diameter 4 cm is partly filled with water. 300 lead balls are dropped in it. The rise in water level is 0.8 cm. The diameter of each ball is ____.- a)0.8 cm
- b)0.4 cm
- c)0.2 cm
- d)0.5 cm
Correct answer is option 'B'. Can you explain this answer?
A cylindrical vessel of diameter 4 cm is partly filled with water. 300 lead balls are dropped in it. The rise in water level is 0.8 cm. The diameter of each ball is ____.
a)
0.8 cm
b)
0.4 cm
c)
0.2 cm
d)
0.5 cm
|
|
Ritu Saxena answered |
Radius of vessel (R) = 2 cm
Rise in water level = 0.8 cm
lume of water displaced by 300 lead balls
= πR2h = π x 4 x 0 .8 = 3.2m
∴ Volume displaced by one ball = 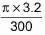
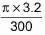
Let radius of each ball be r cm .
∴ 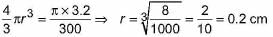
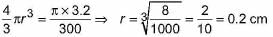
∴ Diameter = 2 x r= 0.4 cm
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed into the tub. If the radius of the hemisphere is 3.5 cm and the height of the cone outside the hemisphere is 5 cm, find the volume of water left in the tub. (Take π = 22/7)- a)616 cm3
- b)600 cm3
- c)535 cm3
- d)716 cm3
Correct answer is option 'A'. Can you explain this answer?
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed into the tub. If the radius of the hemisphere is 3.5 cm and the height of the cone outside the hemisphere is 5 cm, find the volume of water left in the tub. (Take π = 22/7)
a)
616 cm3
b)
600 cm3
c)
535 cm3
d)
716 cm3
|
|
Ritu Saxena answered |
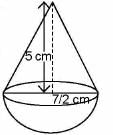
Volume of water in the cylinder tub = Volume of the tub
= 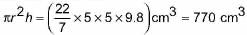
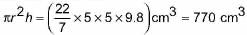
Volume of the solid immersed in the tub = Volume of the hemisphere + Volume of the cone
= 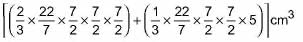
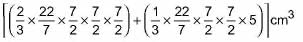
= 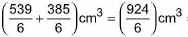
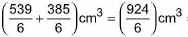
= 154 cm3
Volume of water left in the tub = Volume of the tub - Volume of solid immersed
= ( 770 - 154) cm3 = 616 cm3
The ratio of the volumes of two spheres is 27 : 8. Find the ratio of their surface areas.- a)4 : 9
- b)9 : 4
- c)2 : 3
- d)1 : 3
Correct answer is option 'B'. Can you explain this answer?
The ratio of the volumes of two spheres is 27 : 8. Find the ratio of their surface areas.
a)
4 : 9
b)
9 : 4
c)
2 : 3
d)
1 : 3
|
|
Priyanka Kapoor answered |
Ratio of volumes of spheres of radii r1 and r2 respectively
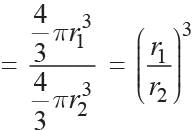
Similarly,
ratio of surface areas
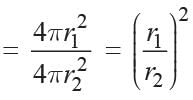
According to condition
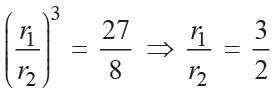
∴ Ratio of surface areas

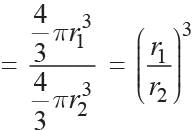
Similarly,
ratio of surface areas
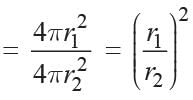
According to condition
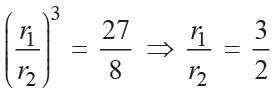
∴ Ratio of surface areas

A solid cylinder has height 12 cm and diameter 10 cm. A conical cavity of same height and same diameter is hollowed out. What is the total surface area of the remaining solid?- a)660 cm2
- b)600 cm2
- c)560 cm2
- d)760 cm2
Correct answer is option 'A'. Can you explain this answer?
A solid cylinder has height 12 cm and diameter 10 cm. A conical cavity of same height and same diameter is hollowed out. What is the total surface area of the remaining solid?
a)
660 cm2
b)
600 cm2
c)
560 cm2
d)
760 cm2
|
|
Priyanka Kapoor answered |
Total surface area of the remaining solid = curved surface area of the cylinder + curved surface area of the cone + area of upper base of the cylinder
= 2πrh + πrl + πr2
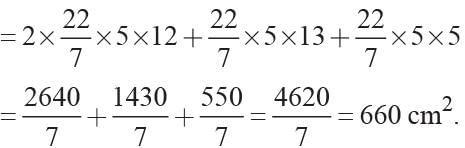
= 2πrh + πrl + πr2
The total surface area of a right cone is 1760 cm2 and the radius of its base is 14 cm. What is the lateral surface area of the cone?- a)1148 cm2
- b)1144 cm2
- c)1198 cm2
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The total surface area of a right cone is 1760 cm2 and the radius of its base is 14 cm. What is the lateral surface area of the cone?
a)
1148 cm2
b)
1144 cm2
c)
1198 cm2
d)
None of these
|
|
Swati verma answered |
To find the lateral surface area of a cone, we need to know the slant height of the cone. However, the given information only includes the total surface area and the radius of the base.
Let's break down the formula for the total surface area of a cone:
Total Surface Area of Cone = Lateral Surface Area of Cone + Base Area of Cone
The base area of a cone is given by the formula:
Base Area of Cone = πr^2
Given that the radius of the base is 14 cm, we can calculate the base area:
Base Area of Cone = π(14 cm)^2 = 196π cm^2
Now, we can substitute the base area into the total surface area formula to find the lateral surface area:
1760 cm^2 = Lateral Surface Area of Cone + 196π cm^2
To find the lateral surface area, we need to isolate it on one side of the equation:
Lateral Surface Area of Cone = 1760 cm^2 - 196π cm^2
To calculate the value of the lateral surface area, we need to know the value of π (pi). However, the value of π is not given in the question. Therefore, we cannot determine the exact value of the lateral surface area.
Hence, the correct answer is option 'D' (None of these) since we do not have enough information to calculate the lateral surface area of the cone.
Let's break down the formula for the total surface area of a cone:
Total Surface Area of Cone = Lateral Surface Area of Cone + Base Area of Cone
The base area of a cone is given by the formula:
Base Area of Cone = πr^2
Given that the radius of the base is 14 cm, we can calculate the base area:
Base Area of Cone = π(14 cm)^2 = 196π cm^2
Now, we can substitute the base area into the total surface area formula to find the lateral surface area:
1760 cm^2 = Lateral Surface Area of Cone + 196π cm^2
To find the lateral surface area, we need to isolate it on one side of the equation:
Lateral Surface Area of Cone = 1760 cm^2 - 196π cm^2
To calculate the value of the lateral surface area, we need to know the value of π (pi). However, the value of π is not given in the question. Therefore, we cannot determine the exact value of the lateral surface area.
Hence, the correct answer is option 'D' (None of these) since we do not have enough information to calculate the lateral surface area of the cone.
A cylinder, whose height is two-thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.- a)4 cm
- b)5 cm
- c)3 cm
- d)6 cm
Correct answer is option 'A'. Can you explain this answer?
A cylinder, whose height is two-thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.
a)
4 cm
b)
5 cm
c)
3 cm
d)
6 cm

|
Snehal Choudhury answered |
Given:
Height of the cylinder = 2/3 of its diameter
Volume of the cylinder = Volume of the sphere
To find: Radius of the base of the cylinder
Let's solve this step by step.
1) Formula for the volume of a cylinder is given by:
Volume = πr^2h, where r is the radius and h is the height.
2) Formula for the volume of a sphere is given by:
Volume = 4/3πr^3, where r is the radius of the sphere.
3) Since the volume of the cylinder is equal to the volume of the sphere, we can equate the two formulas:
πr^2h = 4/3πr^3
4) Canceling out π and dividing both sides by r^2, we get:
h = 4/3r
5) Given that the height of the cylinder is 2/3 of its diameter, which means h = 2/3d, where d is the diameter of the cylinder.
6) Substituting h = 2/3d in the equation from step 4, we get:
2/3d = 4/3r
7) Canceling out 2/3 on both sides and solving for r, we have:
d = 2r
r = d/2
8) Substituting r = d/2 in the equation from step 6, we get:
2/3d = 4/3(d/2)
9) Canceling out 2/3 on both sides and solving for d, we have:
1 = 4/3
This is not possible.
10) Therefore, the given information is inconsistent, and we cannot determine the radius of the base of the cylinder.
Height of the cylinder = 2/3 of its diameter
Volume of the cylinder = Volume of the sphere
To find: Radius of the base of the cylinder
Let's solve this step by step.
1) Formula for the volume of a cylinder is given by:
Volume = πr^2h, where r is the radius and h is the height.
2) Formula for the volume of a sphere is given by:
Volume = 4/3πr^3, where r is the radius of the sphere.
3) Since the volume of the cylinder is equal to the volume of the sphere, we can equate the two formulas:
πr^2h = 4/3πr^3
4) Canceling out π and dividing both sides by r^2, we get:
h = 4/3r
5) Given that the height of the cylinder is 2/3 of its diameter, which means h = 2/3d, where d is the diameter of the cylinder.
6) Substituting h = 2/3d in the equation from step 4, we get:
2/3d = 4/3r
7) Canceling out 2/3 on both sides and solving for r, we have:
d = 2r
r = d/2
8) Substituting r = d/2 in the equation from step 6, we get:
2/3d = 4/3(d/2)
9) Canceling out 2/3 on both sides and solving for d, we have:
1 = 4/3
This is not possible.
10) Therefore, the given information is inconsistent, and we cannot determine the radius of the base of the cylinder.
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.- a)12 cm
- b)16 cm
- c)14 cm
- d)7 cm
Correct answer is option 'C'. Can you explain this answer?
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
a)
12 cm
b)
16 cm
c)
14 cm
d)
7 cm
|
|
Anoushka sengupta answered |
Volume of the Hollow Sphere
To find the height of the cone formed by melting the hollow sphere, we first need to calculate the volume of the hollow sphere.
- External diameter: 8 cm
- Internal diameter: 4 cm
- External radius (R): 8 cm / 2 = 4 cm
- Internal radius (r): 4 cm / 2 = 2 cm
The volume of a hollow sphere is given by the formula:
Volume = (4/3)π(R³ - r³)
Calculating the volume:
- R³ = 4³ = 64
- r³ = 2³ = 8
- R³ - r³ = 64 - 8 = 56
Thus,
Volume of the hollow sphere = (4/3)π(56) = (224/3)π cm³
Volume of the Cone
Now, the volume of the cone formed from this hollow sphere is equal to the volume of the hollow sphere.
- Base diameter of the cone: 8 cm
- Radius of the cone (r_cone): 8 cm / 2 = 4 cm
Let the height of the cone be h. The volume of the cone is given by:
Volume = (1/3)πr_cone²h
Setting the volumes equal:
(224/3)π = (1/3)π(4²)h
Cancelling π and (1/3):
224 = 16h
Solving for h:
h = 224 / 16 = 14 cm
Conclusion
The height of the cone is 14 cm. Thus, the correct answer is option 'C'.
To find the height of the cone formed by melting the hollow sphere, we first need to calculate the volume of the hollow sphere.
- External diameter: 8 cm
- Internal diameter: 4 cm
- External radius (R): 8 cm / 2 = 4 cm
- Internal radius (r): 4 cm / 2 = 2 cm
The volume of a hollow sphere is given by the formula:
Volume = (4/3)π(R³ - r³)
Calculating the volume:
- R³ = 4³ = 64
- r³ = 2³ = 8
- R³ - r³ = 64 - 8 = 56
Thus,
Volume of the hollow sphere = (4/3)π(56) = (224/3)π cm³
Volume of the Cone
Now, the volume of the cone formed from this hollow sphere is equal to the volume of the hollow sphere.
- Base diameter of the cone: 8 cm
- Radius of the cone (r_cone): 8 cm / 2 = 4 cm
Let the height of the cone be h. The volume of the cone is given by:
Volume = (1/3)πr_cone²h
Setting the volumes equal:
(224/3)π = (1/3)π(4²)h
Cancelling π and (1/3):
224 = 16h
Solving for h:
h = 224 / 16 = 14 cm
Conclusion
The height of the cone is 14 cm. Thus, the correct answer is option 'C'.
If the radius of a sphere is doubled then how many times will its surface area?- a)8
- b)4
- c)2
- d)0.5
Correct answer is option 'B'. Can you explain this answer?
If the radius of a sphere is doubled then how many times will its surface area?
a)
8
b)
4
c)
2
d)
0.5
|
|
Priyanka Kapoor answered |
Surface area of sphere = 4πR2
If the radius of sphere is doubled, i.e., R becomes 2R, then
New surface area = 4π(2R)2 = 16πR2
= 4 (4πR2)
= 4 (surface area)
∴ Surface area will become 4 times.
If the radius of sphere is doubled, i.e., R becomes 2R, then
New surface area = 4π(2R)2 = 16πR2
= 4 (4πR2)
= 4 (surface area)
∴ Surface area will become 4 times.
Study the question and the statements given below and decide which of the statement(s) is/are necessary to answer the question.
What is the capacity of the cylindrical tank?
I. The area of the base is 61,600 sq. cm.
II. The height of the tank is 1.5 times the radius.
III. The circumference of base is 880 cm.- a)Only I and II
- b)Only II and III
- c)Only I and III
- d)Only II and either I or III
Correct answer is option 'D'. Can you explain this answer?
Study the question and the statements given below and decide which of the statement(s) is/are necessary to answer the question.
What is the capacity of the cylindrical tank?
I. The area of the base is 61,600 sq. cm.
II. The height of the tank is 1.5 times the radius.
III. The circumference of base is 880 cm.
What is the capacity of the cylindrical tank?
I. The area of the base is 61,600 sq. cm.
II. The height of the tank is 1.5 times the radius.
III. The circumference of base is 880 cm.
a)
Only I and II
b)
Only II and III
c)
Only I and III
d)
Only II and either I or III
|
|
Vivek Bansal answered |
Volume of cylindrical tank = πr2h
So, we need radius and height.
Radius can be found from either statement I or III and height from statement II.
Radius can be found from either statement I or III and height from statement II.
Th e in terna l an d exte rn al dia mete rs of a hollow hemispherical vessel are 24 cm and 25 cm respectively. The cost to paint 1 cm2 of the surface is ₹ 0.05. Find the total cost to painting the vessel all over.- a)₹ 108.32
- b)₹ 296.28
- c)₹ 101.59
- d)₹ 96.28
Correct answer is option 'D'. Can you explain this answer?
Th e in terna l an d exte rn al dia mete rs of a hollow hemispherical vessel are 24 cm and 25 cm respectively. The cost to paint 1 cm2 of the surface is ₹ 0.05. Find the total cost to painting the vessel all over.
a)
₹ 108.32
b)
₹ 296.28
c)
₹ 101.59
d)
₹ 96.28
|
|
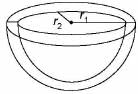
Ritu Saxena answered |
External radius of hemispherical vessel
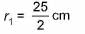
Internal radius of hemispherical vessel
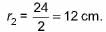
External curved surface area of hemispherical vessel = 2πr12
= 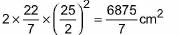
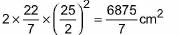
Internal curved surface area of hemispherical vessel = 2πr22
= 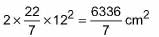
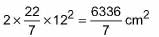
Area of top of the hemispherical vessel
= 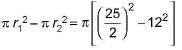
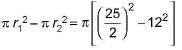
= 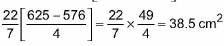
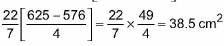
Total surface area of the vessel
=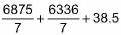
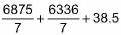
= 1925.78 cm2
Cost of painting the vessel at the rate of ₹ 0.05 per cm2 = 1925.78 » 0.05
= ₹ 96.28
A circus tent is cylindrical to a height of 4 cm and cone above it. If its diameter is 105 m and its lant height is 40 m. What is the total area of canvas required?- a)1760 m2
- b)3960 m2
- c)7920 m2
- d)2640 m2
Correct answer is option 'C'. Can you explain this answer?
A circus tent is cylindrical to a height of 4 cm and cone above it. If its diameter is 105 m and its lant height is 40 m. What is the total area of canvas required?
a)
1760 m2
b)
3960 m2
c)
7920 m2
d)
2640 m2
|
|
Ritu Saxena answered |
Area of canvas = 2πrh + πrl
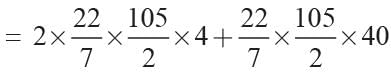
= 1320 + 6600 = 7920 cm2.
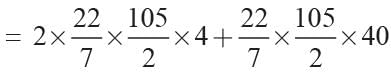
= 1320 + 6600 = 7920 cm2.
The ratio between the volumes of two spheres is 8 : 27. What is the ratio between their surface area?- a)2 : 3
- b)4 : 5
- c)5 : 6
- d)4 : 9
Correct answer is option 'D'. Can you explain this answer?
The ratio between the volumes of two spheres is 8 : 27. What is the ratio between their surface area?
a)
2 : 3
b)
4 : 5
c)
5 : 6
d)
4 : 9
|
|
Priyanka Kapoor answered |
Let the radius of two spheres be R and r.
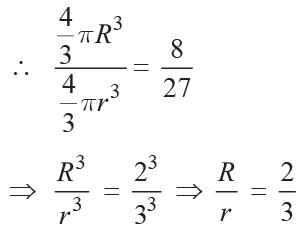
Ratio of their surface area
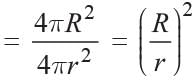
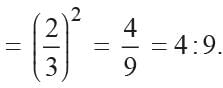
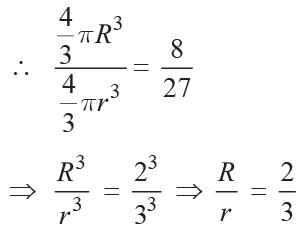
Ratio of their surface area
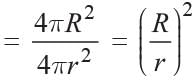
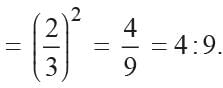
The surface area of a sphere is 616 cm2, what is the diameter of the sphere?- a)7 cm
- b)14 cm
- c)16 cm
- d)24 cm
Correct answer is option 'B'. Can you explain this answer?
The surface area of a sphere is 616 cm2, what is the diameter of the sphere?
a)
7 cm
b)
14 cm
c)
16 cm
d)
24 cm
|
|
Priyanka Kapoor answered |
Surface area of sphere = 4πr2 = 616
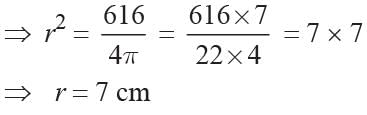
∴ diameter = 2r = 2 × 7 = 14 cm
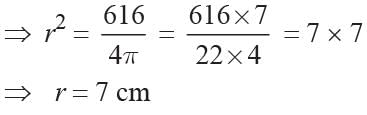
∴ diameter = 2r = 2 × 7 = 14 cm
The aspherical shell of lead whose external and internal diameters are 24 cm and 18 cm respectively is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.- a)6 cm
- b)12 cm
- c)18 cm
- d)24 cm
Correct answer is option 'B'. Can you explain this answer?
The aspherical shell of lead whose external and internal diameters are 24 cm and 18 cm respectively is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
a)
6 cm
b)
12 cm
c)
18 cm
d)
24 cm
|
|
Ritu Saxena answered |
The volume of lead in the shell = volume of a cylinder
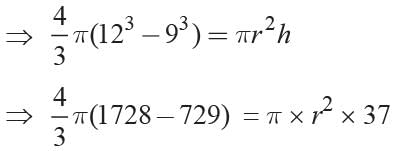
⇒ r2 = 36 ⇒ r = 6
∴ diameter = 2r = 2 × 6 = 12 cm
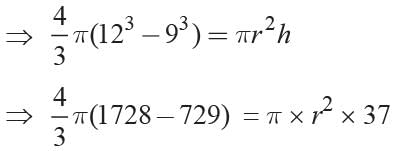
⇒ r2 = 36 ⇒ r = 6
∴ diameter = 2r = 2 × 6 = 12 cm
A cylindrical container is filled with icecream whose diameter is 12 cm and height 15 cm. The whole ice-cream cone?- a)6 cm
- b)4 cm
- c)8 cm
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A cylindrical container is filled with icecream whose diameter is 12 cm and height 15 cm. The whole ice-cream cone?
a)
6 cm
b)
4 cm
c)
8 cm
d)
None of these
|
|
Ritu Saxena answered |
Let r be the radius of base of the conical part.
Height of the conical part = 4r
Volume of cone with hemispherical top = volume of cone + volume of hemispherical top
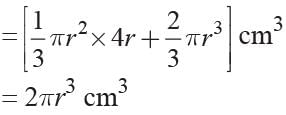
Volume of 10 such cones with hemispherical top
= 10 × 2πr3 = 20πr3 cm3
Volume of cylindrical container
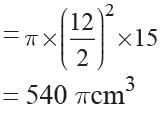
20πr3 = 540π
r3 = 27 ⇒ r = 3 cm.
diameter = 3 × 2 = 6 cm
Height of the conical part = 4r
Volume of cone with hemispherical top = volume of cone + volume of hemispherical top
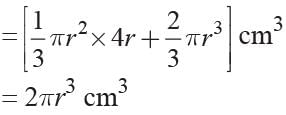
Volume of 10 such cones with hemispherical top
= 10 × 2πr3 = 20πr3 cm3
Volume of cylindrical container
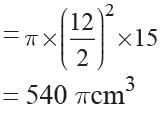
20πr3 = 540π
r3 = 27 ⇒ r = 3 cm.
diameter = 3 × 2 = 6 cm
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r.- a)4/3πr3
- b)2πr3
- c)1/3πr3
- d)2/3πr3
Correct answer is option 'C'. Can you explain this answer?
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r.
a)
4/3πr3
b)
2πr3
c)
1/3πr3
d)
2/3πr3
|
|
Priyanka Kapoor answered |
To cut out maximum area, radius of the cone = radius of the hemisphere = r and height of the cone = radius of the hemisphere = r
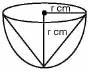
∴ Volume of the cone = 1/3πr
2
h
= 1/3πr3
A bucket is in the form of a frustum of a cone, its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm respectively. How many litres can the bucket hold?- a)13 L
- b)27 L
- c)42.94 L
- d)28.49 L
Correct answer is option 'A'. Can you explain this answer?
A bucket is in the form of a frustum of a cone, its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm respectively. How many litres can the bucket hold?
a)
13 L
b)
27 L
c)
42.94 L
d)
28.49 L
|
|
Priyanka Kapoor answered |
Volume of bucket = 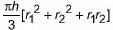
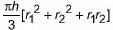
= 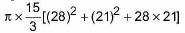
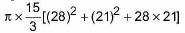
= 28490 cm3
∴ Volume of bucket = 28490 cm3 = 28.49 L
The number of solid spheres, each of diameter 6 cm that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is ____.- a)3
- b)4
- c)5
- d)6
Correct answer is option 'C'. Can you explain this answer?
The number of solid spheres, each of diameter 6 cm that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is ____.
a)
3
b)
4
c)
5
d)
6
|
|
Vivek Bansal answered |
Volume o f one solid sphere = 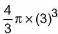
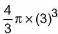
Volume of cylinder = πr2h = π x 4 x 45
Now, Number of spheres x Volume of one sphere = Volume of cylinder
⇒ Number of spheres x 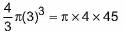
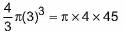
⇒ Number of spheres = 45/9 = 5
A cuboidal metal of dimensions 44 cm × 30 cm × 15 cm was melted and cast into a cylinder of height 28 cm. Its radius is _____.- a)20 cm
- b)15 cm
- c)10 cm
- d)25 cm
Correct answer is option 'B'. Can you explain this answer?
A cuboidal metal of dimensions 44 cm × 30 cm × 15 cm was melted and cast into a cylinder of height 28 cm. Its radius is _____.
a)
20 cm
b)
15 cm
c)
10 cm
d)
25 cm
|
|
Ritu Saxena answered |
Volume of cuboid = 44 x 30 x 15 cm3
This volume is equal to volume of cylinder
∴ 44 x 30 x 15 = π x r2 x 28
∴ r = 15 cm
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. What is the height of the pillar?- a)4 m
- b)5 m
- c)6 m
- d)7 m
Correct answer is option 'C'. Can you explain this answer?
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. What is the height of the pillar?
a)
4 m
b)
5 m
c)
6 m
d)
7 m
|
|
Priyanka Kapoor answered |
Curved surface area of cylindrical pillar = 264
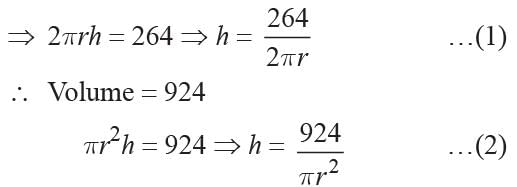
From (1) and (2)

264r = 924 × 2
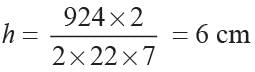
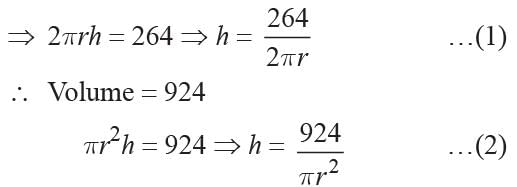
From (1) and (2)

264r = 924 × 2
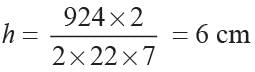
A right cylinder, a right cone and a hemisphere have the same height and same base area. What is ratio of their volumes?- a)1 : 2: 3
- b)3 : 1 : 2
- c)2 : 3 : 1
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A right cylinder, a right cone and a hemisphere have the same height and same base area. What is ratio of their volumes?
a)
1 : 2: 3
b)
3 : 1 : 2
c)
2 : 3 : 1
d)
None of these
|
|
Ritu Saxena answered |
Let the base areas and heights be A and h respectively.
For cylinder, volume = VC = πr2h = Ah
For cone, volume = VCO = 1/3 πr2h = 1/3 Ah
For hemisphere, volume = Vh = 2/3 πr3
∴ Ratio of their volumes = 2/3 (πr2)r
= 2/3 Ah [∵ h =r]
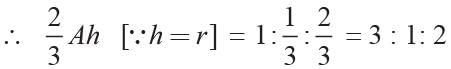
For cylinder, volume = VC = πr2h = Ah
For cone, volume = VCO = 1/3 πr2h = 1/3 Ah
For hemisphere, volume = Vh = 2/3 πr3
∴ Ratio of their volumes = 2/3 (πr2)r
= 2/3 Ah [∵ h =r]
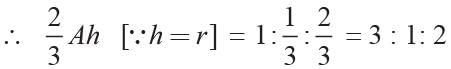
The inner and outer surface areas of a spherical shell are 324 πcm2 and 576 πcm2. What is the thickness of the shell?- a)6 cm
- b)3 cm
- c)2 cm
- d)4 cm
Correct answer is option 'B'. Can you explain this answer?
The inner and outer surface areas of a spherical shell are 324 πcm2 and 576 πcm2. What is the thickness of the shell?
a)
6 cm
b)
3 cm
c)
2 cm
d)
4 cm
|
|
Priyanka Kapoor answered |
Inner surface Area = 4πr2 = 324π cm2
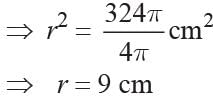
∴ Outer radius
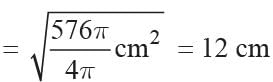
∴ thickness of the shell = (12 - 9) = 3 cm
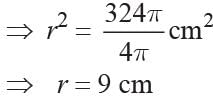
∴ Outer radius
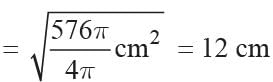
∴ thickness of the shell = (12 - 9) = 3 cm
If the radii of the circular ends of bucket in the form of frustum are 28 cm and 7 cm and the height is 45 cm. The capacity of the bucket is _____.- a)48150 cm3
- b)48510 cm3
- c)48105 cm3
- d)48205 cm3
Correct answer is option 'B'. Can you explain this answer?
If the radii of the circular ends of bucket in the form of frustum are 28 cm and 7 cm and the height is 45 cm. The capacity of the bucket is _____.
a)
48150 cm3
b)
48510 cm3
c)
48105 cm3
d)
48205 cm3
|
|
Vivek Bansal answered |
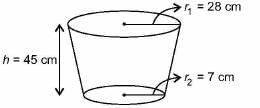
Volume of frustum/bucket = 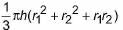
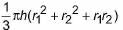
= 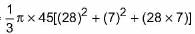
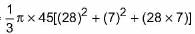
= 48510 cm3
The surface area of the cylinder is 2992 cm2 and its height is 20 cm, what is the diameter of the cylinder?- a)14 cm
- b)28 cm
- c)7 cm
- d)56 cm
Correct answer is option 'B'. Can you explain this answer?
The surface area of the cylinder is 2992 cm2 and its height is 20 cm, what is the diameter of the cylinder?
a)
14 cm
b)
28 cm
c)
7 cm
d)
56 cm
|
|
Priyanka Kapoor answered |
Let r be the radius of the cylinder Total surface area = 2πr (h + r)
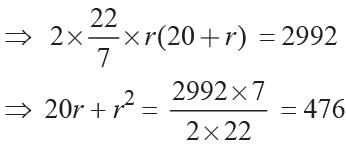
⇒ r2 + 20r - 476 = 0
⇒ r2 + 34r - 14r - 476 = 0
⇒ r(r + 34) - 14(r + 34) = 0
⇒ (r - 14) (r + 34) = 0
⇒ r = 14; r = -34 (Not possible)
diameter = 2 × 14 = 28 cm
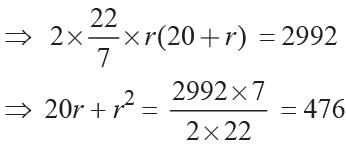
⇒ r2 + 20r - 476 = 0
⇒ r2 + 34r - 14r - 476 = 0
⇒ r(r + 34) - 14(r + 34) = 0
⇒ (r - 14) (r + 34) = 0
⇒ r = 14; r = -34 (Not possible)
diameter = 2 × 14 = 28 cm
To const ruct a wall 24 m long, 0. 4 m thick and 6 m high, bricks of diamensions 25 cm × 16 cm × 10 cm each are used. If the mortar occupies 1/10th of the volume of the wall, find the number of bricks used.- a)12960
- b)14420
- c)24566
- d)14296
Correct answer is option 'A'. Can you explain this answer?
To const ruct a wall 24 m long, 0. 4 m thick and 6 m high, bricks of diamensions 25 cm × 16 cm × 10 cm each are used. If the mortar occupies 1/10th of the volume of the wall, find the number of bricks used.
a)
12960
b)
14420
c)
24566
d)
14296
|
|
Ritu Saxena answered |
Volume of the wall = 24 x 0.4 x 6 = 57.6m
Volume of mortar = 57.6/10 = 5.76 m3
Volume of mortar = 57.6/10 = 5.76 m3
Volume of used bricks = (57.6 - 5.76) m3 = 51.84 m
Volume of each brick = (25 x 16 x 10) cm3 = 4000 cm3
= 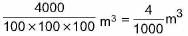
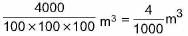
∴ Number o f bricks used = 51.84 / 4/1000
= 12960
Chapter doubts & questions for Surface Area and Volume - International Mathematics Olympiad (IMO) for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Surface Area and Volume - International Mathematics Olympiad (IMO) for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
International Mathematics Olympiad (IMO) for Class 10
28 videos|149 docs|72 tests
|
Related Class 10 Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup