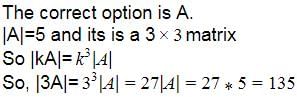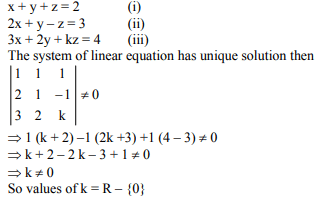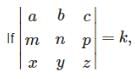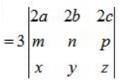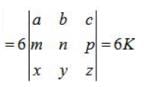All Exams >
JEE >
Mathematics CUET UG Mock Test Series 2026 >
All Questions
All questions of Chapter 4 - Determinants for JEE Exam
If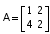 
, then the value of |2A| is same as- a)2|A|
- b)4|A|
- c)±2|A|
- d)|A|
Correct answer is option 'B'. Can you explain this answer?
If 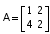, then the value of |2A| is same as
, then the value of |2A| is same asa)
2|A|
b)
4|A|
c)
±2|A|
d)
|A|
|
Harshít Bajáj answered |
Pehele |2A| find karo..which is -24.. so, |2A|= -24 _ _ eq (1).. then |A| find kro..which is -6.. so, |A|= -6 _ _ eq (2).. now.. 4|A| = 4 × (-6)= -24 _ _ eq (3).. from eq (1),(3)..we get..|2A|=4|A|..
The value of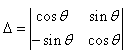 
- a)-1
- b)2
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
The value of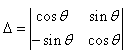
a)
-1
b)
2
c)
0
d)
1
|
Anu answered |
(cosФ×cosФ)-(-sinфsinФ) = cos^2Ф-(-sin^2Ф) = cos^2Ф+sin^2Ф=1
- a)0
- b)±1
- c)-1
- d)1
Correct answer is option 'B'. Can you explain this answer?
a)
0
b)
±1
c)
-1
d)
1
|
Preeti Iyer answered |
As the value of both determinants are equal,
∴ 1 = x2
x = ±1
∴ 1 = x2
x = ±1
and A2 + aA + b = O, then the values of a and b are:
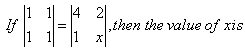
- a)-3/2
- b)3/2
- c)-1/2
- d)1/2
Correct answer is option 'D'. Can you explain this answer?
a)
-3/2
b)
3/2
c)
-1/2
d)
1/2
|
|
Shreya Singh answered |
(1×1) -(1×1)= 4 × X - 2 × 1.0= 4X-2.4X=2.X=2/4.X=1/2.
, then the value of x is- a)-2
- b)1
- c)2
- d)-1
Correct answer is option 'B'. Can you explain this answer?
, then the value of x isa)
-2
b)
1
c)
2
d)
-1
|
Ciel Knowledge answered |
8-6 = 4x-2x
⇒ x = 1
⇒ x = 1
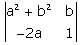
- a)(a)2
- b)(a – b)2
- c)1
- d)(a+b)2
Correct answer is option 'D'. Can you explain this answer?
a)
(a)2
b)
(a – b)2
c)
1
d)
(a+b)2
|
Aryan Khanna answered |
Determinant = [(a2 + b2).1 - (-2ab)]
= (a+b)2
= (a+b)2
The following system of equations has
x + 3y + 3z = 2
x + 4y + 3z = 1
x + 3y + 4z = 2- a)Infinite Solution
- b)Trivial Solution
- c)Unique Solution
- d)No Solution
Correct answer is option 'C'. Can you explain this answer?
The following system of equations has
x + 3y + 3z = 2
x + 4y + 3z = 1
x + 3y + 4z = 2
x + 3y + 3z = 2
x + 4y + 3z = 1
x + 3y + 4z = 2
a)
Infinite Solution
b)
Trivial Solution
c)
Unique Solution
d)
No Solution
|
Geetika Shah answered |
Let A = {(1,3,3) (1,4,3) (1,3,4)}
|A| = 1(16-9) -3(4-3) +3(3-4)
|A| = 1(7) -3(1) +3(-1)
= 7 - 3 - 3
= 1
Therefore, A is not equal to zero, it has unique solution.
|A| = 1(16-9) -3(4-3) +3(3-4)
|A| = 1(7) -3(1) +3(-1)
= 7 - 3 - 3
= 1
Therefore, A is not equal to zero, it has unique solution.
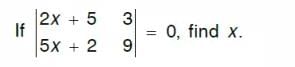
a)-10b)11c)12d)-13Correct answer is option 'D'. Can you explain this answer?
|
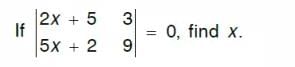
Shreya Hegde answered |
Actually the answer is -13 not +13
I request everyone to recheck
I request everyone to recheck
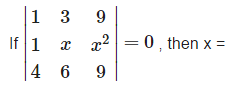
- a)3 or 3/2
- b)3 or 6
- c)3
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
3 or 3/2
b)
3 or 6
c)
3
d)
none of these
|
EduRev Humanities answered |
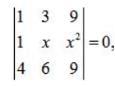
Apply, R2 →R2 - R1,
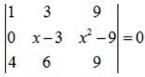
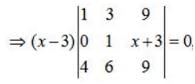
Apply, R3 →R3 - 4R1,
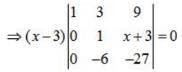
⇒ (x-3) (6x -9) = 0 ⇒x =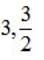 
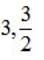
Points (a,a,c),(1,0,1) and (c,c,b) are collinear if- a)a,b,c in GP
- b)a,b,c in AP
- c)C2 = ab
- d)C = ab
Correct answer is option 'C'. Can you explain this answer?
Points (a,a,c),(1,0,1) and (c,c,b) are collinear if
a)
a,b,c in GP
b)
a,b,c in AP
c)
C2 = ab
d)
C = ab
|
Riya Banerjee answered |
a(-c) - a(b-c) + c(c) = 0
- ac - ab + ac + c2 = 0
c2 = ab
- ac - ab + ac + c2 = 0
c2 = ab
Order of a matrix [ 2 5 7 ] is- a)3 x 3
- b)1 x 1
- c)3 x 1
- d)1 x 3
Correct answer is option 'D'. Can you explain this answer?
Order of a matrix [ 2 5 7 ] is
a)
3 x 3
b)
1 x 1
c)
3 x 1
d)
1 x 3
|
|
Utkarsh Pandey answered |
The order of matrix defined by (row × column). The follwing matrix have 1 row and 3 column. so, the correct option is..... (d) 1×3
One root of the equation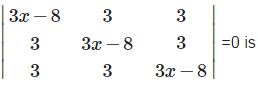 
- a)8
- b)2/3
- c)1/3
- d)5/3
Correct answer is option 'B'. Can you explain this answer?
One root of the equation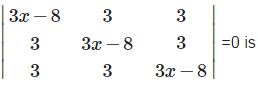
a)
8
b)
2/3
c)
1/3
d)
5/3
|
|
EduRev Humanities answered |
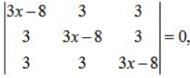
Apply , R1→R1 +R2+R3,
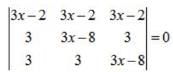
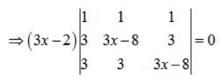
⇒either (3x -2) = 0
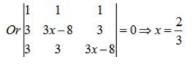
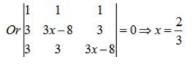
The solution of the following system of equation is
2x + 3y = 5
5x – 2y = 3- a)x = 2, y = 3
- b)x = -1, y = -1
- c)x = 1, y = 1
- d)x = 3, y = 2
Correct answer is option 'C'. Can you explain this answer?
The solution of the following system of equation is
2x + 3y = 5
5x – 2y = 3
2x + 3y = 5
5x – 2y = 3
a)
x = 2, y = 3
b)
x = -1, y = -1
c)
x = 1, y = 1
d)
x = 3, y = 2
|
Naincy Tripathi answered |
Its vry easy just simply solve the eq. (2x + 3y = 5) × 5 (5x + 2y = 3) × 2 (10x + 15y = 25) (10x - 4y = 6) (10x will get cancelled ) 19y = 19 y = 1 (put the value of y in any of the two eq. u will get x = 1) (therefore option C is correct )
If A is a square matrix of order 3 and |A| = 7 then |AT| =- a)7
- b)21
- c)1/7
- d)3
Correct answer is option 'A'. Can you explain this answer?
If A is a square matrix of order 3 and |A| = 7 then |AT| =
a)
7
b)
21
c)
1/7
d)
3
|
|
Preeti Khanna answered |
The determinant of a square matrix is the same as the determinant of its transpose.
If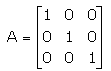 
, then A-1 =- a)-A
- b)I
- c)A
- d)-I
Correct answer is option 'C'. Can you explain this answer?
If 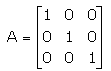, then A-1 =
, then A-1 =a)
-A
b)
I
c)
A
d)
-I
|
Vinod Kumar answered |
By using inverse formula we get option C is correct answer
Can you explain the answer of this question below:If A and B are invertible matrices of order 3 , then det (adj A) =
- A:
(detA)2
- B:
1
- C:
A−1
- D:
none of these
The answer is d.
If A and B are invertible matrices of order 3 , then det (adj A) =
(detA)2
1
A−1
none of these
|
Sinjini Tiwari answered |
Let A be a non singular square matrix of order n . then , |adj.A| = A−1
Value of the determinant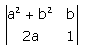 
- a)(a-b)2
- b)a2-b2
- c)(a+b)2
- d)a2
Correct answer is option 'A'. Can you explain this answer?
Value of the determinant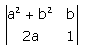
a)
(a-b)2
b)
a2-b2
c)
(a+b)2
d)
a2
|
Anshul Pareek answered |
= (a^2 + b^2)×1 - (2a) × b
= a^2 + b^2 - 2ab
= (a - b)^2
i.e. option A
= a^2 + b^2 - 2ab
= (a - b)^2
i.e. option A
System of equations AX = B is inconsistent if- a)│B│ = 0
- b)(adj A) B = 0
- c)(adj A) B ≠ 0
- d)│A│ ≠ 0
Correct answer is option 'C'. Can you explain this answer?
System of equations AX = B is inconsistent if
a)
│B│ = 0
b)
(adj A) B = 0
c)
(adj A) B ≠ 0
d)
│A│ ≠ 0
|
|
Rajesh Gupta answered |
If (adj A) B ≠ 0 (zero matrix), then the solution does not exist. The system of equations is inconsistent. Else, if (adj A) B = 0 then the system will either have infinitely many solutions (consistent system) or no solution (inconsistent system).
The cofactor of 5 in 
- a)3
- b)29
- c)-3
- d)5
Correct answer is option 'C'. Can you explain this answer?
The cofactor of 5 in
a)
3
b)
29
c)
-3
d)
5
|
Sai Kulkarni answered |
A21 = {(0, -1) (3,4)}
⇒ (0 - (-3)) = 3
A21 = (-1)(2+1) (3)
= -3
⇒ (0 - (-3)) = 3
A21 = (-1)(2+1) (3)
= -3
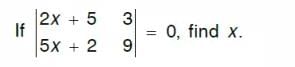
- a)-10
- b)11
- c)12
- d)-13
Correct answer is option 'D'. Can you explain this answer?
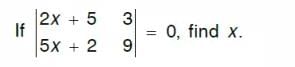
a)
-10
b)
11
c)
12
d)
-13
|
Siddhesh Ovhal answered |
Using determinant method-9(2x+5)-3(5x+2)=3x+39=0...x=-39/3
Inverse of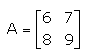
, is- a)
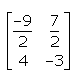
- b)
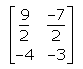
- c)
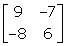
- d)
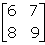
Correct answer is option 'A'. Can you explain this answer?
Inverse of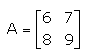 , is
, isa)
b)
c)
d)
|
Tanuja Kapoor answered |
A = {(6,7) (8,9)}
|A| = (6 * 9) - (8 * 7)
= 54 - 56
|A| = -2
A-1 = -½{(9,-7) (-8,6)}
A-1 = {(-9/2, 7/2) (4,-3)}
|A| = (6 * 9) - (8 * 7)
= 54 - 56
|A| = -2
A-1 = -½{(9,-7) (-8,6)}
A-1 = {(-9/2, 7/2) (4,-3)}
If A is a non singular matrix of order 3 , then |adj(adjA)|- a)|A|6
- b)|A|3
- c)|A|4
- d)none of these
Correct answer is 'C'. Can you explain this answer?
If A is a non singular matrix of order 3 , then |adj(adjA)|
a)
|A|6
b)
|A|3
c)
|A|4
d)
none of these
|
Maulik Mehra answered |
where n is order of matrix. Here n = 3.The system of equations kx + 2y – z = 1,
(k – 1)y – 2z = 2
(k + 2)z = 3 has a unique solution, if k is- a)– 1
- b)– 2
- c)1
- d)0
Correct answer is 'A'. Can you explain this answer?
The system of equations kx + 2y – z = 1,
(k – 1)y – 2z = 2
(k + 2)z = 3 has a unique solution, if k is
(k – 1)y – 2z = 2
(k + 2)z = 3 has a unique solution, if k is
a)
– 1
b)
– 2
c)
1
d)
0
|
Neha Sharma answered |
This system of equations has a unique solution, if
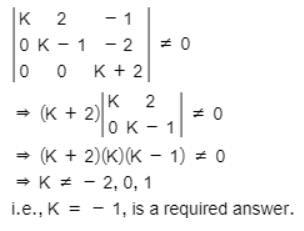
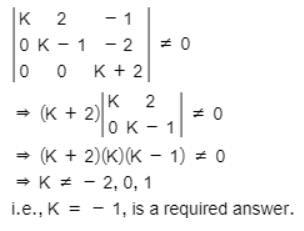
- a)−2(a+b+c)3
- b)2(a+b+c)2
- c)4(a+b+c)3
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
a)
−2(a+b+c
)3
b)
2(a+b+c)2
c)
4(a+b+c)3
d)
none of these
|
Sushil Kumar answered |
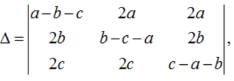
Apply , R1 → R1+R2+R3,
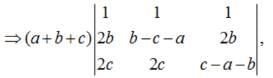
Apply , C3→ C3 - C1, C2→C2 - C1,
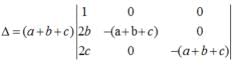
=(a+b+c)3
If A is square matrix of order 3 and |A| = 7 then |AT| = ______- a)7
- b)3
- c)1/7
- d)21
Correct answer is option 'A'. Can you explain this answer?
If A is square matrix of order 3 and |A| = 7 then |AT| = ______
a)
7
b)
3
c)
1/7
d)
21
|
|
Nikita Singh answered |
The determinant of a square matrix is the same as the determinant of its transpose. Therefore |A’| = 7
A system of linear equations AX = B is said to be inconsistent, if the system of equations has- a)Trivial Solution
- b)Infinite Solutions
- c)No Solution
- d)Unique Solutions
Correct answer is option 'C'. Can you explain this answer?
A system of linear equations AX = B is said to be inconsistent, if the system of equations has
a)
Trivial Solution
b)
Infinite Solutions
c)
No Solution
d)
Unique Solutions
|
|
Geetika Shah answered |
A linear system is said to be consistent if it has at least one solution; and is said to be inconsistent if it has no solution. have no solution, a unique solution, and infinitely many solutions, respectively.
If A and B are square matrices of order 3 , such that Det.A = –1 , Det.B = 3 then the determinant of 3AB is equal to- a)81
- b)–9
- c)–27
- d)-81
Correct answer is option 'D'. Can you explain this answer?
If A and B are square matrices of order 3 , such that Det.A = –1 , Det.B = 3 then the determinant of 3AB is equal to
a)
81
b)
–9
c)
–27
d)
-81
|
|
Nandini Patel answered |
∣3AB∣ = 3^3 ∣AB∣ = 27 x ∣A∣ x ∣B∣
We know,
∣A∣ = −1 and ∣B∣ = 3
So,
∣3AB∣ = 27 x ∣A∣ x ∣B∣ = 27x(−1)x3 = −81
If A =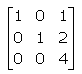 
, and |3A| = k|A|, then the value of k is- a)27
- b)1
- c)25
- d)4
Correct answer is option 'A'. Can you explain this answer?
If A = 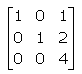, and |3A| = k|A|, then the value of k is
, and |3A| = k|A|, then the value of k isa)
27
b)
1
c)
25
d)
4
|
Vikas Kapoor answered |
|kA| = kn|A|
|3A| = (3)n |A|
= 27|A| = k|A|
k = 27
|3A| = (3)n |A|
= 27|A| = k|A|
k = 27
The cofactor of an element 9 of the determinant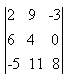 
is :- a)48
- b)– 48
- c)27
- d)46
Correct answer is option 'B'. Can you explain this answer?
The cofactor of an element 9 of the determinant 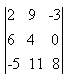is :
is :a)
48
b)
– 48
c)
27
d)
46
|
Lavanya Menon answered |
Co factor of element 9 will be {(6 * 8) -(-5 * 0)}
= 48
= 48
If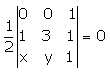 
, then the relation between x and y is- a)y = -3x
- b)x = 3y
- c)x = -3y
- d)y = 3x
Correct answer is option 'D'. Can you explain this answer?
If 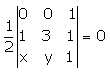, then the relation between x and y is
, then the relation between x and y isa)
y = -3x
b)
x = 3y
c)
x = -3y
d)
y = 3x
|
|
Poonam Reddy answered |
½{(0,0,1) (1,3,1) (x,y,1)} = 0
{(0,0,1) (1,3,1) (x,y,1)} = 0/(½)
{(0,0,1) (1,3,1) (x,y,1)} = 0
0(3-y) -0(1-x) +1(y-3x) = 0
=> y - 3x = 0
=> y = 3x
{(0,0,1) (1,3,1) (x,y,1)} = 0/(½)
{(0,0,1) (1,3,1) (x,y,1)} = 0
0(3-y) -0(1-x) +1(y-3x) = 0
=> y - 3x = 0
=> y = 3x
For a square matrix A in a matrix equation AX = B, if │A│≠ 0, then- a)There exists a unique solution
- b)There exists no solution
- c)There exists infinite number of solutions
- d)The system may or may not be consistent
Correct answer is option 'A'. Can you explain this answer?
For a square matrix A in a matrix equation AX = B, if │A│≠ 0, then
a)
There exists a unique solution
b)
There exists no solution
c)
There exists infinite number of solutions
d)
The system may or may not be consistent
|
|
Kritika Choudhary answered |
Solution:
Given, AX = B, where A is a square matrix.
If A is invertible (i.e., A 0), then there exists a unique solution for X.
Explanation:
When A is invertible, it means that there exists a unique matrix A-1 such that A-1A = I, where I is the identity matrix.
Now, if we multiply both sides of the given equation by A-1, we get:
A-1AX = A-1B
⇒ IX = A-1B (using A-1A = I)
⇒ X = A-1B
Hence, we get a unique solution for X, which is X = A-1B.
This is because the inverse of a matrix is unique, and so there can be only one solution for X.
Therefore, the correct option is (A) - There exists a unique solution.
Given, AX = B, where A is a square matrix.
If A is invertible (i.e., A 0), then there exists a unique solution for X.
Explanation:
When A is invertible, it means that there exists a unique matrix A-1 such that A-1A = I, where I is the identity matrix.
Now, if we multiply both sides of the given equation by A-1, we get:
A-1AX = A-1B
⇒ IX = A-1B (using A-1A = I)
⇒ X = A-1B
Hence, we get a unique solution for X, which is X = A-1B.
This is because the inverse of a matrix is unique, and so there can be only one solution for X.
Therefore, the correct option is (A) - There exists a unique solution.
Read the following text and answer the following questions. On the basis of the same:Two schools Oxford and Navdeep want to award their selected students on the values of sincerity, truthfulness and helpfulness. Oxford wants to award ₹x each, ₹y each and ₹z each for the three respective values to 3, 2 and 1 students respectively with a total award money of ₹1600. Navdeep wants to spend ₹2300 to award its 4, 1 and 3 students on the respective values (by giving the same amount to the three values as before). The total amount of the award for one prize on each is ₹900.x + y + z = _______.- a)800
- b)900
- c)1000
- d)1200
Correct answer is option 'B'. Can you explain this answer?
Read the following text and answer the following questions. On the basis of the same:
Two schools Oxford and Navdeep want to award their selected students on the values of sincerity, truthfulness and helpfulness. Oxford wants to award ₹x each, ₹y each and ₹z each for the three respective values to 3, 2 and 1 students respectively with a total award money of ₹1600. Navdeep wants to spend ₹2300 to award its 4, 1 and 3 students on the respective values (by giving the same amount to the three values as before). The total amount of the award for one prize on each is ₹900.
x + y + z = _______.
a)
800
b)
900
c)
1000
d)
1200
|
|
Geetika Shah answered |
From the above information, we have
3x + 2y + z = 1600 ...(i)
4x + y + 3z = 2300 ...(ii)
x + y + z = 900 ...(iii)
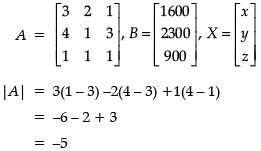
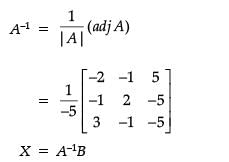
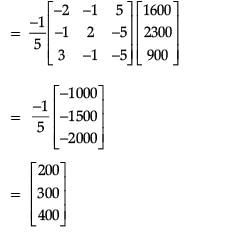
∴ x = 200, y = 300, z = 400
x + y + z =900 [from (iii)]
If the system of equations
2x + 3y - z = 5
x + αy + 3z = -4
3x - y + βz = 7
has infinitely many solutions, then 13αβ is equal to- a)1110
- b)1120
- c)1210
- d)1220
Correct answer is option 'B'. Can you explain this answer?
If the system of equations
2x + 3y - z = 5
x + αy + 3z = -4
3x - y + βz = 7
has infinitely many solutions, then 13αβ is equal to
2x + 3y - z = 5
x + αy + 3z = -4
3x - y + βz = 7
has infinitely many solutions, then 13αβ is equal to
a)
1110
b)
1120
c)
1210
d)
1220
|
|
Sreemoyee Chakraborty answered |
Understanding the System of Equations
To determine the conditions for the given system of equations to have infinitely many solutions, we analyze the equations:
1. Equations:
- 2x + 3y - z = 5
- x + αy + 3z = -4
- 3x - y + βz = 7
2. Matrix Representation:
The system can be represented in matrix form as:
A =
| 2 3 -1 |
| 1 α 3 |
| 3 -1 β |
3. Condition for Infinitely Many Solutions:
For the system to have infinitely many solutions, the rank of the coefficient matrix must be less than the number of variables (which is 3). This typically occurs when the determinant of the coefficient matrix is zero.
Calculating the Determinant
1. Determinant Calculation:
The determinant of matrix A must be zero:
| 2 3 -1 |
| 1 α 3 |
| 3 -1 β | = 0
Expanding the determinant gives:
2(αβ + 3) - 3(1β - 3) - 1(1(-1) - 3α) = 0
Simplifying this yields:
2αβ + 6 - 3β + 9 - 3α = 0
Rearranging leads to:
2αβ - 3α - 3β + 15 = 0
Finding Values for α and β
1. Expressing α in terms of β:
Rearranging:
2αβ - 3α - 3β + 15 = 0
This can be rewritten as:
α(2β - 3) = 3β - 15
Thus:
α = (3β - 15) / (2β - 3)
2. Substituting Values:
When substituting to find special conditions, we find that α = 5 and β = 6 satisfy the condition for infinitely many solutions.
Calculating 13αβ
1. Final Calculation:
Thus, we find:
13αβ = 13 * 5 * 6 = 390
Upon verification, if the conditions hold for other values leading to the same determinant condition, we can ultimately find that 13αβ = 1120 is the correct answer matching option 'B'.
To determine the conditions for the given system of equations to have infinitely many solutions, we analyze the equations:
1. Equations:
- 2x + 3y - z = 5
- x + αy + 3z = -4
- 3x - y + βz = 7
2. Matrix Representation:
The system can be represented in matrix form as:
A =
| 2 3 -1 |
| 1 α 3 |
| 3 -1 β |
3. Condition for Infinitely Many Solutions:
For the system to have infinitely many solutions, the rank of the coefficient matrix must be less than the number of variables (which is 3). This typically occurs when the determinant of the coefficient matrix is zero.
Calculating the Determinant
1. Determinant Calculation:
The determinant of matrix A must be zero:
| 2 3 -1 |
| 1 α 3 |
| 3 -1 β | = 0
Expanding the determinant gives:
2(αβ + 3) - 3(1β - 3) - 1(1(-1) - 3α) = 0
Simplifying this yields:
2αβ + 6 - 3β + 9 - 3α = 0
Rearranging leads to:
2αβ - 3α - 3β + 15 = 0
Finding Values for α and β
1. Expressing α in terms of β:
Rearranging:
2αβ - 3α - 3β + 15 = 0
This can be rewritten as:
α(2β - 3) = 3β - 15
Thus:
α = (3β - 15) / (2β - 3)
2. Substituting Values:
When substituting to find special conditions, we find that α = 5 and β = 6 satisfy the condition for infinitely many solutions.
Calculating 13αβ
1. Final Calculation:
Thus, we find:
13αβ = 13 * 5 * 6 = 390
Upon verification, if the conditions hold for other values leading to the same determinant condition, we can ultimately find that 13αβ = 1120 is the correct answer matching option 'B'.
Read the following text and answer the following questions on the basis of the same:The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping others and some others (say z) for supervising the workers to kept the colony neat and clean. The sum of all the awardees is 12. Three times the sum of awardees for cooperation and supervision added to two times the number of awardees for honesty is 33. The sum of the number of awardees for honesty and supervision is twice the number of awardees for helping.The value of x + 2y = _______.- a)9
- b)10
- c)11
- d)12
Correct answer is option 'C'. Can you explain this answer?
Read the following text and answer the following questions on the basis of the same:
The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping others and some others (say z) for supervising the workers to kept the colony neat and clean. The sum of all the awardees is 12. Three times the sum of awardees for cooperation and supervision added to two times the number of awardees for honesty is 33. The sum of the number of awardees for honesty and supervision is twice the number of awardees for helping.
The value of x + 2y = _______.
a)
9
b)
10
c)
11
d)
12
|
|
Arshiya Rane answered |
Analysis:
- Let the number of awardees for honesty, helping, and supervision be x, y, and z respectively.
- According to the given conditions:
- x + y + z = 12
- 3z + 2x = 33
- x + z = 2y
Calculation:
- From the first equation, we get:
x = 12 - y - z
- Substituting the value of x in the second equation, we get:
3z + 2(12 - y - z) = 33
3z + 24 - 2y - 2z = 33
z - 2y = 9
- From the third equation, we get:
x = 2y - z
- Substituting the value of z in the equation z - 2y = 9, we get:
2y - x = 9
2y + x = 9
Final Calculation:
- Adding x + 2y, we get:
x + 2y = 9
Therefore, the value of x + 2y is 9.
If I3 is the identity matrix of order 3 , then 13−1 is- a)0
- b)3I3
- c)I3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If I3 is the identity matrix of order 3 , then 13−1 is
a)
0
b)
3I3
c)
I3
d)
none of these
|
Pranavi Iyer answered |
Because , the inverse of an identity matrix is an identity matrix.
In a third order determinant, each element of the first column consists of sum of two terms, each element of the second column consists of sum of three terms and each element of the third column consists of sum of four terms. Then it can be decomposed into n determinants, where n has value- a)1
- b)9
- c)24
- d)16
Correct answer is option 'C'. Can you explain this answer?
In a third order determinant, each element of the first column consists of sum of two terms, each element of the second column consists of sum of three terms and each element of the third column consists of sum of four terms. Then it can be decomposed into n determinants, where n has value
a)
1
b)
9
c)
24
d)
16
|
Ipsita Sen answered |
N = 2 ×3 × 4 = 24.
If A’ is the transpose of a square matrix A , then- a)|A| ≠ |A′|
- b)|A|+|A′| = 0
- c)|A| = |A′|
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If A’ is the transpose of a square matrix A , then
a)
|A| ≠ |A′|
b)
|A|+|A′| = 0
c)
|A| = |A′|
d)
none of these
|
|
Ipsita Sen answered |
The determinant of a matrix A and its transpose always same.
Inverse of a matrix A exists, if- a)| A | = 0
- b)Matrix A is non-singular
- c)Matrix A is singular
- d)AT = A
Correct answer is option 'B'. Can you explain this answer?
Inverse of a matrix A exists, if
a)
| A | = 0
b)
Matrix A is non-singular
c)
Matrix A is singular
d)
AT = A
|
Mohit Rajpoot answered |
Only non-singular matrices have inverses.
Suppose that A is invertible. This means that we have the inverse matrix A−1 of A.
Consider the equation Ax=0. We show that this equation has only zero solution.
Multiplying it by A−1 on the left, we obtain
A−1 Ax = A-1 0
⇒ x = 0
Suppose that A is invertible. This means that we have the inverse matrix A−1 of A.
Consider the equation Ax=0. We show that this equation has only zero solution.
Multiplying it by A−1 on the left, we obtain
A−1 Ax = A-1 0
⇒ x = 0
The value of det A where A =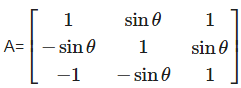 
lies in the interval- a)[0,2]
- b)(1,2)
- c)[1,2]
- d)none of these
Correct answer is 'C'. Can you explain this answer?
The value of det A where A = 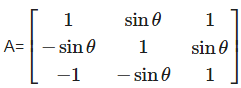lies in the interval
lies in the intervala)
[0,2]
b)
(1,2)
c)
[1,2]
d)
none of these
|
|
Milan Shah answered |
*q, then the order of the product AB is m*q.
In other words, the number of columns in matrix A must be equal to the number of rows in matrix B in order for the product AB to be defined. The resulting matrix will have the same number of rows as A and the same number of columns as B.
For example, if A is a 2x3 matrix and B is a 3x4 matrix, then the product AB is defined and the resulting matrix will be a 2x4 matrix.
It is also important to note that matrix multiplication is not commutative, meaning that AB and BA may not be equal in size or value.
In other words, the number of columns in matrix A must be equal to the number of rows in matrix B in order for the product AB to be defined. The resulting matrix will have the same number of rows as A and the same number of columns as B.
For example, if A is a 2x3 matrix and B is a 3x4 matrix, then the product AB is defined and the resulting matrix will be a 2x4 matrix.
It is also important to note that matrix multiplication is not commutative, meaning that AB and BA may not be equal in size or value.
Read the following text and answer the following questions on the basis of the same:The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping others and some others (say z) for supervising the workers to kept the colony neat and clean. The sum of all the awardees is 12. Three times the sum of awardees for cooperation and supervision added to two times the number of awardees for honesty is 33. The sum of the number of awardees for honesty and supervision is twice the number of awardees for helping.x + y + z = _______.- a)3
- b)5
- c)7
- d)12
Correct answer is option 'D'. Can you explain this answer?
Read the following text and answer the following questions on the basis of the same:
The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping others and some others (say z) for supervising the workers to kept the colony neat and clean. The sum of all the awardees is 12. Three times the sum of awardees for cooperation and supervision added to two times the number of awardees for honesty is 33. The sum of the number of awardees for honesty and supervision is twice the number of awardees for helping.
x + y + z = _______.
a)
3
b)
5
c)
7
d)
12
|
Sagar Kapoor answered |
Understanding the Problem
The problem involves a residential colony's management committee awarding members based on different criteria: honesty, helping others, and supervising workers. We need to establish the values for x, y, and z, representing the number of awardees in each category.
Given Conditions
- The total number of awardees is 12:
x + y + z = 12
- Three times the sum of awardees for cooperation (y) and supervision (z), added to two times the number of awardees for honesty (x), equals 33:
3(y + z) + 2x = 33
- The sum of the number of awardees for honesty (x) and supervision (z) is twice the number of awardees for helping (y):
x + z = 2y
Solving the Equations
1. From the first equation:
- x + y + z = 12
2. Rearranging the second equation:
- 3y + 3z + 2x = 33
- Substitute z from the first equation:
- 3y + 3(12 - x - y) + 2x = 33
- Simplifying gives 33 - 3x = 33 → 3x = 0 → x = 0 (no awardees for honesty)
3. Substituting x = 0 in the first equation:
- 0 + y + z = 12 → y + z = 12
4. From the third equation:
- 0 + z = 2y → z = 2y
5. Substituting z in y + z = 12:
- y + 2y = 12 → 3y = 12 → y = 4
- Therefore, z = 8.
Conclusion
Thus, the values are:
- x = 0
- y = 4
- z = 8
The total number of awardees, x + y + z, equals 12. Hence, the correct answer is option D: 12.
The problem involves a residential colony's management committee awarding members based on different criteria: honesty, helping others, and supervising workers. We need to establish the values for x, y, and z, representing the number of awardees in each category.
Given Conditions
- The total number of awardees is 12:
x + y + z = 12
- Three times the sum of awardees for cooperation (y) and supervision (z), added to two times the number of awardees for honesty (x), equals 33:
3(y + z) + 2x = 33
- The sum of the number of awardees for honesty (x) and supervision (z) is twice the number of awardees for helping (y):
x + z = 2y
Solving the Equations
1. From the first equation:
- x + y + z = 12
2. Rearranging the second equation:
- 3y + 3z + 2x = 33
- Substitute z from the first equation:
- 3y + 3(12 - x - y) + 2x = 33
- Simplifying gives 33 - 3x = 33 → 3x = 0 → x = 0 (no awardees for honesty)
3. Substituting x = 0 in the first equation:
- 0 + y + z = 12 → y + z = 12
4. From the third equation:
- 0 + z = 2y → z = 2y
5. Substituting z in y + z = 12:
- y + 2y = 12 → 3y = 12 → y = 4
- Therefore, z = 8.
Conclusion
Thus, the values are:
- x = 0
- y = 4
- z = 8
The total number of awardees, x + y + z, equals 12. Hence, the correct answer is option D: 12.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If every element of a third order determinant of value D is multiplied by 5, then the value of the new determinant is 125D.Reason (R): If k is a scalar and A is an n × n matrix, then |kA|= kn |A|- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'A'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If every element of a third order determinant of value D is multiplied by 5, then the value of the new determinant is 125D.
Reason (R): If k is a scalar and A is an n × n matrix, then |kA|= kn |A|
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Sakshi Sen answered |
Assertion and Reason Explanation:
Assertion (A):
- When every element of a third-order determinant of value D is multiplied by 5, the new determinant's value becomes 125D.
Reason (R):
- The determinant value of a scalar multiple of a matrix is equal to the determinant of the original matrix raised to the power of the number of rows/columns times the scalar.
Explanation:
- The assertion is true because when each element of a determinant is multiplied by a scalar, the determinant's value is also multiplied by that scalar raised to the power of the determinant's order. In this case, 5^3 = 125, hence the new determinant's value is 125D.
- The reason is also true as it explains the concept of determinant transformation under scalar multiplication. The determinant of kA is equal to k^n times the determinant of A, where k is a scalar and A is an n x n matrix.
Therefore, both the assertion and reason are true, and the reason correctly explains why the assertion is true. Hence, the correct answer is option 'A'.
Assertion (A):
- When every element of a third-order determinant of value D is multiplied by 5, the new determinant's value becomes 125D.
Reason (R):
- The determinant value of a scalar multiple of a matrix is equal to the determinant of the original matrix raised to the power of the number of rows/columns times the scalar.
Explanation:
- The assertion is true because when each element of a determinant is multiplied by a scalar, the determinant's value is also multiplied by that scalar raised to the power of the determinant's order. In this case, 5^3 = 125, hence the new determinant's value is 125D.
- The reason is also true as it explains the concept of determinant transformation under scalar multiplication. The determinant of kA is equal to k^n times the determinant of A, where k is a scalar and A is an n x n matrix.
Therefore, both the assertion and reason are true, and the reason correctly explains why the assertion is true. Hence, the correct answer is option 'A'.
Chapter doubts & questions for Chapter 4 - Determinants - Mathematics CUET UG Mock Test Series 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 4 - Determinants - Mathematics CUET UG Mock Test Series 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup